Đề Olympic 30 tháng 4 Toán 11 năm 2021 trường chuyên Lê Hồng Phong – TP HCM

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI OLYMPIC TRUYỀN THỐNG 30 THÁNG 4 THÀNH PHỐ HỒ CHÍ MINH LẦN THỨ XXVI - NĂM 2021 TRƯỜNG THPT CHUYÊN Ngày thi: 03/4/2021 LÊ HỒNG PHONG
MÔN THI: TOÁN – KHỐI: 11 ĐỀ CHÍNH THỨC THỜI GIAN: 180 phút
Hình thức làm bài: Tự luận Đề thi có 01 trang
Lưu ý: - Thí sinh làm mỗi câu trên một tờ giấy riêng và ghi rõ câu số mấy ở trang 1 của mỗi tờ giấy làm bài
- Thí sinh không được sử dụng máy tính cầm tay. Câu 1. (4,0 điểm) Cho , a ,
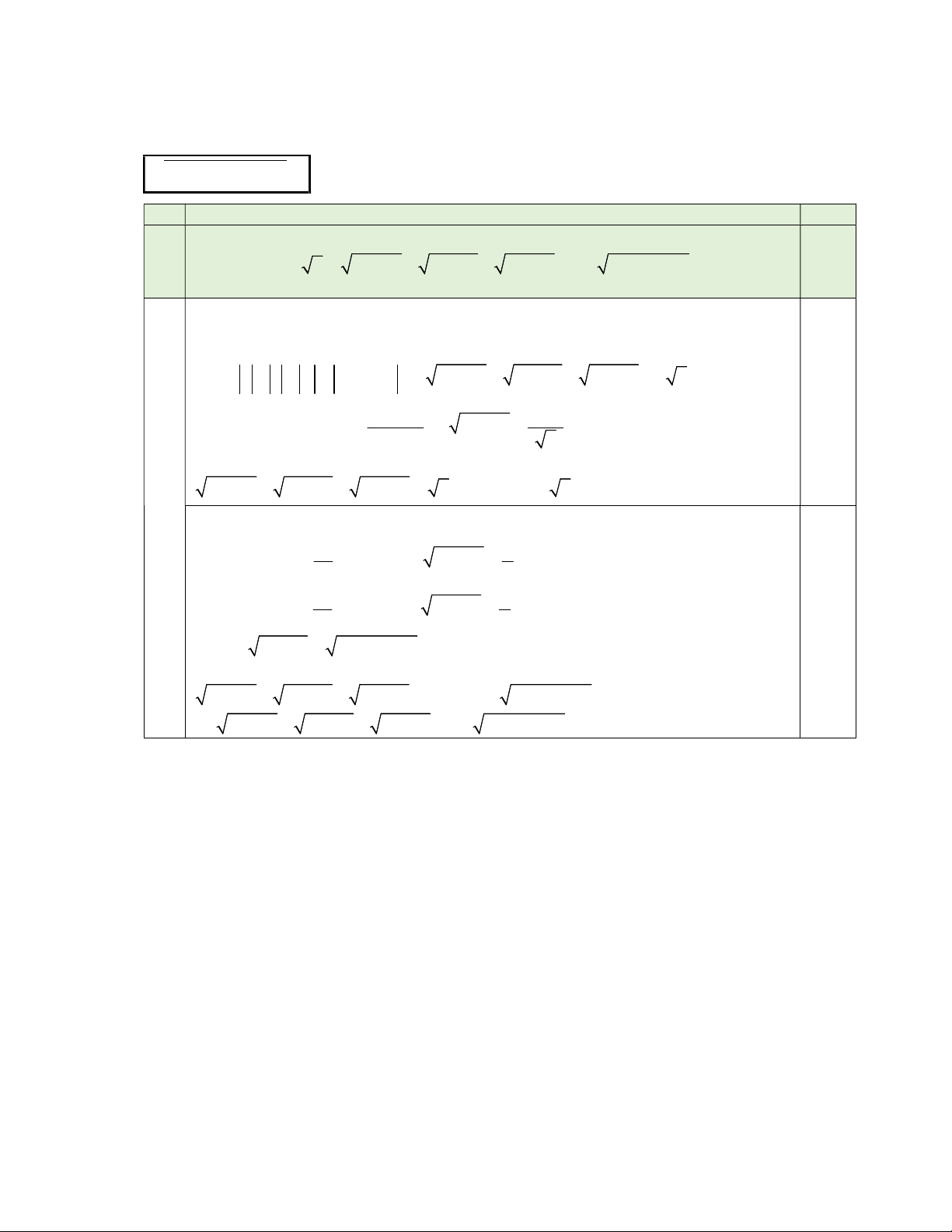
b c là các số thực dương có tổng bằng 2. Chứng minh rằng: 2 2 2 2 2 2 2 2 2
2 2  a  b  b  c  c  a  2  a  b  c .
Câu 2. (3,0 điểm) Tìm tất cả các hàm số f : (0; )   (0; )
 thỏa mãn điều kiện   y  f (x  f (y))  xf 1 f    với mọi , x y (0; )  .   x  Câu 3. (4,0 điểm) a. Cho ,
m n là các số nguyên dương sao cho 2m  n là ước dương của n 1.
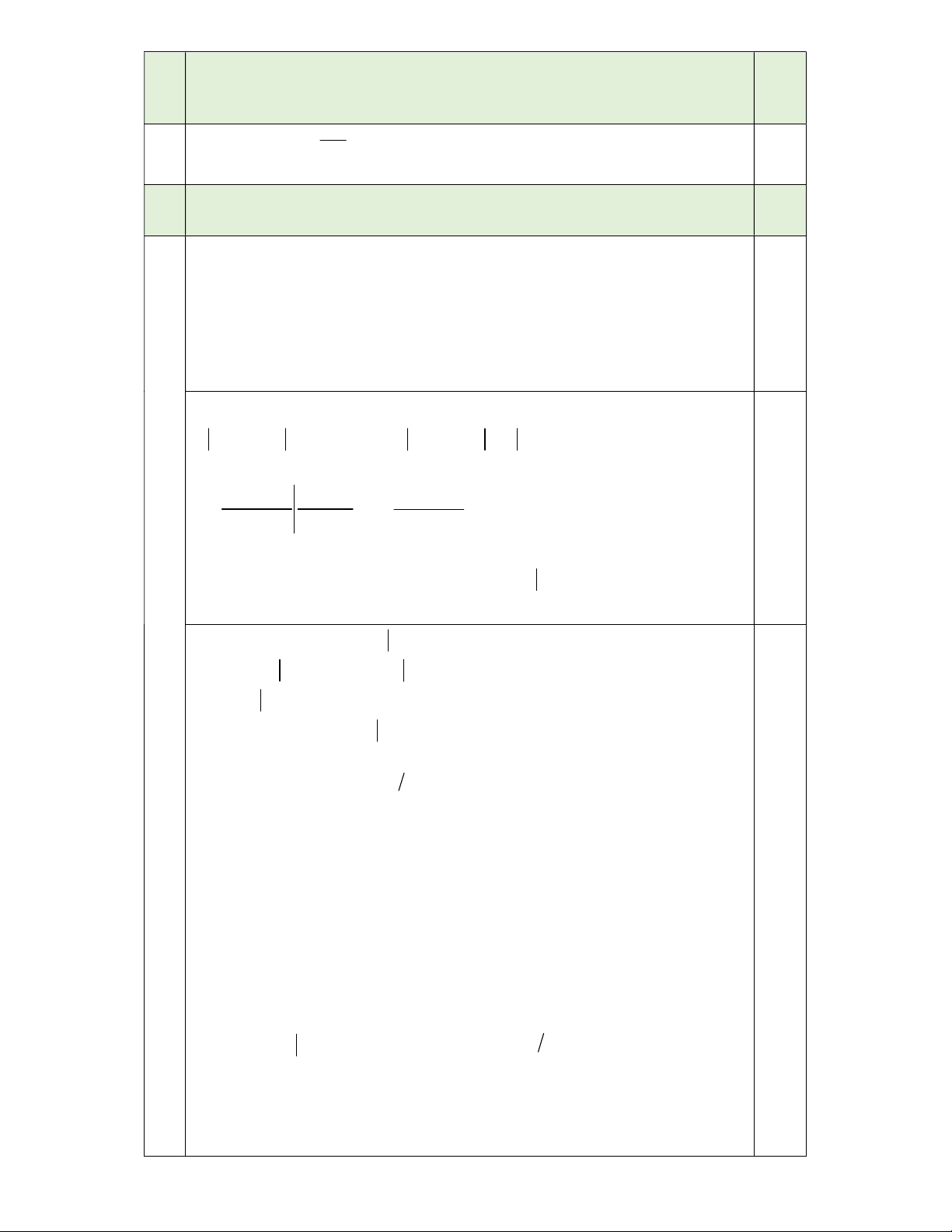
Chứng minh rằng phương trình 2m 2m   (  )n x y
x y có nghiệm nguyên dương.
b. Có bao nhiêu số nguyên dương n sao cho phương trình 304 304   (  )n x y x y có nghiệm nguyên dương?
Câu 4. (5,0 điểm) Cho tam giác nhọn không cân ABC nội tiếp đường tròn (O). Gọi A , B ,C
là chân đường cao hạ từ các đỉnh ,
A B, C. Một đường tròn qua B , C tiếp xúc với cung nhỏ 
BC của (O) tại A . Các điểm B ,C xác định tương tự. 1 1 1 A B cot B a. Chứng minh rằng 1  . A C cot C 1
b. Vẽ các hình bình hành B ABX , C ACY. Chứng minh rằng các điểm X , Y, A 1 1 1
và A thuộc một đường tròn với AA là đường kính của (O). 0 0
c. Vẽ các hình bình hành BACA ,CB AB , AC BC . Chứng minh rằng đường tròn 1 2 1 2 1 2
ngoại tiếp tam giác A B C đi qua trực tâm của tam giác ABC. 2 2 2
Câu 5. (4,0 điểm) Bộ hai số nguyên khác không  ,
x y được gọi là “bộ số đẹp” nếu x là số lẻ, y là số chẵn, ,
x y nguyên tố cùng nhau và 2 2
x  y là số chính phương. a. Chứng minh rằng  ,
x y là “bộ số đẹp” khi và chỉ khi tồn tại 2 số nguyên u,v
khác 0 và khác tính chẵn lẻ, nguyên tố cùng nhau sao cho  x y   2 2 , u  v , 2uv.
b. Với mỗi “bộ số đẹp”  ,
x y ta có thể tạo ra 1 “bộ số đẹp” mới bởi 1 trong 2 phép
biến đổi: hoặc đổi dấu của 1 trong 2 số hoặc cộng 1 số nguyên k nào đó vào cả 2 số
sao cho  x  k, y  k là “bộ số đẹp”. Chứng minh rằng với bất kỳ 2 bộ số đẹp  , x y
và  z,t cho trước ta luôn có thể biến đổi từ  ,
x y thành  z,t sau hữu hạn các
bước biến đổi như trên. HẾT
Họ tên thí sinh: ...................................................................... SBD: ................................
Trường: ................................................................................. Tỉnh/TP: .........................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI OLYMPIC TRUYỀN THỐNG 30 THÁNG 4 THÀNH PHỐ HỒ CHÍ MINH LẦN THỨ XXVI - NĂM 2021 TRƯỜNG THPT CHUYÊN Ngày thi: 03/4/2021 LÊ HỒNG PHONG
MÔN THI: TOÁN 11 - THỜI GIAN: 180 phút ĐÁP ÁN
Hình thức làm bài: Tự luận Đáp án có 06 trang Nội dung Điểm Cho a, ,
b c là các số thực dương thay đổi có tổng bằng 2. Chứng minh rằng Bài 2 2 2 2 2 2 2 2 2 4 1
2 2  a  b  b  c  c  a  2  a  b  c .   
Cách 1: Xét u  a,b , v   , b c , w  c,a .   
 u  v  w  a  b  c, a  b  c  2;2       Ta có 2 2 2 2 2 2
u  v  w  u  v  w  a  b  b  c  c  a  2 2 . 2 a  b a  b 2 2  2 Cách 2: Ta có 2 2 a  b   a  b  . 2 2
Tương tự cho các số hạng còn lại, ta được 2 2 2 2 2 2
a  b  b  c  c  a  2 a  b  c  2 2 .
Do bất đẳng thức đối xứng nên ta có thể giả sử a  mina, , b  c . 2 a a Ta có 2 2 2 2 2 a  b 
 ab  b  a  b   b . 4 2 2 a a 2 2 2 2 2 a  c 
 ac  c  a  c   c . 4 2 2 2 2 2 2 2 b  c  a  b  c .
Cộng vế với vế, ta được 2 2 2 2 2 2 2 2 2
a  b  b  c  c  a  a  b  c  a  b  c 2 2 2 2 2 2 2 2 2
 a  b  b  c  c  a  2  a  b  c .
Tìm tất cả các hàm số thực f : (0; )   (0; )
 thỏa mãn điều kiện Bài   y  3 2 f (x  f (y))  xf 1 f 
  với mọi số thực , x y (0; )  .  x   
Ta có f (x  f (x))  xf 1 f  
1   cx với mọi x(0; )  (1) và 1 c  f 1 f (1) .
Thay x thành x  f (x) vào (1) 1
Suy ra f (x  f (x)  f (x  f (x)))  c(x  f (x)) với mọi x (0; )  (2).
Thế (1) vào (2): f (x  f (x)  cx)  c(x  f (x)) với mọi x (0; )  .
 f ((c 1)x  f (x))  c(x  f (x)) với mọi x (0; )  (3).   1 
Mặt khác theo đề bài thì f ((c 1)x  f (x))  (c 1)xf 1 f    (4).   c 1      1 
Từ (3) và (4), suy ra (c 1)xf 1 f  c(x  f (x))    với mọi 1   c 1    x(0; )  .
Suy ra f (x)  ax với mọi x (0; )  . Do f : (0; )   (0; )  nên a (0; )  .
Thử lại thấy thỏa mãn. a) Cho ,
m n là các số nguyên dương sao cho 2m  n là ước nguyên dương của Bài m m n 1 3
n 1. Chứng minh rằng phương trình 2 2
x  y  (x  y) có nghiệm nguyên dương. n 1    m m n a) Chọn 2   2 m n x y  thì 2 2 x  y  (x  y) . 1
Suy ra phương trình có nghiệm nguyên dương.
b) Có mấy số nguyên dương n sao cho phương trình 304 304   (  )n x y x y có 2 nghiệm nguyên dương. Nếu n  304 , vì , x y  0 ta có ngay 304 304 (  )n n n x y  x  y  x  y nên
phương trình không có nghiệm nguyên dương. Nếu n 1 thì 304 304 x
 y  x  y có nghiệm nguyên dương x  y 1 .
Xét 2  n  303. Giả sử phương trình có nghiệm nguyên dương (x, y). 0,5
Đặt x  da, y  db với (a,b) 1. Ta được 304  304 304      n n d a b d a b  304n 304 304 (  )  (  )n d a b a b . (1)
Cách 1. Đặt    304 304  ,(  )n d a b
a b  1. Nếu d có ước nguyên tố lẻ p thì p a  b  304 304 p a  b nên 304 p 2a  p a, p b vô lý. Vậy k * d  2 , k   .
Do d chẵn nên a,b cùng lẻ. Khi đó 304 304 a  b  2(mod 4) nên d  2. 304 304  (  )n a b a b 304 304 a  b Do nên  1 a  b  1. 2,5 2 2 2 Thế vào (1): 304 n n 1 d  2   2. Suy ra 2k d  với *
k  và n 1 k(304 ) n .
Suy ra n 1  n  304  303(304  n)  304  n 303. Suy ra n 303,301,20 
3 . Các giá trị này đều thỏa mãn (theo câu a). Cách 2. Từ (1) suy ra 304n 304 304 a  b d (a  b ). Lại có 2 2 304n 304 304
a  b (a  b )  a  b d (a  b ) nên 304n 304 a  b 2d .a Do a  b, a  1  304 2 n a b d   (2)
Trường hợp 1: a,b cùng lẻ. 304  2 n  (  )k d
a b .r với r  a  b,k  1 Thế vào (1):  304 304  2 n k r a b a b     (3) Nếu n  k thì r  304 304 a  b  304 304  2  r  1 a  b  2 (do a, b cùng lẻ)
 r 1 a  b . Trường hợp này đã xét ở cách 1.
Nếu n  k thì (3)  r  304 304 a  b 2a  b 2,5 Mà r  304 304 a  b  2 2 a  b 2a  b
Cộng vế với vế ta được 304  ra a  b Mà  304
a , a  b 1 nên r(a  b) (mâu thuẫn).
Trường hợp 2: a, b khác tính chẵn lẻ  a  b là số lẻ. Từ (2) 304n 304n     (  )l a b d d
a b .s l 1,s  (a  ) b  . Thế vào (1): 304 304 nl s a  b  a  b   s  304 304 ( ) ( ) 2 a  b a  b. Mà s  304 304 a  b  2 2
a  b a  b. Cộng vế với vế ta được 304  2sa a  b Mà  304
2a , a  b  1 nên s(a  b) (mâu thuẫn).
Cho tam giác nhọn không cân ABC nội tiếp đường tròn (O). Gọi A , B ,C là
Bài chân đường cao hạ từ các đỉnh ,
A B, C. Một đường tròn qua B ,C tiếp xúc với 5 4 cung nhỏ 
BC của (O) tại A . Các điểm B ,C xác định tương tự. 1 1 1 A B cot B a) Chứng minh 1  . A C cot C 2 1
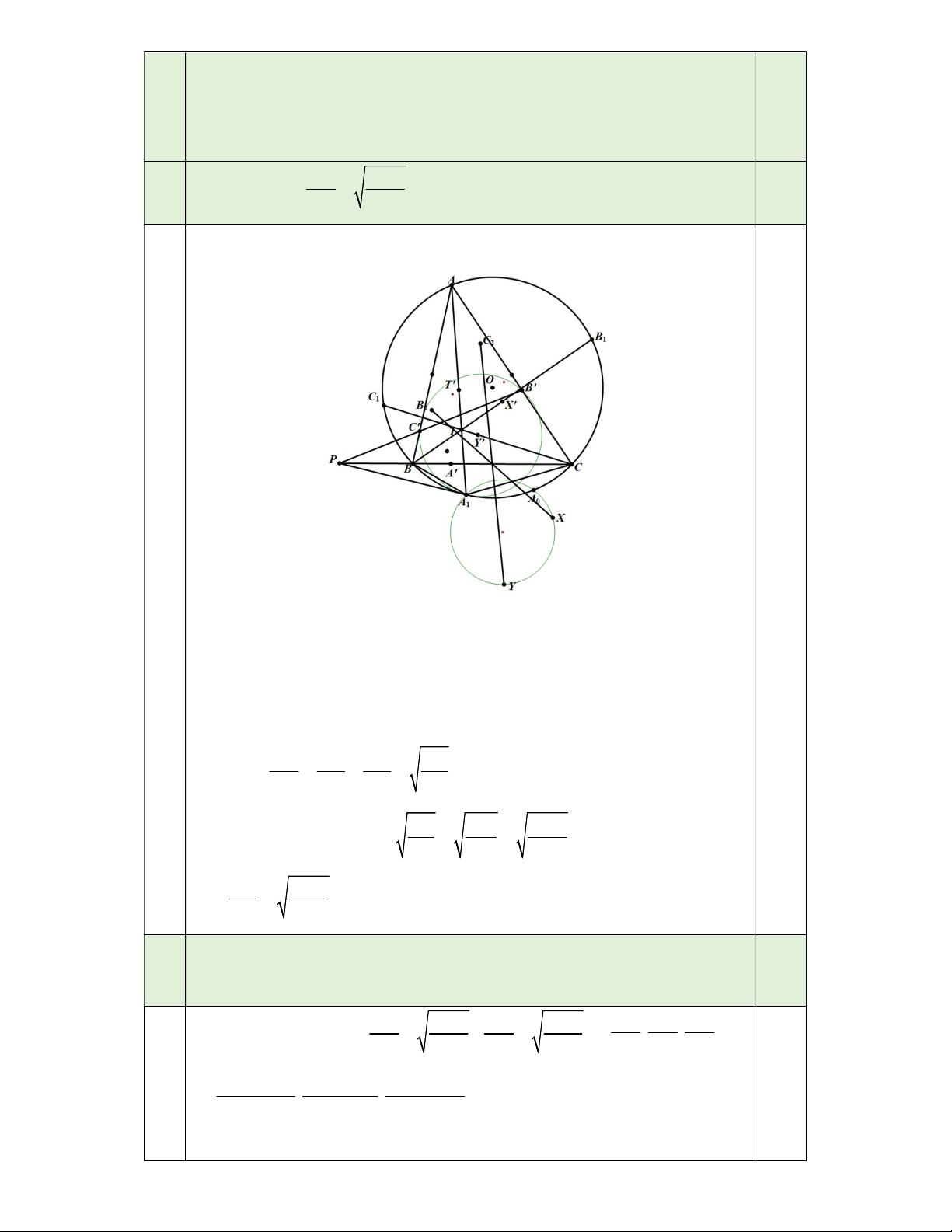
Giả sử các điểm có vị trí như hình vẽ, các trường hợp khác chứng minh tương tự. a) Các đường tròn (A B C  ),(O),(BCB C
 ) có các trục đẳng phương của 1
từng cặp đường tròn đồng quy tại tâm đẳng phương P
 PA là tiếp tuyến chung của đường tròn (A B C  ),(O) 1 1
 tam giác PA B đồng dạng tam giác PCA 1 1 A B PB PA PB 1 1     . 2 AC PA PC PC 1 1 PB AB cot B
Chú ý (PA’BC)=-1, ta được   . PC A C  cot C A B cot B Vậy 1  . A C cot C 1
b) Vẽ các hình bình hành B ABX , C ACY. Chứng minh A  (XYA ) với AA 1 1 1 0 0 2
là đường kính của (O). B C cot C C A cot A A B B C C A
Tương tự câu a) ta được 1  , 1  1 1 1  . .  1. B A cot A C B cot B AC B A C B 1 1 1 1 1 sin  BAA sin CBB sin ACC 1    1   1  2   . . 1 . sin A AC sin B BA sin C CB 1    1    1 
Theo định lý Ceva sin ta có AA , BB ,CC đồng quy tại T . 1 1 1
Gọi X ' là trung điểm AX . Do AB XB là hình bình hành nên X ' là trung 1 điểm BB . Suy ra  0 OX 'T  90 . 1
Gọi Y ',T ' là trung điểm AY , AA . Chứng minh tương tự, ta được 1  OT T   0 ' OY 'T  90
Suy ra X ',Y ',T ' thuộc đường tròn đường kính OT . Suy ra O (X 'Y 'T ').
Xét phép vị tự tâm A tỉ số 2: X '  X Y '  Y T '  A 1 O  A 0
Do X ',Y ',T ',O đồng viên nên X ,Y, A , A đồng viên. 1 0 Vậy A (XYA ) . 0 1
c) Vẽ các hình bình hành BACA ,CB AB , AC BC . Chứng minh (A B C ) đi 1 2 1 2 1 2 2 2 2 1
qua trực tâm của tam giác ABC.    
Do CY  AC ( C ACY là hình bình hành) và AC  C B ( AC BC là hình bình 1 1 1 2 1 2  
hành) nên CY  C B nên C đối xứng Y qua trung điểm BC. 2 2
Tương tự B đối xứng X qua trung điểm BC. 2
Do trực tâm H của tam giác ABC đối xứng A qua trung điểm BC. 0
Gọi I là trung điểm BC. Xét phép đối xứng tâm I. Y  C 1 2 X  B 2 A  A 1 2 A  H 0
Theo câu b ta có X ,Y , A , A đồng viên nên H , A , B ,C đồng viên 1 0 2 2 2 Vậy H (A B C ) . 2 2 2
Bộ hai số nguyên khác không  ,
x y được gọi là “bộ số đẹp” nếu x là số lẻ, y Bài 4 5 là số chẵn, ,
x y nguyên tố cùng nhau và 2 2
x  y là số chính phương. a) Chứng minh rằng  ,
x y là “bộ số đẹp” khi và chỉ khi tồn tại 2 số nguyên
u, v khác 0 và khác tính chẵn lẻ, nguyên tố cùng nhau sao cho 1,5 x y   2 2 , u  v , 2uv.
Nhận xét nếu cặp  x, y là cặp số đẹp thì tồn tại số nguyên dương z sao cho 2 2 2 x  y  z
Có z là số lẻ và nguyên tố cùng nhau với x và y (do (x, y) = 1). Giả sử 0,5 ,
x y  0 , x là số lẻ và y  2t là số chẵn. Ta có 2 2 2 2
x  4t  z  4t  (z  x)(z  x)
Ta có z – x, z + x là hai số cùng chẵn suy ra tồn tại hai số nguyên m, n sao cho z  x  2 , m z  x  2n và 2 . m n  t . z  m  n 0.5   . x  m  n
Do (z, x) = 1 nên (m, n) = 1. Mà 2 .
m n  t nên tồn tại hai số nguyên u, v nguyên tố cùng nhau sao cho 2 0.5 m  u , 2 n  v và u.v  t . Vậy 2 2 x  u  v , y  2uv .
b) Với mỗi “bộ số đẹp”  ,
x y ta có thể tạo ra 1 “bộ số đẹp” mới bởi 1 trong 2
phép biến đổi: hoặc đổi dấu của 1 trong 2 số hoặc cộng 1 số nguyên k nào đó
vào cả 2 số sao cho  x  k, y  k là “bộ số đẹp”. Chứng minh rằng với bất kỳ 2,5 2 bộ số đẹp  ,
x y và z,t cho trước ta luôn có thể biến đổi từ  , x y thành
z,t sau hữu hạn các bước biến đổi như trên.
Ta thực hiện biến đổi:
Bước 1: Biến đổi  x, y thành  x , y với x , y  0 . 0 0  0 0
Bước 2: Với bộ  x , y ở trên, ta có hai số u,v tương ứng ( u  v ) thỏa mãn 0 0  2 2
x  u  v  0, y  2uv . 0 0
Nếu u  2v thì ta biến đổi bằng cách cộng vào 2 số x , y một số 2 4  uv  4v , 0 0 2,5 ta được 2 2 2 2 2
u  v  4uv  4v  (2v  u)  v , 2
2uv  4uv  4v  2v(2v  u) . Khi
đó ta đã biến đổi bộ  2 2 u  v ; 2uv thành  2 2
(2v  u)  v , 2v(2v  u) .
Ta có u  2v  u . Suy ra quá trình trên phải kết thúc sau một số phép biến
đổi. Khi đó ta có u  2v . Vì u,v  1 (2v,v)  1  v  1 u  2 .
Do vậy mọi “bộ số đẹp” có thể biến đổi về (3,4) và ngược lại, đpcm.