Đề ôn tập toán rời rạc Môn Toán thống kê | Trường Đại học Huế

ĐỀ SỐ 4
Câu 1(1.5đ).Trong một cuộc họp lấy ý kiến về 7 vấn đề ,người được hỏi
ghi vào một phiếu trả lời sẵn bằng cách để nguyên hoặc phủ định các
câu trả lời tương ứng với 7 vấn đề đã nêu.Chứng minh rằng với 1153
người được hỏi luôn tìm được ít nhất 10 người trả lời giống hệt nhau. Giải:
Xếp những người có cùng câu trả lời giống nhau thành 1 nhóm.
Có tất cả 7 câu trả lời và với mỗi câu trả lời có 2 lựa chọn.
Vậy theo nguyên lý Dirichlet tồn tại một nhóm có ít nhất [ 1153 ]=10 người. 2∗ 2∗ ∗2 ∗ 2 ∗ ∗ 2 2 2
Câu 2(1.5đ).Có bao nhiêu xâu khác nhau có thể lập từ các chữ cái trong từ ANAMARAM.
Giải: Từ này chứa 4 chữ A ,2 chữ M ,1 chữ N,1 chữ R.Để xác
định số xâu khác nhau ta thấy có C(8,4) cách chọn 4 chỗ cho 4
chữ A,còn lại 4 chỗ trống.Có C(4,2) cách chọn 2 chỗ cho 2 chữ
M,còn lại 2 chỗ trống.Có thể đặt chữ N bằng C(2,1) cách và
C(1,1) cách đặt chữ R vào xâu.Theo nguyên lý nhân ,số các xâu
khác nhau có thể tạo được là : C4 8 ! 10* C46*C12*C11=
8 !∗4 !∗2 !∗1! = =840 xâu.
4 !∗2 !∗4 !∗2 !∗1!∗1 !∗1!∗0
4 !∗2!∗1 !∗1!
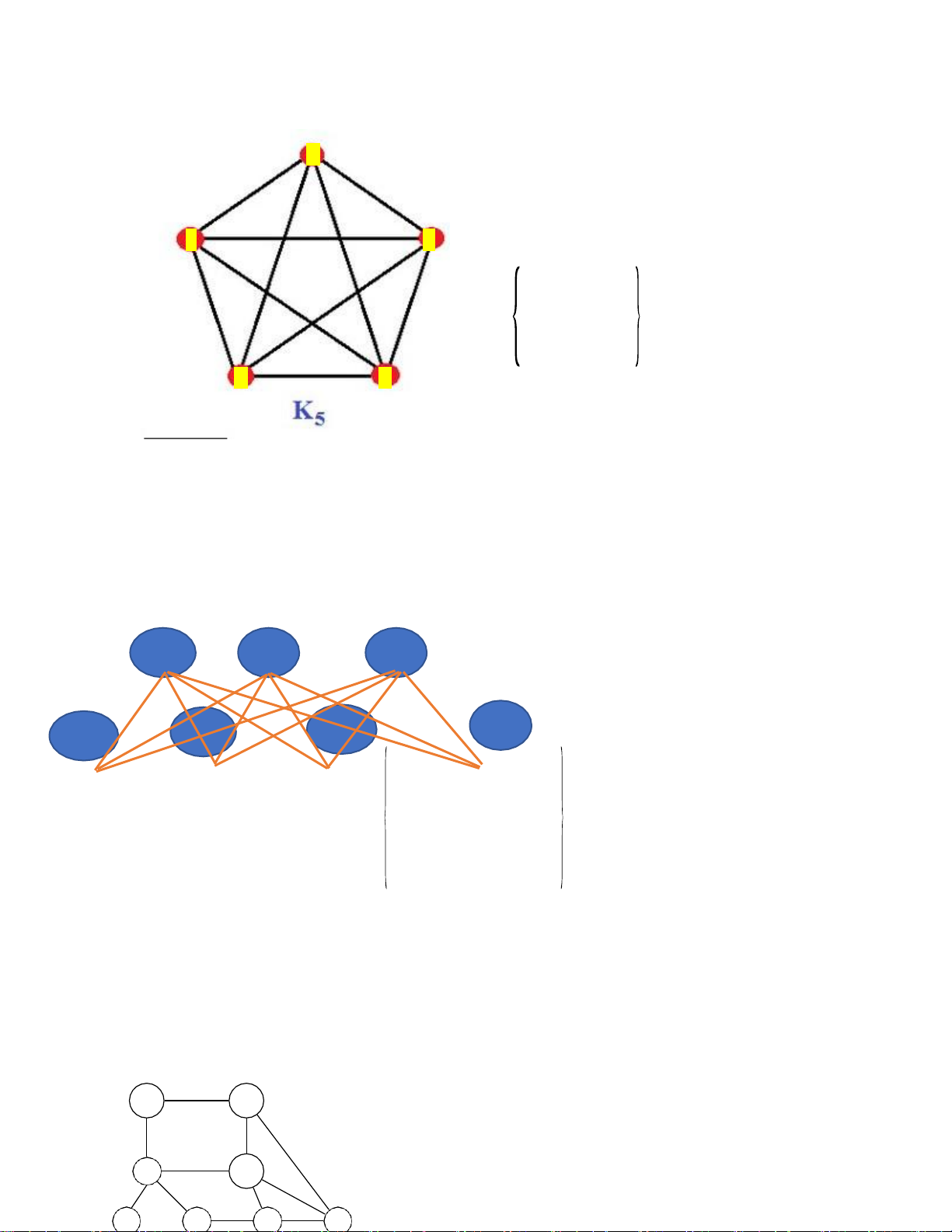
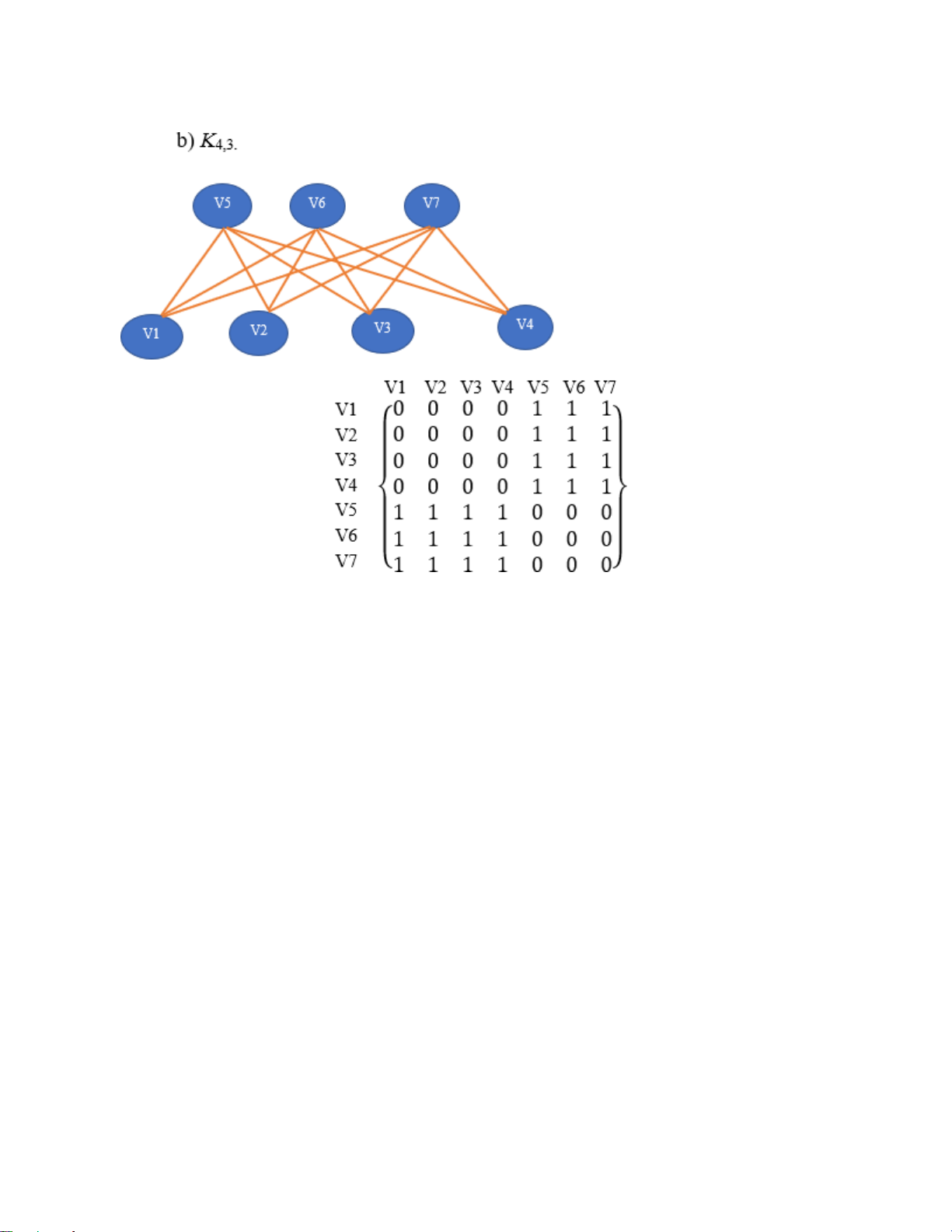
Câu 3(2.0đ).Tìm ma trận liền kề cho các đồ thị sau: a) K5. A E B 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 D C b) K4,3. V5 V6 V7 V4 V1 V2 VV 3 1 0 V2 0 0 V3 0 V4 1 V 1 5 1 V1 0 0 0 0 1 1 1 V2 0 0 0 0 1 1 1 0 0 0 0 1 1 1 V3 1 1 1 1 0 0 0 V4 1 1 1 1 0 0 0 V5 1 1 1 1 0 0 0 V6 V7 V6 V7 Giải:
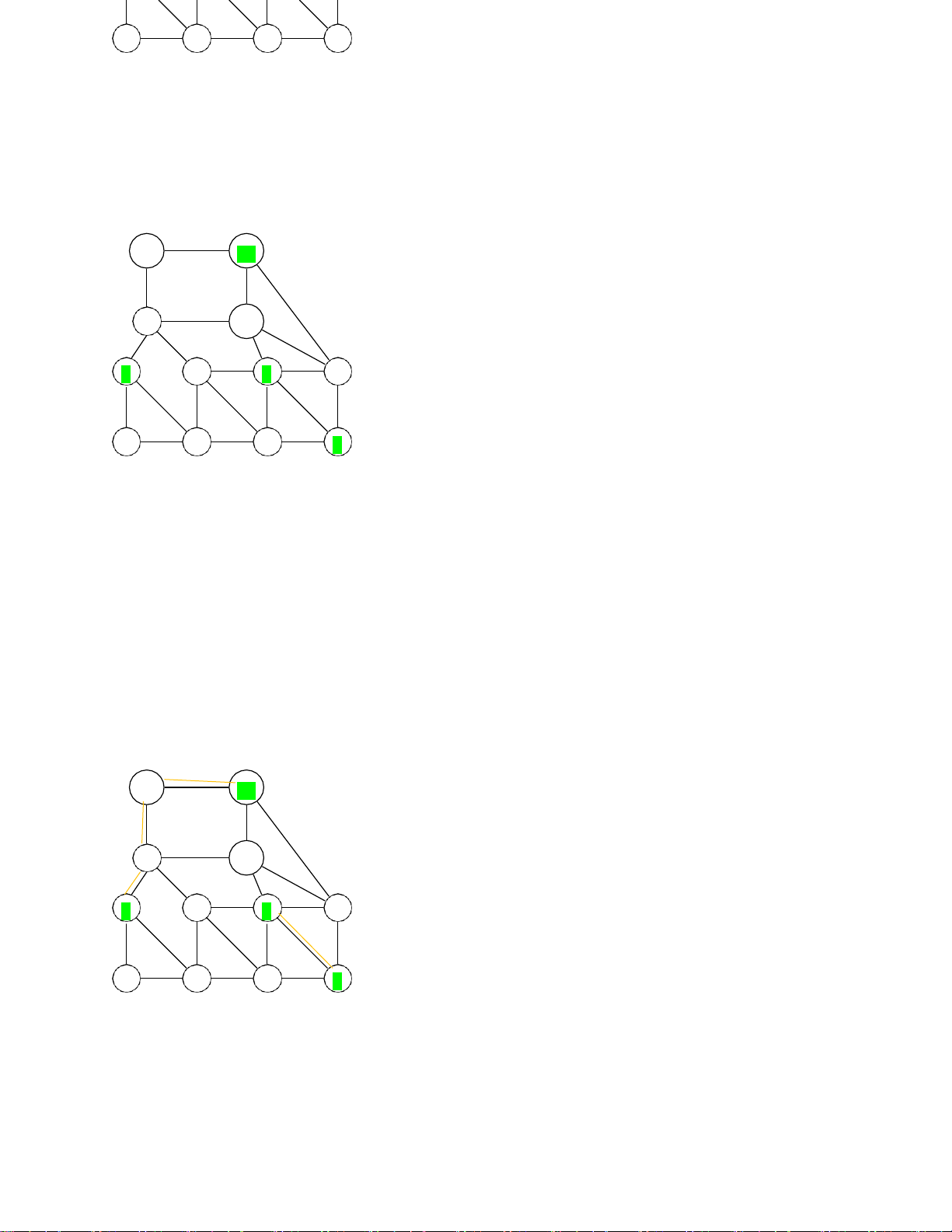
Câu 4(2.0đ).Giải bài toán người phát thư Trung Hoa với đồ thị cho trong hình sau: 12 11 9 10 5 6 7 8 Giải: 12 11 9 10 1 2 3 4 5 6 7 8 1) v0(g)={1 , 3, 8 , 11}
2) p1={(1 , 3),(8 , 11)}; p2={(1 , 8),(3 , 11)};p3={(1 , 11),(3 , 8)}; 3)-D(p1)=3+2=5 -D(p2)=3+2=5 -D(p3)=3+1=4
4) Hàng trình có độ dài=21+4=25 12 11 9 10 1 2 3 4 5 6 7 8
5) 1->5->6->1->9->2->6->7->2->3->7->8->3->4->8->3->10->4->11
->10->9->12->11->12->9->1
Câu 5(3.0đ)câu chưa đầy đủ đề .Tìm cây khung nhỏ nhất bằng thuật
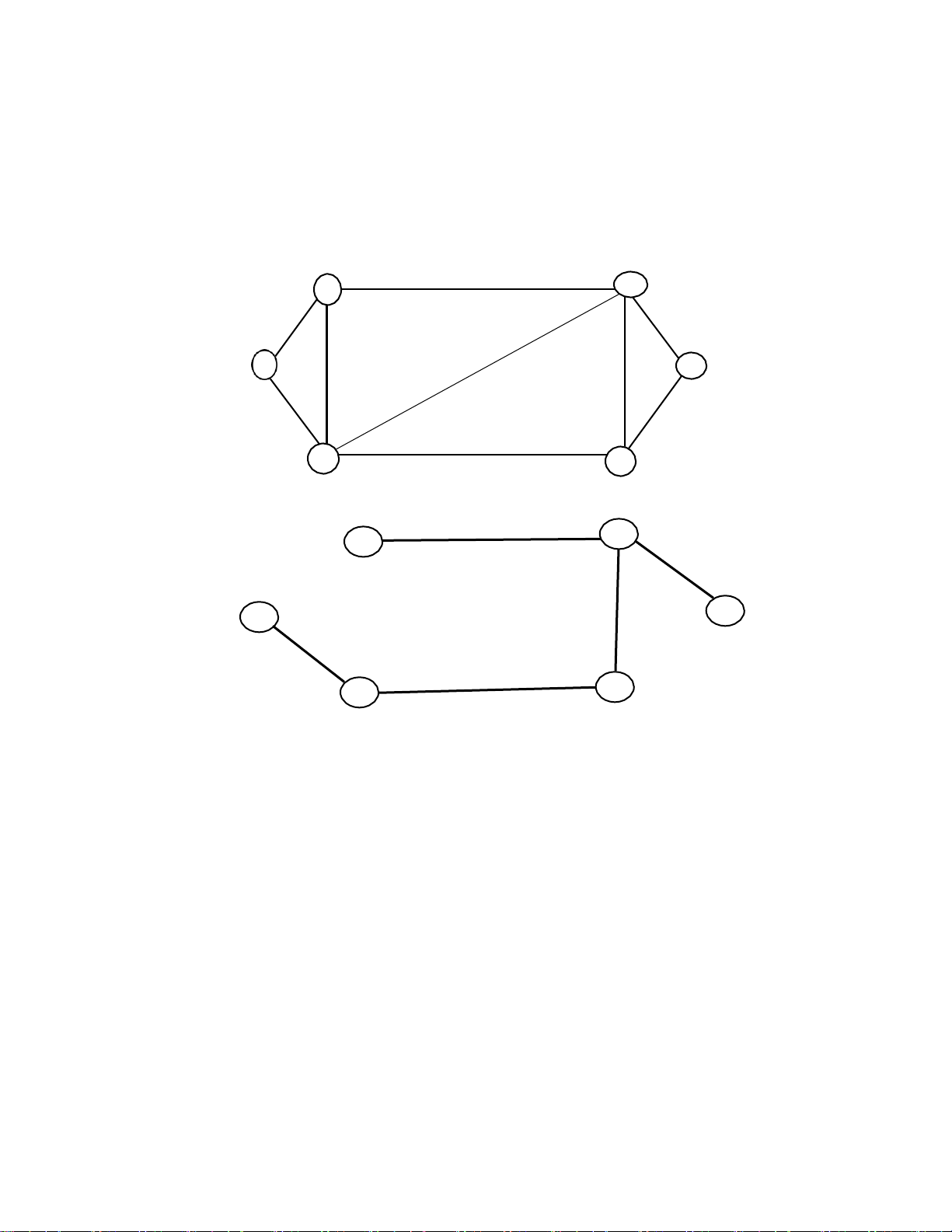
toán Kruskal cho đồ thị như sau: 13 V V 4 2 8 Giải : 14 16 V 1 V6 14 9 10 8 V3 V5 12 13 V V4 2 8 V V 6 1 9 8 V V5 3 12
Bước 1:Sắp xếp thứ tự các cạnh theo trọng số tăng dần
S={(v1v3: 8), (v4v6: 8), (v4v5: 9), (v5v6: 10), (v3v5: 12), (v2v4: 13), (v1v2: 14 ), (v2v3:14), (v3v4: 16)} Bước 2:lặp ET={} - s = v1v3, ET = {v1v3}. - s = v5v6, ET = ET U {v5v6}. ET= ET \ {v5v6} - s = v4v6, ET = ET U{v4v6}. - s = v3v5, ET = ET U {v3v5}. - s = v4v5, ET = ET U {v4v5}.
- s = v2v4, ET = ET U{v2v4},stop. ĐỀ SỐ 8
Câu 1(1.5đ).Trong giỏ trái cây có 5 loại trái là
Cầu ,Dừa ,Đủ ,Xoài ,Cam mỗi loại có ít nhất 7 trái. Hỏi có bao nhiêu
cách xếp lên dĩa với 7 trái mà không cần phân biệt thứ tự cũng như loại trái.
Giải : Vì ta không kể tới thứ tự loại trái và vì ta chọn đúng 7 lần, mỗi lần
lấy 1 trong 5 loại trái nên mỗi cách chọn 5 loại trái này chính là một tổ
hợp chập 7 từ 5 phần tử. Do đó số cần tìm là C 7 5+7-1 = 330 cách
Câu 2(1.5đ).Trong tổng số 2504 sinh viên của một khoa công nghệ
thông tin,có 1876 theo học môn ngôn ngữ lập trình Pascal, 999 học môn
ngôn ngữ Fortran và 345 học ngôn ngữ C. Ngoài ra còn biết 876 sinh
viên học cả Pascal và Fortran, 232 học cả Fortran và C, 290 học cả
Pascal và C. Nếu 189 sinh viên học cả 3 môn Pascal,Fortran và C thì
trong trường hợp đó có bao nhiêu sinh viên không học môn nào trong 3
ngôn ngữ lập trình kể trên . Giải : Gọi:
A là tập các sinh viên học ngôn ngữ Pascal
B là tập các sinh viên học ngôn ngữ Fortran
C là tập các sinh viên học ngôn ngữ C N là tổng số sinh viên
K là tổng số sinh viên học ít nhất 1 môn
Áp dụng nguyên lý bù trừ ta có:
K = |A| + |B| +|C | - |A ∩ B|- |A ∩ C| - |B ∩ C|+ | A∩ B ∩ C|
= 1876+999+345-876-232-290+189 =2011
Số học sinh không học bất cứ môn nào trong cả 3 môn là:
N-K= 2504-2011= 493 ( sinh viên)
Câu 3(2.0đ).Cho G là một đồ thị phẳng liên thông có 10 miền và tất cả
các đỉnh đều có bậc 4. Tìm số đỉnh của G. Giải :
Câu 4(2.0đ).Viết các biểu thức sau đây theo ký pháp quen thuộc.
−* ↑ / − − a b * 3 c 2 4 ↑ −c d 5 * − − a c d / ↑ − b * 2 d 4 3 Giải :
−* ↑ / − (a – b) 3c 2 4 (c-d)5 * (a – c – d) / ↑ (b − 2d) 4 3 − – –
* ↑ (a b 3c) 4 (c-d)5 * (a – c – d) / (b − 2d)4 3 2 − – –
* ( (a b 3c) )4 (c-d)5 * (a – c – d) (b−2d)4 2 3
− (a – b – 3 c ) (b−2 d)4 (
)4(c-d)5 (a – c – d) 2 3
(a – b – 3 c ) (b−2 d)4 (
)4(c-d)5 − (a – c – d) 2 3
Câu 5(3.0đ).Tìm cây khung nhỏ nhất bằng thuật toán Prim của đồ thị
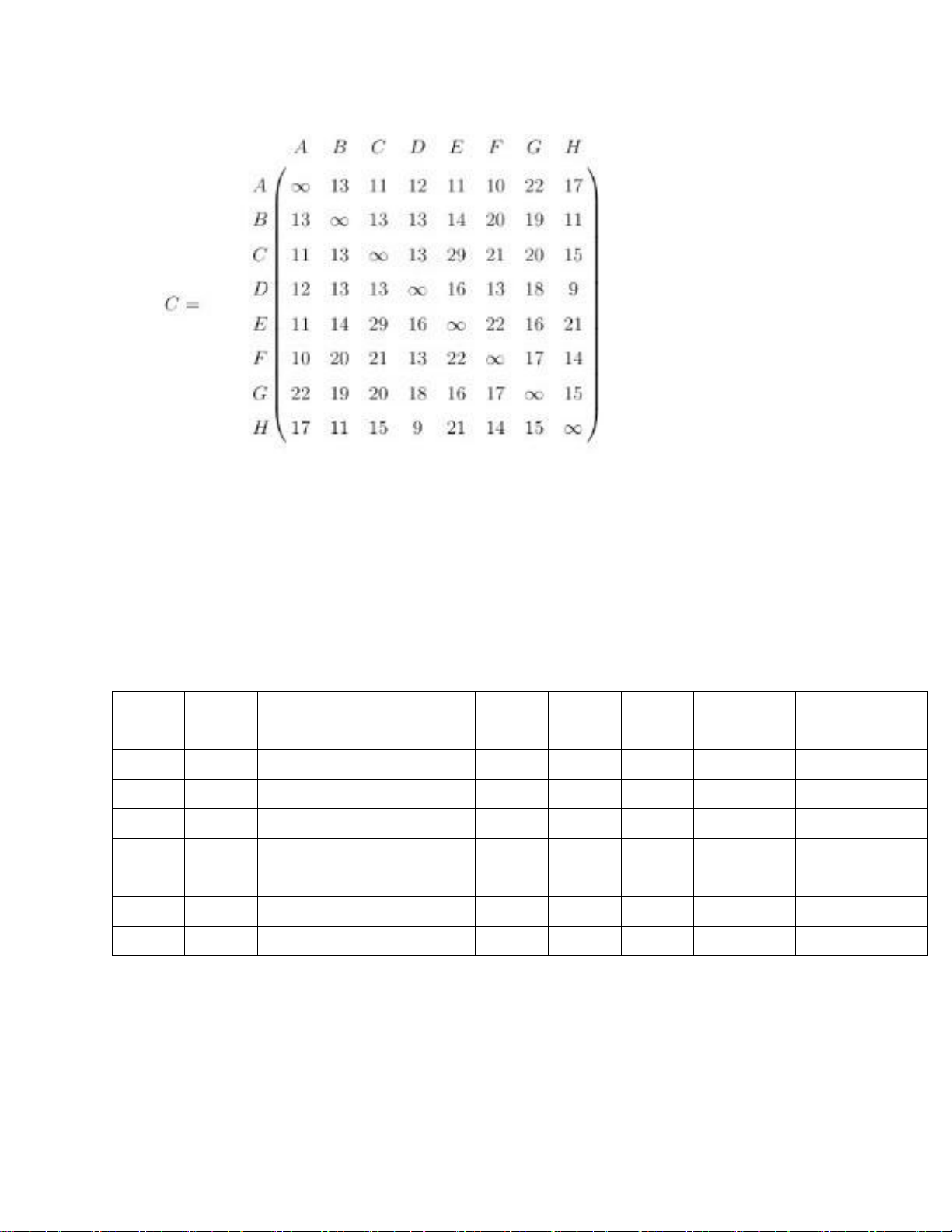
với ma trận trọng số sau:
Yêu cầu: Viết kết quả trung gian trong từng bước lặp , kết quả cuối cùng
được đưa ra trong từng tập cạnh và độ dài nhỏ nhất của cây khung cần tìm. Giải : A B C D E F G H VT ET 0,A
13,A 11,A 12,A 11,A 10,A 22,A 17,A A {} -
13,A 11,A 12,A 11,A 10,A 17,F 14,F U {F} (F,A) - 13,A 11,A 12,A 11,A - 17,F 14,F U {C} U {(C,A)} - 13,A - 12,A 11,A - 16,E 14,F U {E} U {(E,A)} - 13,A - 12,A - - 16,E 9,D U {D} U {(D,A)} - 11,H - - - - 15,H 9,D U {H} U {(H,D)} - 11,H - - - - 15,H - U {B} U {(B,H)} - - - - - - 15,H - U {G} U {(G,H)}
SUM(T) = 0 + 11 + 11 + 12 + 11 + 10 + 15 + 9 =79
ET= {(F,A), (C,A), (E,A), (D,A), (H,D), (B,H), (G,H)} ĐỀ SỐ 16
Câu 1(1.5đ).Đếm xem trong khoảng từ 1 đến 100 có bao nhiêu số chia
hết cho 3 hoặc chia hết cho 5 hoặc chia hết cho 7. Giải :
Gọi A là tập chia hết cho 3,|A| =[ 100 ] = 33 3
Gọi B là tập chia hết cho 5,|B| =[ 100 ] = 20 5
Gọi C là tập chia hết cho 7,|C| =[ 100 ] = 14 7 Ta có : |A∩B| = 15 [ 100 ] = 6 |A∩C| = 21 [ 100 ] = 4 |B∩C| = 35 [ 100 ] = 2 Và |A∩B∩C| = 105 [ 100 ] = 0
Suy ra:|A∪B∪C|=N1-N2+N3=(33+20+14)-(6+4+2)+0
=>|A∪B∪C|=33+20+14-6-4-2+0= 55.
Câu 2(1.5đ).Một cuộc họp gồm 12 người tham dự để bàn về 3 vấn đề.
Có 8 người phát biểu vấn đề I, 5 người phát biểu vấn đề II và 7 người
phát biểu vấn đề III. Ngoài ra, có đúng 1 người không phát biểu vấn đề
nào.Hỏi nhiều lắm là có bao nhiêu người phát biểu cả 3 vấn đề. Giải :
Gọi A là tập bàn luận về vấn đề I ,|A| = 8
Gọi B là tập bàn luận về vấn đề II ,|B| = 5
Gọi C là tập bàn luận về vấn đề III ,|C| = 7 Biết N=12,N4=1
Ta có : N = N - |A∪B∪C|=N-(|A|+|B|+|C|)-( |A∩B|+ |A∩C|+ |B∩C|)+(| A∩B∩C|)
Bài này ta sử dụng công thức tính nhanh:
|A∩B∩C|=N1 + N2 + N3 + N4 – N=9 |A∩B∩C| = 9=4 2
=>Có 4 người phát biểu 3 vấn đề
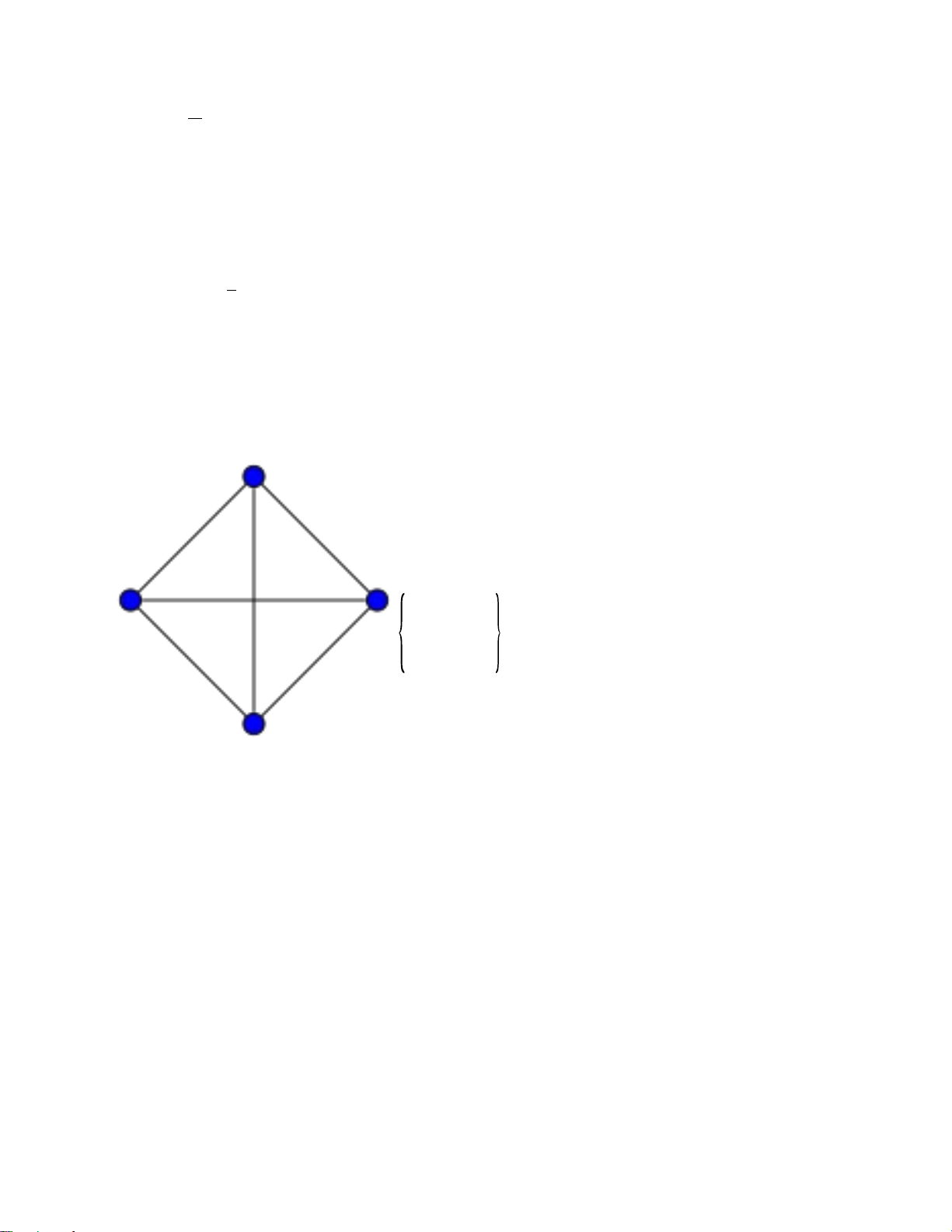
Câu 3(2.0đ).Tìm ma trận liền kề cho các đồ thị sau: a) K4; 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 0 b) K4,3. Giải:
Câu 4(2.0đ).Trong một cuộc hội thảo quốc tế, có 17 đại biểu đến từ 17
quốc gia tham dự, mỗi ngày ngồi họp với nhau một lần quanh một bàn
tròn.Biết rằng mọi người rất muốn làm quen với nhau, nên cần sắp xếp
chỗ ngồi.Hỏi hội thảo kéo dài bao nhiêu ngày và sắp xếp các đại biểu
như thế nào sao cho mỗi lần ngồi họp ,mỗi đại biểu có hai người kế bên là bạn mới ? Giải:
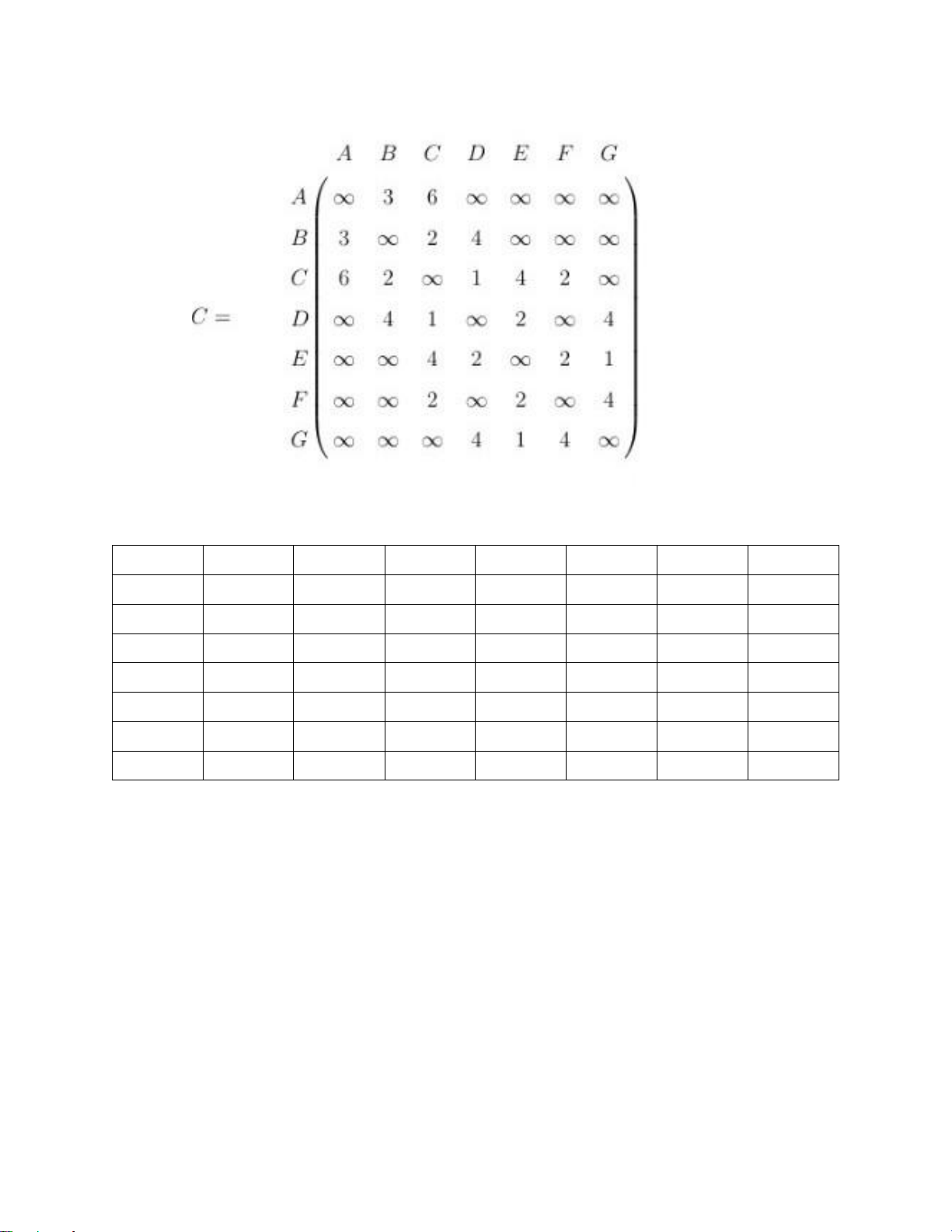
Câu 5(3.0đ).Tìm đường đi ngắn nhất xuất phát từ đỉnh A đến các đỉnh
còn lại của đồ thị biểu diễn bằng ma trận trọng số sau bằng thuật toán
Dijktra. Yêu cầu viết kết quả trung gian trong từng bước lặp và liệt kê
chi tiết các đường đi. Giải: A B C D E F G VT 0,A 3,A 6,A 00,A 00,A 00,A 00,A A - 3,A 5,B 7,B 00,A 00,A 00,A U {B} - - 5,B 6,C 9,C 7,C 00,A U {C} - - - 6,C 8,D 7,C 10,D U {D} - - - - 8,D 6,C 10,D U {F} - - - - 8,D - 9,E U {E} - - - - - - 9,E U {G} TRUY XUẤT BẢNG: A->B: 3 ; A->B;
A->D:6; A->B->C->D;
A->C:5 ; A->B->C;
A->E:8; A->B->C->D->E;
A->F: 6 A->B->C->F;
A->G:9; A->B->C->D->E->G;
1. Tìm hệ thức truy hồi và điều kiện đầu để đếm số cách đi lên cầu
thang n bậc với bước từng bậc một, bước 2 bậc một hoặc 3 bước một. Giải:
Trường hợp 1: Cầu thang 1 bậc ( n = 1 ) Ta có:
Người đó có thể bước theo cách: 1 bậc một. => Có 1 cách đi
Trường hợp 2: Cầu thang 2 bậc ( n = 2) Ta có:
Người đó có thể bước theo cách: 1 bậc - 1 bậc ; 2 bậc => có 2 cách
Trường hợp 3: Cầu thang 3 bậc ( n = 3 ) Ta có:
Người đó có thể bước theo cách: 1 bậc - 1 bậc - 1 bậc; 2 bậc - 1
bậc; 1 bậc - 2 bậc; 3 bậc => có 4 cách
Trường hợp 4: Cầu thang 4 bậc Ta có:
Người đó có thể bước theo cách: 1 bậc - 1 bậc - 1 bậc - 1 bậc; 2
bậc - 1 bậc - 1 bậc; 1 bậc - 1 bậc - 2 bậc; 1 bậc - 2 bậc - 1 bậc ; 2
bậc - 2 bậc; 3 bậc - 1 bậc ; 1 bậc - 3 bậc => có 7 cách
Suy ra trong trường hợp tổng quát để đếm số cách đi ta có thể
liệt kê dãy số trên theo cách:
Những số đứng sau bằng tổng của ba số đứng ngay trước nó.
Vậy ta xậy dựng được: Sn = Sn-1 + Sn-2 +Sn-3
Với các điều kiện đầu: S1=1;S2=2;S3=3.
2. Tìm nghiệm của hệ thức truy hồi sau:
an = 6an−1 − 11an−2 + 6an−3 với các điều kiện đầu a0 = 2, a1 = 5 và a2 = 15 Giải:
Đa thức đặc trưng của hệ thức truy hồi này là r3 - 6r2 + 11r – 6.
Các nghiệm đặc trưng là : r = 1 , r = 2 , r = 3.Do vậy nghiệm của
hệ thức truy hồi có dạng: an= ∝11n+∝22n+∝33n
Các điều kiện ban đầu a0=2= ∝1+∝2+∝3 a1=5= ∝1+∝22+∝33 a2=15= ∝1+∝24 +∝39
Giải hệ phương trình này ta nhận được ∝1¿ 1 ,∝2¿−1 ,∝3=2.
Vì thế,nghiệm duy nhất của các hệ thức truy hồi này và các điều
kiện ban đầu đã cho là dãy {an} với an=1-2n+2*3n
3. Tìm nghiệm của hệ thức truy hồi sau:
an = 2an−1 + 5an−2 − 6an−3 với các điều kiện đầu a0 = 7, a1 = −4, a2 = 8 Giải:
Phương trình đặc trưng là : r3 - 2r2 -5r + 6.
Nó có nghiệm là : r = -2 , r = 1 , r = 3.
Do đó, lời giải của hệ thức truy hồi có dạng: an= ∝1(-2)n+∝21n+∝33n
Để tìm các hệ số ∝1, ∝2, ∝3.Sử dụng các điều kiện ban đầu a0=7= ∝1+∝2+∝3
a1=-4= ∝1(−2)+∝2+∝33 a2=8= ∝14 +∝2+∝39
Giải hệ phương trình này ta nhận được ∝1¿ 3 , ∝2¿ 5 , ∝3=-1.
Vì thế,nghiệm duy nhất của các hệ thức truy hồi này và các điều
kiện ban đầu đã cho là dãy {an} với an=3*(-2)n+5n+(-3)n
4. Tìm nghiệm của hệ thức truy hồi sau:
an = 5an−1 + 6an−2 với các điều kiện đầu a0 = 1, a1 = 3 Giải:
Phương trình đặc trưng là : r2 - 5r – 6 ,có các nghiệm là r = 6 và r = -1.
Do đó, dãy {an} là một lời giải đối với hệ thức truy hồi khi và chỉ khi
an= ∝16n+∝2(-1)n ,với các giá trị ∝1, ∝2 nào đó.
Từ điều kiện ban đầu, suy ra rằng a0=1= ∝1+∝2 a1=3= ∝16+∝2(-1)
Giải hệ phương trình này ta được ∝ 4 3 1¿ , ∝2¿ . 7 7
Vì thế,nghiệm duy nhất của các hệ thức truy hồi này và các điều
kiện ban đầu đã cho là dãy {an} với an= 4 * 6n + 3∗¿(-1)n 7 7
5. Có bao nhiêu xâu nhị phân có độ dài bằng n = 10 và có 5 số 0
liền nhau hoặc 5 số 1 liền nhau. Giải:
Gọi A là tập hợp các xâu nhị phân có độ dài n=10 có 5 số 0 liền nhau.
Cấu hình 1: [0][0][0][0][0][x][x][x][x][x]= 25
Cấu hình 2: [1][0][0][0][0][0][x][x][x][x]=24
Cấu hình 3: [x][1][0][0][0][0][0][x][x][x]=24
Cấu hình 4: [x][x][1][0][0][0][0][0][x][x]=24
Cấu hình 5: [x][x][x][1][0][0][0][0][0][x] =24
Cấu hình 6: [x][x][x][x][1][0][0][0][0][0]= 24
- Ta có số nhị phân có 5 số 0 liên tiếp với độ dài n=10 là: A= 112
Gọi B là tập hợp các xâu nhị phân có độ dài n=10 có 5 số 1 liền nhau.
Cấu hình 1: [1][1][1][1][1][x][x][x][x][x]= 25
Cấu hình 2: [0][1][1][1][1][1][x][x][x][x]=24
Cấu hình 3: [x][0][1][1][1][1][1][x][x][x]=24
Cấu hình 4: [x][x][0][1][1][1][1][1][x][x]=24
Cấu hình 5: [x][x][x][0][1][1][1][1][1][x] =24
Cấu hình 6: [x][x][x][x][0][1][1][1][1][1]= 24
- Ta có số nhị phân có 5 số 1 liên tiếp với độ dài n=10 là: B= 112
- Có 2 trường hợp trùng nhau giữa A và B:
Cấu hình 1: : [0][0][0][0][0][1][1][1][1][1]
Cấu hình 2: : [1][1][1][1][1][0][0][0][0][0]
Số nhị phân có độ dài là 10 và hoặc có 5 số 0 liên tiếp hoặc 5 số 1 liên tiếp là: A+ B -2= 222
6. Đếm xem có bao nhiêu xâu nhị phân độ dài n = 8 có 3 số 0 liên
tiếp hoặc 4 số 1 liên tiếp nhau. Giải:
Gọi A là tập hợp các xâu nhị phân có độ dài n=8 có 3 số 0 liên tiếp .
Cấu hình 1: [0][0][0][x][x][x][x][x]= có 25 xâu.
Cấu hình 2: [1][0][0][0][x][x][x][x]=có 24 xâu.
Cấu hình 3: [x][1][0][0][0][x][x][x]=có 24 xâu.
Cấu hình 4: [x][x][1][0][0][0][x][x]=có 24 xâu.
Cấu hình 5: [x][x][x][1][0][0][0][x]=có 24 - 2 xâu(đã xuất hiện 2 lần ở cấu hình 1).
Cấu hình 6: [x][x][x][x][1][0][0][0]=có 24 -3 xâu(đã xuất hiện 2 lần ở cấu hình 1 và 1 mo
- Ta có số nhị phân có 3 số 0 liên tiếp với độ dài n = 8 là: A= 107
Gọi B là tập hợp các xâu nhị phân có độ dài n=8 có 4 số 1 liên tiếp .
Cấu hình 1: [1][1][1][1][x][x][x][x]=có 24 xâu
Cấu hình 2: [0][1][1][1][1][x][x][x]=có 23 xâu
Cấu hình 3: [x][0][1][1][1][1][x][x]=có 23 xâu
Cấu hình 4: [x][x][0][1][1][1][1][x]=có 23 xâu
Cấu hình 5: [x][x][x][0][1][1][1][1]=có 23 xâu
- Ta có số nhị phân có 4 số 1 liên tiếp với độ dài n=8 là: B= 48
- Có 4 trường hợp trùng nhau giữa A và B:
Cấu hình 1: [1][1][1][1][0][0][0][0]
Cấu hình 2: [0][0][0][0][1][1][1][1]
Câu hình 3: [1][1][1][1][1][0][0][0]
Cấu hình 4: [0][0][0][1][1][1][1][1]
Cấu hình 5: [0][0][0][1][1][1][1][0]
Cấu hình 6: [0][1][1][1][1][0][0][0]
Câu hình 7: [1][0][0][0][1][1][1][1]
Cấu hình 8: [1][1][1][1][0][0][0][1]
Số xâu nhị phân độ dài n = 8 có 3 số 0 liên tiếp hoặc 4 số 1 liên tiếp nhau à: A+ B - 8=147
Bài tập 1.4 Tài khoản của thí sinh trên trang web
oj.hueuni.edu.vn gồm 6 ký tự, trong đó 2 ký tự đầu tiên lấy
trong 26 chữ cái (không dùng chữ O và I ). 4 chữ số còn lại lấy từ tập 0..9.
Hỏi quản lý được bao nhiêu handle (username) bao nhiêu? Giải :
Gọi tài khoản thí sinh trang web oj.hueuni.edu.vn là XYabcd
Với X, Y là 1 kí tự trong 24 chữ cái (không dùng chữ O và I trong bảng 26 chữ cái)
abcd là 4 chữ số lấy từ tập {0;..;9}
Suy ra có 24*24*10*10*10*10 = 5760000 cách lập ra 1 handle (username)
Số tài khoản handle (username) được là 5760000 tài khoản
Bài tập 1.5 Cho tập hợp X = {0, 1, 2, 3, 4, 5} Có thể lập được
bao nhiêu số tự nhiên có bốn chữ số khác nhau từ X, ví dụ 1234, 3425. Giải:
Gọi ABCD là số được lập nên từ X Ta có:
A có 5 cách chọn ( trừ 0 ) B có 5 cách chọn C có 4 cách chọn D có 3 cách chọn
Vậy tổng số tự nhiên có bốn chữ số khác nhau được lập từ X là: 5*5*4*3= 300 cách
Bài tập 1.6 Cho một lưới gồm các ô vuông. Các nút được
đánh số từ 0 đến n theo chiều từ trái sang phải và từ 0 đến k
theo chiều từ dưới lên trên. Hỏi có bao nhiêu đường đi khác
nhau từ nút (0, 0) đến nút (n, k) nếu chỉ cho phép đi trên cạnh
các ô vuông theo chiều sang phải hoặc lên trên? Giải:
Đường đi từ từ nút(0,0) đến nút(n,k) cần đi hết n+ k bước (n sang phải và k lên trên)
Ta coi đường đi là xâu nhị phân có độ dài n+k , coi mỗi bước lên
là 1, bước sang phải là 0
Từ đó bài toán trở thành tìm số xâu nhị phân có độ dài n+k với đúng n bit 0 và k bit 1.
Ví dụ với n = 3, k = 2 ta có các xâu thõa mãn
00011 ; 00101 ; 00110 ; 01001 ; 01100 ; 01010 ; 10001 ; 10010 ; 10100 ; 11000 =>Có 10 xâu thõa mãn
Suy ra, tổng quát ta có C(n,n+k) xâu nhị phân thõa mãn bài toán tìm xâu nhị phân
Vậy có C(n,n+k) đường đi khác nhau từ nút (0,0) đến nút (n,k)
Bài tập 1.7 Phương trình x1 + x2 + x3 + x4 + x5 = 21 có bao nhiêu
nghiệm nguyên không âm? Giải:
Chúng ta nhận thấy mỗi nghiệm của phương trình ứng với một
cách chọn phần tử từ một tập có 5 loại áo cho x1 phần tử loại 1,x2
phần tử loại 2,x3 phần tử loại 3,x4 phần tử loại 4,x5 phần tử loại
5được chọn.Vì vậy số nghiệm bằng số tổ hợp lập chập 21 từ tập
có 5 phần tử và bằng C215+21-1=12650 nghiệm.
Bài tập 1.8 Có bao nhiêu xâu khác nhau nếu hoán vị các ký tự
của từ ’MISSISSIPI’. Giải:
Từ này chứa 1 chữ M ,4 chữ S ,4 chữ I,1 chữ P.Để xác định số
xâu khác nhau ta thấy có C(10,4) cách chọn 4 chỗ cho 4 chữ
S,còn lại 6 chỗ trống.Có C(6,4) cách chọn 4 chỗ cho 4 chữ I,còn
lại 2 chỗ trống.Có thể đặt chữ M bằng C(2,1) cách và C(1,1) cách
đặt chữ P vào xâu.Theo nguyên lý nhân ,số các xâu khác nhau
có thể tạo được là : C410* C46*C12*C11=
10 !∗6 !∗2!∗1 ! = 10 ! =6300 xâu.
4 !∗6 !∗4 !∗2!∗1 !∗1!∗1 !∗0
4 !∗4 !∗1!∗1 !
Bài tập 1.9 Chỉ ra rằng có ít nhất 4 người trong số 25.000.000
người có cùng tên họ viết tắt bằng ba chữ cái viết hoa sinh
cùng một ngày trong năm (không nhất thiết phải cùng một năm). Giải: