






















































































Preview text:
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng
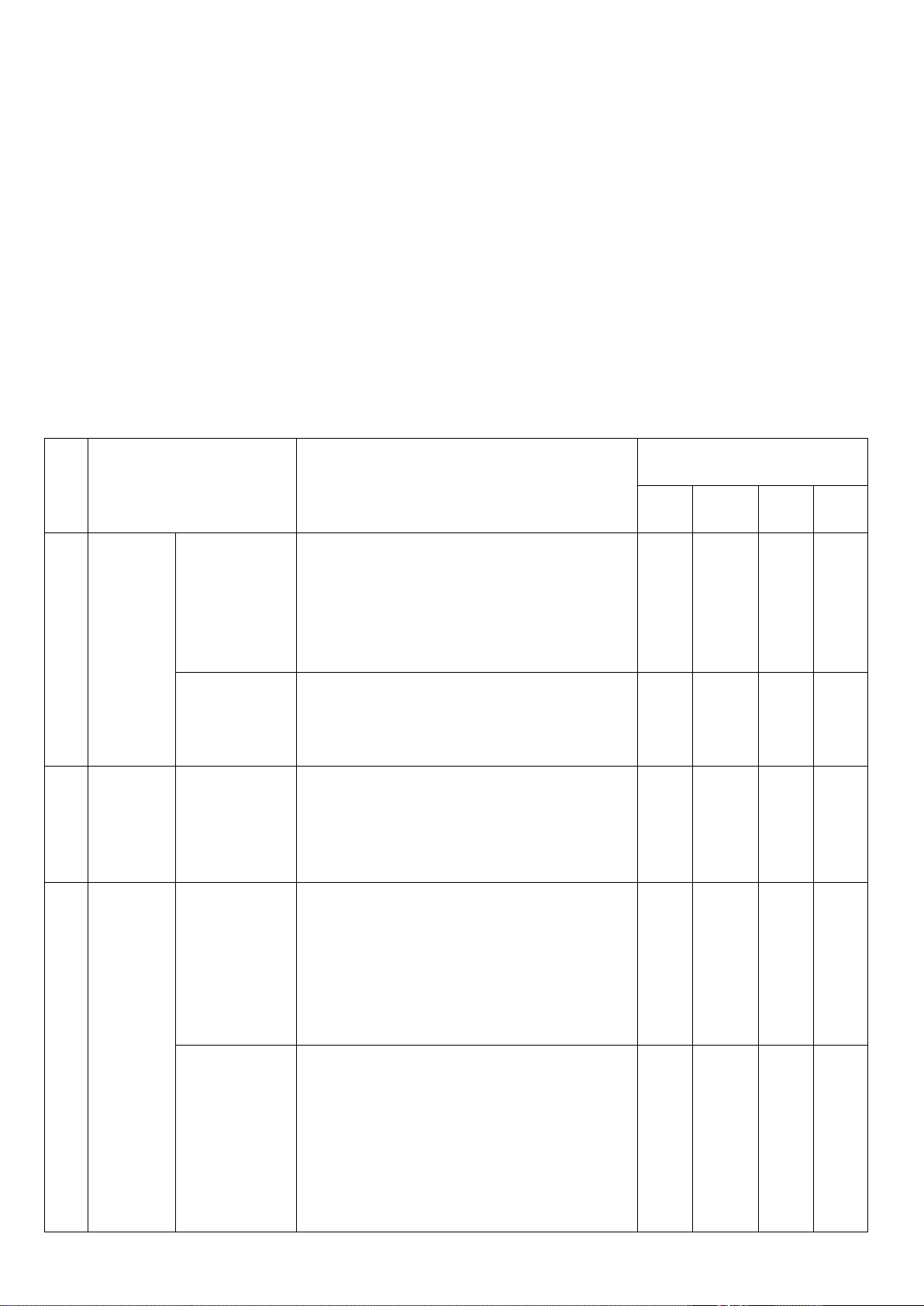
TT Chủ đề Nội dung/Đơn vị kiến điểm thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TN TL TN TL TN TL TN TL
Vẽ đồ thị hàm số 𝑦𝑦 = 1
𝑎𝑎𝑥𝑥2 (P) và y = ax + b (Bài a) 1 Đồ thị (d) (1,0đ) hàm số 2đ 1 Tìm tọa độ giao điểm (Bài b) của (P) và (d) (1,0đ) Hệ thức 1 2 Vi-et và (Bài 2) ứng Hệ thức Vi-et (1,5 đ) 1,5đ dụng Giải bài toán bằng 1 cách lập hệ phương (Bài 3) trình. (1,5đ) Bài tập 3 ứng Dạng ứng dụng tăng 1 1 dụng 4đ giảm Bài 4a Bài 4b thực tế (1,0đ) (0,5đ) Dạng toán ứng dụng 1 1 hình không gian (Bài 5a) (Bài 5b) (0,5đ) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài 6b) (Bài 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng Đồ thị hàm số 1 y = ax2 (P) và Vận dụng: (Bài
y = ax + b (d) - Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ 1a) 1 Đồ thị trục tọa độ hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong việc (Bài (P) và (d)
tìm tọa độ giao điểm của (P) và (d). 1b) Thông hiểu: Hệ thức
- Tính được tổng, tích, x 2 2 1 +x2 các nghiệm của 2 Vi-et và
Hệ thức Vi -et phương trình bậc hai một ẩn bằng hệ thức 1 ứng dụng
Vi-et . Sự dụng kiến thức nhân đa với đa để (Bài 2)
tính giá trị của biểu thức Giải bài toán Thông hiểu:
bằng cách lập - Phân tích đề bài, tìm mối quan hệ giữa số tờ tiền hệ phương
và số tiền cho trong đề bài, gọi ẩn, từ đó lập được 1 trình.
hệ 2 phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu: Bài tập
- Tính được số tiền phải trả bằng công thức
3 ứng dụng Dạng ứng tăng/giảm 1 1 thực tế dụng tăng Vận dụng: Bài giảm
- Vận dụng kiến thức về tăng giảm, tỉ số % để Bài 4a 4b tính tiền vốn
Dạng toán ứng Thông hiểu: dụng hình
- Tính được thể tích của hình 1 1 không gian
Vận dụng cao: Bài 5a Bài
- Vận dụng hợp lí công thức thể tích hình trụ, 5b
hình cầu để giải quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc 4
với đường tròn, mối quan hệ giữa các góc, phối
Hình học Tứ giác nội tiếp
hợp các kiến thức để chứng minh hai góc bằng nhau 1 1
Vận dụng cao: (Bài (Bài
- Phối hợp tổng hợp các kiến thức tính chất 6b) 6c)
các góc trong đường tròn, tam giac đồng dạng ,
hệ thức trong tam giác vuông để chứng minh tứ giác nội tiếp
ỦY BAN NHÂN DÂN HUYỆN CỦ CHI
ĐỀ KIỂM TRA CUỐI KỲ 2
TRƯỜNG TRUNG HỌC CƠ SỞ NĂM HỌC 2023 - 2024 AN NHƠN TÂY MÔN: TOÁN 9 Thời gian: 90 phút
(Đề thi gồm 2 trang)
(Không kể thời gian phát đề)
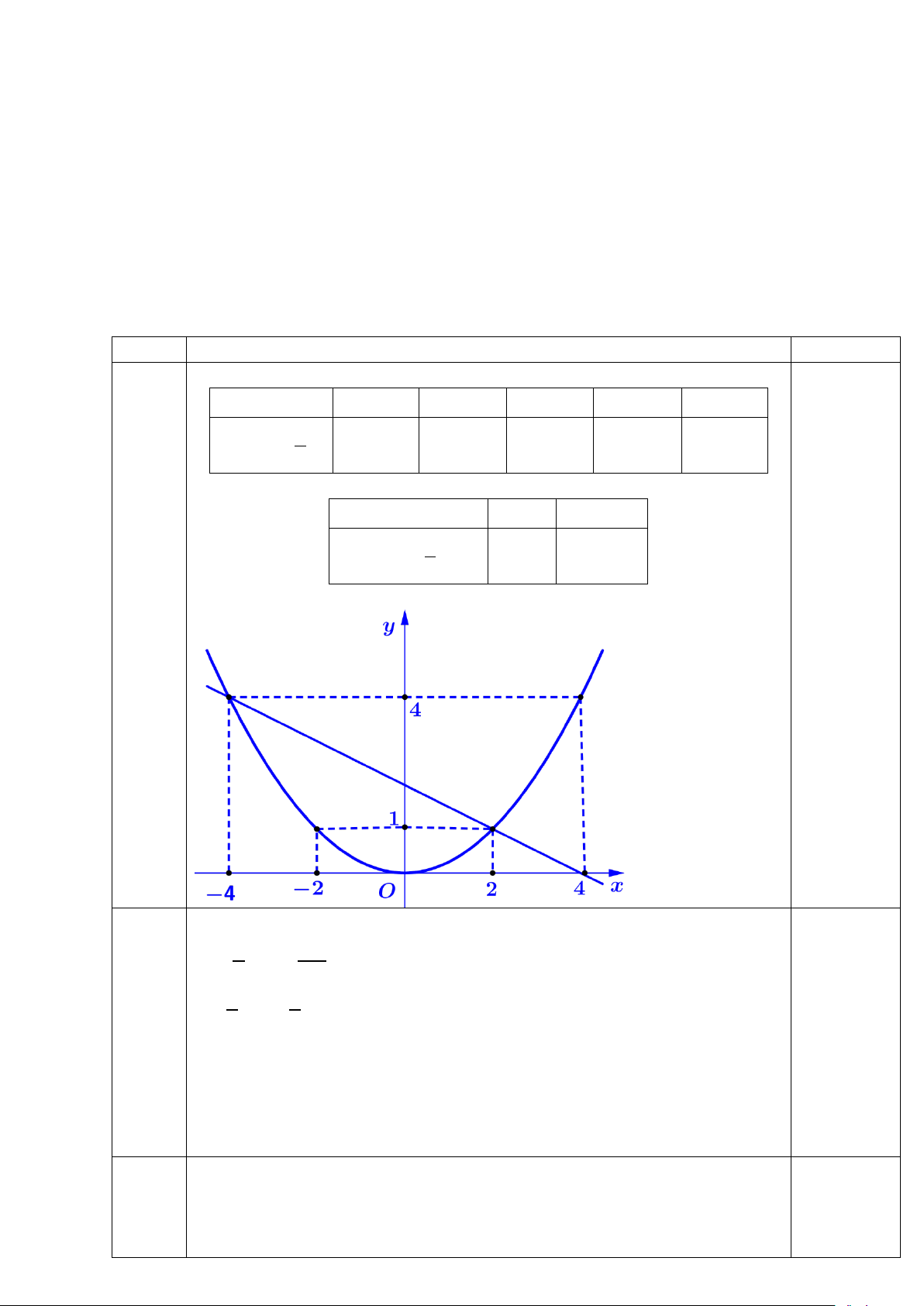
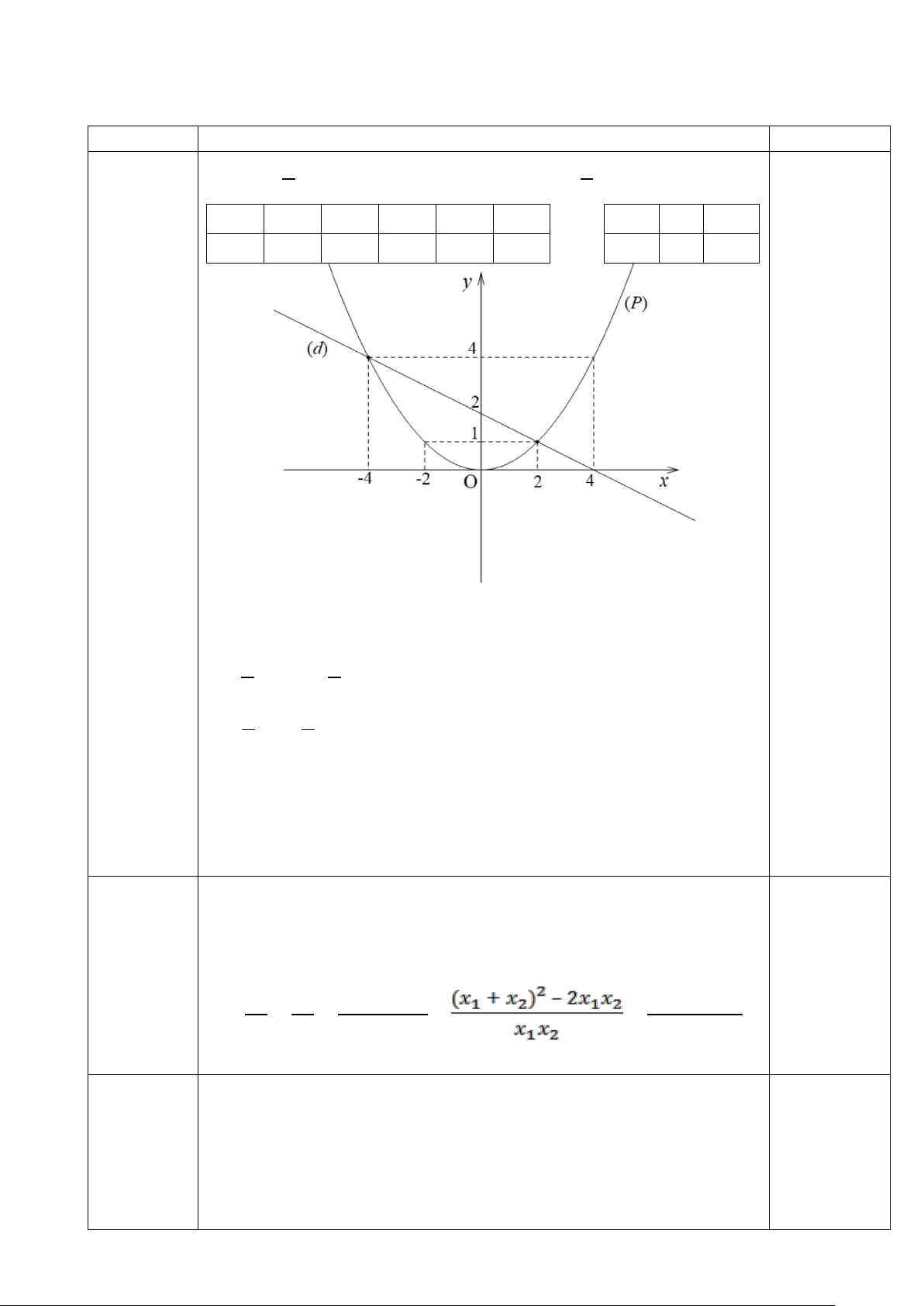
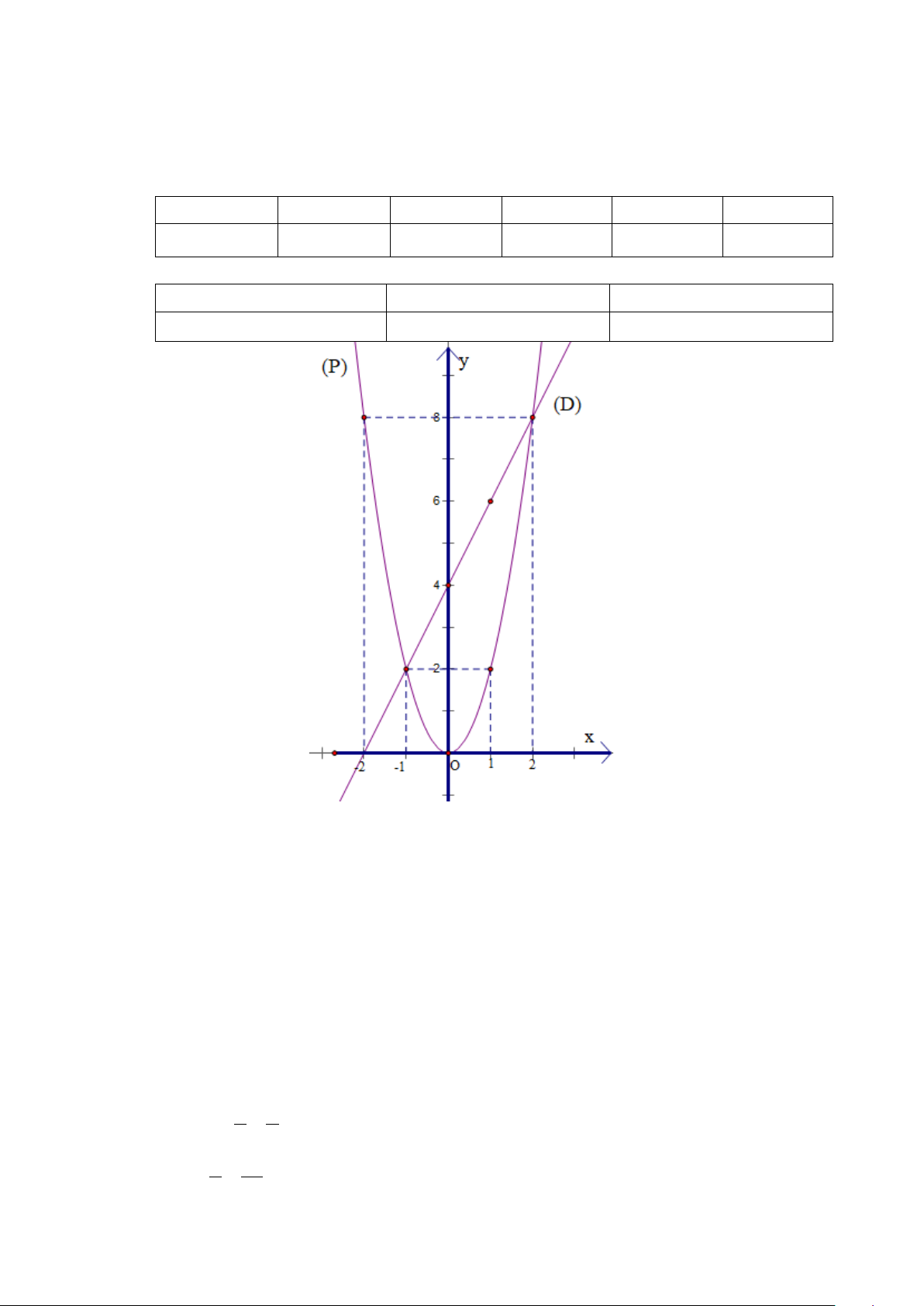
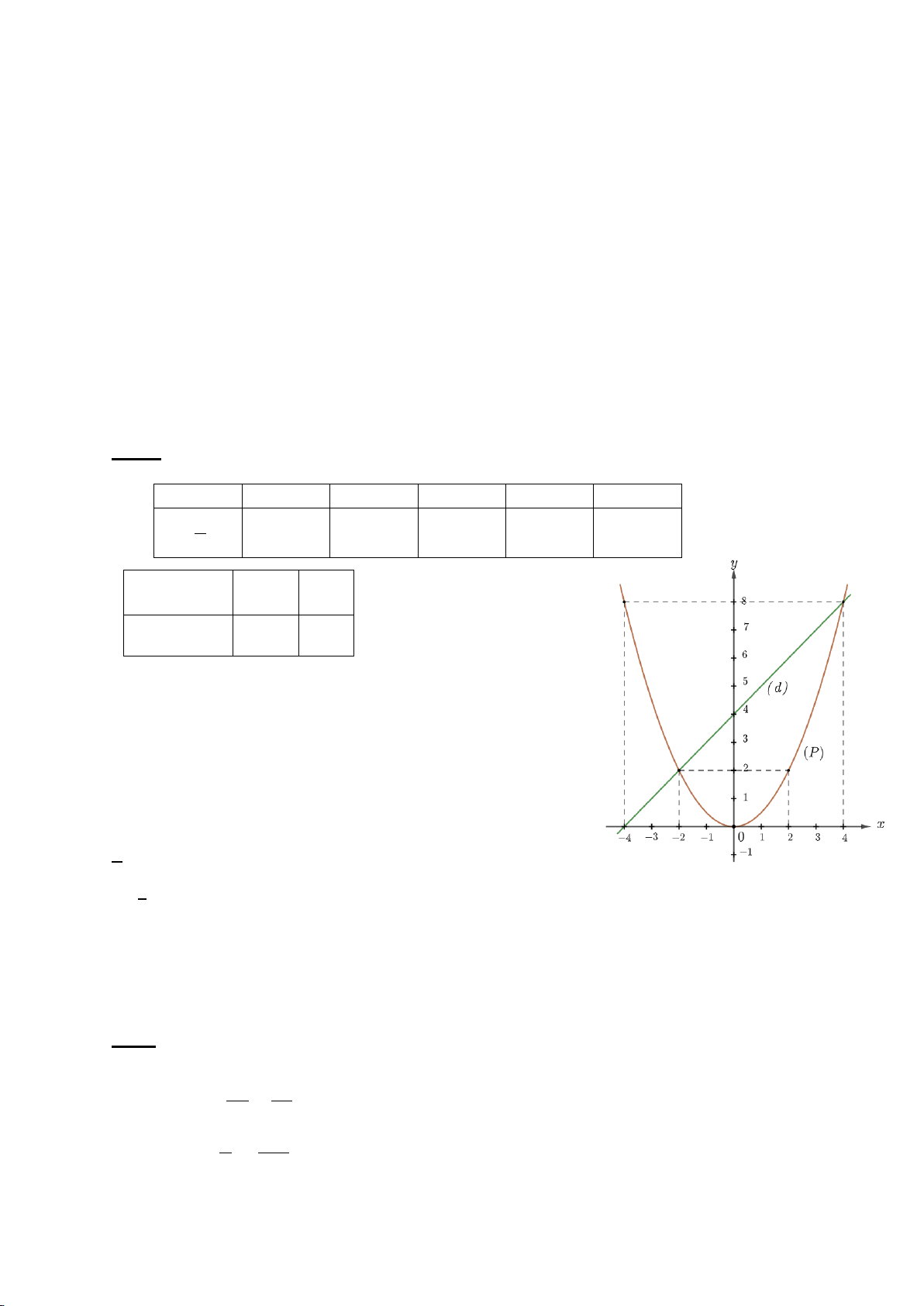
Bài 1: (2 điểm) Cho hàm số 𝑦𝑦 = 1 x2 và (d): y = −1 x + 2 4 2
a) Vẽ hai đồ thị (P) và (d) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Bài 2: (1.5 điểm) Cho phương trình: 2
2x + 7x − 5 = 0 có 2 nghiệm x và x . 1 2
Không giải phương trình, hãy tính giá trị biểu thức: 𝐴𝐴 = (𝑥𝑥1 − 5𝑥𝑥2)(𝑥𝑥2 − 5𝑥𝑥1)
Bài 3: (1.5 điểm) Bạn Mai dự định để dành tiền mua quà nhân ngày 8/3 cho
mẹ nên đã bỏ heo đất. Hôm đó bạn đập heo đất và đếm được có tất cả 40 tờ
tiền loại 5000 đồng và 10000 đồng. Vì tính mua cho mẹ cái áo ấm có giá 350
000 đồng nên bạn Mai xin ba thêm 25000 đồng. Hỏi bạn Mai để dành được bao
nhiêu tờ tiền mỗi loại?
Bài 4: (1.5 điểm) Một công ty giao cho cửa hàng 100 hộp khẩu trang y tế để bán
ra thị trường. Lúc đầu cửa hàng bán 29 hộp khẩu trang với giá bán một hộp khẩu
trang là 50 000 đồng. Do nhu cầu của thị trường nên từ hộp khẩu trang thứ 30 đến
hộp khẩu trang thứ 70 mỗi hộp khẩu trang có giá bán tăng 15% so với giá lúc đầu,
từ hộp khẩu trang thứ 71 đến hộp khẩu trang thứ 100 mỗi hộp khẩu trang có giá
bán giảm 10% so với giá lúc đầu.
a) Hỏi số tiền cửa hàng thu được khi bán 100 hộp khẩu trang là bao nhiêu ?
b) Biết rằng: với số tiền thu được khi bán 100 hộp khẩu trang, sau khi trừ đi
10% tiền thuế giá trị gia tăng VAT cửa hàng vẫn lãi 1 641 750 đồng. Hỏi mỗi hộp
khẩu trang công ty giao cho cửa hàng có giá là bao nhiêu?
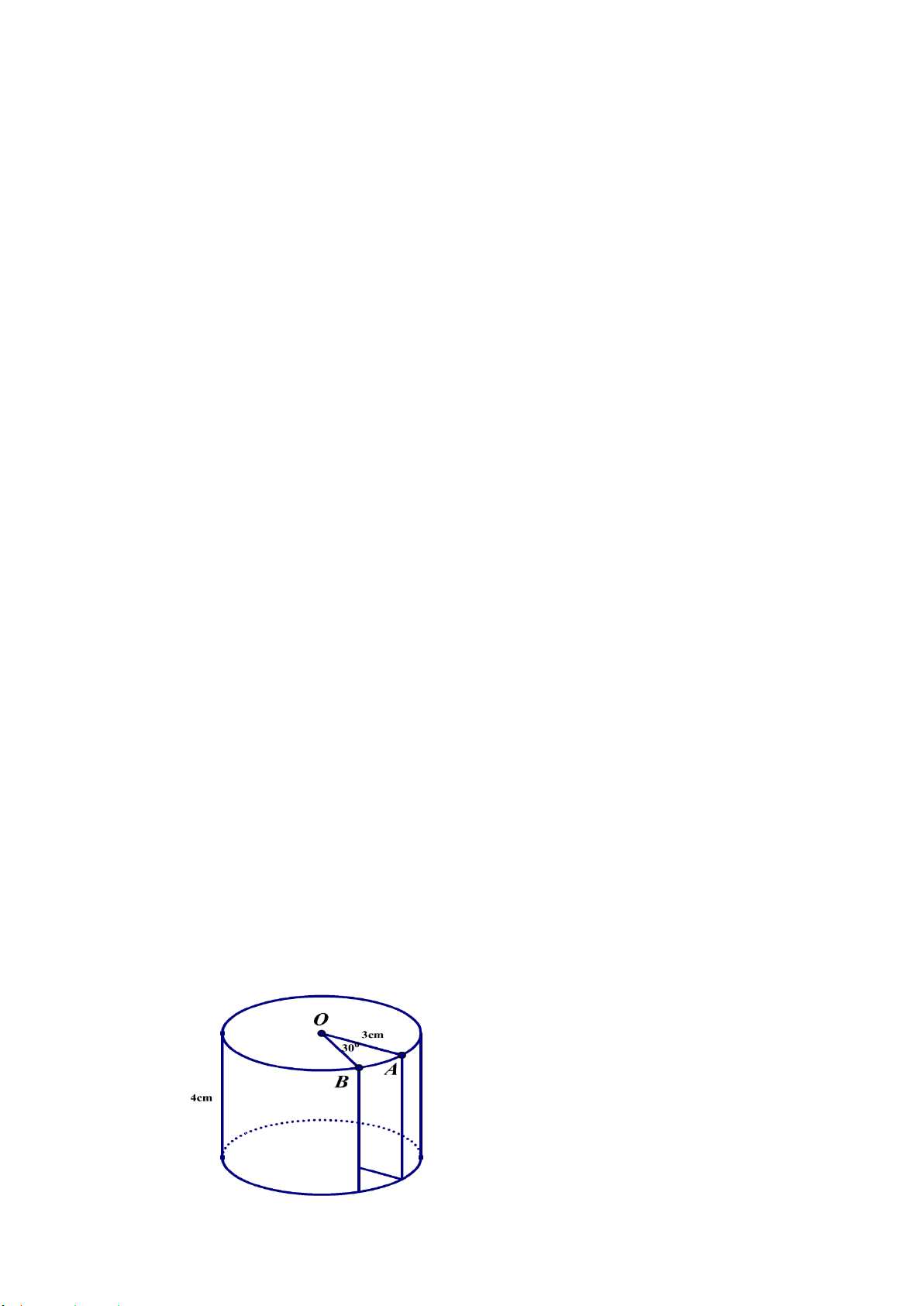
Bài 5: (1 điểm) Một ly nước dạng hình trụ có chiều cao là 15 cm, đường kính
đáy là 5 cm, lượng nước tinh khiết trong ly cao 10 cm.
a) Lượng nước được chứa trong ly là bao nhiêu centimet khối ?
b) Người ta thả vào ly nước 5 viên bi hình cầu có cùng thể tích, đồng chất
và ngập hoàn toàn trong nước làm nước trong ly dâng lên bằng miệng ly. Hỏi
thể tích của mỗi viên bi là bao nhiêu milimet khối (Giả sử độ dày của ly, đế ly là không đáng kể).
Cho biết công thức tính thể tích hình trụ là: V = 𝜋𝜋r2 h
Trong đó r là bán kính đáy, h là chiều cao hình trụ, 𝜋𝜋 ≈ 3,14
Công thức tính thể tích hình cầu là V = 4 𝜋𝜋R3 3
Trong đó R là bán kính của hình cầu
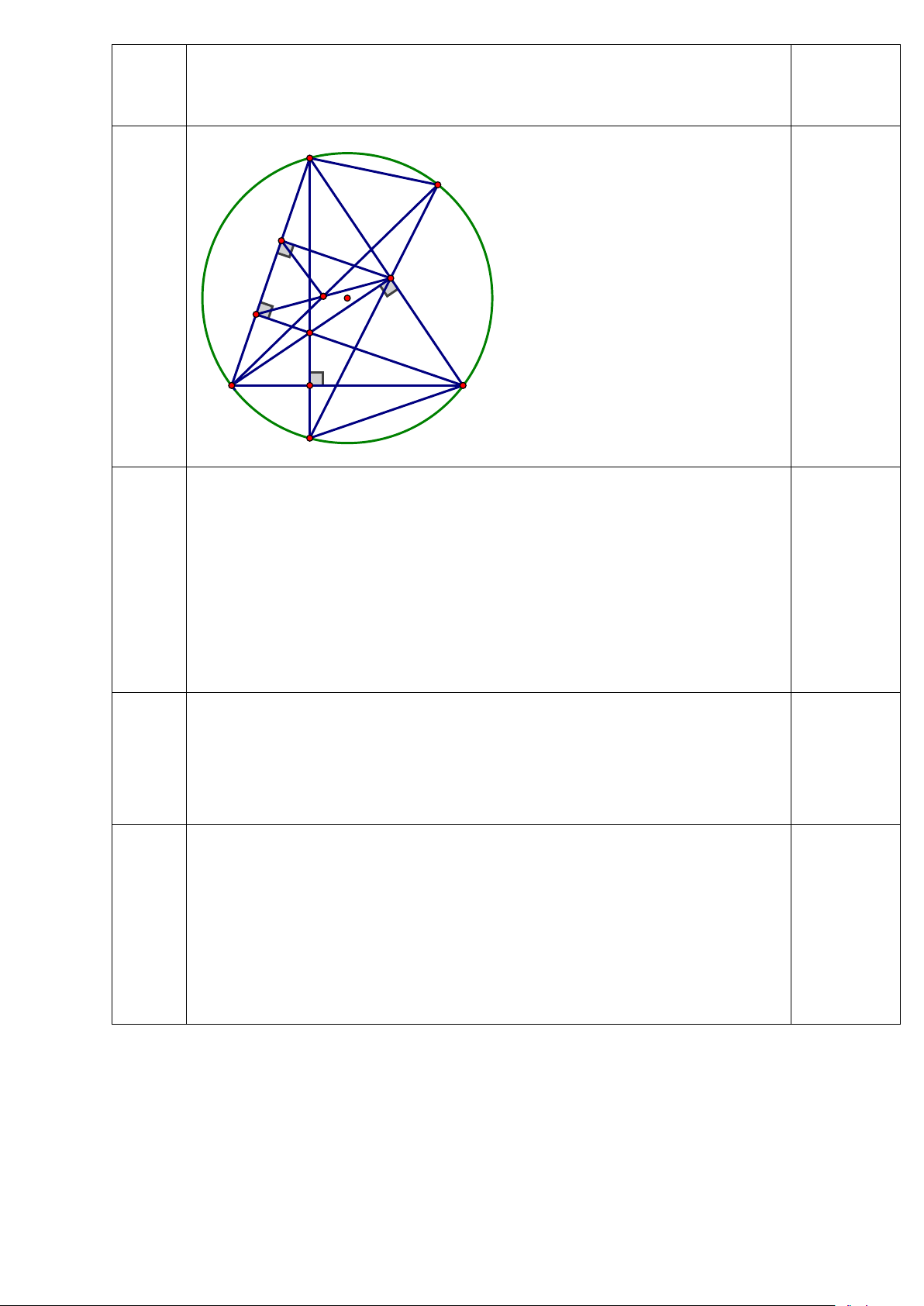
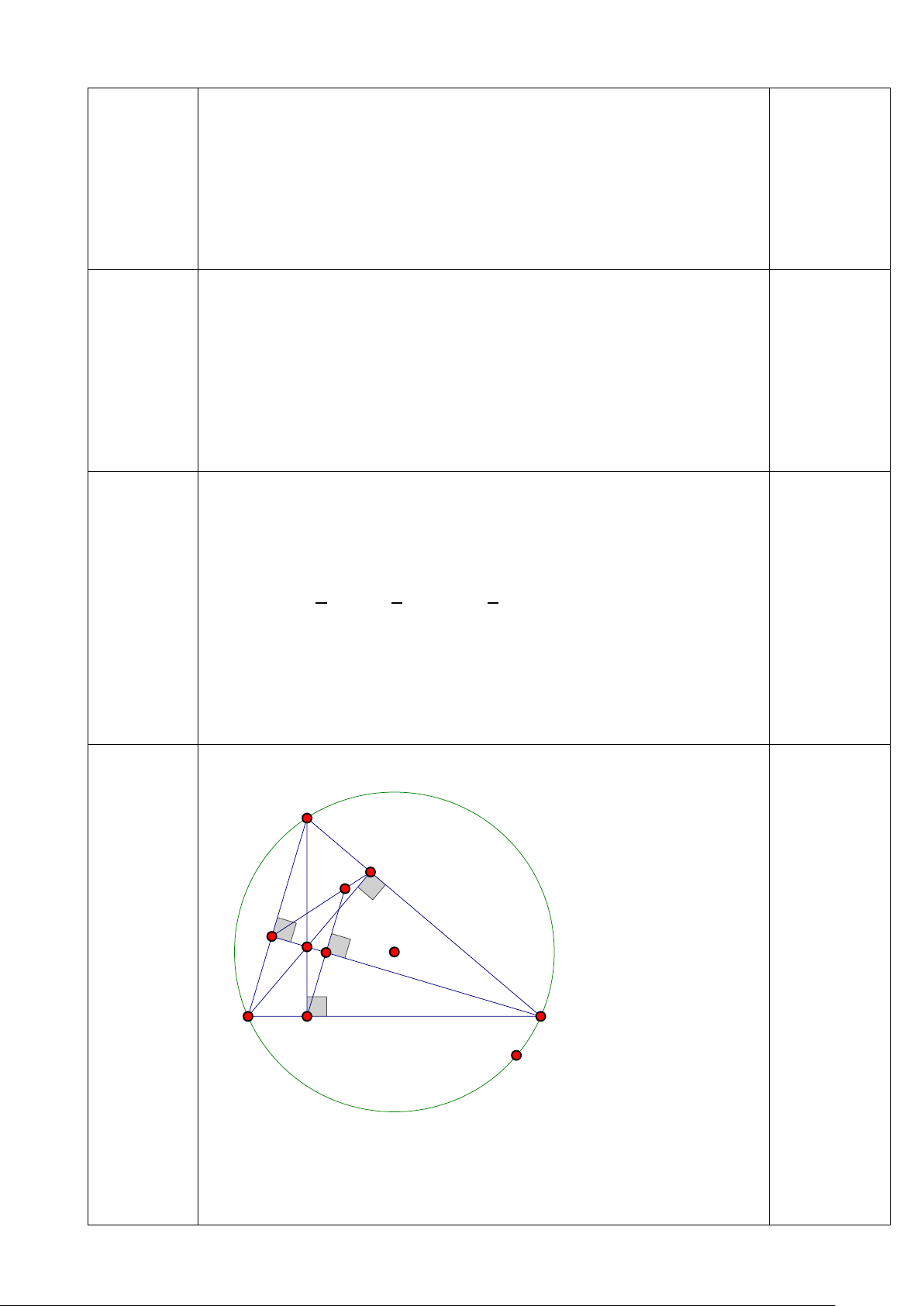
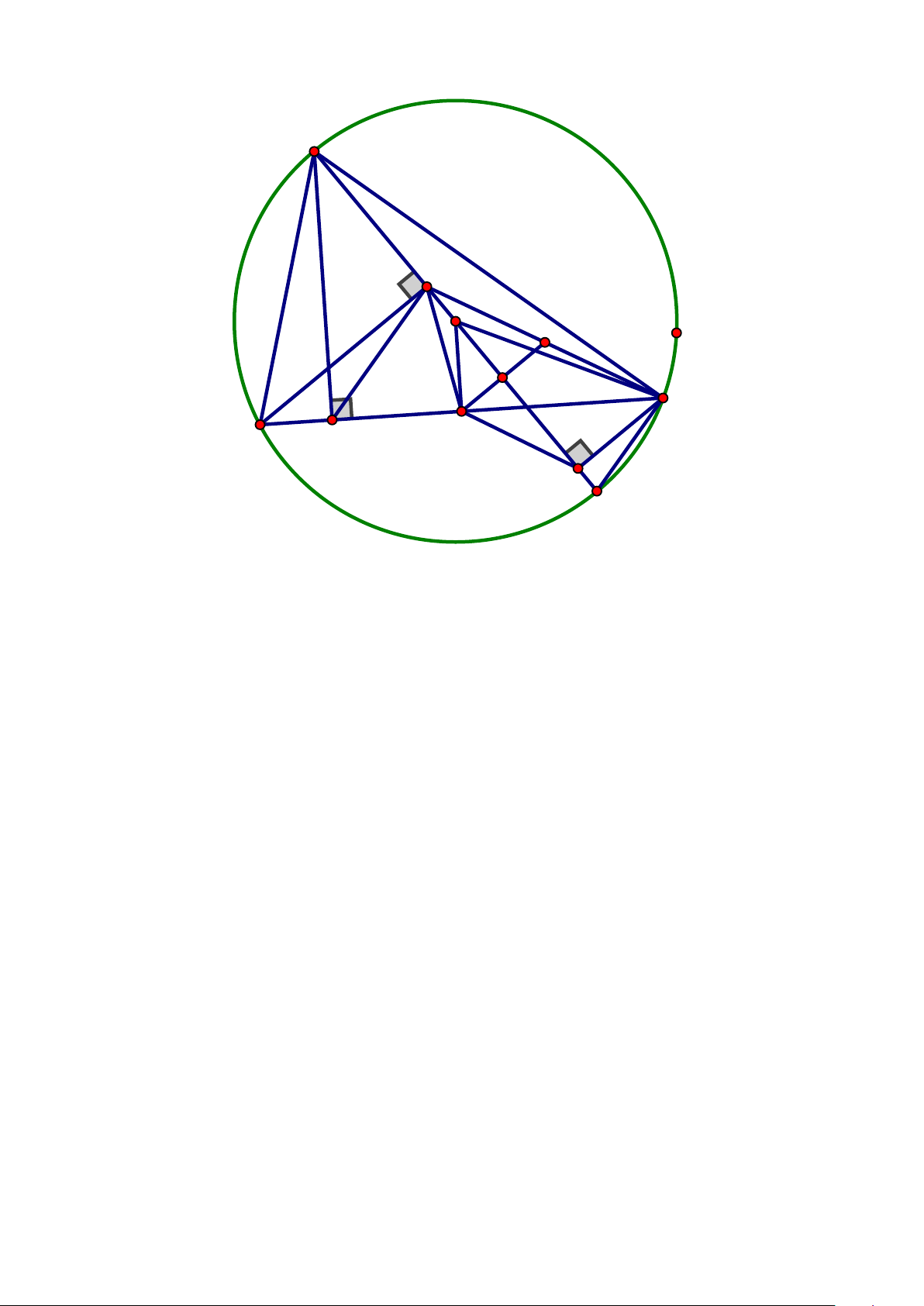
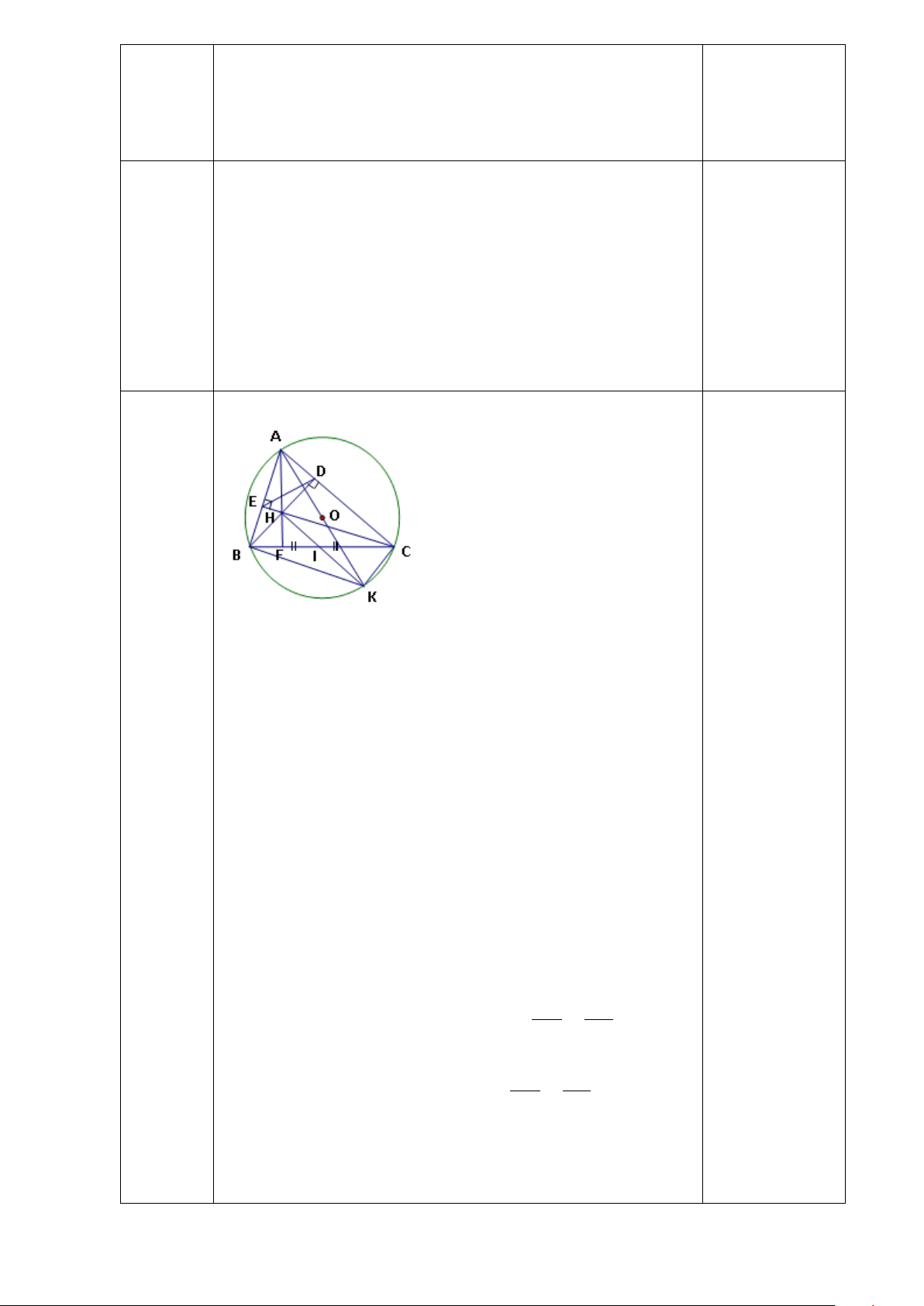
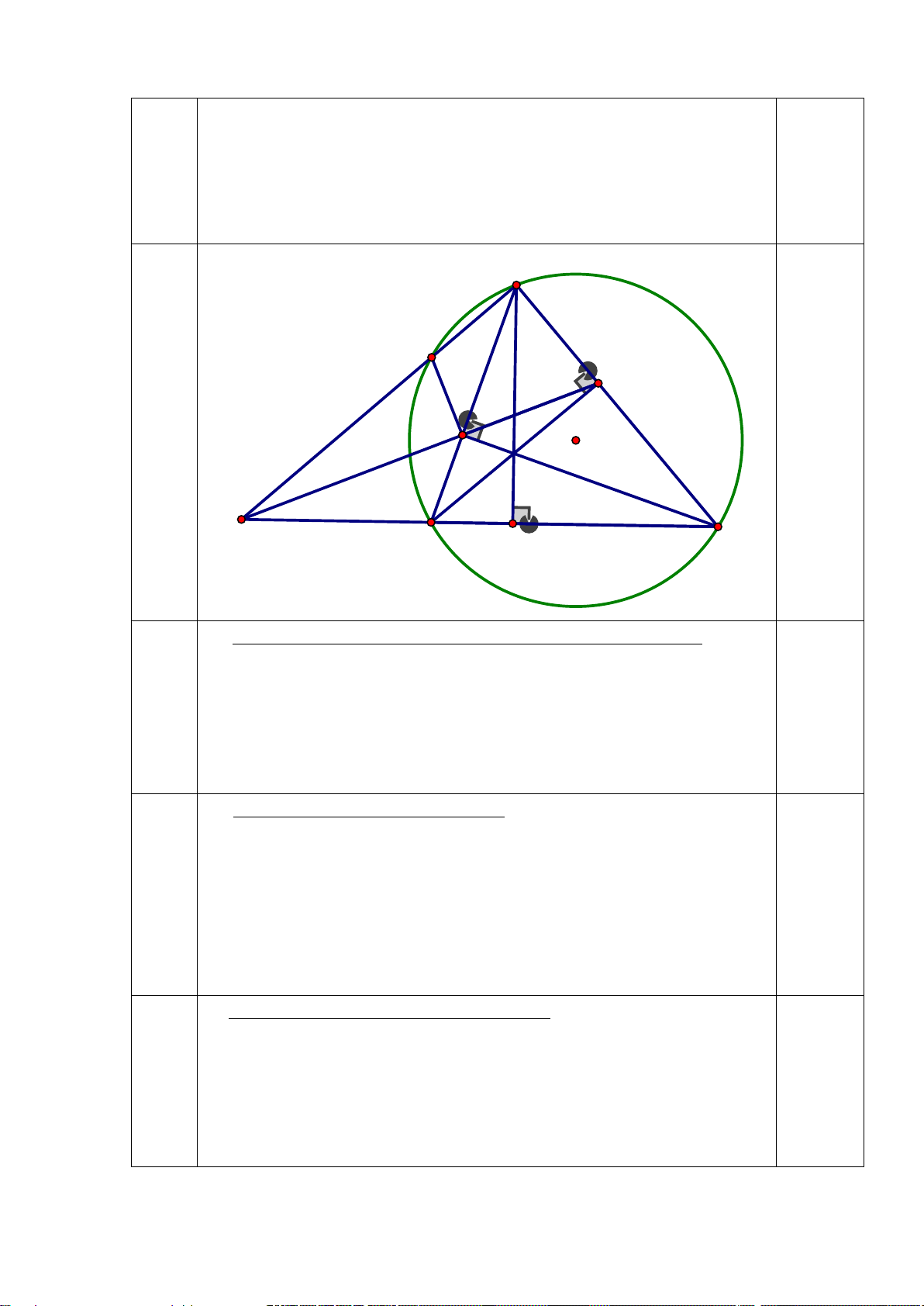
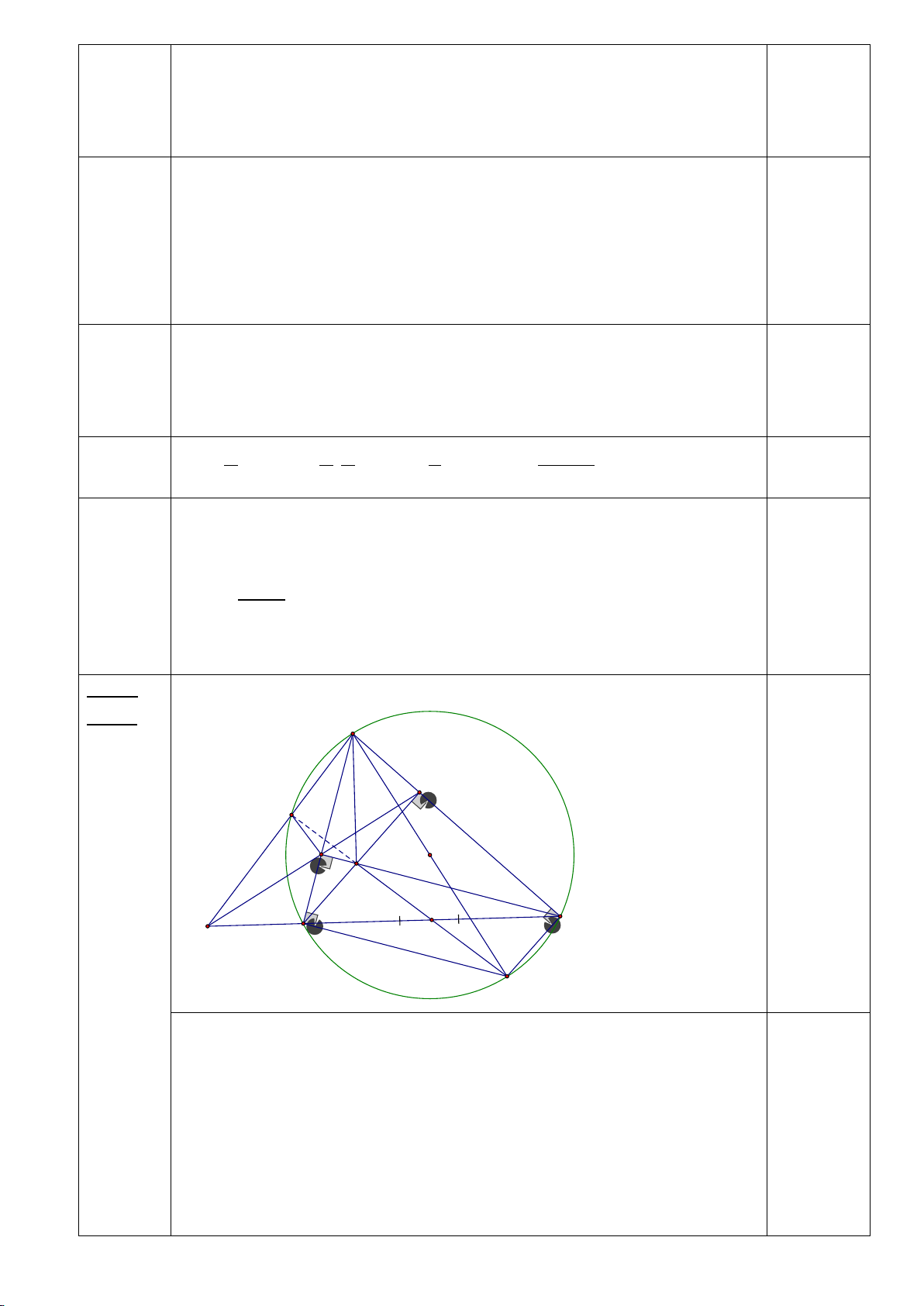
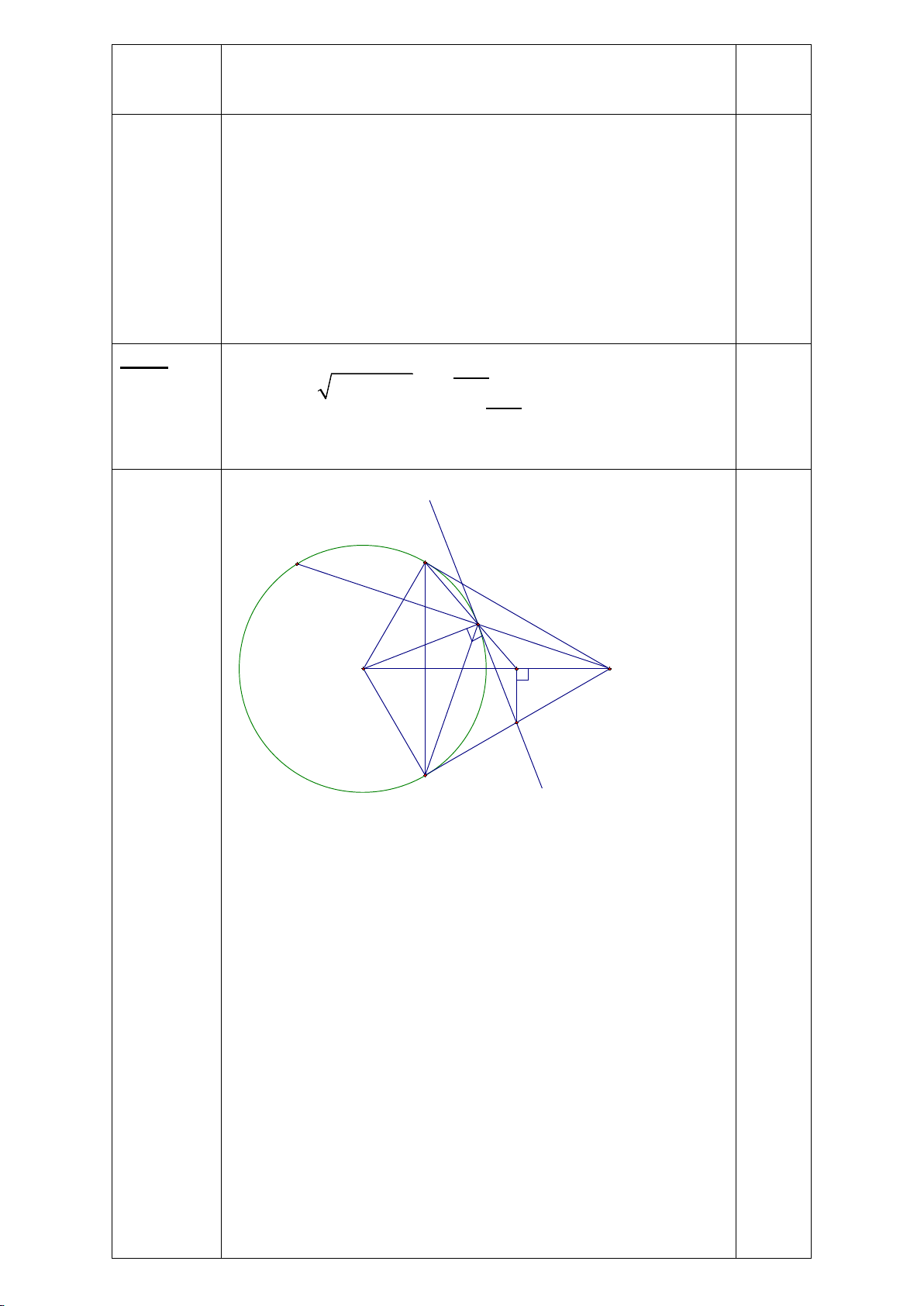
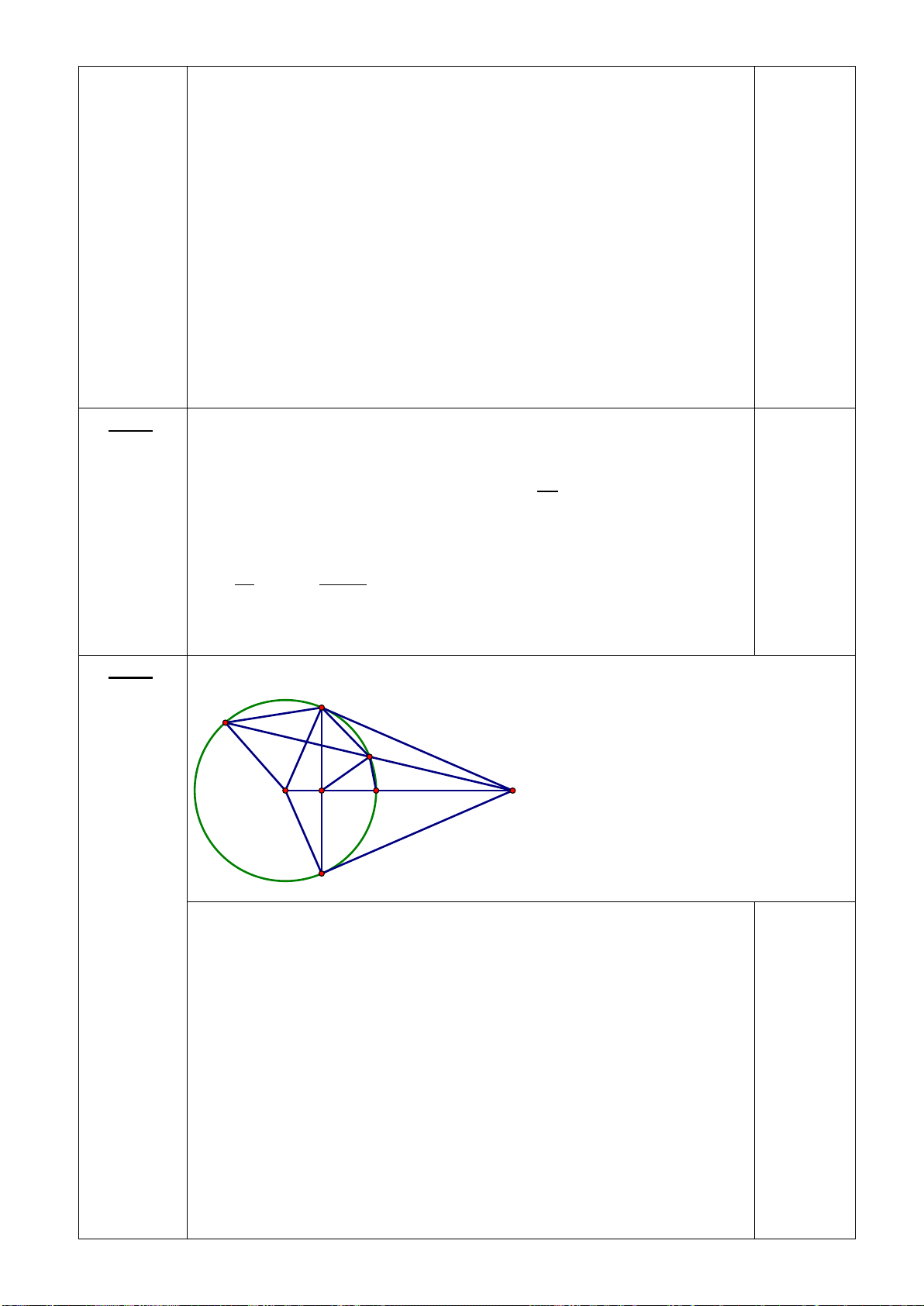
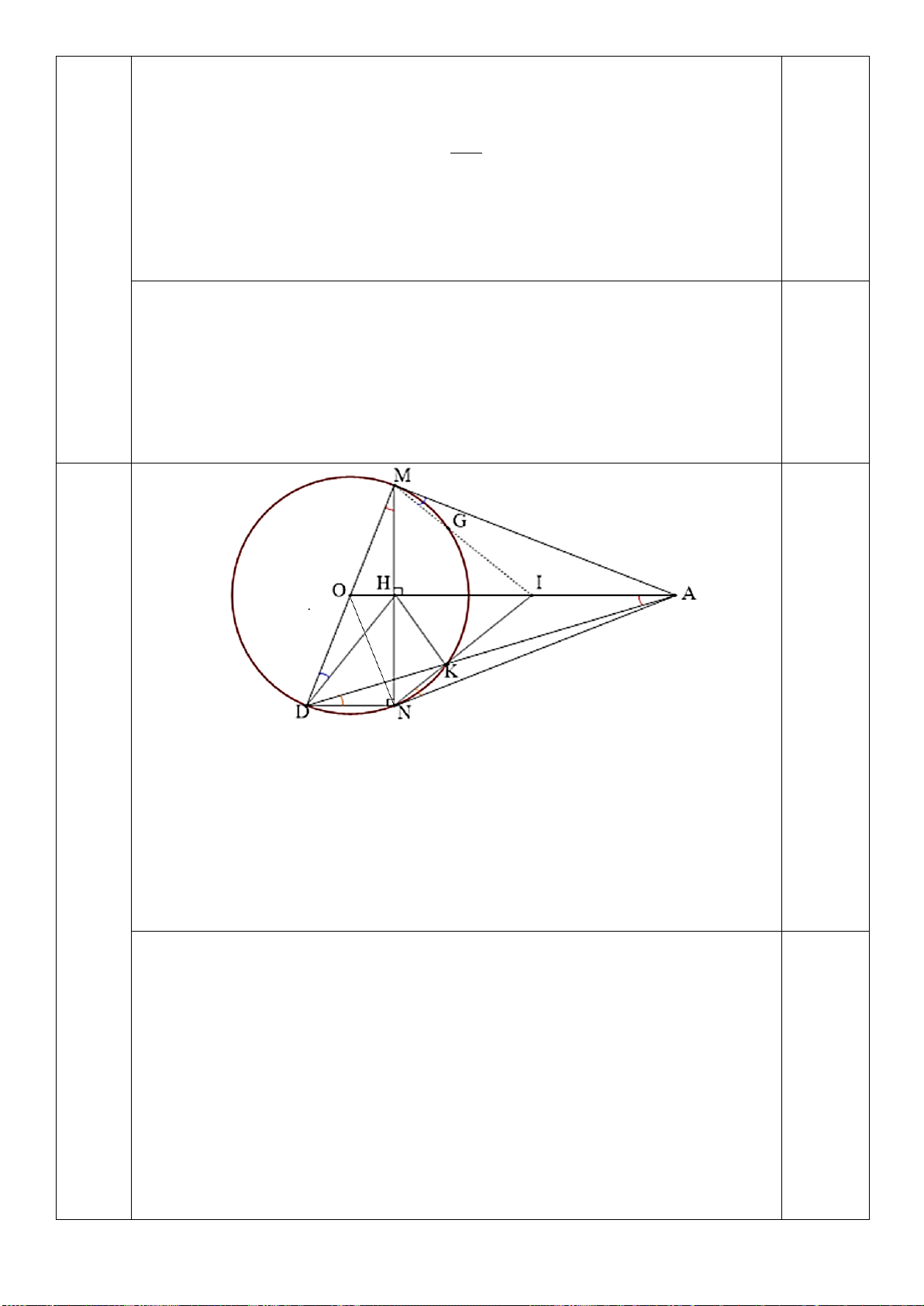
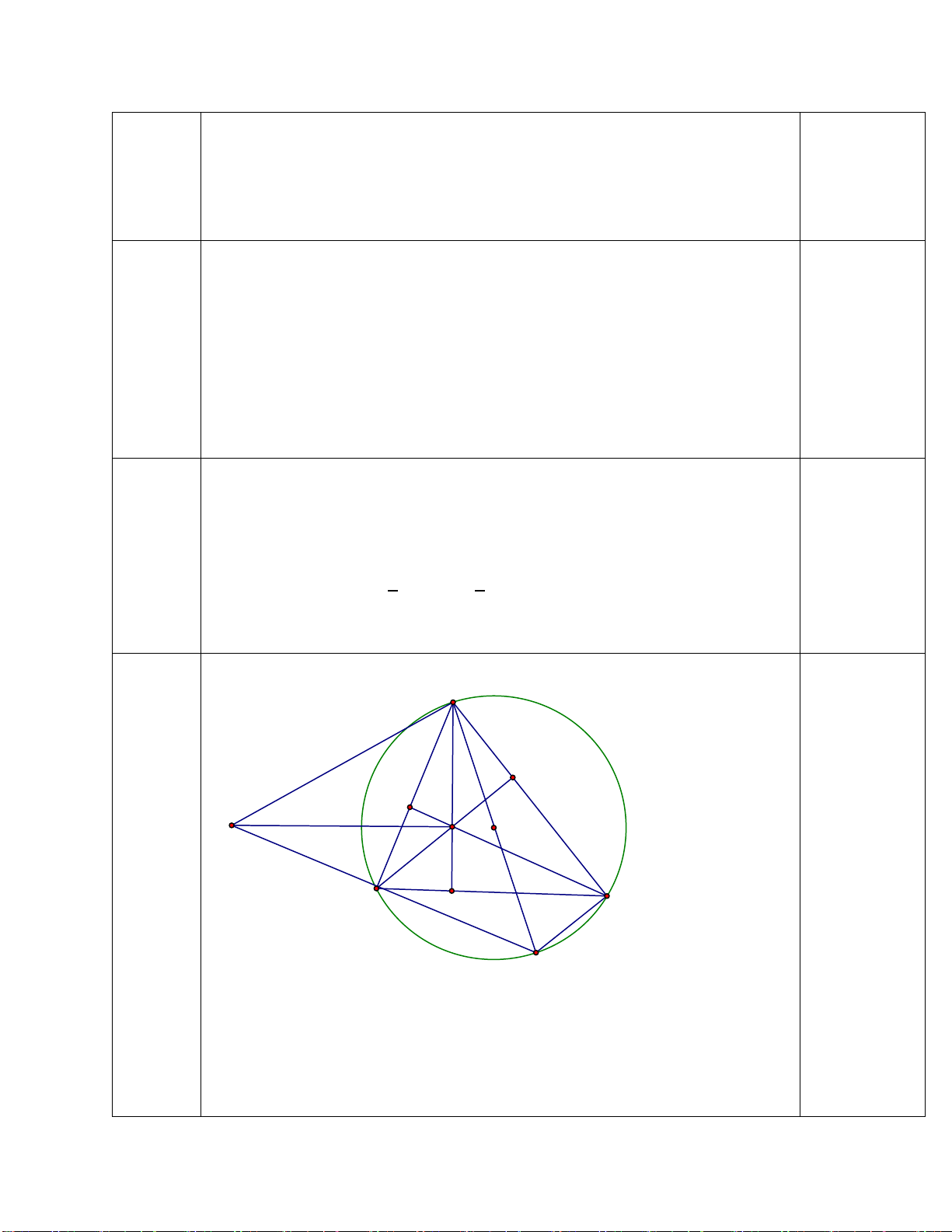
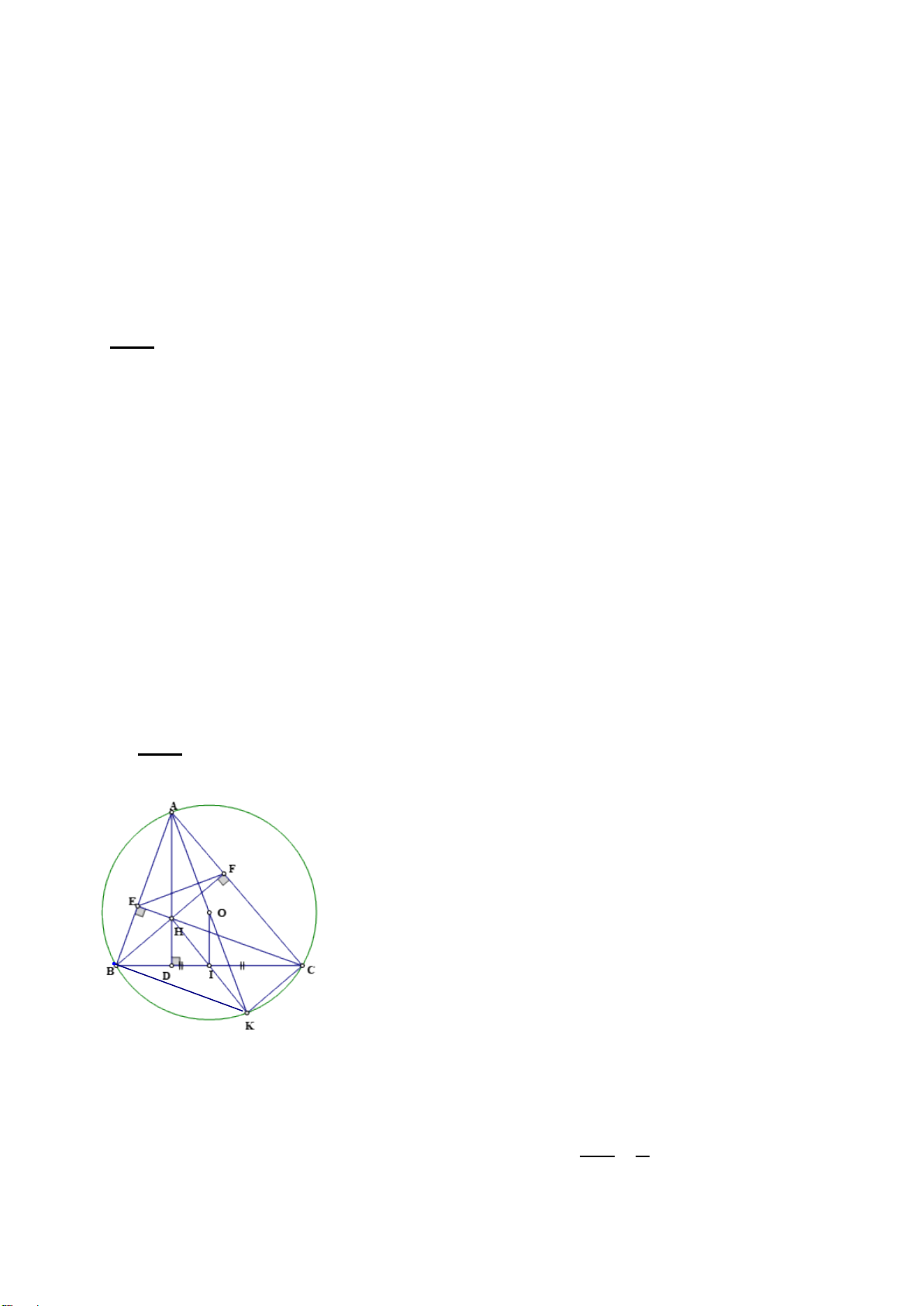
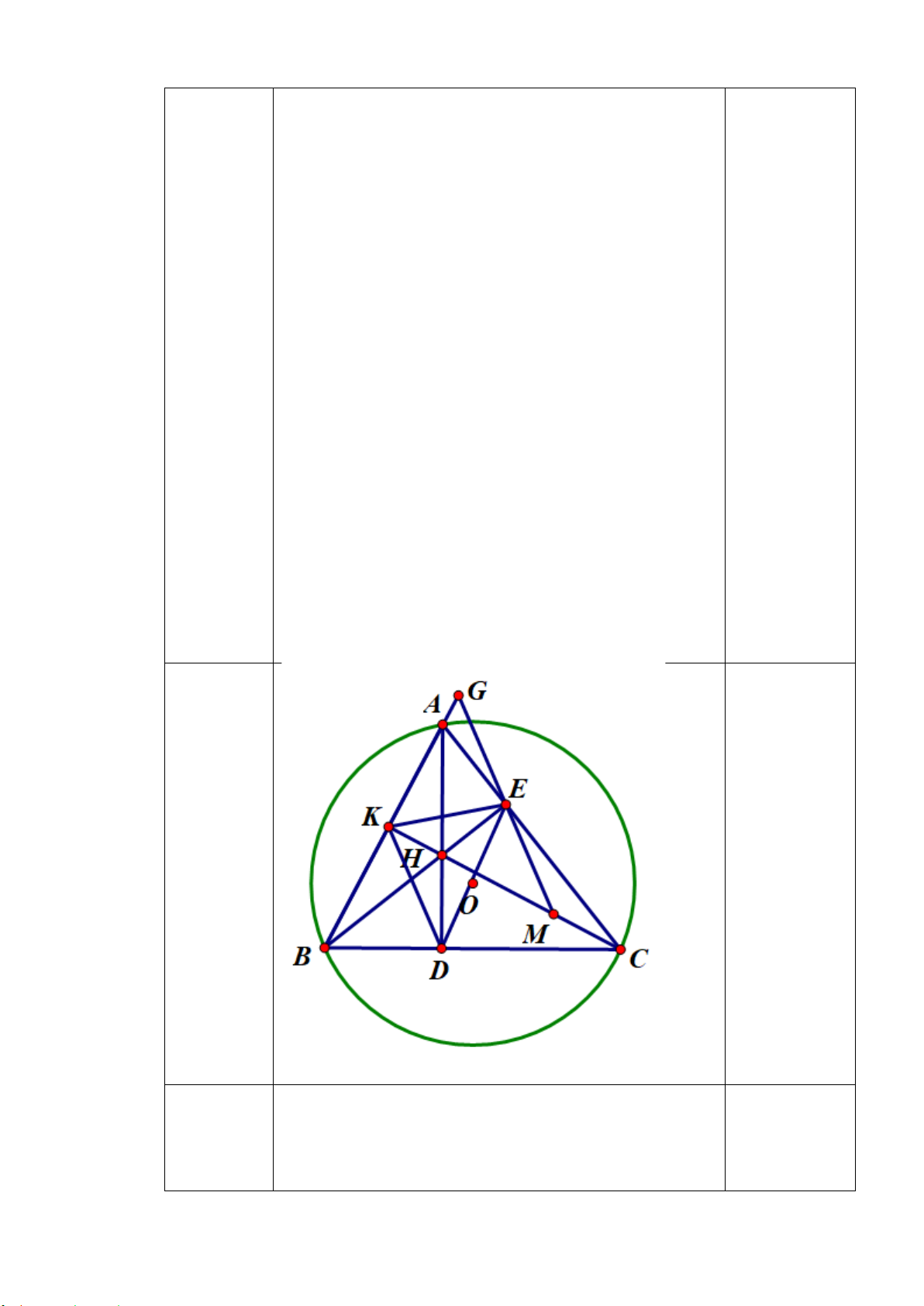
Bài 6: (2.5 điểm) Cho ∆ABC (AB < AC) nội tiếp (O;R) có ba đường cao AD, BE, BF cắt nhau tại H
a) Chứng minh tứ giác BFEC nội tiếp, tứ giác CEHD nội tiếp
b) Tia AD cắt đường trong tâm O tại K ( K ≠ A). Tia KE cắt (O) tại M ( M
≠ K). Chứng minh 𝐵𝐵𝐵𝐵𝐵𝐵 � = 𝐵𝐵𝐵𝐵𝐵𝐵 �
c) Gọi I là giao điểm của BM và EF. Qua E vẽ đường thẳng vuông góc với
AB tại S. Chứng minh tứ giác ASIM nội tiếp
------------------HẾT------------------
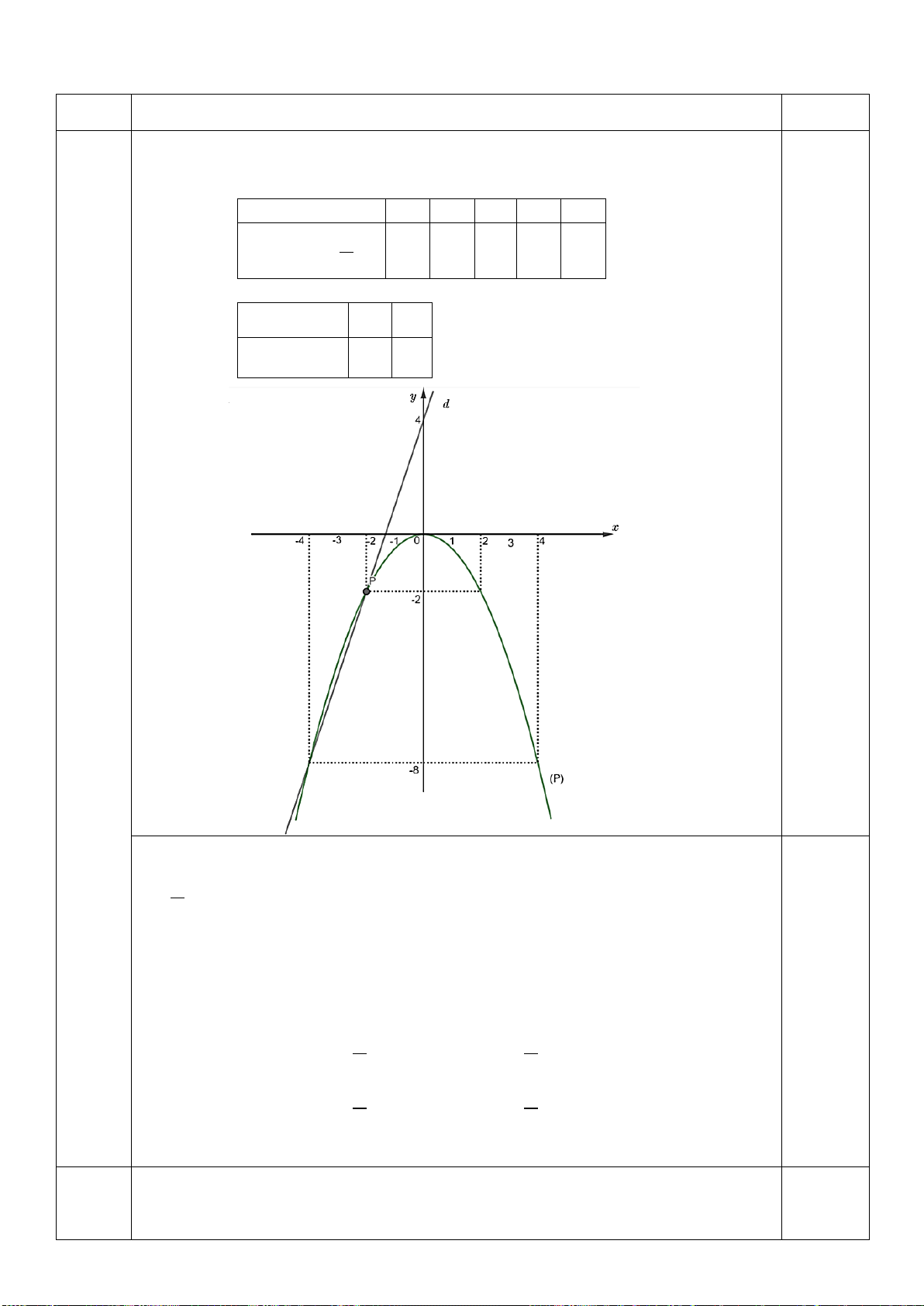
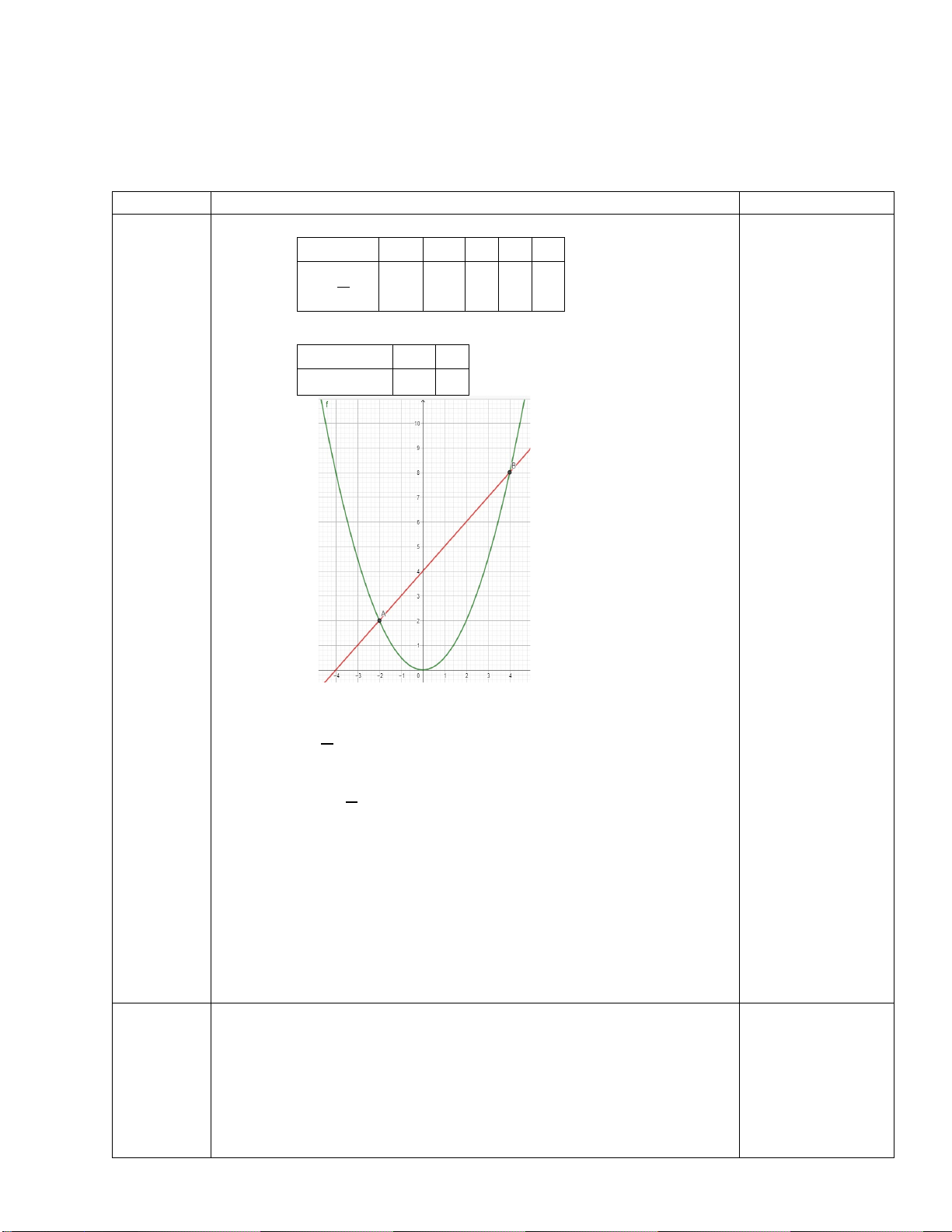
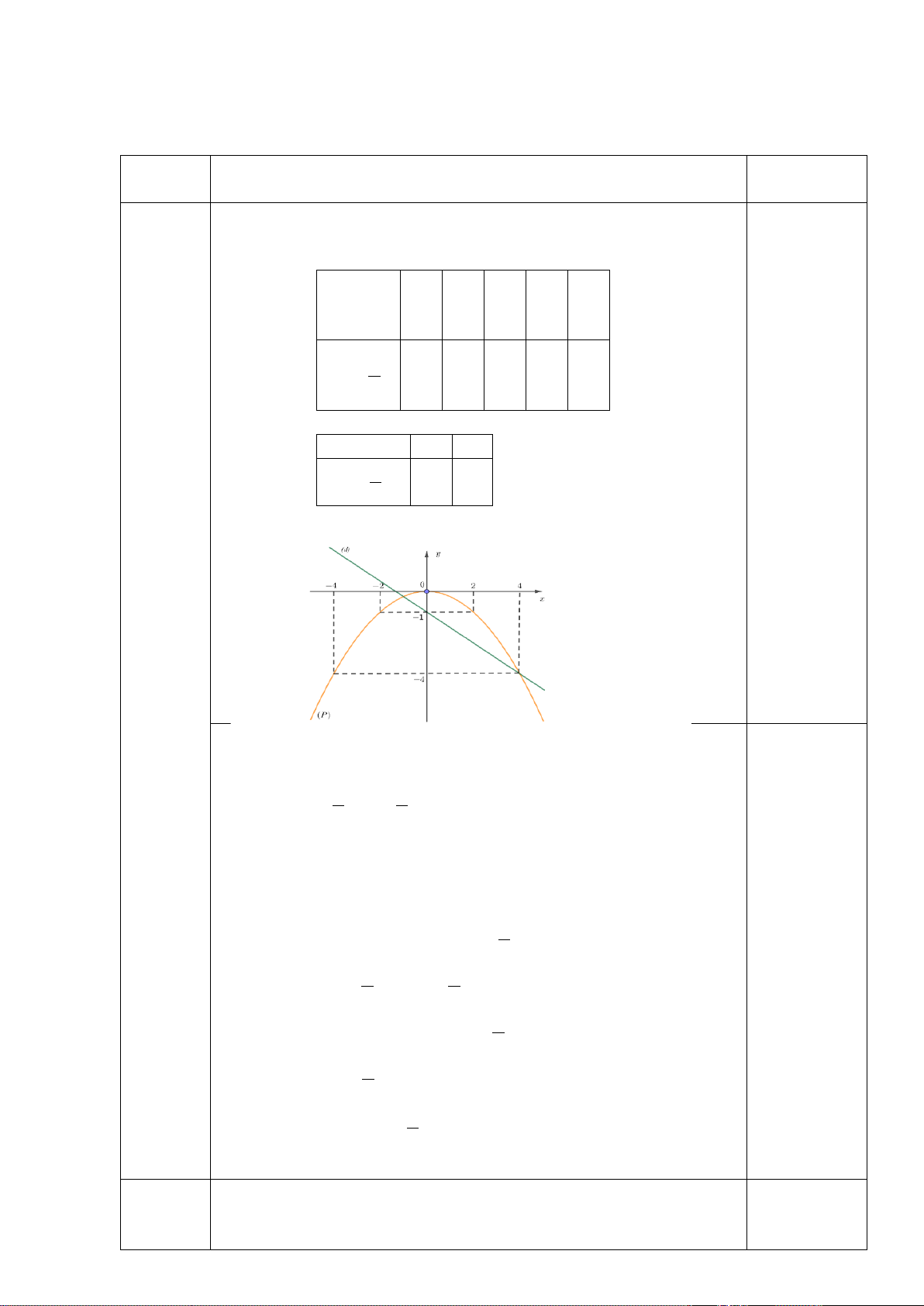
HƯỚNG DẪN CHẤM TOÁN 9 Nội dung Điểm Bài 1 (2 đ)a x 4 2 0 2 4 0,25đ 1 2
(P) : y x 4 1 0 1 4 4 x 0 4 1
(d) : y x 2 2 0 0,25đ 2 0,25đ + 0,25đ b
Phương trình hoành độ giao điểm của (P) và (d) là: 1 −1 4x2 = 2 x + 2 1 1 0,5đ ⟺ 4x2 + 2x − 2 = 0
Giải phương trình ta được: x1 = 2 ⇒ y1 = 1 x2 = −4 ⇒ y2 = 4
Vậy toạ độ giao điểm của (P) và (d) là (2; 1) và (-4; 4) 0,5đ Bài
Theo hệ thức Vi-ét ta có : 2(1,5 đ) 0,25đ −b 7 x + x − = = 1 2 a 2 0,25đ c 5 x x − = = 1 2 a 2 Khi đó : 𝐴𝐴 = (𝑥𝑥
1 − 5𝑥𝑥2)(𝑥𝑥2 − 5𝑥𝑥1) 0,25đ 𝐴𝐴 = 𝑥𝑥 2 2
1𝑥𝑥2 − 5𝑥𝑥1 − 5𝑥𝑥2 + 25𝑥𝑥1𝑥𝑥2 0,25đ 𝐴𝐴 = 26𝑥𝑥 2 2
1𝑥𝑥2 − 5(𝑥𝑥1 + 𝑥𝑥2 ) 0,25đ
𝐴𝐴 = 26𝑥𝑥1𝑥𝑥2 − 5[(𝑥𝑥1 + 𝑥𝑥2)2 − 2𝑥𝑥1𝑥𝑥2] 2
𝑃𝑃 = 26. −5 − 5 ��−7� − 2. −5� 2 2 2 𝑃𝑃 = −605 0,25đ 4
Bài 3 Gọi x (tờ) là số tờ tiền loại 5000 đồng
(1.5đ) Gọi y (tờ) là số tờ tiền loại 5000 đồng 0,25đ ĐK: x,y nguyên dương
Vì Mai để dành được 40 tờ tiền 0,25đ
Nên ta có phương trình : x+y = 40 (1)
Vì Mai tính mua cho mẹ cái áo ấm có giá 350000 đồng nên bạn
Mai xin ba thêm 25000 đồng 0,25đ
ta có phương trình : 5000x + 10000y = 350 000- 25000 ( 2)
Từ (1) và (2) ta có hệ phương trình : x+y = 40 5000x + 10000y = 325 000
Giải hệ phương trình ta được : x =15, y = 25 0,25đ
Vậy Mai để dành được 15 tờ 5000 đồng và 25 tờ 10 000 đồng
Bài 5 a) Số tiền mua 29 hộp đầu tiên
(1.5đ) 29. 50 000 = 1 450 000 (đồng) 0,25đ
Số tiền mua 41 hộp (từ hộp 30 đến hộp 70)
41. 50 000. 115% = 2 357 500 (đồng) 0,25đ
Số tiền mua 30 hộp (từ hộp 71 đến hộp 100)
30. 50 000. 90% = 1 350 000 ( đồng) 0,25đ
Hỏi số tiền cửa hàng thu được khi bán 100 hộp khẩu trang là
1 450 000+2 357 500+1 350 000 = 5 157 500 (đồng) 0,25đ
b) Giá 1 hộp khẩu trang công ty giao cho cửa hàng là
( 5 157 500.90% - 1 641 750) : 100 = 30 000 (đồng) 0,5đ Bài 6
a) Lượng nước chứa trong ly là : 3,14. 2,52.10= 196.25 (cm3) 0,5đ (1đ)
b) Lượng nước dâng lên chính là thể tích của cả 5 viên bi
3,14. 2,52.(15 – 10) = 98,125 (cm3)
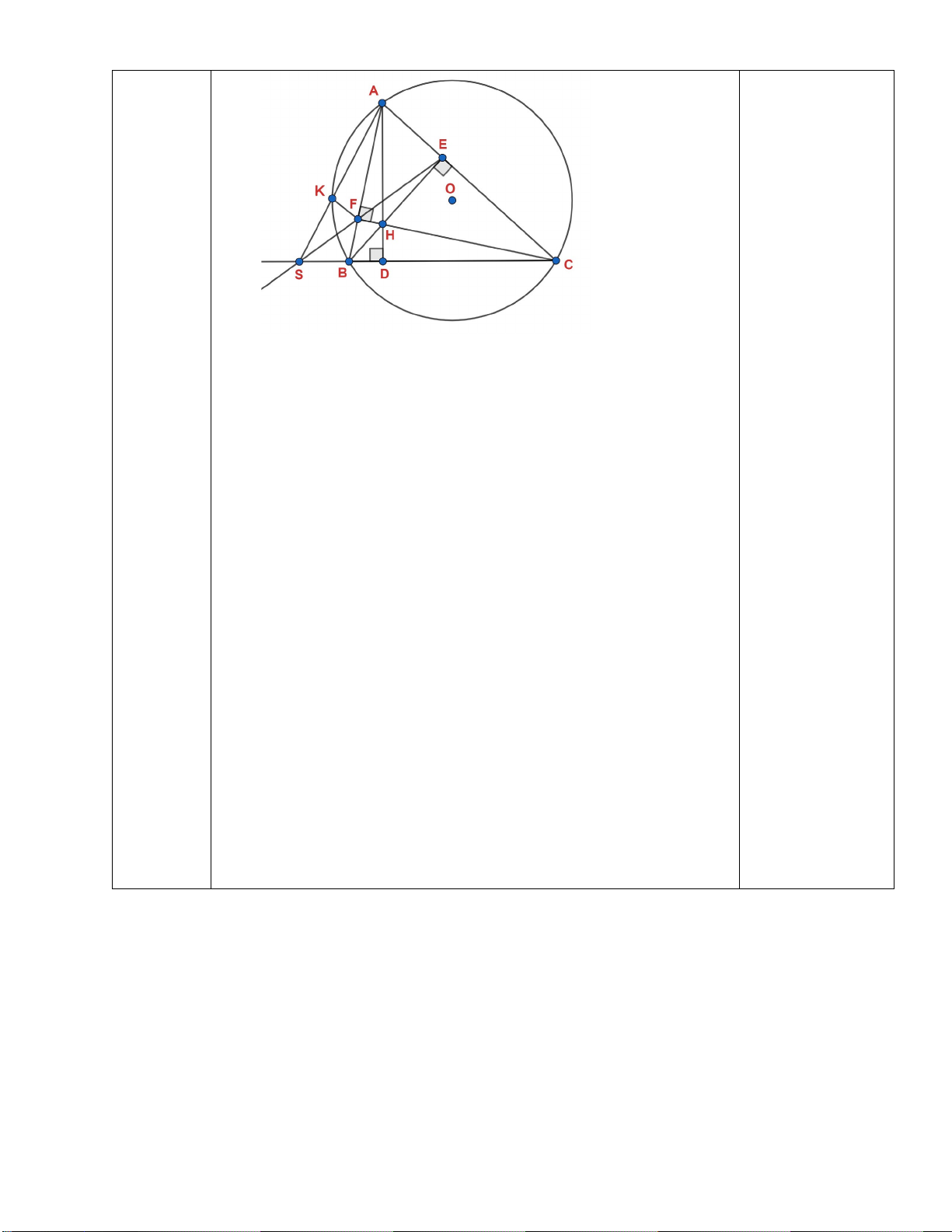
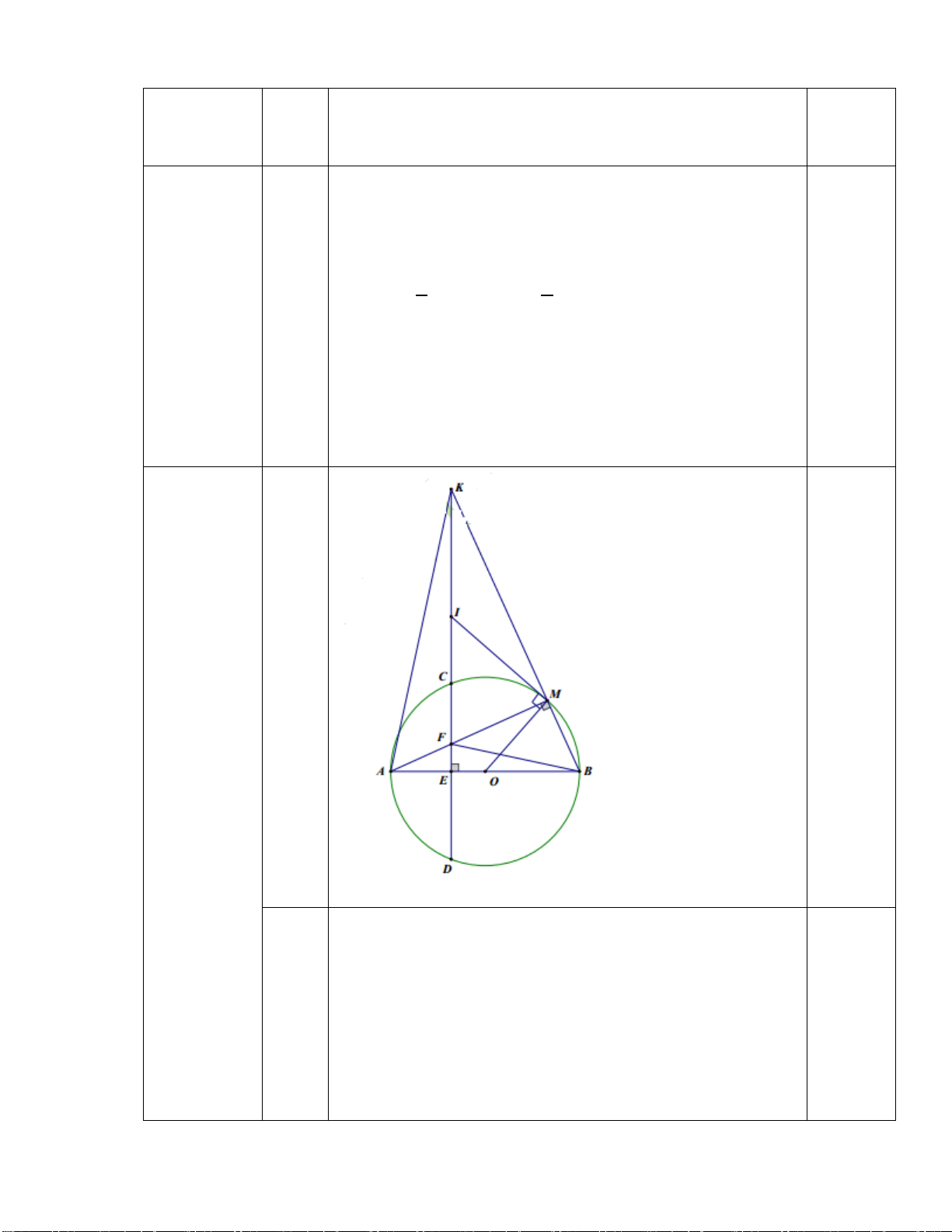
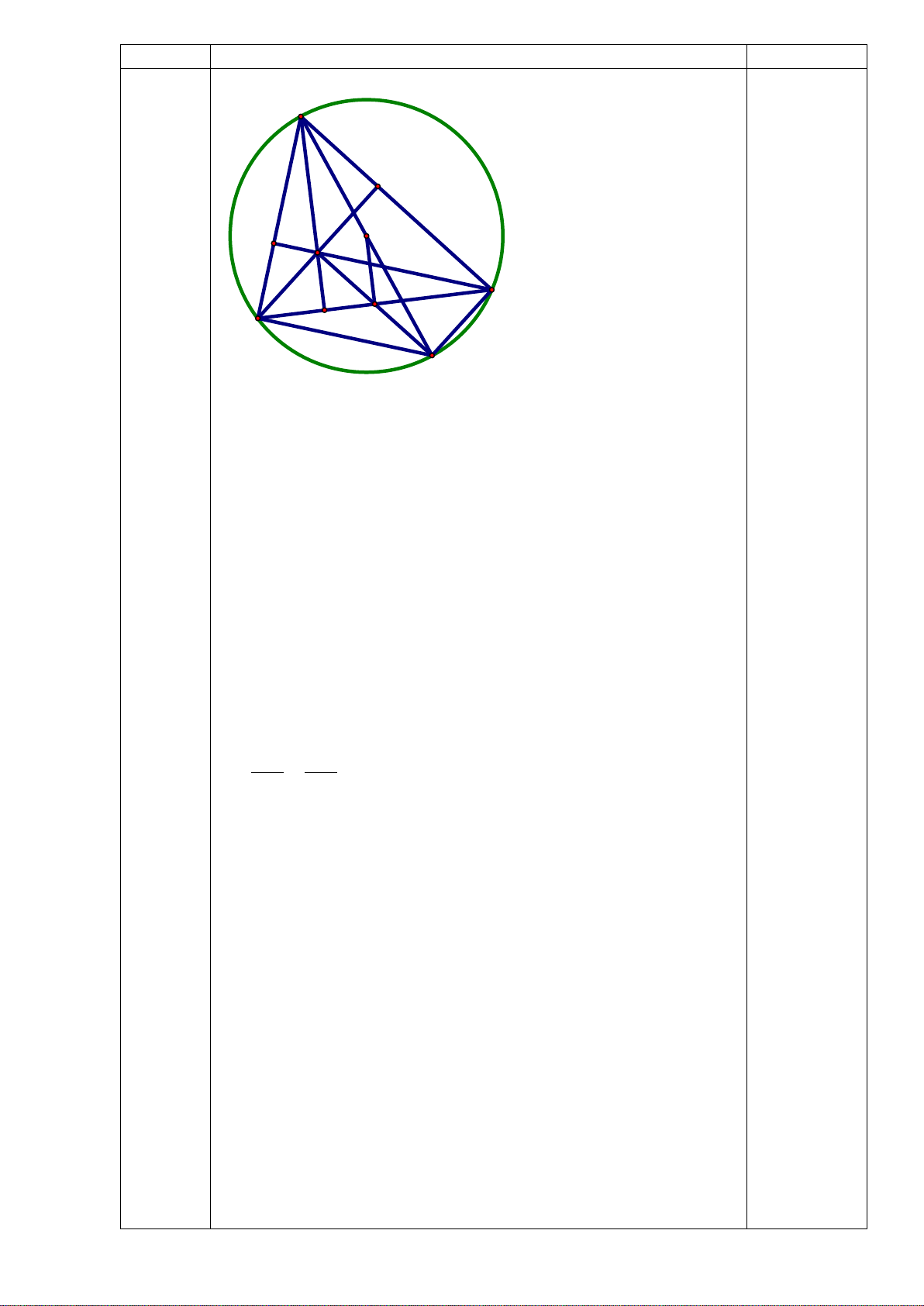
Thể tích của một viên bi 0,25đ 98,125 : 5 = 19,625 (cm3) 19,625 cm3 = 19 625 mm3 0,25đ Bài 7 A (2.5 M đ) S E F I H B D C K a Xét tứ giác BFEC có: BFC � = BEC
� = 900 ( Vì CF,BE là đường cao) 0,25đ
Mà F,E là hai đỉnh kề nhìn cạnh BC với một góc vuông Nên BFEC nội tiếp *Xét tứ giác CEHD có: 0,25đ CEH � = CDH
� = 900 ( Vì AD,BE là đường cao) CEH � + CDH � = 900 + 900 = 1800 0,25đ
Nên tứ giác CEHD nội tiếp 0,25đ b
Chứng minh tứ giác AEHF nội tiếp 0,25đ Suy ra BEF � = BAK � 0,25đ BCK � = BAK � 0,25đ Nên 𝐵𝐵𝐵𝐵𝐵𝐵 � = 𝐵𝐵𝐵𝐵𝐵𝐵 � 0,25đ c
Chứng minh 𝐵𝐵𝐵𝐵2 = 𝐵𝐵𝐵𝐵. 𝐵𝐵𝐴𝐴
Chứng minh 𝐵𝐵𝐵𝐵2 = 𝐵𝐵𝐵𝐵. 𝐵𝐵𝐵𝐵 Do đó : BS . BA = BI. BM 0,25đ
Ta chứng minh được ∆BSI ∽∆BMA
Suy ra 𝐵𝐵𝐵𝐵𝐵𝐵 � = 𝐵𝐵𝐵𝐵𝐴𝐴 �
Vậy tứ giác ASIM nội tiếp 0,25đ
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng điểm T Chủ Nội dung/Đơn vị T đề kiến thức
Nhận biết Thông hiểu Vận dụng Vận dụng cao T N TL T N TL T N TL T N TL Vẽ đồ thị hàm số 1
Đồ thị 𝑦𝑦 = 𝑎𝑎𝑥𝑥2 (P) và y = (Bài a) 1 hàm ax + b (d) (1,0đ) 2đ số 1 Tìm tọa độ giao (Bài b) điểm của (P) và (d) (1,0đ) Hệ 1 thức (Bài 2) 2 Vi-et Hệ thức Vi-et (1,5 đ) 1,5đ và ứng dụng Giải bài toán bằng 1 cách lập hệ (Bài 3) phương trình. (1,5đ) Bài tập Dạng ứng dụng 1 1 3 ứng tăng giảm Bài 4a Bài 4b 4đ dụng (1,0đ) (0,5đ)
thực tế Dạng toán ứng 1 1 dụng hình không (Bài 5a) (Bài gian (0,5đ) 5b) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài (Bài 6b) 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100 % Tỉ lệ chung 65% 35% 100 %
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 T Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ T nhận thức Nhận Thông Vận VD
biết hiểu dụng cao Đồ thị hàm 1 số y = ax2 (Bài (P) và Vận dụng: 1a) y = ax + b
- Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ trục tọa độ 1 Đồ thị (d) hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1 giao điểm
- Vận dụng phương trình bậc hai một ẩn (Bài của (P) và
trong việc tìm tọa độ giao điểm của (P) và 1b) (d) (d). Hệ thức Thông hiểu:
- Tính được tổng, tích, x12+x22 các 1
2 Vi-et và Hệ thức Vi - ứng et
nghiệm của phương trình bậc hai một (Bài dụng
ẩn bằng hệ thức Vi-et (Biến đổi đơn 2) giản)
Giải bài toán Thông hiểu: bằng cách
- Phân tích đề bài, tìm mối quan hệ giữa lập hệ
các đại lượng cho trong đề bài, gọi ẩn, từ 1 phương
đó lập được hệ 2 phương trình bậc nhất 2 Bài 3 trình. ẩn.
- Giải hệ phương trình, đối chiếu điều
kiện để trả lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức tăng/giảm
Bài tập Dạng ứng 1 1 dụng tăng Vận dụng: Bài Bài 3 ứng
- Vận dụng kiến thức về tăng giảm, tỉ dụng giảm
số % giải quyết một số vấn đề trong 4a 4b thực tế thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện Dạng toán
tích toàn phần, thể tích của hình trụ (hoặc ứng dụng hình nón, hình cầu) 1 1
hình không Vận dụng cao: Bài Bài gian
- Vận dụng hợp lí công thức tính diện 5a 5b
tích, thể tích hình trụ (hoặc hình nón,
hình cầu) để giải quyết một số bài toán thực tiễn. 4 Hình Tứ giác nội Nhận biết: 1 học tiếp
- Nhận biết được tứ giác nội tiếp đường (Bài tròn. 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các
loại góc với đường tròn, mối quan hệ
giữa các góc, phối hợp các kiến thức để chứng minh.
- Vận dụng các phương pháp chứng 1 1
minh hai tam giác đồng dạng, chứng (Bài (Bài
minh song song, vuông góc, 3 điểm 6b) 6c)
thẳng hàng giải quyết yêu cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức
trong hình học phẳng để giải quyết yêu cầu đề bài. UBND HUYỆN CỦ CHI
ĐỀ KIỂM TRA CUỐI KÌ II NĂM HỌC : 2023– 2024 TRƯỜNG THCS AN PHÚ Môn: TOÁN 9 Thời gian : 90 Phút
(Không kể thời gian phát đề) Bài 1(2.0 điểm):
a) Vẽ trên cùng hệ trục Oxy đồ thị (P) 𝑦𝑦 = −𝑥𝑥2 và (d) y = x – 4 2
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. Bài 2. (1,5 điểm).
Cho phương trình: 2x2 + 3x – 14 = 0 có 2 nghiệm là x , x 1 2
a) Không giải phương trình, hãy tính tổng và tích 2 nghiệm của phương trình.
b) Tính giá trị của biểu thức sau: 2 2
P = x + x − 5x x 1 2 1 2
Bài 3: (1,5 điểm)
Bà Hai đi chợ mua 23 kg xoài và ổi hết 420 000 đồng. Biết giá 1 kg xoài là 20 000 đồng,
giá 1 kg ổi 12000 đồng. Hỏi bà Hai đã mua bao nhiêukg xoài, bao nhiêu kg ổi?
Bài 4: (1,5 điểm)
Thực hiện chương trình khuyến mãi “Ngày chủ nhật vàng”, một cửa hàng điện máy giảm
giá 50% trên một tivi cho lô hàng tivi 50 cái với giá bán lẻ trước đó là 6500000 đồng/cái.
Đến trưa cùng ngày thì cửa hàng đã bán được 30 cái và cửa hàng quyết định giảm thêm
10% nữa (so với giá đã giảm lần 1 ) cho số tivi còn lại.
a/ Tính số tiền mà cửa hàng thu được khi bán hết lô hàng 50 tivi.
b/ Biết rằng giá vốn là 3000 000 đồng/cái tivi. Hỏi cửa hàng lời hay lỗ khi bán hết lô hàng tivi đó. Bài 5:(1.0 điểm )
Một xe chở xăng dầu, bên trên có chở một bồn chứa hình trụ chiều dài 2,6 mét và
đường kính đáy là 1,4 mét .
a./Thể tích bồn chứa hình trụ
b./Theo tiêu chuẩn an toàn, thì bồn chỉ chứa tối đa 80% thể tích khi xe di chuyển trên
đường. Vậy bồn đó có thể chứa được nhiều nhất là bao nhiêu lít nhiên liệu ? (làm tròn đến
hàng đơn vị).Cho biết: 2
V = π.r .h Bài 6: (2,5 điểm)
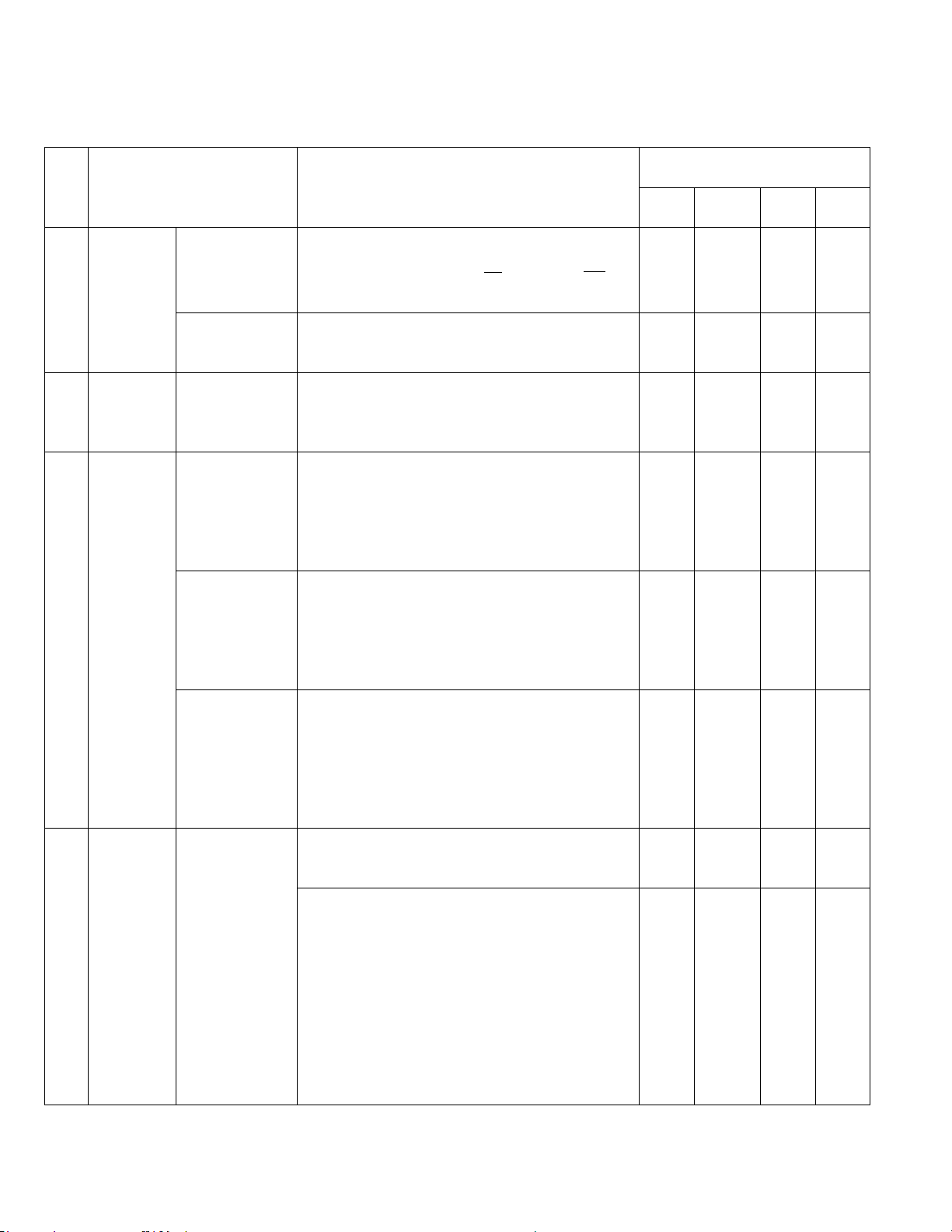
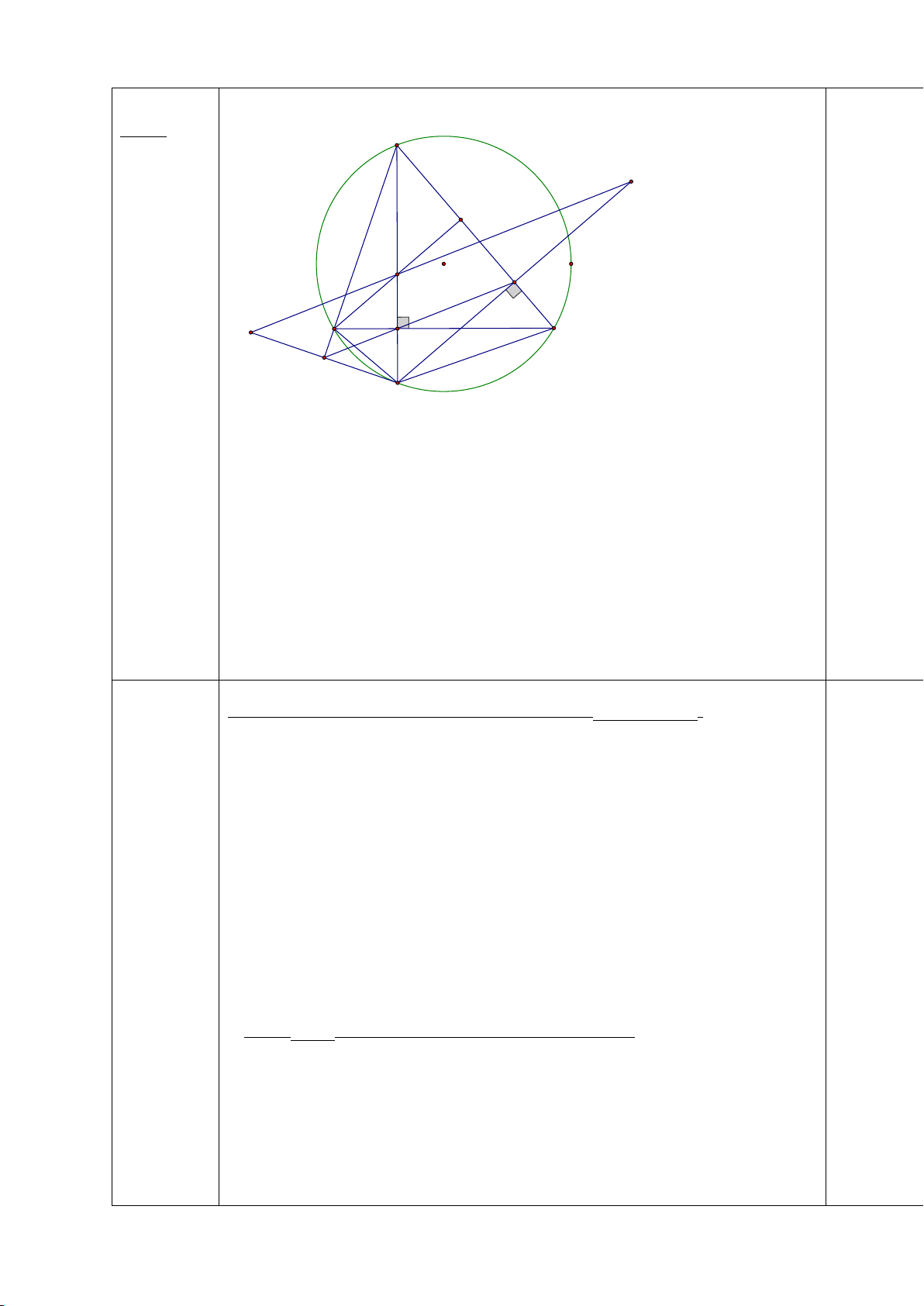
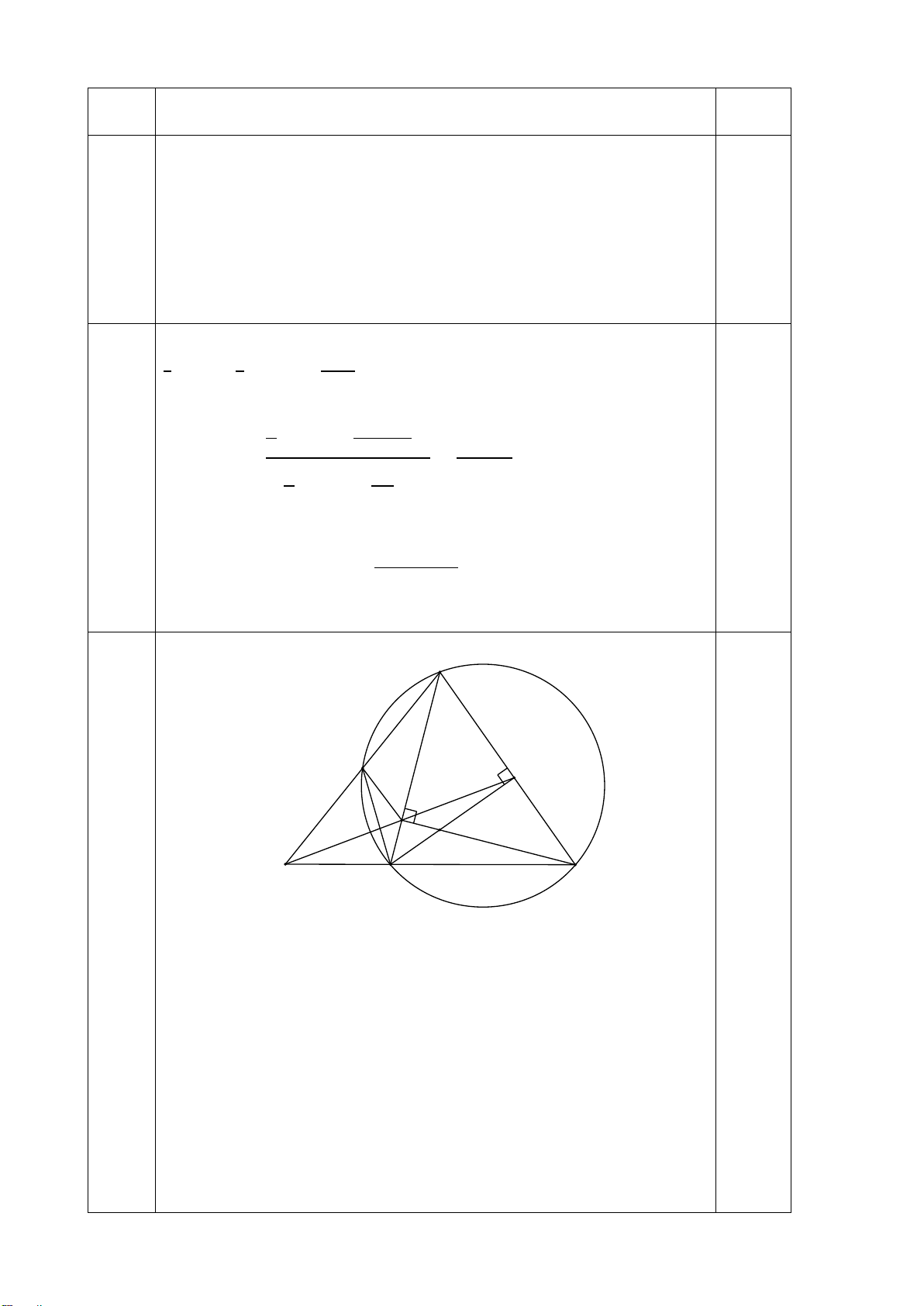
Từ điểm M ở ngoài đường tròn (O; R) vẽ cát tuyến MCD (MC < MD) và hai tiếp
tuyến MA và MB đến (O) (A, B là các tiếp điểm)
a) Chứng minh : 4 điểm M, A, O, B cùng thuộc một đường tròn, hãy xác định tâm I của đường tròn.
b) Gọi H là giao điểm của AB và MO. Chứng minh: MH.MO=MC.MD
c) Chứng minh: HB là phân giác CHD .
..............Hết................... UBND HUYỆN CỦ CHI
HƯỚNG DẪN CHẤM KIỂM TRA CUỐI KÌ TRƯỜNG THCS AN PHÚ NĂM HỌC 2023-2024 Môn: TOÁN 9 Thời gian: 90 phút Thứ tự Lời giải Thang điểm bài (điểm) Bài 1
a)Vẽ trên cùng hệ trục Oxy đồ thị
(2,0 điểm) (P) y = -x2và (d) y = x – 4 2 0,5 điểm Bảng giá trị đúng Vẽ đúng (P) và (D) 0,5 điểm 0,5 điểm
b)Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm : −𝑥𝑥2 = x – 4 2 ⇔x2 + 2x – 8 = 0 0,5 điểm Giải ra x1 = 2; x2 = – 4
Tìm ra tọa độ giao điểm (2; – 2) và ( – 4; – 8) Bài 2:
a) Vì phương trình có hai nghiệm là x1, x2 nên:
(1,5 điểm) Theo hệ thức Vi-et b − 3 S x x − = + = = 0,5 điểm 1 2 a 2 c 14 P x . x − = = = = 7 − 1 2 a 2
b) Tính giá trị của biểu thức 0,5 điểm P = 2 2
P = x + x − 5x x 1 2 1 2
P = (x + x )2 − 2x x −5x x 1 2 1 2 1 2
= (x + x )2 − 7x x 1 2 1 2 0,5 điểm 2 = 3 − − (− ) 205 7. 7 = 2 4 Bài 3
Gọi x là số kg xoài ; y là số kg ổi ( x, y thuộc N*) 0,25 điểm
(1,5 điểm) Số tiền mua xoài 20000 x Số tiền mua ổi 12000 y 0,5 điểm
Ta được hệ phương trình � x + y = 23 0,5 điểm 20000x + 12000y = 420000 Giải hệ pt ta được x = 18 0,25 điểm y = 5 (thỏa đk)
Vậy số kg xoài 18 kg, số kg ổi: 5 kg. Bài 4:
a/ Số tiền cửa hàng thu được khi bán hết lô hàng là: (1,5 điểm) 30.50%. 6500000 +
20. (1– 10%). 50%. 6500000=156000000đ 0,5 điểm
b/ Tiền vốn là 50.3000000 = 150000000đ 0,5 điểm
Vậy cửa hàng có lời khi bán hết lô hàng tivi đó 0,5 điểm Bài 5:
Đổi đơn vị: 1,4m = 14 dm 2,6m = 26 dm
(1 điểm) a./ Bán kinh đáy bồn chứa hình trụ : R = 14 : 2 = 7dm 0,5 điểm
Thể tích bồn chứa hình trụ :
V = 3,14.49. 26 = 4 000,36 dm3
b./ Thể tích nhiên liệu được chở trên xe:
4 000,36 . 0,8 = 3200,288 dm3 ≈ 3200 lít 0,5 điểm
* Vậy nhiên liệu trên xe được chở tối đa là : 3200 lít Bài 6: A (2,5 điểm) M H O C D B
a./- Chứng minh: 4 điểm M, A, O, B cùng thuộc một
đường tròn, hãy xác định tâm I của đường tròn. 0,25 điểm Ta có 0,25 điểm = 0 MAO MBO = 90 0,25 điểm ⇒ + 0 MAO MBO =180
Tứ giác M,A,O,B nội tiếp 0,25 điểm
- Suy ra M, A, O, B cùng thuộc đường tròn có tâm I là trung điểm của MO b/ Chứng minh: MH.MO=MC.MD Chúng minh M
∆ ABcân , MH đường cao 0,25 điểm
áp dung hệ thức lượng : 2 MA = . MO MH (1) 0,25 điểm ChỨng minh: MA ∆
C đồng dạng MD ∆ A 2
⇒ MA = MC.MD(2) 0,25 điểm
Từ(1),(2) suy ra MH.MO=MC.MD 0,25 điểm
c./Chứng minh: HB là phân giác CHD chứng minh được
tam giác MHC đồng dạng tam giác MDO (c.g.c)
Chứng minh tứ giác CHOD nội tiếp ⇒ = MHC ODC 0,25 điểm = ODC OCD ⇒ = OCD OHD ⇒ = CHB DHB Suy ra HB là phân giác CHD 0,25 điểm Lưu ý:
Học sinh có cách giải khác nếu đúng thì giáo viên theo thang điểm trên để chấm. UBND HUYỆN CỦ CHI
ĐỀ KIỂM TRA CUỐI KỲ II TRƯỜNG THCS BÌNH HÒA Năm học 2023-2024 Môn: Toán 9 Ma trận đề
Thời gian làm bài: 90 phút
(Không kể thời gian ghi đề)
A. MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 Mức độ đánh giá Tổng Nội dung/Đơn vị kiến điểm TT Chủ đề thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TN TL TN TL TN TL TN TL
Vẽ đồ thị hàm số 𝑦𝑦 = 1 (Bài a) Đồ thị
𝑎𝑎𝑥𝑥2 (P) và y = ax + b (d) (1,0đ) 1 2đ hàm số 1 Tìm tọa độ giao điểm (Bài b) của (P) và (d) (1,0đ) Hệ thức 1 2 Vi-et và Hệ thức Vi-et (Bài 2) 1,5đ ứng (1,5 đ) dụng Giải bài toán bằng 1 cách lập hệ phương (Bài 3) trình. (1,5đ) Bài tập ứng Dạng ứng dụng tăng 1 1 3 4đ dụng giảm Bài 4a Bài 4b thực tế (1,0đ) (0,5đ) Dạng toán ứng dụng 1 1 hình không gian (Bài 5a) (Bài 5b) (0,5đ) (0,5đ) 1 (Bài 6a) (1,0đ) 4
Hình học Tứ giác nội tiếp 2,5đ 1 1 (Bài 6b) (Bài 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
B. BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng Đồ thị hàm số 1 y = ax2 (P) và Vận dụng: (Bài
y = ax + b (d) - Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ 1a) 1 Đồ thị trục tọa độ hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong việc (Bài (P) và (d)
tìm tọa độ giao điểm của (P) và (d). 1b) Hệ thức Thông hiểu: 2 2 2 Vi-et và
Hệ thức Vi -et - Tính được tổng, tích, x1 +x2 các nghiệm của 1 ứng dụng
phương trình bậc hai một ẩn bằng hệ thức (Bài 2)
Vi-et (Biến đổi đơn giản) Giải bài toán Thông hiểu:
bằng cách lập - Phân tích đề bài, tìm mối quan hệ giữa các đại hệ phương
lượng cho trong đề bài, gọi ẩn, từ đó lập được hệ 1 trình.
2 phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức Dạng ứng tăng/giảm 1 Bài tập dụng tăng Vận dụng: 1 Bài 3 ứng dụng giảm
- Vận dụng kiến thức về tăng giảm, tỉ số % Bài 4a 4b thực tế
giải quyết một số vấn đề trong thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện tích toàn
Dạng toán ứng phần, thể tích của hình trụ (hoặc hình nón, hình dụng hình cầu) 1 1 không gian
Vận dụng cao: Bài 5a Bài
- Vận dụng hợp lí công thức tính diện tích, thể 5b
tích hình trụ (hoặc hình nón, hình cầu) để giải
quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc
với đường tròn, mối quan hệ giữa các góc, phối 4
hợp các kiến thức để chứng minh.
Hình học Tứ giác nội tiếp
- Vận dụng các phương pháp chứng minh hai 1 1
tam giác đồng dạng, chứng minh song song, (Bài (Bài
vuông góc, 3 điểm thẳng hàng giải quyết yêu 6b) 6c) cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình
học phẳng để giải quyết yêu cầu đề bài.
C. ĐỀ KIỂM TRA CUỐI KỲ 2 TOÁN 9 Năm Học 2023-2024 UBND HUYỆN CỦ CHI
ĐỀ KIỂM TRA HỌC KỲ II TRƯỜNG THCS BÌNH HÒA Năm học 2023-2024 Môn: Toán 9
Đề thi có 2 trang
Thời gian làm bài: 90 phút
(Không kể thời gian ghi đề)
Câu 1: (2 điểm) Cho parabol (P): y = 1 x2 và đường thẳng (d): y = – 1 x + 2 4 2
a/ Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b/ Tìm tọa độ giao điểm của (P) và (d) bằng phép toán.
Câu 2: (1,5 điểm)
Cho phương trình x2 – 3x = 1 có 2 nghiệm 𝑥𝑥1, 𝑥𝑥2. Không giải phương trình. Tính
giá trị biểu thức A = (𝑥𝑥1 – 𝑥𝑥2)2 và B = 𝑥𝑥1 + 𝑥𝑥2 𝑥𝑥2 𝑥𝑥1
Câu 3: (1,5 điểm)
Mục tiêu là để rèn luyện sức khỏe, anh An và anh Bình đề ra mục tiêu mỗi ngày một
người phải đi bộ ít nhất 6000 bước. Hai người cùng đi bộ ở công viên và thấy rằng, nếu
cùng đi trong 2 phút thì anh An bước nhiều hơn anh Bình 20 bước. Hai người cùng giữ
nguyên tốc độ như vậy nhưng anh Bình đi trong 5 phút thì lại nhiều hơn anh An đi
trong 3 phút là 160 bước. Hỏi mỗi ngày anh An và anh Bình cùng đi bộ trong 1 giờ thì
họ đã đạt được số bước tối thiểu mà mục tiêu đề ra hay chưa? (Giả sử tốc độ đi bộ hàng
ngày của hai người không đổi).
Câu 4: (1,5 điểm)
Anh An làm việc cho một công ty sản xuất hàng cao cấp, anh được trả 5760000
đồng cho 48 tiếng làm việc trong một tuần. Sau đó để tăng thêm thu nhập, anh An đã
đăng ký làm thêm một số giờ nửa trong tuần, mỗi giờ làm thêm này anh An được trả
bằng 150% số tiền mà mỗi giờ anh An được trả trong 48 giờ đầu. Cuối tuần sau khi
xong việc, anh An được lãnh số tiền là 7200000 đồng. Hỏi anh An đã làm thêm bao
nhiêu giờ trong tuần đó?
Câu 5: (1,0 điểm)
Các viên kẹo mút có dang hình cầu, bán kính
1,6cm. Người ta dùng môt que nhựa hình trụ tròn,
bán kính 0,2cm cắm vào đến phân nửa viên kẹo để
người dùng dễ sử dụng.
a) Tính thể tích phần ống nhựa hình trụ cắm vào phân nửa viên kẹo.
b) Tính thể tích thực của viên kẹo sau khi trừ phần ống nhựa cắm vào.
Câu 6: (2,5 điểm)
Cho ∆ABC nhọn nội tiếp (O), các đường cao BE, CF cắt nhau tại H.
a./ Chứng minh: AH ⊥ BC tại D và BFEC nội tiếp.
b./ Chứng minh: EH là tia phân giác của góc FED.
c./ Từ D kẻ một đường thẳng vuông góc với đường thẳng FC cắt EF tại I.
Chứng minh: tứ giác DEIH nội tiếp. HẾT
D HƯỚNG DẪN CHẤM Câu Đáp án Điểm Câu1 0,5đ
(2 điểm) (P): y = 1 x2
(d) : y = – 1 x + 2 4 2 x –4 –2 0 2 4 x 0 2 y 4 1 0 1 4 y 2 1 0,5đ 0,5đ
b) Phương trình hoành độ giao điểm của (P) và (d) 1 x2 = – 1 x + 2 4 2 ⇔ 1 x2 + 1 x – 2 = 0 4 2 x = 2 ⇔ x = 4 − 0,5đ
Tọa độ giao điểm của (P) và (d) là (2;1) và (– 4; 4) Câu 2
(1,5điểm) � 𝑥𝑥1 + 𝑥𝑥2 = 3 𝑥𝑥1 . 𝑥𝑥2 = − 1 0,5đ A = (𝑥𝑥 2 2
1 – 𝑥𝑥2)2 = 𝑥𝑥1 + 𝑥𝑥2 – 2𝑥𝑥1𝑥𝑥2 = (𝑥𝑥1 + 𝑥𝑥2)2 – 4𝑥𝑥1𝑥𝑥2 0,5đ = 32 – 4.( –1) = 13 2 2
B = 𝑥𝑥1 + 𝑥𝑥2 = 𝑥𝑥1 + 𝑥𝑥2 = = 32−2.(−1) = 0,25đ 𝑥𝑥2 𝑥𝑥1 𝑥𝑥1𝑥𝑥2 − 1 0,25đ – 11
Câu 3 Gọi số bước anh An đi bộ trong 1 phút là x (bước) (x ∈ N*). 0,25đ
(1,5 điểm) Gọi số bước anh Bình đi trong 1 phút là y (bước) (y ∈ N*).
Vì nếu cùng đi trong 2 phút thì anh An bước nhiều hơn anh Bình 0,25đ
20 bước nên ta có phương trình: 2x – 2y = 20 ⇔ x – y = 10
anh Bình đi trong 5 phút thì lại nhiều hơn anh An đi trong
3 phút là 160 bước nên ta có phương trình: 5y – 3x = 160 0,25đ
Ta có hệ phương trình: x − y =10 x =105 (nha ) n ⇔ 5 y 3x 160 − = y = 95 (nha ) n 0,25đ
Mỗi ngày anh An và anh Bình cùng đi bộ trong 1 giờ nên số
bước anh An đi là 105.60 = 6300, anh Bình đi được 95.60 = 5700 0,25đ bước.
Vậy anh An đạt được mục tiêu đề ra còn anh Bình thì không. 0,25đ
Câu 4 a) Số tiền mỗi giờ anh An làm trong 48 giờ đầu:
(1,5 điểm) 5.760.000 : 48 = 120.000 (đồng)
Số tiền anh An làm thêm là: 7.200.000 – 5.760.000 = 1.440.000 0,5đ (đồng)
Số tiền mỗi giờ làm thêm anh An được trả là: 120.000 × 150% 0,5đ = 180.000 (đồng)
Số giờ mà anh An làm thêm là: 1.440.000 : 180.000 = 8 (giờ) 0,5đ
Câu 5 a) Thể tích phần ống nhựa hình trụ cắm vào viên kẹo: (1,0 điểm)
𝑉𝑉 = 𝜋𝜋𝑟𝑟2ℎ = 𝜋𝜋. 0,22. 1,6 = 0,064𝜋𝜋 (𝑐𝑐𝑐𝑐3) 0.5 điểm
b) Thể tích hình cầu có bán kính 1,6cm: 4 4 4 0.25 điểm
𝑉𝑉 = 3𝜋𝜋𝑅𝑅3 = 3𝜋𝜋.1,63 = 3𝜋𝜋4,096 = 5,46𝜋𝜋(𝑐𝑐𝑐𝑐3)
Thể tích thực của viên kẹo: 0.25 điểm
5,46𝜋𝜋 − 0,064𝜋𝜋 = 5,396𝜋𝜋(𝑐𝑐𝑐𝑐3) Câu 6 (2,5 điểm) A E I F H B D C
a./ Chứng minh: AH ⊥ BC tại D và BFEC nội tiếp.
∆ ABC có hai đường cao BE và CF cắt nhau tại H (gt) 0,25đ H là trực tâm
AH là đường cao thứ ba
AH ⊥ BC tại D 0,25đ 0
B ˆFC = B ˆEC = 90 0,25đ
=>Tứ giác BFEC nội tiếp đường tròn đường kính BC 0,25đ
b./ Chứng minh: EH là tia phân giác của góc FED. F ˆ = ˆ
EH FCB ( cùng chắn cung BF) ˆ = ˆ
HED HCD (cùng chắn cung HD của tứ giác EHDC nội tiếp) 0,25đx4
=> F ˆEH = H ˆED
=> EH là tia phân giác của góc FED
c./ Chứng minh: tứ giác DEIH nội tiếp. Ta có: ˆ = ˆ
HDI DCH (cùng phụ góc DHC) Mà ˆ DCH = ˆ IEH ( cmt) 0,25x2 Nên ˆ
HDI = I ˆEH
Vậy tứ giác IHDE nội tiếp ----HẾT---
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng
TT Chủ đề Nội dung/Đơn vị kiến điểm thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TN TL TN TL TN TL TN TL
Vẽ đồ thị hàm số 𝒚𝒚 = 1
𝒂𝒂𝒙𝒙𝟐𝟐 (P) và y = ax + b (Bài a) 1 Đồ thị (d) (1,0đ) hàm số 2đ 1 Tìm tọa độ giao điểm (Bài b) của (P) và (d) (1,0đ) Hệ thức 1 2 Vi-et và (Bài 2) ứng Hệ thức Vi-et (1,5 đ) 1,5đ dụng Giải bài toán bằng 1 cách lập hệ phương (Bài 3) trình. (1,5đ) Bài tập 3 ứng Dạng ứng dụng tăng 1 1 dụng 4đ giảm Bài 4a Bài 4b thực tế (1,0đ) (0,5đ) Dạng toán ứng dụng 1 1 hình không gian (Bài 5a) (Bài 5b) (0,5đ) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài 6b) (Bài 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng Đồ thị hàm số 1 y = ax2 (P) và Vận dụng: (Bài
y = ax + b (d) - Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ 1a) 1 Đồ thị trục tọa độ hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong việc (Bài (P) và (d)
tìm tọa độ giao điểm của (P) và (d). 1b) Hệ thức Thông hiểu: 2 2 2 Vi-et và
Hệ thức Vi -et - Tính được tổng, tích, x1 +x2 các nghiệm của 1 ứng dụng
phương trình bậc hai một ẩn bằng hệ thức (Bài 2)
Vi-et (Biến đổi đơn giản) Giải bài toán Thông hiểu:
bằng cách lập - Phân tích đề bài, tìm mối quan hệ giữa các đại hệ phương
lượng cho trong đề bài, gọi ẩn, từ đó lập được hệ 1 trình.
2 phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức Dạng ứng tăng/giảm 1 Bài tập dụng tăng Vận dụng: 1 Bài 3 ứng dụng giảm
- Vận dụng kiến thức về tăng giảm, tỉ số % Bài 4a 4b thực tế
giải quyết một số vấn đề trong thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện tích toàn
Dạng toán ứng phần, thể tích của hình trụ (hoặc hình nón, hình dụng hình cầu) 1 1 không gian
Vận dụng cao: Bài 5a Bài
- Vận dụng hợp lí công thức tính diện tích, thể 5b
tích hình trụ (hoặc hình nón, hình cầu) để giải
quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc
với đường tròn, mối quan hệ giữa các góc, phối 4
hợp các kiến thức để chứng minh.
Hình học Tứ giác nội tiếp
- Vận dụng các phương pháp chứng minh hai 1 1
tam giác đồng dạng, chứng minh song song, (Bài (Bài
vuông góc, 3 điểm thẳng hàng giải quyết yêu 6b) 6c) cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình
học phẳng để giải quyết yêu cầu đề bài.
ĐỀ THAM KHẢO CUỐI HỌC KỲ II TOÁN 9 NH: 2023 – 2024
TRƯỜNG THCS HÒA PHÚ
Bài 1: (2 điểm) Cho hàm số 2
y = 2x có đồ thị là parabol (P) và hàm số y = 2x + 4 có đồ thị
là đường thẳng (D).
a/ Vẽ đồ thị (P) và (D) trên cùng hệ trục tọa độ;
b/ Tìm tọa độ giao điểm của (P) và (D) bằng phép toán.
Bài 2: (1,5 điểm) Cho phương trình: 2
3x − 4x −1= 0 có hai nghiệm x1, x2. Không giải x −1 x −1
phương trình, hãy tính giá trị của biểu thức sau: 1 2 A = + x x 2 1
Bài 3: (1,5 điểm) Hai phân xưởng A và B có tất cả 64 công nhân cùng sản xuất một mặt
hàng. Xưởng A trung bình mỗi người làm được 30 sản phẩm mỗi ngày, xưởng B trung bình
mỗi người làm được 28 sản phẩm mỗi ngày. Biết hai xưởng trong một ngày làm ra tổng cộng
1860 sản phẩm. Tìm số công nhân mỗi phân xưởng Bài 4: (1,5 điểm)
Một cửa hàng A bán loại bánh A như sau: nếu mua không quá 3 hộp thì giá 35 nghìn đồng
mỗi hộp, nếu mua nhiều hơn 3 hộp thì bắt đầu từ hộp thứ tư trở đi giá mỗi hộp sẽ giảm đi 20% giá ban đầu.
a) Bạn An đến cửa hàng A mua 5 hộp bánh A. Hỏi An phải trả bao nhiêu cho cửa hàng?
b) Lan và Hồng đều mua loại bánh A với số hộp nhiều hơn 3. Hỏi mỗi bạn mua bao nhiêu
hộp biết rằng số hộp bánh Lan mua gấp đôi số hộp Hồng mua, đồng thời số tiền mua bánh
của Lan nhiều hơn Hồng 140 nghìn đồng.
Bài 5: (1 điểm) Một xe chở xăng dầu, bên trên có chở một bồn chứa hình trụ chiều dài 2,6
mét và đường kính đáy là 1,4 mét .
a/ Tính thể tích của bồn chứa.
b/ Theo tiêu chuẩn an toàn, thì bồn chỉ chứa tối đa 80% thể tích khi xe di chuyển trên đường.
Vậy bồn đó có thể chứa được nhiều nhất là bao nhiêu lít nhiên liệu?
Bài 6: (2,5 điểm) Cho tam giác ABC có 3 góc nhọn, nội tiếp đường tròn tâm (𝑶𝑶) và ABVẽ đường kính AD của đường tròn (𝑶𝑶). Kẻ BE và CF vuông góc với AD (E,F thuộc AD).
Kẻ AH vuông góc với BC (H thuộc BC).
a/ Chứng minh : tứ giác AEHB nội tiếp.
b/ Chứng minh HE song song với CD
c/ Gọi M là trung điểm BC. Chứng minh ME=MF Đáp án Bài 1. a/ Bảng giá trị: x 2 − 1 − 0 1 2 2 y = 2x 8 2 0 2 8 x 0 -1 y = 2x + 4 4 2
b/ Hoành độ giao điểm của (P) và (D) là nghiệm của phương trình: 2 2
2x = 2x + 4 ⇔ 2x − 2x − 4 = 0
⇒ Phương trình có hai nghiệm phân biệt: x = 1 − ; x = 2 1 2 + Với x = 1 − ⇒ y = 2 1 1
+ Với x = 2 ⇒ y = 8 2 2
Vậy toạ độ giao điểm của (P) và (D)là ( 1; − 2);(2;8) . Bài 2. 2
3x − 4x −1= 0
Theo định lí Vi - ét ta có: b 4 S = x + x = − = 1 2 a 3 c 1 P x . x − = = = 1 2 a 3 x −1 x −1 1 2 A = + x x 2 1 ... 10 − = 3
Bài 3 Gọi x,y lần lượt là số công nhân ở phân xưởng A và B (0Tổng số công nhân ở 2 phân xưởng là 64 công nhân : x+y=64 (1)
Số sản phẩm làm trong 1 ngày của phân xưởng A : 30x
Số sản phẩm làm trong 1 ngày của phân xưởng B : 28y
Tổng sản phẩm làm trong một ngày của cả hai phân xưởng : 30x+28y=1860 (2)
Từ (𝟏𝟏) và (𝟐𝟐) ta có hệ phương trình: �𝐱𝐱 + 𝐲𝐲 = 𝟔𝟔𝟔𝟔
𝟑𝟑𝟑𝟑𝐱𝐱 + 𝟐𝟐𝟐𝟐𝐲𝐲 = 𝟏𝟏𝟐𝟐𝟔𝟔𝟑𝟑
⇔ �𝐲𝐲 = 𝟑𝟑𝟑𝟑 𝐱𝐱 = 𝟑𝟑𝟔𝟔
Vậy số công nhân ở hai phân xưởng A và B lần lượt là 34 và 30 công nhân Bài 4:
a/ Số tiền An phải trả cho cửa hàng A là
35 000.3 + 2.(35 000.80%) = 161 000 đồng.
b) Gọi x (hộp) là số hộp bánh Hồng mua. (x > 3)
Khi đó 2x (hộp) là số hộp bánh Lan mua. Theo giả thiết, ta có:
(28000.2x + 21000) – ( 28000.x + 21000) = 140000
⇔ 56000x − 28000x =140000 ⇔ 28000x =140000 ⇔ x = 5 (nhận)
Vậy số hộp bánh Hồng mua là 5 hộp và số hộp bánh Lan mua là 10 hộp. Bài 5.
a/ Bán kính của bồn chứa hình trụ là: 1,4 R = = 0,7(m). 2
Đổi đơn vị: R = 7(dm), h = 26(dm).
Thể tích của bồn chứa hình trụ là: 2 2
V = π R h = π.7 .26 =1274π (dm3) = 1274π (lít)
b/ Theo tiêu chuẩn an toàn bồn chỉ chứa tối đa 80% thể tích khi xe di chuyển trên đường do
đó số lít nhiên liệu nhiều nhất mà bồn chứa được là: V.80% =1274π.80% ≈ 3201,911233 (lít)
Vậy bồn đó có thể chứa được nhiều nhất khoảng 3201 lít nhiên liệu. Bài 6. A E K O I C B H M F D a) Xét tứ giác AEHB có:
góc AEB = góc AHB = 90 độ
Mà 2 góc này ở vị trí cùng nhìn cạnh AB
⇒Tứ giác AEHB nội tiếp b) Ta có: Tứ giác AEHB nội tiếp
⇒góc DEH = góc HBA (tính chất) →góc DEH = góc CBA
Ta có: Đường tròn (O) có: góc CDA = góc CBA
⇒góc CDA = góc DEH = góc CBA
mà 2 góc này ở vị trí so le trong →HE//CD
c) Gọi K là trung điểm EC, I là giao điểm của MK và ED
Khi đó: MK là đường trung bình của tam giác BCE
=> MK//BE mà BE vuông góc AD (gt) => MK vuông góc AD
Hay: MK vuông góc với EF (1)
Lại có: CF vuông góc AD (gt) => MK//CF Hay: KI//CF
Tam giác ECF có: KI//CF, KE=KC nên IE=IF (2)
Từ (1) và (2) suy ra: MK là đường trung trực EF Hay: ME = MF
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng điểm T Chủ Nội dung/Đơn vị T đề kiến thức
Nhận biết Thông hiểu Vận dụng Vận dụng cao T N TL T N TL T N TL T N TL Vẽ đồ thị hàm số 1
Đồ thị 𝑦𝑦 = 𝑎𝑎𝑥𝑥2 (P) và y = (Bài a) 1 hàm ax + b (d) (1,0đ) 2đ số 1 Tìm tọa độ giao (Bài b) điểm của (P) và (d) (1,0đ) Hệ 1 thức (Bài 2) 2 Vi-et Hệ thức Vi-et (1,5 đ) 1,5đ và ứng dụng Giải bài toán bằng 1 cách lập hệ (Bài 3) phương trình. (1,5đ) Bài tập Dạng ứng dụng 1 1 3 ứng tăng giảm Bài 4a Bài 4b 4đ dụng (1,0đ) (0,5đ)
thực tế Dạng toán ứng 1 1 dụng hình không (Bài 5a) (Bài gian (0,5đ) 5b) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài (Bài 6b) 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100 % Tỉ lệ chung 65% 35% 100 %
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 T Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ T nhận thức Nhận Thông Vận VD
biết hiểu dụng cao Đồ thị hàm 1 số y = ax2 (Bài (P) và Vận dụng: 1a) y = ax + b
- Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ trục tọa độ 1 Đồ thị (d) hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1 giao điểm
- Vận dụng phương trình bậc hai một ẩn (Bài của (P) và
trong việc tìm tọa độ giao điểm của (P) và 1b) (d) (d). Hệ thức Thông hiểu:
- Tính được tổng, tích, x12+x22 các 1
2 Vi-et và Hệ thức Vi ứng –et
nghiệm của phương trình bậc hai một (Bài dụng
ẩn bằng hệ thức Vi-et (Biến đổi đơn 2) giản)
Giải bài toán Thông hiểu: bằng cách
- Phân tích đề bài, tìm mối quan hệ giữa lập hệ
các đại lượng cho trong đề bài, gọi ẩn, từ 1 phương
đó lập được hệ 2 phương trình bậc nhất 2 Bài 3 trình. ẩn.
- Giải hệ phương trình, đối chiếu điều
kiện để trả lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức tăng/giảm
Bài tập Dạng ứng 1 1 dụng tăng Vận dụng: Bài Bài 3 ứng
- Vận dụng kiến thức về tăng giảm, tỉ dụng giảm
số % giải quyết một số vấn đề trong 4a 4b thực tế thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện Dạng toán
tích toàn phần, thể tích của hình trụ (hoặc ứng dụng hình nón, hình cầu) 1 1
hình không Vận dụng cao: Bài Bài gian
- Vận dụng hợp lí công thức tính diện 5a 5b
tích, thể tích hình trụ (hoặc hình nón,
hình cầu) để giải quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường (Bài 4 Hình Tứ giác nội tròn. 6a) học tiếp Vận dụng: 1 1
- Vận dụng các định lý, hệ quả của các (Bài (Bài
loại góc với đường tròn, mối quan hệ 6b) 6c)
giữa các góc, phối hợp các kiến thức để chứng minh.
- Vận dụng các phương pháp chứng
minh hai tam giác đồng dạng, chứng
minh song song, vuông góc, 3 điểm
thẳng hàng giải quyết yêu cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức
trong hình học phẳng để giải quyết yêu cầu đề bài.
UỶ BAN NHÂN DÂN HUYỆN CỦ CHI
ĐỀ KIỂM TRA CUỐI KỲ II NH 2023-2024
TRƯỜNG TRUNG HỌC CƠ SỞ MÔN: TOÁN - LỚP 9 NHUẬN ĐỨC
Thời gian: 90 phút (Không kể thời gian phát đề) Bài 1:(2 điểm) 1
Cho hàm số: y = x2 (P) và y = –x + 4 (D) 2
a) Vẽ đồ thị (P) và (D) của 2 hàm số trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán Bài 2: (1,5 điểm)
Cho phương trình x2 - 4x -1 = 0 có 2 nghiệm là x ,x . Không giải phương trình, 1 2
hãy tính giá trị của biểu thức A = 2 x + 2 x + 3x x . 1 2 1 2 Bài 3: (1,5 điểm)
Trước ngày kết thúc năm học tập thể các học sinh lớp 9A muốn mua quà tặng
cho các giáo viên giảng dạy lớp mình trong suốt năm học để tỏ lòng tri ân, mỗi món quà
tặng cho thầy với giá là 50 ngàn đồng, mỗi món quà tặng cho cô có giá là 65 ngàn
đồng, biết lớp tặng quà cho 15 giáo viên và tổng số tiền mà lớp mua quà là 870 ngàn
đồng. Em hãy tính số thầy giáo và số cô giáo lớp 9A dự định mua quà tặng.
Bài 4 : ( 1,5 điểm)
Một công ty giao cho cửa hàng 100 hộp bánh để bán ra thị trường. Lúc đầu cửa hàng
bán 24 hộp bánh với giá bán một hộp bánh là 200000 đồng. Do nhu cầu của thị trường
nên từ hộp bánh thứ 25 đến hộp bánh thứ 80 mỗi hộp bánh có giá bán tăng 15% so với
giá bán lúc đầu, từ hộp bánh thứ 81 đến hộp bánh thứ 100 mỗi hộp bánh có giá bán
giảm 10% so với giá bán lúc đầu.
a) Hỏi số tiền thu cửa hàng được khi bán 100 hộp bánh là bao nhiêu?
b)Biết rằng: Với số tiền thu được khi bán 100 hộp bánh, sau khi trừ đi 10% tiền
thuế giá trị gia tăng VAT cửa hàng vẫn lãi 1152000 đồng. Hỏi mỗi hộp bánh
công ty giao cho cửa hàng có giá là bao nhiêu? Bài 5: (1 điểm)
Một xe chở xăng dầu, bên trên có một bồn chứa hình trụ dài 2,6 m và đường
kính đáy là 1,4 m. Theo tiêu chuẩn an toàn thì bồn chỉ chứa được tối đa 80 % thể tích
khi xe di chuyển trên đường.
a) Mỗi chuyến xe có thể chở nhiều nhất bao nhiêu lít nhiên liệu? (cho 3,14 ).
b) Trên đường vận chuyển, xe chở xăng dầu trên phải đi qua 1 cây cầu có tải trọng
5 tấn. Biết xe khi chưa chở hàng nặng 3 tấn. Hỏi nếu muốn đi qua cây cầu đó thì xe
chở tối đa bao nhiêu lít xăng? Biết khối lượng riêng của xăng là 0,713 kg/lít (Các kết
quả làm tròn đến hàng đơn vị). Bài 6: (2,5 điểm)
Cho tam giác nhọn ABC nội tiếp đường tròn (O ; R). Gọi H là giao điểm của 2 đường cao BD và CE.
a) Chứng minh tứ giác BCDE nội tiếp và xác định tâm I của đường tròn này.
b) Vẽ đường kính AK của đường tròn (O ; R). Chứng minh: Tứ giác BHCK là
hình bình hành rồi suy ra ba điểm H , I , K thẳng hàng.
c) Giả sử BC = 3 AK. Tính tổng AB.CK + AC.BK theo R 4 ………. Hết ………
UỶ BAN NHÂN DÂN HUYỆN CỦ CHI
ĐÁP ÁN KIỂM TRA CUỐI KỲ II NH 2023-2024
TRƯỜNG TRUNG HỌC CƠ SỞ MÔN: TOÁN - LỚP 9 NHUẬN ĐỨC
Thời gian: 90 phút (Không kể thời gian phát đề)
CÂU HƯỚNG DẪN CHẤM BIỂU ĐIỂM Bài 1(2
a)Lập bảng giá trị đúng: 0,25+0,25 điểm )
Vẽ đồ thị đúng và đầy đủ thông tin 0,25+0,25
b)Phương trình hoành độ giao điểm của (P) và (D): 1 x2 = –x + 4 2 ⇔ x + 2x − 8 = 0 0,25 2
Giải phương trình này ta được: x 1 = 2 ; x2 = –4 Với x = 2 suy ra y = 2 0,25 Với x = –4 suy ra y = 8 0,25
Vậy tọa độ giao điểm của (P) và (D) là: (2 ;2), (–4 ; 8) 0,25 Bài 2: (,5
Vì a.c 0 nên phương trình có hai nghiệm phân điểm) biệt x ,x . 0,25 1
2 Theo định lí Vi-et, ta có: b −4
S = x + x = − = − = 4 1 2 a 2 c − 0,25 1
P = x .x = = = −1 1 2 a 1 0,25 Ta có 2 2 2
x + x = S − P = − − = 1 2 2 42 2( ) 1 18 0,25 Ta có: A = 2 x + 2
x + 3x x =18+3.(-) =15 1 2 1 2 0,5 Bài 3 (
Gọi số thầy giáo và số cô giáo của lớp 9A dự định 1,5
mua quà tặng lần lượt là ∈ 0,25 điểm) x, y Đk x,y * N
Vì lớp tặng quà cho 15 giáo viên và tổng số tiền
mà lớp mua quà là 870 ngàn đồng nên từ đề bài ta có hệ phương trình x + y = 15 0,5
50x + 65y = 870
Giải hệ phương trình ta được x = 7(n) 0,25 y = ( 8 n)
Vậy lớp 9A dự định mua quà tặng cho 7 thầy giáo và 0,5 8 cô giáo. Bài 4 (
a) Số tiền thu được khi bán 24 hộp bánh đầu là: 1,5 24.200000 = 4800000 (đồng) 0,25 điểm)
Số tiền thu được khi bán được từ hộp bánh thứ 25 đến
hộp bánh thứ 80 là: 56.200000(1+15%) =12880000 (đồng) 0,25
Số tiền thu được khi bán được từ hộp bánh thứ 81 đến
hộp bánh thứ 100 là: 20.200000(1−10%) = 3600000 (đồng)
Số tiền thu cửa hàng được khi bán 0,25 100 hộp bánh là:
4800000 +12880000 + 3600000 = 21280000(đồng) 0,25
b) Số tiền thuế giá trị gia tăng VAT là
10%.21280000 = 2128000(đồng) 0,25
Số tiền mỗi hộp bánh công ty giao cho cửa hàng có giá là:
(21280000− 2128000)−1152000 :100 =180000 (đồng) 0,25 Bài 5 (1 1, 4 : 2 0,7 m điểm) a)Bán kính đáy: 0,25
Số lít nhiên liệu xe có thể chở nhiều nhất: 2 2 3
V.80% = π.R . .80% h
= 3.14.0.7 .2,6.80% ≈ 3,2(m ) = 3200(l) 0,25 b)
Khối lượng xăng xe có thể chở tối đa để qua cầu 0,25
5 3 2 (tấn) 2000 kg
Số lít xăng xe chở tối đa để qua cầu: 0,25 2000 : 713 , 0 ≈ 2805 Bài 6:(2,5điể m ) a)Xét tứ giác BCDE
Ta có : góc BEC = góc BDC = 900 (gt) 0,5
Suy ra BCDE nội tiếp đường tròn. 0,25
Tâm I của đường tròn đi qua 4 điểm B,D,C,E là 0,25 trung điểm của BC
b) Ta có BH // CK (cùng vuông góc với AC). 0,25
Và CH // BK (cùng vuông góc với AB).
Nên BHCK là hình bình hành.
Do đó hai đường chéo BC và HK giao nhau tại trung 0,25
điểm của mỗi đường. 0,25
Mà I là trung điểm của BC
⇒ I cũng là trung điểm của HK. Nên H, I, K thẳng hàng. 0,25
c) Gọi F là giao điểm của AH và BC.
Cm H là trực tâm của tam giác ABC
Ta có ∆ ABF ∽ ∆ AKC (g.g) ⇒ AB BF = ⇒ AB. AK KC 0,25 KC = AK. BF (1) Và ∆ ACF ∽ ∆ AKB (g.g) ⇒ AC CF = ⇒ AC. KB AK KB = AK. CF (2)
Cộng (1) và (2) theo vế ta có: AB. KC + AC. KB =
AK. BF + AK. CF = AK.(BF + CF) = AK.BC 0,25
Mà BC = 3 AK ⇒ AB. KC + AC. KB = AK. 3 AK = 3 4 4 4
AK2 = 3 .(2R)2 = 3R2 4
Lưu ý: học sinh làm cách khác đúng vẫn trọn điểm
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng điểm TT Chủ đề
Nội dung/Đơn vị kiến thức
Nhận biết Thông hiểu Vận dụng Vận dụng cao T N TL T N TL T N TL T N TL Vẽ đồ thị hàm số 1
𝑦𝑦 = 𝑎𝑎𝑥𝑥2 (P) và y = ax + b (d) (Bài a) 1 Đồ thị hàm số (1,0đ) 2đ 1
Tìm tọa độ giao điểm của (P) và (d) (Bài b) (1,0đ) 1 2 Hệ thức Vi-et và ứng dụng Hệ thức Vi-et (Bài 2) 1,5đ (1,5 đ)
Giải bài toán bằng cách lập hệ phương 1 trình. (Bài 3) (1,5đ)
Dạng ứng dụng tăng giảm 1 1 3
Bài tập ứng dụng Bài 4a Bài 4b thực tế 4đ (1,0đ) (0,5đ) 1 1
Dạng toán ứng dụng hình không gian (Bài 5a) (Bài (0,5đ) 5b) (0,5đ) 1 4 Hình học Tứ giác nội tiếp (Bài 6a) 2,5đ (1,0đ) 1 1 (Bài (Bài 6b) 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100 % Tỉ lệ chung 65% 35% 100 %
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức Nhận Thông Vận VD
biết hiểu dụng cao
Đồ thị hàm số y = ax2 (P) và Vận dụng: 1 y = ax + b (d)
- Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ trục (Bài 1 Đồ thị (a khác 0) tọa độ 1a)
hàm số Tìm tọa độ giao điểm của (P) và Thông hiểu: 1 (d)
- Vận dụng phương trình bậc hai một ẩn trong việc tìm tọa (Bài
độ giao điểm của (P) và (d). 1b) Hệ thức Thông hiểu: 1 2 Vi-et và
- Tính được tổng, tích, x12+x22 các nghiệm của ứng Hệ thức Vi -et
phương trình bậc hai một ẩn bằng hệ thức Vi-et (Bài dụng (Biến đổi đơn giản) 2) 3
Bài tập Giải bài toán bằng cách lập hệ Thông hiểu: 1 ứng phương trình. Bài 3 dụng
- Phân tích đề bài, tìm mối quan hệ giữa các đại lượng cho thực tế
trong đề bài, gọi ẩn, từ đó lập được hệ 2 phương trình bậc nhất 2 ẩn.
- Giải hệ phương trình, đối chiếu điều kiện để trả lời câu
hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức tăng/giảm 1 1
Dạng ứng dụng tăng giảm Vận dụng:
- Vận dụng kiến thức về tăng giảm, tỉ số % giải quyết Bài Bài
một số vấn đề trong thực tiễn. 4a 4b Thông hiểu:
- Tính được diện tích xung quanh, diện tích toàn phần, thể
Dạng toán ứng dụng hình không tích của hình trụ (hoặc hình nón, hình cầu) 1 1 gian
Vận dụng cao: Bài Bài
- Vận dụng hợp lí công thức tính diện tích, thể tích hình 5a 5b
trụ (hoặc hình nón, hình cầu) để giải quyết một số bài
toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc với 4
Hình Tứ giác nội tiếp
đường tròn, mối quan hệ giữa các góc, phối hợp các học
kiến thức để chứng minh.
- Vận dụng các phương pháp chứng minh hai tam giác 1 1
đồng dạng, chứng minh song song, vuông góc, 3 điểm (Bài (Bài
thẳng hàng giải quyết yêu cầu bài toán. 6b) 6c)
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình học
phẳng để giải quyết yêu cầu đề bài. UBND HUYỆN CỦ CHI
ĐỀ THAM KHẢO CUỐI KÌ II
TRƯỜNG THCS NGUYỄN VĂN XƠ NĂM HỌC 2023 – 2024 MÔN: TOÁN – LỚP 9 Thời gian: 90 phút
(không kể thời gian phát đề) Bài 1(2,0đ):
a) Vẽ trên cùng hệ trục Oxy đồ thị (P) 𝑦𝑦 = −𝑥𝑥2 và (d) y = x – 4 2
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Bài 2(1,5đ): Cho phương trình: x2 – 3x – 5 = 0 (1) (x là ẩn số) coa hai nghiệm x1;x2. Không
giải phương trình hãy tính giá trị biểu thức (x1 – x2)2
Bài 3 (1,5 đ): Cô Lan đi đến cửa hàng sách để mua 17 quyển bao gồm cả tập và sách tham
khảo làm quà tặng cho một học sinh có hoàn cảnh khó khăn trong lớp. Em hãy tính xem cô
Lan mua bao nhiêu quyển tập ? bao nhiêu quyển sách tham khảo ? Biết rằng giá mỗi quyển
tập là 10 nghìn đồng ; giá mỗi quyển sách tham khảo là 50 nghìn đồng và tổng số tiền cô
Lan đã trả là 250 nghìn đồng.
Bài 4 (1,5đ) : Cửa hàng A thực hiện chương trình khuyến mãi giảm giá cho khách hàng
mua giày hiệu BITI’S như sau: Nếu mua một đôi giày thì được giảm 5% so với giá niêm
yết. Nếu mua hai dôi giày thì đôi thứ nhất được giảm 5%, đôi thứ hai được giảm 10% so
với giá niêm yết. Nếu mua 3 đôi trở lên thì ngoài hai đôi đầu được hưởng chương trình giảm
giá như trên từ đôi thứ ba trở đi mỗi đôi sẽ được giảm 15 % so với giá niêm yết.
a)Bạn Nam mua 3 đôi giày hiệu BITI’S có cùng kiểu ở cửa hàng A thì phải trả số tiền là
bao nhiêu? Biết rằng mỗi đôi giày đó có giá niêm yết là 500 000 đồng.
b)Nếu cửa hàng A đưa ra hình thức giảm giá thứ hai cho giày hiệu BITI’S nêu trên là: Nếu
nếu mua từ 3 đôi trở lên thì sẽ giảm giá 12% cho mỗi đôi thì bạn Nam nên chọn hình thức
khuyến mãi nào có lợi hơn?
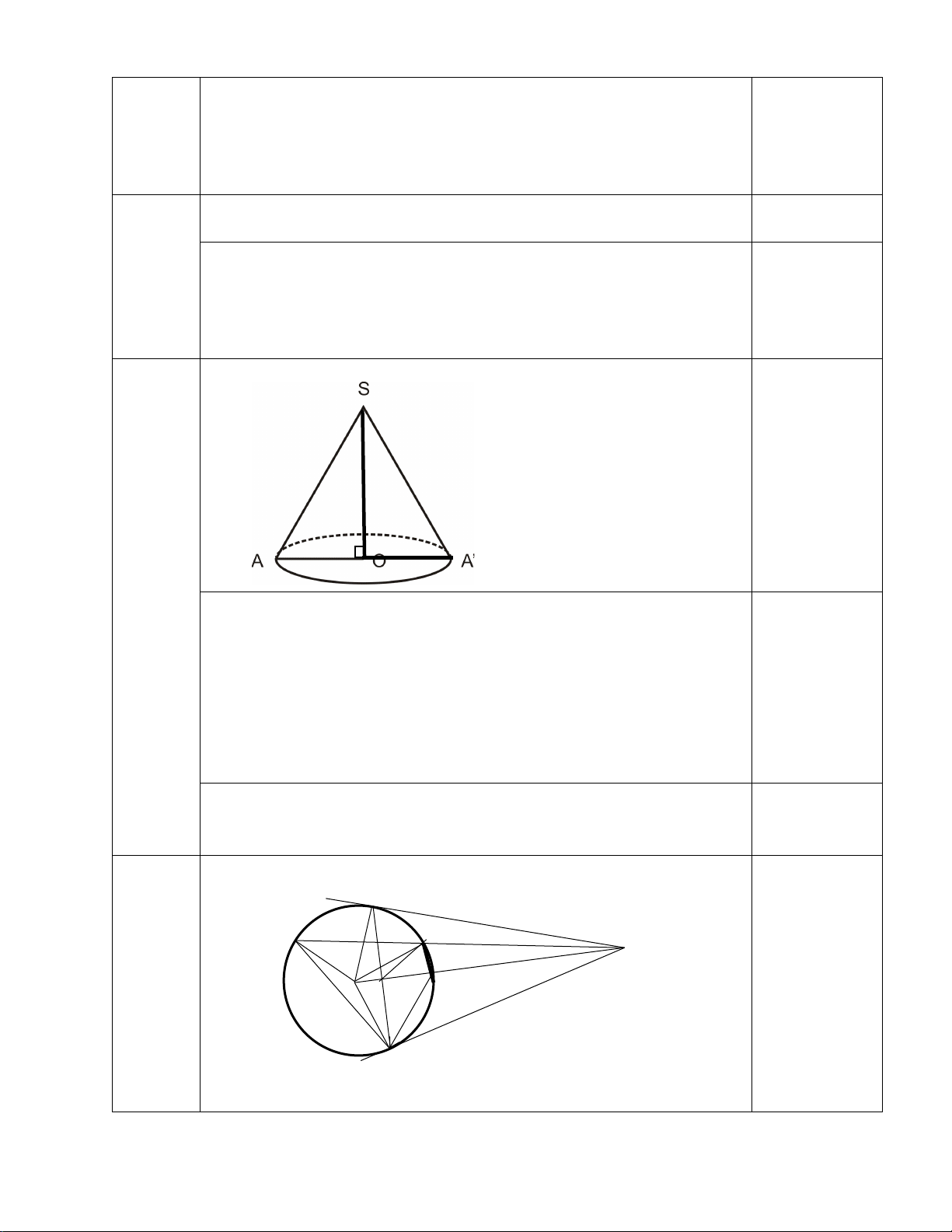
Bài 5 (1,0đ): Chiếc nón lá Việt Nam có dạng mặt xung quanh của một hình nón. Biết rằng
đáy của nón lá là một hình tròn có đường kính d=AA’=50cm, chiều cao h = SO= 30cm.
a)Tính độ dài đường sinh l (SA) của chiếc nón(Kết quả làm tròn đến chữ số thập phân thứ nhất)
b)Để trang trí nón người ta dùng vải màu có in hình hoa sen – Quốc hoa của nước Việt Nam
là loài hoa tượng trưng cho sự thanh cao và bất khuất của con người trước mọi nghịch cảnh.
Em hãy tính diện tích vải bao xung quanh bên ngoài nón lá bao gồm 10% các nếp gấp((Các
kết quả làm tròn đến hàng đơn vị) l h r
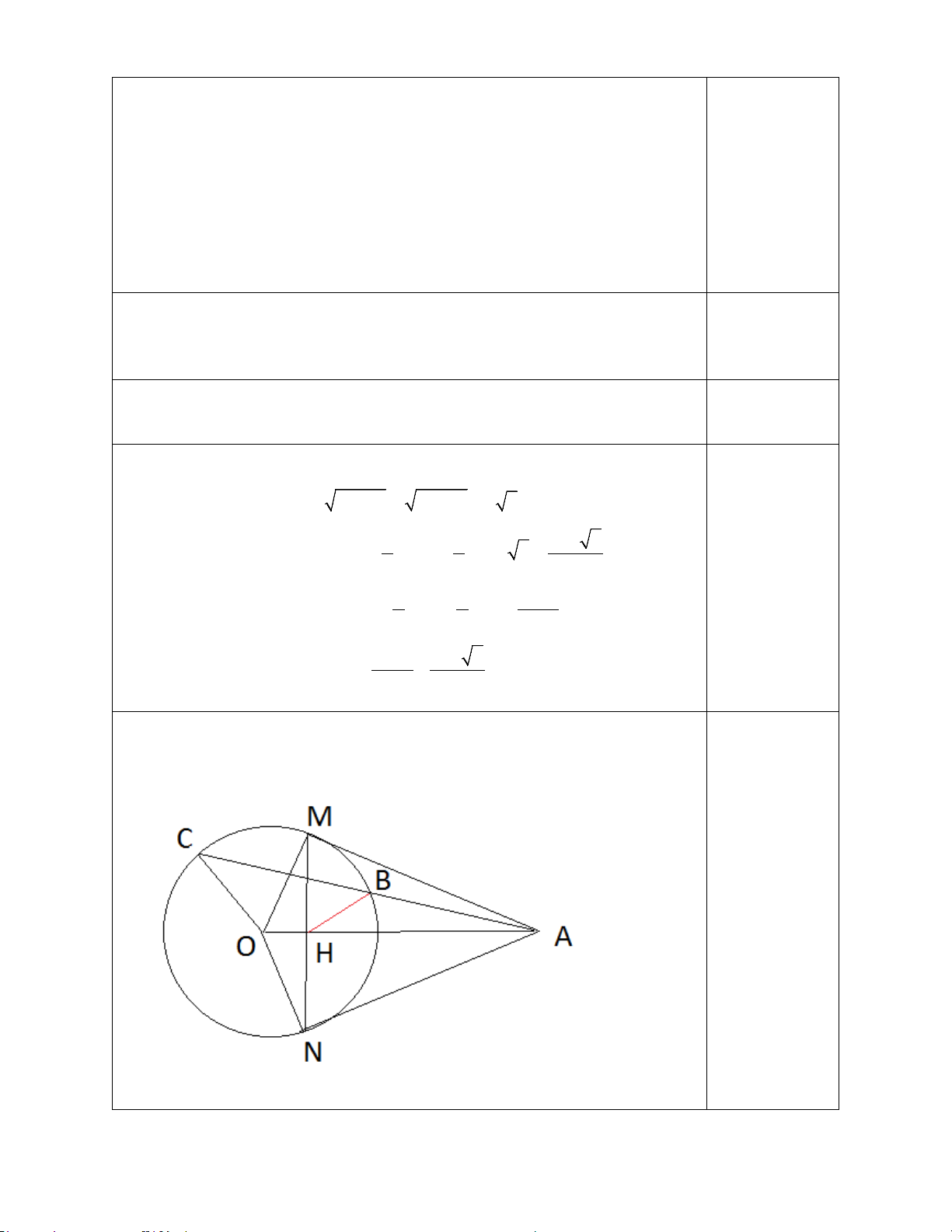
Bài 6(2,5đ): Từ điểm A bên ngoài đường tròn (O;R) dựng hai tiếp tuyến AB, AC và cát
tuyến AMN ( B, C là tiếp điểm, tia AN nằm giữa hai tia AB và AO, M nằm giữa A và N).
Gọi H là giao điểm của AO và BC.
a) Cm : AO vuông góc BC và tứ giác ABOC nội tiếp được đường tròn b) Cm: AM . AN = AH . AO
c) Đoạn thẳng AO cắt đường tròn (O) tại I. Cm: MI là phân giác của góc AMH -------- Hết --------
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM Bài Đáp án Thang điểm
1 (2,0đ) a)Vẽ trên cùng hệ trục Oxy đồ thị (P) y = -x2và (d) y = x – 4 2 0,25+0,25 Bảng giá trị đúng 0,25+0,25 Vẽ đúng (P) và (D)
b)Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm : −𝑥𝑥2 = x – 4 0,25 2 ⇔x2 + 2x – 8 = 0 0,25 Giải ra x1 = 2; x2 = – 4
Tìm ra tọa độ giao điểm (2; – 2) và ( – 4; – 8) 0,5 2(1,5đ) x 1 + x2 = −𝑏𝑏 = 3 𝑎𝑎 0,5 x1.x2 = 𝑐𝑐 = – 5 𝑎𝑎 0,5
(x1 – x2)2 = x12 – 2x1x2 +x22 = (x1 + x2)2 – 4x1x2 = 9 + 20 = 29 0,5
3(1,5 đ) Gọi x (quyển) là số quyển tập cô Lan đã mua. y(quyển) là số quyển 0,25
sách tham khảo cô Lan đã mua. 0
Vì cô Lan đã mua 17 quyển bao gồm cả tập và sách . Nên x + y = 17 (1) 0,25
Vì tập có giá 10 nghìn đồng / quyển ; sách tham khảo có giá 50
nghìn đồng / quyển và cô đã trả là 250 nghìn đồng. Nên 10x + 50y = 250 (2) 0,25
Từ (1) và (2) ta có hệ phương trình � 𝑥𝑥 + 𝑦𝑦 = 17 0,25 10𝑥𝑥 + 50𝑦𝑦 = 250
Giải hệ ta được �𝑥𝑥 = 15 0,25 𝑦𝑦 = 2
Vậy cô Lan đã mua 15 quyển tập ; 2 quyển sách tham khảo 0,25
4(1,5 đ) a)Số tiền bạn Nam phải trả khi mua ba đôi giày BITI’S là : 0,75
500 000.95% + 500 000.90%+ 500 000.85%=1 350 000 đồng
b) Số tiền bạn Nam phải trả khi mua ba đôi giày BITI’S khi chọn
hình thức khuyến mãi thứ hai là :
2.500 000.88% = 1 320 000 đồng. 0,55
Vì 1 320 000 < 1 350 000 nên bạn Nam chọn hình thức khuyến 0,25
mãi thứ hai thì có lợi hơn. 5(1,0đ) l h r
a)Tính độ dài đường sinh l (SA) của chiếc nón
Ta có tam giác SAO vuông tại O
⇒SA2 = SO2 + AO2 ( Py ta go) 0,25 ⇒ l2 = 302 + (50:2)2 = 900 + 625 = 1525 ⇒l ≈39,1 cm 0,25
b)Diện tích vải cần chuẩn bị bao xung quanh của chiếc nón : 0,5
110%.Sxq =110%.πrl =110%.π.25.39,1 ≈3378cm2 6 (2,5đ) B N M A O I H C
a)Cm: AO vuông góc BC và tứ giác ABOC nội tiếp Ta có: OB = OC ( bán kính)
AB = AC ( tính chất hai tiếp tuyến cắt nhau)
⇒ OA là đường trung trực của BC 0,25 Vậy AO vuông góc BC 0,25 Xét tứ giác ABOC: 𝐴𝐴𝐴𝐴𝐴𝐴
�=900( AB là tiếp tuyến) 𝐴𝐴𝐴𝐴𝐴𝐴
�=900 (AC là tiếp tuyến) ⇒𝐴𝐴𝐴𝐴𝐴𝐴 �+𝐴𝐴𝐴𝐴𝐴𝐴 � = 1800 0,25
Vậy tứ giác ABOC nội tiếp được đường tròn 0,25 b)Cm : Cm: AM . AN = AH . AO Cm được AM . AN= AB2 0,5 Cm được AH . AO= AB2 0,25 Suy ra AM . AN = AH . AO 0,25
c) Cm: MI là phân giác của góc AMH
Cm: Tam giác AMH đồng dạng với tam giác AON
Suy ra 𝐴𝐴𝐴𝐴𝐴𝐴 � = 𝐴𝐴𝐴𝐴𝐴𝐴 � 0,25
Lại có: 𝐴𝐴𝐴𝐴𝐴𝐴 � = 2𝐴𝐴𝐴𝐴
�𝑁𝑁 (góc ở tâm và góc nội tiếp cùng chắn cung NMI) 𝐴𝐴𝐴𝐴𝑁𝑁 � = 𝐴𝐴𝐴𝐴
�𝑁𝑁( tứ giác CIMN nội tiếp)
Suy ra 𝐴𝐴𝐴𝐴𝐴𝐴
� = 2𝐴𝐴𝐴𝐴𝑁𝑁 �
Vậy : MI là tia phân giác của góc AMH 0,25
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng điểm TT Chủ đề Nội dung/Đơn vị kiến thức Vận dụng Nhận biết Thông hiểu Vận dụng cao TN TL TN TL TN TL TN TL
Vẽ đồ thị hàm số 𝑦𝑦 = 1
𝑎𝑎𝑥𝑥2 (P) và y = ax + b (Bài a) 1 Đồ thị (d) (1,0đ) hàm số 2đ 1 Tìm tọa độ giao điểm (Bài b) của (P) và (d) (1,0đ) Hệ 1 thức (Bài 2)
2 Vi-et và Hệ thức Vi-et (1,5 đ) 1,5đ ứng dụng Giải bài toán bằng 1 cách lập hệ phương (Bài 3) trình. (1,5đ) Bài tập 3 ứng Dạng ứng dụng tăng 1 1 dụng 4đ giảm Bài 4a Bài 4b thực tế (1,0đ) (0,5đ) Dạng toán ứng dụng 1 1 hình không gian (Bài 5a) (Bài 5b) (0,5đ) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài 6b) (Bài 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng
Đồ thị hàm số Vận dụng: 1 y = ax2 (P) và - Vẽ đồ thị hàm số 2 x − (Bài y = ax + b (d) (P): y = và ( ) x d : y = + 2 4 2 1a) 1 Đồ thị hàm số (a khác 0)
trên cùng hệ trục tọa độ Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong việc (Bài (P) và (d)
tìm tọa độ giao điểm của (P) và (d). 1b) Hệ thức Thông hiểu: 2 2 2 Vi-et và
Hệ thức Vi -et - Tính được tổng, tích, x1 +x2 các nghiệm của 1 ứng dụng
phương trình bậc hai một ẩn bằng hệ thức (Bài 2)
Vi-et (Biến đổi đơn giản) Giải bài toán Thông hiểu: bằng cách lập
- Phân tích đề bài, tìm mối quan hệ giữa các đại hệ phương
lượng cho trong đề bài, gọi ẩn, từ đó lập được hệ 1 trình.
2 phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức Bài tập Dạng ứng tăng/giảm 1 1
3 ứng dụng dụng tăng Vận dụng: Bài 4a Bài thực tế giảm
- Vận dụng kiến thức về tăng giảm, tỉ số % 4b
giải quyết một số vấn đề trong thực tiễn. Thông hiểu:
Dạng toán ứng - Tính được chiều cao của hình nón khi biết bán dụng hình
kính và đường sinh, thể tích của nón 1 1 không gian
Vận dụng cao: Bài 5a Bài
- Vận dụng hợp lí công thức tính thể tích hình 5b
nón và hình cầu để giải quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc
với đường tròn, mối quan hệ giữa các góc, phối 4
hợp các kiến thức để chứng minh.
Hình học Tứ giác nội tiếp
- Vận dụng các phương pháp chứng minh hai 1 1
tam giác đồng dạng, chứng minh song song, (Bài (Bài
vuông góc, 3 điểm thẳng hàng giải quyết yêu 6b) 6c) cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình
học phẳng để giải quyết yêu cầu đề bài.
ỦY BAN NHÂN DÂN HUYỆN CỦ CHI
ĐỀ KIỂM TRA CUỐI HỌC KÌ II
TRƯỜNG TRUNG HỌC CƠ SỞ Môn: TOÁN - LỚP 9 PHÚ MỸ HƯNG NĂM HỌC 2023-2024
Thời gian làm bài: 90 phút ĐÈ THAM KHẢO: 2 − Bài 1: x
( 2,0 đ) Cho parabol (P) : y = và đường thẳng ( ) x d : y = + 2 4 2
a/ Vẽ (P) và (d) trên cùng một hệ trục tọa độ Oxy
b/ Tìm tọa độ các giao điểm của (P) và (d) bằng phép toán
Bài 2: (1,5 đ) Cho phương trình 2 2
x − 5x − 6 = 0 có hai nghiệm là x ,x Không giải phương 1 2 trình.
a/ Tính x + x x .x 2 1 2 ; 1 2 ; 2 x + x 1 2
b/ Tính giá trị của các biểu thức: x + 2 x + 2 1 2 A = + x x 2 1
Bài 3 ( 1,5 đ) Lớp 9A có 16 nam và 24 nữ. Biết điểm trung bình của lớp 9A là 7,7 và điểm trung
bình của các bạn nam hơn điểm trung bình của các bạn nữ là 0,5. Tính điểm trung bình của các
bạn nam và của các bạn nữ ở lớp 9A?
Bài 4 ( 1,5 đ) Nhân ngày quốc tế phụ nữ 8/3. Một cửa hàng bán quà lưu niệm bán đồng giá 50
000 đồng một món và có chương trình giảm giá 15% cho một món hàng và nếu khách hàng mua
5 món trở lên thì từ món thứ 5 trở đi khách hàng chỉ phải trả 70% giá đã giảm. Đặc biệt, nếu
khách hàng mua trên 10 món thì cũng được khuyến mãi như trên và chỉ phải trả 80% tổng số tiền trên hóa đơn.
a/Cô Mai đến cửa hàng và mua tổng cộng 10 món hàng. Em hãy tính xem cô Mai phải trả bao nhiêu tiền ? .
b/Cùng thời điểm ấy chị Lan cũng đến mua hàng. Khi ra quầy tính tiền chị Lan đã trả tổng số
tiền là 397 800 đồng. Em hãy tính xem chị Lan đã mua bao nhiêu món hàng?
Bài 5: (1 điểm) Một cây kem có phần bánh hình nón, người ta đựng đầy kem trong phần bánh và
thêm một nửa hình cầu kem phía trên (xem hình). Đường kính của hình tròn đáy (phía bên trong
bánh hình nón) là 4cm và độ dài đường sinh bên của hình nón là 8cm .
a) Tính chiều cao và thể tích của chiếc bánh hình nón
b) Tính thể tích của phần kem trong cả cây kem.
Cho biết: Thể tích hình nón: 1 V = π 2 R h 3
(Với R : bán kính đường tròn đáy; h : chiều cao hình nón) Thể tích hình cầu: 4 V = π 3 R 3
(Với R : bán kính hình cầu)
Bài 6 : (2,5 điểm) Từ điểm A nằm bên ngoài đường tròn (O), kẻ hai tiếp tuyến AM, AN của (O).
a) Chứng minh: tứ giác AMON nội tiếp.
b) Kẻ cát tuyến ABC của (O) (B nằm giữa A và C). Gọi H là giao điểm của AO và MN.
Chứng minh : AB . AC = AH . AO.
c) Chứng minh : góc OHB = 1800 – góc OCB.
------------------------------Hết------------------------- Hướng dẫn chấm
ĐỀ KIỂM TRA CUỐI KÌ II - Môn: TOÁN - LỚP 9 NĂM HỌC 2023-2024 Thời gian: 90 phút ĐÈ THAM KHẢO: Bài 1: ( 1,5 đ)
a/Lập đúng 2 bảng giá trị, 1 Vẽ đúng hai đồ thị
b/ Phương trình hoành độ giao điểm của (P) và (d): 2 x 1 = − x + 2 4 2 0,5
Tìm được 2 nghiệm x1 = 2; x2 = -4 0,25 Tính được y 1 = 1; y2 = 4
Vậy tọa độ giao điểm của (P) và (d) là (2;1); (-4; 4) 0,25
Bài 2: ( 1,5 đ) Gọi x ,x là hai nghiệm của phương trình 2 x − 5x − 6 = 0 . 1 2
Không giải phương trình.
a/ Tính tổng và tích của hai nghiệm x ,x 1 2 − b 5 S c − = x + x = = 6 P = x x = = = − 1. 2 3 1 2 a 2 a 2 0,5 2 2 2 5 2 49
x + x = x + x − x x = − − = 1 2 ( 1 2 ) 2 1 2 ( ) 2.( ) 3 2 4 0,5
b/ Tính giá trị của các biểu thức: x + 2 x + 2 1 2 A = + x x 2 1 49 5 2 2 2 2 +
x + x + x + x x + x + x + A = x − 1 2 1 2 2 2 ( 1 2 ) ( 2 1 2 ) 4 2 59 = = = 0,5 x x x x − 1 2 1 2 3 12 Bài 3:
Gọi x là điểm trung bình của các bạn nam, y là điểm trung bình của các bạn 0,25 nữ ( ĐK: x, y > 0 )
Vì điểm trung bình của lớp 9A là 7,7. Nên ta có pt: 0,25
16x + 24y = 40.7,7 16x + 24y =308 (1)
Vì điểm trung bình của các bạn nam hơn điểm trung bình của các bạn nữ là 0,5. Nên ta có pt: x – y = 0,5 (2) 0,25 Từ (1) và (2) ta có hpt
16x + 24y = 308 x − y = 5 , 0 Giải hpt được x = 8 nhận y = 5 , 7 0,5
Vậy điểm trung bình của các bạn nam là 8,0 và điểm trung bình của các bạn nữ là 7,5 0,25 Bài 4
a/ Số tiền cô Mai phãi trả cho 10 món hàng là
4.50000 . 85% + 6.50000.85%.70.% = 34 8000 (đồng) 1,0 đ
b/ vì 397 800 > 348500 nên chị Lan mua nhiều họn 10 món hàng 0,5 đ
Số món hàng chị lan đã mua là:
( 397800 : 80% - 348500 ) : (50000. 85% .70%) +10 = 15 (món) Bài 5.
a/ Chiều cao hình nón: h = 2l − 2 R = 2 − 2 8 4 = 4 3cm 0,25 đ
Thể tích chiếc bánh hình nón: 1 2 1 2 π 64 3
V = π R h = π 4 .4 3 = 3 cm 1 3 3 3 0,25 đ
b/ Thể tích phần kem hình cầu: 4 3 4 3 π 256
V = π R = π 4 = 3 cm 2 3 3 3 0,25 đ Thể tích phần kem: π 256 π 64 3
V = V + V = + ≈ 3 384cm 1 2 3 3 0,25 đ Bài 6. 0,5 0,25 a)Xét tứ giác AMON 0,25
ta có góc AMO = góc ANO = 900 ( gt)
=> Góc AMO + góc ANO = 1800
=> tứ giác AMON nội tiếp
b)Chứng minh : AB . AC = AH . AO.
Ta có: AM = AN ( tính chất hai tiếp tuyến cắt nhau tại A)
Ta lại có: OM = ON ( bán kính)
=> OA là đường trung trực của đoạn thẳng MN
=> 𝑂𝑂𝑂𝑂 ⊥ 𝑀𝑀𝑀𝑀 tại H. 0,25
Chứng minh tam giác AMB đồng dạng tam giác ACB ( g-g) Suy ra AM2 = AB . AC 0,25
Sử dụng hệ thức lượng trong tam giác vuông AMO đường cao MH Suy ra AM 2 = AH . AO 0,25
Từ đó ta có AB . AC = AH . AO 0,25
c) chứng minh : OCBH là tứ giác nội tiếp. 0,5 đ
Chứng minh tam giác ABH đồng dạng tam giác AOC ( c-g-c)
Từ đó suy ra góc AHB = góc ACO
Suy ra tứ giác OCBH nội tiếp.
Suy ra: góc OHB = 1800 – góc OCB
UBND HUYỆN CỦ CHI ĐỀ THAM KHẢOKIỂM TRA CUỐI KÌ II
TRƯỜNG THCS PHƯỚC THẠNH MÔN: TOÁN 9 - NH: 2023 – 2024
Thời gian làm bài: 90 phút
(Không kể thời gian phát đề)
Bài 1. (2 điểm) Cho hàm số: 1 2 y − =
x có đồ thị là (P) và hàm số : y = x – 4 có đồ thị là (D). 2
a/ Vẽ (P) và (D) trên cùng một hệ trục tọa độ.
b/ Tìm các tọa độ giao điểm của (P) và đường thẳng (D) bằng phép toán.
Bài 2. (1,5 điểm) Cho phương trình: x2 - x - 12 = 0 có 2 nghiệm x và x . Không 1 2
giải phương trình, hãy tính giá trị biểu thức: N = (x − x )2 − 3x − 3x 1 2 1 2
Bài 3. (1,5 điểm)
Cỡ giày (Size) y của một người thay đổi phụ thuộc vào chiều dài bàn chân x
(inch) của người đó . Mối liên hệ giữa 2 đại lượng này là một hàm số bậc nhất
y = ax + b . Biết rằng cỡ giày người lớn nhỏ nhất là Size 5 và vừa với bàn chân dài 9
inch; bàn chân dài 11 inch có Size là 11. a) Hãy tìm a, b.
b) Bạn Bình có chiều dài bàn chân là 25,4 cm. Hỏi theo cách quy đổi trên bạn
Bình đi giày Size bao nhiêu? Biết 1 inch ≈ 2,54 cm
Bài 4. (1,5 điểm)
Đầu năm 2021, bác An mua 5000 cổ phiếu của công ty B với giá 300 000 đồng
/1 cổ phiếu. Đầu năm 2022 giá cổ phiếu tăng 30% so với giá đầu năm 2021 nên bác
An đã bán 3000 cổ phiếu.
a/ Hỏi sau khi bán 3000 cổ phiếu trên, bác An đã thu về số tiền là bao nhiêu?
b/ Sang đầu năm 2023, giá cổ phiếu giảm 35% so với giá đầu năm 2022 nên
bác An quyết định bán hết số cổ phiếu còn lại vì lo ngại giá sẽ tiếp tục giảm. Hỏi sau
2 năm đầu tư và đã bán hết toàn bộ cổ phiếu đã mua thì bác An lời bao nhiêu?
Bài 5. (1 điểm)
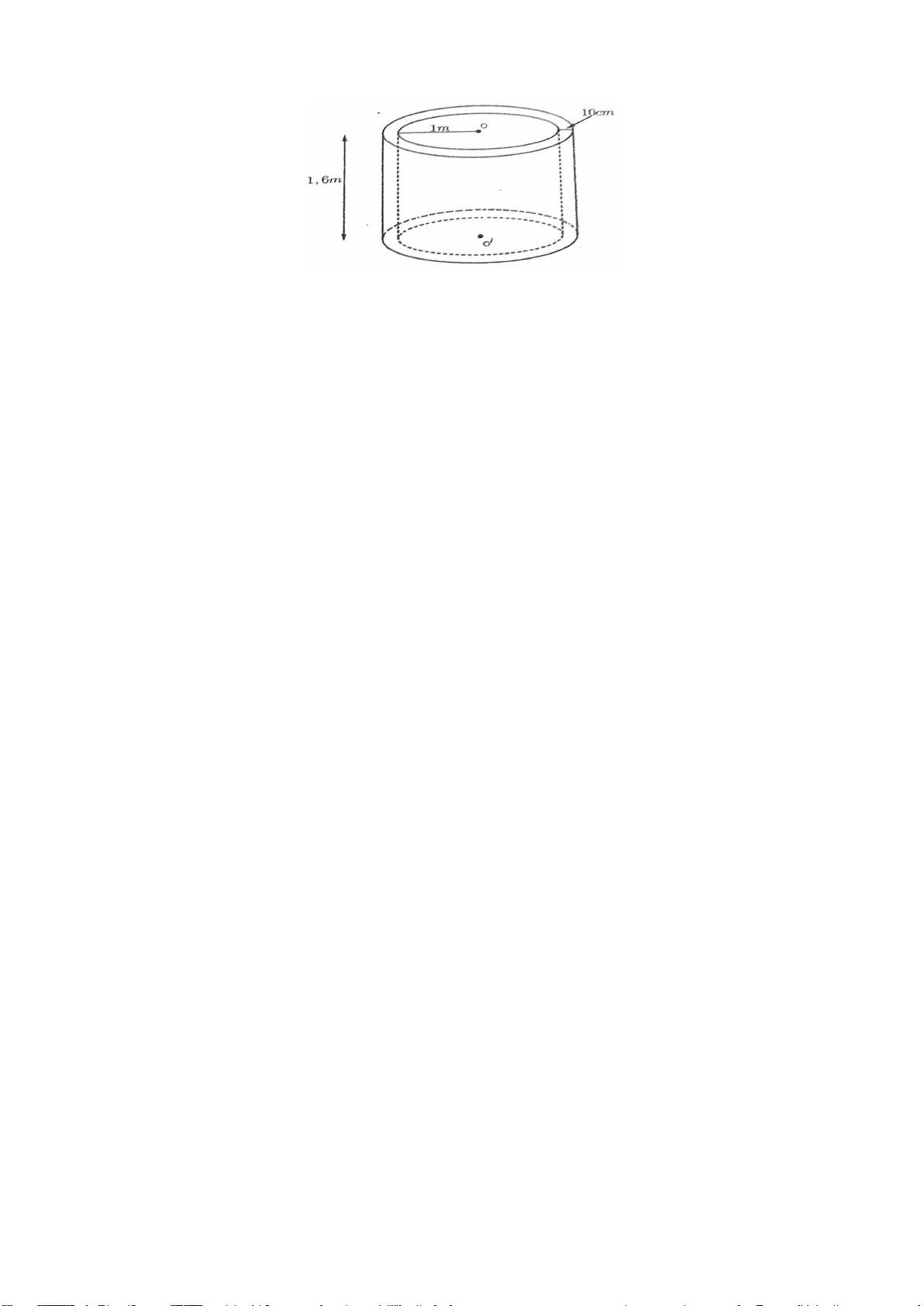
Một nhà kính trồng rau sạch có dạng nửa hình trụ đường kính đáy là 30 m,
chiều dài là 45 m. Người ta dùng màng nhà kính Politiv – Israel để bao quanh phần
diện tích xung quanh nửa hình trụ và hai nửa đáy hình trụ. Khi thi công hao phí
khoảng 10% diện tích nhà kính.
a) Tính diện tích phần màng cần cho nhà trồng rau trên (làm tròn đến hàng đơn 2 vị). Biết S = 2 Rh π ; xq S = R π d
, trong đó Sxq là diện tích xung quanh của hình trụ Sđ
là diện tích đáy của hình trụ, h là chiều cao hình trụ, R là bán kính hình trụ.
b) Tính chi phí cần có để mua màng làm kính trên biết rằng màng có khổ rộng
2,2 m và dài 100m có giá 13 000 đồng/m2 (chỉ bán theo cuộn).
Bài 6. (2,5 điểm)
Cho tam giác ABC nhọn (ABAD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh: tứ giác BCEF và tứ giác BDHF nội tiếp.
b) Gọi K là giao điểm của EF và BC. Chứng minh: KB. KC=KF. KE
c) Gọi M là giao điểm của AK và đường tròn (O). Chứng minh tứ giác AEFM nội tiếp được. ĐÁP ÁN Bà Đáp án Thang điểm a)
Vẽ (P) và (D) trên cùng một hệ trục tọa độ. Lập bảng giá trị của (P ) 0.25 0.5 0.25
Lập bảng giá trị của (D ) 0.25 Vẽ (P) 0.25 Vẽ (D) b)
Tìm các tọa độ giao điểm của (P) và đường thẳng (D)
Phương trình hoành độ giao điểm: 1 2 − x = x − 4 0,25 2 1 2
⇔ − x − x + 4= 0 0.25 2
⇔ x = 2 ; x = − 4 1 2 0,25 0.25 0.25
Vậy tọa độ giao điểm của (P) và (D) là: (2; -2) và (− 4; −8) Bài 2 1,5
phương trình: x2 - x - 12 = 0 có 2 nghiệm x và x 1 2
Theo hệ thức Vi-ét ta có : −b −(− ) 1 S = x + x = = = 1 1 2 a 1 0.25x2 c 12 P x x − = = = = 12 − 1 2 a 1 Khi đó : N = (x − x )2 − 3x − 3x 0.25x2 1 2 1 2 2 2 = x + x − 2x x − 3 x + x 1 2 1 2 ( 1 2) 0,25 2 = S − 3S − 4P 0,25 2 =1 − 3.1− 4.( 12 − ) = 46 Bài 3 1,5 a)
Thay x = 9; y = 5 vào công thức hàm số bậc nhất y = ax + b ta
được: 5 = 9a + b 0,25
Thay x = 11; y = 11 vào công thức hàm số bậc nhất y = ax + b ta
được: 11 =11a + b 0,25 9 a + b = 5 0,25
Giải hệ phương trình: 11 a + b = 11 Ta được: a = 3; b = - 22 0,25 Vậy y = 3x – 22 b)
Ta có 25,4cm≈10inch 0,25
Thay x =10 vào hàm số y = 3x − 22 , ta được: y = 3.10 − 22 = 8
Vậy bạn Bình đi giày Size 8. 0,25 Bài 4 1,5 a)
Giá một cổ phiếu vào đầu năm 2022 là:
300000.(1 + 30%) = 390 000 (đồng) 0.5x2
+ Sau khi bán 3000 cổ phiếu trên, bác An đã thu về số tiền là:
390000.3000 = 1 170 000 000 (đồng) b)
+ Giá một cổ phiếu vào đầu năm 2023 là:
390000.(1 – 35%) = 253500 (đồng)
+ Sau khi bán 3000 cổ phiếu trên, bác An đã thu về số tiền là: 0,25
253500.(5000 – 3000) = 507 000 000 (đồng)
+ Sau 2 năm đầu tư và đã bán hết toàn bộ cổ phiếu đã mua thì
bác An lời số tiền là:
(1 170 000 000 + 507 000 000) – 5000.300000 = 177 000 000 0,25 (đồng) Bài 5 a)
Bán kính đáy hình trụ là: 30: 2 =15 (m)
Diện tích xung quanh hình trụ là: 2 .15.45 π =1350π 2 (m )
Diện tích 1 đáy hình trụ là: 2 .15 π = 225π ( 2 m ) 0,25đ
Diện tích toàn phần hình trụ là: 1350π+ 2.225π =1800π 2 (m ) 0,25đ
b) Tính chi phí cần có để mua màng làm kính
1 .1800 .π(1+10%) =990π ≈3110
Diện tích phần màng cần là: 2 m2 0,25đ
Diện tích màng của một cuộn là: 2,2.100 = 220 2 (m )
Số tiền mua 1 cuộn màng là: 220.13000 = 2860000 (đồng)
Số cuộn cần mua làm màng là: 3110: 220 ≈14,1 (cuộn)
Vì chỉ bán theo cuộn nên để làm màng kính cần mua 15 cuộn.
Tổng chi phí cần có để mua màng làm kính là: 15.2860000 = 42900000 0,25 (đồng) Bài 6 A M E F O K B D C
a/ Chứng minh: tứ giác BCEF và tứ giác BDHF nội tiếp. góc BEC=góc BFC=900 0,25 Suy ra BCEF nt 0,25 Góc BFH+góc BDH=1800 Suy ra BDHF nội tiếp 0,25 x2
b/ Chứng minh: KB. KC=KF. KE xét ∆KBF và ∆KEC 0.25 ta có: góc K chung 0.25 góc KFB=góc KCE 0.25 suy ra ∆KBF đd ∆KEC (gg) 0.25 suy ra KB. KC=KF. KE
c) Chứng minh tứ giác AEFM nội tiếp. Cm được KM.KA=KF.KE 0.25
Cm được ∆KFM đd ∆KAE (cgc) Suy ra góc KFM =gócKAE 0.25 Suy ra AEFM nội tiếp UBND HUYỆN CỦ CHI
ĐỀ THAM KHẢO KIỂM TRA CUỐI KỲ 2
TRƯỜNG THCS PHƯỚC VĨNH AN NĂM HỌC 2023 – 2024 MÔN: TOÁN – LỚP 9 Thời gian: 90 phút Bài 1. (2 điểm)
a) Vẽ trên cùng hệ trục Oxy đồ thị (P) y = −𝑥𝑥2 và (d) y = x – 4 2
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính. BÀI 2 (1.5 điểm):
Cho phương trình bậc hai 2x2 + 4x + 7 = 0 có hai nghiệm x , x . Không giải phương trình, tính 1 2
giá trị của biểu thức: (x − 3x )(x − 3x ) 1 2 2 1 BÀI 3 (1.5 điểm)
Tổng số học sinh của lớp 9A và 9B vào đầu năm học là 85 học sinh. Đến đầu học kì II , lớp 9A có
1 học sinh đi du học và 2 học sinh chuyển qua lớp 9B nên lúc này số học sinh lớp 9A bằng số học
sinh lớp 9B. Tính số học sinh đầu năm của lớp 9A và 9B . BÀI 4 (1.5 điểm)
Bác Hùng nhập kho 500 trái dừa sáp với giá vốn 150 000 đồng một trái và chi phí vận chuyển là 2
triệu đồng. Biết rằng 12% số trái bị hỏng trong quá trình vận chuyển và số trái còn lại được bán hết.
a) Hỏi nếu giá bán mỗi trái dừa sáp là 210 000 đồng thì bác Hùng lời được bao nhiêu tiền?
b) Bạn An làm việc cho bác Hùng và được bác trả lương như sau: lương cơ bản 5 triệu đồng và tiền
thưởng bằng 20% tiền lời của số trái dừa bán vượt chỉ tiêu (trong đó chỉ tiêu bác Hùng đưa ra là
mỗi ngày phải bán được 14 trái dừa). Hỏi trong tháng 4, bạn An nhận được bao nhiêu tiền lương?
Biết trong tháng 4 bạn đã giúp bác Hùng bán hết số dừa không bị hỏng. BÀI 5 (1 điểm)
Một cái thùng dùng để đựng gạo có dạng nửa hình cầu với đường kính 50cm, phần gạo vun lên có dạng hình nón cao 12cm.
a) Tính thể tích phần gạo trong thùng (Làm tròn đến chữ số thập phân thứ nhất ).
b) Nhà bạn An dùng lon sữa bò dạng hình trụ với bán kính đáy là 5cm, chiều cao là 14cm dùng để
đong gạo mỗi ngày. Biết rằng mỗi ngày nhà An ăn 4 lon gạo và mỗi lần đong thì lượng gạo chiếm
90% thể tích của lon. Hỏi cần ít nhất bao nhiêu ngày để nhà An có thể ăn hết số gạo trong thùng? (Biết 1 2 2 4 3
V = π R h V = π R h V = π R ) n . . ; t . . ; c . 3 3 BÀI 6 (2.5 điểm)
Cho ∆ABC (AB < AC ) có ba góc nhọn nội tiếp đường tròn (O) và hai đường cao BE và CF cắt
nhau tại 𝐻𝐻 (𝐸𝐸 ∈ 𝐴𝐴𝐴𝐴; 𝐹𝐹 ∈ 𝐴𝐴𝐴𝐴). Tia EF và CB cắt nhau tại K.
a. Chứng minh: tứ giác AEHF nội tiếp và AH vuông góc với BC.
b. Chứng minh : 𝐾𝐾𝐸𝐸. 𝐾𝐾𝐹𝐹 = 𝐾𝐾𝐴𝐴. 𝐾𝐾𝐴𝐴
c. Gọi I là trung điểm của BC. AK cắt (𝑂𝑂) tại N (N khác 𝐴𝐴).
Chứng minh: ba điểm N, H, I thẳng hàng.
…………………….HẾT………………….. HƯỚNG DẪN CHẤM BÀI ĐÁP ÁN ĐIỂM 1a Bảng giá trị đúng 0,25+0,25 Vẽ đúng (P) và (d) 0,25+0,25 1b PT hoành độ giao điểm: 0,25 2 2 − x 0,25 = − 4 − <=> x x − x + 4 = 0 2 2 -Tìm được x 0,25 1 = 2; x2 = -4 -Tìm được y 1 = -2; y2 = -8 0,25
-Kết luận đúng 2 tọa độ giao điểm (2;-2) và (-4;-8) 2
Cho phương trình: 2x2 - 7x + 5 = 0 ∆ = 9 > 0
Vậy pt có 2 nghiệm phân biệt 0,25 Theo Viet, có: − b 7
S = x + x = = 1 2 a 2 0,25 c 5 P = x x = = 1 2 a 2 0,25
*(x −3x )(x −3x ) 1 2 2 1
= x x − x − x + x x 0,25 1 2 3 21 3 22 9 1 2 = P − ( 3 2
S − 2P) + 9P 0,25 5 7 2 5 5 = − . 3 ( ) − . 2 + . 9 2 2 2 2 13 = 0,25 4 3
Gọi số học sinh đầu năm của lớp 9A là x(hoïc sinh)
Gọi số học sinh đầu năm của lớp 9B là y(hoïc sinh) 0,25 (đk: x,y nguyên dương) 0,25
Vì tổng số học sinh của lớp 9A và 9B vào đầu năm học là 85 học sinh
nên ta có phương trình: x + y = 85 0,25
Vì Đến đầu học kì II , lớp 9A có 1 học sinh đi du học và 2 học sinh
chuyển qua lớp 9B nên lúc này số học sinh lớp 9A bằng số học sinh lớp
9B nên ta có phương trình:
x – 3 = y + 2 <=> x – y = 5 0,25 Ta có hệ phương trình: x + y = 85 x – y = 5 0,25
<=> x = 45 (Nhận) y = 40 (nhận)
Vậy Số học sinh đầu năm của lớp 9Alà 45 học sinh 0,25
Số học sinh đầu năm của lớp 9B là 40 học sinh 4a
Tổng số vốn mà bác Hùng bỏ ra là:
500.150 000 + 2 000 000 = 77 000 000 (đồng) 0,25
Số trái dừa không bị hỏng là:
500.(100% – 12%) = 440 (trái)
Tổng số tiền bác Hùng thu được là: 0,25
440.210000 = 92400000 (đồng) 0,25
Vậy bác Hùng lời: 92 400 000 – 77 000 000 = 15 400 000 đồng 0,25 4b
Tiền lời khi bán 1 trái dừa là: 210 000 – 150 000 = 60 000 (đồng)
Vì tháng 4 có 30 ngày nên số trái dừa bán vượt chỉ tiêu là: 0,25 440 – 30.14 = 20 (trái)
Tiền lương bạn An nhận được khi bán hết 440 trái dừa trong tháng 4 là: 5
000 000 + 20%.60000.20 = 5 240 000 (đồng) 0,25 5a 1 1 4 3 1 2 38750 0,25
V = V +V = π + π = π ≈ cm g c n . . .25 .25 .12 40578,9( 3) 2 2 3 3 3 0,25 5b Thể tích lon: 2 π = π ( 3 .5 .14 350 cm ) 0,25
Thể tích gạo một ngày múc: 2 π = π ( 3
4.90%. .5 .14 1260 cm )
Ta có: 38750π :1260π ≈10,3 3
Vậy cần ít nhất 11 ngày để dùng hết số gạo trong thùng 0,25 Bài 6: (2.5đ) A E N F O H K C B I P a) Xét tứ giác BFEC có: �AEH � = 90o(gt) ⇒ AEH � + AFH � = 180o 0,25 AFH � = 90o(gt) 0,25 ⇒BFEC nội tiếp Xét ∆ABC
Ta có: BE và CF là 2 đường cao cắt nhau tại H => H là trực tâm
=> AH là đường cao thứ ba 0,25 => AH ⊥ BC 0,25 b. *Tứ giác BCEF nội tiếp 0,5 Xét ΔKBFvà ΔKEC có : + KBF � = KEC
� (tứ giác BFEC nội tiếp) + K� ∶ chung ⇒ ΔKBF ∼ ΔKEC(g. g) 0,25 KB KF ⇒ KE = KC ⇒ KB. KC = KF. KE 0,25 c. Kẻ đường kính AP
*Tứ giác BHCP là hbh => I là trung điểm HP
*ΔKNF ∼ ΔKEA(c. g. c) ⇒ KFN � = KAE �
⇒ Tứ giác ANFE nội tiếp (góc ngoài bằng góc trong đối ) ⇒5 điểm ,
A N,F,H,E cùng thuộc đường tròn đường kính AN 0,25 ⇒ ANH
� = 90o (góc nội tiếp chắn nửa đường tròn) ⇒ AN ⊥ NH
Ta lại có: 𝐴𝐴𝐴𝐴𝐴𝐴
� = 90𝑜𝑜 (góc nội tiếp chắn nửa đường tròn)
⇒ 𝐴𝐴𝐴𝐴 ⊥ 𝐴𝐴𝐴𝐴
⇒N,H,P thẳng hàng 0,25
Mà I là trung điểm HP nên N,H,I thẳng hàng. UBND HUYỆN CỦ CHI
ĐỀ KIỂM TRA CUỐI KỲ II
TRƯỜNG THCS PHẠM VĂN CỘI NĂM HỌC 2023–2024 MÔN: TOÁN – LỚP 9 ĐỀ THAM KHẢO
(Đề thi có 02 trang)
Thời gian: 90 phút (Không kể thời gian phát đề) Bài 1 : (2 điểm) 2 Cho parabol (P) : x y =
và đường thẳng (d) : y = x + 4 2
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ các giao điểm của (P) và (d) bằng phép tính.
Bài 2 :(1,5 điểm) Cho phương trình: x2 + 4x – 1 = 0.
Không giải phương trình, hãy tính giá trị của biểu thức: x x 5 1 2 A= x x 2 2 1 Bài 3 :(1,5 điểm)
Hai trường A, B có 250 học sinh lớp 9 dự thi vào lớp 10, kết quả có 210 học
sinh đã trúng tuyển. Tính riêng tỉ lệ đỗ thì trường A đạt 80%, trường B đạt
90%. Hỏi mỗi trường có bao nhiêu học sinh lớp 9 dự thi vào lớp 10. Bài 4: ( 1,5 điểm)
Một chủ cửa hàng đã nhập 700 cái điện thoại với giá 18 triệu đồng mỗi cái.
Đợt 1 ông đã bán 525 cái với giá 25,2 triệu đồng một cái.
a/ Tính số tiền thu được sau đợt 1 ?
b/ Sau đó ông giảm giá để bán hết số điện thoại còn lại. Vậy ông phải bán mỗi
cái điện thoại còn lại với giá bao nhiêu để có lợi nhuận đạt tỉ lệ 20% ? Bài 5 :(1 điểm)
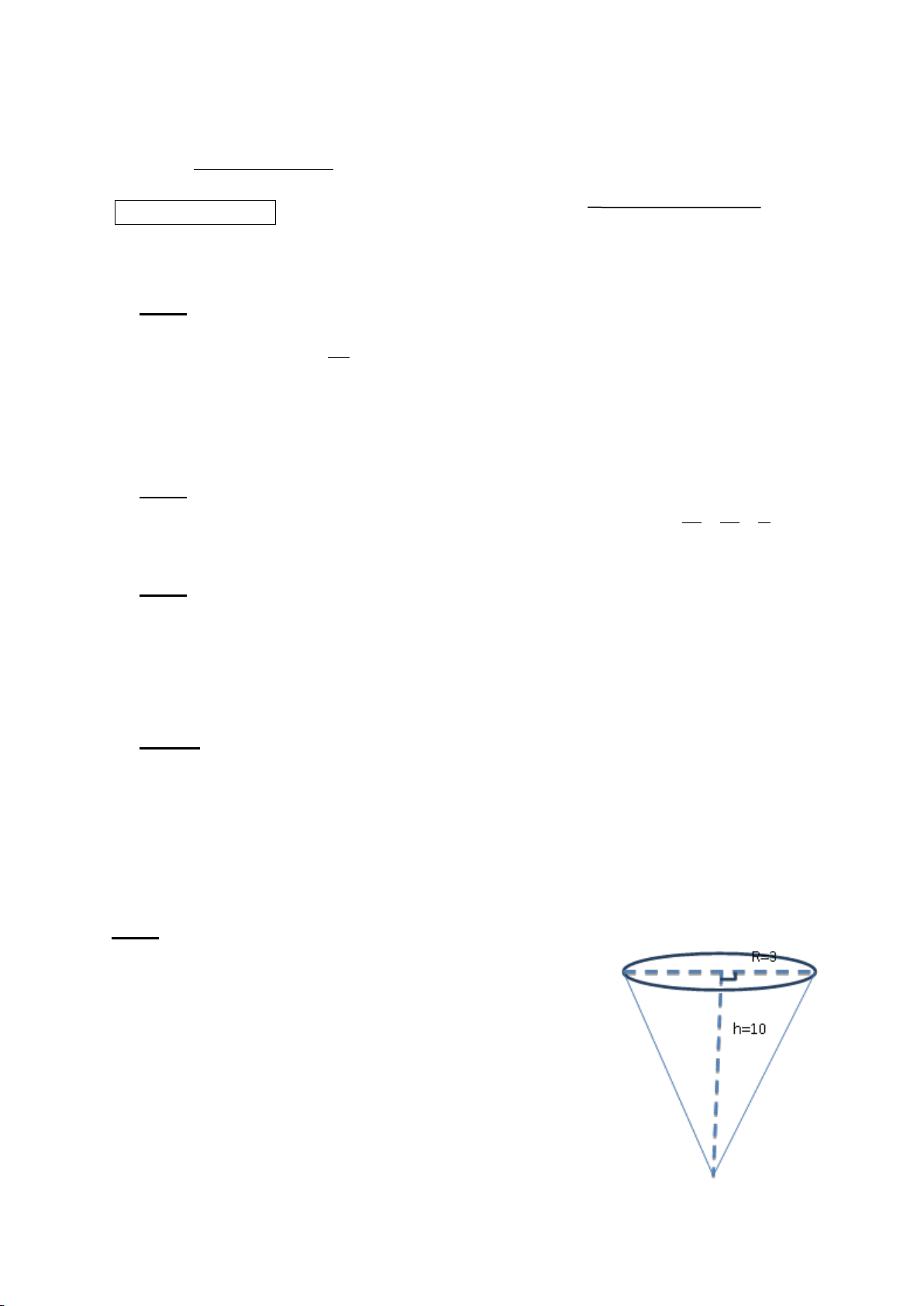
Một chiếc bánh ống quế đựng kem Ý có dạng
một hình nón có kích thước như hình vẽ: R=
3cm, h= 10 cm. Cho biết 1 cm2 bánh quế có khối lượng 0,12 gam.
a/ Tính thể tích có thể chứa kem của chiếc bánh quế ?
b/Tính khối lượng bánh ống quế khi học sinh
ăn một cây kem (cho 3,14). Bài 6: (2,5 điểm)
Cho ∆ABC nhọn (AB < AC) nội tiếp đường tròn (O), có đường cao AD, AD cắt
(O) tại điểm thứ hai là M. Vẽ ME vuông góc với AC (E thuộc AC), đường thẳng
ED cắt đường thẳng AB tại I.
a) Chứng minh tứ giác MDEC nội tiếp và = IBM IDM . b) Tính
AIM và chứng minh AB.AI = AD.AM.
c) Gọi N là điểm đối xứng với M qua I, F là điểm đối xứng với M qua E. NF
cắt AD tại H. Chứng minh BH // MF. HẾT ĐÁP ÁN Bài 1 : - Bảng giá trị 1 điểm (2 điểm) - Đồ thị 1 điểm
Toạ độ giao điểm (4; -8) và (-2 ;2) Bài 2 :
∆ = 20 > 0 .Phương trình có hai nghiệm phân biệt 0,25điểm
(1,5điểm) S = – 4 ; P = – 1 0,25điểm x x 5 1 2 A = - x x 2 2 1 2 S 2P 5 P 2 0,5điểm 31 2 0,5điểm Bài 3 :
-Gọi x ; y (x,y > 0,hoc sinh) lớp 9 trường A , trường B 0,25điểm
(1,5điểm) -Số học sinh đỗ lớp 10 trường A : 80%x = 0,8x
-Số học sinh đỗ lớp 10 trường B : 90%x = 0,9x
-Vì tổng số học sinh lớp 9 hai trường là 250 hoc sinh nên : x + y = 250
-Vì tổng số học sinh đỗ lớp 10 hai trường là 210 hoc sinh nên : 0,8x 1 điểm + 0,9y =210 0,25điểm
Ta có hệ phương trình : x+ y =250 x =150 ⇔
0,8x + 0,9y = 210 y =100
Trường A : 150 học sinh ; trường B : 100 học sinh Bài 4:
a/ số tiền thu được trong đợt 1 là 1 điểm (1,5 điểm)
525.25,2 13230 (triệu đồng)
b/ Số tiền vốn bỏ ra lúc đầu là: 700.18 12600 (triệu đồng) Để có lợi nhuận 0,5 điểm
20% số tiền vốn cần thu về là:
12600.(1 20%) 15120 (triệu đồng)
Số tiền cần thu về khi bán 175 cái điện thoại ở đợt 2 là:
15120 13230 1890 (triệu đồng)
Giá bán một cái điện thoại lúc sau là: 1890 : 175 10,8 (triệu đồng) Bài 5 :
a/ Thể tích có thể chứa kem của bánh là: 1 . 32. 𝜋𝜋. 10 ≈94,2cm2 0,5 điểm (1điểm) 3
b/Đường sinh của hình nón: l 2 2 3 10 0,25điểm
Diện tích xung quanh hình nón: 3,14.3. 2 2 3 10
Khối lượng bánh quế là: 0,12.98,35 11,80 gam 0,25điểm 0,25điểm Bài 6 : A (0,75điểm 1 0,25điểm ) F 0,25điểm L H E 1 1 2 N B D C I M
Cho ∆ABC nhọn (AB < AC) nội tiếp đường tròn (O), có đường cao
AD, AD cắt (O) tại điểm thứ hai là M. Vẽ ME vuông góc với AC (E
thuộc AC), đường thẳng ED cắt đường thẳng AB tại I.
a) Chứng minh tứ giác MDEC nội tiếp và = IBM IDM b) Tính
AIM và chứng minh AB.AI = AD.AM.
c) Gọi N là điểm đối xứng với M qua I, F là điểm đối xứng với M
qua E. NF cắt AD tại H. Chứng minh BH // MF.
a/ Chứng minh tứ giác MDEC nội tiếp và 0,5 điểm = IBM IDM . 0,5điểm * Ta có: 0 MDC = MEC = 90
⇒MDEC nội tiếp ( Hai đỉnh kề D, E cùng nhìn MC dưới 2 góc bằng nhau)
* Ta có ABMC nội tiếp (O) ⇒ = IBM ACM = Mà ACM IDM(MDEC nt) ⇒ = IBM IDM b/Tính
AIM và chứng minh AB.AI = AD.AM. *Cmđ IBDM nội tiếp 0,5điểm 0,5điểm 0 BIM + BDM = 180 0 ⇒ BIM = 90 *Cmđ AD ∆ B ∽ AI ∆ M (g.g) ⇒ AB.AI = AD.AM c/Cm: BH // MF
Cmđ: IE là đường trung bình ∆MNF ⇒ IE // NF Cmđ: D là trung điểm MH 0,5điểm Cmđ: BC là phân giác MBH ⇒ = = B B A 1 2 1 Mà + 0 = ⇒ + 0 A C 90
B C = 90 ⇒ ∆BLC vuông tại L 1 1 1 1
⇒ BH ⊥ AC mà MF ⊥ AC ⇒ BH // MF
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 Mức độ đánh giá Tổng Nội dung/Đơn vị kiến điểm TT Chủ đề thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TN TL TN TL TN TL TN TL
Vẽ đồ thị hàm số 𝑦𝑦 = 1 (Bài a) Đồ thị
𝑎𝑎𝑥𝑥2 (P) và y = ax + b (d) (1,0đ) 1 2đ hàm số 1 Tìm tọa độ giao điểm (Bài b) của (P) và (d) (1,0đ) Hệ thức 1 Vi-et và (Bài 2) 2 Hệ thức Vi-et 1,5đ ứng (1,5 đ) dụng Giải bài toán bằng 1 cách lập hệ phương (Bài 3) trình. (1,5đ) Bài tập ứng Dạng ứng dụng tăng 1 1 3 4đ dụng giảm Bài 4a Bài 4b thực tế (1,0đ) (0,5đ) Dạng toán ứng dụng 1 1 hình không gian (Bài 5a) (Bài 5b) (0,5đ) (0,5đ) 1 (Bài 6a) (1,0đ) 4
Hình học Tứ giác nội tiếp 2,5đ 1 1 (Bài 6b) (Bài 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng Đồ thị hàm số 1 y = ax2 (P) và Vận dụng: (Bài
y = ax + b (d) - Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ 1a) 1 Đồ thị trục tọa độ hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong việc (Bài (P) và (d)
tìm tọa độ giao điểm của (P) và (d). 1b) Hệ thức Thông hiểu: 2 2 2 Vi-et và
Hệ thức Vi -et - Tính được tổng, tích, x1 +x2 các nghiệm của 1 ứng dụng
phương trình bậc hai một ẩn bằng hệ thức (Bài 2)
Vi-et (Biến đổi đơn giản) Giải bài toán Thông hiểu: bằng cách lập
- Phân tích đề bài, tìm mối quan hệ giữa các đại hệ phương
lượng cho trong đề bài, gọi ẩn, từ đó lập được hệ 1 trình.
2 phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức Dạng ứng tăng/giảm 1 Bài tập dụng tăng Vận dụng: 1 Bài 3 ứng dụng giảm
- Vận dụng kiến thức về tăng giảm, tỉ số % Bài 4a 4b thực tế
giải quyết một số vấn đề trong thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện tích toàn
Dạng toán ứng phần, thể tích của hình trụ (hoặc hình nón, hình dụng hình cầu) 1 1 không gian
Vận dụng cao: Bài 5a Bài
- Vận dụng hợp lí công thức tính diện tích, thể 5b
tích hình trụ (hoặc hình nón, hình cầu) để giải
quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc
với đường tròn, mối quan hệ giữa các góc, phối 4
hợp các kiến thức để chứng minh.
Hình học Tứ giác nội tiếp
- Vận dụng các phương pháp chứng minh hai 1 1
tam giác đồng dạng, chứng minh song song, (Bài (Bài
vuông góc, 3 điểm thẳng hàng giải quyết yêu 6b) 6c) cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình
học phẳng để giải quyết yêu cầu đề bài.
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng
TT Chủ đề Nội dung/Đơn vị kiến điểm thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TN TL TN TL TN TL TN TL
Vẽ đồ thị hàm số 𝑦𝑦 = 1
𝑎𝑎𝑥𝑥2 (P) và y = ax + b (Bài a) 1 Đồ thị (d) (1,0đ) hàm số 2đ 1 Tìm tọa độ giao điểm (Bài b) của (P) và (d) (1,0đ) Hệ thức 1 2 Vi-et và (Bài 2) ứng Hệ thức Vi-et (1,5 đ) 1,5đ dụng Giải bài toán bằng 1 cách lập hệ phương (Bài 3) trình. (1,5đ) Bài tập 3 ứng Dạng ứng dụng tăng 1 1 dụng 4đ giảm Bài 4a Bài 4b thực tế (1,0đ) (0,5đ) Dạng toán ứng dụng 1 1 hình không gian (Bài 5a) (Bài 5b) (0,5đ) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài 6b) (Bài 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng Đồ thị hàm số 1 y = ax2 (P) và Vận dụng: (Bài
y = ax + b (d) - Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ 1a) 1 Đồ thị trục tọa độ hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong việc (Bài (P) và (d)
tìm tọa độ giao điểm của (P) và (d). 1b) Hệ thức Thông hiểu: 2 2 2 Vi-et và
Hệ thức Vi -et - Tính được tổng, tích, x1 +x2 các nghiệm của 1 ứng dụng
phương trình bậc hai một ẩn bằng hệ thức (Bài 2)
Vi-et (Biến đổi đơn giản) Giải bài toán Thông hiểu:
bằng cách lập - Phân tích đề bài, tìm mối quan hệ giữa các đại hệ phương
lượng cho trong đề bài, gọi ẩn, từ đó lập được hệ 1 trình.
2 phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức Dạng ứng tăng/giảm 1 Bài tập dụng tăng Vận dụng: 1 Bài 3 ứng dụng giảm
- Vận dụng kiến thức về tăng giảm, tỉ số % Bài 4a 4b thực tế
giải quyết một số vấn đề trong thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện tích toàn
Dạng toán ứng phần, thể tích của hình trụ (hoặc hình nón, hình dụng hình cầu) 1 1 không gian
Vận dụng cao: Bài 5a Bài
- Vận dụng hợp lí công thức tính diện tích, thể 5b
tích hình trụ (hoặc hình nón, hình cầu) để giải
quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc
với đường tròn, mối quan hệ giữa các góc, phối 4
hợp các kiến thức để chứng minh.
Hình học Tứ giác nội tiếp
- Vận dụng các phương pháp chứng minh hai 1 1
tam giác đồng dạng, chứng minh song song, (Bài (Bài
vuông góc, 3 điểm thẳng hàng giải quyết yêu 6b) 6c) cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình
học phẳng để giải quyết yêu cầu đề bài. UBND HUYỆN CỦ CHI
ĐỀ THAM KHẢO KIỂM TRA CUỐI KỲ II
TRƯỜNG THCS PHƯỚC HIỆP NĂM HỌC 2023 - 2024 Môn: TOÁN - LỚP 9
Thời gian : 90 phút
Bài 1. (2,0 điểm Cho hàm số y = 1 2
x có đồ thị (P) và hàm số y = x + 4 có đồ thị là 2 (D).
a/ Vẽ đồ thị (P) và (D) trên cùng mặt phẳng tọa độ.
b/ Tìm tọa độ giao điểm của (P) và (D) bằng phép toán.
Bài 2. (1,5 điểm). Cho phương trình: 2x2 + 3x – 14 = 0 có 2 nghiệm là x , x . Tính giá 1 2
trị của biểu thức sau: 𝑃𝑃 = 𝑥𝑥 2 2
1 + 𝑥𝑥2 − 7𝑥𝑥1𝑥𝑥2
Bài 3: (1,5 điểm) Để có tủ sách chung của lớp, giáo viên chủ nhiệm lớp 9A phát động
và giao chỉ tiêu cho lớp đóng góp 200 quyển sách cũ. Nhằm nâng cao tinh thần thi đua
giữa nam và nữ trong lớp, lớp trưởng cho hai đội thi đua thu góp sách cũ. Cả hai đội
đều rất tích cực. Đội nam thu gom vượt chỉ tiêu 20%, đội nữ thu gom vượt chỉ tiêu 25%
nên tổng số sách của lớp 9A thu được là 246 quyển. Hỏi mỗi đội được giao chỉ tiêu góp bao nhiêu quyển sách?
Bài 4: (1,5 điểm) Nhân dịp tựu trường, cửa hàng sách A thực hiện chương trình
giảm giá cho học sinh khi mua các loại sách bài tập, sách giáo khoa, sách tham
khảo,… Chương trình áp dụng với bộ sách bài tập môn Toán lớp 9 (trọn bộ bao
gồm 5 quyển) như sau: Nếu mua quyển tập 1 thì được giảm 5% so với giá niêm
yết. Nếu mua quyển tập 2 thì quyển tập 1 được giảm 5% còn quyển tập 2 được
giảm 10% so với giá niêm yết. Nếu mua trọn bộ 5 quyển thì ngoài hai quyển đầu
được giảm giá như trên, từ quyển tập 3 trở đi mỗi quyển sẽ được giảm 20% so với giá niêm yết.
a) Bạn Bình mua trọn bộ 5 quyển sách bài tập Toán lớp 9 ở cửa hàng sách A thì
phải trả số tiền là bao nhiêu, biết rằng mỗi quyển sách bài tập Toán lớp 9 có giá
niêm yết là 30 000 đồng.
b) Cửa hàng sách B áp dụng hình thức giảm giá khác cho loại sách bài tập Toán
lớp 9 nêu trên là: nếu mua từ 3 quyển trở lên thì sẽ giảm giá 5000 đồng cho mỗi
quyển. Nếu bạn Bình mua trọn bộ 5 quyển sách bài tập Toán lớp 9 thì bạn Bình
nên mua ở cửa hàng sách nào để số tiền phải trả ít hơn? Biết rằng giá niêm yết
của hai cửa hàng sách là như nhau.
Bài 5: (1 điểm) Nước giải khát thường đựng trong lon nhôm
và cỡ lon phổ biến chứa được khoảng 330ml chất lỏng, được
thiết kế hình trụ với chiều cao khoảng 10,2 cm (phần chứa
chất lỏng), đường kính đáy khoảng 6,42 cm.
Nhưng hiện nay các nhà sản xuất có xu hướng tạo ra
những lon nhôm với kiểu dáng cao thon hơn. Tuy chi phí sản
xuất những chiếc lon cao này tốn kém hơn, nhưng nó lại dễ
đánh lừa thị giác và được người tiêu dùng ưa chuộng hơn.
a/ Một lon nước ngọt cao 13,41 cm (phần chứa chất lỏng), đường kính đáy là 5,6
cm. Hỏi lon nước ngọt cao này có thể chứa được hết lượng nước ngọt của một lon có
cỡ phổ biến không ? Vì sao ?
(Biết thể tích hình trụ: V = πr2h, với π ≈ 3,14).
b/ Vì sao chi phí sản xuất chiếc lon cao tốn kém hơn chiếc lon cỡ phổ biến ?
Biết diện tích xung quanh, diện tích toàn phần hình trụ được tính theo công thức:
Sxq = 2πrh và Stp = Sxq + 2Sđáy
Bài 6: (2,5 điểm) Cho ∆ABC nhọn ( AB < AC). Vẽ đường tròn tâm O có đường kính BC cắt
2 cạnh AB và AC theo thứ tự tại E và F. BF và CE cắt nhau tại H. AH cắt BC tại D. Gọi I là trung điểm AH.
a/ Chứng minh tứ giác AEHF nội tiếp đường tròn tâm I và AD ⊥ BC.
b/ Chứng minh: AE.AB = AF.AC
c/ Chứng minh tứ giác EDOF nội tiếp. HƯỚNG DẪN CHẤM Bài 1. (2,0 điểm). a/-BGT: ( 0,5 điểm) x -2 -4 0 2 4 1 2 y = x 2 2 8 0 2 8 x 0 4 Yy =x+4 4 8 H ọc sinh vẽ đúng 0 ( ,5đ)
b/ Phương trình hoành độ giao điểm của (P) và (d) là: 1 2 𝑥𝑥2 = 𝑥𝑥 + 4
⇔ 1 𝑥𝑥2 − 𝑥𝑥 − 4 = 0 ( 0,25 điểm) 2 ⇔ �𝑥𝑥 = 4 ( 0,25 điểm) 𝑥𝑥 = −2
Thay x = 4 vào y = x + 4, ta có: y = 4 + 4 = 8 ( 0,25 điểm)
Thay x = -2 vào y = x + 4, ta có y = -2 + 4 = 2 ( 0,25 điểm )
Vậy tọa độ giao điểm của (P) và (d) là ( 4;8) và ( -2; 2) Bài 2. (1,5 điểm) Theo hệ thức Vi-et b − 3 S x x − = + = = ( 0,25 điểm) 1 2 a 2 c 14 P x . x − = = = = 7 − ( 0,25 điểm) 1 2 a 2
Tính giá trị của biểu thức P = 𝑥𝑥 2 2
1 + 𝑥𝑥2 − 7𝑥𝑥1𝑥𝑥2
P = (𝑥𝑥1 + 𝑥𝑥2)2 − 2𝑥𝑥1𝑥𝑥2 − 7𝑥𝑥1𝑥𝑥2 (0,25 điểm)
= (x + x )2 −9x x 1 2 1 2 (0,25 điểm) 2
= �−3� − 9. (−7) (0,25 điểm) 2 =261 ( 0,25 điểm) 4
Bài 3: (1,5 điểm)
Gọi x,y (quyển) lần lượt là số sách củ đội nam và đội nữ góp được theo chỉ tiêu ( *
x, y ∈ N ) (0,25điểm)
Vì giáo viên chủ nhiệm lớp 9A phát động và giao chỉ tiêu cho lớp đóng góp 200 quyể n
sách cũ nên ta có phương trình: x + y = 200 (1) (0,25điểm)
Vì đội nam thu gom vượt chỉ tiêu 20%, đội nữ thu gom vượt chỉ tiêu 25% và tổn g số
sách của lớp 9A thu được là 246 quyển nên ta có phương trình: 120%x+125%y = 246 (2) (0,25điểm)
Từ (1) và (2) ta có hệ phương trình: x + y = 200 ( 0,25 điểm) 120% x +125%y = 246
Giải hệ phương trình ta được x = 80 (nhận) ( 0,25 điểm) y = 120
Vậy đội nam được giao chỉ tiêu góp 80 quyển, đội nữ được giao chỉ tiêu góp 120 quyển ( 0,25 điểm)
Bài 4: (1,5 điểm)
a) Giá của quyển tập 1: 30 000.(100% - 5%) = 28 500 (đồng) ( 0,25 điểm)
Giá của quyển tập 2: 30 000.(100% - 10%) = 27 000 (đồng)
( 0,25 điểm )
Giá của 3 quyển còn lại: 30 000.(100% - 20%).3 = 72 000 (đồng) ( 0,25 điểm )
Vậy nếu bạn Bình mua trọn bộ 5 quyển sách bài tập Toán lớp 9 ở cửa hàng sác h
A thì phải trả số tiền là:
28 500 + 27 000 + 72 000 = 127 500 (đồng) ( 0,25 điểm)
b) Nếu bạn Bình mua trọn bộ 5 quyển sách bài tập Toán lớp 9 ở cửa hàng sách
B thì phải trả số tiền là:
(30 000 – 5 000).5 = 125 000 (đồng) < 127 500 đồng ( 0,25 điểm)
Vậy bạn Bình nên ở cửa hàng sách B để số tiền phải trả ít hơn. ( 0,25 điểm)
Bài 5: (1 điểm)
a/ . Thể tích lon nước ngọt cao là: 2
π. �5,6� . 13,41 ≈ 330,1 cm3 = 330,1 𝑚𝑚𝑚𝑚. ( 0,25 điểm) 2
Vậy lon nước ngọt cao này có thể chứa được hết lượng nước ngọt của một lon có cỡ phổ biến. ( 0,25 điểm)
b/ Diện tích vỏ nhôm của lon cao: 2
S = π. 5,6. 13,41 + 2. π. �5,6� ≈ 285 cm2 ( 0,25 điểm) 2
Diện tích vỏ nhôm của lon cũ: 2
S = π. 6,42. 10, 2 + 2. π. �6,42� ≈ 270,5 cm2 ( 0,25 điểm) 2
Vậy giá thành lon cao mắc hơn.
Bài 6: (2,5 điểm) A I F E H B D C O
a) Chứng minh: tứ giác AEHF nội tiếp đường tròn tâm I
BEC = 900 (gnt chắn nửa (O))=> AEH =900
BFC = 900 (gnt chắn nửa (O))=> AFH =900 ( 0,25 điểm)
=> AEH + AFH = 1800 ( 0,25 điểm )
=> tứ giác AEHF nội tiếp đường tròn đường kính AH
Mà I là trung điểm của AH
Vậy tứ giác AEHF nội tiếp đường tròn tâm I ( 0,25 điểm) c/m: AD ⊥ BC C E
B ˆ = 900 ( góc nội tiếp chắn nửa đường tròn) C F
B ˆ = 900 ( góc nội tiếp chắn nửa đường tròn)
=> BF và CE là hai đường cao của ∆ABC => H là trực tâm => AD là đ.cao thứ ba => AD ⊥ BC ( 0,25 điểm)
b/ Chứng minh: AE.AB = AF.AC
∆AEH ∼∆ADB => AE.AB = AH.AD ( 0,5 điểm)
∆AFH∼∆AD C => AF.AC = AH.AD ( 0,25 điể m ) Suy ra: AE.AB = AF.AC ( 0,25 điểm )
c) Chứng minh tứ giác EDOF nội tiếp. *Tứ giác BEHD nội tiếp
=> HED = HBD (cùng chắn cung HD) ( 0,25 điểm) *Tứ giác BEFC nội tiếp
=> FBC = FEC (cùng chắn cung FC) => FED = 2.FBC Mà FOC = 2.FBC => FED = FOC
=> tứ giác EDOF nội tiếp ( 0,25 điểm) ỦY BAN NHÂN DÂN CỦ CHI
TRƯỜNG THCS PHÚ HÒA ĐÔNG
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng điểm TT Chủ đề Nội dung/Đơn vị kiến thức Nhận biết Thông hiểu Vận dụng Vận dụng cao T N TL T N TL T N TL T N TL
Vẽ đồ thị hàm số 𝑦𝑦 = 1
𝑎𝑎𝑥𝑥2 (P) và y = ax + b (Bài a) 1 Đồ thị (d) (1,0đ) hàm số 2đ 1 Tìm tọa độ giao điểm (Bài b) của (P) và (d) (1,0đ) Hệ 1 thức (Bài 2) 2 Vi-et Hệ thức Vi-et (1,5 đ) 1,5đ và ứng dụng Giải bài toán bằng 1 cách lập hệ phương (Bài 3) trình. (1,5đ)
Bài tập Dạng ứng dụng tăng 1 1 3 ứng dụng giảm Bài 4a Bài 4b 4đ thực tế (1,0đ) (0,5đ) Dạng toán ứng dụng 1 1 hình không gian (Bài 5a) (Bài (0,5đ) 5b) (0,5đ) 1 (Bài 6a) (1,0đ) 4 Hình học Tứ giác nội tiếp 1 1 2,5đ (Bài (Bài 6b) 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng Đồ thị hàm số 1 y = ax2 (P) và Vận dụng: (Bài
y = ax + b (d) - Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ 1a) 1 Đồ thị trục tọa độ hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong việc (Bài (P) và (d)
tìm tọa độ giao điểm của (P) và (d). 1b) Hệ thức Thông hiểu: 2 2 2 Vi-et và
Hệ thức Vi -et - Tính được tổng, tích, x1 +x2 các nghiệm của 1 ứng dụng
phương trình bậc hai một ẩn bằng hệ thức (Bài 2)
Vi-et (Biến đổi đơn giản) Giải bài toán Thông hiểu:
bằng cách lập - Phân tích đề bài, tìm mối quan hệ giữa các đại hệ phương
lượng cho trong đề bài, gọi ẩn, từ đó lập được hệ 1 trình.
2 phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức Dạng ứng tăng/giảm 1 Bài tập dụng tăng Vận dụng: 1 Bài 3 ứng dụng giảm
- Vận dụng kiến thức về tăng giảm, tỉ số % Bài 4a 4b thực tế
giải quyết một số vấn đề trong thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện tích toàn
Dạng toán ứng phần, thể tích của hình trụ (hoặc hình nón, hình dụng hình cầu) 1 1 không gian
Vận dụng cao: Bài 5a Bài
- Vận dụng hợp lí công thức tính diện tích, thể 5b
tích hình trụ (hoặc hình nón, hình cầu) để giải
quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc
với đường tròn, mối quan hệ giữa các góc, phối 4
hợp các kiến thức để chứng minh.
Hình học Tứ giác nội tiếp
- Vận dụng các phương pháp chứng minh hai 1 1
tam giác đồng dạng, chứng minh song song, (Bài (Bài
vuông góc, 3 điểm thẳng hàng giải quyết yêu 6b) 6c) cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình
học phẳng để giải quyết yêu cầu đề bài. UBND HUYỆN CỦ CHI
ĐỀ KIỂM TRA CUỐI KÌ II NĂM HỌC: 2023– 2024
TRƯỜNG THCS PHÚ HÒA ĐÔNG Môn: TOÁN 9 Thời gian: 90 Phút
(Không kể thời gian phát đề)
Bài 1. (2 điểm). Cho hai hàm số : Cho parabol (P): 1 2
y = x và đường thẳng (d): 2 y = x + 4 .
a) Vẽ (P) và (d) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính
Bài 2. (1,5 điểm). Cho phương trình: 2x2 + 3x – 14 = 0 có 2 nghiệm là x , x 1 2
a) Không giải phương trình, hãy tính tổng và tích 2 nghiệm của phương trình.
b) Tính giá trị của biểu thức sau: A = 𝑥𝑥1 + 𝑥𝑥2 𝑥𝑥2 𝑥𝑥1
Bài 3. (1,5 điểm). An đi siêu thị mua một túi kẹo nặng 500g trong đó gồm có hai loại
kẹo là kẹo màu xanh và kẹo màu đỏ, về đếm được tổng cộng có 140 chiếc kẹo. Biết mỗi
chiếc kẹo màu xanh nặng 3g và mỗi chiếc kẹo màu đỏ nặng 5g. Hỏi có bao nhiêu chiếc
kẹo mỗi loại trong túi kẹo mà An đã mua.
Bài 4. (1,5 điểm). Cửa hàng đồng giá 40 000 đồng một món có chương trình giảm giá
20% cho một món hàng và nếu khách hàng mua 5 món trở lên thì từ món thứ 5 trở đi
khách hàng chỉ phải trả 60% giá ban đầu.
a) Tính số tiền một khách hàng phải trả khi mua 7 món hàng.
b) Nếu có khách hàng đã trả 272 000 đồng thì khách hàng này đã mua bao nhiêu món hàng ?
Bài 5. (1 điểm) Khung của nón lá có dạng hình nón được làm bởi các thanh gỗ
nối từ đỉnh tới đáy như các đường sinh (l), 16 vành nón được làm từ những thanh
tre mảnh nhỏ, dẻo dai uốn thành những vòng tròn có đường kính to, nhỏ khác
nhau, cái nhỏ nhất to bằng đồng xu.
– Đường kính (d = 2r) của chiếc nón lá khoảng 40 (cm);
– Chiều cao (h) của chiếc nón lá khoảng 19 (cm)
a) Tính độ dài của thanh tre uốn thành vòng tròn lớn nhất của vành chiếc nón
lá.(không kể phần chắp nối, tính gần đúng đến 2 chữ số thập phân, biết π ≃ 3,14)
b) Tính diện tích phần lá phủ xung quanh của chiếc nón lá. (không kể phần
chắp nối,tính gần đúng đến 2 chữ số thập phân). Biết diện tích xung quanh
của hình nón là S = π r l
Bài 6. (2,5 điểm). Từ điểm M nằm ngoài (O;R) vẽ hai tiếp tuyến MA , MB và cát tuyến
MCD với (O) (A, B là tiếp điểm và cát tuyến MCD nằm trong
AMO , MC < MD). Gọi
H là giao điểm của OM và AB.
a) Chứng minh: tứ giác MAOB nội tiếp và OM ⊥ AB.
b) Chứng minh: AC. BD = AD. BC
c) Tiếp tuyến tại C của (O) cắt MB tại E. Gọi I là hình chiếu vuông góc của E lên
đường thẳng MO. Chứng minh: A, C, I thẳng hàng. - HẾT –
ĐÁP ÁN ĐỀ KIỂM HỌC KỲ II NĂM HỌC 2022 - 2023 MÔN TOÁN LỚP 9 BÀI NỘI DUNG ĐIỂM Bài 1:
a) Vẽ (P) và (d) trên cùng một hệ trục tọa độ. (2điểm)
Lập bảng giá trị của (P ) 0. 25 Vẽ (P) 0.25
Lập bảng giá trị của (d ) 0.25 0.25 Vẽ (d)
b) Phương trình hoành độ giao điểm: 1 𝑥𝑥2 = 𝑥𝑥 + 4 2 1 ⇔ 0,25
2 𝑥𝑥2 − 𝑥𝑥 − 2 = 0
⇔ 𝑥𝑥1 = 4; 𝑥𝑥2 = −2 0,25
Thay x1 = 4 vào y = 1x2 ⇔ y = 8 0,25 2 0,25
Thay x2 = -2 vào y = 1x2 ⇔ y = 2 2
Vậy tọa độ giao điểm của (P) và (d) là: (4; 8) và (−2; 2) Bài 2.
a) Vì phương trình có hai nghiệm là x1, x2 nên:
(1,5điểm) Theo hệ thức Vi-et b − 3 S x x − = + = = 1 2 0,25 a 2 c 14 P x . x − = = = = 7 − 0,25 1 2 a 2 37 𝑥𝑥2 2 0,25
1 + 𝑥𝑥2 = (𝑥𝑥1 + 𝑥𝑥2 ) 2 – 2. 𝑥𝑥1. 𝑥𝑥2 = (−3)2 – 2.(-7) = 2 4
b) Tính giá trị của biểu thức A = 𝑥𝑥1 + 𝑥𝑥2 𝑥𝑥2 𝑥𝑥1 2 2 A = 𝑥𝑥1+ 𝑥𝑥1 0,25 𝑥𝑥1.𝑥𝑥2 A = 37: (-7) 0,25 4 A = 37 28 0,25 Bài 3.
Gọi x, y lần lượt là số kẹo màu xanh và số kẹo màu đỏ trong 0,25
(1,5điểm) túi kẹo (x, y * ∈ N )
Tổng số kẹo là 140 nên: x + y =140 0,25
Khối lượng túi kẹo là 500g nên: 3x +5y =500 0,25 Ta có hệ phương trình: 0,25 �𝑥𝑥 + 𝑦𝑦 = 140 3𝑥𝑥 + 5𝑦𝑦 = 500 ⇔ 0,25 �𝑥𝑥 = 100 𝑦𝑦 = 40
Vậy có 100 viên kẹo màu xanh, 40 viên kẹo màu đỏ 0,25 Bài 4.
a) Số tiền khách hàng phải trả khi mua 7 món hàng là:
(1,5điểm) 4. 40 000. 80% + 3.40 000. 60% = 200 000 (đồng) 1,0
b)Số tiền khách hàng phải trả khi mua từ món hàng thứ 5 trở
đi là: 272 000 - 4. 40 000. 80% = 144 000 (đồng) 0,25
Số món hàng mà khách hàng đã mua là:
4 + 144 000: 40 000. 60% = 10 (món hàng) 0,25 Bài 5.
a) C = πd ≃ 3,14. 40 ⇒ C ≃125, 6 cm 0,5 (1 điểm) b) l = 2 2 20 +19 = √761 cm 0,25
S = π r l ≃ 3,14. 20. √761 ⇒ S ≃ 1732,42 cm2 0,25 Bài 6. (2,5 điểm) D A C I O M E B
a) Chứng minh tứ giác MAOB nội tiếp -Xét tứ giác MAOB có : 𝑂𝑂𝑂𝑂𝑂𝑂
� = 900; 𝑂𝑂𝑂𝑂𝑂𝑂 � = 900 0,25 ⇒ 𝑂𝑂𝑂𝑂𝑂𝑂 � + 𝑂𝑂𝑂𝑂𝑂𝑂 � = 900 + 900 = 1800
Vậy tứ giác MAOB nội tiếp đường tròn có tâm là trung điểm của OM 0,25
- Ta có MA=MB (t/c 2 tiếp tuyến cắt nhau) OA=OB=R 0,25
⇒ OA là trung trực của đoạn thẳng AB ⇒ OM ⊥ AB 0,25
b) Chứng minh AM2 =MC. MD
Xét 𝛥𝛥𝑂𝑂𝑂𝑂𝛥𝛥 và 𝛥𝛥𝑂𝑂𝑂𝑂𝛥𝛥 ta có: 𝑂𝑂𝑂𝑂𝛥𝛥 � chung Và 𝑂𝑂𝑂𝑂𝛥𝛥 � = 𝑂𝑂𝛥𝛥𝑂𝑂
� ( cùng chắn 𝑂𝑂𝛥𝛥 � ) 0, 25
⇒ 𝛥𝛥𝑂𝑂𝑂𝑂𝛥𝛥 ∼ 𝛥𝛥𝑂𝑂𝛥𝛥𝑂𝑂 (gg) 0 , 25
⇒ 𝑀𝑀𝑀𝑀 = 𝑀𝑀𝑀𝑀 ⇒ 𝑂𝑂𝑂𝑂2 = 𝑂𝑂𝛥𝛥. 𝑂𝑂𝛥𝛥 0,5 𝑀𝑀𝑀𝑀 𝑀𝑀𝑀𝑀
c) Chứng minh: A, C, I thẳng hàng
Chứng minh 5 điểm C, I, E, B, O cùng thuộc 1 đường
tròn. Nên tứ giác CIEB nội tiếp ⇒ 𝑂𝑂𝛥𝛥𝐵𝐵 � = 𝐵𝐵𝐼𝐼𝑂𝑂 � 𝑂𝑂𝛥𝛥𝑂𝑂 � = 𝐵𝐵𝐼𝐼𝑂𝑂 �(= 𝑂𝑂𝑂𝑂𝐼𝐼 �) 0,25 ⇒ 𝑂𝑂𝛥𝛥𝐵𝐵 � = 𝑂𝑂𝛥𝛥𝑂𝑂 � Mà 𝑂𝑂𝛥𝛥𝑂𝑂 � + 𝑂𝑂𝛥𝛥𝑂𝑂
� = 1800(𝑂𝑂𝛥𝛥𝑂𝑂𝛥𝛥 𝑛𝑛𝑛𝑛) ⇒ 𝑂𝑂𝛥𝛥𝐵𝐵 � + 𝑂𝑂𝛥𝛥𝑂𝑂 � = 1800 Vậy A, C, I thẳng hàng. 0,25
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng điểm T Chủ Nội dung/Đơn vị T đề kiến thức
Nhận biết Thông hiểu Vận dụng Vận dụng cao T N TL T N TL T N TL T N TL Vẽ đồ thị hàm số 1
Đồ thị 𝑦𝑦 = 𝑎𝑎𝑥𝑥2 (P) và y = (Bài a) 1 hàm ax + b (d) (1,0đ) 2đ số 1 Tìm tọa độ giao (Bài b) điểm của (P) và (d) (1,0đ) Hệ 1 thức (Bài 2) 2 Vi-et Hệ thức Vi-et (1,5 đ) 1,5đ và ứng dụng Giải bài toán bằng 1 cách lập hệ (Bài 3) phương trình. (1,5đ) Bài tập Dạng ứng dụng 1 1 3 ứng tăng giảm Bài 4a Bài 4b 4đ dụng (1,0đ) (0,5đ)
thực tế Dạng toán ứng 1 1 dụng hình không (Bài 5a) (Bài gian (0,5đ) 5b) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài (Bài 6b) 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng Đồ thị hàm số 1 y = ax2 (P) và Vận dụng: (Bài
y = ax + b (d) - Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ 1a) 1 Đồ thị trục tọa độ hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong việc (Bài (P) và (d)
tìm tọa độ giao điểm của (P) và (d). 1b) Hệ thức Thông hiểu: 2 2 2 Vi-et và
Hệ thức Vi -et - Tính được tổng, tích, x1 +x2 các nghiệm của 1 ứng dụng
phương trình bậc hai một ẩn bằng hệ thức Vi- (Bài 2)
et (Biến đổi đơn giản) Giải bài toán Thông hiểu: bằng cách lập
- Phân tích đề bài, tìm mối quan hệ giữa các đại hệ phương
lượng cho trong đề bài, gọi ẩn, từ đó lập được hệ 2 1 trình.
phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức Bài tập Dạng ứng tăng/giảm 1 1
3 ứng dụng dụng tăng Vận dụng: Bài 4a Bài thực tế giảm
- Vận dụng kiến thức về tăng giảm, tỉ số % giải 4b
quyết một số vấn đề trong thực tiễn. Thông hiểu:
Dạng toán ứng - Tính được diện tích xung quanh, diện tích toàn dụng hình
phần, thể tích của hình trụ (hoặc hình nón, hình cầu) 1 1 không gian
Vận dụng cao: Bài 5a Bài
- Vận dụng hợp lí công thức tính diện tích, thể tích 5b
hình trụ (hoặc hình nón, hình cầu) để giải quyết
một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc
với đường tròn, mối quan hệ giữa các góc, phối 4
hợp các kiến thức để chứng minh.
Hình học Tứ giác nội tiếp
- Vận dụng các phương pháp chứng minh hai 1 1
tam giác đồng dạng, chứng minh song song, (Bài (Bài
vuông góc, 3 điểm thẳng hàng giải quyết yêu 6b) 6c) cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình
học phẳng để giải quyết yêu cầu đề bài. UBND HUYỆN CỦ CHI
ĐỀ KTCK II NĂM HỌC 2023 – 2024
TRƯỜNG THCS TÂN AN HỘI MÔN: TOÁN 9
Thời gian: 90 phút. (không kể thời gian phát đề) (Đề gồm 02 trang)
Bài 1. (2 điểm) Cho hàm số: 𝑦𝑦 = 1 𝑥𝑥2 có đồ thị là (P) và hàm số: 𝑦𝑦 = 3𝑥𝑥 − 4 có đồ thị là (D). 2
a) Vẽ (P) và (D) trên cùng mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của (P) và đường thẳng (D) bằng phép toán
Bài 2. (1,5 điểm) Gọi x ,x là các nghiệm của phương trình 2
x 3x 7 0. Không giải phương 1 2
trình, tính giá trị của biểu thức A (x 3)(x 3) 5x x . 1 2 1 2
Bài 3. (1,5 điểm)
Mối liên hệ giữa chiều dài y(cm) của một sợi dây xích và số mắt xích x là một hàm số bậc nhất y = ax + .
b Biết đoạn xích có 5 mắt xích thì dài 22cm, đoạn xích có 8 mắt xích thì dài 34 cm.
a) Hãy xác định hệ số a; b.
b) Hãy tính xem một sợi xích dài 1,5m thì gồm bao nhiêu mắt xích?
Bài 4. (1,5 điểm)
Một cửa hàng cần bán một lô hàng gồm 32 sản phẩm cùng loại với giá bán ban đầu là 2400 000
đồng. Nhân dịp lễ Noel, cửa hàng giảm 10% so với giá bán ban đầu thì bán được 12 sản phẩm.
Vào dịp tết Tây, mỗi sản phẩm được giảm 200000 đồng (so với giá đã giảm ở dịp lễ Noel) thì cửa
hàng bán được hết số sản phẩm còn lại. Sau khi bán hết thì cửa hàng lãi được 60% so với tổng số
tiền bỏ ra gồm giá vốn của các sản phẩm và giá vận chuyển 2000000 đồng. Hỏi giá vốn của mỗi
sản phẩm trong lô hàng cần bán là bao nhiêu tiền?
Bài 5. (1,0 điểm)
Có một bình thủy tinh hình trụ phía bên trong có đường kính đáy là 30cm , chiều cao 20cm , đựng
một nửa bình nước và một khối thủy tinh hình trụ có bán kính đáy là
14cm, chiều cao là 11cm . (Cho thể tích hình trụ tính theo công thức: 2
V = π R h với R là bán kính đáy, h là chiều cao của hình trụ)
a) Tính thể tích khối thủy tinh (làm tròn đến chữ số thập phân thứ nhất)
b) Hỏi nếu bỏ lọt khối thủy tinh vào bình thủy tinh thì lượng
nước trong bình có bị tràn ra ngoài hay không? Tại sao?
Bài 6. (2,5 điểm) Từ điểm M nằm ngoài đường tròn tâm O, vẽ hai tiếp tuyến MA, MB (A, B là
các tiếp điểm) và cát tuyến MCD không đi qua O (C nằm giữa M và D) của đường tròn tâm O.
Đoạn thẳng OM cắt AB và (O) theo thứ tự tại H và I. Chứng minh rằng:
a) Tứ giác MAOB là tứ giác nội tiếp và MC.MD = MA2
b) Bốn điểm O, H, C, D thuộc một đường tròn.
c) CI là tia phân giác của 𝐻𝐻𝐻𝐻𝐻𝐻 � . ---HẾT---
ĐÁP ÁN ĐỀ KTCK2_TOÁN 9_NH 2023 – 2024 BÀI HƯỚNG DẪN CHẤM ĐIỂM Bài 1. a/-BGT: 0, 25đ (2 điểm) x -4 -2 0 2 4 1 2 y = x 8 2 0 2 8 2 x 0 2 0,25đ y = 3x − 4 -4 2 -HS vẽ đúng: 0, 5đ
b/Phương trình hoành độ giao điểm của (P) và (D) là: 1 2 x = 3x − 4 2 0,25đ 1 2
⇔ x − 3x + 4 = 0 0,25đ 2 ⇒ x = 4; x = 2 1 2 0,25đ ⇒ y = 8; y = 2 1 2
Vậy tọa độ giao điểm của (P) và (D) là (2;2);(4;8) 0 , 25đ Bài 2. 2
x 3x 7 0 (1,5 điểm) S
x x 3
Theo định lý Vi-et ta có: 1 2 0,25đx2 P
x .x 7 1 2
A (x 3)(x 3) 5x x x x 3x 3x 9 5x x 0,25đ 1 2 1 2 1 2 1 2 1 2
3(x x ) 4x x 9 1 2 1 2 0,25đ
3(3) 4(7) 9 28 0,5đ Bài 3.
(1,5 điểm) Hàm số: y = ax + b . Theo đề bài có: 0,25đ
*Khi x = 5 thì y = 22 ⇒ 5a + b = 22 0,25đ
*Khi x = 8 thì y = 34 ⇒ 8a + b = 34 5 a + b = 22 a = 4
Ta có hệ phương trình: ⇔ 8 a b 34 + = b = 2 0,5đ
b) Hàm số là: y = 4x + 2
1,5m =150cm. Thay y = 150 vào 0,25đ
y = 4x + 2 được:
4x + 2 =150 ⇒ x = 37 . 0,25đ Bài 4. (1,5 điểm)
Giá tiền 1 sản phẩm khi được giảm 10% 0,25đ
2400000(1−10%) = 2160000 (đồng)
Số tiền bán được sau khi bán hết 32 sản phẩm:
12 + 2160000 + (32 −12)(2160000 − 200000) = 65120000 0,25đ (đồng)
Gọi x (đồng) là số tiền vốn của mỗi sản phẩm, x > 0 0,25đ
Số tiền vốn và lãi sau khi bán 32 sản phẩm là:
(32x+ 2000000)(1+60%) = 1,6(32x+ 2000000) 0,25đ Ta có phương trình:
1,6(32x + 2000000) = 65120000 0,25đ x = 1209375 (đồng)
Vậy giá vốn của mỗi sản phẩm là 1209375 đồng 0,25đ Bài 5.
a) Thể tích khối thủy tinh là: 2
V 3,14.14 .11 6769, 8 3 cm . 0,25đ 2 (1 điểm) 2
b) Thể tích bình thủy tinh là: 30 V 3,14. .20 14130 3 cm . 0,25đ 1 2
Thể tích khi bỏ khối thủy tinh vào bình thủy tinh là: V 14130 1 V
6769, 8 13834, 8 cm V . 0,25đ 2 3 1 2 2
Vậy nước không bị tràn ra ngoài. 0,25đ Bài 6. (2,5 điểm) A D C M O H I B
a)Chứng minh tứ giác MAOB là tứ giác nội tiếp 0.25
Vì MA, MB là các tiếp tuyến của (O) tại A và B
=> MA ⊥ OA tại A và MB ⊥ OB tại B 0.25 Xét tứ giác MAOB có: 𝐻𝐻𝑀𝑀𝑀𝑀 � + 𝐻𝐻𝑀𝑀𝑀𝑀 � = 900 + 900 = 1800
=> tứ giác MAOB nội tiếp đường tròn (tứ giác có tổng 2 góc đối 0.25 bằng 1800) + Chứng minh MC.MD = MA2 0.25 Xét ΔMCA và ΔMAD có: 𝑀𝑀𝐻𝐻𝐻𝐻 � chung 𝐻𝐻𝑀𝑀𝐻𝐻 � = 𝑀𝑀𝐴𝐴𝐻𝐻
� (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AC)
=> ΔMCA đồng dạng ΔMAD (gg)
=> 𝑀𝑀𝑀𝑀 = 𝑀𝑀𝑀𝑀 => MC . MD = MA2 𝑀𝑀𝑀𝑀 𝑀𝑀𝑀𝑀
b) Vì MA = MD (t/c 2 tiếp tuyến cắt nhau) OA = OB (bán kính) 0. 25
=> MO là đường trung trực của AB => MO ⊥ AB tại H 0.25
Xét ΔOAM vuông tại A, đường cao AH, ta có:
AM2 = MH . MO (hệ thức lượng) Mà AM2 = MC.MD (cmt) 0.25 => MH.MO = MC.MD
=> 𝑀𝑀𝑀𝑀 = 𝑀𝑀𝑀𝑀 𝑀𝑀𝑀𝑀 𝑀𝑀𝑀𝑀 Xét ΔMDO và ΔMHC có: 0,25 𝐻𝐻𝐻𝐻𝐻𝐻 � chung
𝑀𝑀𝑀𝑀 = 𝑀𝑀𝑀𝑀 (cmt) 𝑀𝑀𝑀𝑀 𝑀𝑀𝑀𝑀
=> ΔMDO đồng dạng ΔMHC (cgc) => 𝐻𝐻𝐻𝐻𝐻𝐻 � = 𝐻𝐻𝐴𝐴𝑀𝑀 �
=> Tứ giác OHCD nội tiếp đường tròn(góc ngoài tại một đỉnh
bằng góc trong của đỉnh đối diện)
Hay O, H, C, D cùng thuộc một đường tròn. 0. 25
c) Chứng minh AI là tia phân giác của 𝐻𝐻𝑀𝑀𝐻𝐻 � 0.25 ⇒ IH = AH ( ) 1 IM AM
∆MHC và ∆MDO đồng dạng (cmt) ⇒ CH = OD CM OM OD=OA=R nên CH = OA (2) CM OM
Chứng minh ∆AMH, ∆OMA đồng dạng ⇒ OA = AH (3) OM AM
Từ (1), (2) và (3) ⇒ IH = CH . IM CM
Do đó chứng minh được CI là tia phân giác của 𝐻𝐻𝐻𝐻𝐻𝐻 � .
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng
TT Chủ đề Nội dung/Đơn vị kiến điểm thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TN TL TN TL TN TL TN TL
Vẽ đồ thị hàm số 𝑦𝑦 = 1
𝑎𝑎𝑥𝑥2 (P) và y = ax + b (Bài a) 1 Đồ thị (d) (1,0đ) hàm số 2đ 1 Tìm tọa độ giao điểm (Bài b) của (P) và (d) (1,0đ) Hệ thức 1 2 Vi-et và (Bài 2) ứng Hệ thức Vi-et (1,5 đ) 1,5đ dụng Giải bài toán bằng 1 cách lập hệ phương (Bài 3) trình. (1,5đ) Bài tập 3 ứng Dạng ứng dụng tăng 1 1 dụng 4đ giảm Bài 4a Bài 4b thực tế (1,0đ) (0,5đ) Dạng toán ứng dụng 1 1 hình không gian (Bài 5a) (Bài 5b) (0,5đ) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài 6b) (Bài 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng Đồ thị hàm số 1 y = ax2 (P) và Vận dụng: (Bài
y = ax + b (d) - Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ 1a) 1 Đồ thị trục tọa độ hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong việc (Bài (P) và (d)
tìm tọa độ giao điểm của (P) và (d). 1b) Hệ thức Thông hiểu: 2 2 2 Vi-et và
Hệ thức Vi -et - Tính được tổng, tích, x1 +x2 các nghiệm của 1 ứng dụng
phương trình bậc hai một ẩn bằng hệ thức (Bài 2)
Vi-et (Biến đổi đơn giản) Giải bài toán Thông hiểu:
bằng cách lập - Phân tích đề bài, tìm mối quan hệ giữa các đại hệ phương
lượng cho trong đề bài, gọi ẩn, từ đó lập được hệ 1 trình.
2 phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức Dạng ứng tăng/giảm 1 Bài tập dụng tăng Vận dụng: 1 Bài 3 ứng dụng giảm
- Vận dụng kiến thức về tăng giảm, tỉ số % Bài 4a 4b thực tế
giải quyết một số vấn đề trong thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện tích toàn
Dạng toán ứng phần, thể tích của hình trụ (hoặc hình nón, hình dụng hình cầu) 1 1 không gian
Vận dụng cao: Bài 5a Bài
- Vận dụng hợp lí công thức tính diện tích, thể 5b
tích hình trụ (hoặc hình nón, hình cầu) để giải
quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc
với đường tròn, mối quan hệ giữa các góc, phối 4
hợp các kiến thức để chứng minh.
Hình học Tứ giác nội tiếp
- Vận dụng các phương pháp chứng minh hai 1 1
tam giác đồng dạng, chứng minh song song, (Bài (Bài
vuông góc, 3 điểm thẳng hàng giải quyết yêu 6b) 6c) cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình
học phẳng để giải quyết yêu cầu đề bài.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI KỲ II HUYỆN CỦ CHI NĂM HỌC 2023–2024
TRƯỜNG TH – THCS TÂN TRUNG MÔN: TOÁN – LỚP 9 ĐỀ THAM KHẢO
Thời gian: 90 phút (Không kể thời gian phát đề)
(Đề thi có 02 trang)
Bài 1: (2 điểm) Cho (P) 1 2
: y = − x và đường thẳng (d ) : y = 3x + 4. 2
a) Vẽ đồ thị (P) và (d ) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của và (d ) bằng phép tính.
Bài 2: (1,5đ) Gọi x , x là các nghiệm của phương trình 2
x − x −12 = 0 . Không giải phương 1 2 x +1 x +1
trình, tính giá trị của biểu thức 1 2 A = + . x x 2 1
Bài 3: (1,5đ) Trong tháng Giêng hai tổ công nhân đã may được 800 chiếc áo. Tháng Hai, tổ
1 may vượt mức 15% , tổ hai may vượt mức 20% so với tháng Giêng do đó cả hai tổ đã may
được 945 cái áo. Hỏi trong tháng Giêng mỗi tổ đã may được bao nhiêu chiếc áo?
Bài 4: (1,5đ) Một công ty giao cho cửa hàng 100 hộp bánh để bán ra thị trường. Lúc đầu cửa
hàng bán 24 hộp bánh với giá bán một hộp bánh là 200000 đồng. Do nhu cầu của thị trường
nên từ hộp bánh thứ 25 đến hộp bánh thứ 80 mỗi hộp bánh có giá bán tăng 15% so với giá
bán lúc đầu, từ hộp bánh thứ 81 đến hộp bánh thứ 100 mỗi hộp bánh có giá bán giảm 10% so với giá bán lúc đầu.
a/Hỏi số tiền thu cửa hàng được khi bán 100 hộp bánh là bao nhiêu?
b/Biết rằng: Với số tiền thu được khi bán 100 hộp bánh, sau khi trừ đi 10% tiền thuế giá trị
gia tăng VAT cửa hàng vẫn lãi 1152000 đồng. Hỏi mỗi hộp bánh công ty giao cho cửa hàng có giá là bao nhiêu?
Bài 5: (1,0đ) Gạch ống là một sản phẩm được tạo hình thành từ đất sét và nước, được kết hợp
lại với nhau theo một công thức chung hợp lý mới có thể tạo
ra hỗn hợp dẻo quánh, sau đó chúng được đổ vào khuôn, rồi
đem phơi hoặc sấy khô và cuối cùng là đưa vào lò nung. Một
viên gạch hình hộp chữ nhật có kích thước dài 20cm , rộng
8cm. Bên trong có bốn lỗ hình trụ bằng nhau có đường kính 2,5cm.
a) Tính thể tích đất sét để làm một viên gạch. (Biết công thức tính thể tích hình trụ là 2 V = π R h
, trong đó R là bán kính đáy, h là chiều cao của hình trụ. Lấy π = 3,14)
b) Theo tính toán, bác Ba muốn xây một ngôi nhà phải mua 10 thiên gạch, 1 thiên gạch là
1000 viên. Nhưng khi thi công, bác Ba phải mua dư 2% số gạch cần dùng dự phòng cho
hư hao. Để vận chuyển số gạch đến nơi xây dựng, bác Ba dự định thuê một chiếc xe tải với
giá 550000 đồng mỗi chuyến (chưa kể tiền công bốc xếp gạch). Hỏi bác Ba cần chuẩn bị
bao nhiêu tiền để trả chi phí vận chuyển (không kể tiền công bốc xếp gạch), biết mỗi chuyến
xe tải chở được 1800 viên gạch.
Bài 6: (2,5đ) Cho ( ;
O R) và điểm A nằm ngoài (O) kẻ hai tiếp tuyến AM , AN ( M , N là
hai tiếp điểm). Kẻ đường kính MD , AD cắt (O) tại K , NK cắt AH tại I .
a) Chứng minh tứ giác ANOM nội tiếp. b) Chứng minh rằng 2
AI = IK.IN .
c) Chứng minh rằng I là trung điểm của AH .
.............Hết............. Bài ĐÁP ÁN Điểm
a) Vẽ đồ thị (P) và (d ) trên cùng hệ trục tọa độ. BGT: x 4 − 2 − 0 2 4 0,25 1 (P) 2 : y = − x 8 − 2 − 0 2 − 8 − 2 x 1 − 0 0,25 y = 3x + 4 1 4 0,25x2 Bài 1 2,0đ
b) Phương trình hoành độ giao điểm của (P) và (d ) : 1 2 − x = 3x + 4 0,25 2 2
⇔ x + 6x + 8 = 0 x = 2 − ⇔ 0,25 x = 4 − 1 1 0,25 Thay x = 2 − vào 2
y = − x , ta được: y = − ( 2 − )2 = 2 − . 2 2 1 1 Thay x = 4 − vào 2
y = − x , ta được: y = − ( 4 − )2 = 8 − . 0,25 2 2 Vậy ( 2; − − 2) , ( 4;
− − 8) là hai giao điểm cần tìm. Vì 2
∆ = b − 4ac = (− )2 1 − 4.(− ) 1 .12 = 49 > 0 0,25
Nên phương trình có hai nghiệm phân biệt x , x . 1 2 − 0,25x2 = + = b S x x = 1 Bài 2 1 2
Theo định lí Vi-et, ta có: a 1,5đ = . = c P x x = 12 − 1 2 a x +1 x +1 Ta có: 1 2 A = + x x 2 1 x x +1 + x x +1 1 ( 1 ) 2 ( 2 ) A = x .x 0,25 1. 2 2 2
x + x + x + x 1 2 1 2 A = x .x 1. 2 0,25 2 S − 2P + = S A P 0,25 13 − A = 6
Gọi x, y (chiếc áo) lần lượt là số chiếc áo tổ 1 và tổ 2 đã may được trong 0,5 tháng Giêng. ( * x, y ∈ )
Theo đề bài, ta có hệ phương trình: x + y = 800 Bài 3 0,25x2 105% x +120%y = 945 1,5đ x = 300 ⇔ (TM ) 0,25 y = 500
Vậy trong tháng Giêng, tổ 1 đã may được 300 chiếc áo và tổ 2 đã may được 0,25 500 chiếc áo.
a) Số tiền thu được khi bán 24 hộp bánh đầu là: 24.200000 = 4800000(đồng) 0,25
Số tiền thu được khi bán được từ hộp bánh thứ 25 đến hộp bánh thứ 80 là:
56.200000(1+15%) =12880000 (đồng) 0,25
Số tiền thu được khi bán được từ hộp bánh thứ 81 đến hộp bánh thứ 100 là: Bài 4
20.200000(1−10%) = 3600000(đồng) 0,25
1,5đ Số tiền thu cửa hàng được khi bán 100 hộp bánh là:
4800000 +12880000 + 3600000 = 21280000(đồng) 0,25
b) Số tiền thuế giá trị gia tăng VAT là 10%.21280000 = 2128000(đồng) 0,25
Số tiền mỗi hộp bánh công ty giao cho cửa hàng có giá là:
(21280000 − 2128000) −1152000 :100 =180000 (đồng) 0,25
a) Thể tích đất sét làm viên gạch hình hộp chữ nhật chưa trừ bốn lỗ rỗng bên trong là: V = = ( 3 8.8.20 1280 cm )
Thể tích của bốn lỗ hình trụ bằng nhau là: 2 2,5 V ( 2 π R h).4 3,14. = = .20.4 = 0,25 392,5( 3 cm 1 ) Bài 5 2
Thể tích đất sét để làm một viên gạch là: 1,0đ
V = V −V =1280 − 392,5 = 887,5( 3 cm 0,25 2 1 )
b) Số viên gạch bác Ba cần mua là:
10.1000.(1+ 2%) =10200(viên gạch)
Ta có: 10200 =1800.5 +1200 ⇒ [10200 :1800] = 6 0,25
Nên bác Ba cần thuê 6 chuyến xe để vận chuyển gạch.
Số tiền bác Ba cần chuẩn bị là: 550000.6 0,25 = 3300000(đồng).
a) Chứng minh tứ giác ANOM nội tiếp .
Xét tứ giác ANOM , ta có: 0,25
AMO = 90° (vì AM là tiếp tuyến của (O)) 0,25
ANO = 90°(vì AN là tiếp tuyến của (O)) ⇒ AMO +
ANO = 90° + 90° =180° 0,25
Suy ra tứ giác ANOM nội tiếp (tổng hai góc đối bù nhau). 0,25 Bài 6 b) Chứng minh 2
AI = IK.IN 2,5đ
Ta có: AM = AN (tính chất 2 tiếp tuyến cắt nhau)
Và OM = ON (= R)
⇒ AO là đường trung trực của MN Ta có:
DN ⊥ MN (vì
MND = 90° , góc nội tiếp chắn nửa đường tròn)
Và AO ⊥ MN (vì AO là đường trung trực của MN ). ⇒ AO // DN 0,25 ⇒ IAK = KDN (so le trong) Mà INA =
KDN (góc tạo bởi tiếp tuyến và góc nội tiếp cùng chắn cung NK ) 0,25 ⇒ IAK = INA
Xét ∆AIK và ∆NIA có : I là góc chung Và IAK = INA(cmt) 0,25
⇒ ∆AIK ∽∆NIA (g-g) 0,25 IA IK 2 ⇒ =
⇒ AI = IK.IN IN IA
c) Chứng minh rằng I là trung điểm của AH .
Xét ∆NHI và ∆DMA ta có: NHI = DMA = 90° Và HNI =
MDA (góc nội tiếp cùng chắn NI )
⇒ ∆NHI ∽∆DMA (g-g) ⇒ HI HN = ⇒ HI AM = AM MD HN MD
Mà AM = AN (tính chất 2 tiếp tuyến cắt nhau) ⇒ HI AN = ( ) 1 HN MD 0,25
Xét ∆AHN và ∆MND ta có: AHN = MND = 90° Và HNA =
NDM (Góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn NM )
⇒ ∆AHN ∽∆MND (g-g) ⇒ AH = AN (2) MN MD AH HI AN Từ ( ) 1 và (2) suy ra = = MN HN MD
Mà H là trung điểm của MN (vì OA vuông góc với MN tại H ) ⇒ = 2
⇒ AH = HI ⇒ AH MN HN = HI 0,25 2HN HN 2
Vậy I là trung điểm của AH .
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng
TT Chủ đề Nội dung/Đơn vị kiến điểm thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TN TL TN TL TN TL TN TL
Vẽ đồ thị hàm số 𝑦𝑦 = 1
𝑎𝑎𝑥𝑥2 (P) và y = ax + b (Bài a) 1 Đồ thị (d) (1,0đ) hàm số 2đ 1 Tìm tọa độ giao điểm (Bài b) của (P) và (d) (1,0đ) Hệ thức 1 2 Vi-et và (Bài 2) ứng Hệ thức Vi-et (1,5 đ) 1,5đ dụng Giải bài toán bằng 1 cách lập hệ phương (Bài 3) trình. (1,5đ) Bài tập 3 ứng Dạng ứng dụng tăng 1 1 dụng 4đ giảm Bài 4a Bài 4b thực tế (1,0đ) (0,5đ) Dạng toán ứng dụng 1 1 hình không gian (Bài 5a) (Bài 5b) (0,5đ) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài 6b) (Bài 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng Đồ thị hàm số 1 y = ax2 (P) và Vận dụng: (Bài
y = ax + b (d) - Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ 1a) 1 Đồ thị trục tọa độ hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong việc (Bài (P) và (d)
tìm tọa độ giao điểm của (P) và (d). 1b) Hệ thức Thông hiểu: 2 2 2 Vi-et và
Hệ thức Vi -et - Tính được tổng, tích, x1 +x2 các nghiệm của 1 ứng dụng
phương trình bậc hai một ẩn bằng hệ thức (Bài 2)
Vi-et (Biến đổi đơn giản) Giải bài toán Thông hiểu:
bằng cách lập - Phân tích đề bài, tìm mối quan hệ giữa các đại hệ phương
lượng cho trong đề bài, gọi ẩn, từ đó lập được hệ 1 trình.
2 phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức Dạng ứng tăng/giảm 1 Bài tập dụng tăng Vận dụng: 1 Bài 3 ứng dụng giảm
- Vận dụng kiến thức về tăng giảm, tỉ số % Bài 4a 4b thực tế
giải quyết một số vấn đề trong thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện tích toàn
Dạng toán ứng phần, thể tích của hình trụ (hoặc hình nón, hình dụng hình cầu) 1 1 không gian
Vận dụng cao: Bài 5a Bài
- Vận dụng hợp lí công thức tính diện tích, thể 5b
tích hình trụ (hoặc hình nón, hình cầu) để giải
quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc
với đường tròn, mối quan hệ giữa các góc, phối 4
hợp các kiến thức để chứng minh.
Hình học Tứ giác nội tiếp
- Vận dụng các phương pháp chứng minh hai 1 1
tam giác đồng dạng, chứng minh song song, (Bài (Bài
vuông góc, 3 điểm thẳng hàng giải quyết yêu 6b) 6c) cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình
học phẳng để giải quyết yêu cầu đề bài. UBND HUYỆN CỦ CHI
ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II
TRƯỜNG THCS TRUNG LẬP NĂM HỌC 2023 - 2024
MÔN: TOÁN – LỚP 9 Thời gian: 90 phút
(Không kể thời gian phát đề)
Bài 1: ( 2điểm) Cho parabol (P) 1 2
: y = x và đường thẳng (d ): y = x + 4 2
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Bài 2: (1,5 điểm) Cho phương trình 2
x 3x 7 0
a/ Chứng minh phương trình trên có nghiệm. Không giải phương trình, hãy
tính tổng và tích hai nghiệm của phương trình trên?
b/ Gọi x1, x2 là hai nghiệm của phương trình trên. Tính giá trị của biểu thức:
A = x (x − 5) + x (x − 5) 1 1 2 2 Bài 3: (1,5đ)
Nam đi siêu thị mua một túi kẹo nặng 500g trong đó gồm có hai loại kẹo là kẹo màu
xanh và kẹo màu đỏ, về đếm được tổng cộng có 140 chiếc kẹo. Biết mỗi chiếc kẹo màu
xanh nặng 3g và mỗi chiếc kẹo màu đỏ nặng 5g. Hỏi có bao nhiêu chiếc kẹo mỗi loại trong túi kẹo mà Nam đã mua. Bài 4: ( 1,5 điểm)
Cửa hàng đồng giá 40 000 đồng một món có chương trình giảm giá 20% cho
một món hàng và nếu khách hàng mua 5 món trở lên thì từ món thứ 5 trở đi khách
hàng chỉ phải trả 60% giá đang bán.
a/ Tính số tiền một khách hàng phải trả khi mua 7 món hàng.
b/ Nếu có khách hàng đã trả 272 000 đồng thì khách hàng này đã mua bao nhiêu món hàng ? Bài 5: ( 1điểm)
Người ta muốn làm một thùng rác văn phòng như
hình bên có đường cao 0,8m, đường kính 0,4m.
a/ Tính diện tích tôn cần thiết để gò nên thùng rác theo kích thước đã cho.
b/ Hãy tính thể tích của thùng rác này? Bài 6: ( 3điểm)
Cho tam giác ABC có 3 góc nhọn (ABtiếp đường tròn (O). Kẻ các đường cao AD, BE, CF của
tam giác, gọi H là giao điểm của AD, BE, CF.
a/ Chứng minh: tứ giác BEFC, BFHD nội tiếp đường tròn.
b/ Gọi S là giao điểm của 2 đường thẳng BC và EF. Chứng minh: SE.SF = SB.SC.
c/ Gọi K là giao điểm của AS và đường tròn ( O). Chứng minh tứ giác AEFM nội tiếp.
--------------------------------------Hết------------------------------------------ ĐÁP ÁN Bài Đáp án Điểm Bài 1: a) Bảng giá trị 2 điểm x 4 − 2 − 0 2 4 1 2 y = x 8 2 0 2 8 2 x 2 − 4 y = x + 4 2 8 1,0đ
b) Phương trình hoành độ giao điểm của (P) và (d) : 1 2 x = x + 4 2 1 2
⇔ x − x − 4 = 0 2 x = 4 ⇔ x = 2 −
Với x = 4 ⇒ y = 4 + 4 = 8 Với x = 2 − ⇒ y = 2 − + 4 = 2
Vậy (P) cắt (d) tại B(4;8) và A( 2; − 2) 1,0 đ Bài 2 2
x 3x 7 0 - 1,5 điểm
a)Chứng minh: phương trình luôn có 2 nghiệm phân biệt.
Ta có a và c trái dấu nên ∆ > 0 (0,25 đ x 2)
Nên phương trình luôn có 2 nghiệm phân biệt x1,,x2.
b/ Vì x1 và x2 là hai nghiệm của phương trình nên
Theo định lý Vi-et ta có: S x x 3 1 2 0,25đ P
x .x 7 1 2 0,25đ Ta có: 2 2 x
1 + x 2 = S2 – 2P = 23
A = x (x − 5) + x (x − 5) 1 1 2 2 = x 2 2 1 – 5x1 + x2 - 5x2 = x 2 2 0,25 đ 1 + x2 - 5(x1+ x2) = 23 – 5. (-3) = 38 0,25đ Bài 3 1,5 điểm
Gọi số viên kẹo màu xanh và màu đỏ lần lượt là: x, y (viên) (x, y ∈ N*) 0,25đ x + y =140 x =100 0,5đ ⇒ Hệ phương trình : ⇔ 3 x 5y 500 + = y = 40 0,5đ
Vậy số viên kẹo màu xanh là 100 viên và số viên kẹo màu đỏ là 0,25đ 40 viên. Bài 4:
a/ Tính số tiền một khách hàng phải trả khi mua 7 món 1,5 điểm hàng.
40000.(100% − 20%).4 + 40000.60%.3 = 200.000 đồng 0,5 đ
b/ Gọi x là số món hàng khách hàng mua khi đã trả 272
000 đồng ( vì 272 000đ> 200 000đ nên x > 7) 0,25đ
Ta có: 40000(1 – 20%).4 + 40000.60%. ( x – 4) = 272 000 0,25đ
128000 + 24000( x -4) = 272000 24000( x -4) = 144000 x – 4 = 6 => x = 10 0,25đ
Vậy khách hàng mua 10 món hàng 0,25đ Bài 5:
a/ diện tích tôn cần thiết để gò nên thùng rác: 1 điểm
2. π .R.h+π R2 = 2. π .0,4.0,8 + π .0,42 = 0.8π (m)
b/Thể tích của thùng rác 0,5đ V = π R2.h 0,25đ = π .0,42.0,8 = 0,128π (m3)
Vậy thể tích thùng rác là = 0,128π (m3) 0,25đ Bài 6: 2,5 đ
a)Chứng minh: tứ giác BCEF và tứ giác BDHF nội tiếp. Xét : tứ giác BCEF có: 0,25đ góc BEC=góc BFC=900 Suy ra BCEF nt 0,25đ Xét tứ giác BDHF có: Góc BFH= 900 góc BDH - 900 0,25đ Góc BFH+góc BDH=1800 0,25đ Suy ra BDHF nt
b) Chứng minh: SB. SC=SE. SF xét ∆SBF và ∆SEC ta có: góc S chung
góc SFB=góc SCE ( tứ giác BFEC nội tiếp) suy ra ∆SBF đd ∆SEC (gg) 0,5đ suy ra SB. SC=SE. SF 0,25đ
c) Chứng minh tứ giác AEFK nội tiếp Cm được SK.SA = SE.SF 0,25đ
Cm được ∆SKF đd ∆SEA (cgc) 0,25đ Suy ra góc SFK =góc SAE Suy ra AEFK nội tiếp 0,25 đ
UBND HUYỆN CỦ CHI
ĐỀ THAM KHẢO CUỐI KỲ II NĂM HỌC 2023 -2024
TRƯỜNG THCS TRUNG LẬP HẠ MÔN: TOÁN LỚP 9 Thời gian : 90 phút
(Không kể thời gian phát đề)
Bài 1: (2,0 điểm)Cho (P) : y = 1 2
x và (D) : y = 3x − 4 2
a) Vẽ (P) và (D) trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán.
Bài 2: (1,5 điểm): Cho pt: x2 – 5x – 2 = 0. Không giải phương trình trên, hãy tính
giá trị của biểu thức: A = 2
(x − x ) − x .x 1 2 1 2
Bài 3: (1,5 điểm) Để chuẩn bị cho lễ tri ân Thầy Cô giáo của trường, lớp 9A1
muốn mua quà tặng cho 15 giáo viên giảng dạy lớp mình trong suốt năm học để
tỏ lòng tri ân. Biết rằng mỗi món quà tặng cho thầy với giá 50 nghìn đồng, mỗi
món quà tặng cho cô với giá 65 nghìn đồng và tổng số tiền mà lớp mua quà là 870
nghìn đồng. Em hãy tính xem lớp 9A1 dự định tặng quà cho bao nhiêu thầy giáo
và bao nhiêu cô giáo?
Bài 4: (1,5 điểm) Cửa hàng A đưa ra hình thức khuyến mãi như sau: Nếu bạn mua
một đôi giày với mức giá thông thường, bạn sẽ được giảm 35% khi mua đôi thứ hai
và mua đôi thứ ba với một nửa giá lúc đầu. Bạn Ngọc đã trả 1 290 000 đồng cho 3 đôi giày.
a) Hỏi giá tiền lúc đầu của một đôi giày là bao nhiêu?
b) Nếu cửa hàng đưa ra hình thức khuyến mãi thứ hai là giảm 30% cho mỗi
đôi giày. Bạn Ngọc nên chọn hình thức khuyến mãi nào sẽ có lợi hơn nếu mua ba đôi giày?
Bài 5: (1,0 điểm) Một hộp kem hình trụ có đường kính 12 cm và chiều cao 15 cm đựng
đầy kem. Kem sẽ được người bán hàng chia vào các bánh ốc quế hình nón có chiều cao 12
cm và đường kính 6 cm, có hình bán cầu trên đỉnh như hình vẽ.
a) Tính thể tích hộp kem hình trụ?
b) Tính số que kem có thể chia được? Biết rằng người bán hàng đã chia kem vào bánh
ốc quế ít hơn 5% so với thể tích thực của chiếc bánh như hình vẽ trên tính luôn phần bán
cầu. Cho biết công thức tính thể tích:
Hình trụ là: 𝑉𝑉 = 𝑆𝑆. ℎ trong đó S là diện tích đáy hình trụ, h là chiều cao hình trụ
Hình nón: 𝑉𝑉 = 1 𝑆𝑆. ℎ trong đó S là diện tích đáy hình nón, h là chiều cao hình nón 3
Hình cầu: 𝑉𝑉 = 4 𝜋𝜋𝑅𝑅3 trong đó 𝜋𝜋 ≈ 3,14, R là bán kính hình cầu 3
Bài 6: (2,5 điểm) Cho đường tròn tâm O đường kính AB. Dây CD vuông góc với
AB tại E (E nằm giữa A và O; E không trùng A, không trùng O). Lấy điểm M thuộc
cung nhỏ BC sao cho cung MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM
cắt đường thẳng CD tại K.
a. Chứng minh tứ giác BMFE nội tiếp.
b. Chứng minh BF vuông góc với AK và EK.EF = EA.EB
c. Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.
ĐÁP ÁN VÀ BIỂU ĐIỂM Bài Câu Lời giải Điểm Bài 1 a 1 (2,0 điểm) a)Vẽ (P) : y = 2
x và (D) : y = 3x − 4 2 0,25x2 Bảng giá trị 0,25x2 x y = 3x − 4 4 1 x -4 -2 0 2 4 y = 1 2 x 8 2 0 2 8 2 Vẽ đúng mỗi đồ thị b
b) Phương trình hoành độ giao điểm của (P) và (D) là: 1 2 x = 3x − 4 2
⇔ x − 6x + 8 = 0 0,25 2 x = 0,5 1 4 ⇔ x = 2 2 Với x1 = 4 Þ y1 = 8 Với x2 = 2 Þ y2 = 2
Vậy: Tọa độ các giao điểm của (P) và (D) là: (4 ; 8) 0,25 và (2 ; 2) Bài 2
Vì a.c = 1.( - 2) < 0 nên phương trình có hai 0,5 (1,5 điểm) nghiệm x 1;x2 Theo định lí Viet ta có: 0,5 0,25 b x x − + = = 5 1 2 a 0,25 c x x = = 2 − 1 2 a 2 2 2 2
x + x = (x + x ) − 2x x = 5 − 2.( 2) − = 29 1 2 1 2 1 2 2
A = (x − x ) − x x 1 2 1 2 2 2
= x + x − 2x x − x x 1 2 1 2 1 2 = 29 − 3.( 2) − = 35 Bài 3
Gọi x là số thầy giáo mà lớp 9A1 dự định mua quà (1,5 điểm) tặng
y là số cô giáo mà lớp 9A1 dự định mua quà tặng
( ĐK: x, y nguyên dương và x, y < 15) 0,25
Lớp 9A1 muốn mua quà tặng cho 15 giáo viên nên ta có: 0,25 x + y = 15 (1)
Mỗi món quà tặng cho thầy với giá 50 nghìn đồng,
mỗi món quà tặng cho cô với giá 65 nghìn đồng và 0,25
tổng số tiền mà lớp mua quà là 870 nghìn đồng ⇒ 50x + 65y = 870 (2) 0,25
Từ (1) và (2) ta có hệ phương trình: � 𝑥𝑥 + 𝑦𝑦 = 15
50 𝑥𝑥 + 65 𝑦𝑦 = 870 ⇔ �𝑥𝑥 = 7 𝑦𝑦 = 8 ( TĐK) 0,25
Vậy lớp 9A1 dự định mua quà tặng cho 7 thầy giáo 0,25 và 8 cô giáo. Bài 4
a)Gọi x ( đồng) là giá tiền lúc đầu của đôi giày (1,5điểm) ( x >0) 0,5
Theo đề bài, ta có phương trình 1 x + 65%x + x =1 290 000 2 0,5 Giải pt, ta có x = 600 000
Vậy giá của đôi giày lúc đầu là 600 000 đồng.
b) Khi mua theo hình thức khuyến mãi thứ hai thì
số tiền phải trả cho 3 đôi giày là
600 000. 3. 70% = 1 260 000 (đồng) 0,25
Vậy bạn Ngọc nên chọn hình thức khuyến mãi 2 sẽ có lợi hơn. 0,25 Bài 5
a) Thể tích hộp kem hình trụ: (1,0điểm) 0,5
𝑉𝑉 = 𝑆𝑆. ℎ = 𝜋𝜋𝑅𝑅2ℎ = 𝜋𝜋. 62. 15 ≈ 1695,6 (𝑐𝑐𝑐𝑐3)
b) Thể tích que kem hình bánh ốc quế là: 1 4
𝑉𝑉 = 3.𝜋𝜋.32.12 + 3.𝜋𝜋.33 ≈ 226,08 (𝑐𝑐𝑐𝑐3)
Lượng kem mà người bán bỏ vào bánh là:
𝑉𝑉 = 226,08.0,9 ≈ 203,472 (𝑐𝑐𝑐𝑐3) 0,25
Số que kem có thể chia được là: 1695,6: 203,472 ≈
8,3 ≈ 8 (𝑞𝑞𝑞𝑞𝑞𝑞) 0,25 Bài 6 (2,5 điểm) a
a. Chứng minh tứ giác BMFE nội tiếp. Xét tứ giác BMFE ta có: 0,25 ∧ 0
AMB = 90 (góc nội tiếp chắn nửa (O) ∧ 0,25 0 EFM = 90 ( giả thiết ) 0,5 ∧ ∧ 0 AMB+ EFM = 180
=> tứ giác BMFE nội tiếp. b
b. Chứng minh BF vuông góc với AK và EK.EF = EA.EB • Xét tam giác AKB
AM ⊥ BK, KE ⊥ AB , AM và KE cắt nhau tại F 0,25
Nên F là trực tâm, suy ra BF là đường cao thứ ba của tam giác
=> BF ⊥ AK
• Xét tam giác AEF vuông tại E và tam giác KEB vuông tại E có: ∧ ∧
KFM = AFE ( đối đỉnh ) 0,25 ∧ ∧
KFM = KBE ( góc ngoài bằng góc đối trong ) ∧ ∧ AFE = KBE 0,25 A ∆ EF = K
∆ EB(g − g) => AE FE ⇒ = KE EB
⇒ AE.EB = KE.FE 0,25 c
c. Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF. ∧ ∧ Ta có :
IMF = MBA ( cùn chắn cung AB) ∧ ∧
IFM = MBA ( góc ngoài bằng góc đối trong) ∧ ∧
=> IFM = IMF
=> tam giác IFM cân tại I 0,25 => IF=IM (1) ∧ ∧
Ta có: IMK = 90 − IMF ∧ ∧ MKI = 90 − IFM ∧ ∧
Mà IFM = IMF ( cmt) ∧ ∧ => MIK = MKI
=> Tam giác MIK cân tại I => IK = IM ( 2) 0,25
Từ (1) và ( 2) suy ra IK= IF
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng điểm T Chủ Nội dung/Đơn vị T đề kiến thức
Nhận biết Thông hiểu Vận dụng Vận dụng cao T N TL T N TL T N TL T N TL Vẽ đồ thị hàm số 1
Đồ thị 𝑦𝑦 = 𝑎𝑎𝑥𝑥2 (P) và y = (Bài a) 1 hàm ax + b (d) (1,0đ) 2đ số 1 Tìm tọa độ giao (Bài b) điểm của (P) và (d) (1,0đ) Hệ 1 thức (Bài 2) 2 Vi-et Hệ thức Vi-et (1,5 đ) 1,5đ và ứng dụng Giải bài toán bằng 1 cách lập hệ (Bài 3) phương trình. (1,5đ) Bài tập Dạng ứng dụng 1 1 3 ứng tăng giảm Bài 4a Bài 4b 4đ dụng (1,0đ) (0,5đ)
thực tế Dạng toán ứng 1 1 dụng hình không (Bài 5a) (Bài gian (0,5đ) 5b) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài (Bài 6b) 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100 % Tỉ lệ chung 65% 35% 100 %
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 T Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ T nhận thức Nhận Thông Vận VD
biết hiểu dụng cao Đồ thị hàm 1 số y = ax2 (Bài (P) và Vận dụng: 1a) y = ax + b
- Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ trục tọa độ 1 Đồ thị (d) hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1 giao điểm
- Vận dụng phương trình bậc hai một ẩn (Bài của (P) và
trong việc tìm tọa độ giao điểm của (P) và 1b) (d) (d). Hệ thức Thông hiểu:
- Tính được tổng, tích, x12+x22 các 1
2 Vi-et và Hệ thức Vi - ứng et
nghiệm của phương trình bậc hai một (Bài dụng
ẩn bằng hệ thức Vi-et (Biến đổi đơn 2) giản)
Giải bài toán Thông hiểu: bằng cách
- Phân tích đề bài, tìm mối quan hệ giữa lập hệ
các đại lượng cho trong đề bài, gọi ẩn, từ 1 phương
đó lập được hệ 2 phương trình bậc nhất 2 Bài 3 trình. ẩn. Bài tập
- Giải hệ phương trình, đối chiếu điều
kiện để trả lời câu hỏi đề bài yêu cầu. 3 ứng dụng Thông hiểu: thực tế
- Tính được số tiền phải trả bằng công Dạng ứng thức tăng/giảm 1 1 dụng tăng Vận dụng: Bài Bài giảm
- Vận dụng kiến thức về tăng giảm, tỉ
số % giải quyết một số vấn đề trong 4a 4b thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện Dạng toán
tích toàn phần, thể tích của hình trụ (hoặc ứng dụng hình nón, hình cầu) 1 1
hình không Vận dụng cao: Bài Bài gian
- Vận dụng hợp lí công thức tính diện 5a 5b
tích, thể tích hình trụ (hoặc hình nón,
hình cầu) để giải quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường (Bài tròn. 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các
loại góc với đường tròn, mối quan hệ
giữa các góc, phối hợp các kiến thức để 4 Hình Tứ giác nội chứng minh. học tiếp
- Vận dụng các phương pháp chứng 1 1
minh hai tam giác đồng dạng, chứng (Bài (Bài
minh song song, vuông góc, 3 điểm 6b) 6c)
thẳng hàng giải quyết yêu cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức
trong hình học phẳng để giải quyết yêu cầu đề bài. UBND HUYỆN CỦ CHI
ĐỀ KIỂM TRA CUỐI HỌC KỲ II-NH: 2023 – 2024
TRƯỜNG TRUNG HỌC CƠ SỞ MÔN: TOÁN 9 TÂN PHÚ TRUNG
Thời gian làm bài: 90 phút
Bài 1:(2 điểm): Cho Parabol P 1 2
: y x và đường thẳng D 3
: y x 1. 4 4
a) Vẽ (P) và (D) trên cùng hệ trục tọa độ
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính
Bài 2:(1,5 điểm) Cho phương trình: 2
3x − x −1 = 0 .
a/ Chứng tỏ phương trình luôn có hai nghiệm phân biệt x , x 1 2
b/Không giải phương trình, hãy tính giá trị của biểu thức 2 2
A = x + x + x x 1 2 1 2
Bài 3: (1,5 điểm) Một lớp học có 40 học sinh, trong đó nam nhiều hơn nữ. Trong giờ
ra chơi, cô giáo đưa cả lớp 260 000 đồng để mỗi bạn nam mua một ly Coca giá 5000
đồng/ly, mỗi bạn nữ mua một bánh phô mai giá 8000 đồng/cái và được căn tin thối lại
3000 đồng. Hỏi lớp có bao nhiêu học sinh nam và bao nhiêu học sinh nữ?
Bài 4: (1,5 điểm) Cửa hàng A thực hiện chương trình giảm giá cho khách hàng mua sỉ
tập học sinh loại B theo thùng 100 quyển/thùng với giá niêm yết của mỗi thùng tập loại
100 quyển/thùng là 550 000 đồng như sau:
Nếu mua 1 thùng thì giảm 5% so với giá niêm yết.
Nếu mua 2 thùng thì thùng thứ nhất giảm 5% còn thùng thứ hai được giảm 10% so với giá niêm yết.
Nếu mua 3 thùng trở lên thì thì ngoài hai thùng đầu được hưởng chương trình
giảm giá như trên thì từ thùng thứ ba trở đi mỗi thùng sẽ được giảm 20% so với giá niêm yết.
Nếu tổng hoá đơn nhiều hơn 4 triệu đồng thì được giảm thêm 2% trên giá đã giảm.
a) Cô Lan mua 5 thùng tập loại B mỗi thùng 100 quyển ở cửa hàng A đó thì sẽ
phải trả bao nhiêu tiền?
b) Chú Bình cũng mua tập loại B mỗi thùng 100 quyển ở cửa hàng A đó và phải
trả số tiền 4 015 550 đồng. Hỏi chú Bình đã mua bao nhiêu thùng tập?
Bài 5: (1 điểm) Một thùng đựng nước có dạng hình trụ chiều cao là 35 cm đường kính đáy 30 cm.
a) Tính thể tích của thùng.
b) Người ta sử dụng thùng trên để múc nước đổ vào một bể chứa có dung tích1m3. Hỏi
cần phải đổ ít nhất bao nhiêu thùng thì đầy bể chứa? Biết rằng mỗi lần xách người ta
chỉ đổ đầy 90% thùng để nước không đổ ra ngoài.
Bài 6: (2,5 điểm) Cho ∆ABC (AB < AC) có 3 góc nhọn nội tiếp đường tròn (O;R). Gọi
H là giao điểm của 3 đường cao AD, BE, CF của ∆ABC.
a) Chứng minh: tứ giác BFEC và BFHD nội tiếp đường tròn.
b) Vẽ đường kính AK của đường tròn (O). Chứng minh: AB.AC = 2R.AD.
c) Gọi I là trung điểm của BC.So sánh OI và AH. Hết
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM BÀI HƯỚNG DẪN CHẤM BIỂU ĐIỂM Bài 1
a) Vẽ đồ thị (P) và (D) trên cùng hệ trục tọa độ. (2,0 đ ) BGT: 4 − x – 2 4 − 0 2 0,25đ 4 2 4 1 4 − 1 − 1 − 4 − 2 y = − x – – 0 – – 4 4 1 1 4 0,25đ x 0 4 3 y = − x −1 4 1 − 4 − 0,25đ+0,25đ
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (D) 1 2 3
− x = − x −1 4 4 0,25đ ⇔ 2
x − 3x − 4 = 0 x = −1 ⇔ x = 4 0,25đ Thay x = −1 vào 1 2
y = − x , ta được: 4 1 y = − (− )2 1 1 = − 4 4 0,25đ Thay x = 4 vào 1 2
y = − x , ta được: 4 1 y = − .(4)2 = 4 − 4 0,25đ Vậy 1 −1; −
, (4; − 4) là hai giao điểm cần tìm. 4
Bài 2 a/Vì a.c =3.(-1) =-3<0 nên phương trình có 2 nghiệm phân biệt 0,5đ (1,5đ) x , x 1 2
b/Theo định lý Viét ta có 1
S = x + x = , 1 P = x x = − 0,5đ 1 2 3 1 2 3 2 2 2 1 1 7
x + x = x + x − 2x x = − 2 − = 1 2 ( 1 2)2 1 2 3 3 0,25đ 9 Ta có 2 2 7 1 4 A x x x .x = + + = + − = 0,25đ 1 2 1 2 9 3 9 Bài 3
Gọi x (học sinh) là số học sinh nam, y (học sinh) là số học sinh 0,25 đ ( 1,5 đ)
nữ (điều kiện: 𝑥𝑥, 𝑦𝑦 ∈ ℕ ∗, 𝑥𝑥 > 𝑦𝑦)
Theo đề bài, ta lập hệ phương trình: x + y = 40 0,5 đ 5x + 8y = 257 x = 21 ⇔ 0,5 đ y = 19
Vậy có 21 học sinh nam và 19 học sinh nữ. 0,25 đ Bài 4
a) Giá bán của thùng tập thứ nhất: ( 1,5 đ)
550000. (100% − 5%) = 522500 (đồng) 0,25 đ
Giá bán của thùng tập thứ hai: 0,25 đ
550000. (100% − 10%) = 495000 (đồng)
Giá bán của mỗi thùng tập tính từng thùng thứ ba:
550000. (100% − 20%) = 440000 (đồng) 0,25 đ
Số tiền cô Lan phải trả khi mua 5 thùng tập loại B mỗi thùng 100 quyển ở cửa hàng A:
522500 + 495000 + 3 . 440000 = 2337500 (đồng) 0,25 đ
b)Gọi x là số thùng tập chú Bình đã mua (x ∈ N ) Ta có phương trình: 522500+ 495000+ 0,25 đ
(x−2).440000.(100%−2%) = 4015550 ⇔ x = 9 (N ) 0,25 đ
Vậy chú Bình đã mua 9 thùng tập. Bài 5
a) Bán kính đáy hình trụ là R = 30: 2 =15(cm). 0,25 đ ( 1 đ) Thể tích trụ: 2 2 V = R π h = π = π ≈ ( 3 .15 .35 7875 24740 cm )
b)Thể tích nước mỗi lần xách là: 0,25 đ = ( 3 cm ) = ( 3 24740.90% 22266 0,022266 cm ).
Số thùng ít nhất cần đổ để đầy bể là: 0,25 đ
1: 0,022266 = 44,91 nên số thùng cần là 45 thùng. 0,25 đ Bài 6 ( 2,5 đ) A E O H F C B D I K a) Tứ giác BFEC có: 𝐵𝐵𝐵𝐵𝐵𝐵 � = 𝐵𝐵𝐵𝐵𝐵𝐵
� = 90𝑜𝑜 (BE, CF là 2 đường 0,25 đ cao của ∆ABC)
⇒ Tứ giác BFEC nội tiếp đường tròn( vì có hai đỉnh cùng nhìn 0,25 đ 1 cạnh dưới 1 góc 900). Xét tứ giác BFHD ta có 𝐻𝐻𝐻𝐻𝐵𝐵 � = 90𝑜𝑜 (gt) 0,25 đ 𝐵𝐵𝐵𝐵𝐵𝐵 � = 90𝑜𝑜 (gt) ⇒ 𝐵𝐵𝐵𝐵𝐻𝐻 + � 𝐻𝐻𝐻𝐻𝐵𝐵 � = 180𝑜𝑜 0,25đ
⇒ Tứ giác BFHD nội tiếp đường tròn.
b) Ta có: 𝐴𝐴𝐴𝐴𝐵𝐵
� = 90𝑜𝑜 (góc nội tiếp chắn nửa đường tròn) Xét ∆ ABD và ∆ AKC có: 𝐴𝐴𝐵𝐵𝐻𝐻 � = 𝐴𝐴𝐴𝐴𝐵𝐵
� (hai góc nội tiếp cùng chắn cung AC); 𝐴𝐴𝐻𝐻𝐵𝐵 � = 𝐴𝐴𝐵𝐵𝐴𝐴 � = 90𝑜𝑜
Do đó: ∆ ABD ∽∆ AKC (g.g) 0,25đ AB AD ⇒ = ⇒ AB.AC = AK.AD AK AC 0,25 đ Mà AK = 2R Suy ra: AB.AC 0,25 đ = 2R.AD c)
Ta có: 𝐴𝐴𝐵𝐵𝐴𝐴
� = 90𝑜𝑜 (góc nội tiếp chắn nửa đường tròn) Suy ra BK ⊥ AB Mà CF ⊥ AB(gt)
Do đó BK//CF suy ra BK//HC (1)
Ta có 𝐴𝐴𝐵𝐵𝐴𝐴 � = 90𝑜𝑜 (cmt)
Suy ra CK ⊥ AC mà BE ⊥ AC(gt)
Do đó CK//BE Suy ra CK//BH (2)
Từ (1) và (2) Suy ra Tứ giác BHCK là hình bình hành 0,25 đ
Mà I là trung điểm BC (gt)
Suy ra I cũng là trung điểm HK 0,25đ Xét tam giác AHK ta có I là trung điểm HK (cmt) O là trung điểm AK (gt)
Suy ra OI là đường trung bình của tam giác AHK 0,25đ Do đó AH = 2OI
Lưu ý: học sinh làm cách khác đúng vẫn trọn điểm. UBND HUYỆN CỦ CHI
ĐỀ THAM KHẢO KT CUỐI KỲ 2
TRƯỜNG THCS THỊ TRẤN NĂM HỌC 2023 - 2024 Môn: TOÁN 9
Thời gian làm bài: 90 phút (Không kể thời gian phát đề)
Bài 1 : (2 điểm) Cho các hàm số (P) 1 2
y = x và (D) 3
y = x −1 2 2
a/ Vẽ (P) và (D) trên cùng một mặt phẳng tọa độ
b/ Tìm tọa độ giao điểm của chúng bằng phép toán
Bài 2 : (1,5 điểm) Cho pt 2
2x − 3x −10 = 0 . Phương trình có 2 nghiệm x , x , không giải 1 2
phương trình hãy tính giá trị biểu thức 2 2
A = x − 3x + x − 3x − 5 1 1 2 2
Bài 3 : (1,5 điểm) Sau khi xem bảng giá, mẹ bạn An đưa 350 000 đồng nhờ bạn mua 1 bàn
ủi, 1 bộ lau nhà. Hôm nay đúng đợt khuyến mãi, bàn ủi giảm 10 %, bộ lau nhà giảm 20 %
nên bạn chỉ trả 300 000 đồng. Hỏi giá tiền của bàn ủi, bộ lau nhà khi chưa giảm là bao nhiêu?
Bài 4 : (1,5điểm)
Bác Nam trồng cây ăn quả trúng mùa nên cuối vụ thu hoạch bác tiết kiệm được 200 triệu đồng.
Bác quyết định gửi hết số tiền tiết kiệm đó vào ngân hàng theo hình thức tiết kiệm online, phương
thức đáo hạn quay vòng cả gốc lãi. Bác gửi kỳ hạn 1 năm với lãi suất 5,5%.
a) Hỏi sau hai năm, nếu bác Nam rút tiền, thì bác nhận được tất cả bao nhiêu tiền.
b) Do chưa cần dùng đến số tiền lớn nên sau hai năm bác chưa rút tiền về, bác gửi thêm một năm nữa,
nhưng năm này ngân hàng đã giảm lãi suất. Sau 3 năm, tổng số tiền bác nhận về được 233 735 250
đồng. Hỏi lãi suất năm thứ ba là bao nhiêu phần trăm.
Bài 5 : (1điểm)
Một cốc nước hình trụ có chiều cao 15cm, bán kính đáy là 3cm và lượng nước ban đầu trong cốc
cao 12cm. Thả chìm hoàn toàn vào cốc nước 3 viên bi thủy tinh hình cầu có cùng bán kính là 2cm.
(Giả sử độ dày của thành cốc và đáy cốc không đáng kể - mô phỏng bằng hình vẽ) 3cm 15cm 2cm 2cm 2cm
a) Tính thể tích của nước trong cốc.
b) Khi thả 3 viên bi hình cầu vào cốc thì nước trong cốc có bị tràn ra ngoài không? Nếu có hãy
tính thể tích nước bị tràn ra ngoài?
Bài 6 : (2,5 điểm)
Cho tam giác ABC có ba góc nhọn (ABđường cao BE và CF cắt nhau tại H, AH cắt BC tại I.
a/ Chứng minh: tứ giác AFHE nội tiếp đường tròn và 0 ˆ
BAC =180 − B ˆHC
b/ Kẻ đường kính AK của (O). Chứng minh: AB.AC = 2R.AI
c/Vẽ điểm L đối xứng K qua AB. Chứng minh : HA ⟂ HL -HẾT- ĐÁP ÁN Bài 1
a/ Mỗi bảng giá trị đúng 0,5
(2 điểm) Vẽ đúng một đồ thị 0,5
b/ Phương trình hoành độ giao điểm của (P) và (D) 1 2 1 x = x + 3 2 2 1 0,25 2 1
⇔ x + x −1 = 0 2 2
Giải pt ta được : x = 3; x = 2 − 0,25 1 2 Tìm được đúng y 0,25
Giải và tìm được tọa độ giao điểm : 9 3; ;( 2 − 0,25 ;2) 2 Bài 2 2
2x − 3x −10 = 0 (1,5điểm)
Phương trình có 2 nghiệm, theo vi-ét b − 3 0,25
S = x + x = = 1 2 a 2 0,25 = . c P x x = = 5 − 1 2 a 2 2
A = x − 3x + x − 3x − 5 1 1 2 2 = ( 2 2
x + x − 3 x + x − 5 1 2 ) ( 1 2) 0,25 2
= S − 2P − 3S − 5 0,25 2 3 = − (− ) 3 11 2 5 − 3 − 5 = 0,25+0,25 2 2 4 Bài 3
(1,5điểm) Gọi x,y ( đ ) lần lượt là giá 1 bàn ủi và giá 1 bộ lau nhà khi chưa giảm 0,25 ( 0 < x,y < 350000 )
Vì giá 1 bàn ủi và giá 1 bộ lau nhà khi chưa giảm là 350000 đồng 0,25
Nên ta có pt: x + y = 350000 (1)
Giá bàn ủi sau khi giảm 10% là : 90%x (đ) 0,25
Giá bộ lau nhà sau khi giảm 20% là : 80%y (đ)
Vì số tiền phải trả là 300000 đồng nên ta có pt: 0,25 90%x + 80%y = 300000 (2)
x + y = 350000 x = 200000
Từ (1) và (2) ta có hệ pt: ⇔ (N ) 90%
x + 80%y = 300000 y = 150000 0,25
Vậy giá lúc đầu của 1 bàn ủi là 200000 đồng , 1 bộ lau nhà là 150000 đồng 0,25 Bài 4
a) Số tiền cả vốn lẫn lãi sau 1 năm: (1,5điểm)
200. (100% + 5,5%) = 211 ( 𝑡𝑡𝑡𝑡𝑡𝑡ệ𝑢𝑢 đồ𝑛𝑛𝑛𝑛) 0,5
Sau 2 năm, bác Nam nhận được số tiền là:
211. (100% + 5,5%) = 222,605 ( 𝑡𝑡𝑡𝑡𝑡𝑡ệ𝑢𝑢 đồ𝑛𝑛𝑛𝑛) 0,5
b) Gọi x là lãi suất của năm thứ ba ( 0 < x < 1)
Vì số tiền sau 3 năm là 233, 73525 triệu đồng
⇒ 𝑝𝑝𝑡𝑡: 222,605. (100% + 𝑥𝑥) = 233,73525 0,25 ⟺ 1 + 𝑥𝑥 = 1,05 ⟺ 𝑥𝑥 = 0,05 = 5%
Vậy lãi suất năm thứ 3 của ngân hàng là 5%/năm. 0,25 Bài 5
a) Thể tích nước trong cốc có chiều cao h = 12cm (1,0điểm)
𝑉𝑉 = 𝜋𝜋𝑡𝑡2ℎ = 3,14. 32. 12 = 339,12 𝑐𝑐𝑐𝑐3 0,5
b) Thể tích phần không chứa nước của cốc
𝑉𝑉′ = 𝜋𝜋𝑡𝑡2. ℎ′ = 3,14. 32. (15 − 12) = 84,78 𝑐𝑐𝑐𝑐3 0,25
Thể tích 3 viên bi thả vào cốc 4 4
𝑉𝑉1 = 3. 3𝜋𝜋𝑅𝑅3 = 3.3.3,14.23 = 100,48 𝑐𝑐𝑐𝑐3
Vì 𝑉𝑉1 > 𝑉𝑉′ nên khi thả 3 vên bi vào cốc thì nước bị tràn ra ngoài 1 lượng là: 0,25
100,48 − 84,78 = 15,7 𝑐𝑐𝑐𝑐3 Bài 6 (2,5điểm) A E F L H O B I C K
a/ Chứng minh: tứ giác AFHE nội tiếp đường tròn và 0 B
∠ AC =180 − B ∠ HC Xét tứ giác AEHF 0 A ∠ EH = 90 0,25 Có : 0 A ∠ FH = 90 0 0 0 ⇒ A ∠ EH + A ∠ FH = 90 + 90 =180 0,25
⇒ AEHF nội tiếp đường tròn 0 ⇒ B ∠ AC + E ∠ HF =180 0,25 0 ⇒ ∠ = − ∠ BAC 180 EHF Mà : E ∠ HF = B ∠ HC 0 ⇒ B
∠ AC =180 − B ∠ HC 0,25
b/ Chứng minh : AB.AC = 2R.AI
Xét tam giác ABC Có : BE và CF là hai đường cao cắt nhau tại H
⇒ H là trực tâm của tam giác ABC
⇒ AH là đường cao thứ ba
⇒ AH ⊥ BC tại I 0 ⇒ AˆIB = 90 0,25 Có : 0 ˆ
ACK = 90 ( Góc nội tiếp chắn nửa đường tròn) ⇒ Aˆ = ˆ IB ACK HS CHỨNG MINH ĐƯỢC IB ∆ A∽ CKA ∆ 0,25 AB AI ⇒ = AK AC 0,25 ⇒ AB.AC = AK.AI= 2R.AI 0,25
c/ Chứng minh : AH ⊥ LH
- HS chứng minh được: A ˆLB = A ˆKB
- HS chứng minh được: A ˆKB = A ˆHE
Suy ra: A ˆLB = A ˆHE 0,25
Suy ra : tứ giác AHBL nội tiếp 0
⇒ A ˆBL = A ˆ HL = 90 ⇒ HA ⊥ HL 0,25
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng
TT Chủ đề Nội dung/Đơn vị kiến điểm thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TN TL TN TL TN TL TN TL
Vẽ đồ thị hàm số 𝑦𝑦 = 1
𝑎𝑎𝑥𝑥2 (P) và y = ax + b (Bài a) 1 Đồ thị (d) (1,0đ) hàm số 2đ 1 Tìm tọa độ giao điểm (Bài b) của (P) và (d) (1,0đ) Hệ thức 1 2 Vi-et và (Bài 2) ứng Hệ thức Vi-et (1,5 đ) 1,5đ dụng Giải bài toán bằng 1 cách lập hệ phương (Bài 3) trình. (1,5đ) Bài tập 3 ứng Dạng ứng dụng tăng 1 1 dụng 4đ giảm Bài 4a Bài 4b thực tế (1,0đ) (0,5đ) Dạng toán ứng dụng 1 1 hình không gian (Bài 5a) (Bài 5b) (0,5đ) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài 6b) (Bài 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng Đồ thị hàm số 1 y = ax2 (P) và Vận dụng: (Bài
y = ax + b (d) - Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ 1a) 1 Đồ thị trục tọa độ hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong việc (Bài (P) và (d)
tìm tọa độ giao điểm của (P) và (d). 1b) Hệ thức Thông hiểu: 2 2 2 Vi-et và
Hệ thức Vi -et - Tính được tổng, tích, x1 +x2 các nghiệm của 1 ứng dụng
phương trình bậc hai một ẩn bằng hệ thức (Bài 2)
Vi-et (Biến đổi đơn giản) Giải bài toán Thông hiểu:
bằng cách lập - Phân tích đề bài, tìm mối quan hệ giữa các đại hệ phương
lượng cho trong đề bài, gọi ẩn, từ đó lập được hệ 1 trình.
2 phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức Dạng ứng tăng/giảm 1 Bài tập dụng tăng Vận dụng: 1 Bài 3 ứng dụng giảm
- Vận dụng kiến thức về tăng giảm, tỉ số % Bài 4a 4b thực tế
giải quyết một số vấn đề trong thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện tích toàn
Dạng toán ứng phần, thể tích của hình trụ (hoặc hình nón, hình dụng hình cầu) 1 1 không gian
Vận dụng cao: Bài 5a Bài
- Vận dụng hợp lí công thức tính diện tích, thể 5b
tích hình trụ (hoặc hình nón, hình cầu) để giải
quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc
với đường tròn, mối quan hệ giữa các góc, phối 4
hợp các kiến thức để chứng minh.
Hình học Tứ giác nội tiếp
- Vận dụng các phương pháp chứng minh hai 1 1
tam giác đồng dạng, chứng minh song song, (Bài (Bài
vuông góc, 3 điểm thẳng hàng giải quyết yêu 6b) 6c) cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình
học phẳng để giải quyết yêu cầu đề bài. UBND HUYỆN CỦ CHI
ĐỀ KIỂM TRA CUỐI KỲ II TRƯỜNG THCS THỊ TRẤN 2 NĂM HỌC 2023–2024 MÔN: TOÁN – LỚP 9 ĐỀ THAM KHẢO
(Đề thi có 02 trang) Thời gian: 90 phút
Bài 1.( 2 điểm) Cho Parabol (P) 1 2
y = − x và đường thẳng (d) y = x − 4 2
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép toán.
Bài 2.(1,5 điểm) Cho phương trình 2
2x − 5x −1= 0. Không giải phương trình, hãy
tính giá trị của biểu thức M = (2x − x 2x − x 1 2 ) ( 2 1 )
Bài 3.(1,5 điểm) Hôm qua mẹ của bạn Hồng qua tiệm tạp hóa gần nhà mua 20 quả
trứng gồm 10 quả trứng gà và 10 quả trứng vịt hết 45 000 đồng. Hôm nay mẹ của
bạn Hồng cũng qua tiệm tạp hóa gần nhà mua 20 quả trứng gồm 15 quả trứng gà và
5 quả trứng vịt chỉ hết 42 500 đồng mà giá trứng thì vẫn như cũ. Hỏi nếu ngày mai
mẹ bạn Hồng nhờ bạn Hồng qua tiệm tạp hóa trên mua 30 quả trứng gồm 20 quả
trứng gà và 10 quả trứng vịt thì mẹ bạn Hồng phải đưa cho bạn Hồng số tiền vừa đủ
là bao nhiêu biết giá trứng không thay đổi?
Bài 4.(1,5 điểm) Nhân ngày quốc tế phụ nữ 8/3. Một cửa hàng bán quà lưu niệm bán
đồng giá 50 000 đồng một món và có chương trình giảm giá 15% cho một món hàng
và nếu khách hàng mua 5 món trở lên thì từ món thứ 5 trở đi khách hàng chỉ phải trả
70% giá đã giảm. Đặc biệt, nếu khách hàng mua trên 10 món thì cũng được khuyến
mãi như trên và chỉ phải trả 80% tổng số tiền trên hóa đơn.
a) Cô Hương đến cửa hàng và mua tổng cộng 10 món hàng. Em hãy tính xem
Cô Hương phải trả bao nhiêu tiền?.
b) Cùng thời điểm ấy Chị Phương cũng đến mua hàng. Khi ra quầy tính tiền Chị
Phương đã trả tổng số tiền là 397 800 đồng. Em hãy tính xem Chị Phương đã mua bao nhiêu món hàng?
Bài 5.(1 điểm) Để lắp đặt hệ thống thoát nước cho một khu vực dân cư, đội công
nhân cần đúc 500 ống cống bê tông dạng hình trụ có đường kính trong là 2 m, chiều
dài mỗi ống là 1,6 m và độ dày thành ống là 10 cm.
a) Tính lượng bê tông (m3) cần dùng để đúc cho một ống cống như trên? Biết
công thức tính thể tích hình trụ là 2
V = π R h (lấy π = 3,14).
b) Hỏi đội công nhân cần ít nhất bao nhiêu bao xi măng loại 50 kg/bao để làm
đủ số ống cống bê tông trên? Biết mỗi mét khối bê tông cần 289 kg xi măng.
Bài 6.(2,5 điểm) Cho AB ∆
C nhọn (AB < AC) nội tiếp đường tròn (O) có 3 đường cao
AD , BF và CE cắt nhau tại H. Vẽ đường kính AK của đường tròn (O).
a) Chứng minh tứ giác BCFE nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác BCFE.
b) Chứng minh: AD⋅CK = AC⋅DB c) Tính tỉ số OI và AH.
.............Hết............. HƯỚNG DẪN CHẤM Môn Toán lớp 9 Bài 1: (2đ)
a) – Mỗi bảng giá trị đúng cho 0,25đ x 2
- Vẽ đúng mỗi đồ thị cho 0,25đ x 2
b) - Phương trình hoành độ giao điểm của (P) và (d) đúng cho 0,25đ
- Tìm đúng tọa độ giao điểm cho 0,5đ - Kết luận 0,25đ Bài 2: (1,5đ) Vì . a c = 2.(− ) 1 = 2 − < 0
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 0,25đ −b 5
S = x + x = = 1 2
Theo định lí Vi-et, ta có: a 2 0,25đ + 0,25đ c 1 P x . − = x = = 1 2 a 2
- Thực hiện phép tính và thu gọn M = (2x − x 2x − x 1 2 )( 2 1 ) = 5x x − 2( 2 2 x + x 0,25đ 1 2 1 2 ) 1 − 29 = 5. − 2. 0,25đ 2 4 = 17 − 0,25đ Bài 3: (1,5đ) Gọi :
Giá tiền một quả trứng gà là x (đồng) 0,25đ x 2
Giá tiền một quả trứng vịt là y (đồng) Đk : x,y > 0
Ta có hệ phương trình sau : 10 x +10y = 45 000 x = 2000 ⇔ 0,25đ x 3 15 x 5y 42 500 + = y = 2500
Số tiền mẹ của bạn Hồng phải đưa là :
20⋅ 2000 +10⋅ 2500 = 65 000 (đồng) 0,25đ Bài 4: (1,5đ) a)
Giá tiền món hàng khi giảm 15% là
85% ⋅ 50 000 = 42 500 đồng. 0,25đ
Giá tiền món hàng khi trả 70% trên giá đã giảm là
70% ⋅ 42 500 = 29 750 đồng. 0,25đ
Số tiền cô Hương phải trả khi mua 10 món hàng là
4⋅ 42 500 + 6⋅ 29 750 = 348 500 đồng. 0,5đ b)
Vì 397 800 > 348 250 nên chị Phương mua trên 10 món.
Số tiền chị Phương phải trả khi chưa giảm giá là
397 800 :80% = 497 250 đồng 0,25đ
Số món hàng chị Phương mua trên 10 món là :
(497 250 −348500):29 750 = 5 (món)
Số món hàng Chị Phương mua được là : 10 + 5 =15 món 0,25đ Bài 5: (1,5đ)
a)Thể tích hình trụ nhỏ có bán kính là 1m 2 2 3 V = π⋅ R ⋅ h = 3 14
, ⋅1 ⋅1,6 = 5,024m n 0,25đ
Thể tích hình trụ lớn có bán kính là 1,1m 2 2 3 V = π⋅ R ⋅ h = 3 14 , ⋅1 1
, ⋅1,6 = 6,07904 m l 0,25đ
Lượng bê tông cần đúc cho một ống cống là : 3
6,07904 − 5,024 =1,05504 m 0,5đ
b)Lượng bê tông cần đúc cho 500 ống cống là 3
500⋅1,05504 = 527,52 m s 0,25đ
Lượng xi măng cần đúc 500 ống cống là 527,52 289 .
=152453,28(kg)
Ta có : 152453,28:50 = 3049,06...
Vậy cần ít nhất 3050 bao xi măng. 0,25đ Bài 6: (2,5đ)
a)(1đ) Chứng minh : tứ giác BCFE nội tiếp. Xác định tâm I Xét tứ giác BCFE có : = 0 BFC BEC = 90
Suy ra tứ giác BCFE nội tiếp đường tròn đường kính
BC. Tâm I là trung điểm của BC.
b)(1đ)Chứng minh : AD ⋅CK = AC⋅ DB
AK là đường kính nên 0 ACK = 90 Cm : AD ∆ B # AC ∆ K suy ra kết quả AD ⋅ CK = AC ⋅ DB
c)(0,5đ)Tính tỉ số OI và AH.
Cm tứ giác BHCK là hình bình hành.
Cm OI là đường trung bình AH ∆ K suy ra tỉ số OI 1 = AH 2
Ghi chú: Học sinh giải cách khác nhưng đúng vẫn cho điểm. …………Hết……..
A. MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ 2 MÔN TOÁN – LỚP 9
Mức độ đánh giá Tổng
TT Chủ Nội dung/Đơn vị đề kiến thức
Nhận biết Thông hiểu Vận dụng Vận dụng % cao điểm TN TL TN TL
TN TL TN TL Vẽ đồ thị hàm số 1 (Bài Đồ
𝑦𝑦 = 𝑎𝑎𝑥𝑥2 (P) và y = ax + b (d) a) 1 thị (1,0đ) hàm 20 1 số Tìm tọa độ giao (Bài điểm của (P) và (d) b) (1,0đ) Hệ 1 thức (Bài 2 Vi-et 2) và Hệ thức Vi-et (1,5 đ) 15 ứng dụng Giải bài toán 1 bằng cách lập hệ (Bài 3) Bài phương trình. (1,5đ) tập 1 1 3 ứng Dạng ứng dụng Bài 4a Bài dụng 40 tăng giảm (1,0đ) 4b thực (0,5đ) tế Dạng toán ứng 1 1 dụng hình không (Bài (Bài gian 5a) 5b) (0,5đ) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 25 1 1 (Bài (Bài 6b) 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
B. BẢN ĐẶC TẢ ĐỀ KIỂM TRA CUỐI KÌ 2 MÔN TOÁN – LỚP 9 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức Nhận Thông Vận VD
biết hiểu dụng cao Đồ thị hàm 1 số y = ax2 Vận dụng: (Bài 1 Đồ thị (P) và 1a) hàm số y = ax + b
- Vẽ đồ thị hàm số y = ax2 và y = ax + b trên (d) cùng hệ trục tọa độ (a khác 0) Tìm tọa độ Thông hiểu: 1 giao điểm
- Vận dụng phương trình bậc hai một ẩn (Bài của (P) và
trong việc tìm tọa độ giao điểm của (P) và 1b) (d) (d). Hệ Thông hiểu: thức
- Tính được tổng, tích, x 2 2 1 +x2 các 1
2 Vi-et và Hệ thức Vi - nghiệm của phương trình bậc hai một (Bài ứng et
ẩn bằng hệ thức Vi-et (Biến đổi đơn 2) dụng giản) Giải bài Thông hiểu: toán bằng
- Phân tích đề bài, tìm mối quan hệ giữa
cách lập hệ các đại lượng cho trong đề bài, gọi ẩn, từ 1 phương
đó lập được hệ 2 phương trình bậc nhất 2 Bài 3 trình. ẩn.
- Giải hệ phương trình, đối chiếu điều
kiện để trả lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức tăng/giảm
Bài tập Dạng ứng 1 1 dụng tăng Vận dụng: Bài Bài 3 ứng
- Vận dụng kiến thức về tăng giảm, tỉ dụng giảm
số % giải quyết một số vấn đề trong 4a 4b thực tế thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện Dạng toán
tích toàn phần, thể tích của hình trụ (hoặc ứng dụng hình nón, hình cầu) 1 1
hình không Vận dụng cao: Bài Bài gian
- Vận dụng hợp lí công thức tính diện 5a 5b
tích, thể tích hình trụ (hoặc hình nón,
hình cầu) để giải quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường (Bài tròn. 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các
loại góc với đường tròn, mối quan hệ
giữa các góc, phối hợp các kiến thức để 4 Hình Tứ giác nội chứng minh. học tiếp
- Vận dụng các phương pháp chứng 1 1
minh hai tam giác đồng dạng, chứng (Bài (Bài
minh song song, vuông góc, 3 điểm 6b) 6c)
thẳng hàng giải quyết yêu cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức
trong hình học phẳng để giải quyết yêu cầu đề bài.
C. ĐỀ KIỂM TRA CUỐI HỌC KÌ 2 MÔN TOÁN – LỚP 9
ỦY BAN NHÂN DÂN HUYỆN CỦ CHI
KIỂM TRA CUỐI HỌC KÌ 2
TRƯỜNG THCS TÂN THẠNH ĐÔNG
NĂM HỌC 2023 – 2024
(Đề gồm có 02 trang) Môn: TOÁN 9 Thời gian: 90 phút
(không kể thời gian giao đề)
Bài 1 (2 điểm). Cho parabol (𝑃𝑃): 𝑦𝑦 = 1 𝑥𝑥2 và đường thẳng (𝐷𝐷): 𝑦𝑦 = 3𝑥𝑥 − 4. 2
a) Vẽ (𝑃𝑃) và (𝐷𝐷) trên cùng một mặt phẳng tọa độ 𝑂𝑂𝑥𝑥𝑦𝑦.
b) Tìm tọa độ giao điểm của (𝑃𝑃) và (𝐷𝐷) bằng phép toán.
Bài 2 (1,5 điểm). Cho phương trình 3𝑥𝑥2 + 5𝑥𝑥 − 6 = 0 có 2 nghiệm phân biệt
𝑥𝑥1; 𝑥𝑥2. Không giải phương trình, hãy tính giá trị của các biểu thức: a) 𝐴𝐴 = 𝑥𝑥2 2 1 + 𝑥𝑥2 ;
b) 𝐵𝐵 = (𝑥𝑥1 + 2𝑥𝑥2)(2𝑥𝑥1 + 𝑥𝑥2).
Bài 3 (1,5 điểm). Trong kỳ thi học kì II môn Toán lớp 9, một phòng thi của trường
THCS A có 24 thi sinh dự thi. Các thi sinh đều phải làm bài trên giấy thi của trường
phát cho. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng cộng 53 tờ giấy
thi. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 2 tờ giấy thi, bao nhiêu thí sinh
làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi và không có thí sinh
nào làm nhiều hơn 3 tờ giấy thi.
Bài 4 (1,5 điểm). Một cửa hàng trà sữa có chương trình khuyến mại giảm 20%
trên giá bán ban đầu cho 10 ly đầu tiên, từ ly thứ 11 trở đi mỗi ly được giảm thêm 10% trên giá đã giảm.
a) Bạn Bình mua 12 ly trà sữa A ở của hàng trên có giá niêm yết là 20 000 đồng/ly
thì phải trả tất cả bao nhiêu tiền?
b) Bạn Thái mua 20 ly trà sữa B ở cửa hàng trên phải trả 380 000 đồng. Hỏi giá
niêm yết của mỗi ly trà sữa B là bao nhiêu?
Bài 5 (1 điểm). Một quả dưa hấu không hạt ruột đỏ dạng hình cầu có đường kính
25 cm và phần vỏ dày 2 cm.
a) Coi phần ruột màu đỏ cũng có dạng hình cầu và đặc. Thể tích phần ruột màu đỏ
chiếm bao nhiêu phần trăm thể tích quả dưa hấu? (Kết quả làm tròn tới chữ số thập phân thứ hai).
Cho biết công thức tính thể tích hình cầu là 𝑉𝑉 = 4 𝜋𝜋𝑅𝑅3, với 𝑅𝑅 là bán kính hình cầu, 3 𝜋𝜋 = 3,14. 2 cm 25 cm
b) Người ta ép phần ruột màu đỏ của quả dưa hấu trên thì thể tích nước ép thu được
bằng 80% thể tích phần ruột. Nước ép dưa hấu được đựng trong một một ly thủy tinh,
phần lòng trong dạng hình trụ có chiều cao 10 cm và đường kính đáy lòng trong là 5 cm.
Mỗi ly chỉ chứa 70% nước ép dưa hấu. Hỏi dùng nước ép của một quả dưa hấu nói trên
thì đủ nguyên liệu làm ra bao nhiêu ly nước ép dưa hấu?
Cho biết công thức tính thể tích hình trụ là 𝑉𝑉 = 𝜋𝜋𝑟𝑟2ℎ, trong đó 𝑟𝑟 là bán kính đáy
hình trụ, ℎ là chiều cao.
Bài 6 (2,5 điểm). Cho ∆𝐷𝐷𝐷𝐷𝐷𝐷 nhọn (𝐷𝐷𝐷𝐷 < 𝐷𝐷𝐷𝐷) nội tiếp đường tròn (O). Hai đường
cao 𝐷𝐷𝐸𝐸 và 𝐷𝐷𝐹𝐹 cắt nhau tại 𝐴𝐴.
a) Chứng minh các tứ giác 𝐷𝐷𝐹𝐹𝐴𝐴𝐸𝐸 và 𝐷𝐷𝐷𝐷𝐸𝐸𝐹𝐹 nội tiếp.
b) Gọi 𝐼𝐼 là giao điểm của 𝐹𝐹𝐸𝐸 và 𝐷𝐷𝐷𝐷. Chứng minh rằng 𝐼𝐼𝐷𝐷 ⋅ 𝐼𝐼𝐷𝐷 = 𝐼𝐼𝐹𝐹 ⋅ 𝐼𝐼𝐸𝐸.
c) Gọi giao điểm của 𝐼𝐼𝐷𝐷 và đường tròn (O) là 𝐾𝐾 (𝐾𝐾 khác 𝐷𝐷). Chứng minh rằng 5
điểm 𝐷𝐷, 𝐾𝐾, 𝐹𝐹, 𝐴𝐴, 𝐸𝐸 cùng nằm trên một đường tròn. ---o0o--- HẾT
D. ĐÁP ÁN VÀ THANG ĐIỂM
ỦY BAN NHÂN DÂN HUYỆN CỦ CHI
ĐÁP ÁN VÀ THANG ĐIỂM
TRƯỜNG THCS TÂN THẠNH ĐÔNG Môn Toán 9 Bài Đáp án Điểm a) Bảng giá trị x 0 1 y = 3x − 4 – 4 -1 0,25 x -4 -2 0 2 4 y = 1 2 x 8 2 0 2 8 1 2 0,25
(2đ) Vẽ đúng mỗi đồ thị
b) Phương trình hoành độ giao điểm của (P) và (D) là: 0,25x2 1 0,25 2 𝑥𝑥2 = 3𝑥𝑥 − 4
⇔ 𝑥𝑥 = 4 hoặc 𝑥𝑥 = 2. 0,25
Với 𝑥𝑥 = 4 ⇒ 𝑦𝑦 = 8 0,25 Với 𝑥𝑥 = 2 ⇒ y = 2 0,25
Vậy tọa độ giao điểm của (P) và (D) là: (4; 8) và (2; 2)
Ta có 𝑎𝑎 ⋅ 𝑐𝑐 = 3 ⋅ (−6) = −18 < 0. Vậy phương trình có hai 0,25 nghiệm phân biệt.
Theo định lí Vi-ét, ta có −b −5 0,25 S = 𝑥𝑥1 + 𝑥𝑥2 = 2 � a = 3 c 0,25 (1,5đ)
P = 𝑥𝑥1𝑥𝑥2 = a = −2 2 a) 𝐴𝐴 = 𝑥𝑥2 2 0,25
1 + 𝑥𝑥2 = 𝑆𝑆2 − 2𝑃𝑃 = �−5� − 2 ⋅ (−2) = 61. 3 9 b) 𝐵𝐵 = (𝑥𝑥 2 2
1 + 2𝑥𝑥2)(2𝑥𝑥1 + 𝑥𝑥2) = 2𝑥𝑥1 + 𝑥𝑥1𝑥𝑥2 + 4𝑥𝑥1𝑥𝑥2 + 2𝑥𝑥2 0,25 = 2(𝑥𝑥2 2
1 + 𝑥𝑥2 ) + 5𝑥𝑥1𝑥𝑥2 = 2 ⋅ �61� + 5 ⋅ (−2) = 32. 0,25 9 9
Gọi 𝑥𝑥, 𝑦𝑦 (thí sinh) lần lượt là số thí sinh làm 2 tờ và 3 tờ giấy thi.
Điều kiện: 𝑥𝑥, 𝑦𝑦 nguyên dương. 0,25
Vì một phòng thi của trường THCS A có 24 thi sinh dự thi nên ta có phương trình
𝑥𝑥 + 𝑦𝑦 + 3 = 24 ⇔ 𝑥𝑥 + 𝑦𝑦 = 21 (1) 0,25 3
Vì sau khi thu bài, giám thị coi thi đếm được tổng cộng 53 tờ giấy
(1,5đ) thi nên ta có phương trình
2𝑥𝑥 + 3𝑦𝑦 + 3 = 53 ⇔ 2𝑥𝑥 + 3𝑦𝑦 = 50 (2) 0,25
Từ (1) và (2) ta có hệ phương trình �2𝑥𝑥 + 3𝑦𝑦 = 50 𝑥𝑥 + 𝑦𝑦 = 21 0,25
Giải hệ phương trình ta được �𝑥𝑥 = 13 𝑦𝑦 = 8 (thỏa mãn). 0,25
Vậy số thí sinh làm 2 tờ và 3 tờ giấy thi lần lượt là 13 thí sinh và 8 thí sinh. 0,25
a) Số tiền bạn Bình mua 12 ly trà sữa là 0,25x4
10.20.80% + 2.20.80%. 90% = 188,8 (nghìn đồng).
b) Gọi giá niêm yết của mỗi ly trà sữa B là 𝑥𝑥 (nghìn đồng), 𝑥𝑥 > 0. 0,25 4
Vì bạn thái mua 20 ly trà sữa B ở cửa hàng trên phải trả 380 000
(1,5đ) đồng nên ta có phương trình
10. 𝑥𝑥. 80% + 2. 𝑥𝑥. 80%. 90% = 380
⇔ 𝑥𝑥 = 25 (thỏa mãn)
Vậy giá niêm yết của mỗi ly trà sữa B là 25 (nghìn đồng). 0,25
a) Thể tích phần ruột quả dưa hấu là 4 3
𝜋𝜋𝑅𝑅3 = 4 ⋅ 3,14 ⋅ �25−4� = 4846,59 (cm3). 0,25 3 3 2
Phần trăm thể tích phần ruột so với quả dưa là 4 3 3 ⋅ 3,14 ⋅ �25 − 4 2 � 9261 0,25 5 4 3 = 15625 ≈ 59,27% (1đ) 3 ⋅ 3,14 ⋅ �25 2 �
b) Thể tích lòng trong ly thủy tinh là
𝜋𝜋𝑟𝑟2ℎ = 3,14 ⋅ 2,52 ⋅ 10 = 196,25 (cm3) 0,25
Số ly nước em dưa hấu là 4846,59⋅80% ≈ 28,2 (ly) 196,25⋅70%
Vậy dùng nước ép của một quả dưa hấu nói trên thì đủ nguyên liệu làm ra 28 ly. 0,25 D K H G A I E F 6
(2,5đ) a) Xét tứ giác DGAH có 𝐷𝐷𝐹𝐹𝐴𝐴 � = 𝐷𝐷𝐴𝐴𝐸𝐸
� = 90° (FG, EH là đường cao). ⇒ 𝐷𝐷𝐹𝐹𝐴𝐴 � + 𝐷𝐷𝐴𝐴𝐸𝐸 � = 90° + 90° = 180° 0,25
Vậy tứ giác DGAH nội tiếp. (1) 0,25 Xét tứ giác EFHG có 𝐷𝐷𝐹𝐹𝐷𝐷 � = 𝐷𝐷𝐸𝐸𝐷𝐷
� = 90° (FG, EH là đường cao). 0,25
⇒ G và H là hai đỉnh kề nhau cùng nhìn EF dưới một góc không đổi bằng 90°.
Vậy tứ giác EFHG nội tiếp. 0,25
b) Xét ∆𝐼𝐼𝐷𝐷𝐹𝐹 và ∆𝐼𝐼𝐸𝐸𝐷𝐷 có 𝐼𝐼̂ chung ; 0,25 𝐼𝐼𝐷𝐷𝐹𝐹 � = 𝐼𝐼𝐸𝐸𝐷𝐷
� (tứ giác EFHG nội tiếp, góc ngoài bằng góc đối trong). 0,25
Vậy ∆𝐼𝐼𝐷𝐷𝐹𝐹 # ∆𝐼𝐼𝐸𝐸𝐷𝐷 (c.g.c) 0,25
⇒ 𝐼𝐼𝐼𝐼 = 𝐼𝐼𝐼𝐼 ⇒ 𝐼𝐼𝐷𝐷 ⋅ 𝐼𝐼𝐷𝐷 = 𝐼𝐼𝐹𝐹 ⋅ 𝐼𝐼𝐸𝐸 (2) 0,25 𝐼𝐼𝐼𝐼 𝐼𝐼𝐼𝐼
c) Xét ∆𝐼𝐼𝐷𝐷𝐾𝐾 và ∆𝐼𝐼𝐷𝐷𝐷𝐷 có 𝐼𝐼̂ chung ; 𝐼𝐼𝐷𝐷𝐾𝐾 � = 𝐼𝐼𝐷𝐷𝐷𝐷
� (tứ giác EFDK nội tiếp (O), góc ngoài bằng góc đối trong).
Vậy ∆𝐼𝐼𝐷𝐷𝐾𝐾 # ∆𝐼𝐼𝐷𝐷𝐷𝐷 (c.g.c)
⇒ 𝐼𝐼𝐼𝐼 = 𝐼𝐼𝐼𝐼 ⇒ 𝐼𝐼𝐷𝐷 ⋅ 𝐼𝐼𝐷𝐷 = 𝐼𝐼𝐷𝐷 ⋅ 𝐼𝐼𝐾𝐾 (3) 𝐼𝐼𝐼𝐼 𝐼𝐼𝐼𝐼
Từ (2) và (3) suy ra 𝐼𝐼𝐾𝐾 ⋅ 𝐼𝐼𝐷𝐷 = 𝐼𝐼𝐹𝐹 ⋅ 𝐼𝐼𝐸𝐸. 0,25
Xét ∆𝐼𝐼𝐹𝐹𝐾𝐾 và ∆𝐼𝐼𝐷𝐷𝐸𝐸 có 𝐼𝐼̂ chung ;
𝐼𝐼𝐼𝐼 = 𝐼𝐼𝐼𝐼 (vì 𝐼𝐼𝐾𝐾 ⋅ 𝐼𝐼𝐷𝐷 = 𝐼𝐼𝐹𝐹 ⋅ 𝐼𝐼𝐸𝐸). 𝐼𝐼𝐼𝐼 𝐼𝐼𝐼𝐼
Vậy ∆𝐼𝐼𝐹𝐹𝐾𝐾 # ∆𝐼𝐼𝐷𝐷𝐸𝐸 (c.g.c) ⇒ 𝐼𝐼𝐹𝐹𝐾𝐾 � = 𝐼𝐼𝐷𝐷𝐸𝐸 � .
Vậy tứ giác DKGH nội tiếp (góc ngoài bằng góc đối trong). (4)
Từ (1) và (4) suy ra 5 điểm 𝐷𝐷, 𝐾𝐾, 𝐹𝐹, 𝐴𝐴, 𝐸𝐸 cùng nằm trên một đường tròn. 0,25
Ghi chú : - Học sinh không vẽ hình hoặc vẽ hình sai bài 6 thì không chấm điểm.
- Học sinh làm theo cách khác sử dụng kiến thức đã học mà đúng cho điểm tối đa. UBND HUYỆN CỦ CHI
ĐỀ KIỂM TRA CUỐI KỲ
TRƯỜNG TRUNG HỌC CƠ SỞ
HỌC KỲ II MÔN TOÁN 9 TÂN TIẾN
NĂM HỌC: 2023 - 2024
Thời gian làm bài 90 phút
(Không kể thời gian phát đề) ĐỀ THAM KHẢO 2
Câu 1 (2 điểm): Cho hàm số y = x có đồ thị (P) và đường thẳng (D): y = −x + 4 2
a) Vẽ (P) và (D) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán
Câu 2 (1,5 điểm): Cho phương trình 2
x − 6x − 9 = 0 có 2 nghiệm x , x . 1 2
a) Tính tổng và tích của 2 nghiệm 𝑥𝑥1, 𝑥𝑥2.
b) Tính giá trị của A = (x − ) 1 (x − ) 2 2 1 − x − x 1 2 1 2
Câu 3 (1,5 điểm): Để chuẩn bị cho hội trại 26 tháng 3, lớp 9A đi đặt may áo lớp.
Giá mỗi áo nam là 120 nghìn đồng, mỗi áo nữ là 110 nghìn đồng. Vì mua số lượng
nhiều nên được giảm 10% trên tổng giá tiền do đó cả lớp trả số tiền tổng cộng là
4437 nghìn đồng. Hỏi lớp 9A có bao nhiêu bạn nam và bao nhiêu bạn nữ. Biết rằng
sĩ số của lớp là 43 học sinh.
Câu 4 (1,5 điểm) Một công ty giao cho cửa hàng 100 hộp bánh để bán ra thị trường.
Lúc đầu cửa hàng bán 24 hộp bánh với giá bán một hộp bánh là 200 000 đồng. Do
nhu cầu của thị trường nên 56 hộp bánh tiếp theo mỗi hộp bánh có giá bán tăng 15%
so với giá bán lúc đầu. Còn 20 hộp bánh cuối cùng mỗi hộp bánh có giá bán giảm
10% so với giá bán lúc đầu.
a) Hỏi số tiền thu cửa hàng được khi bán 100 hộp bánh là bao nhiêu?
b) Biết rằng: Với số tiền thu được khi bán 100 hộp bánh, sau khi trừ đi 10%
tiền thuế giá trị gia tăng VAT cửa hàng vẫn lãi 1 152 000 đồng. Hỏi mỗi
hộp bánh công ty giao cho cửa hàng có giá là bao nhiêu?
Câu 5 (1 điểm) Cho hình dưới đây là một thúng gạo vun đầy. Thúng có dạng nửa
hình cầu với đường kính 50cm, phần gạo vun lên có dạng hình nón cao 15cm.
a) Giả sử khoảng cách của các hạt gạo là không đáng kể. Tính thể tích phần gạo.
(Làm tròn đến chữ số thập phân thứ nhất).
b) Nhà Danh dùng lon sữa bò cũ có dạng hình trụ (bán kính đáy bằng 5cm, chiều
cao 12cm) để đong gạo mỗi ngày. Biết mỗi ngày nhà Danh ăn 4 lon gạo và
mỗi lần đong thì lượng gạo chiếm 110% thể tích lon. Hỏi với lượng gạo ở
thúng trên thì nhà Danh có thể ăn nhiều nhất là bao nhiêu ngày?
Biết thể tích hình nón là 1 2
V = .π.R .h , thể tích hình cầu là 4 3
V = .π.R và thể 3 3 tích hình trụ là 2
V = π.r .h (với π ≈ 3,14)
Câu 6 (2,5 điểm): Cho ∆ABC nhọn (AB < AC) nội tiếp đường tròn (O), các đường
cao AD, BE và CF cắt nhau tại H.
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
b) Hai đường thẳng EF và BC cắt nhau tại M. Chứng minh MB . MC = ME . MF
c) AM cắt đường tròn (O) tại N. Đường thẳng qua B và song song với AC cắt
AM tại I và cắt AH tại K. Chứng minh AN ⊥ HN và HI = HK ------HẾT------ ĐÁP ÁN
Câu 1 a)Bảng giá trị: (2 (P): điểm) 𝑥𝑥 −4 −2 0 2 4 𝑥𝑥2 8 2 0 2 8 0,25đ 𝑦𝑦 = 2 (d): 𝑥𝑥 0 2 0,25đ 𝑦𝑦 = −𝑥𝑥 + 4 4 2 Vẽ đúng (P) 0,25đ Vẽ đúng (d) 0,25đ
b)Phương trình hoành độ giao điểm của (P) và (d) là : 𝑥𝑥2 2 = −𝑥𝑥 + 4 0,25đ 𝑥𝑥2 2 + 𝑥𝑥 − 4 = 0 0,25đ
Tọa độ giao điểm của (P) và (d) là: (2;2) (-4;8) 0,25đ Câu 2
𝑥𝑥2 − 6𝑥𝑥 − 9 = 0 (1,5
a) Vì phương trình có hai nghiệm x , x 0,25đ 1
2 nên theo hệ thức Vi-ét, ta có: điểm) 𝑏𝑏
𝑆𝑆 = 𝑥𝑥1 + 𝑥𝑥2 = − 0,25đ � 𝑎𝑎 = 6 𝑐𝑐 𝑃𝑃 = 𝑥𝑥 0,25đ 1𝑥𝑥2 = 𝑎𝑎 = −9 b) 2 2 x + x 1 2 2 = S − 2P 2 = 6 − 2 ⋅( 9 − ) 0,25đ = 54 A = (x − ) 1 (x − ) 2 2 1 − x − x 1 2 1 2 0,25đ
= P − S +1− ( 2 2 x + x 1 2 ) = 68 − 0,25đ
Câu 3 Gọi số bạn nam, bạn nữ của lớp 9A lần lượt là 𝑥𝑥, 𝑦𝑦 ( 𝑏𝑏ạ𝑛𝑛) (𝑥𝑥, 𝑦𝑦 ∈ (1,5
𝑁𝑁∗, 𝑥𝑥, 𝑦𝑦 < 43) 0,25đ
điểm) + Vì sĩ số lớp 9A là 43 học sinh nên ta có phương trình: 𝑥𝑥 + 𝑦𝑦 = 43 (1) 0,25đ
+ Vì giá mỗi áo nam là 120 nghìn đồng, mỗi áo nữ là 110 nghìn đồng và
mua số lượng nhiều nên được giảm 10% trên tổng giá tiền do đó cả lớp
trả số tiền tổng cộng là 4437 nghìn đồng nên ta có phương trình:
120𝑥𝑥 + 110𝑦𝑦 = 4437: 90% 0,25đ
120𝑥𝑥 + 110𝑦𝑦 = 4930 (2)
Từ (1) và (2) ta có hệ pt: 0,25đ � 𝑥𝑥 + 𝑦𝑦 = 43
12𝑥𝑥 + 110𝑦𝑦 = 4930 0,25đ �𝑥𝑥 = 20
𝑦𝑦 = 23(𝑛𝑛ℎậ𝑛𝑛) 0,25đ
Vạy lớp 9A có 20 nam,23 nữ.
Câu 4 a) Số tiền bán bánh lần thứ nhất là: (1,5
24 . 200 000 = 4 800 000 (đồng)
điểm) Số tiền bán bánh lần thứ hai là:
56 . 200 000 . 115% = 12 880 000 (đồng)
Số tiền bán bánh lần thứ ba là:
20 . 200 000 . 90% = 3 600 000 (đồng)
Tổng số tiền thu được sau khi bán hết 100 cái bánh là:
4 800 000 + 12 880 000 + 3 600 000 = 21 280 000 (đồng) b) Số tiền thuế VAT:
21 280 000 . 10% = 2 128 000 (đồng)
Tổng số tiền thu được sau khi trừ thuế là:
21 280 000 – 2 128 000 = 19 152 000 (đồng)
Số tiền vốn của 100 cái bánh:
19 152 000 – 1 152 000 = 18 000 000 (đồng)
Số tiền vốn của 1 hộp bánh là:
18 000 000 : 100 = 180 000 (đồng) Câu 5
a) Bán kính hình cầu là: 50 : 2 = 25 (cm) 0,25đ (1 Thể tích gạo là: điểm) 1 4 3 1 2 1 4 3 1 2 40625. . . π
π R + .π.R .h = . .π.25 + .π.25 .15 = ≈ 42520,8 ( 3 cm ) 2 3 3 2 3 3 3 0,25đ b) Thể tích lon sữa bò: 2 2 V = π r h = π = π ( 3 . . .5 .12 300. cm ) 0,25đ
Số ngày bạn Danh đong gạo cho đến khi hết gạo là:
40625.π :(300.π.110%.4) ≈ 10,3 3
Vậy nhà Danh có thể ăn nhiều nhất là 11 ngày là hết gạo 0,25đ Câu 6 (2,5 A điểm) E N O F I 2 H 1 B C M D K
a) Chứng minh tứ giác AEHF, BCEF nội tiếp 0,5+0,5đ
b) Chứng minh MB . MC = ME . MF
Chứng minh ∆𝑀𝑀𝑀𝑀𝑀𝑀 đồng dạng ∆𝑀𝑀𝑀𝑀𝑀𝑀 (g-g) 0,5đ
Suy ra : 𝑀𝑀𝑀𝑀 = 𝑀𝑀𝑀𝑀 𝑀𝑀𝑀𝑀 𝑀𝑀𝑀𝑀 Suy ra: MB.MC = ME.MF 0,25đ
c) Chứng minh AN ⊥ HN và HI = HK
Chứng minh được MN.MA=ME.MF
Suy ra tứ giác AEFN nội tiếp 0,25đ
Chứng minh được AN ⊥ HN Chứng minh được 𝐻𝐻 0,25đ 1 � = 𝐻𝐻2 � (=𝑀𝑀𝑁𝑁𝑀𝑀 � = 𝐴𝐴𝑀𝑀𝑀𝑀 �) Chứng minh được: HI=HK 0,25đ
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9 NĂM HỌC 2023-2024
Mức độ đánh giá Tổng điểm T Chủ Nội dung/Đơn vị T đề kiến thức
Nhận biết Thông hiểu Vận dụng Vận dụng cao T N TL T N TL T N TL T N TL Vẽ đồ thị hàm số 1
Đồ thị 𝑦𝑦 = 𝑎𝑎𝑥𝑥2 (P) và y = (Bài a) 1 hàm ax + b (d) (1,0đ) 2đ số 1 Tìm tọa độ giao (Bài b) điểm của (P) và (d) (1,0đ) Hệ 1 thức (Bài 2) 2 Vi-et Hệ thức Vi-et (1,5 đ) 1,5đ và ứng dụng Giải bài toán bằng 1 cách lập hệ (Bài 3) phương trình. (1,5đ) Bài tập Dạng ứng dụng 1 1 3 ứng tăng giảm Bài 4a Bài 4b 4đ dụng (1,0đ) (0,5đ)
thực tế Dạng toán ứng 1 1 dụng hình không (Bài 5a) (Bài gian (0,5đ) 5b) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài (Bài 6b) 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100 % Tỉ lệ chung 65% 35% 100 %
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9 NĂM HỌC 2023-2024 T Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ T nhận thức Nhận Thông Vận VD
biết hiểu dụng cao Đồ thị hàm 1 số y = ax2 (Bài (P) và Vận dụng: 1a) y = ax + b
- Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ trục tọa độ 1 Đồ thị (d) hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1 giao điểm
- Vận dụng phương trình bậc hai một ẩn (Bài của (P) và
trong việc tìm tọa độ giao điểm của (P) và 1b) (d) (d). Hệ thức Thông hiểu:
- Tính được tổng, tích, x12+x22 các 1
2 Vi-et và Hệ thức Vi - ứng et
nghiệm của phương trình bậc hai một (Bài dụng
ẩn bằng hệ thức Vi-et (Biến đổi đơn 2) giản)
Giải bài toán Thông hiểu: bằng cách
- Phân tích đề bài, tìm mối quan hệ giữa lập hệ
các đại lượng cho trong đề bài, gọi ẩn, từ 1 phương
đó lập được hệ 2 phương trình bậc nhất 2 Bài 3 trình. ẩn.
- Giải hệ phương trình, đối chiếu điều
kiện để trả lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức tăng/giảm
Bài tập Dạng ứng 1 1 dụng tăng Vận dụng: Bài Bài 3 ứng
- Vận dụng kiến thức về tăng giảm, tỉ dụng giảm
số % giải quyết một số vấn đề trong 4a 4b thực tế thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện Dạng toán
tích toàn phần, thể tích của hình trụ (hoặc ứng dụng hình nón, hình cầu) 1 1
hình không Vận dụng cao: Bài Bài gian
- Vận dụng hợp lí công thức tính diện 5a 5b
tích, thể tích hình trụ (hoặc hình nón,
hình cầu) để giải quyết một số bài toán thực tiễn. Nhận biết: 1 4 Hình Tứ giác nội
- Nhận biết được tứ giác nội tiếp đường (Bài học tiếp tròn. 6a) Vận dụng: 1 1
- Vận dụng các định lý, hệ quả của các (Bài (Bài
loại góc với đường tròn, mối quan hệ 6b) 6c)
giữa các góc, phối hợp các kiến thức để chứng minh.
- Vận dụng các phương pháp chứng
minh hai tam giác đồng dạng, chứng
minh song song, vuông góc, 3 điểm
thẳng hàng giải quyết yêu cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức
trong hình học phẳng để giải quyết yêu cầu đề bài. UBND HUYỆN CỦ CHI
ĐỀ THAM KHẢO HỌC KÌ II
TRƯỜNG THCS TÂN THẠNH TÂY
MÔN: TOÁN 9 - NH: 2023 – 2024
Thời gian làm bài: 90 phút
(Không kể thời gian phát đề)
Bài 1. (2,0 điểm) Cho hàm số (P): 2
y = −x và (D): y = 2x − 3 .
a) Vẽ (P) và (D) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính.
Bài 2. (1,5 điểm) Cho phương trình: 2
2x − 3x − 5 = 0 có hai nghiệm x1, x2 . Không giải
phương trình, tính giá trị biểu thức: 2 2
A = 2x + 2x 1 2
Bài 3. (1,5 điểm) Một giáo viên mua viết xanh và viết đỏ làm phần thưởng tặng học sinh
làm kiểm tra đạt điểm tốt. Viết xanh giá 3.000 đồng 1 cây, viết đỏ loại tốt nên giá 5.000
đồng 1 cây. Biết tổng số viết xanh và viết đỏ là 40 cây, giáo viên đã trả tiền mua viết là
148.000 đồng. Hỏi giáo viên đã mua bao nhiêu cây viết xanh, viết đỏ ?
Bài 4. (1,5 điểm) Thực hiện chương trình khuyến mãi “Ngày Chủ Nhật vàng”, 1 cửa hàng
điện máy giảm giá 50 % trên một tivi cho lô hàng tivi gồm có 40 cái với giá bán lẻ trước
đó là 6.500.000 đ /cái.Đến trưa cùng ngày thì cửa hàng đã bán được 20 cái và cửa hang
đã quyết định giảm thêm 10 % nữa (so với giá đã giảm lần 1) cho số tivi còn lại.
a/Tính số tiền mà cửa hàng thu được khi bán hết lô hàng tivi ?
b/ Biết rằng giá vốn là 2.850.000 đ /1 cái tivi . Hỏi cửa hang lời hay lỗ khi bán hết lô hàng tivi đó ?
Bài 5. (1,0 điểm) Một hình trụ có bán kính đường tròn đáy là 3cm, chiều cao 4cm được
đặt đứng trên mặt bàn. Một phần của hình trụ bị cắt rời ra theo bán kính OA, OB và theo
chiều thẳng đứng từ trên xuống dưới với
AOB = 30 . (như hình vẽ). Hãy tính:
a) Thể tích hình trụ ban đầu.
b) Thể tích phần còn lại.
Bài 6. (2,5 điểm) Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Vẽ các tiếp
tuyến AM, AN với (O) ( M,N là các tiếp điểm ). Qua A vẽ đường thẳng cắt đường tròn
(O) tại hai điểm B và C phân biệt ( B nằm giữa A và C ). Gọi H là trung điểm BC .
a) Chứng minh tứ giác AMHN nội tiếp b) Chứng minh 2 AM = . AB AC
c) Đường thẳng qua B song song AM với cắt đoạn thẳng MN tại E. Chứng minh EH // MC Hết.
HƯỚNG DẪN CHẤM ĐỀ THAM KHẢO KIỂM TRA HỌC KỲ II NĂM HỌC 2023-2024 MÔN: TOÁN 9 1
a) Bảng GT đúng + vẽ đúng 0,5đ x2
( 2,0đ) b) Tìm đúng 2 giao điểm 0,25đ x2 2
Vì a.c = 2.(-5) = - 10 < 0 nên pt có nghiệm 0,25đ ( 1,5đ) b − 3
S = x + x = = 1 2 0,25đ Theo vi-ét a 2 c 5 P x .x − = = = 1 2 a 2 0,25đ 2 2 Ta có : x x x + x 1 2 1 2 M = + = 0,25đ x x x .x 2 1 1 2 2 3 5 2 − − 2 S 2P 2 2 − 29 0,5đ M − = = = P 5 − 10 2 3
Gọi x (cây), y (cây) lần lượt là số cây viết xanh và viết đỏ. 0,25đ
( 1,5đ) Đk x, y nguyên dương
Vì: Tổng số cây viết xanh và viết đỏ là 40 cây nên ta có pt: 0,25đ x + y = 40 (1) 0,25đ
Số tiền giáo viên phải trả là 148000 đ nên ta có phương trình: 3000x + 5000y = 148000 (2) 0,25đ
Từ (1) và (2) ta có hệ pt: x + y = 40 3000
x + 5000y =148000 0,25đ
Giải hpt ta được x = 26 ( nhận) y =14 0,25đ
Vậy gv đã mua 26 cây viết xanh và 14 cây viết đỏ 4
a)số tiền mà cửa hàng thu được khi bán hết lô hàng tivi
( 1,5đ) 6 500 000.20.50 0,75đ
% + 6 500 000.20. 50 %.90% = 123 500 000 đồng
b)Giá vốn của 40 cái TV là: 0,5đ
2 850 000.40 =114 000 000 đồng 0,25đ
Vây cửa hàng bán có lời (Vì 123 500 000 > 114 000 000) 5
a) Thể tích hình trụ ban đầu là: 2 V = h S = π = π ( 3 . 4. .3 36 cm ) 0,5đ ( 1,0đ) b) Diện tích hình quạt 30 3 OAB là: 2 S = π.3 . = .π OAB ( 3 cm ) 360 4
Thể tích phần bị cắt là: 3 .π.4 = 3π ( 3 cm ) 0,25đ 4
Thể tích phần trụ còn lại: π − π = π ( 3 36 3 33 cm ) 0,25đ 8 M ( 2,5đ) C H E B O A N
a) Chứng minh tứ giác AMHN nội tiếp và. 0,25đ Ta có H là trung điểm BC ⇒ OH ⊥ BC
Mà AM ⊥ MO, AN ⊥ NO 0,25đ
⇒ AHO = AMO = ANO = 90°
⇒ H, M,N cùng thuộc một đường tròn đường kính AO . 0,25đ
⇒ H, M,N,O,A cùng thuộc một đường tròn. 0,25đ
⇒ tứ giác AMHN nội tiếp. b)Chứng minh: 2 AM = . AB AC
Xét ∆AMB và ∆ACM có MAB chung 0,25đ
AMB = ACM (góc nội tiếp và góc tạo bởi tiếp tuyến và
dây cung cùng chắn cung MB) 0,25đ
⇒ ∆AMB ∆ACM (g – g). AM AB 0,25đ ⇒ = AC AM ⇒ 2 AM = . AB AC 0,25đ
c)Chứng minh : EH // MC Ta có BE// AM
⇒ EBH = MAH (hai góc đồng vị) Mà
MAH = ENH (hai góc nội tiếp cùng chắn cung EH
của đường tròn (AMHON)) 0,25đ ⇒ EBH = ENH
⇒ tứ giác BEHN nội tiếp. ⇒ BHE = BNM Mà
BNM = BCM (hai góc nội tiếp cùng chắn cung BM của đường tròn (O) ) ⇒ BHE = BCM Mà BHE và
BCM là hai góc đồng vị 0,25đ ⇒ EH // MC . UBND HUYỆN CỦ CHI
KIỂM TRA CUỐI KÌ II-NĂM HỌC 2023-20242
TRƯỜNG TRUNG HỌC CƠ SỞ MÔN: TOÁN – KHỐI:9 TÂN THÔNG HỘI THỜI GIAN: 90 phút
(Không kể thời gian phát đề)
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng điểm
TT Chủ đề Nội dung/Đơn vị kiến thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TN TL TN TL TN TL TN TL 1
Vẽ đồ thị hàm số 𝑦𝑦 =
𝑎𝑎𝑥𝑥2 (P) và y = ax + b (Bài a) (d) (1,0đ) 1 Đồ thị hàm số 2đ 1 Tìm tọa độ giao điểm (Bài b) của (P) và (d) (1,0đ) Hệ thức 1 2 Vi-et và ứng Hệ thức Vi-et (Bài 2) 1,5đ dụng (1,5 đ) Giải bài toán bằng 1 cách lập hệ phương trình. (Bài 3) (1,5đ)
Bài tập Dạng ứng dụng tăng 1 1 3 ứng giảm dụng Bài 4a Bài 4b 4đ thực tế (1,0đ) (0,5đ) Dạng toán ứng dụng 1 1 hình không gian (Bài 5a) (Bài 5b) (0,5đ) (0,5đ) 1 4 Hình học Tứ giác nội tiếp 2,5đ (Bài 6a) (1,0đ) 1 1 (Bài 6b) (Bài 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng Đồ thị hàm số 1 y = ax2 (P) và Vận dụng: (Bài
y = ax + b (d) - Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng hệ 1a) trục tọa độ 1 Đồ thị (a khác 0) hàm số Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong việc (Bài (P) và (d)
tìm tọa độ giao điểm của (P) và (d). 1b) Thông hiểu: Hệ thức 1 2 Vi-et và
Hệ thức Vi -et - Tính được tổng, tích, x 2 2 1 +x2 các nghiệm của ứng dụng
phương trình bậc hai một ẩn bằng hệ thức (Bài 2)
Vi-et (Biến đổi đơn giản) Thông hiểu: Giải bài toán bằng cách lập
- Phân tích đề bài, tìm mối quan hệ giữa các đại hệ phương
lượng cho trong đề bài, gọi ẩn, từ đó lập được hệ 1 trình.
2 phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu: Bài tập
- Tính được số tiền phải trả bằng công thức 3 ứng dụng tăng/giảm thực tế Dạng ứng 1 1 dụng tăng Vận dụng: Bài giảm Bài 4a
- Vận dụng kiến thức về tăng giảm, tỉ số % 4b
giải quyết một số vấn đề trong thực tiễn.
Dạng toán ứng Thông hiểu: 1 1 dụng hình Bài không gian Bài 5a 5b
- Tính được diện tích xung quanh, diện tích toàn
phần, thể tích của hình trụ (hoặc hình nón, hình cầu)
Vận dụng cao:
- Vận dụng hợp lí công thức tính diện tích, thể
tích hình trụ (hoặc hình nón, hình cầu) để giải
quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc
với đường tròn, mối quan hệ giữa các góc, phối 4 Tứ giác nội tiếp Hình học
hợp các kiến thức để chứng minh.
- Vận dụng các phương pháp chứng minh hai 1 1
tam giác đồng dạng, chứng minh song song, (Bài (Bài
vuông góc, 3 điểm thẳng hàng giải quyết yêu 6b) 6c) cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình
học phẳng để giải quyết yêu cầu đề bài. UBND HUYỆN CỦ CHI
KIỂM TRA CUỐI HỌC KỲ II
TRƯỜNG TRUNG HỌC CƠ SỞ NĂM HỌC 2023-2024 TÂN THÔNG HỘI
MÔN: TOÁN – KHỐI : 9 THỜI GIAN: 90 phút
(Không kể thời gian phát đề) ĐỀ THAM KHẢO
Bài 1 (2 điểm): Cho parabol (P) 1 2
: y = x và đường thẳng (d ): y = x + 4 2
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Bài 2 (1,5 điểm): Cho phương trình 2
3x + 2x − 6 = 0 có hai nghiệm x ;x . Không 1 2
giải phương trình, tính giá trị biểu thức A = (x − 2x x − 2x 1 2 ) ( 2 1 )
Bài 3: (1,5 điểm) Trường THCS A có tất cả 250 học sinh tham dự kì thi tuyển
sinh vào lớp 10. Biết rằng, 2 số học sinh nam và 3 số học sinh nữ của trường 3 5
trúng tuyển thì số học sinh nam trúng tuyển nhiều hơn số học sinh nữ trúng tuyển
là 2 học sinh. Tính số học sinh nam và nữ tham dự kì thi trên.
Bài 4: (1,5 điểm) Một công ty cung cấp dịch vụ internet bằng cáp quang đưa ra
chi phí sử dụng như sau: số tiền phải trả trong 3 tháng đầu tiên được xác định theo
công thức 260 000.x + 300 000 (đồng), trong đó x là số tháng sử dụng.Từ tháng
thứ tư trở đi số tiền phải trả sẽ được tính theo công thức 250 000.x (đồng) với x
là số tháng sử dụng tính từ tháng thứ tư.
a) Tính số tiền người sử dụng dịch vụ internet phải trả sau 7 tháng?
b) Công ty có chương trình khuyến mãi, nếu đóng trước một năm thì được
tặng hai tháng sử dụng miễn phí. Hỏi với số tiền 3 580 000 đồng thì người sử
dụng dịch vụ internet đã dùng trong bao nhiêu tháng kể từ khi lắp đặt ?
Bài 5: (1 điểm) : Một xô nước hình trụ có đường kính là 25 cm và chiều cao là
28 cm, được dùng để lấy nước từ một hồ trữ nước hình lập phương có cạnh là
2m. Hồ đang chứa đầy nước
a) Tính thể tích của xô nước. Biết rằng thể tích hình trụ được tính theo công thức 2
V = 3,14R h Trong đó R là bán kính mặt đáy ; h là chiều cao của hình trụ
b) Giả sử mỗi ngày gia đình bạn A sử dụng 30 xô nước lấy từ hồ. Hỏi nước
trong hồ sử dụng đến ngày thứ mấy sẽ hết nước ( bỏ qua thể tích thành hồ, múc đầy xô nước)
Bài 6. (2,5 điểm) : Cho ∆ABC nội tiếp đường tròn (O) ( AB < AC ) có 2 đường
cao BE, CK cắt nhau tại H.
a) Chứng minh các tứ giác AKHE, BCEK nội tiếp.
b) AH cắt BC tại D. Từ E kẻ đường thẳng song với KD cắt KC và đường
thẳng AB lần lượt tại tại M và G. Chứng minh HK.KC = KA.KB và KC là phân giác của góc DKE
c) Chứng minh E là trung điểm của MG. ------HẾT------ ĐÁP ÁN Bài Đáp án Điểm Bài1a a) Bảng giá trị (1,0 điểm) x 4 − 2 − 0 2 4 0,25đ + 0,25đ 1 2 y = x 8 2 0 2 8 2 x 2 − 4 y = x + 4 2 8 0,25đ + 0,25đ Bài 1b
b) Phương trình hoành độ giao điểm ( 1 điểm)
của (P) và (d): 1 2 x = x + 4 2 0,25đ 1 2
⇔ x − x − 4 = 0 2 x = 4 ⇔ x = 2 − 0,25đ
Với x = 4 ⇒ y = 4+ 4 = 8 Với x = 2 − ⇒ y = 2 − + 4 = 2 0,25đ
Vậy (P) cắt (d) tại B(4;8)và A( 2; − 2) 0,25đ Bài 2
Áp dụng định lí Vi - ét (1,5 b − 2 x x − + = = 0,5đ điểm) 1 2 a 3 c 6 x x − = = = 2 − 1 2 a 3 0,5đ
A = (x − 2x x − 2x 1 2 ) ( 2 1 ) 2 2
A = x x − 2x − 2x + 4x x 1 2 1 2 1 2 0,25đ 2 2
A = 5x x − 2(x + x ) 1 2 1 2 2
A = 5x x − 2 (x + x ) − 2x x 1 2 1 2 1 2 2 A = 2(
− x + x ) + 9x x 1 2 1 2 0,25đ 2 2 A − = − + (− ) 170 2 9 2 − = 3 9 Bài 3
Gọi x ( học sinh) là số học sinh nam của trường (1,5
THCS A tham dự kì thi tuyển sinh 10 0,25đ điểm)
Gọi y ( học sinh) là số học sinhn nữ của trường
THCS A tham dự kì thi tuyển sinh 10
(0 < x, y < 250 ; *
x, y ∈ N )
Vì tổng số học sinh dự thi của trường THCS A là
250 học sinh, nên ta có phương trình: 0,5đ
x + y = 250 (1)
Vì số học sinh nam trúng tuyển nhiều hơn số học
sinh nữ trúng tuyển là 2 học sinh, nên ta có phương trình: 2 3 x − y = 2 (2) 0,25đ 3 5
Từ (1) và (2) ta có hệ phương trình x + y = 250 0,25đ x =120 2 3 ⇔ x − y = 2 y =130 3 5
Vậy số học sinh nam dự thi của trường THCS A 0,25đ là 120 học sinh.
Số học sinh nữ dự thi của trường THCS A là 130 học sinh. Bài 4
a) Số tiền phải trả sau 7 tháng:
(1,5điểm) (260 000.3 + 300 000) + 250 000. (7 – 3) 0,5đ+0,5đ =2 080 000 (đồng)
b) Gọi x (tháng) là số tháng người sử dụng dịch vụ internet kể
từ khi lắp đặt ( x > 0) Theo đề ta có:
(260 000.3 +300 000) + 250 000(x – 3) = 3 580 0,25đ 000
1 080 000 + 250 000x – 750 000 = 3 580 000 250 000x = 3 250 000 x = 13 0,25đ
Vậy số tháng sử dụng kể từ khi lắp đặt: 15 tháng Bài 5
Một xô nước hình trụ có đường kính là 25 cm và (1điểm)
chiều cao là 28 cm, được dùng để lấy nước từ một
hồ trữ nước hình lập phương có cạnh là 2m. Hồ đang chứa đầy nước
a) Tính thể tích của xô nước R = 25: 2 = 12,5 cm = 1,25 dm 0,25đ + V= 3,14. 1,252. 2,8 ≈ ( 3 13,7 dm ) 0,25đ
b) Giả sử mỗi ngày gia đình bạn A sử dụng 30 xô
nước. Hỏi nước trong hồ sử dụng đến ngày thứ
mấy sẽ hết nước.( bỏ qua thể tích thành hồ)
Thể tích nước mỗi ngày sử dạng 0,25đ
= 30 (3,14. 1,252. 2,8) =412,125 (dm3)
Thể tích của nước trong hồ là: 203 = 8000 (dm3)
Vì 8000 : 412,125 = 19, 411 nên lượng nước 0,25đ
trong hồ sử dụng đến ngày thứ 20 sẽ hết Bài 6 (2,5 điểm)
a)Chứng minh tứ giác AKHE , BCEK nội tiếp.
Chứng minh tứ giác AKHE nội tiếp Xét tứ giác AKHE có: ˆK
A H = 900 (CK ⊥ AB) ˆH E A
= 900 (BE ⊥ AC) 0,25đ 0 0 0 ˆK A H + ˆH E A = 90 + 90 = 180
Vậy tứ giác AKHE nội tiếp( Tứ giác có tổng hai góc đối bằng 1800) 0,25đ
Chứng minh tứ giác BCEK nội tiếp Xét tứ giác BCEK có: ˆK
B C = 900 (CK ⊥ AB) ˆ C E B
= 900 (BE ⊥ AC) 0,25đ 0 ˆK B C = ˆC E B = 90
Vậy tứ giác BCEK nội tiếp( Tứ giác có K, E là hai
đỉnh kề nhau cùng nhìn cạnh BC dưới góc 900 0,25đ
b)Chứng minh: HK.KC = KA.KB và KC là phân giác của góc DKE 0,25đ
Chứng minh ∆BKH ∽ ∆CKA 0,25đ Chứng minh HK.KC = KA.KB 0,5đ
Chứng minh: KC là phân giác của góc DKE
c)Chứng minh E là trung điểm của MG. Chứng minh KE = EM 0,25đ Chứng minh KE = EG
Chứng minh E là trung điểm của MG. 0,25đ
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024
Mức độ đánh giá Tổng
TT Chủ đề Nội dung/Đơn vị kiến điểm thức Nhận biết Thông hiểu Vận dụng Vận dụng cao TN TL TN TL TN TL TN TL Vẽ đồ thị hàm số 1 (P) và y = ax + (Bài a) 1 Đồ thị b (d) (1,0đ) hàm số 2đ 1 Tìm tọa độ giao điểm (Bài b) của (P) và (d) (1,0đ) Hệ thức 1 2 Vi-et và (Bài 2) ứng Hệ thức Vi-et (1,5 đ) 1,5đ dụng Giải bài toán bằng 1 cách lập hệ phương (Bài 3) trình. (1,5đ) Bài tập 3 ứng Dạng ứng dụng tăng 1 1 dụng 4đ giảm Bài 4a Bài 4b thực tế (1,0đ) (0,5đ) Dạng toán ứng dụng 1 1 hình không gian (Bài 5a) (Bài 5b) (0,5đ) (0,5đ) 1 (Bài 6a) 4 Hình (1,0đ) học Tứ giác nội tiếp 2,5đ 1 1 (Bài 6b) (Bài 6c) (1đ) (0,5đ) Tổng: Số câu 1 5 3 2 11 Điểm 1đ 5,5đ 2,5đ 1đ 10 đ Tỉ lệ % 10% 55% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
BẢN ĐẶC TẢ ĐỀ THAM KHẢO KIỂM TRA CUỐI KÌ II TOÁN 9. NĂM HỌC 2023-2024 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận Thông Vận VD cao biết hiểu dụng Đồ thị hàm số 1 y = ax2 (P) và Vận dụng: (Bài
y = ax + b (d) - Vẽ đồ thị hàm số y = ax2 và y = ax + b trên cùng 1a) 1 Đồ thị hệ trục tọa độ hàm số (a khác 0) Tìm tọa độ Thông hiểu: 1
giao điểm của - Vận dụng phương trình bậc hai một ẩn trong (Bài (P) và (d)
việc tìm tọa độ giao điểm của (P) và (d). 1b) Hệ thức Thông hiểu: 2 2 2 Vi-et và
Hệ thức Vi -et - Tính được tổng, tích, x1 +x2 các nghiệm của 1 ứng dụng
phương trình bậc hai một ẩn bằng hệ thức (Bài 2)
Vi-et (Biến đổi đơn giản) Giải bài toán Thông hiểu:
bằng cách lập - Phân tích đề bài, tìm mối quan hệ giữa các đại hệ phương
lượng cho trong đề bài, gọi ẩn, từ đó lập được hệ 1 trình.
2 phương trình bậc nhất 2 ẩn. Bài 3
- Giải hệ phương trình, đối chiếu điều kiện để trả
lời câu hỏi đề bài yêu cầu. Thông hiểu:
- Tính được số tiền phải trả bằng công thức Dạng ứng tăng/giảm 1 Bài tập dụng tăng Vận dụng: 1 Bài 3 ứng dụng giảm
- Vận dụng kiến thức về tăng giảm, tỉ số % Bài 4a 4b thực tế
giải quyết một số vấn đề trong thực tiễn. Thông hiểu:
- Tính được diện tích xung quanh, diện tích toàn
Dạng toán ứng phần, thể tích của hình trụ (hoặc hình nón, hình dụng hình cầu) 1 1 không gian
Vận dụng cao: Bài 5a Bài
- Vận dụng hợp lí công thức tính diện tích, thể 5b
tích hình trụ (hoặc hình nón, hình cầu) để giải
quyết một số bài toán thực tiễn. Nhận biết: 1
- Nhận biết được tứ giác nội tiếp đường tròn. (Bài 6a) Vận dụng:
- Vận dụng các định lý, hệ quả của các loại góc
với đường tròn, mối quan hệ giữa các góc, phối 4
hợp các kiến thức để chứng minh.
Hình học Tứ giác nội tiếp
- Vận dụng các phương pháp chứng minh hai 1 1
tam giác đồng dạng, chứng minh song song, (Bài (Bài
vuông góc, 3 điểm thẳng hàng giải quyết yêu 6b) 6c) cầu bài toán.
Vận dụng cao:
- Phối hợp tổng hợp các kiến thức trong hình
học phẳng để giải quyết yêu cầu đề bài.
PHÒNG GD & ĐT HUYỆN CỦ CHI
ĐỀ THAM KHẢO KIỂM TRA HỌC KÌ II
TRƯỜNG THCS TRUNG AN NĂM HỌC: 2023-2024
MÔN TOÁN LỚP 9 – Thời gian 90’ 2
Bài 1:(2điểm) Cho (P) : =− x y 1
2 (D): y = x − 3 2
a) Vẽ (P) và (D) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán
Bài 2(1.5 điểm) : Cho phương trình: 3x2 - 10x +2 = 0. Không giải phương trình
hãy tính giá trị của biểu thức A =2x12 + 2x22 – x1x2
Bài 3:(1.5đ) Bạn Bình mua một món quà hết 78000đồng. Bạn đưa 22 tờ tiển
mệnh giá 2000đồng và 5000đồng và được người bán trả lại 2000đồng. Hỏi số tờ tiền mỗi loại?
Bài 4: (1.5đ) Cô An đi siêu thị mua nồi cơm điện đang khuyến mãi và giảm gia
20% . Do cô có thẻ khách hàng thân thiết của siêu thị nên được giảm thêm 2%
trên giá đã giảm. do đó Cô chỉ phải trả 196000 đồng cho nồi cơm điện.
a/ Hỏi giá ban đầu của nồi cơm điện khi chưa khuyến mãi là bao nhiêu ?
b/ Hỏi ông Bình mua 2 nồi cơm điện khi không là khách hàng thân thiết thì phải trả bao nhiêu tiền ?
Bài 5 (1 điểm). Một bồn đựng nước có dạng hình hộp chữ nhật có các kích thước cho trên hình vẽ
a) Tính diện tích bề mặt của bồn (không tính nắp)?
b) Một vòi bơm với công suất 120 lít/phút để bơm một lượng nước
vào bồn không có nước lên độ cao cách nắp bồn là 1,5 m thì phải mất
bao lâu? Biết rằng trong quá trình bơm thì hệ thống bơm bị rò rỉ, hao tổn hết 5%. 2,3 m 11,5m 3,1 m
Bài 6(2.5) : Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn tâm
( O). Các đường cao BE và CF cắt nhau tại H, AH cắt BC tại D.
a/ Chứng minh tứ giác BCEF nội tiếp
b/ Từ A kẻ Ax là tiếp tuyến tại A của (O) Chứng minh: EF vuông góc AO
c/ BE và CF cắt (O) lần lượt tại M và M
chứng minh MN song song với Ax.
-----------------HẾT-----------------
HƯỚNG DẪN ĐÁP ÁN MÔN TOÁN - LỚP 9 – HKII 2023-2024 Bài 2: (2đ)
a) BGT đúng (0, 5) + vẽ đúng (0, 5)
b) Phương trình hoành độ giao điểm, giải đúng hai giá trị x (0,25)
Tìm y tương ứng, đúng tọa độ điểm (0,75) Bài 2: (1.5đ) Tính đúng đenta 0,25đ
Tính đúng tổng và tích 0.25đ+0.25đ Tính đúng x21 + x22 0.25đ
Tính đúng biểu thức A 0. 5đ Bài 3 1.5đ
Gọi x là số tờ tiền loại 2000
Gọi y là số tờ tiền loại 5000 ( 0. 5đ)
Ta có hpt x + y = 22 0. 5đ
2000x + 5000y = 80000 X=10,y= 12 0,25đ Vậy 0.25đ Bài 4: (1.5đ)
Gọi giá ban đầu của nồi cơm điện là x (đồng), x>0.
Giảm giá 20%, giá bán còn lại là x – 20%x = 0,8x. (0,25)
Giảm thêm 2% của giá đã giảm, giá bán còn lại là 0,8x – 2%.0.8x=0,784x (0,25) Ta có 0,784x=196000 (0,25) x=250000 (đồng).
Vậy giá ban đầu của nồi cơm điện là 250000 đồng (0,25)
b/ tổng số tiền 2 nồ cơm điện khi không là khách hàng thân thiết là 2.250000(100% - 20%) = 0,25đ Vậy 0,25
Câu 5 1đ a) Diện tích bề mặt bồn nước (không tính nắp) là : 2
2. 3,1 11,5 .2,33,1.11,5 102,81m
b) Tổng lượng nước cần bơm vào bể là: 3
3,1.11,5.1,5 53,475m 53475l
Vì trong quá trình bơm bị hao phí 5%, nên thời gian bơm nước là: 53475.15 % 468(phút). 120 Bài 6: (2.5đ)
b/ Chứng minh tứ giác BCEF nội tiếp
Xét tứ giác BCEF có:Góc BEC = góc BFC = 900 ( tính chất đường cao) 0,75đ
=> tứ giác BCEF nội tiếp 0,25đ
b/ Chứng minh: EF vuông góc AO ta có: BÂx = C
B ˆA ( cùng chắn cung AB) 0,25đ E F A ˆ = C B ˆA 0,25đ =>BÂx = E F
A ˆ => Ax //FE. Mà Ax ⊥ OA nên EF ⊥ OA 0.5đ
c/ chứng minh MN // EF 0,25đ kết luân MN // Ax 0,25đ
Document Outline
- ANT- KTCK2 TOÁN 9 - 2324
- AP- KTCK2 TOÁN 9- 2324
- BH- KTCK2 TOÁN 9 - 2324
- HP- KTCK2 TOÁN 9 - 2324
- NĐ- KTCK2 TOÁN 9- 2324
- NVX- KTCK2 TOÁN 9 - 2324
- PMH- KTCK2 TOÁN 9 - 2324
- PT- KTCK2 TOÁN 9 - 2324
- PVA- KTCK2 TOÁN 9 - 2324
- PVC- KTCK2 TOÁN 9 - 2324
- PH- KTCK2 TOÁN 9- 2324
- PHĐ- KTCK2 TOÁN 9 - 2324
- TAH- KTCK2 TOÁN 9- 2324
- TânTrung- KTCK2 TOÁN 9- 2324
- TL- KTCK2 TOÁN 9 - 2324
- TLH- KTCK2 TOÁN 9 - 2324
- TPT- KTCK2 TOÁN 9 - 2324
- TT- KTCK2 TOÁN 9- 2324
- TT2- KTCK2 TOÁN 9- 2324
- TTĐ- KTCK2 TOÁN 9 - 2324
- TTien- KTCK2 TOÁN 9 - 2324
- TTT- KTCK2 TOÁN 9 - 2324
- TTH- KTCK2 TOÁN 9 - 2324
- TrAn- KTCK2 TOÁN 9 - 2324




