





























Preview text:
ỦY BAN NHÂN DÂN QUẬN 3
ĐỀ KIỂM TRA THAM KHẢO HỌC KÌ II
TRƯỜNG THCS LƯƠNG THẾ
NĂM HỌC 2023 – 2024 VINH Môn : TOÁN LỚP 9
Thời gian làm bài 90 phút
(không kể thời gian phát đề)
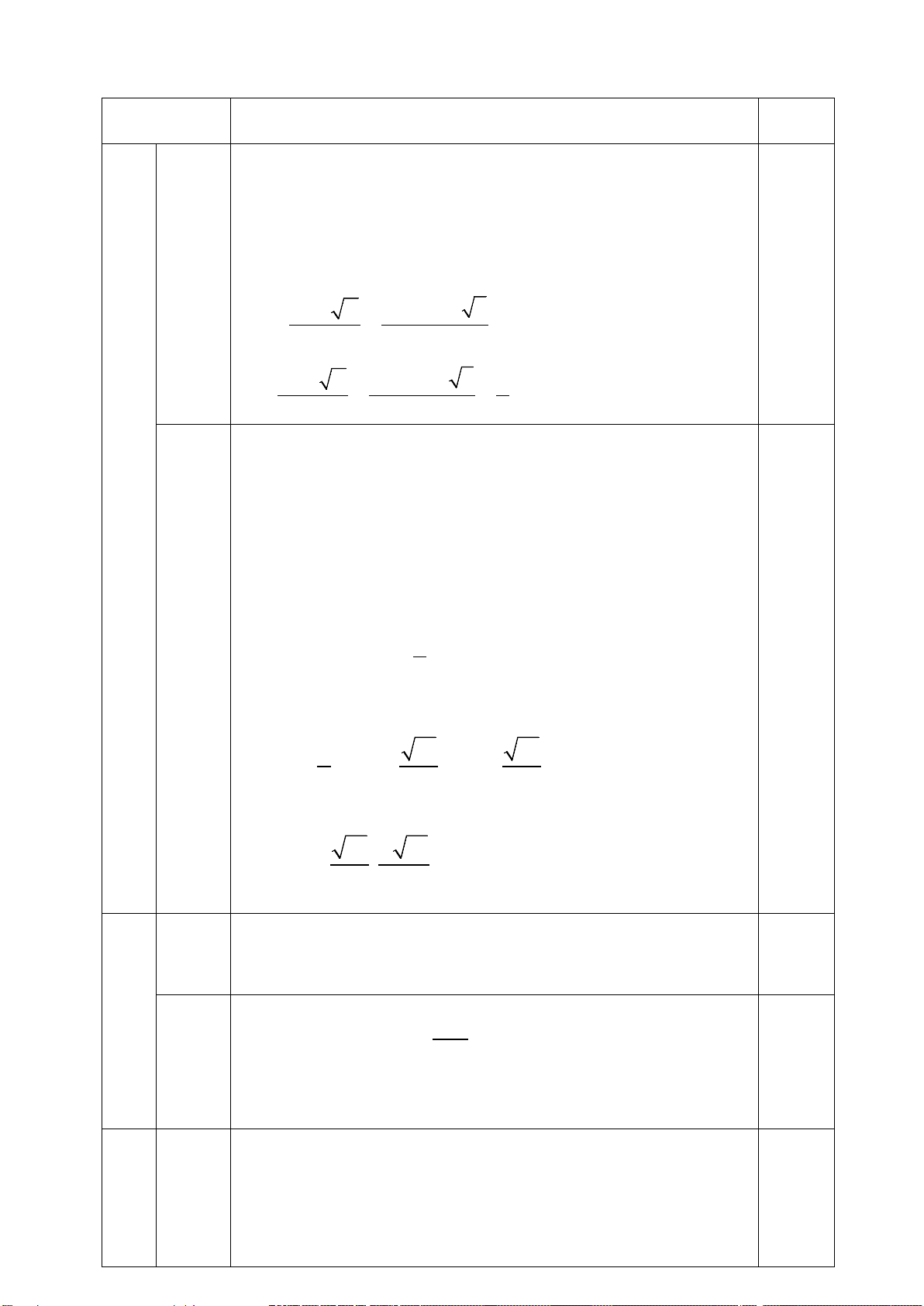
Bài 1 (1,5 điểm).:Giải phương trình, hệ phương trình: a) 2
x – 4x – 11 0 b) 4 2
x – 5x – 6 0
Bài 2 (1,5 điểm). Cho 3 P 1 : y 2 x và (d) : y x 2 2 2
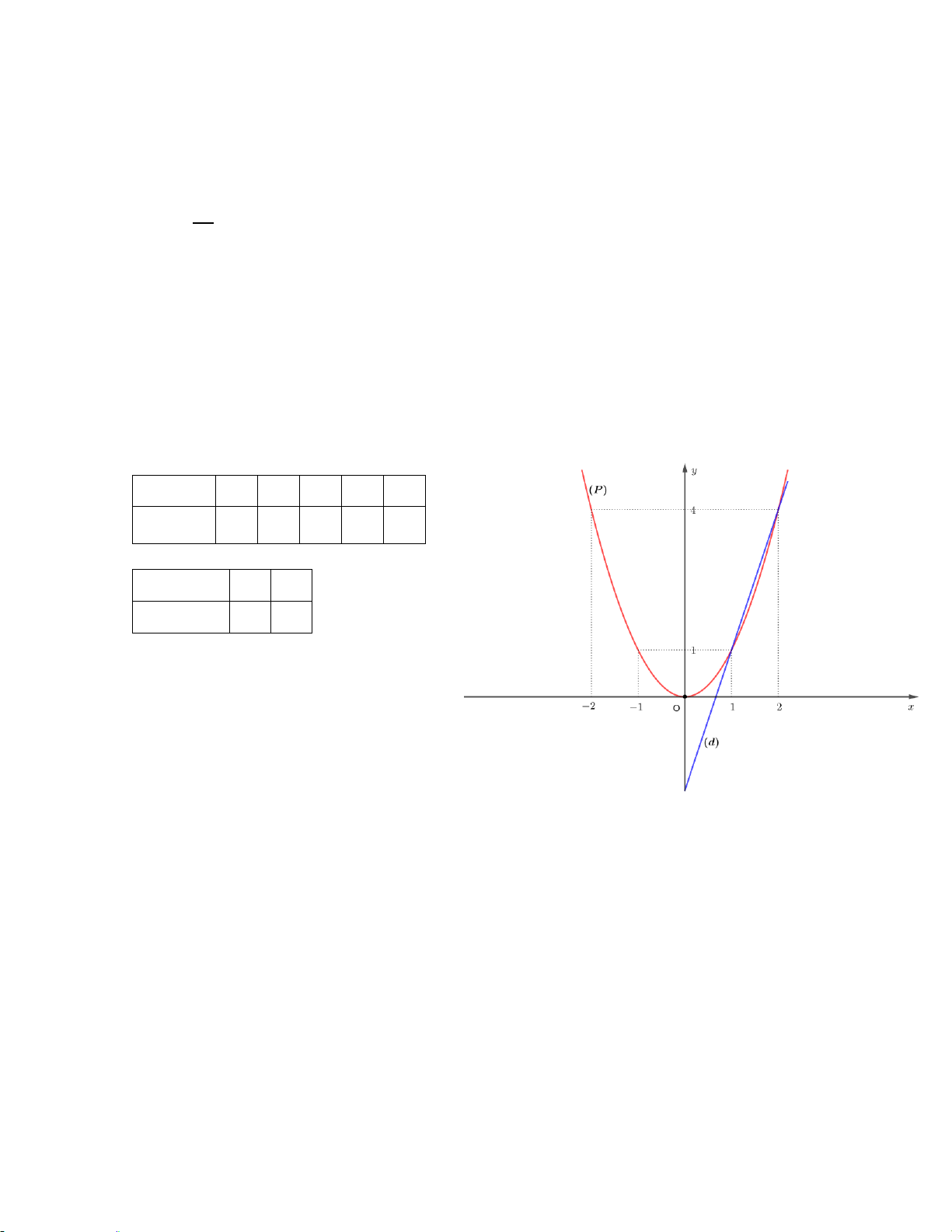
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ
b) Xác định tọa độ giao điểm của (P) và (d) bằng phép toán
Bài 3 (1,5 điểm). Gọi x ,x là hai nghiệm của phương trình ẩn x: 2
3x 12x 5 0 . Không giải phương 1 2 2 x 4x
trình, hãy tính giá trị của biểu thức x x T 1 2 1 2 4x 2 x x x 1 2 1 2
Bài 4 (1 điểm). Nhà bạn Lan có một mảnh vườn trồng rau cải bắp. Vườn được đánh thành nhiều luống,
mỗi luống trồng cùng một số cây cải bắp. Lan tính rằng: Nếu tăng thêm 8 luống rau, nhưng mỗi luống trồng
ít đi 4 cây thì số cây toàn vườn ít đi 48 cây. Nếu giảm đi 4 luống, nhưng mỗi luống trồng tăng thêm 3 cây
thì số rau toàn vườn sẽ tăng thêm 32 cây. Hỏi vườn nhà Lan trồng được bao nhiêu cây rau cải bắp?
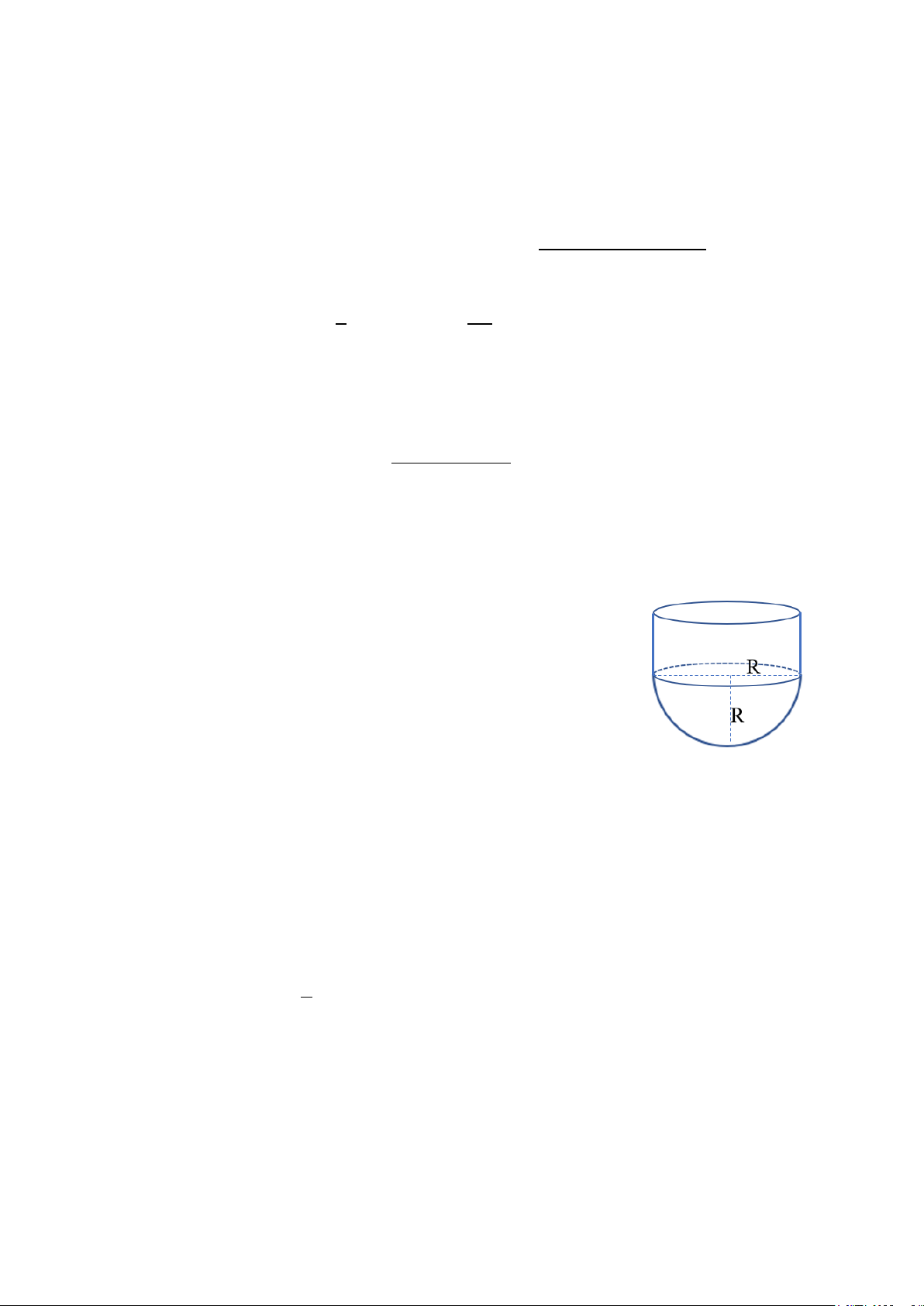
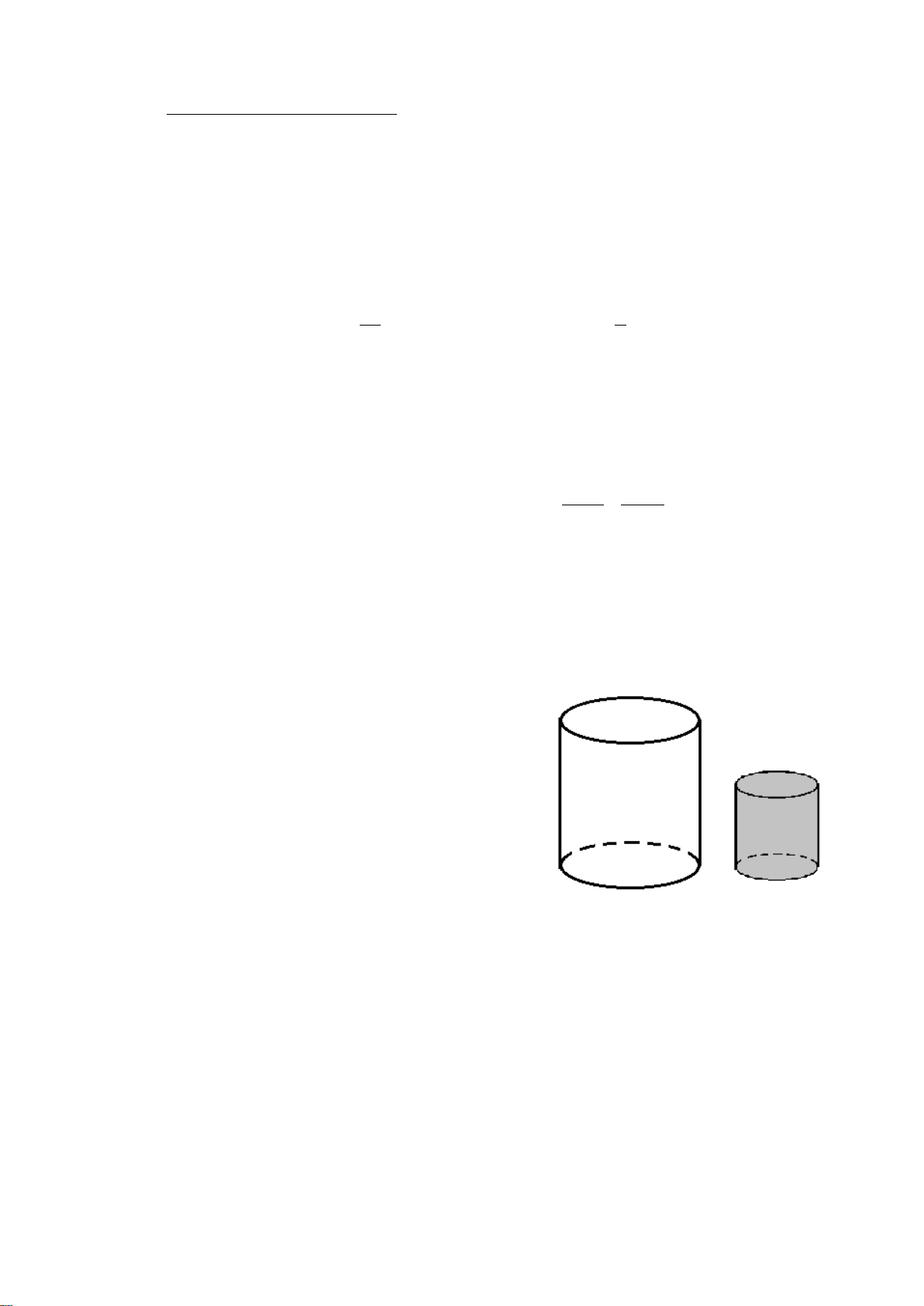
Bài 5 (0,5 điểm). Một chụp nhựa bảo vệ chuông điện có cấu trúc gồm một
phần hình trụ có bán kính R, chiều cao 6cm và một bán cầu bán kính R (hình
vẽ bên). Cho biết diện tích mặt xung quanh khối chụp 2 120 cm . Tính thể tích
khối chụp (kết quả làm tròn đến chữ
Bài 6 (1 điểm). Một xí nghiệp may cứ mỗi tháng thì phải trả tiền lương cho
công nhân viên, tiền vật liệu, tiền điện, tiền thuế,… tổng cộng là 410 000 000
(VNĐ). Mỗi chiếc áo được bán với giá là 350 000 (VNĐ). Gọi số tiền lời
(hoặc lỗ) mà xí nghiệp thu được sau mỗi tháng là T (VNĐ) và mỗi tháng xí nghiệp sản xuất được A chiếc áo.
a) Lập hàm số của T theo A.
b) Hỏi cần phải sản xuất trung bình bao nhiêu chiếc áo mỗi tháng để sau 1 năm, xí nghiệp thu được tiền lời là 1 380 000 000 (VNĐ)?
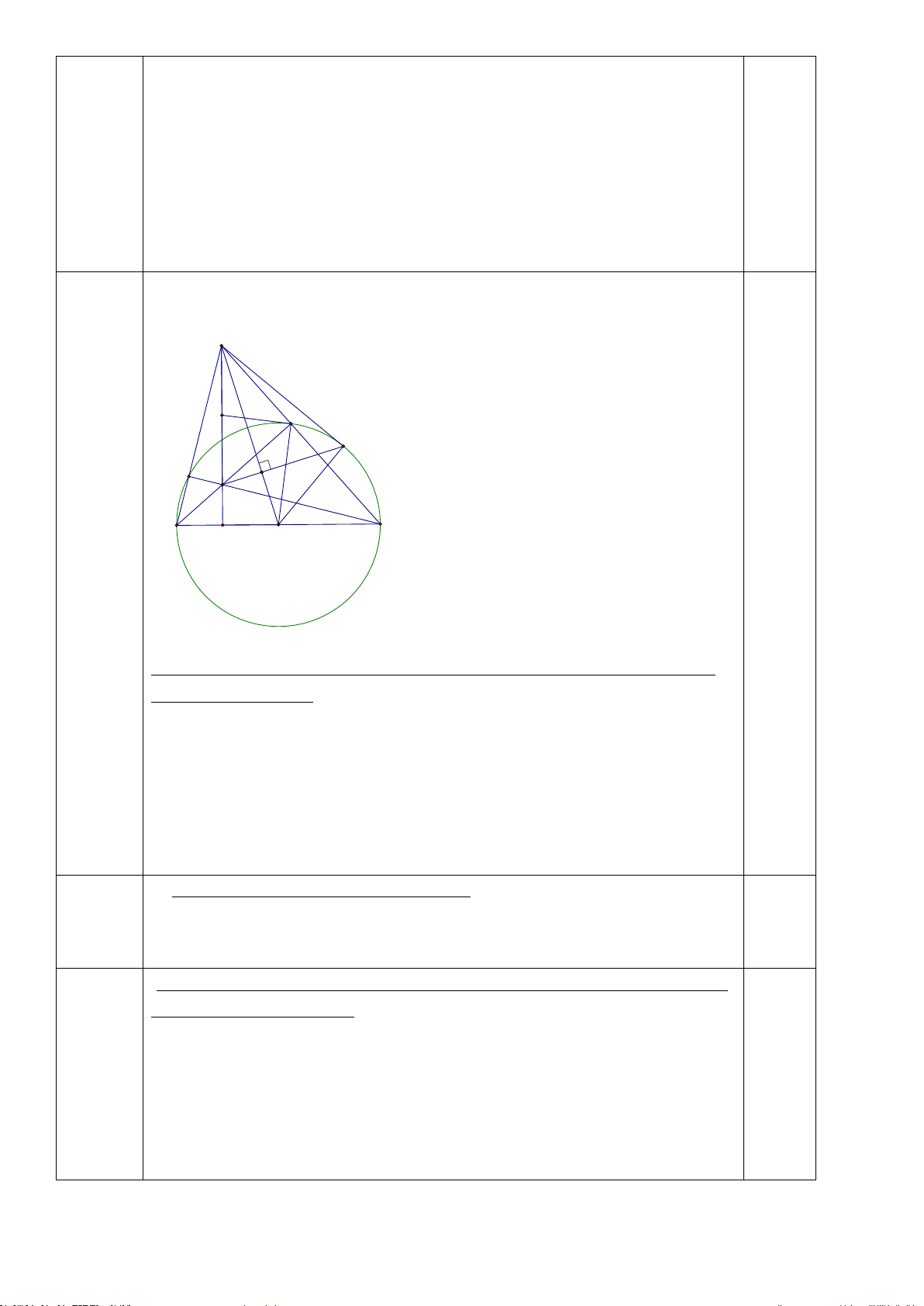
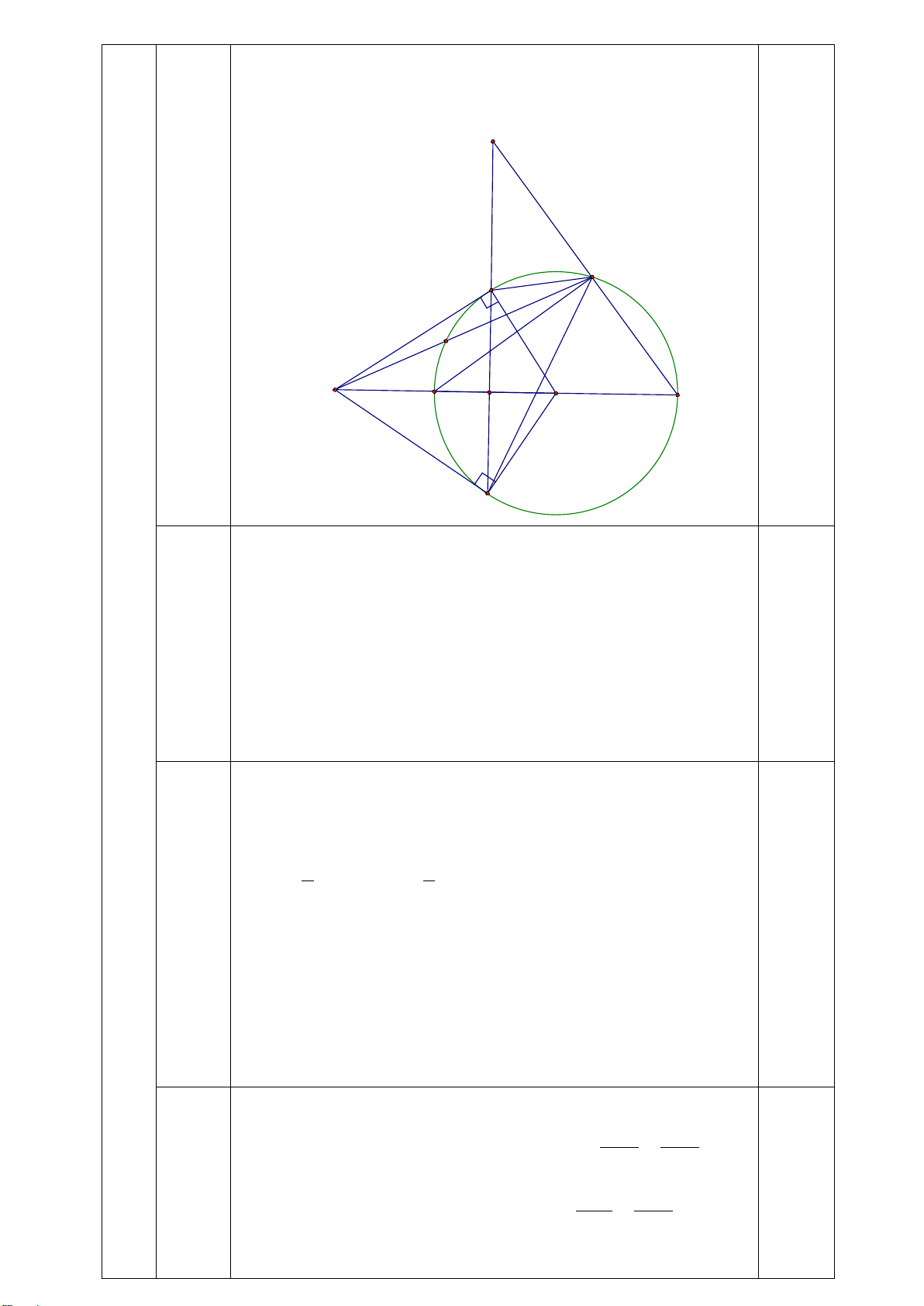
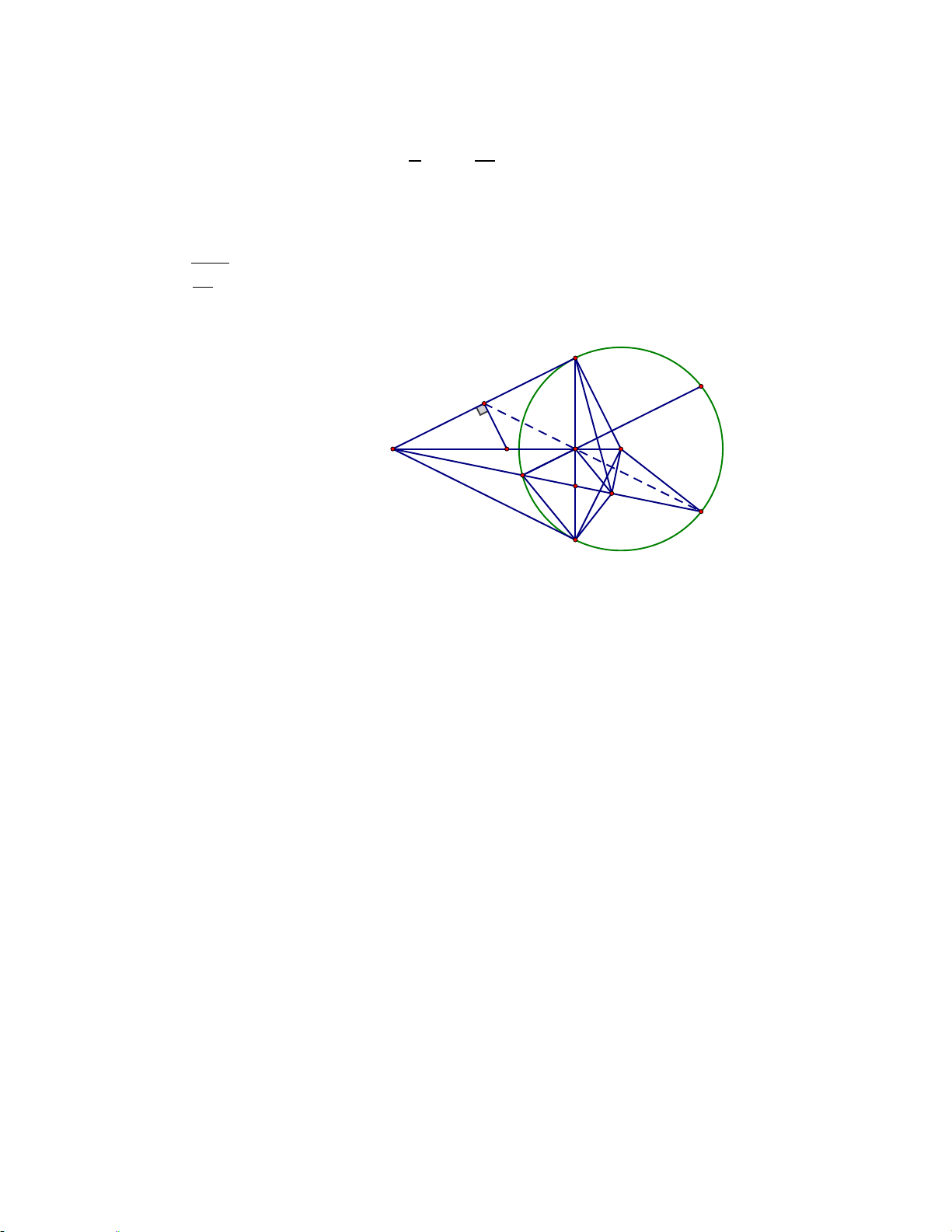
Bài 7 (3 điểm). Cho tam giác nhọn ABC nội tiếp đường tròn (O; R). Gọi H là giao điểm hai đường cao BD và CE của ∆ABC.
a) Chứng minh tứ giác BCDE nội tiếp một đường tròn và xác định tâm I của đường tròn này.
b) Gọi AK là đường kính của (O). Chứng minh AED � = AKB � và OA ⊥ ED. c) Trong trường hợp 3
BC AK , tính tổng AB.CK + AC.BK theo R. 4 ----- HẾT -----
(Giám thị không giải thích gì thêm)
HƯỚNG DẪN CHẤM TOÁN 9 - HKII
Bài 1: (1.5 điểm) Giải phương trình, hệ phương trình a) 2
x – 4x – 11 0 0,75 b) 4 2
x – 5x – 6 0 0,75 Bài 2: (1.5 điểm)
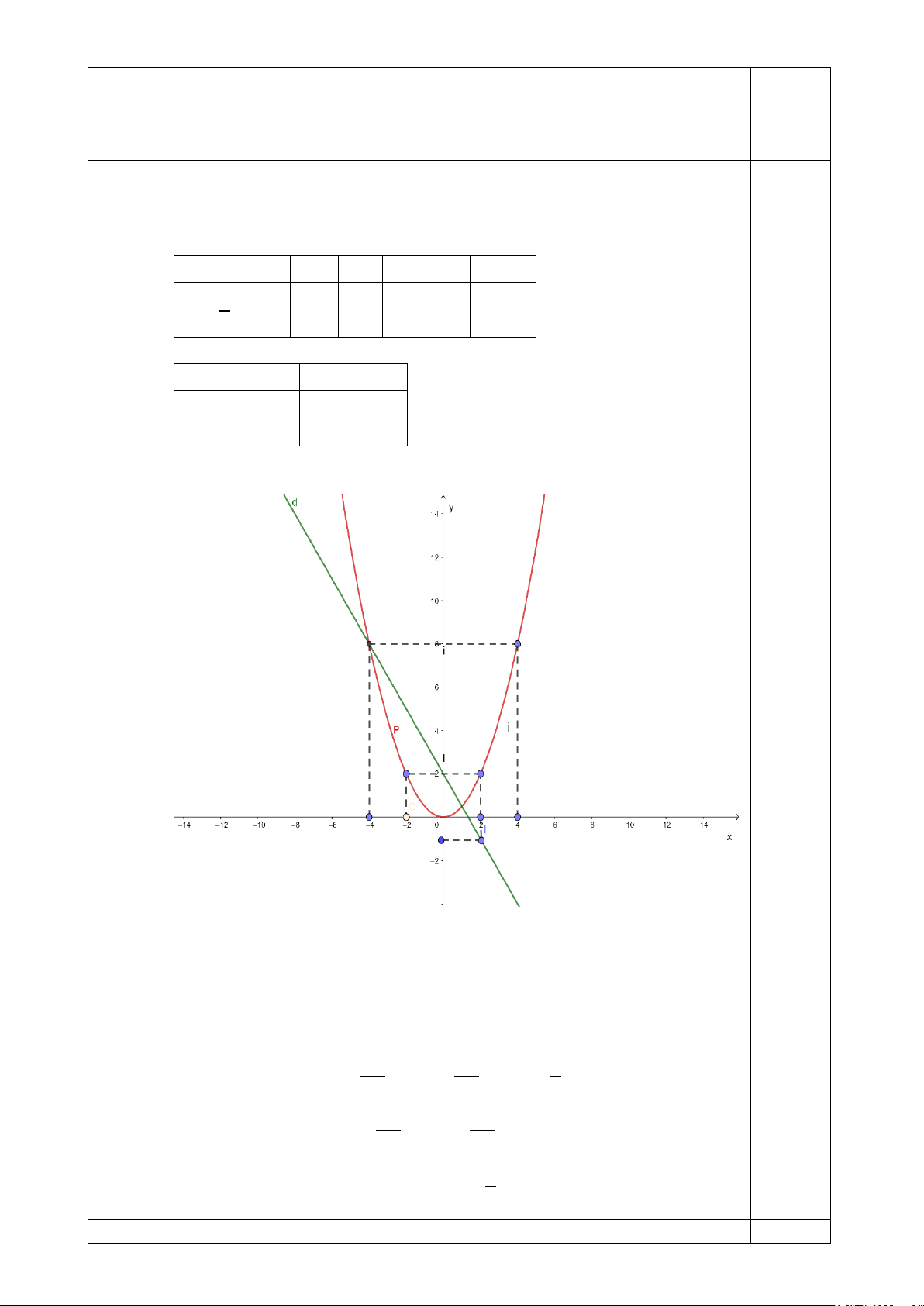
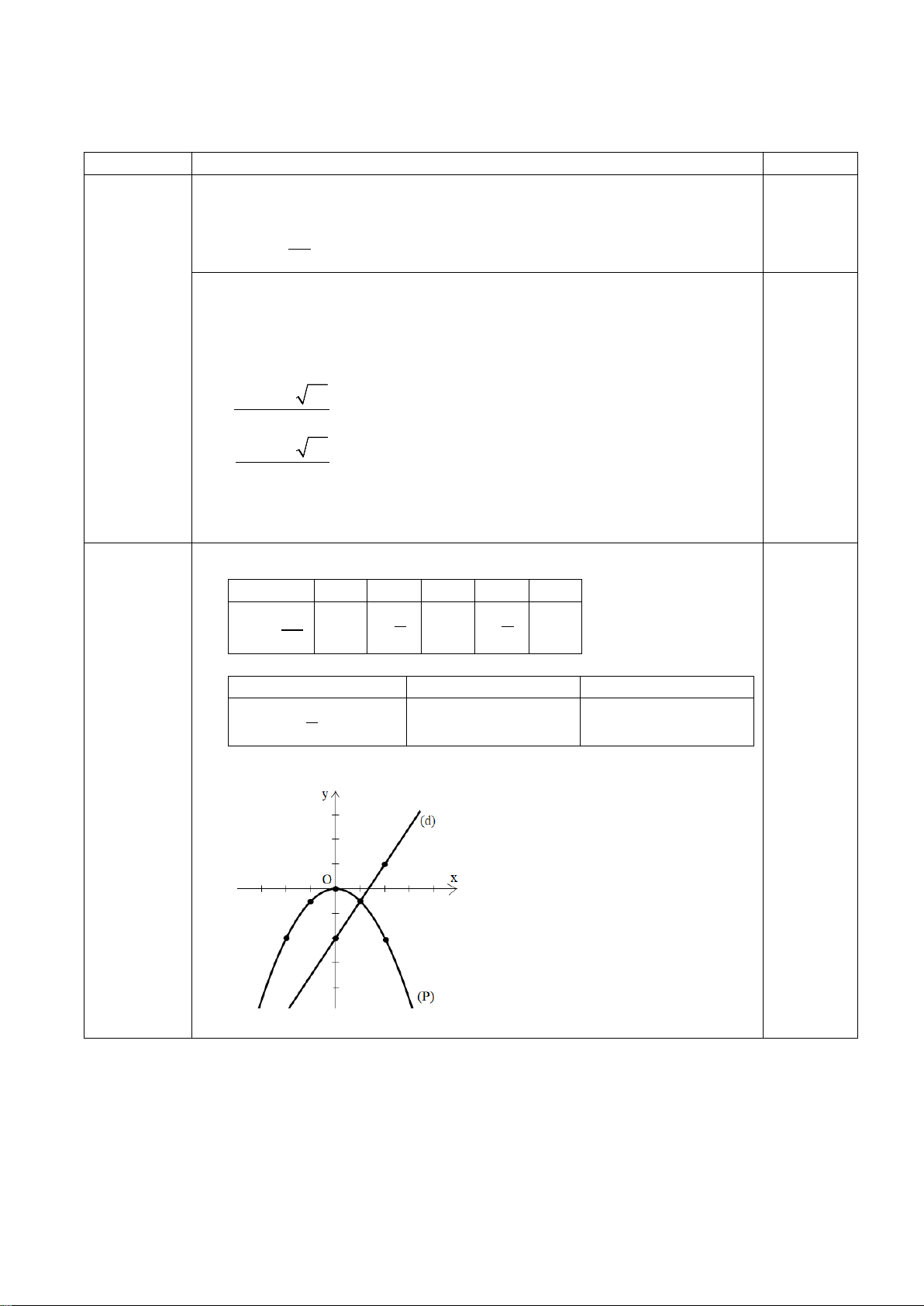
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ Bảng giá trị: x -4 -2 0 2 4 1 8 2 0 2 8 y 2 x 2 0,5 x 0 -4 3 2 8 y x 2 2 Đồ thị: 0,5
b) Phương trình hoành độ giao điểm của (P) và (d): 1 2 3 x x 2 2 2
Giải ra ta được: x 1;x 4 1 2 Với 3 3 1 x 1 thay vào y x 2 .1 2 2 2 2 0,5 với 3 3 x 4 thay vào y x 2 . ( 4) 2 8 2 2
Vậy tọa độ giao điểm của (P) và (d) là 1 1; và 4;8 2 Bài 3 (1,5 điểm)
Vì a.c = 3.(-5) = -15 < 0 nên phương trình có 2 nghiệm phân biệt 0,5 Theo Vi-et: b c 5
S x x 4 ;
P x .x 1 2 a 1 2 a 3 0,5 x 4x 2 2 x x x x x x x x x x 1 1 2 2 2 1 2 2 T 1 2 1 2 1 2 0,5 2 4x x x x x x x x x x x 2x x x 1 2 1 2 1 2 2 2 2 1 2 1 2 1 1 2 2 x x 2x x 1 2 2 29 1 2 x x 2 24 1 2 Bài 4 (1 điểm).
Gọi x là số luống cây và y là số cây cải bắp trồng trên một luống (x, y ∈ N*) 0.25đ
Với giả thiết thứ nhất, ta có: 0.25đ
xy – (x + 8)(y – 4) = 48 ⇔ 4x – 8y = 16 0,25đ
Với giả thiết thứ hai, ta có:
(x – 4)(y + 3) – xy = 32 ⇔ 3x – 4y = 44 0.25đ 0.25đ 0,25đ
Từ đó, ta có hệ phương trình: 4x 8y 16 x 36 x 36 ⇔ ⇔ 3x 4y 44 3.36 4y 44 y 16 0,25đ
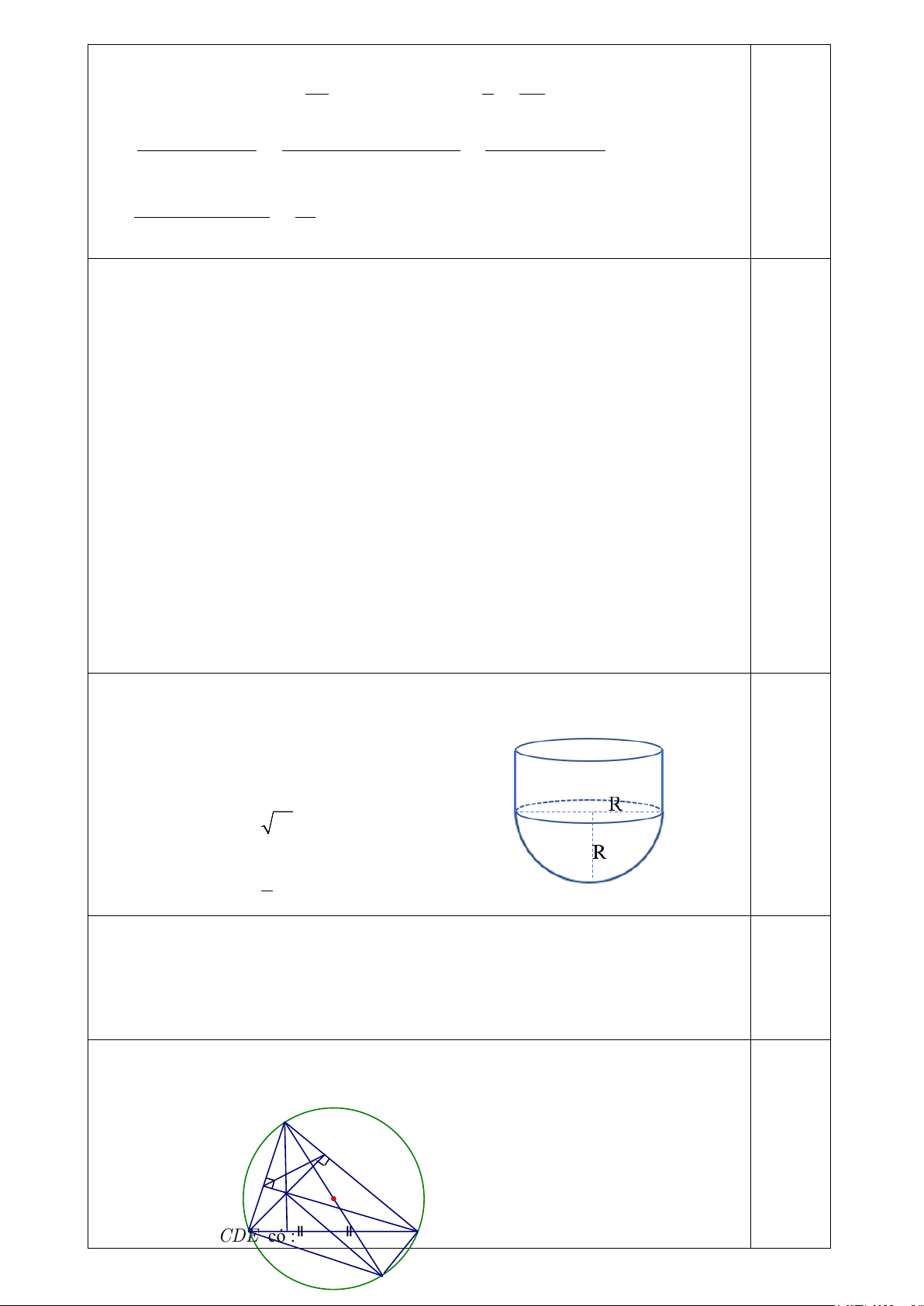
Vậy số cây rau nhà bạn Lan trồng được là: 36.16 = 576 (cây) Bài 5: (0,5 điểm)
Ta có diện tích xung quanh S 2 . R h 2 2 R 0,25 2
120 12R 2R 2
R 6R 60 0 0.25 R 3 69 Thể tích khối chụp 2 V 2
R .h 3 R 3 845,1(cm ) 3 Bài 6: ( 1 điểm)
a) Lập hàm số của T theo A 0.5
b) Tổng số tiền khi bán được A chiếc áo là: 350000.A đồng 0.25 0.25
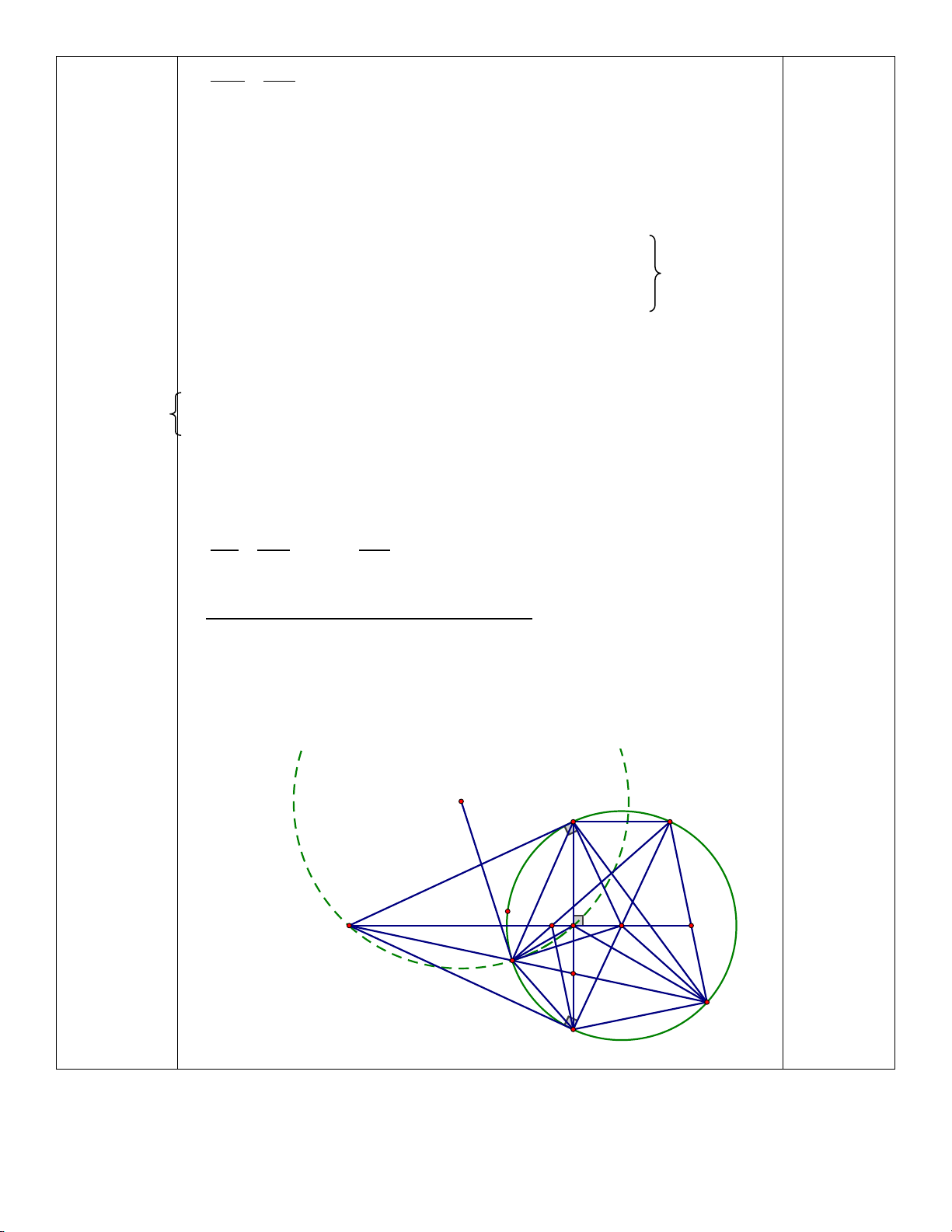
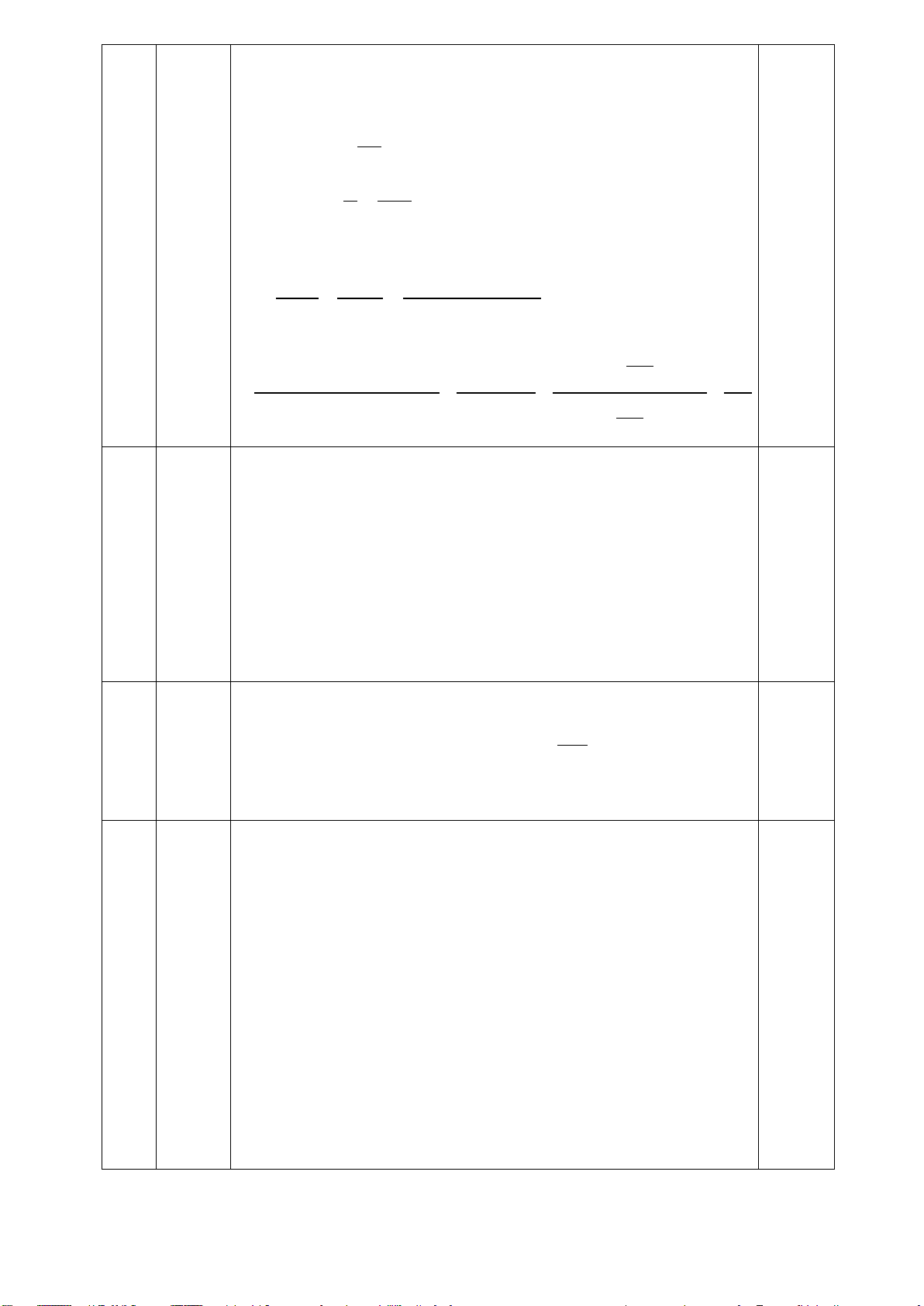
Hàm số của T (số tiền lời hoặc lỗ) theo A là: T 350000.A 410000000 Bài 7: (3,0 điểm) A D E H O a) Xét tứ giác BCDE B có F : I C K
góc BEC = góc BDC 0 90 …..(0.25đ)
2 đỉnh E;D liên tiếp cùng nhìn cạnh BC
tứ giác BCDE nội tiếp đường tròn tâm I đường kính BC) (0.25đ)
Tâm I là trung điểm của đường kính BC. (0.25đ)
b) Ta có tứ giác BCDE nội tiếp (cmt) => góc AED = góc ACB (góc ngoài bằng góc đối
trong)………………….(0.25đ)
Mà góc ACB = góc AKB (góc nội tiếp cùng chắn cung AB)……….(0.25đ)
=> Góc AED = góc AKB…………..(0.25đ)
Ta có tam giác ABK nội tiếp đường tròn đường kính AK => Tam giác ABK vuông tại B …….(0.25đ)
=> Góc BAK + góc BKA = 900
=> góc BAK + góc AED = 900
=> OA vuông góc với ED…………(0.25đ)
c) Gọi F là giao điểm của AH và BC. Ta có ∆ ABF AB BF ∽ ∆ AKC (g.g) ⇒
⇒ AB. KC = AK. BF (1) 0.25 AK KC Và ∆ ACF AC CF ∽ ∆ AKB (g.g) ⇒
⇒ AC. KB = AK. CF (2) AK KB (0.25đ)
Cộng (1) và (2) theo vế ta có: AB. KC + AC. KB = AK. BF + AK. CF
= AK.(BF + CF) = AK.BC (0.25đ)
Mà BC = 3 AK ⇒ AB. KC + AC. KB = AK. 3 AK = 3 AK2 = 3 .(2R)2 = 3R2 4 4 4 4 0.25
UỶ BAN NHÂN DÂN QUẬN 3
ĐỀ THAM KHẢO HỌC KỲ II
TRƯỜNG THCS BẠCH ĐẰNG
Năm học : 2023 – 2024 Môn : Toán 9
Thời gian : 90 phút ( không kể thời gian phát đề 2
Câu 1 : ( 1,5 điểm) Cho hàm số x y 1 =
có đồ thị (P) và đường thẳng (D) có phương trình y = x + 2 4 2
a) Vẽ đồ thị (P) và (D) trên cùng mặt phẳng toạ độ
b) Tìm toạ độ giao điểm của (P( và (D)
Câu 2 : (1,5 điểm) Cho phương trình x2–3x + 2 = 0 có 2 nghiệm x1, x2 .Không giải phương trình ,hãy
tính giá trị của biểu thức 2 2 2 2 A = ( 1 x − 4 1
x − 2)(x2 + 4x2 − 2) + 2( 1 x + x2)
Câu 3 : (1 điểm) Giá bán của ấm đun nước được xác định bởi hàm số 11R C = + 50 (trong đó: C là giá 8
bán, đơn vị tính: nghìn đồng; R là bán kính của đáy ấm, đơn vị tính cm). Bạn Mai mua 2 cái ấm có bán
kính của đáy ấm lần lượt là 24 cm và 32 cm. Khi đi mua hàng, Mai mang theo 200.000 đồng. Hỏi Mai
có đủ tiền để trả không?
Câu 4 : (1 điểm) Một đoàn y tế từ thiện của tỉnh gồm các bác sĩ và y tá về xã để khám chữa bệnh miễn
phí cho người dân trong tỉnh. Đoàn gồm 45 người và có tuổi trung bình là 40 tuổi. Tính số bác sĩ và y
tá biết tuổi trung bình của các bác sĩ là 50 tuổi và tuổi trung bình của các y tá là 35 tuổi.
Câu 5 : ( 1 điểm) Sau buổi sinh hoạt ngoại khóa, nhóm bạn của Hồng rủ nhau đi ăn kem ở một quán
gần trường. Mỗi ly kem đồng giá là 15000 đồng. Do quán mới khai trương nên có khuyến mãi, mua từ
ly thứ 4 trở đi giá mỗi ly kem là 12000 đồng. Hỏi nhóm của Hồng mua bao nhiêu ly, biết số tiền phải trả là 105000 đồng? A
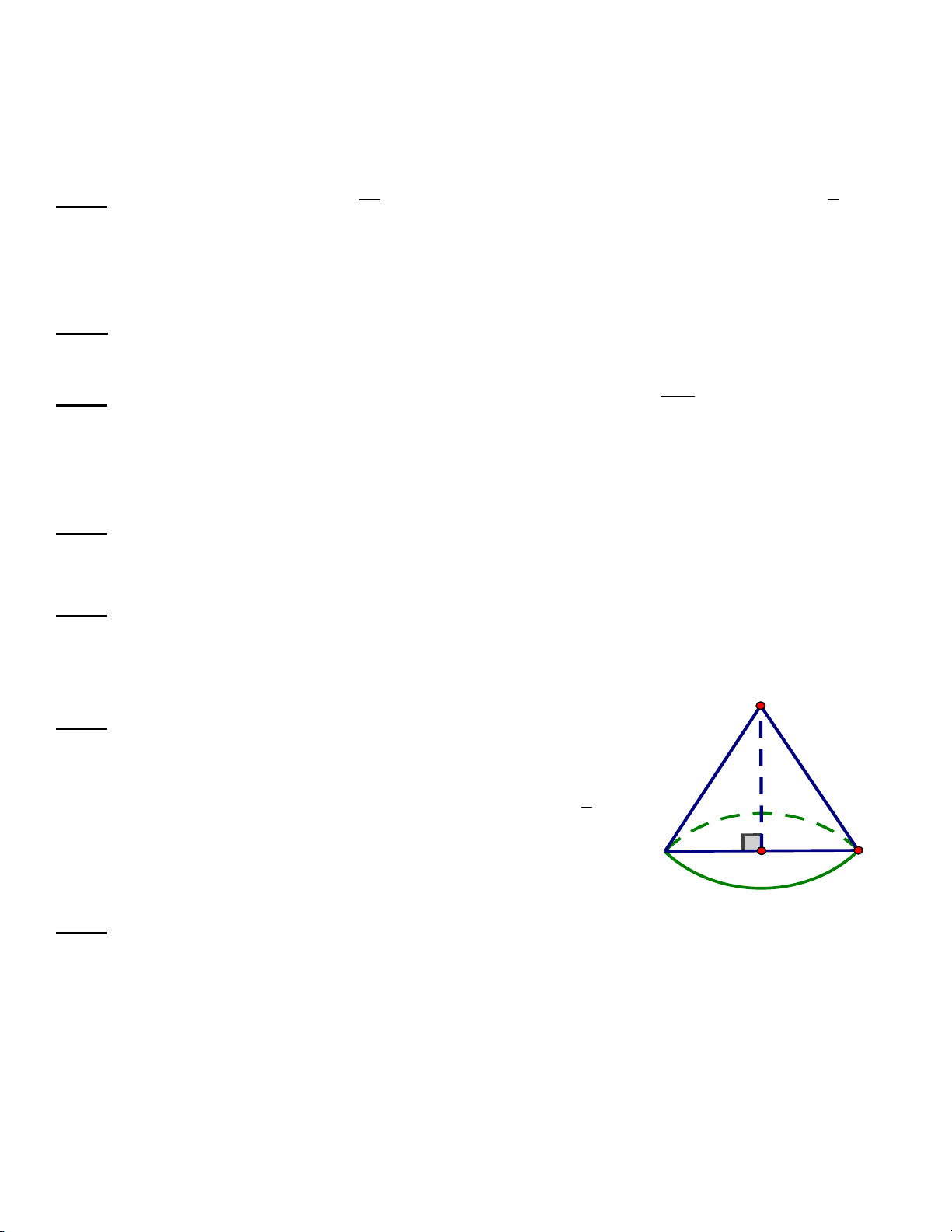
Câu 6 : (1 điểm) Khi quay tam giác vuông AOC một vòng quanh cạnh góc
vuông OA cố định thì được một hình nón h l
Tính thể tích V của hình nón biết AC = 13cm , OC =5cm và 1 2 V = πr h 3 (π = 3,14 ) r C O
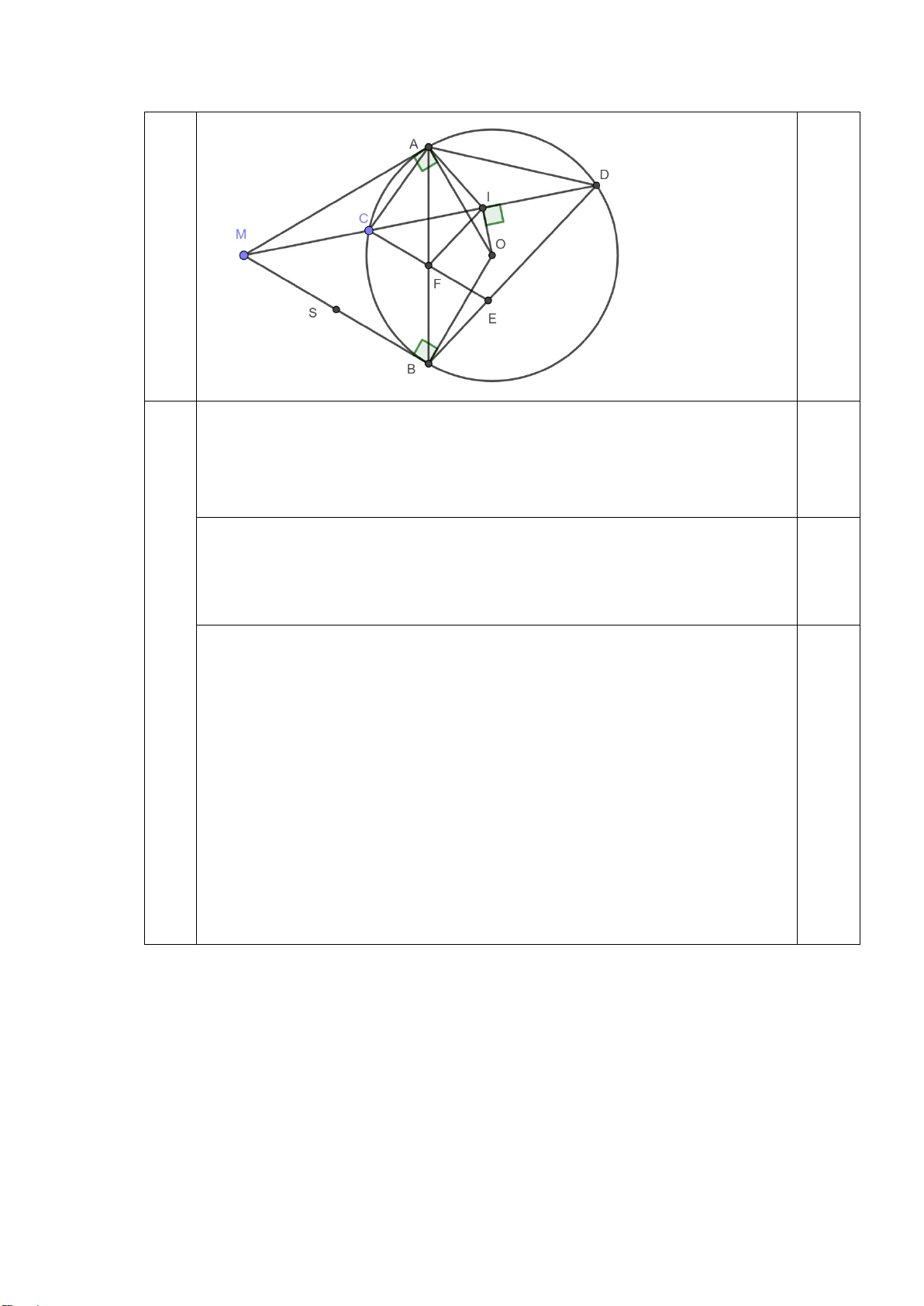
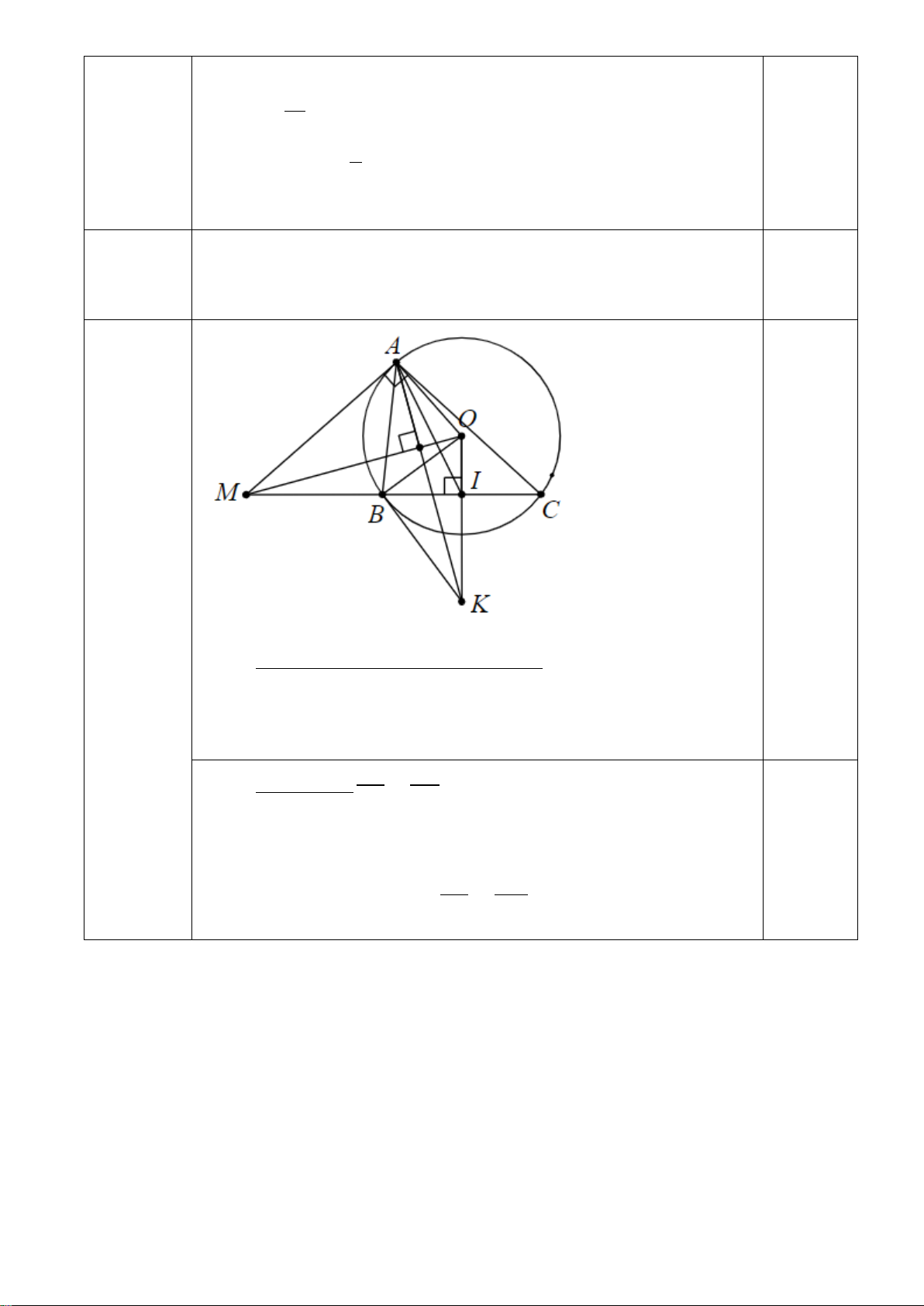
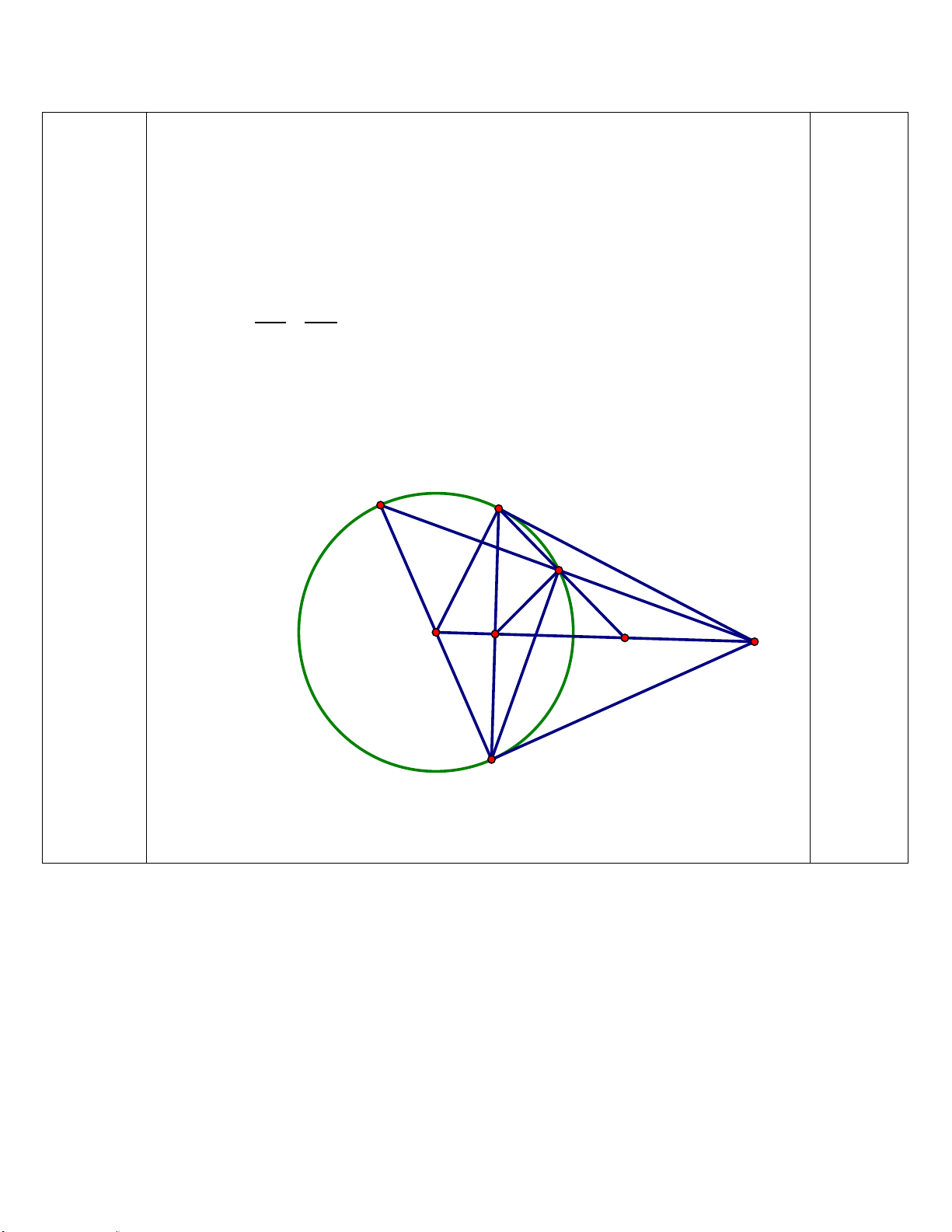
Câu 7 : (3 điểm) Từ điểm M nằm ngoài đường tròn (O;R) (OM > 2R), vẽ 2 tiếp tuyến MA, MB (A, B
là hai tiếp điểm. Gọi H là giao điểm của OM và AB. Lấy C thuộc đoạn HB. Đường thẳng MC cắt (O)
tại D và E (D nằm giữa M và C)
a) Chứng minh: AD. BE = AE.BD
b) Chứng minh tứ giác OHDE nội tiếp. Chứng minh CD.ME = CE.MD
c) Gọi K là tâm đường tròn ngoại tiếp tam giác MHD. Chứng minh KD là tiếp tuyến của (O). ĐÁP ÁN Câu 1 :
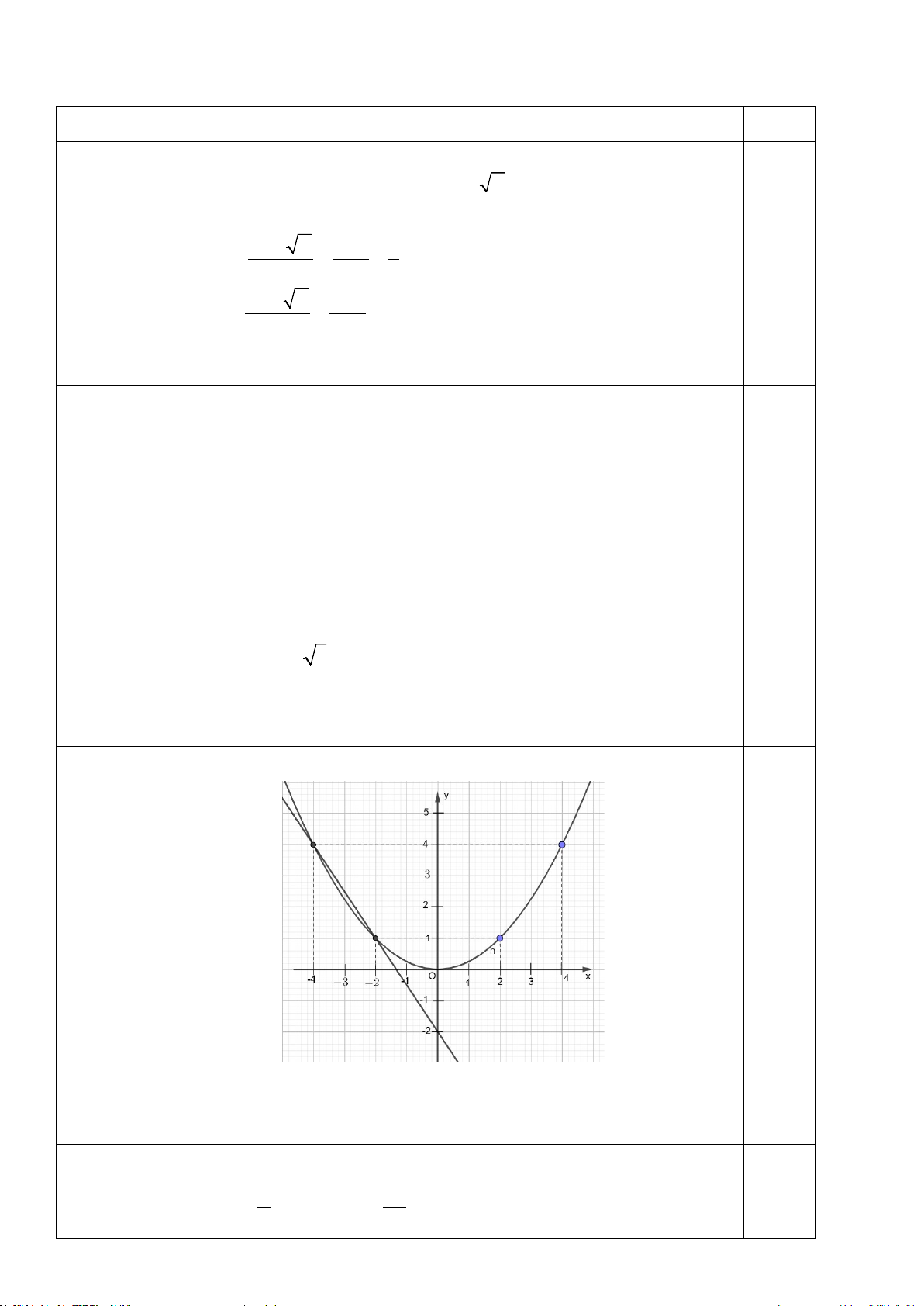
-Bảng giá trị đúng 0,5 điểm
( 1,5 điểm) -Đồ thị đúng 0,5 điểm
-Toạ độ giao điểm (4 ;4 ) và (-2 ;1) 0,5 điểm Câu 2 : S = 3 ; P = - 2 0,5 điểm
( 1,5 điểm) A = P.(S2 – 16)+2.(S2 – 2P) = 40 1 điểm Câu 3 : ( 1 điểm)
Giá của cái ấm đun có bán kính đáy ấm 24cm: 11.24 + 50 = 83 (nghìn 8 0,25 điểm đồng)
Giá của cái ấm đun có bán kính đáy ấm 32cm: 11.32 + 50 = 94 (nghìn 0,25 điểm 8 đồng) 0,25 điểm
Số tiền Mai phải trả: 83+ 94 = 177 (nghìn đồng) 0,25 điểm
Vì 177 000 < 200 000 nên Mai có đủ tiền để trả. Câu 4 :
Gọi x (người) là số bác sĩ và y (người) là số y tá ( x,y ∈ * ) 0,25 điểm ( 1 điểm) x + y = 45 50x + 35y = 45.40 0,25 điểm x + y = 45 0,25 điểm 50x + 35y = 45.40 0,25 điểm ⇒ x = 15, y = 30 Câu 5 :
Gọi số ly kem nhóm đã mua là x (ly), x∈ N * 0,25 điểm ( 1 điểm)
Ta có phương trình : 15000×3 + 12000(x-3) = 105000 0,25 điểm
x= 8. Vậy nhóm đã mua 8 ly kem 0,5 điểm Câu 6 : h= 12 cm 0,5 điểm ( 1 điểm) 1 2 1 2 2
V = π r h = .3,14.5 .12 = 314cm 0,5 điểm 3 3 Câu 7 :
a) Chứng minh: AD. BE = AE.BD (1đ) ( 3 điểm) cm MA ∆ D ∽ ME ∆ A (g-g) MD AD ⇒ = MA EA cm MB ∆ D ∽ ME ∆ B (g-g) MD BD ⇒ = AD BD ⇒ = MB EB EA EB ⇒ A . D EB = E . A BD
mà MA = MB (t/c 2 tiếp tuyến cắt nhau)
b) Chứng minh tứ giác OHDE nội tiếp. Chứng minh CD.ME = CE.MD (1đ) cm MO ⊥ AB tại H cm 2
MH.MO = MB (Hệ thức lượng trong MB ∆
O vuông tại B, có BH là đường cao) cm 2 .
MD ME = MB ( MB ∆ D ∽ ME ∆ B ) ⇒MH.MO= . MD ME MH MD ⇒ = ME MO ⇒ MH ∆ D ∽ ME ∆ O (c-g-c) ⇒ = MHD MEO
⇒ OHDE nội tiếp (góc ngoài = góc đối trong) cm = MHD MEO (cmt) = MEO ODE ( ODE ∆ cân tại O) ⇒ = MHD OHE =
ODE OHE (OHDE nội tiếp, 2 đỉnh kề cùng nhìn 1 cạnh) mà + 0 MHD DHB = 90 + 0 OHE EHB = 90 ⇒ = DHB EHB
⇒ HB là phân giác của DHE
mà HM ⊥ HB⇒HM là phân giác ngoài của DHE CD MD ⇒ =
(cùng = HD ) ⇒ C .
D ME = CE.MD CE ME HE
c) Chứng minh KD là tiếp tuyến của (O) (1đ) cm 2 2
OH.OM = OA = OD (Hệ thức lượng trong ∆ vuông OAM) ⇒ ODH ∆ ∽ O ∆ MD (c-g-c) ⇒ = ODH OMD
⇒ DO là tia tiếp tuyến của (K) (định lý đảo về góc tạo bởi tia tiếp tuyến và dây cung) ⇒ DO ⊥ DK tại D
⇒ DK là tiếp tuyến của (O) K A F I M O N H D C E B
MA TRẬN ĐỀ KIỂM TRA: Chủ đề Nhận Thông hiểu Vận dụng Tổng biết Mức độ thấp Mức độ cao Nội Vẽ đồ thị Tìm tọa độ giao điểm dung Hàm số Số 1 1 2 câu Điểm 1 0,5 1,5 % 10% 5% 15% Nội Tính tổng và tích hai Tính giá trị dung nghiệm biểu thức
Định lí Vi-ét Số 1 1 2 câu Điểm 0,5 1 1,5 % 5% 110% 15% Nội Hệ phương trình, hàm dung số, hình nón ,mua Toán thực hàng giảm giá tế Số 4 4 câu Điểm 4 4 % 40% 40% Nội
Chứng minh Chứng minh tứ giác Chứng minh dung hệ thức
nội tiếp .Chứng minh tiếp tuyến với hệ thức đường tròn Hình học Số 1 1 1 3 câu Điểm 1 1 1 3 % 10% 10% 10% Số 2 7 2 11 Tổng câu Điểm 2 6 2 10 % 20% 60% 20% 100%
ĐỀ THAM KHẢO CUỐI HỌC KỲ 2/ 2023 – 2024 MÔN: TOÁN 9
Câu 1: (1,0 điểm) Giải các phương trình sau: a) x2 + 2x – 2= 0 b) x4 – 7x2 – 18 = 0
Câu 2: (1,5 điểm) a) Vẽ (P) 1 2
: y = − x và (D): y = x – 4 trên cùng mặt phẳng toạ độ. 2
b) Tìm tọa độ giao điểm của (D) và (P) bằng phép toán.
Câu 3: (1,5 điểm) Cho phöông trình: x2 + 2mx – 2m2 = 0 (x là ẩn số)
a) Chứng tỏ phương trình luôn có nghiệm với mọi giá trị của m.
b) Tìm m để phương trình có hai nghiệm x1, x2 sao cho tổng hai nghiệm bằng tích của chúng
Câu 4: (1 điểm) Một vật rơi ở độ cao so với mặt đất là 100m. Quãng đường chuyển động s (mét) của vật rơi phụ
thuộc vào thời gian t (giây) bởi công thức: s = 4t2.
a) Sau 2 giây, vật này cách mặt đất bao nhiêu mét?
b) Hỏi sau bao lâu vật này tiếp đất?
Câu 5: (1 điểm) Bạn Tèo đi siêu thị mua hai loại hàng và phải trả tổng cộng 2,17 triệu đồng, kể cả thuế giá trị gia
tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai. Nếu thuế VAT là 9% đối với cả
hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế VAT thì bạn Tèo phải trả bao
nhiêu tiền cho mỗi loại hàng?
Câu 6: (1 điểm) Có hai lọ thủy tinh hình trụ, lọ thứ nhất phía bên trong có đường kính đáy là 30cm, chiều cao 20cm,
đựng đầy nước. Lọ thứ hai bên trong có đường kính đáy là 40cm, chiều cao 12cm. Hỏi nếu đổ hết nước từ trong lọ
thứ nhất sang lọ thứ hai nước có bị tràn ra ngoài không? Vì sao? (thể tích hình trụ: V = πR2h trong đó R là bán kính
đáy, h là chiều cao của hình trụ ; lấy π = 3,14)
Câu 7: (3,0 điểm) Cho A
∆ BC nhoïn (AB < AC) noäi tieáp ñöôøng troøn (O) coù 2 ñöôøng cao AD, CE caét nhau taïi H
( D∈BC, E∈AB). Veõ ñöôøng kính AK cuûa (O) caét CE taïi M. Tia AD caét tia CK taïi N.
a) Chöùng minh: BEHD, HMKN laø caùc töù giaùc noäi tieáp. b) Chöùng minh: = EAD OCA
c) Goïi I laø trung ñieåm cuûa ñoaïn BC. Tia EI caét AK taïi P. Chöùng minh: AD.AN = AP.AK
------------------ Hết --------------------
Học sinh không được sử dụng tài liệu
Giám thi coi thi không được giải thích gì thêm.
Không được có cảm xúc, ý kiến, bình luận về đề thi
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN 3
Trường THCS Đoàn Thị Điểm
ĐỀ THAM KHẢO HỌC KỲ II - NĂM HỌC 2023 – 2024
MÔN : TOÁN – LỚP 9
THỜI GIAN LÀM BÀI : 90 phút
Câu 1: (2 điểm) Giải các phương trình sau : a) 2
3x + 2x − 5 = 0 b) 2 x 1 x 1 x 720 0
Câu 2: (1, 5 điểm) Cho hàm số 1 2 y −
= x có đồ thị (P) và hàm số 3 y =
x − 2 có đồ thị (D) 4 2
a/ Vẽ (P) và (D) trên cùng mặt phẳng toạ độ.
b/ Tìm tọa độ giao điểm của (P) và (D) bằng phép tính.
Câu 3: (1, 5 điểm) Cho phương trình: 2 x − 5x − 4 = 0.
a) Chứng tỏ phương trình luôn có 2 nghiệm phân biệt. − −
b) Không giải phương trình, hãy tính giá trị biểu thức : x x x x 1 2 2 1 A = + x x 2 1
Câu 4: (0,75 điểm) Để đảm bảo dinh dưỡng trong bữa ăn hàng ngày thì mỗi gia đình 4 thành viên
cần 900 đơn vị protêin và 400 đơn vị Lipit trong thức ăn mỗi ngày. Mỗi kilogam thịt bò chứa 800 đơn
vị protêin và 200 đơn vị Lipit, còn mỗi kilogam thịt heo chứa 600 đơn vị protêin và 400 đơn vị Lipit.
Biết giá thịt bò là 240 000 đồng/kg và giá thịt heo là 160 000 đồng/kg. Hỏi cần bao nhiêu tiền mua
thịt bò và thị heo để đảm bảo dinh dưỡng trong một ngày cho 4 người?
Câu 5: ( 0, 5 điểm)
a) Người ta muốn làm một xô nước dạng chóp cụt như hình bên, hãy tính diện
tích tôn cần thiết để gò nên xô nước theo các kích thước đã cho (xem phần ghép
mí không đáng kể). Công thức tính diện tích xung quanh hình chóp cụt là
S = π ⋅(r + r ⋅l xq 1 2 )
b) Hỏi xô nước đã làm có thể chứa được tối đa bao nhiêu lít nước? Công thức
tính thể tích hình chóp cụt là 1 V = π h ⋅( 2 2
r + r + r .r 1 2 1 2 ) 3
Câu 6: ( 0,75 điểm)
Theo quy định của cửa hàng xe máy, để hoàn thành chỉ tiêu
trong một tháng, mỗi nhân viên phải bán được trung bình
một chiếc xe máy trong một ngày. Nhân viên nào hoàn
thành chỉ tiêu trong một tháng thì nhận lương cơ bản là 12
000 000 đồng. Nếu trong một tháng nhân viên nào vượt chỉ
tiêu thì được thưởng thêm 8% tiền lời của số xe bán vượt
chỉ tiêu. Trong tháng 5 (có 31 ngày), anh Thành nhận được
số tiền là 14 880 000 đồng (bao gồm cả lương cơ bản và
tiền thưởng thêm tháng đó). Hỏi anh Thành đã bán được
bao nhiêu chiếc xe máy trong tháng 5, biết rằng mỗi xe
máy bán ra thì cửa hàng thu được tiền lời là 4 000 000 đồng. Câu 7: (3 điểm)
Cho ∆ABC nhọn (ABtại H.
a) Chứng minh: AH⊥BC tại D và tứ giác AEHF nội tiếp. Xác định tâm I của đường tròn này.
b) Chứng minh: Tứ giác IEOD nội tiếp.
c) Qua H vẽ tia Hx vuông góc với AO tại K và cắt (O) tại L. Chứng minh AL là tiếp tuyến của (O).
ĐÁP ÁN ĐỀ THAM KHẢO CÂU ĐÁP ÁN ĐIỂM 1a 2
3x + 2x − 5 = 0 (1 đ) 2 2
∆ = b − 4ac = 2 − 4.3.( 5 − ) = 64 ⇒ ∆ = 8
∆ > 0 ⇒ pt có 2 nghiệm phân biệt : b − + ∆ 2 + 8 5 x = = = ; 1 0,5 2a 2.3 3 b − − ∆ 2 −8 x = = = 1 − 2 2a 2.3 0.25x2 1b x 1 x 1 2 x 720 0 (1 đ) 4 2 x 6x 27 0 0.25 Đăt t = x2 (Đk: t 0) Phương trình trở thành: 2t + 6t − 27 = 0 a= 1; b = 6 ; c= -18 0.25 2 2
∆ = b − 4ac = 6 − 4.1.( 27 − ) =144
∆ > 0 ⇒ pt (2) có 2 nghiệm phân biệt : ⇒ t = 3 (nhận) ; t = 9 − (loại) 2 t = x = 3 ⇒ x = ± 3 0.25x2 2a BGT 0.5 (1đ) 0,5
(lưu ý: HS xác định độ dài đơn vị trên trục tung – trục hoành khác nhau thì không cho điểm) 2b
Phương trình hoành độ giao điểm của (P) và (D): (0,5đ) b/ (P) : 1 2 y − = x ; (D) : 3 y = x − 2 0.25 4 2
Phương trình hoành độ giao điểm giữa (P) và (D)là: 1 3 − 1 3 x = 2 − ⇒ y =1 2 2 x = x − 2 ⇔ x + x + 2 = 0 ⇔ 4 2 4 2 0.25 x = 4 − ⇒ y = 4
Vậy tọa độ giao điểm giữa (P) và (D) là: (-2; 1) và (- 4; 4) 3a 2 x − 5x − 4 = 0
(0.5đ) Ta có a.c=1.(-4)=-4<0 0.25
Nên phương trình có 2 nghiệm phân biệt x và x 1 2 0.25 3b Theo định lý Vi ét (1 đ) − = + = b S x x = 5 1 2 a 0.5 = . = c P x x = 4 − 1 2 a 2 2 2 x − x x − x x − x x + x − x x S − 4P 1 2 2 1 1 1 2 2 1 2 A = + = = 0.25 x x x x P 2 1 1 2 2 5 − 4( 4) − 41 A − = = 4 − 4 0.25 4
Gọi x (kg) là lượng thịt bò; y (l) là lượng thịt heo cần để đảm bảo dinh
(0,75đ) dưỡng trong một ngày cho 4 người.( x, y>0)
Vì tổng đơn vị protein trong thịt heo và thịt bò là 900 nên: 0.25
800x + 600y = 900
Vì tổng đơn vị lipit trong thịt heo và thịt bò là 400 nên:
200x + 400y = 400 0.25 Ta có hệ phương trình 800 x + 600y = 900 x = 0,6 ⇔ 200x 400y 400 + = y = 0,7
Số tiền cần mua thịt bò và thịt heo là: 0.25
240000. 0,6+160000.0,7=256000 đ 5
a) Diện tích tôn cần thiết để gò nên xô nước theo các kích thước đã cho (0,5đ) là:
S = S + S = π ⋅(r + r ) 2 ⋅l + π r 2
= π ⋅(20 +10)⋅30 + π.10 0.25 xq day 1 2 2 ≈ ( 2 3142 cm ).
b) Chiều cao xô nước là: 2 2
h = 30 −10 = 800 = 20 2 (cm) .
Xô nước đã làm có thể chứa được tối đa số lít nước là: 1 0.25 V = π h ⋅( 2 2
r + r + r .r 1 = ⋅π ⋅ 20 2 ⋅( 2 2 20 +10 + 20⋅10) 1 2 1 2 ) 3 3 ≈ ( 3
20722,94273 cm ) ≈ 20,72294 (lít). 6
Gọi x là số xe anh Thành bán được trong tháng 5. Điều kiện: xÎN*. 0.25 (0,75đ)
Số tiền anh Thành nhận hơn số lương cơ bản là:
14880000 −12000000 = 2880000, nên anh Thành bán vượt chỉ tiêu.
Số tiền anh Thành nhận được do bán vượt chỉ tiêu: 0.25 (x − ) 31 .4000000.8% = 2880000 ⇔ x − 31 = 9 ⇔ x = 40 0.25
Vậy tháng 5 anh Thành bán được 40 chiếc. 7a (1 đ) A I E L F H K B D C O
Chứng minh: AH⊥BC tại D và tứ giác AEHF nội tiếp. Xác định tâm I của đường tròn này. 0.25 0 = 0 BFC 90 ; BEC = 90
H là trực tâm ∆ABC⇒ AH⊥BC tại D. 0.25
Chứng minh được tứ giác AEHF nội tiếp. 0.25 Tâm I là trung điểm AH 0.25 7b
Chứng minh: Tứ giác IEOD nội tiếp. 2x0.25 (1đ)
Chứng minh được IE⊥OE.
Chứng minh được tứ giác IEOD nội tiếp 2x0.25 7c
Qua H vẽ tia Hx vuông góc với AO tại K và cắt (O) tại L. Chứng minh (1đ)
AL là tiếp tuyến của (O). 0.25
Chứng minh được năm điểm A, E, K, H, F cùng thuộc một đường tròn Chứng minh được: 2 OE = OK.OA 0.25 ⇒ 2
OL = OK.OA và ∆OKL∽∆OLA 0.25
Chứng minh AL là tiếp tuyến của (O) 0.25 UỶ BAN NHÂN DÂN QUẬN 3
ĐỀ KIỂM TRA CUỐI KỲ 2
TRƯỜNG QUỐC TẾ Á CHÂU NĂM HỌC 2023-2024 MÔN: TOÁN - KHỐI 9 Ngày kiểm tra: ĐỀ THAM KHẢO
Thời gian: 90 phút (không kể thời gian phát đề)
Câu 1: (2điểm) Giải các phương trình sau: a) 2
x − 9x + 20 = 0 b) 4 2
4x + 3x −1 = 0 2
Câu 2: (1,5 điểm) Cho parabol ( ) : x P y =
và đường thẳng (d ) : y = x + 4 . 2
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép toán
Câu 3: (1,5 điểm) Cho phương trình: 2
3x 5x1 0.
a) Chứng tỏ phương trình trên có hai nghiệm phân biệt x1, x2 rồi tính tổng và tích của hai nghiệm đó
b) Không giải phương trình để tìm hai nghiệm x1, x2, hãy tính giá trị của biểu thức: 2 2
A = 3x + x x + 3x 1 1 2 2 3 3 x x + x x 1 2 1 2
Câu 4: (0,75 điểm) Anh Ba có 900 000 000 đồng. Anh Ba dùng 600 000 000 gửi ngân
hàng với lãi suất 7,5% một năm và phần còn lại anh dùng để đầu tư chứng khoán. Sau một
năm, anh thu về cả vốn lẫn lãi từ hai nguồn trên là 1 020 000 000 đồng. Hỏi anh Ba đầu tư
chứng khoán lãi bao nhiêu phần trăm.
Câu 5: (0,5 điểm) Một cái ly thủy tinh có dạng hình nón như hình
vẽ, người ta đổ rượu vào ly sao cho chiều cao của lượng rượu trong
ly bằng 1 chiều cao của phần hình nón. Biết rằng thể tích của rượu 3
là 2cm3. Hãy tính thể tích của cái ly.
Câu 6: (0,75 điểm) Trong một đợt khuyến mãi, siêu thị giảm giá
cho mặt hàng A là 20% và mặt hàng B là 15% so với giá niêm yết. Một khách hàng mua 2
món hàng A và 1 món hàng B phải trả số tiền là 362 000 đồng. Nhưng nếu mua trong
khung giờ vàng thì món hàng A được giảm giá 30% còn món hàng B được giảm giá 25%
so với giá niêm yết. Một người mua 3 món hàng A và 2 món hàng B trong khung giờ vàng
nên chỉ trả số tiến là 552 000 đồng. Tính giá niêm yết của mỗi món hàng A và B.
Câu 7: (3,0 điểm) Cho đường tròn ( ;
O R). Từ một điểm M nằm ngoài đường tròn tâm, kẻ hai tiếp tuyến ,
MA MB đến (O) (với ,
A B là các tiếp điểm). Qua A kẻ đường thẳng
song song với MO cắt đường tròn tại E, đường thẳng ME cắt đường tròn tại F, đường
thẳng AF cắt MO tại N.
a) Chứng minh tứ giác MAOB nội tiếp đường tròn. b) Chứng minh 2 MN = NF. . NA 2
c) Gọi H là giao điểm của MO và A .
B Chứng minh MN = NH và HB EF − = 1. 2 HF MF UBND QUẬN 3
ĐỀ ĐỀ NGHỊ KIỂM TRA HỌC KỲ II
TRƯỜNG THCS THĂNG LONG
NĂM HỌC 2023 – 2024 MÔN TOÁN LỚP 9 ĐỀ THAM KHẢO
Thời gian 90 phút (Không kể thời gian phát đề) 2
Bài 1: (2 điểm) Cho Parabol ( ) x P : y =
và đường thẳng (D) : y = x + 3 4
a) Vẽ đồ thị (P) và (D) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (D) bằng phép tính.
Bài 2: (1,5 điểm) Cho phương trình 3x2 + 5x - 6 = 0 có 2 nghiệm x1, x2
a) Tính tổng và tích 2 nghiệm 𝑥𝑥1, 𝑥𝑥2
b) Không giải phương trình, hãy tính giá trị của biểu thức: A = (x1-2)(x2-2) + x12 + x22
Bài 3: (1,5 điểm) Trong buổi sinh hoạt câu lạc bộ môn Toán của trường, mỗi học sinh khối 9
tham gia trả lời 20 câu hỏi. Biết rằng mỗi câu trả lời đúng được cộng 5 điểm và mỗi câu trả lời
sai bị trừ 2 điểm. Kết quả nhóm của bạn Thư đạt được 51 điểm. Hỏi nhóm của bạn Thư đã trả
lời được bao nhiêu câu đúng và bao nhiêu câu sai?
Bài 4: (1đ) ) Bạn An chọn ngẫu nhiên một số tự nhiên có 2 chữ số
Gọi A: “Số được chọn là bình phương của một số tự nhiên”.
B: “Số được chọn có tổng các chữ số chia hết cho 9”.
a) Xác định tập hợp các kết quả thuận lợi cho các biến cố trên và
b) Tính xác suất của mỗi biến cố A;B nêu trên. Bài 5: ( 1 điểm)
Vòng đệm là một trong những chi tiết lót không thể thiếu giữa đai ốc và
các thiết bị ghép nối trong các máy móc công nghiệp. Vòng đệm có tác
dụng phân bố đều lực ép lên đai ốc, làm tăng độ chặt giữa các mối ghép.
Một vòng đệm có thiết kế như hình vẽ bên, với A là tâm của hai đường
tròn bán kính AD và AC. Biết D là trung điểm của AC và AD = 5cm. Tính
diện tích phần tô đậm, kết quả làm tròn đến cm ( cho 𝜋𝜋 = 3,14).
Bài 6: (3 điểm). Từ điểm M ở ngoài đường tròn (O, R), vẽ 2 tiếp tuyến MA và MB (A, B là 2 tiếp
điểm) và cát tuyến MCD không đi qua tâm (C nằm giữa M và D, tia MO nằm giữa hai tia MO,
MA). Vẽ OI vuông góc CD (I ∈ CD).
a) Chứng minh tứ giác AOBM nội tiếp và 5 điểm M, A, O, B, I cùng thuộc một đường tròn.
b) Chứng minh MA.MB = MC . MD.
c) Từ C vẽ đường thẳng song song với MB cắt AB, DB lần lượt tại F và E. Gọi S là trung
điểm MB. Chứng minh AIFC là tứ giác nội tiếp và D, F, S thẳng hàng.
ĐÁP ÁN VÀ THANG ĐIỂM Bài Đáp án Điểm 1 2 x
2,0đ Cho hàm số y = Cho Parabol (P) : y =
và đường thẳng (D) : y = x + 3 4
a)Vẽ đồ thị (P) và (D) trên cùng một hệ trục tọa độ.
• Lập bảng giá trị và vẽ (P) 0,5
• Lập bảng giá trị và vẽ (D) 0,5
b)Tìm tọa độ giao điểm của (P) và (D) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (D): 1 𝑥𝑥2 = 𝑥𝑥 + 3 4 0,25 1
⇔ 4𝑥𝑥2 − 𝑥𝑥 − 3 = 0 0,25 ⇔ x = 6 hay x = −2 0,25
Vậy tọa độ giao điểm của (P) và (D) là: (-2; 1) và (6; 9) 0,25 2
Cho phương trình 3x2 + 5x - 6 = 0 có 2 nghiệm x1, x2 1,5đ a) S = x 0,25 1 + x2 = −𝑏𝑏= − 5 𝑎𝑎 3 0,25 P = x1.x2 =𝑐𝑐= -2 𝑎𝑎
b) Tính giá trị của biểu thức: A = (x 1-2)(x2-2) + x12 + x22 A = x 0,25 1x2 -2x1 -2x2 +4 + x12 + x22 = x 0,25
1x2 – 2( x1 + x2) + 4 + x12 + x22 = P – 2S +4 + S2 -2P 0,25 0,25 = 109 9 3
1,5đ Gọi x,y lần lượt là số câu trả lời đúng và số câu trả lời sai. (x,y ∈ N*)
Vì trả lời 20 câu hỏi nên ta có pt: 0,25 x + y = 20 (1)
Vì mỗi câu trả lời đúng được cộng 5 điểm và mỗi cẫu trả lời sai bị trừ 2
điểm và tổng số điểm là 51 nên ta có pt: 0,25 5x – 2y = 51 (2) Từ (1),(2) ta có hệ pt: � x + y = 20 5x – 2y = 51 0,5 �𝑥𝑥 = 13 𝑦𝑦 = 7 KL: 0,25 0,25 4 1,0 1,0đ
. Không gian mẫu Ω = {10 ; 11 ; 12 ; … ; 99}. 0,25
⇒ Số phần tử của không gian mẫu Ω là n(Ω) = 90.
* A: “Số được chọn là bình phương của một số tự nhiên”. 0,25
A = {16 ; 25 ; 36; … ; 81} (42 ; 52 ; … ; 92)
⇒ Số kết quả thuận lợi của biến cố A: n(A) = 6. n A
b) Xác suất của biến cố A: P( A) ( ) 6 1 = n( ) = = Ω 90 15 0,25
* B: “Số được chọn có tổng các chữ số chia hết cho 9”. 0,25
B = {18 ; 27 ; 36 ; … ; 99}.
⇒ Số kết quả thuận lợi của biến cố B: n(B) = 10. n B
Xác suất của biến cố B: P(B) ( ) 10 5 = n( ) = = Ω 90 45 5 1,0 1,0đ
• Diện tích hình tròn (A; AD) S 0,25
1= 𝜋𝜋. r2 = 25𝜋𝜋 (cm2) AC= 2.AD= 2.5=10 (cm) 0,25
• Diện tích hình tròn (A; AC) 0,25
S2 = 𝜋𝜋.R2 = 100𝜋𝜋 (cm2)
• Diện tích phần tô đậm
100𝜋𝜋 - 25𝜋𝜋 = 75𝜋𝜋 = 75.3,14 ≈ 236 (cm2) 0,25 6 3,0 3,0đ
a)Chứng minh tứ giác AOBM nội tiếp và 5 điểm M, A, O, B, I cùng thuộc một đường tròn.
• Chứng minh AOBM nội tiếp. 0,5
• Chứng minh 5 điểm M, A, O, B, I cùng thuộc một đường tròn. 0,5 b)Chứng minh MA.MB = MC MD. Chứng minh ∆MAC ~ ∆MDA. 0,5 Chứng minh MA.MB = MC . MD 0,5
c/ Từ C vẽ đường thẳng song song với MB cắt AB, DB lần lượt tại F và
E. Gọi S là trung điểm MB. Chứng minh AIFC là tứ giác nội tiếp và D, F, S thẳng hàng. 0,25 • Chứng minh F Cˆ I = I B Mˆ • Chứng minh I B Mˆ = IAˆF
• Chứng minh AIFC nội tiếp. 0,25 • Chứng minh IF // DB.
• Chứng minh F trung điểm EC 0,25 0,25
• Chứng minh minh D, F, S thẳng hàng. ỦY BAN NHÂN DÂN QUẬN 3
ĐỀ THAM KHẢO HỌC KỲ II
TRƯỜNG THCS PHAN SÀO NAM
NĂM HỌC: 2023 – 2024
Môn: TOÁN – LỚP 9
Thời gian làn bài: 90 phút
(Không kể thời gian phát đề)
Câu 1. (2,0 điểm) Giải phương trình a/ 2
7x −12x +5 = 0 b/ 4 2
5x – 7x + 2 = 0
Câu 2. (1,5 điểm): 2 x Cho hàm số y − =
có đồ thị là (P) và hàm số y = x − 4 có đồ thị là (d). 2
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 3. (1,5 điểm) Cho phương trình 6x2 + 6x – 13 = 0 có hai nghiệm là 𝑥𝑥1 và 𝑥𝑥2 .
a) Chứng tỏ phương trình luôn có hai nghiệm phân biệt x và x . 1 2
b) Không giải phương trình, tính giá trị của biểu thức x −1 x −1 1 2 A = + . x x 2 1
Câu 4. (0,75 điểm) Thư viện trường A có 2 kệ sách. Kệ thứ nhất có 120 quyển sách, kệ thứ hai
có 90 quyển. Để sắp xếp lại thư viện, cô phụ trách đã lấy ra ở kệ thứ nhất một số sách gấp 3 lần
số sách lấy ra ở kệ thứ hai, khi đó số sách còn lại trong kệ thứ hai gấp đôi số sách còn lại trong
kệ thứ nhất. Tính số sách còn lại ở mỗi kệ?
Câu 5. (0,5 điểm) Một xe chở xăng dầu, bên trên có chở một bồn chứa hình trụ chiều dài 2,6
mét và đường kính đáy là 1,4 mét. Theo tiêu chuẩn an toàn, thì bồn chỉ chứa tối đa 80% thể
tích khi xe di chuyển trên đường. Vậy bồn đó có thể chứa được nhiều nhất là bao nhiêu lít nhiên
liệu (làm tròn đến hàng đơn vị).
Câu 6. (0,75 điểm)
Bạn Hùng mua bánh liên hoan cuối niên học cho lớp. Tại cửa hàng bánh A giá bánh bạn
Hùng muốn mua là 15 000 đồng 1 cái bánh, nhưng nếu mua trên 10 cái bánh sẽ được của hàng bánh giảm 10% trên tổng số tiền mua bánh.
a) Nếu bạn Hùng mua 44 cái bánh nói trên ở cửa hàng bánh A thì phải trả bao nhiêu
tiền ? b) Tại cửa hàng B (gần cửa hàng A) bán cùng loại bánh nói trên (chất lượng như nhau)
đồng giá 15.000 đồng 1 cái bánh nhưng nếu mua 3 cái bánh chỉ phải trả 40 000 đồng. Bạn Hùng
mua 44 cái bánh nói trên ở cửa hàng nào để tổng số tiền phải trả ít hơn?
Câu 7. (3,0 điểm) Từ một điểm A nằm ngoài đường tròn tâm O, bán kính R (AO < 2R) vẽ hai
tiếp tuyến AD, AE với (O) (D, E là các tiếp điểm). Gọi H là giao điểm của DE và AO. Lấy
điểm M thuộc cung nhỏ DE (M khác D, khác E, MD < ME). Tia AM cắt đường tròn (O;R) tại
N. Đoạn thẳng AO cắt cung nhỏ DE tại K.
a) Chứng minh tứ giác ADOE nội tiếp và AO vuông góc với DE.
b) Chứng minh NK là tia phân giác của góc DNE và tứ giác MHON nội tiếp.
c) Kẻ đường kính KQ của đường tròn (O;R). Tia QN cắt tia ED tại C. Chứng minh MD.CE = ME.CD --- Hết --- ĐÁP ÁN Câu Nội dung Điểm 2
7x −12x +5 = 0 ( a = 7,b = 12 − ,c =15) 2 ∆ = b − 4ac = ( 12 − )2 − 4.7.5 = 4 > 0 a
Vì ∆ > 0 nên phương trình có hai nghiệm phân biệt: 0,5 (1,0 đ) b − + ∆ −( 12 − ) + 4 x = = = 1 1 2a 2.7 b − − ∆ −( 12 − ) − 4 5 x = = = 0,5 1 2a 2.7 7 4 2
5x – 7x + 2 = 0 (1) Đặt 2
x = t . Điều kiện: t ≥ 0. Ta được phương trình: 1 2
5t − 7t + 2 = 0 (2) (2.0 2 ∆ = b − 4ac đ) = ( 7 − )2 − 4.2.(5) = 9 > 0
Vì ∆ > 0 nên phương trình có hai nghiệm phân biệt: 0,25 b t =1 2 t = 2 (Nhận); 2 (Nhận). (1,0 đ) 5 0,25
Với t =1⇒ x =1; x = 1 − 1 2 0,25 2 10 10
Với t = ⇒ x = ;x = − 1 2 5 5 5 0,25
Vậy tập hợp nghiệm của phương trình (1) là: 10 − 10 S 1; 1; ; = − 5 5 a
Lập đúng bảng giá trị. 0,25x2
(1,0 đ) Vẽ đúng đồ thị hàm số (P) và (d) trên cùng một hệ trục tọa độ. 0,25x2 2 (1,5 0,25 2 −x đ) b
Viết pt hoành độ đúng: = x − 4 2 (0,5 đ)
Tìm đúng giao điểm (-4 ;-8) và (2 ;-2) 0,25
Chứng tỏ phương trình luôn có hai nghiệm phân biệt x và x 1 2 3
Ta có: a = 6 > 0,b = 3,c = 1 − 3 < 0 (1,5 a 0,25 đ) (0,5 đ)
Vì a và c trái dấu nên phương trình có hai nghiệm phân biệt x , x . 0,25 1 2 6x2 + 6x – 13 = 0
Theo hệ thức Vi-ét, ta có: b S = x + x − = = 1 − 1 2 a c 13 P x .x − = = = 0,25x2 1 2 a 6 b (1,0đ) Ta có: 2 2 x
−1 x −1 x − x + x − x 1 2 1 1 2 2 A = + = x x x x 2 1 1 2 2 13 − ( 1 − − 2. − 1 x x 2x x x x − + − − + 1 2 )2 1 2 ( 1 2) 2 ( ) ( )
S − 2P − S 6 38 − 0,25x2 = = = = x x P 13 − 13 1 2 6
Gọi x,y( quyển) lần lượt là số sách còn lại ở kệ thứ nhất và kệ 4 thứ hai(x, y ∈ N*)
Lý luận đưa đến hệ phương trình: 0,25 (0,7 5 đ) (0,75 −x + 3y = 150 0,25x2 đ) 2x − y = 0
⇔ x = 30, y = 60 (thỏa điều kiện) 0,25
Vậy số sách còn lại ở kệ thứ nhất và thứ hai lần lượt là 30 quyển và 60 quyển. 5 0,5 đ Thể tích của bồn chứa tối đa là: (0,5 2 1,4 đ) V 80%V 80% π 2 . .R .h π = = = 80% . tru .2,6 0,25 2 ≈ 3,2( 3
m ) ≈ 3200(lit) 0,25
Hùng mua trên 10 cái nên được giảm 10% trên tổng tiền mua 6 bánh (0,7
a. Số tiền Hùng phải trả khi mua 44 cái bánh: 5 đ) (0,75 đ)
44.15000.( 1 -10%) = 594000 đồng
b. Nếu mua ở cửa hàng B thì: 44: 3 = 14 dư 2
Do 3 cái chỉ trả 40 000 đồng nên số tiền Hùng phải trả:
14.40 000 + 2.15000 = 590 000 đồng
Vì 590 000 đồng < 594 000 đồng nên nếu mua 44 cái thì Hùng
mua ở cửa hàng B có lợi hơn C 7 (3,0 đ) N D M A Q K H O E
a) Chứng minh tứ giác ADOE nội tiếp và AO ⊥ DE Ta có : 0
ADO = 90 (AD là tiếp tuyến của (O)) 0
AEO = 90 (AE là tiếp tuyến của (O)) 0,25 a ⇒ + 0
ADO AEO =180 (kề bù với DMC )
(1,0 đ) ⇒ Tứ giác ADOE nội tiếp. 0,25
+ C/m đúng AO là đường trung trực của đoạn DE. 0,25
=> OA ⊥ DE tại H và H là trung điểm của DE. 0,25
b) Chứng minh NK là tia phân giác của góc DNE và tứ giác MHON nội tiếp. Ta có: 1 0,25 = 1 = DNK DOK; ENK EOK 2 2 b (1,0 đ) Mà =
DOK EOK (tính chất 2 tiếp tuyến cắt nhau)
+ Kết luận đúng NK là phân giác của góc DNE 0,25 + C/m đúng AH ∆ M đồng dạng AN ∆ O (c-g-c) 0,25 => góc AHM = góc ANO
=> Tg MHON nội tiếp (góc ngoài bằng góc đối trong) 0,25
c) Chứng minh MD.CE = ME.CD MD AM Chứng minh AD ∆ M đồng dạng AN ∆ D=> = (1) 0,25 c ND AD (1,0 đ) ME AM Tương tự AM ∆ E đồng dạng AE ∆ N => = (2) NE AE Mà AD = AE (3) 0,25 MD ND Từ (1), (2) và (3) => = (4) ME NE
Mặt khác, ta có: góc QNK = 900 (góc nt chắn nửa đường tròn (O)) => CN⊥ NK 0,5
Mà NK là phân giác trong góc DNE của tam giác DNE
=> CN là phân giác ngoài tại đỉnh N của tam giác DNE => CD ND = (5) CE NE Từ (4) và (5) => MD CD = ⇒ MD.CE = ME.CD (đpcm) ME CE
MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II MÔN TOÁN - LỚP 9
Mức độ đánh giá TT Chủ đề
Nội dung/Đơn vị kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao Tổng % TNK điểm Q TL TNK Q TL TN KQ TL TNK Q TL 1 Phương trình
Nhận biết, giải phương trình bậc hai 1 10 bậc hai
Phương trình quy về pt bậc hai 1 ẩn 1 10 2 Hàm số
Vẽ đồ thị hàm số 1 10
Tìm tọa độ giao điểm của (P) và (d) 1 5 3 Hệ thức Vi et
Chứng tỏ phương trình có nghiệm 1 5 và ứng dụng
Tính giá trị biểu thức cho trước 1 10
Giải bài toán bằng cách lập phương trình, hệ phương trình 1 7.5 4 Bài toán thực
Ứng dụng hình không gian để giải các bài toán tế thực tế 1 5
Bài toán thực tế về tăng giảm, phần trăm, tính
tiền hoặc suy luận 1 7.5
Các loại góc trong đường tròn 5 Đường tròn
Tứ giác nội tiếp 1 10
Chứng minh các yếu tố bằng nhau, trung điểm,
hệ thức, vuông góc, song song. 1 1 20 5 Tổng 2 6 3 1 Tỉ lệ % 20% 45% 25% 10%
BẢNG ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ II MÔN TOÁN - LỚP 9
Số câu hỏi theo mức độ nhận thức TT Chủ đề
Mức độ đánh giá Nhận Thông Vận Vận dụng cao biết hiểu dụng
Nhận biết, giải phương Nhận biết: 1
trình bậc hai
Giải được phương trình bậc hai một ẩn 1 Phương
trình bậc hai Phương trình quy về pt Thông hiểu: 1
bậc hai 1 ẩn
Giải được các phương trình có thể quy về
phương trình bậc hai một ẩn Nhận biết: 1
Vẽ đồ thị hàm số
Vẽ được đồ thị của hàm số y = ax2 (a khác 0) 2 Hàm số Thông hiểu: 1
Tìm tọa độ giao điểm của Áp dụng phương trình hoành độ giao điểm (P) và (d)
và giải phương trình bậc hai để tìm tọa độ giao điểm Thông hiểu: 1
Chứng tỏ phương trình có nghiệm
Sử dụng hệ thức để chứng minh phương Hệ thức Vi trình có nghiệm 3 et và ứng Thông hiểu: 1 dụng
Tính giá trị biểu thức cho Ứng dụng được hệ thức để tính nhẩm, trước
tìm ẩn và tính giá trị biểu thức mà không cần giải phương trình Vận dụng: 1
Biết cách lập luận, sử dụng giả thiết để đưa
Giải bài toán bằng cách bài toán về dạng phương trình hoặc hệ 4 Bài toán thực tế
lập phương trình, hệ phương trình
phương trình bậc nhất hai ẩn… Áp dụng
phương trình, hệ phương trình để giải bài toán
Ứng dụng hình không Thông hiểu: 1
gian để giải các bài toán Sử dụng các khái niệm, công thức liên thực tế quan để giải bài toán.
Bài toán thực tế về tăng Vận dụng: 1
giảm, phần trăm, tính
Sử dụng kĩ năng phân tích, tính toán, công
tiền hoặc suy luận
thức .. để suy luận, giải bài toán Nhận biết: Các loại góc trong đường tròn
Nhận biết được các loại góc và áp dụng tính
chất, định lý để giải ra giá trị của góc Thông hiểu: 1
Tứ giác nội tiếp
Sử dụng các định lý, định nghĩa, tính chất, hệ
quả để chứng mình đường tròn ngoại tiếp, 5 Đường tròn nội tiếp Vận dụng: 1
Chứng minh các yếu tố
Chứng minh hệ thức, vuông góc, song song
bằng nhau, trung điểm,
hệ thức, vuông góc, song Vận dụng cao: song.
Chứng minh trung điểm, thẳng hàng, diện 1 tích..
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN 3
ĐỀ KIỂM TRA CUỐI HỌC KỲ II
TRƯỜNG TH VÀ THCS TÂY ÚC
NĂM HỌC: 2023– 2024 ĐỀ THAM KHẢO MÔN: TOÁN - KHỐI 9 (Đề có 02 trang)
Thời gian làm bài: 90 phút
(Không kể thời gian phát đề)
Câu 1. (2 điểm) Giải các phương trình sau: 2 a) x + 3x − 4 = 0 4 2 b) x − 2x −8 = 0 2
Câu 2. (1,5 điểm) Cho hàm số x y = −
có đồ thị là (P) và hàm số 3
y = x − 2 có đồ thị là (d). 2 2
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục Oxy.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép toán.
Câu 3. (1,5 điểm) Cho phương trình 2 3x −5x − 4 = 0
a) Chứng tỏ phương trình có 2 nghiệm x ;x . 1 2
b) Không giải phương trình hãy tính giá trị biểu thức : x +1 x +1 1 2 A = + x x 2 1
Câu 4. (0,75 điểm) Hai lớp 9A và 9B cùng tham gia quyên góp tiền giúp các bạn học sinh có
hoàn cảnh khó khăn mua thiết bị học tập. Trung bình một học sinh lớp 9A góp 18 000 đồng,
một học sinh lớp 9B góp 20 000 đồng. Hỏi mỗi lớp có bao nhiêu học sinh, biết rằng cả hai
lớp có 85 học sinh và tổng số tiền góp được là 1 610 000 đồng?
Câu 5. (0,5 điểm) Có một bình thủy tinh hình trụ phía
bên trong có đường kính đáy là 30cm, chiều cao 20cm,
đựng một nửa bình nước và một khối thủy tinh hình trụ
có bán kính đáy là 14cm, chiều cao là 11cm.
(Cho thể tích hình trụ tính theo công thức: 2 V = πR h
với R là bán kính đáy, h là chiều cao của hình trụ).
a) Tính thể tích khối thủy tinh (làm tròn đến chữ
số thập phân thứ nhất).
b) Hỏi nếu bỏ lọt khối thủy tinh vào bình thủy
tinh thì lượng nước trong bình có bị tràn ra
ngoài hay không? Tại sao?
Câu 6. (0,75 điểm) Sau buổi sinh hoạt ngoại khóa , nhóm bạn của Lan rủ nhau đi uống trà sữa ở một
quán gần trường. Mỗi ly trà sữa đồng giá 15 000 đồng. Do quán mới khai trương nên có chương trình
khuyến mãi giảm giá 20% cho mỗi ly trà sữa. Biết rằng tổng số tiền phải trả cho quán là 120 000 đồng.
a) Hỏi số tiền mua trà sữa của nhóm bạn của Lan lúc chưa giảm giá là bao nhiêu?
b) Hỏi nhóm bạn của Lan đã mua bao nhiêu ly trà sữa?
Câu 7. (3,0 điểm) Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua M kẻ tiếp tuyến
MA và cát tuyến MBC với đường tròn (O) (A là tiếp điểm, B nằm giữa M và C, điểm O nằm trong góc
CMA). Kẻ OI vuông góc BC (I thuộc BC).
a) Chứng minh MAOI là tứ giác nội tiếp. b) Chứng minh CA NC = . CB NB
c) Đường thẳng qua A và vuông góc với đường thẳng MO cắt đường thẳng OI tại K. Chứng minh
KB là tiếp tuyến của đường tròn (O).
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . SBD:. . . . . . . . . .Phòng thi:. . . . . . . . .
Cán bộ coi kiểm tra không giải thích gì thêm về đề - Học sinh không được sử dụng tài liệu.
--------------------Hết-------------------
ĐÁP ÁN VÀ BIỂU ĐIỂM CHẤM Câu Đáp án Điểm Câu 1 2 a) x + 3x − 4 = 0 (2 điểm) Ta có : 1 + 3 + (- 4) = 0 0,5×2 4 x 1; x − = = = 4 − 1 2 1 4 2 b) x − 2x −8 = 0 (*) Đặt 2 t = x (t ≥ 0) (*) 2 ⇔ t − 2t −8 = 0
Phương trình có hai nghiệm phân biệt −( 2) − + 36 t = = 4 (nhận) 0,5×2 1 2.1 −( 2) − − 36 t = = 2 − (loại) 2 2.1 Với t = 4 thì 2 x = 4 ⇔ x = 2 ± Vậy S = {± } 2 Câu 2 a) Bảng giá trị (1,5 điểm) x -2 -1 0 1 2 2 x -2 1 y = − − 0 1 − -2 2 2 2 x 0 2 3 y = x − 2 - 2 1 2 0,25×4
b) Xét phương trình hoành độ giao điểm: 2 x 3 − = x − 2 2 2 2 x 3 ⇔ − − x + 2 = 0 2 2 1 0,25×2 x =1⇒ y = − ⇔ 2 x = 4 − ⇒ y = 8 −
Vậy giao điểm cần tìm là 1 1;− và ( 4; − 8 − ) 2 Câu 3. (1,5 a) 2 3x −5x − 4 = 0 điểm) ∆ = (− )2 5 − 4.3.( 4 − ) = 73 > 0 0,5
⇒ Phương trình luôn có 2 nghiệm phân biệt.
b) Với x1; x2 là 2 nghiệm của phương trình, theo Vi-et, có: b −( 5) − 5 S = x + x = − = = 1 2 a 3 3 c 4 P = x .x − = = 1 2 a 3 x +1 x +1 1 2 A = + x x 2 1 (x +1 x x +1 x 1 ) 1 ( 2 ) 2 A = + x x x x 0,25×4 1 2 1 2 2 2 x + x + x + x 1 1 2 2 A = x x 1 2 (x + x )2 − 2x x + x + x 1 2 1 2 ( 1 2) A = x x 1 2 2 5 4 − 5 − 2. + 3 3 3 17 A − = 4 = − 6 3 Câu 4.
Gọi x, y lần lượt là số học sinh lớp 9A và 9B (0,75 điểm) x + y = 85 Theo đề ta có: 18
000.x + 20 000.y = 1 610 000 0,25×3 x = 45
Giải hệ phương trình, nhận được giá trị: y = 40
Vậy số học sinh lớp 9A là 45 học sinh, số học sinh lớp 9B là 40 học sinh. Câu 5.
a) Thể tích khối thủy tinh là: (0,5 điểm) 2 π.14 .11 0,25×2 = 2156π
b) Thể tích bình thủy tinh là: 2 30 π. .20 = 4500π 2 Vì 1
2156π < .4500π nên khi bỏ lọt khối thủy tinh vào bình thủy 2
tinh thì lượng nước trong bình không bị tràn ra. Câu 6.
a) Số tiền mua trà sữa của nhóm bạn của Lan lúc chưa giảm giá là: (0,75 điểm)
120 000 : (100% - 20%) = 150 000 (đồng)
b) Số ly trà sữa mà nhóm bạn của Lan đã mua là: 0,25×3 150 000 : 15 000 = 10 (ly) âu 7. (3,0 điểm) 0,5×2
a) Chứng minh MAOI là tứ giác nội tiếp.
Vì MA là tiếp tuyến của (O) tại A => 0 OAM = 90 Tứ giác MAOI có + 0 0 0 OAM OIM = 90 + 90 =180
=> MAOI là tứ giác nội tiếp. b) Chứng minh CA NC = CB NB
Xét ∆ MBA và ∆ MAC có: M chung và = MAB MCA (cùng chắn AB ) 0,5×2
=> ∆ MBA ∆ MAC (g – g) => AB MA = AC MC
c) Chứng minh KB là tiếp tuyến của đường tròn Ta có: AMO = AIO (cùng chắn AO ) AMO = KAO (cùng phụ AOM ) => AIO = KAO 0,25×4
Xét ∆ OIA và ∆ OAK , ta có: AIO = KAO và AOK là góc chung.
=> ∆ OIA ∆ OAK (g-g) => OA2 = OI.OK
=> OB2 = OI . OK => ∆ OIB ∆ OBK (c-g-c) => = 0
OBK OIB = 90 => KB là tiếp tuyến của đường tròn (O).
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN 3
ĐỀ THAM KHẢO CUỐI KỲ II
TRƯỜNG THCS BÀN CỜ NĂM HỌC 2023 - 2024
Môn: TOÁN– KHỐI 9
Thời gian làm bài: 90 phút (Không kể thời g ian phát đề)
Câu 1. (2,0 điểm ) Giải phương trình : a) 2
2x 5x 3 0 b) 4 2
3x 12x 9 0
Câu 2. (1,5 điểm ) Cho 𝑦𝑦 = 𝑥𝑥2 (𝑃𝑃) và y = -x +2
a) Vẽ đồ thị (P) và (d ) trên cùng một mặt phẳng tọa độ Oxy .
b) Tìm tọa độ giao điểm của (P) và (d ) bằng phép toán.
Câu 3. (1,5 điểm) Cho phương trình: 2
2x 13x 6 0
a) Chứng tỏ phương trình có hai nghiệm phân biệt x1 ; x2 rồi tính tổng và tích hai nghiệm.
b) Không giải phương trình hãy tính giá trị của biểu thức sau:
A x x 2 4x x 1 2 1 2
Câu 4. (0.75 điểm) Một bạn học sinh A có ý định tiết kiệm để mua một chiếc xe
đạp có giá 2 100 000 đồng. Hiện nay bạn đã tiết kiệm được 600 000 đồng. Mỗi
ngày bạn học sinh A có thể tiết kiệm được 15 000 đồng. Gọi y (đồng) là số tiền bạn
học sinh tiết kiệm được sau x (ngày).
a/ Hãy lập công thức hàm số của y theo biến số x.
b/ Sau bao nhiêu ngày kể từ ngày bắt đầu tiết kiệm, thì bạn học sinh có thể mua được chiếc xe đạp.
Câu 5. (0.5 điểm) Hôm qua mẹ của bạn Minh đến tiệm tạp hóa gần nhà mua 20
quả trứng gồm 10 quả trứng gà và 10 quả trứng vịt hết 45 000 đồng. Hôm nay mẹ
của bạn Minh cũng đến tiệm tạp hóa gần nhà mua 20 quả trứng gồm 15 quả trứng
gà và 5 quả trứng vịt chỉ hết 42 500 đồng mà giá trứng thì vẫn như cũ. Hỏi nếu
ngày mai mẹ bạn Minh nhờ bạn Minh qua tiệm tạp hóa trên mua 30 quả trứng gồm
20 quả trứng gà và 10 quả trứng vịt thì mẹ bạn Minh phải đưa cho bạn Minh số tiền
vừa đủ là bao nhiêu biết giá trứng không thay đổi?
Câu 6. (0.75 điểm). Một bình chứa nước hình hộp chữ nhật có diện tích đáy là
20dm2 và chiều cao 3dm. Người ta rót hết nước trong bình ra những chai nhỏ mỗi
chai có thể tích là 0,35dm3 được tất cả 72 chai. Hỏi lượng nước có trong bình
chiếm bao nhiêu phần trăm thể tích bình?
Câu 7. (3 điểm) Từ điểm A ở ngoài đường tròn (O;R) vẽ hai tiếp tuyến AB và AC
của (O) (với B và C là hai tiếp điểm).
a) Chứng minh: AO vuông góc với BC tại H.
b) Vẽ đường kính CD của (O); AD cắt (O) tại M (M không trùng D). Chứng
minh: Tứ giác AMHC nội tiếp.
c) BM cắt AO tại N. Chứng minh: N là trung điểm của AH. ------ HẾT ------
Học sinh không được sử dụng tài liệu.
Giám thị không giải thích gì thêm. HƯỚNG DẪN CHẤM CÂU NỘI DUNG ĐIỂM a/ 49 0.25 1 x 3 ;x 0.25x2 1 1 2 Vậy 1 0.25 S 3 ; 2 1 b/ 4 2
3x 12x 9 0 (2,0 điểm) Đặt 2
x t 0 2
3t 12t 9 0 0.25
t 3 ( nhận) hay t 1(nhận)
t 3 hay t 1 0.25x2 Vậy S 3; 1 0.25
a/Lập BGT và vẽ đúng (P) và (D ) 0.25x4
b/ Phương trình hoành độ giao điểm : 2x = −x + 2 2 0.25 ⇔ 2 x + x − 2 = 0 (1.5 điểm) x = 1 ⇔ x = − 2 Thay x = 1 vào = 2
y x , ta được: y = 2 1 = 1. Thay x = −2 vào 2
y = −x , ta được: y = (− )2 2 = 4 . Vậy : ( 0.25
1; 1) , (−2; 4) là hai giao điểm cần tìm.
a/ Ta có : a = 2 ; c = 6 => a,c trái dấu 0.25 x2
=> phương trình có hai nghiệm phân biệt x1 ; x2. b 13 S
x x 0.25x2 b/ 1 2 a 2 c 3 P x .x 3 1 2 a (1.5 điểm)
A x x 2 4x x 1 2 1 2 2 0.25 13 A 4.(3) 2 217 0.25 A . 4
a/ Công thức hàm số y = 15 000.x + 600 000 0.25 Câu 4 (0.75
b/ Theo đề ta có 15 000.x + 600 000 = 2 100 000 ⇒ x = 100 0.25x2 điểm)
Gọi x; y (đồng) lần lượt là số tiền của 1 quả trứng gà, 1 quả trứng vịt (x>0; y>0) Câu 5 0.25
(0.5 điểm) Ta có hệ pt: �10𝑥𝑥 + 10𝑦𝑦 = 45000
15𝑥𝑥 + 5𝑦𝑦 = 42500 ⟺ �𝑥𝑥 = 2000 𝑦𝑦 = 2500
Số tiền mẹ bạn Minh cần đưa vừa đủ cho bạn Minh là:
20.2000 + 10.2500 = 65000 (đồng) 0.25
Thể tích của lượng nước trong 72 chai nhỏ: 0,35.72 = 25,2 dm3 0,25 Câu 6 0,25 (0.75
Thể tích của bình hình hộp chữ nhật: 20 . 3 = 60 dm3 điểm) 0.25
Thể tích nước trong bình chiếm: 25,2 : 60 = 42% thể tích bình
a) Chứng minh: AO vuông góc với BC tại H. Ta có:
+) AB = AC (tính chất hai tiếp tuyến cắt nhau) 0.5 +) OB = OC = R
⇒ OA là đường trung trực của đoạn BC
⇒ AO vuông góc với BC tại H. 0.5
b) Vẽ đường kính CD của (O); AD cắt (O) tại M (M không trùng D). Chứng
minh: Tứ giác AMHC nội tiếp. Ta có:
DMC = 90° (góc nội tiếp chắn nửa đường tròn đường kính 0.5 DC) ⇒ CMA = 90°
Xét tứ giác AMHC ta có: = CMA CHA = 90° 0.5
⇒ Tứ giác AMHC nội tiếp (hai đỉnh liên tiếp cùng nhìn một cạnh dưới hai góc bằng nhau) Câu 7
c) BM cắt AO tại N. Chứng minh: N là trung điểm của AH. (3.0 điểm) Ta có: =
ABN BCM (góc tạo bởi tiếp tuyến và dây với góc nội tiếp cùng chắn cung BM)
Lại có: Tứ giác AMHC nội tiếp (cmt) nên =
BCM MAN (hai góc
nội tiếp cùng chắn cung HM) Suy ra = ABN MAN Xét A ∆ BN và MA ∆ N , có: +) N chung +) = ABN MAN (cmt) ⇒ A ∆ BN ∽ M
∆ AN(g − g) AN BN 2 ⇒ =
⇒ AN = MN.BN(1) MN AN Ta có:
+) Tứ giác AMHC nội tiếp suy ra =
MHN MCA (hai góc nội tiếp cùng chắn cung AM) +) =
MCA CDM (góc tạo bởi tiếp tuyến và dây với góc nội tiếp cùng chắn cung MC) +) =
CDM HBN (hai góc nội tiếp cùng chắn cung MC) Suy ra = MHN HBN Xét MH ∆ N và HB ∆ N , ta có: +) N chung +) = MHN HBN ⇒ M ∆ HN ∽ HB ∆
N(g − g) HN MN 2 ⇒ =
⇒ HN = MN.BN(2) BN HN
Từ (1) và (2) suy ra AN = HN ⇒ N là trung điểm của AH. 0.5 x2 D B M O H N A C ------ HẾT ------
ỦY BAN NHÂN DÂN QUẬN 3
ĐỀ THAM KHẢO KIỂM TRA HỌC KÌ 2
TRƯỜNG THCS KIẾN THIẾT NĂM HỌC 2023 - 2024 MÔN THI: TOÁN ĐỀ THAM KHẢO KHỐI 9
Thời gian: 90 phút. (không kể thời gian phát đề)
Bài 1. (1,5 điểm) 2 Cho parabol (P): x y =
và đường thẳng (d): y = −x + 4 2
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Bài 2. (1 điểm)
Cho phương trình : 2x2 −5x – 1 = 0 có hai nghiệm là x1, x2 .
Không giải phương trình, hãy tính giá trị của biểu thức 1 1 A = + 2 2 x x 1 2
Bài 3.(1 điểm)
Bảng cước phí dịch vụ VinaCard áp dụng cho thuê bao trả trước, cước gọi liên mạng trong
nước (đã bao gồm VAT) quy định rằng : nếu gọi trong 6 giây đầu thì tính cước 138 đồng/6
giây đầu, còn kể từ sau giây thứ 6 trở đi, họ tính thêm 23 đồng cho mỗi giây.
a) Gọi y là số tiền phải trả (tính bằng đồng) và t là thời gian gọi nhiều hơn 6 giây
(t > 6). Hãy lập công thức biểu thị y theo t ?
b) Hỏi bạn An gọi trong bao lâu mà bạn trả 3450 đồng ?
Bài 4. (1 điểm)
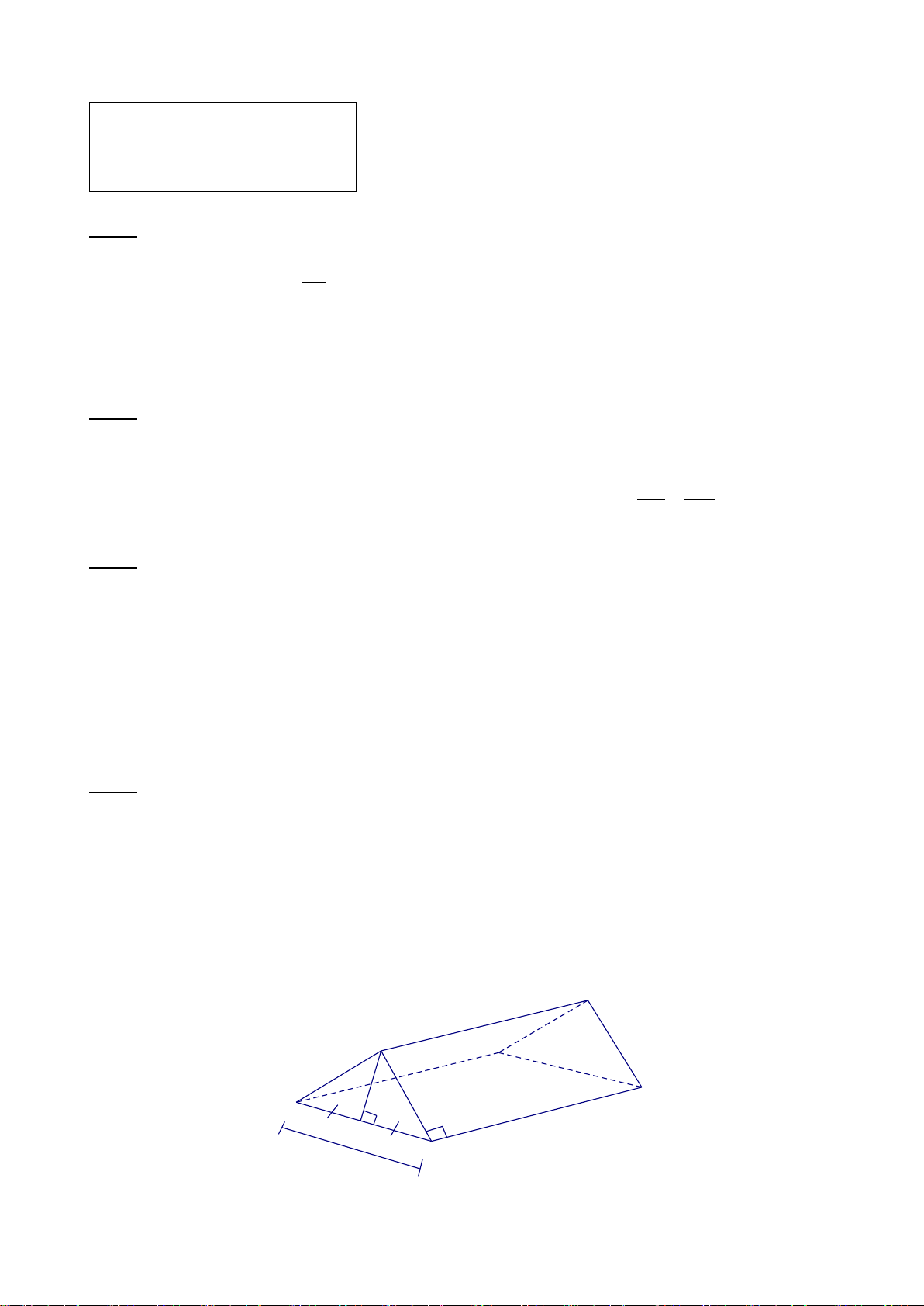
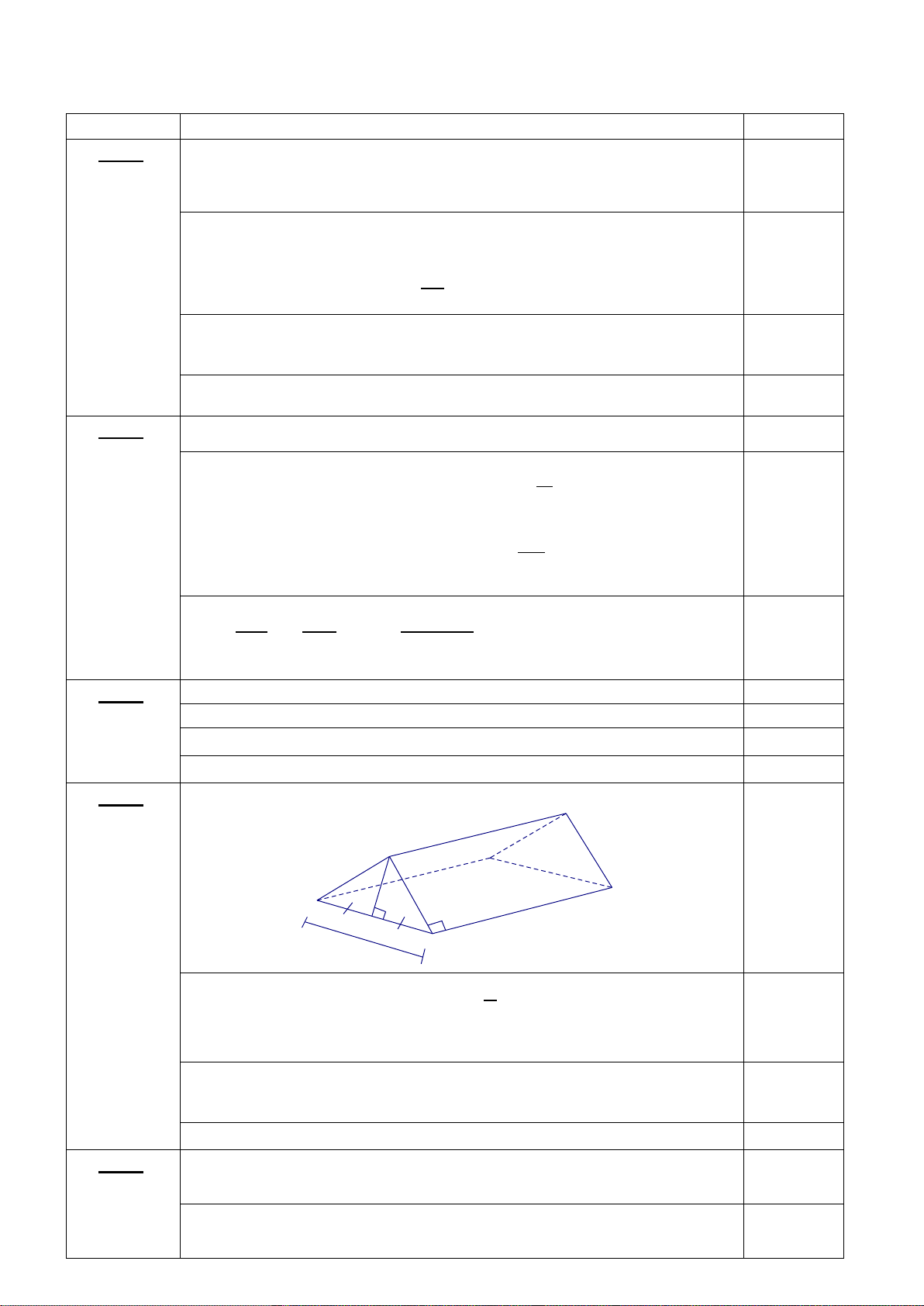
Một cái lều ở trại hè có dạng lăng trụ đứng tam giác (với các kích thước trên hình : AH =1,2m ; BC=3,2m ; CC’=5m).
a) Tính thể tích khoảng không ở bên trong lều.
b) Cần phải có ít nhất bao nhiêu m2 vải bạt để dựng lều đó ?(Không tính các mép và nếp gấp của lều) A' A B' 1,2m C' B 5m H 3,2m C
Bài 5.(1 điểm)
Một cửa hàng điện máy niêm yết giá bán chiếc tivi Smart Samsung 43 inch cao hơn 40%
so với giá nhập vào. Nhân dịp khuyến mãi, cửa hàng đã giảm giá 15% trên giá niêm yết.
Lúc đó, chiếc tivi bán ra lời được 1,9 triệu đồng so với giá nhập vào. Hỏi giá nhập vào của
chiếc tivi đó là bao nhiêu? Bài 6.
(1 điểm)
Một sợi xích có ba vòng tròn kết nối dài 10 cm, có năm
vòng tròn kết nối dài 16 cm. Hỏi sợi xích đó có 15 vòng
tròn kết nối thì dài bao nhiêu ? Bài 7.(1 điểm)
Ở một trường Trung học cơ sở, tuổi trung bình của các giáo viên nữ trong trường là 36,
tuổi trung bình của các giáo viên nam trong trường là 40. Tính tuổi trung bình của các giáo
viên nam và các giáo viên nữ biết rằng số giáo viên nữ gấp ba lần số giáo viên nam ?
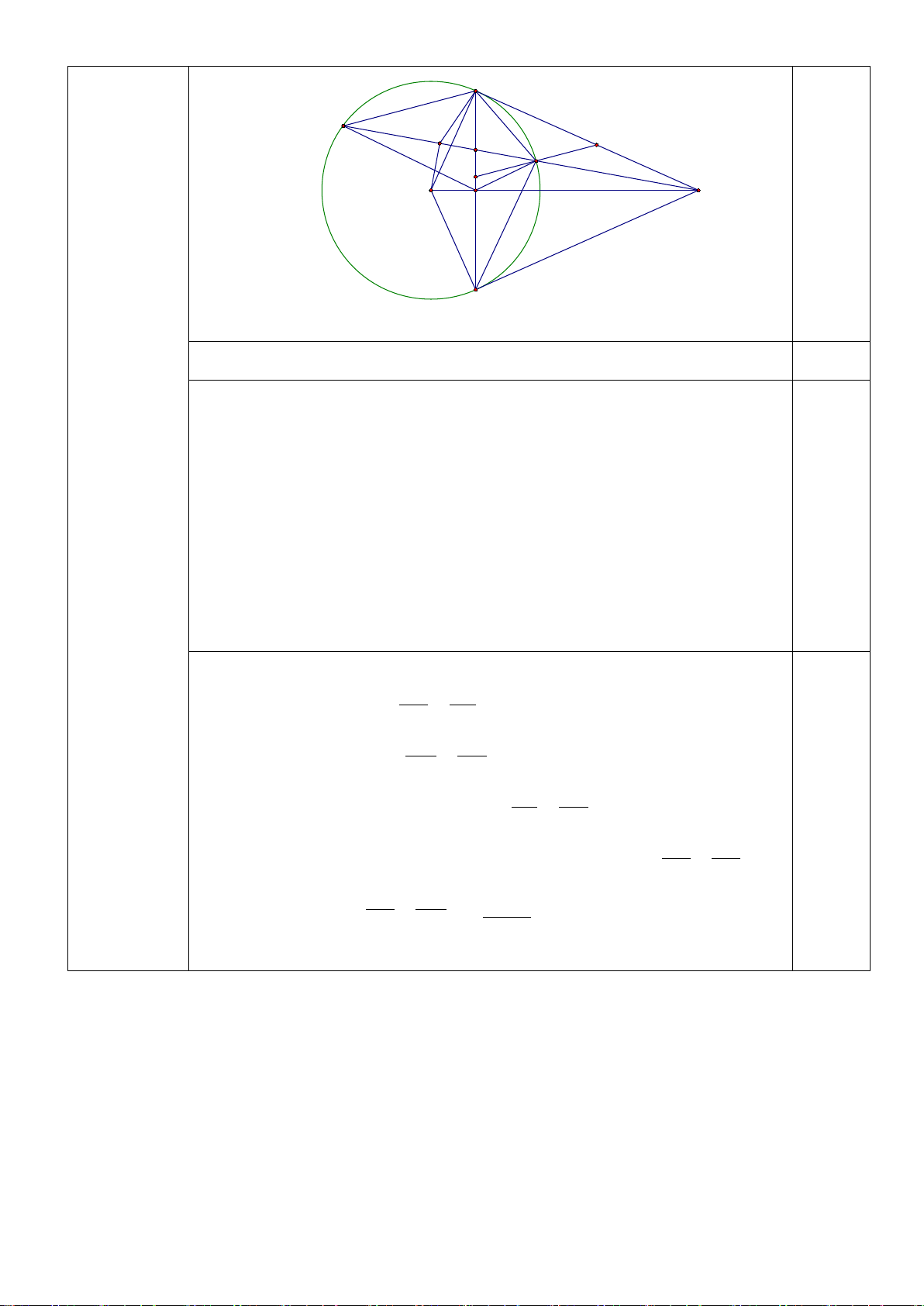
Bài 8.(2,5 điểm) Cho tam giác ABC nhọn (AB > AC), nội tiếp đường tròn (O; R). Các
tiếp tuyến tại B và C cắt nhau tại M. Gọi H là giao điểm của OM và BC. Từ M kẻ đường
thẳng song song với AC, đường thẳng này cắt (O) tại E và F (E thuộc cung nhỏ BC), cắt BC tại I, cắt AB tại K.
a/ Chứng minh: MO ⊥ BC và ME.MF = MH.MO.
b/ Chứng minh rằng tứ giác MBKC là tứ giác nội tiếp. Từ đó suy ra năm điểm M,
B, K, O, C cùng thuộc một đường tròn.
c/ Đường thẳng OK cắt (O) tại N và P (N thuộc cung nhỏ AC). Đường thẳng PI cắt
(O) tại Q (Q khác P). Chứng minh ba điểm M, N, Q thẳng hàng. ---HẾT---
ĐÁP ÁN ĐỀ THI THAM KHẢO HK2 _ NĂM HỌC 2023-2024 ---oOo--- BÀI HƯỚNG DẪN CHẤM ĐIỂM Bài 1. a) (1,5 điểm) • Vẽ (P) 0,5đ • Vẽ (d) 0,25đ b)
Phương trình hoành độ giao điểm của (P) và (d): 2 x 0,25đ = −x + 4 22 ⇔ x + 2x − 8 = 0 0,25đ ⇔ x = 2;x = 4 − 1 2
Suy ra tọa độ giao điểm của (P) và (d) là (2 ; 2) và ( 4 − ; 8) 0,25đ Bài 2. 2x2 −5x – 1 = 0 (1 điểm) 5 S = x + x = 1 2 2
Theo định lý Vi-et ta có: 1 0,25đx2 P x .x − = = 1 2 2 2 1 1 S − 2P A = + = ... = = 29 2 2 2 x x P 0,5đ 1 2 Bài 3. a) y = 23(t − 6)+138 0,5đ
(1 điểm) b) y = 23t ⇒ 3450 = 23t ⇒ t =150 0,25đ
Vậy bạn An đã gọi trong 150 giây 0,25đ Bài 4. (1 điểm) A' A B' 1,2m C' B 5m H C 3,2m
a) Diện tích đáy (tam giác): 1 2 S = .3,2.1,2 =1,92m 2 0,25đx2
Thể tích khoảng không ở bên trong lều 3 V = S.h =1,92.5 = 9,6m b) Tính được AC = 2m
Số m2 vải bạt ít nhất cần có : 2 2(1,92 + 2.5) = 23,84m 0,25đx2 Bài 5.
Gọi giá tiền nhập vào của chiếc tivi là x (triệu đồng) (x>0)
(1 điểm) Giá niêm yết của chiếc tivi là 1,4x (triệu đồng) 0,25đ
Giá bán ra sau khi giảm 15% là :1,4x.(1 − 15%) = 1,19x (triệu đồng) 0,25đ
Ta có : 1,19x = x + 1,9⇒ x =10 0,25đ
Vậy giá nhập vào của chiếc tivi đó là 10 triệu đồng 0,25đ Bài 6.
Gọi x là đường kính của một vòng tròn và y là khoảng cách kết nối
(1 điểm) giữa hai vòng tròn (x>0;y>0) 0,5đ
Ta có hệ phương trình: {3x −2y=10 5x − 4y=16
Giải hệ phương trình ta được x = 4 ; y = 1 0,25đ
Sợi xích có 15 vòng kết nối dài 15.4 −14.1 = 46cm 0,25đ Bài 7.
Gọi số giáo viên nam là x, số giáo viên nữ là 3x (x nguyên dương)
(1 điểm) Gọi y là số tuổi trung bình của GV nam và GV nữ 0,25đ
Ta có : 40x + 36.3x = y(x +3x)
⇒ 148x = 4xy ⇒ y = 37 0,5đ
Vậy tuổi trung bình của GV nam và GV nữ là 37 0,25đ Bài 8. (2,5
điểm) a) OM là đường trung trực của BC ⟹ OM ⊥ BC tại H.(0,5đ)
C/m được ME.MF = MB2(0,25đ) C/m được MH.MO = MB2
⟹ 𝑀𝑀𝑀𝑀. 𝑀𝑀𝑀𝑀 = 𝑀𝑀𝑀𝑀. 𝑀𝑀𝑀𝑀 (0,25đ) b) 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝐵𝐵𝐵𝐵
� (vì MF // AC); 𝑀𝑀𝐵𝐵𝑀𝑀 � = 𝑀𝑀𝐵𝐵𝐵𝐵
� (vì cùng chắn cung BC) ⟹ 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝐵𝐵𝑀𝑀 � (0,25đ)
⟹ Tứ giác MBKC nội tiếp.(0,25đ)
C/m tứ giác MBOC nội tiếp.(0,25đ)
⟹ M, B, K, O, C cùng thuộc một đường tròn. (0,25đ)
c) C/m: IM. IK = IB. IC; IP. IQ = IB. IC ⟹ IM. IK = IP. IQ
⟹ tứ giác MQKP nội tiếp ⟹ MQP � = MKP �(0,25đ) Lại có: MKP � = MKO � = MBO
� = 900 ⟹ 𝑀𝑀𝑀𝑀𝑀𝑀 � = 900 Mà: NQP � = 900 ⟹ NQM
� = 1800 ⟹ N, Q, M thẳng hàng.(0,25đ) ---HẾT---
ĐỀ THAM KHẢO KIỂM TRA HỌC KỲ 2 MÔN: TOÁN 9
Câu 1. (2 điểm) Giải các phương trình sau: a) 2
−x + x +12 = 0 b) 4 2
x −11x +18 = 0
Câu 2. (1,5 điểm) Cho parabol 2
(P) : y = − x và đường thẳng (d) : y = 2x − 3
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (d) và (P) bằng phép tính.
Câu 3. (1,5 điểm) Cho phương trình: 2 3x + 6x −1= 0.
a) Không giải phương trình, chứng tỏ phương trình có hai nghiệm x1 ; x2.
b) Không giải phương trình, hãy tính giá trị của biểu thức: 3 3 A = x + x . 1 2
Câu 4. (0,75 điểm) Bác Phong có 500 triệu đồng, bác dùng một phần số tiền
này để gửi ngân hàng với lãi suất 7% một năm. Phần còn lại, bác đầu tư vào nhà
hàng của một người bạn để nhận lãi kinh doanh. Sau 1 năm, bác thu về số tiền
cả vốn và lãi từ cả hai nguồn trên là 574 triệu đồng. Biết rằng tiền lãi kinh
doanh nhà hàng bằng 20% số tiền đầu tư. Hỏi bác Phong đã sử dụng bao nhiêu
tiền cho mỗi hình thức đầu tư?
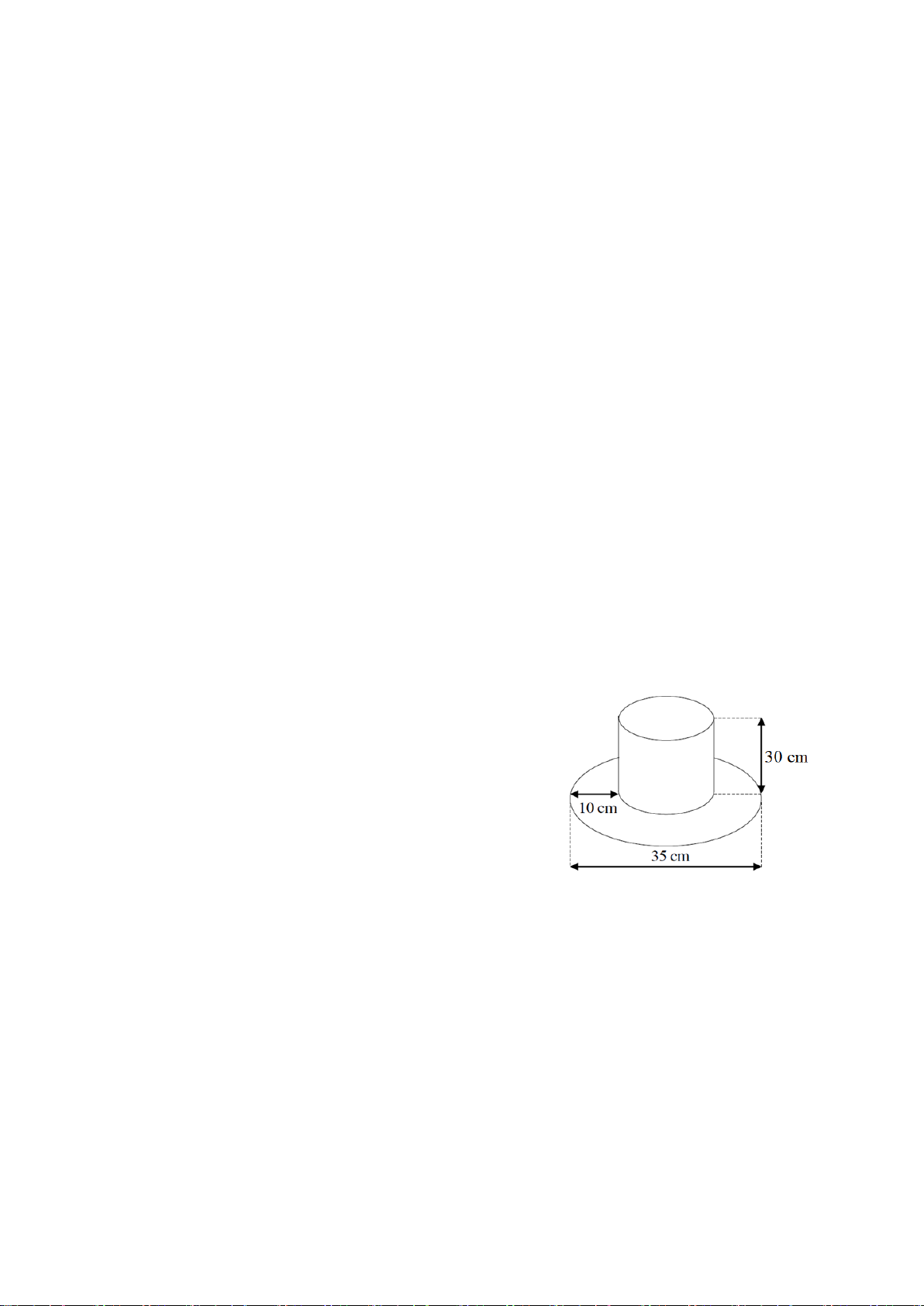
Câu 5. (0,5 điểm) Một cái mũ bằng vải của nhà
ảo thuật có kích thước như hình vẽ. Hãy tính tổng
diện tích vải cần để làm cái mũ đó (không kể
riềm, mép, phần thừa). (Làm tròn đến chữ số thập phân thứ nhất)
(Biết phần ống mũ chỉ có một đáy và diện tích xung quanh của hình trụ là
S = 2.π.r.h với h là chiều cao, r là độ dài bán kính mặt đáy) xq
Câu 6. (0,75 điểm) Nhân dịp Black Friday, một cửa hàng thể thao giảm giá
toàn bộ sản phẩm trong cửa hàng. Một áo thể thao giảm 10%, một quần thể thao
giảm 20%, một đôi giày thể thao giảm 30%. Đặc biệt nếu mua đủ bộ bao gồm 1
quần, 1áo, 1 đôi giày thì sẽ được giảm tiếp 5% (tính theo giá trị của 3 mặt hàng
trên sau khi giảm giá). Bạn Minh vào cửa hàng mua 3 áo giá 300 000 VNĐ/ cái,
2 quần giá 250 000/ cái, 1 đôi giày giá 100 0000 VNĐ/ đôi (các giá trên là giá
chưa giảm). Vậy số tiền bạn Minh phải trả là bao nhiêu ?
Câu 7. (3 điểm) Từ điểm A nằm ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB,
AC với đường tròn (O) (B, C là tiếp điểm) và cát tuyến ADE (AD < AE và tia
AE nằm giữa hai tia AB và AO). Gọi I là trung điểm của DE.
a) Chứng minh các tứ giác ABOC và ABIO nội tiếp.
b) Gọi H là giao điểm của AO và BC. Chứng minh AD . AE = AH. AO và HB
là tia phân giác của góc DHE.
c) Qua D kẻ đường thẳng song song với BE, đường thẳng này cắt AB, BC lần
lượt tại M, N. Chứng minh: MD = DN Câu ĐÁP ÁN Biểu điểm Câu 1 a) 2
−x + x +12 = 0
(2 điểm) Giải được 2 nghiệm x1 = 4; x2 = -3 1,0 b) 4 2
x −11x +18 = 0 (1) Đặt t = x2 (t ≥ 0)
(1) trở thành t2 – 11t + 18 = 0 (2)
Giải (2) được t1 = 2 (nhận) ; t2 = 9 (nhận) 0,5
• Với t1 = 2 thì x = ± √2 • Với t 0,5 2 = 9 thì x = ± 3 Câu 2 a) Vẽ đúng (P) và (d) 0,5*2
(1,5 điểm) b) Phương trình hoành độ giao điểm của (P) và (d) là -x2 = 2x – 3 0,25 x2 + 2x – 3 = 0 x = 1 hay x = -3
Thay x = 1 vào (d) ta được y = -1
Thay x = -3 vào (d) ta được y = -9
Vậy tọa độ giao điểm của (P) và (d) lần lượt là (1 ; -1) và (-3 ; 9) 0,25 Câu 3 Phương trình: 2 3x + 6x −1= 0
(1,5 điểm) a. Tính đúng ∆ = 48 0,25 KL đúng 0,25
- Theo định lí Vi - ét ta có: b − 6 x + x = − = = − 2 1 2 a 3 0,25*2 c −1 x . x = = 1 2 a 3 - Biến đổi đúng: 3 3 A = x + x = x + x − 3x x x + x 0,25 1 2 ( 1 2)3 1 2 ( 1 2 ) - Tính đúng: 0,25 A = −10 Câu 4
Gọi x (triệu đồng) là số tiền bác Phong gửi ngân hàng (0 < x < (0,75 điểm) 500)
y (triệu đồng) là số tiền bác Phong đầu tư vào nhà hàng (0 < y < 500) 0,25
Vì tổng số tiền đầu tư vào cả hai hình thức là 500 triệu đồng nên: x + y = 500
Vì số tiền cả vốn và lãi thu về từ cả hai nguồn trên sau 1 năm là 574 triệu đồng nên:
(1 + 7%)x + (1 + 20%)y = 574 ⇔ 1,07x + 1,2y = 574 0,25 Ta có hệ phương trình: 0,25 � x + y = 500 1,07x + 1,2y = 574
Giải hệ phương trình ta được: x = 200 (nhận), y = 300 (nhận)
Vậy bác Phong gửi 200 (triệu đồng) vào ngân hàng và đầu tư 300
(triệu đồng) vào nhà hàng. Câu 5
Bán kính đáy R = 35 − 2.10 = 7,5 (cm) (0,5 điểm) 2
Diện tích vải để làm ống mũ là:
S1 = 2πRh + πR2 = 2π.7,5.30 + π.7,52 = 506,25π (cm2)
Diện tích vải để là vành mũ là:
S2 = π.17,52 – π.7,52 = 250π (cm2)
Tổng diện tích vải cần để làm cái mũ là:
506,25π + 250π = 756,25π ≈2375,8 (cm2) Câu 6
Tổng giá tiền sản phẩm nếu mua lẻ :
(0,75 điểm) 3.300000.90%+2.250000.80%+1000000.70% =1 910 000 (VNĐ)
Vì mua đủ bộ 3 món nên số tiền được giảm thêm là :
(300000.90%+250000.80%+1000000.70%).5% =58500 (VNĐ)
Số tiền bạn Minh phải trả là: 1910000 - 58500=1851500 (VNĐ) Câu 7 B (3 điểm) E I L M D N A O H C
a. Tứ giác ABOC và ABIO nội tiếp đường tròn 1,0
b. cm ∆𝐴𝐴𝐴𝐴𝐴𝐴 ∽ ∆𝐴𝐴𝐴𝐴𝐴𝐴 (g – g) AD . AE = AB2 0,25
cm ∆𝐴𝐴𝐴𝐴𝐴𝐴 vuông tại B, đường cao BH AH. AO = AB2 cm AD . AE = AH . AO 0,25 cm 𝐴𝐴𝐴𝐴𝐴𝐴 � = 𝐴𝐴𝐴𝐴𝐴𝐴 � 0,25
cm HB là tia phân giác của góc DHE. 0,25
c. Gọi L là giao điểm HB và AE. ∆LBE có DN // BE ⇒ DN LD = (hệ quả Talet) (1) EB LE ∆ABE có DM // BE ⇒ DM AD 0,25 = (hệ quả Talet) (2) EB AE
∆EHD có HL là phân giác DHE ⇒ LD HD = (3) LE HE 0,25
HA ⊥ HL tại H ⇒ HA là phân giác ngoài ∆EHD ⇒ AD HD = (4) AE HE 0,25 (1), (2), (3), (4) ⇒ DN DM = ⇒ đpcm. EB EB 0,25
ỦY BAN NHÂN DÂN QUẬN 3
ĐỀ THAM KHẢO KIỂM TRA HỌC KÌ II
TRƯỜNG THCS LÊ LỢI NĂM HỌC 2023 - 2024 MÔN TOÁN – LỚP 9
Thời gian làm bài: 90 phút
Câu 1 (2,0 điểm): Giải các phương trình sau a) 2
2x − 5x − 3 = 0 b) 4 2
2x − 7x − 4 = 0
Câu 2 (1,5 điểm): Cho Parabol 2
(P) : y = x và đường thẳng (d) : y = 3x − 2.
a) Vẽ đồ thị (P) và (d)trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Câu 3 (1,5 điểm): Cho phương trình: 2
5x − 2x − 7 = 0
a) Chứng tỏ phương trình trên có 2 nghiệm phân biệt x ; x 1 2
b) Không giải phương trình, hãy tính giá trị của biểu thức 2
A = (x + x )(x − 2x ) + 3x 1 2 1 2 2
Câu 4 (0,75 điểm): Trong cuộc thi “Đố vui để học”, mỗi thí sinh phải trả lời 12 câu hỏi
của ban tổ chức. Mỗi câu hỏi gồm bốn phương án, trong đó chỉ có một phương án đúng.
Với mỗi câu hỏi, nếu trả lời đúng thì được cộng 5 điểm, trả lời sai bị trừ 2 điểm. Khi bắt
đầu cuộc thi, mỗi thí sinh có sẵn 20 điểm. Thí sinh nào đạt từ 50 điểm trở lên sẽ được vào
vòng thi tiếp theo. Hỏi thí sinh phải trả lời đúng ít nhất bao nhiêu câu thì được vào vòng thi tiếp theo?
Câu 5 (0,5 điểm): Một cửa hàng mở chương trình khuyến mãi như sau: Nếu mua sản phẩm
thứ nhất nguyên giá thì sản phẩm thứ 2 được giảm 10 nghìn đồng, sản phẩm thứ 3 được
giảm 10%. Từ sản phẩm thứ 4 trở đi khách hàng chỉ phải trả 80% giá niêm yết.
a) Bạn An đến mua 13 sản phẩm và phải trả 1298 nghìn đồng. Hỏi giá bán 1 sản
phẩm khi chưa giảm là bao nhiêu?
b) Khi chủ của hàng nhập vào 100 sản phẩm và chỉ bán được 80 sản phẩm thì khi
bán xong chủ cửa hàng lời hay lỗ bao nhiêu %? Biết giá vốn 1 sản phẩm và 60 nghìn đồng.
Câu 6 (0,75 điểm): Một bình nước hình trụ có chiều cao 20cm và
đường kính đáy bằng 8cm. Bạn Nam đổ nước vào bình cho đến khi
mực nước cách đáy bình 17cm thì dừng lại.
a) Tính thể tích nước trong bình ?
b) Sau đó, Nam lấy các viên đá lạnh hình cầu có cùng bán kính
2cm thả vào bình nước. Bạn Nam có thể thả tối đa bao nhiêu
viên đá để nước không tràn ra khỏi bình?
Câu 7 (3,0 điểm): Cho đường tròn (O) và điểm A ở ngoài đường tròn.
Vẽ tiếp tuyến AM, AN. Gọi H là giao điểm của MN và OA. Kẻ dây
BC của (O) sao cho BC đi qua H và BC ⊥ OM (C thuộc cung nhỏ MN). Đường thẳng AC
cắt (O) tại điểm thứ hai là D. Gọi I là trung điểm CD và F là giao điểm của MN và CD.
a/ Chứng minh tứ giác AMOI nội tiếp đường tròn và xác định tâm K.
b/ Chứng minh CHIN nội tiếp và FI . FA = FC . FD.
c/ Kẻ KE ⊥ AM tại E. Chứng minh E, H, D thẳng hàng.
ĐÁP ÁN ĐỀ THAM KHẢO KIỂM TRA HỌC KÌ II NĂM HỌC 2023 – 2024
Câu 1 : Giải các phương trình sau a) 2
2x − 5x − 3 = 0 1 S 3; − = 2 b) 4 2
2x − 7x − 4 = 0 S = {2; − } 2 Câu 2:
a) Vẽ đồ thị (P) và (d) trên cùng hệ trục tọa độ. BGT: x −2 −1 0 1 2 = 2 y x 4 1 0 1 4 x 1 2
y = 3x − 2 1 4
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Phương trình hoành độ giao điểm của (P) và (d): 2 x = 3x − 2 ⇔ 2
x − 3x + 2 = 0 x = 1 ⇔ x = 2 Thay x = 1 vào = 2
y x , ta được: y = 2 1 = 1. Thay x = 2 vào = 2
y x , ta được: y = 2 2 = 4 .
Vậy (1; 1) , (2; 4) là hai giao điểm cần tìm
Câu 3:Cho phương trình 2
5x − 2x − 7 = 0 có hai nghiệm x1, x2 a) a = 5; c = -7
a và c trái dấu nên phương trình có 2 nghiệm phân biệt. b) Phương trình 2
5x − 2x − 7 = 0 có hai nghiệm x1, x2 thỏa mãn hệ thức Viét: −𝑏𝑏 2
𝑆𝑆 = 𝑥𝑥1 + 𝑥𝑥2 = � 𝑎𝑎 = 5 𝑐𝑐 −7
𝑃𝑃 = 𝑥𝑥1. 𝑥𝑥2 = 𝑎𝑎 = 5 A= (𝑥𝑥 2
1 + 𝑥𝑥2)(𝑥𝑥1 − 2𝑥𝑥2) + 3𝑥𝑥2 = (𝑥𝑥 2
1 + 𝑥𝑥2)(𝑥𝑥1 − 2𝑥𝑥2) + 3𝑥𝑥2 2
= 𝑥𝑥21 − 𝑥𝑥1𝑥𝑥2 + 𝑥𝑥22 = (𝑥𝑥1 + 𝑥𝑥2)2 − 3𝑥𝑥1𝑥𝑥2 = �2� − 3. −7 = 109 5 5 25
Câu 4: Gọi x là số câu trả lời đúng (x ∈N*, x < 12)
Số câu trả lời sai là 12 – x (câu)
Để vào vòng thi tiếp theo cần đạt 50 điểm nên ta có:
5x − 2(12 − x) + 20 ≥ 50 ⇔ 5x − 24 + 2x + 20 ≥ 50 ⇔ 7x ≥ 54 54 ⇔ x ≥ 7
Vậy thí sinh phải trả lời đúng ít nhất 8 câu hỏi thì được vào vòng thi tiếp theo. Câu 5:
a) Gọi x (nghìn đồng) là giá bán của một sản phẩm khi chưa giảm (x > 0) Theo bài ta có:
x + x – 10 + x (100% - 10%) + (13 – 3).80%.x = 1298
<=> x = 120 (nghìn đồng)
b) Tiền vốn bỏ ra để nhập hàng là: 60.100 = 6000 (nghìn đồng)
Số tiền bán 80 sản phẩm:
120 + 120 – 10 + 120.(100% - 10%) + (80 – 3).80%.120 = 7730 (nghìn đồng)
Sô tiền lời cửa hàng thu về: 7730 – 6000 = 1730 (nghìn đồng)
Phần trăm tiền lời là: 1730: 6000 . 100% ≈29% Câu 6:
a) Bán kính bình nước là: 8:2 = 4 (cm)
Thể tích nước trong bình là: 2 3 π.4 .17 = 272π (cm )
b) Thể tích 1 viên đá là: 4 3 32 3 π.2 = π (cm ) 3 3
Thể tích phần không chứa nước là: 2 π ( − ) 3
.4 . 20 17 = 48π (cm ) Ta có: 48π = 4.5 32
. Nên Nam có thể thả tối đa 4 viên đá π 3 Câu 7: M B E H O A K C F I D N
a) (O) có : CD dây cung không qua tâm I là trung điểm CD.
⇒ OI ⊥ CD tại I. (đường kính – dây cung)
∆AMO vuông tại M, ∆AIO vuông tại I.
⇒ ∆AMO, ∆AIO nội tiếp đường tròn đường kính AO
⇒ A, M, O, I thuộc đường tròn đường kính AO
Mà K là tâm đường tròn này ⇒ K là trung điểm AO.
b) Vậy AMOI nội tiếp (K) đường kính AO. Cm: CH // AM Cm: AMIN nội tiếp Cm: AIN � = AMN � = CHN � Suy ra CHIN nội tiếp.
Cm: FI . FA = FM . FN (Sử dụng ∆FIN ∽ ∆FMA)
Cm: FC . FD = FM . FN (Sử dụng ∆CFN ∽ ∆MFD) Suy ra FI . FA = FC . FD. M
c/ Gọi J là giao điểm MD và BC. E B Cm: HI // MD J H
Cm: H trung điểm CJ và E trung điểm AM. A O K C Cm: F ADH � = ADE
�. Suy ra E, H, D thẳng hàng I D N TRƯỜNG THCS COLETTE
ĐỀ THAM KHẢO HỌC KỲ II
Môn : TOÁN 9 - Thời gian : 90 phút
Bài 1: (2,0 điểm) Giải các phương trình sau: a) x2 – 13x – 9 = 0 b) x4 – 4x2 – 45 = 0
Bài 2: (1,5 điểm) Cho (P) 1 2
: y = x và d y = x + 2 ( ) : 4
a) Vẽ (P) và (d) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép toán.
Bài 3: (1,5 điểm) Cho phương trình: 2
7x +14x − 21 = 0.
a) Không giải phương trình. Chứng tỏ phương trình luôn có hai nghiệm phân biệt x1, x2.
b) Tính giá trị biểu thức A = 2 2 x + x − x − x 1 2 1 2
Bài 4: (0,75 điểm) Tại bề mặt nước áp suất khí quyển là 1 (atm) atmosphere. Bên dưới mặt
nước, áp suất là 2 (atm) khi một người thợ lặn ở độ sâu d là 32 (feet). Biết rằng mối liên hệ
giữa áp suất P (atm) và độ sâu d (feet ) dưới mực nước là một hàm số bậc nhất P(d) = ad + b
. a) Xác định các hệ số a và b.
b) Một người thợ lặn ở độ sâu bao nhiêu mét thì chịu áp suất là 2,25 (atm) (làm tròn đến
chữ số thập phân thứ nhất). Biết feet là đơn vị đo độ dài và 1 (feet) = 0,3048 (m).
Bài 5: (0,75 điểm) Để chuần bị cho buổi liên hoan cuối năm của lớp 9A, giáo viên chủ
nhiệm đưa cho lớp trưởng 1,5 triệu đồng đề đi mua 45 cái bánh ngọt cho lớp. Hôm đó tiệm
bánh có chương trình khuyến mãi, mua từ cái bánh thứ 16 trở đi, mỗi cái bánh được giảm
5% so với giá niêm yết. Sau khi trả tiền bánh thì lớp trưởng đưa lại cho giáo viên chủ nhiệm
195 000 đồng tiền thừa. Hỏi giá niêm yết của một cái bánh là bao nhiêu tiền?
Bài 6: (0,5 điểm) Một thùng đựng nước có dạng hình trụ với chiều cao là 35 cm và đường kính đáy là 30 cm.
a) Tính thể tích của thùng nước. (kết quả làm tròn đến hàng đơn vị).
b) Người ta sử dụng thùng nước trên để múc nước đổ vào một bể chứa có dung tích
1m3. Hỏi cần phài đồ it nhất bao nhiêu thùng nước thì đầy bể chứa? Biết rằng, mỗi
lần xách người ta chỉ đổ đầy 90% thùng để nước không đổ ra ngoài. Cho công thức tinh thể tich hình trụ: 2
V = π r ⋅h trong đó h là chiều cao hình trụ, r là bán kính đường tròn đáy.
Bài 7: (3,0 điểm) Từ điểm S ở ngoài đường tròn (O) vẽ tiếp tuyến SA (A là tiếp điểm) và
cát tuyến SBC đến đường tròn (O) (cát tuyến SBC nằm giữa SA và SO). Vẽ OH vuông góc với BC tại H.
a) Chứng minh: tứ giác SAHO nội tiếp đường tròn.
b) Kẻ đường kính AK của (O). Tia SO cắt CK tại E. Chứng minh: EK.BH = AB.OK
c) Tia AE cắt (O) tại D. Chứng minh: ba điểm B, O, D thẳng hàng. ---Hết---
Document Outline
- Lương Thế Vinh
- Bạch Đằng
- Hai Bà Trưng
- Đoàn Thị Điểm
- Á Châu
- Thăng Long
- Phan Sào Nam
- Tây Úc
- Bàn Cờ
- Kiến Thiết
- Lê Quý Đôn
- Lê Lợi
- Colette




