ĐỀ THAM KHẢO SỐ 3 HK1 TOÁN 10

Giảng dạy: Nguyễn Trung Kiên – 096 592 4852
Đây là dòng trên, các em không cần đọc!
ĐỀ THAM KHẢO SỐ 3 – HK1 TOÁN 10 
PHẦN I: TRẮC NGHIỆM (4 điểm)
Câu 1. Cho mệnh đề : 2 " x  ,
 x  3x  2025  0". Mệnh đề phủ định của mệnh đề trên là: A. 2 " x  ,
 x  3x  2025  0". B. 2 " x  ,
 x  3x  2025  0". C. 2 " x  ,
 x  3x  2025  0". D. 2 " x  ,
 x  3x  2025  0".
Câu 2. Cho tập hợp X  a; ;bc. Số tập con của X là: A. 4. B. 6. C. 8. D. 12.
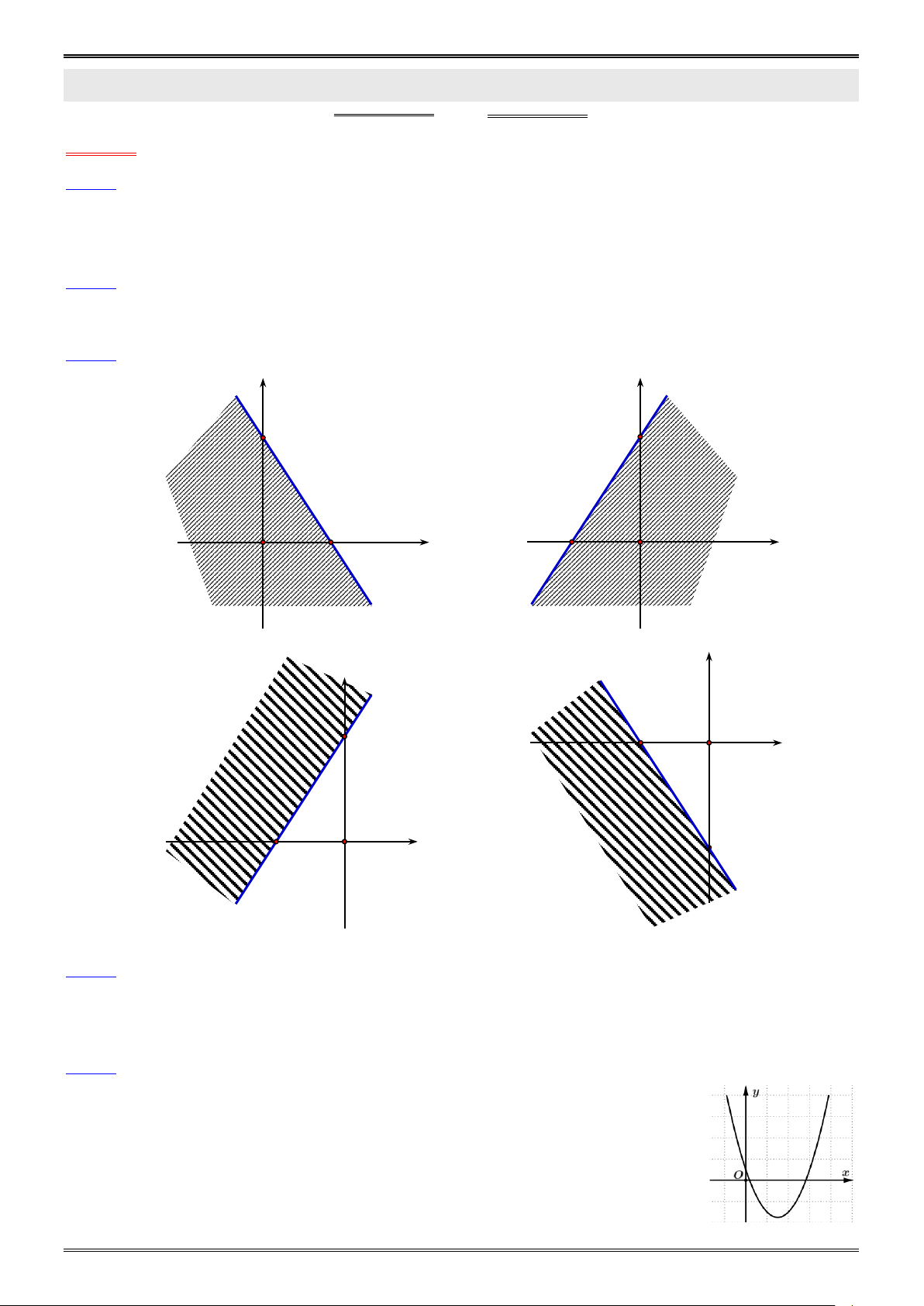
Câu 3. Miền nghiệm của bất phương trình 3x  2y  6 là: y y 3 3 A. B. 2 x 2 − O O x y y 2 − 3 O x C. D. 2 − O x 3 3  y  0
Câu 4. Miền nghiệm của hệ bất phương trình 
chứa điểm nào sau đây? 2
 x  3y  1  0 
A. A3;4.
B. B 4;3.
C. C 7;4.
D. D 4 ; 4.
Câu 5. Cho đồ thị hàm số 2
y  ax  bx  c có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng? A. a  0, 0, b  0 c  . B. a  0, 0, b  0 c  . C. a  0, 0, b  0 c  . D. a  0, 0, b  0 c  .
Còn đây là dòng dưới, chắc chắn sẽ có bạn đọc tới đoạn này!!! Ahihi, đồ ngốc ^^ Trang 1
Giảng dạy: Nguyễn Trung Kiên – 096 592 4852
Đây là dòng trên, các em không cần đọc!
Câu 6. Cho tam thức bậc hai f x 2  x
  4x  5. Tìm tất cả các giá trị của x để f x  0. A. x  5;1   .      B. x   ;  1  5;   .  C. x  1;5   .      D. x   ;  1  5;   . 
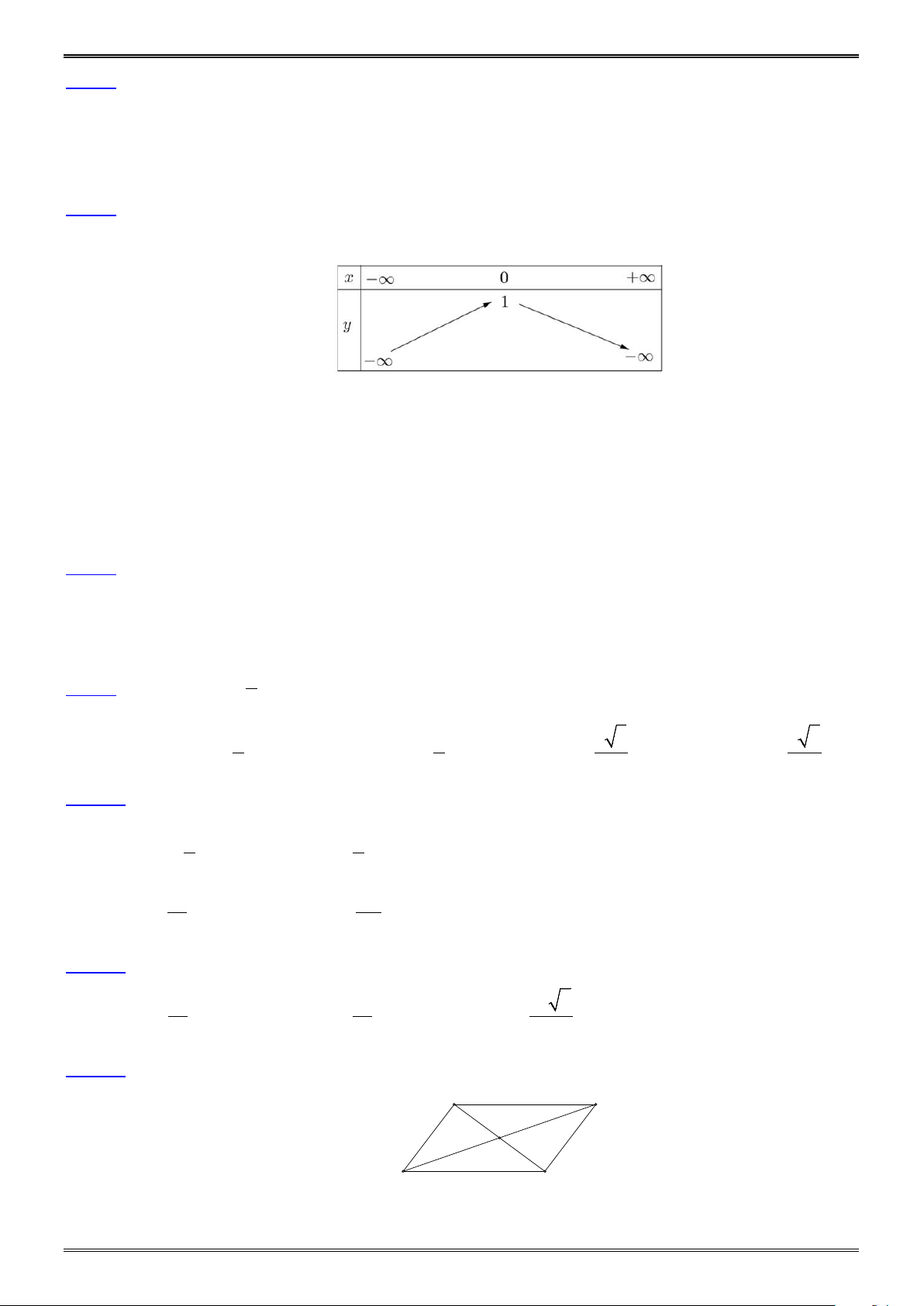
Câu 7. Cho hàm số y  f x có bảng biến thiên như hình bên dưới. Khẳng định nào sao đây là đúng?
A. Hàm số đồng biến trên khoảng  ;  .
B. Hàm số đồng biến trên khoảng   ;1 .
C. Hàm số đồng biến trên khoảng  ;0  .
D. Hàm số đồng biến trên khoảng 1;.
Câu 8. Tập nghiệm của bất phương trình 2
x  2x  3  0 là: A.  ;    1  3;.
B. 1;3. C. .  D. .  Câu 9. Cho 1
sin   , với 90    180. Tính cos .  3 A. 2 cos   . B. 2
cos    . C. 2 2 cos   . D. 2 2 cos    . 3 3 3 3
Câu 10. Tam giác ABC có AB  5, BC  5, AC  3. Giá trị cosA là: A. 2  . B. 1 . 3 2 C. 3  . D. 3 . 10 10
Câu 11. Cho hình thoi ABCD có cạnh bằng a. Góc 
BAD  30. Diện tích hình thoi ABCD là 2 2 2 A. a B. a C. a 3 D. 2 a 4 2 2 
Câu 12. Cho hình bình hành ABCD. Vectơ nào sau đây bằng vectơ CD ? A D O B C     A. AB. B. . BA C. BC. D. AD.
Còn đây là dòng dưới, chắc chắn sẽ có bạn đọc tới đoạn này!!! Ahihi, đồ ngốc ^^ Trang 2
Giảng dạy: Nguyễn Trung Kiên – 096 592 4852
Đây là dòng trên, các em không cần đọc!
Câu 13. Cho hình bình hành ABCD có tâm O. A D O B C
Khẳng định nào sau đây đúng?       
A. OB OD  BD.
B. OB OC  OD  . OA      
C. OA OB  CD.
D. AB  AD  BD.    
Câu 14. Cho b  0 và a  3b. Khẳng định nào sau đây đúng?   A.  
a và b không cùng phương.
B. a và b cùng hướng.       C.  
a và b ngược hướng và a  3 b .
D. a và b ngược hướng và a  3 b .   Câu 15. Cho A  BC có 
AB  5, AC  8, BAC  60. Khi đó AB.AC bằng: A. 40. B. 20 3. C. 40 3. D. 20.   
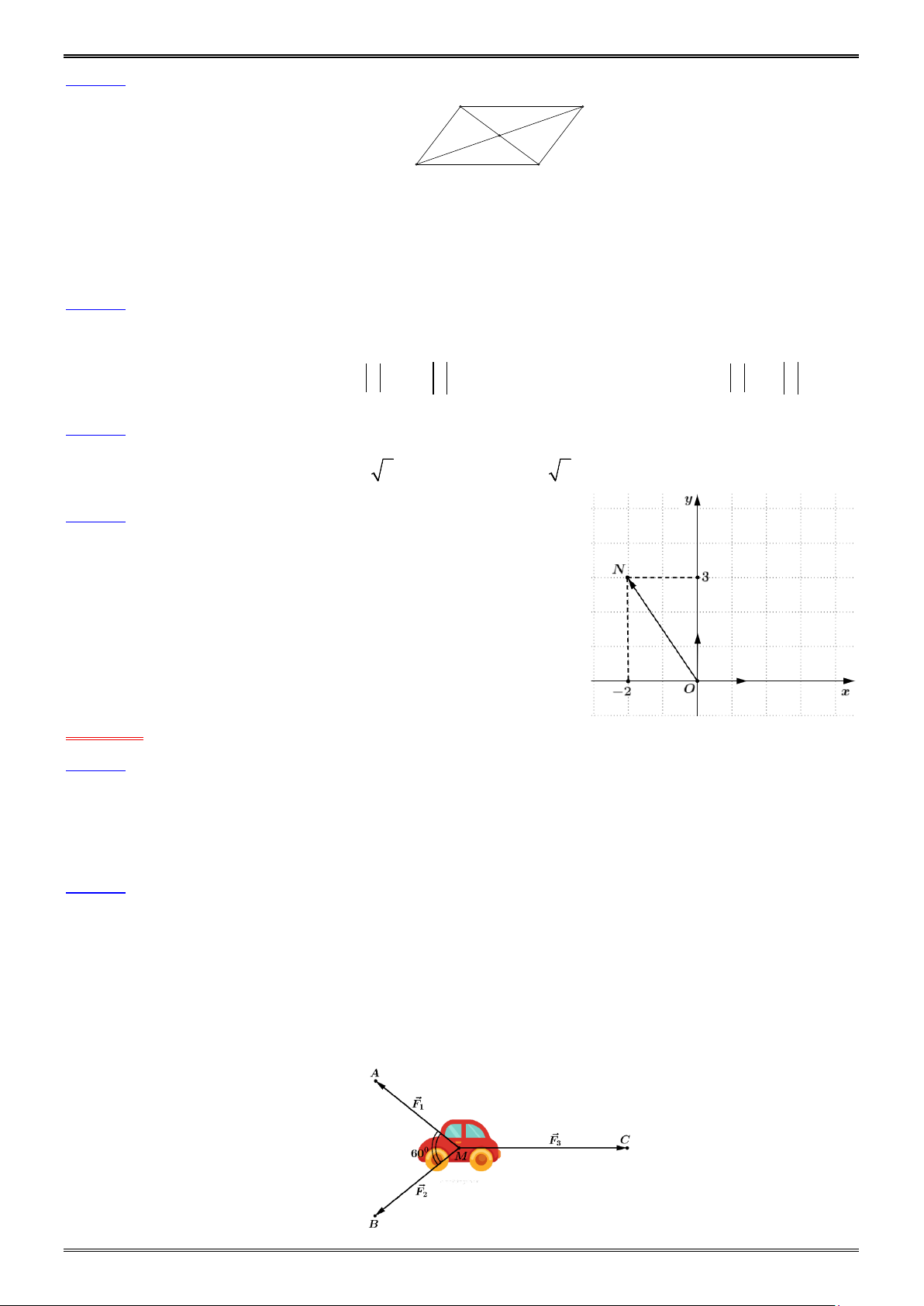
Câu 16. Biểu thị vec tơ ON (hình vẽ) theo các vec tơ i , j ta được:   
A. ON  3i  2j .   
B. ON  2i  3j .   
C. ON  2i  3j .   
D. ON  2i  3j .
PHẦN II: TỰ LUẬN (6 điểm) Câu 17.
a) Cho các tập hợp A  5;2   
 và B  3;3. Tìm A  , B A  , B A \ , B C
 A  B .
b) Lớp 10A có 28 học sinh giỏi Toán, 7 học sinh giỏi cả Văn và Toán. Hỏi có bao nhiêu học
sinh trong lớp 10A giỏi ít nhất một trong hai môn Toán và Văn? Câu 18.
a) Cho tam giác ABC có 
BC  16, AB  10, ABC  60. Tính cos , A AC, . R       b) Cho ba lực F  , MA F  ,
MB F  MC cùng tác động vào một ô tô tại điểm M và ô 1 2 3  
tô đứng yên. Cho biết cường độ hai lực F , F đều bằng 100N và góc  AMB  60. Khi 1 2 
đó tính cường độ F . 3
Còn đây là dòng dưới, chắc chắn sẽ có bạn đọc tới đoạn này!!! Ahihi, đồ ngốc ^^ Trang 3
Giảng dạy: Nguyễn Trung Kiên – 096 592 4852
Đây là dòng trên, các em không cần đọc!
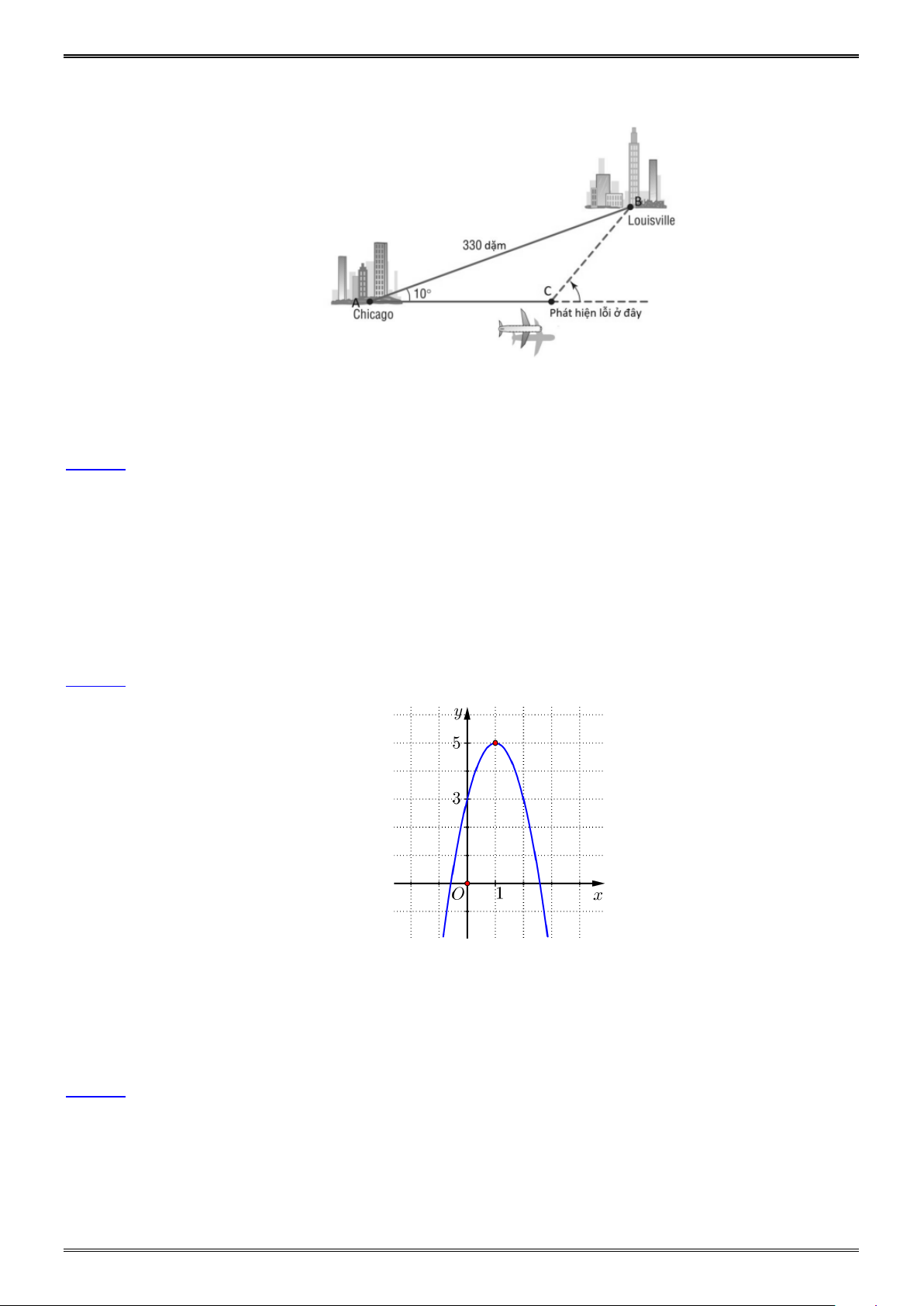
c) Trong một chuyến bay thử nghiệm từ Chicago tới Louisville, khoảng cách là 330 dặm,
viên phi công đã vô tình chọn hướng bay sai lệch đi một góc 10 như hình vẽ dưới đây.
Nếu máy bay duy trì tốc độ trung bình 220 dặm một giờ và nếu lỗi sai về hướng bay
được phát hiện ra sau 15 phút, thì viên phi công nên điều chỉnh hướng bay chếch lên
theo góc nào để bay tới được Lousville?
Câu 19. Trong mặt phẳng tọa độ Ox ,
y cho ba điểm A4; 
1 , B 2;3, C 8;9.
  
a) Tìm tọa độ của vecto , AB AC, BC.
b) Tìm tọa độ I là trung điểm AB và trọng tâm G của tam giác ABC.    
c) Tìm tọa độ điểm D thỏa mãn 30OD  19DB  3DC  0.   d) Tính AC.CB.  
e) Tính góc giữa hai vecto AB và BD.
Câu 20. Cho đồ thị parabol P 2
: y  ax  bx  c như hình bên dưới:
a) Xác định tọa độ đỉnh và trục đối xứng của parabol P.
b) Xác định khoảng đồng biến và nghịch biến của đồ thị trên.
c) Xác định dấu a, , b . c
d) Tính D  a  2b  . c Câu 21. a) P 2
: y  ax  bx  3 có đỉnh I 1;5. b) P 2
: y  2x  bx  c đi qua điểm M 5;9 và có trục đối xứng x  3. c) P 2
: y  x  bx  c đi qua hai điểm M 6;5 và N 1;5.
Còn đây là dòng dưới, chắc chắn sẽ có bạn đọc tới đoạn này!!! Ahihi, đồ ngốc ^^ Trang 4
Giảng dạy: Nguyễn Trung Kiên – 096 592 4852
Đây là dòng trên, các em không cần đọc! Câu 22.
a) Tìm tập xác định của hàm số x  4 y  . x  1
b) Tìm tập xác định của hàm số y  x  2.
c) Tìm tập xác định của hàm số 3x  4 y  . x  1
d) Tìm tập xác định D của hàm số 2x  4 y  . 2 x  9 Câu 23. a) Giải phương trình 2 2
x  2x  1  x   2x  1. b) Giải phương trình 2
3x  4x  4  3x  2.
Câu 24. Cho tam giác đều ABC có độ dài cạnh là a và G là trọng tâm. Tính:     a) AB  BC . c) AB CB .     b) AB  AC . d) BG  BC . Câu 25.
a) Giải bất phương trình 2
36x  12x  1  0.
b) Có bao nhiêu giá trị nguyên của tham số m không lớn hơn 2025 để hàm số 2
y  mx  2mx  5m  2 có tập xác định là  ?
c) Tìm điều kiện của tham số m để tam thức bậc hai f x 2  x
  m  2x  5m 1 luôn
âm với mọi x   ? Câu 26.
a) Cho tam giác ABC. Gọi I là điểm nằm trên cạnh BC sao cho BI  4IC. Phân tích   
vecto AI theo hai vecto AB và AC. b) Cho A
 BC. Gọi M là một điểm trên cạnh BC sao cho MB  2MC. Khi đó   
AM  mAB  nAC. Tổng m  n bằng bao nhiêu?
c) Cho hình chữ nhật ABCD có AB  3, AD  4. Gọi M là điểm thỏa mãn điều kiện  
AM  kAB. Tìm giá trị k để hai đường thẳng AC và DM vuông góc.
Câu 27. Sau khi phát hiện một bệnh dịch, các chuyên gia y tế tính được tốc độ truyền bệnh vào ngày
thứ t (kể từ ngày xuất hiện bệnh nhân đầu tiên) là f t 2
 3t  90t  10. Xác định ngày
mà tốc độ truyền bệnh là lớn nhất.
Câu 28. Một công ty du lịch thông báo giá tiền cho chuyến tham quan của một nhóm du khách như
sau: 50 khách đầu tiên có giá 300000 đồng/người. Nếu nhiều hơn 50 người đăng kí thì cứ
thêm một người, giá vé sẽ giảm 5000 đồng/người cho toàn bộ hành khách. Nếu gọi x là số
người thêm, khi đó f x 2
 5000x  150000x  20000000 là hàm doanh thu của công ty
du lịch. Hỏi số người của nhóm khách du lịch nhiều nhất là bao nhiêu thì công ty không bị
lỗ biết chi phí thực sự cho chuyến đi là 15080000 đồng?
Còn đây là dòng dưới, chắc chắn sẽ có bạn đọc tới đoạn này!!! Ahihi, đồ ngốc ^^ Trang 5
Giảng dạy: Nguyễn Trung Kiên – 096 592 4852
Đây là dòng trên, các em không cần đọc!
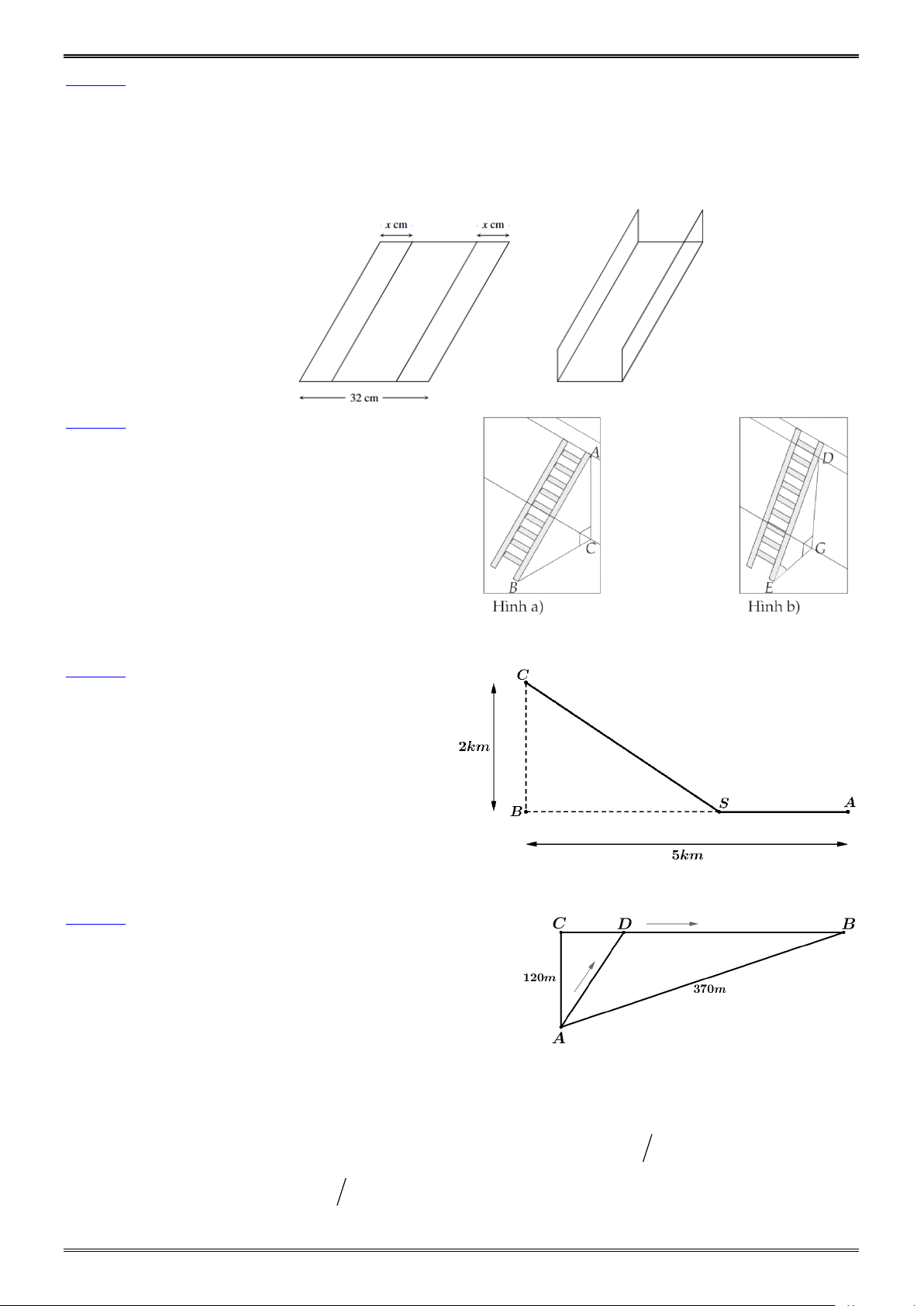
Câu 29. Bác Dũng muốn uốn tấm tôn phẳng có dạng hình chữ nhật với bề ngang 32cm thành một
máng dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc
vuông (như hình vẽ). Để đảm bảo kĩ thuật, diện tích mặt cắt ngang của máng dẫn nước phải lớn hơn hoặc bằng 2
120cm . Khi đó máng dẫn nước phải có độ cao ít nhất là bao nhiêu xăng ti mét?
Câu 30. Để leo lên một bức tường, bác Dũng
dùng một chiếc thang cao hơn bức
tường đó 2m. Ban đầu, bác Dũng đặt
chiếc thang mà đầu trên của chiếc thang
đó vừa chạm đúng vào mép trên của
bức tường. Sau đó, bác Dũng dịch
chuyển chân thang vào gần chân bức
tường thêm 1m thì bác Dũng nhận thấy
thang tạo với mặt đất một góc 45. Bức tường cao bao nhiêu mét?
Câu 31. Một kĩ sư thiết kế đường dây điện từ
vị trí A đến vị trí S và từ vị trí S đến
vị trí C . Tiền công thiết kế mỗi
kilômét đường dây từ A đến S và từ
S đến C lần lượt là 3 triệu đồng và
2 triệu đồng. Biết tổng số tiền công là
17 triệu đồng. Tính số kilômét đường
dây đã thiết kế (làm tròn đến chữ số
thập phân thứ nhất).
Câu 32. Một chú thỏ ngày nào cũng ra bờ suối ở vị trí ,
A cách cửa hang của mình tại vị trí B là 370
mét để uống nước, sau đó chú thỏ sẽ đến vị trí
C cách vị trí A là 120 mét để ăn cỏ rồi trở về
hang. Tuy nhiên, hôm nay sau khi uống nước
ở bờ suối, chú thỏ không đến vị trí C như mọi
ngày mà chạy đến vị trí D để tìm cà rốt rồi mới trở về hang (xem hình bên dưới). Biết rằng,
tổng thời gian chú thỏ chạy từ vị trí A đến vị trí D rồi về hang là 30 giây (không kể thời
gian tìm cà rốt), trên đoạn AD chú thỏ chạy với vận tốc là 13m s, trên đoạn BD chú thỏ
chạy với vận tốc là 15m s. Khoảng cách giữa hai vị trí C và D bằng bao nhiêu?
Còn đây là dòng dưới, chắc chắn sẽ có bạn đọc tới đoạn này!!! Ahihi, đồ ngốc ^^ Trang 6