Đề thi chọn HSG tỉnh Toán 10 THPT năm 2017 – 2018 sở GD và ĐT Hải Dương

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI TỈNH HẢI DƯƠNG
LỚP 10 THPT NĂM HỌC 2017 - 2018 MÔN THI: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 180 phút Ngày thi: 04/04/2018
(Đề thi gồm 01 trang) Câu I (2,0 điểm) 2 6x  4x  2018
1) Tìm tất cả các giá trị của tham số m để hàm số y  có tập xác 2
(m 1)x  2(m 1)x  4 định là . 2) Cho hai hàm số 2
y  x  2 m  
1 x  2m và y  2x  3. Tìm m để đồ thị các hàm số đó cắt
nhau tại hai điểm A và B phân biệt sao cho 2 2
OA  OB nhỏ nhất (trong đó O là gốc tọa độ). Câu II (3,0 điểm) 1) Giải phương trình
3 5  x  3 5x  4  2x  7
2) Giải bất phương trình 2 2
11x  19x  19 
x  x  6  2 2x  1
xy xy  y   2 4
4  y 2y  5 1
3) Giải hệ phương trình  2xy 
x  2y  x 14y  0
Câu III (3,0 điểm)
1) Cho tam giác ABC có AB  6; BC  7;CA  5 .Gọi M là điểm thuộc cạnh AB sao cho
AM  2MB và N là điểm thuộc AC sao cho AN  k AC ( k 
).Tìm k sao cho đường thẳng CM
vuông góc với đường thẳng BN .
2) Cho tam giác ABC có BC  , a CA  ,
b AB  c và p là nửa chu vi của tam giác. Gọi I là tâm   
đường tròn nội tiếp tam giác. Biết c( p a) a( p b) b( p c) 9  
 . Chứng minh rằng tam giác ABC 2 2 2 IA IB IC 2 đều.
3) Trong mặt phẳng toạ độ Oxy , cho hình chữ nhật ABCD có phương trình đường thẳng AB là
x  2y 1  0 . Biết phương trình đường thẳng BD là x  7 y 14  0 và đường thẳng AC đi qua điểm
M (2,1) .Tìm toạ độ các đỉnh của hình chữ nhật. Câu IV (1,0 điểm)
Một xưởng sản xuất có hai máy, sản xuất ra hai loại sản phẩm I và II. Một tấn sản phẩm loại I lãi
2 triệu đồng, một tấn sản phẩm loại II lãi 1,6 triệu đồng. Để sản xuất 1 tấn sản phẩm loại I cần máy thứ
nhất làm việc trong 3 giờ và máy thứ hai làm việc trong 1 giờ. Để sản xuất 1 tấn sản phẩm loại II cần
máy thứ nhất làm việc trong 1 giờ và máy thứ hai làm việc trong 1 giờ. Mỗi máy không đồng thời làm
hai loại sản phẩm cùng lúc. Một ngày máy thứ nhất làm việc không quá 6 giờ, máy thứ hai làm việc
không quá 4 giờ. Hỏi một ngày nên sản xuất bao nhiêu tấn mỗi loại sản phẩm để tiền lãi lớn nhất?
Câu V (1,0 điểm)
Chứng minh rằng với mọi số thực , a ,
b c dương thỏa mãn 2 2 2
a  b  c  27 thì: 1 1 1 12 12 12      . 2 2 2 a  b b  c c  a a  63 b  63 c  63
........................................ Hết ......................................
Họ và tên thí sinh: .............................................. Số báo danh: .............................
Giám thị coi thi số 1: ............................................... Giám thị coi thi số 2: ....................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
DỰ THẢO HƯỚNG DẪN CHẤM HẢI DƯƠNG
ĐỀ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 10
THPT – NĂM HỌC 2017 - 2018 MÔN: TOÁN
(Dự thảo hướng dẫn chấm gồm 6 trang) Câu Nội dung Điể m Câu
Tìm tất cả các giá trị của tham số m để hàm số sau có tập xác định là I.1 2 6x  4x  2018 1,0 đ y  2
(m 1)x  2(m 1)x  4
Hàm số có tập xác định khi và chỉ khi 2 f ( )
x  (m 1)x  2(m 1)x  4  0,  x  . 0,25
Với m  1, ta có f ( ) x  4  0, x
  . Do đó m  1 thỏa mãn. 0,25  m  1
Với m  1, f (x)  0, x     2 
(m 1)  4(m 1)  0 0,25 m  1  
(m 1)(m  5)  0
1  m  5. Vậy1  m  5. 0,25 Câu Cho hàm số 2
y  x  2 m  
1 x  2m và hàm số y  2x  3. Tìm m để đồ thị các hàm số đó I.2 cắt nhau tại hai điểm  nhỏ nhất (trong đó 1,0 đ A và B sao cho 2 2 OA OB
O là gốc tọa độ)
Phương trình hoành độ giao điểm của hai đồ thị 2
x  2 m  
1 x  2m  2x  3 hay 2
x  2mx  2m  3  0 (*) 0,25 Ta có: 2
'  m  2m3  0 với mọi m nên (*) luôn có hai nghiệm phân biệt hay hai đồ 0,25
thị luôn cắt nhau tại hai điểm phân biệt A,B.
Gọi x , x là hai nghiệm của phương trình (*). Khi đó A x ;2x  3, B  x ;2x  3 A A B B  A B
Ta có OA   x ;2x  3, OB   x ;2x  3 . A A B B 
OA  OB  x  x   x  x  0,25 A 2 3 A 2 B 2 3 B 2 2 2 2 2  5 2 2 x  x  x  x  A B  12 A B  18  5x  x  x  x   x x A B 2 12 A B  18 10 A B   1
Theo định lí Vi-et ta có x  x  2 , m x x  2  m  3 A B A B Khi đó (1) trở thành 11 119 2 2 2
OA  OB  20m  44m  48 2  20(m  )  10 5 0,25   Tìm được 11 2 2
OA  OB nhỏ nhất bằng 119 khi m  . Vậy 11 m  là giá trị của m cần 5 10 10 tìm. CâuII.
Giải phương trình: 3 5  x  3 5x  4  2x  7 1 1,0 đ Điề 4 u kiện:  x  5 (*) 5
3 5  x  3 5x  4  2x  7 0,25
 3 5  x  (7  x)  3 5x  4  x  0     2 2 3 4   5 4 5 x  x x x     0
3 5  x  (7  x) 5x  4  x 0,25    1 3  2 4
  5x  x     0 (**)
 3 5  x  (7  x)
5x  4  x  1 3 4 do   0 x  [ ,5] nên
3 5  x  (7  x) 5x  4  x 5 2 (**)  4
  5x  x  0 0,25 x  1  x  4
Đối chiếu điều kiện thấy thỏa mãn. Vậy tập nghiệm của phương trình là S  {1;4} 0,25 CâuII. Giải bất phương trình 2 2
11x  19x  19 
x  x  6  2 2x  1 2 1,0 đ 2 
x  x  6  0  Điều kiện:  2x  1  0  x  3  0,25 2
11x 19x 19  0 
Bất phương trình đã cho tương đương với 2 2
11x  19x  19   (x
2)(x  3  2 2x  1    2  0
1 x  26x  17  4 (2x  1)(x  3) x  2 0,25 2 2
 5(2x  5x  3)  4 2x  5x  3 x  2  (x  2)  0 2 2 2x  5x  3 2x  5x  3  5.  4 1  0 x  2 x  2 2 0,25 2x  5x  3   1 x  2 2 2
 2x  5x  3  x  2  2x  6x  5  0   Ta được 3 19 3 19  x  2 2 
Kết hợp điều kiện x  3 được 3 19 3  x  0,25 2
Vậy tập nghiệm của bất phương trình là: 3  19 S  [3; ) 2 CâuII.
xy xy  y   2 4
4  y 2y  5 1 3
Giải hệ phương trình:  2xy 
x  2y    1,0 đ x 14 y 0   xy  2 2
 y x  y 2 2 1 2  5y   1 Hệ phương trình     x  2y  2xy   1  12 y 2 0,25
Xét y= 0 không là nghiệm hpt
Xét y  0 chia 2 vế phương trình (1) cho 2
y , chia 2 vế phương trình (2) cho y ta được: 2  1   2x    
x  2y  5  y  0,25      x  y  1 2 2x   12      y   1 a  2x  2  a  b  5 a  3  Đặt  y có HPT      ab  12 b   4  b   x  2y 0,25  1 2x   3  hay  y 
x  2y  4    0,25
Giải hệ ta được nghiệm ( 7 1 -2;1) và  ;    2 4  Câu
Cho tam giác ABC có AB = 6 ; BC = 7 ;CA = 5 . M là điểm thuộc cạnh AB sao cho AM III.1
= 2MB ; N thuộc AC sao cho AN  k AC .Tìm k để CM vuông góc với BN 1,0 đ 2
CM  AM  AC 
AB  AC và BN  AN  AB  k AC  AB 3 0,25 2 2 2 2k 2 Suy ra CM BN 
( AB  AC)(k AC  AB)  AB AC 
AB  k AC  AB AC 3 3 3 0,25    2 2 2 2 2
AB  AC  BC AB AC  CB  A . B AC   6 2 0,25 2 2 2k 2
BN  CM  BN.CM  0  A . B AC 
AB  k AC  A . B AC  0 3 3 2k 2 6  0,25
.6  .36  25k  6  0  2
 1k 18  0  k   3 3 7 Câu
Cho tam giác ABC có BC  , a CA  ,
b AB  c và p là nửa chu vi của tam giác. Gọi I là III.2   
tâm đường tròn nội tiếp tam giác. Biết c( p a) a( p b) b( p c) 9    . Chứng minh 2 2 2 IA IB IC 2 1,0 đ
rằng tam giác ABC đều. 0,25
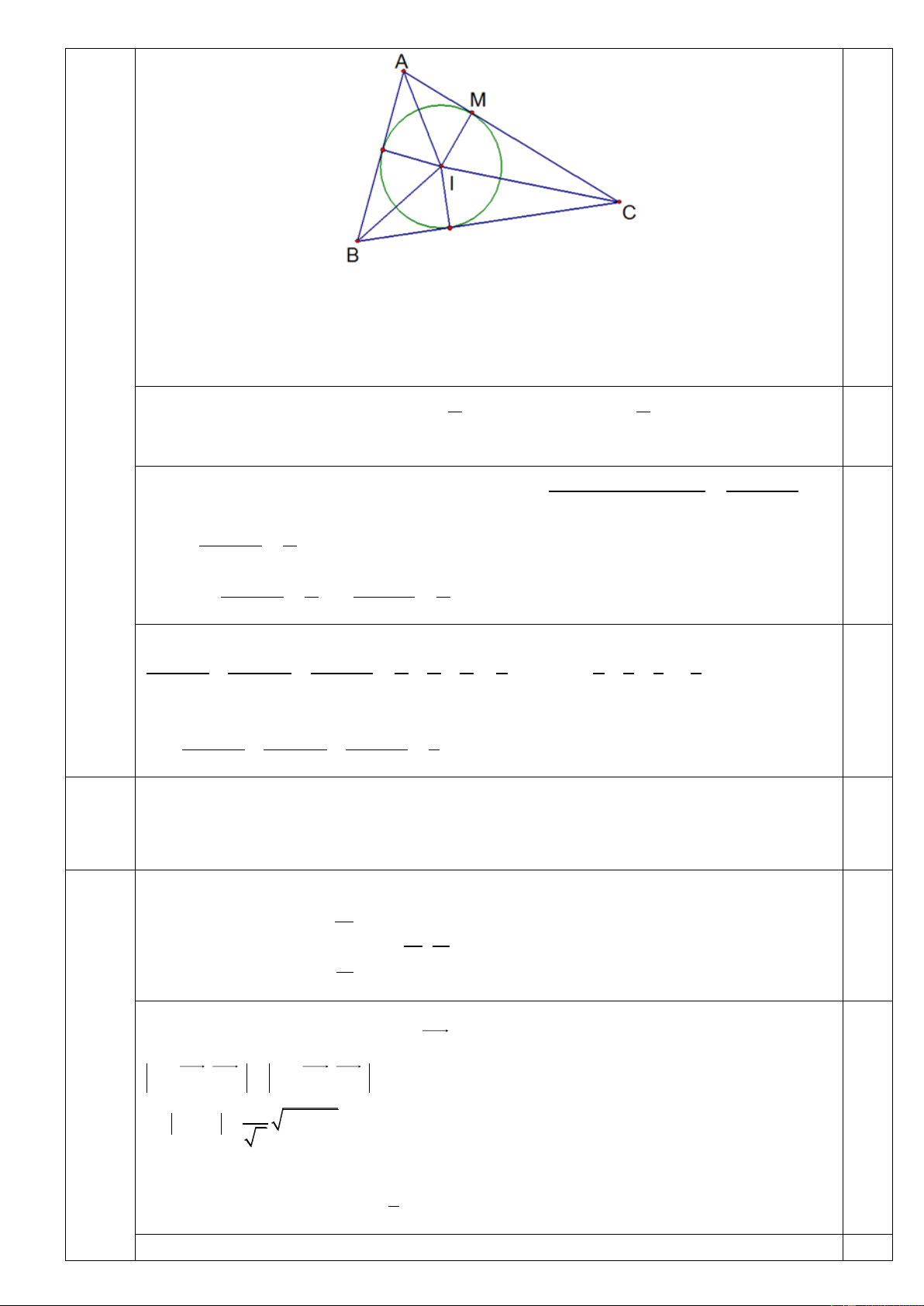
Gọi M là tiếp điểm của AC với đường tròn nội tiếp tam giác ABC. Khi đó ta có AM  p  ,
a IM  r . Áp dụng định lí Pitago trong tam giác AIM ta có 2 2 2 2 2
IA  AM  MI  ( p  ) a  r Gọi S S
S là diện tích tam giác ABC thì r  nên 2 2 2
IA  ( p  a)  ( ) p p 0,25
( p  a)( p  b)( p  c)
( p  a)bc Mà 2 S  ( p p  ) a ( p  ) b ( p  ) c nên 2 2
IA  ( p  a)   p p
c( p  a) p Suy ra  . 2 IA b 0,25  
Tương tự a( p b) p  b( p c) p và  . 2 IB c 2 IC a Từ đó
c( p  a)
a( p  b)
b( p  c)    p p p   1 1 1 1 9
 (a  b  c)(   )  . 2 2 2 IA IB IC a b c 2 a b c 2 0,25
Dấu bằng đạt được khi a  b  c    Vậy c( p a) a( p b) b( p c) 9  
 chỉ khi tam giác ABC đều. 2 2 2 IA IB IC 2 Câu
Trong mặt phẳng toạ độ C , cho hình chữ nhật ABCD có phương trình đường thẳng AB:
x  2y 1  0 , phương trình đường thẳng BD: x  7 y 14  0 , đường thẳng AC đi qua III.3 1,0 đ
M(2; 1). Tìm toạ độ các đỉnh của hình chữ nhật.
Do B là giao của AB và BD nên toạ độ B là nghiệm của hệ:  21 x 
 x  2y 1  0  5 21 13     B( ; )
x  7y 14  0 13 5 5  y   5 0,25
Do ABCD là hình chữ nhật nên góc giữa hai đường thẳng AC và AB bằng góc giữa hai
đường thẳng AB và BD. Giả sử 2 2 n
 (a;b),(a  b  0) là VTPT của AC. Khi đó AC o c s(n , n )  o c s(n , n ) AB BD AC AB 3 2 2  a  2b  a  b 2  0,25 a  b  2 2 
 7a  8ab  b  0  b a    7 + Với a  b  . Chọn a = 1, b = -1.
Phương trình AC: x – y – 1 = 0 0,25
 x  y 1  0  x  3
A  AB  AC nên toạ độ A là nghiệm của hệ:     ( A 3; 2)
x  2y 1  0 y  2
Gọi I là giao của AC và BD thì toạ độ I là nghiệm của hệ:  7 x 
 x  y 1  0  2 7 5     I( ; )
x  7y 14  0 5 2 2 y   2
Do I trung điểm AC và BD nên tính được 14 12 C(4;3); D( ; ) 5 5 + Với b  7
 a ( Loại vì khi đó AC không cắt BD) 0,25 Câu
Một xưởng sản xuất có hai máy sản xuất ra hai loại sản phẩm I và II. Một tấn sản phẩm I
IV 1,0 lãi 2 triệu đồng, một tấn sản phẩm II lãi 1,6 triệu đồng. Để sản xuất 1 tấn sản phẩm loại I thì đ
máy thứ nhất làm việc trong 3 giờ và máy thứ hai làm việc trong 1 giờ. Để sản xuất 1 tấn
sản phẩm loại II thì máy thứ nhất làm việc trong 1 giờ và máy thứ hai làm việc trong 1
giờ . Mỗi máy không đồng thời làm hai loại sản phẩm cùng lúc. Một ngày máy thứ nhất
làm việc không quá 6 giờ , máy thứ hai làm việc không quá 4 giờ. Hỏi một ngày sản xuất
bao nhiêu tấn mỗi loại sản phẩm để tiền lãi lớn nhất?
Gọi x, y là số tấn sản phẩm loại I, II cần sản xuất trong một ngày ( ; x y  0 ).
Tiền lãi một ngày là L  2x 1,6y (triệu đồng). Một ngày máy thứ nhất làm việc 3x  y
giờ, máy thứ hai làm việc x  y giờ.  0,25 ; x y  0  Theo gt có: 3
 x  y  6
 x  y  4 
Khi đó bài toán trở thành tìm x; y thỏa mãn hệ trên sao cho L  2x 1,6y đạt giá trị lớn 0,25 nhất
Vẽ các đường thẳng 3x  y  6, x  y  4 . Ta có các điểm M ( ; x y) với ( ;
x y) là nghiệm của
hệ bất phương trình trên thuộc miền trong tứ giác OABC, kể cả các điểm tr f(x)= ê 6-3 n c x f(x)=4-x ạnh tứ giác. y 8 7 6 5 C 4 B 3 2 1 x A -6 -5 -4 -3 -2 -1 O 1 2 3 4 5 6 7 8 9 10 -1 0,25 -2 -3 -4 -5 -6 -7
L đạt giá trị lớn nhất tại đỉnh của tứ giác.Thay tọa độ các điểm ( O 0;0), ( A 2;0), (
B 1;3),C(0; 4) vào biểu thức L ta được L đạt giá trị lớn nhất tại ( B 1;3) . Khi 0,25
đó L  2x 1,6y  2.11,6.3  6,8. Vậy để thu được tiền lãi cao nhất thì mỗi ngày sản xuất
1 tấn sản phẩm loại I và 3 tấn sản phẩm loại II
Câu V . Chứng minh rằng với mọi số thực , a ,
b c dương thỏa mãn 2 2 2
a  b  c  27 thì: 1,0 đ 1 1 1 12 12 12      . 2 2 2 a  b b  c c  a a  63 b  63 c  63 1 1 1 1 1 4   2  2  a  b b  c
a  b b  c (a  )
b (b  c)
a  2b  c
Chứng minh tương tự ta có 1 1 4   b  c a  c
a  2c  b 0,25 1 1 4   a  b a  c
b  2a  c 1 1 1  1 1 1  Suy ra    2     a  b c  b a  c
 b  2a  c a  2b  c b  2c  a  Ta chứng minh 1 6  . Thật vậy: 2
b  2a  c a  63 1 6  2
b  2a  c a  63 0,25 2 2 2 2
 a  63  6b 12a  6c  2a  b  c  36  6b 12a  6c  0 2 2 2
 2(a  3)  (b  3)  (c  3)  0
Điều này luôn đúng. Dấu bằng đạt được khi và chỉ khi a  b  c  3 Vậy 1 1 1 6 6 6      2 2 2
b  2a  c
a  2b  c
b  2c  a a  63 b  63 c  63 1 1 1 12 12 12 Suy ra      0,25 2 2 2 a  b b  c c  a a  63 b  63 c  63
Dấu bằng xảy ra khi và chỉ khi a = b = c = 3. 0,25
Lưu ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa.