Đề thi chọn HSG Toán 10 năm 2019 – 2020 trường THPT Trần Phú – Hà Tĩnh

NHÓM TOÁN VD – VDC
ĐỀ THI HSG TOÁN
SỞ GD&ĐT HÀ TĨNH
KỲ THI CHỌN HSG LỚP 10 THPT TRẦN PHÚ NĂM HỌC 2019 - 2020 (Đề thi có 01 trang) MÔN: TOÁN –THPT N HÓM Thời gian: 120 phút TOÁ ĐỀ BÀI
Câu 1: (5,0 điểm) Cho hàm số 2 y  m  x 
m  x  m  ( N  2 2  1 2 m là tham số). V D
a) Biết đồ thị là một đường parabol có tung độ đỉnh bằng 3m . Xác định giá trị của m . –
b) Tìm m để hàm số nghịch biến trên khoảng  ;  2. VDC
Câu 2: (4,0 điểm) Trong hệ tọa độ
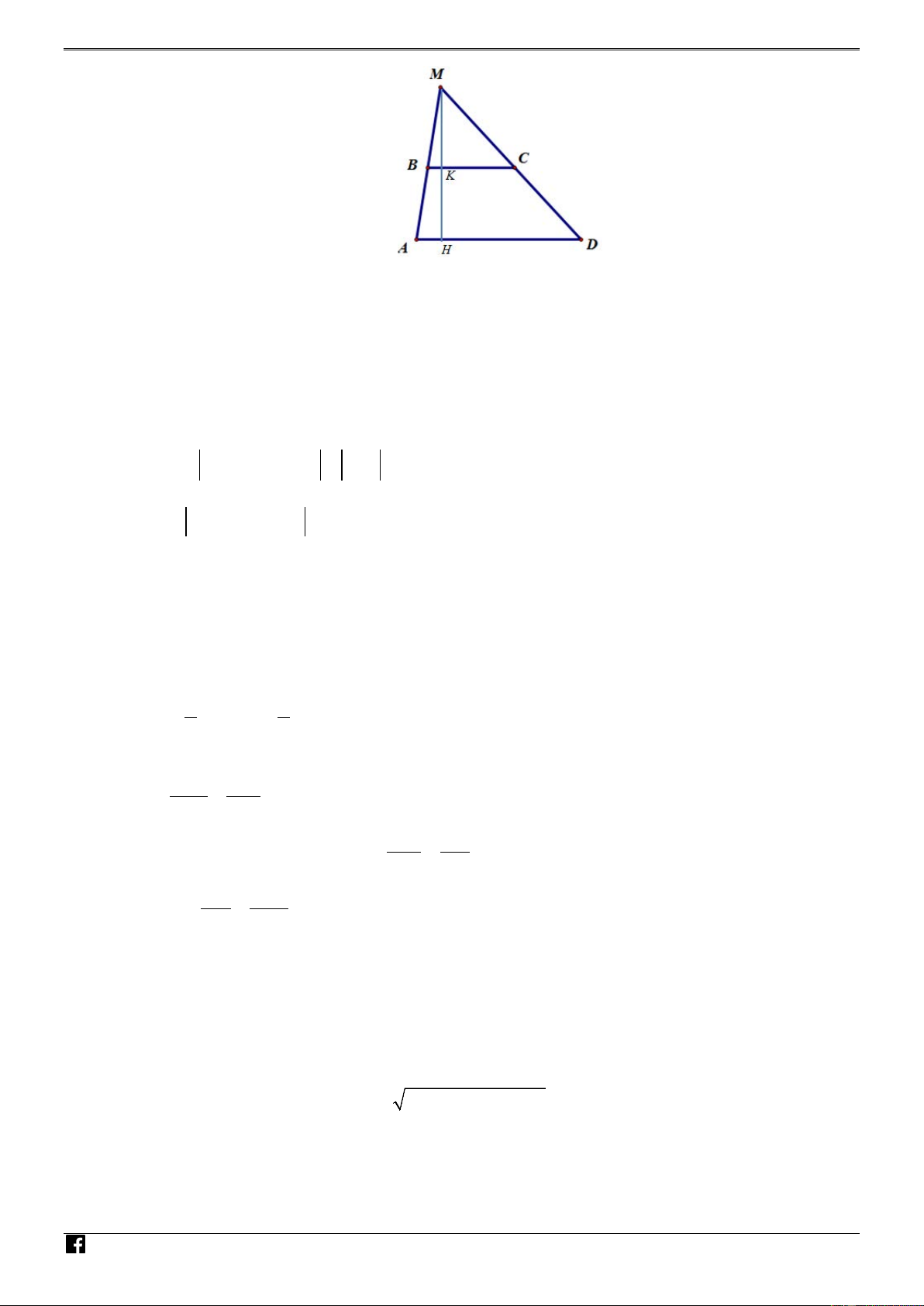
Oxy , cho hình thang ABCD có hai cạnh bên AB và CD cắt
nhau tại điểm M , tọa độ điểm ( A 2; − 2
− ), B(0;4) và C(7;3) .       
a) Tìm tọa độ điểm E để EA + EB + 2EC = 0 và tìm giá trị nhỏ nhất của PA + PB + 2PC
biết P là điểm di động trên trục hoành.
b) Biết diện tích hình thang ABCD gấp 3 lần diện tích tam giác MBC . Tìm tọa độ đỉnh D
Câu 3: (5,0 điểm) Cho phương trình 3 2
2x + mx + 2x − m = x +1 ( m là tham số).
a) Giải phương trình với m = 3 − .
b) Tìm các giá trị của m để phương trình có 3 nghiệm phân biệt.
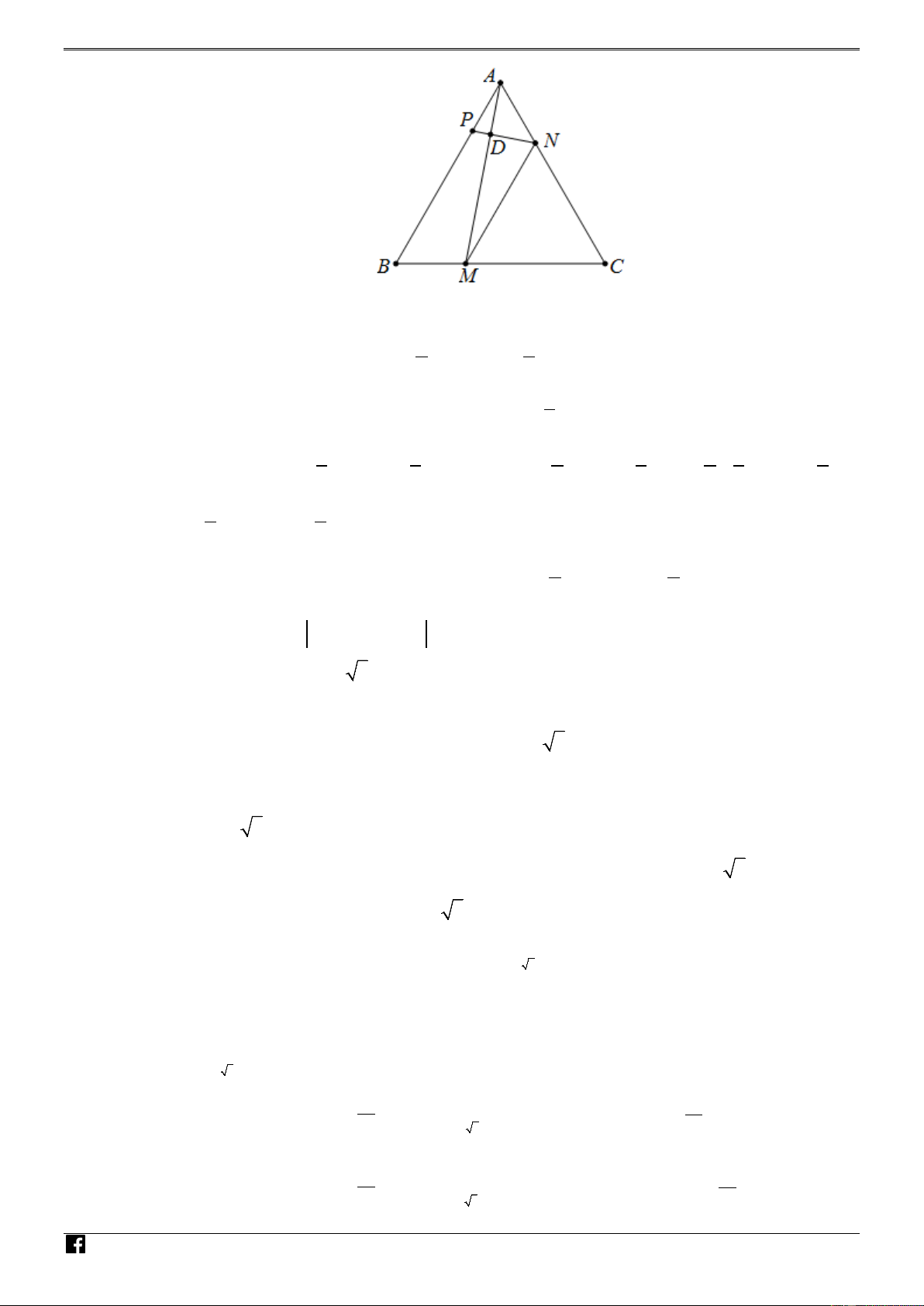
Câu 4: (4,0 điểm) Cho tam giác ABC đều cạnh 3a . Lấy các điểm M , N lần lượt trên các cạnh
BC , CA sao cho BM = a , CN = 2a .  
a. Tìm giá trị của tích vô hướng AM ⋅ BC theo a .
b. Gọi P là điểm nằm trên cạnh AB sao cho AM vuông góc với PN . Tính độ dài PN theo a .
Câu 5: (2,0 điểm) Cho hàm số f (x) 4 2
= x − 4x + 5 + m ( m là tham số). Tìm m để giá trị lớn
nhất của hàm số đã cho trên đoạn  2; − 5  
 đạt giá trị nhỏ nhất.
----------------HẾT----------------
https://www.facebook.com/groups/toanvd.vdc Trang 1 NHÓM TOÁN VD – VDC
ĐỀ THI HSG TOÁN
SỞ GD&ĐT HÀ TĨNH
KỲ THI CHỌN HSG LỚP 10 THPT TRẦN PHÚ NĂM HỌC 2019 - 2020 (Đề thi có 01 trang) MÔN: TOÁN –THPT N HÓM Thời gian: 120 phút TOÁ HƯỚNG DẪN GIẢI
Câu 1: (5,0 điểm). Cho hàm số 2 y  m  x 
m  x  m  ( N  2 2  1 2 m là tham số). V D
a) Biết đồ thị là một đường parabol có tung độ đỉnh bằng 3m . Xác định giá trị của m . –
b) Tìm m để hàm số nghịch biến trên khoảng  ;  2. VDC Lời giải:
a) Để đồ thị là một đường parabol thì m2  0  m  2 .
Đồ thị có tung độ đỉnh bằng 2m 5 3m 
 3m  2m5  3mm2 m  2 m 1  2
 3m 8m 5  0   5 tm . m   3 m 1  Vậy  5 . m   3
b) Để hàm số nghịch biến trên  ;
 2 thì m  2 .
Khi đó hàm số nghịch biến trên khoảng  m 1  ;       m  2
Ta được: m1  2  m1 2m2do m2 0. m  2
 m1 2m4  m  3 Vậy 2  m  3.
Câu 2: Trong hệ tọa độ Oxy , cho hình thang ABCD có hai cạnh bên AB và CD cắt nhau tại
điểm M , tọa độ điểm ( A 2; − 2
− ), B(0;4) và C(7;3) .       
a) Tìm tọa độ điểm E để EA + EB + 2EC = 0 và tìm giá trị nhỏ nhất của PA + PB + 2PC
biết P là điểm di động trên trục hoành.
b) Biết diện tích hình thang ABCD gấp 3 lần diện tích tam giác MBC . Tìm tọa độ đỉnh D . Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN N HÓM TOÁ N V E x y D a) Ta gọi ( ; ) , –    V EA = ( 2 − − x; 2
− − y) ,EB = (−x;4 − y) ,EC = (7 − x;3− y) DC      2
− − x − x + 2  (7 − x) = 0  = nên x 2
EA + EB + 2EC = 0 ⇔  ⇔  .  2
− − y + 4 − y + 2 
(3− y) = 0 y = 3 Vậy E(2;3) .    
Ta có: PA + PB + 2PC = 4PE = 4PE .   
Nên PA + PB + 2PC đạt giá trị nhỏ nhất khi P là hình chiếu của E lên trục hoành. Vậy P(2;0).
b) Gọi M (a;b) và D( ; c d )
Diện tích hình thang ABCD gấp 3 lần diện tích tam giác MBC nên 4S = S MB ∆ C MA ∆ B 1 1
⇔ 4. MH.BC = MK.DA 2 2
⇔ 4MH.BC = MK.AD 4BC MK ⇔ = . AD MH
Mà ABCD là hình thang nên MK AD = . MH BC Do đó AD 4BC = . BC AD   Suy ra 2
AD = 4BC ⇒ AD = 2BC ⇒ AD = 2BC . 
AD = (c + 2;d + 2) c =12  ⇒  .  = − d = 4 BC (7; 1) −
Vậy D(12; 4 − ) .
Câu 3: (5,0 điểm) Cho phương trình 3 2
2x + mx + 2x − m = x +1 ( m là tham số).
a) Giải phương trình với m = 3 − .
b) Tìm các giá trị của m để phương trình có 3 nghiệm phân biệt. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN x +1 ≥ 0
Ta có phương trình đã cho  ⇔  .
2x + mx + 2x − m =  (x + )2 3 2 1 N x ≥ 1 − x ≥ 1 − HÓM   ⇔  ⇔  (*) . 3 2x +  (m − ) 2
1 x − m −1 = 0 (x −  ) 2 1 2x + (m + )
1 x + m +1 = 0    TOÁ x ≥ 1 − a) Với  m = 3 − thì (*) ⇔  2 N (x −  )1 
(2x −2x−2) = 0 V D x ≥ 1 − –  x =1 V x =1  D ⇔  ⇒  1± 5  . C  1± 5 x = x =  2   2  ± 
Vậy tập nghiệm của phương trình 1 5  S = 1  ; .  2   x ≥ 1 − b) Ta có (  *) ⇔ x = 1 .  2 2x +  (m + )
1 x + m +1 = 0 (**) Xét phương trình ( ) 2 ** : 2x + (m + ) 1 x + m +1 = 0 Có ∆ = (m + )2 1 − 8(m + ) 1 = (m + ) 1 (m − 7) .
Phương trình đã cho có 3 nghiệm phân biệt ⇔ Phương trình (**) có 2 nghiệm phân
biệt x , x khác 1 và 1
− ≤ x < x 1 2 1 2 ∆ = (m + ) 1 (m − 7) > 0   m +1 + = − 2  x x 2.1 + (m + ) 1 .1+ m +1 ≠ 0  1 2 ⇔ (với  2 ). (  
x +1 + x +1 > 0  m +1 1 ) ( 2 ) x x = (  1 2 
x +1 . x +1 ≥ 0  2 1 ) ( 2 ) (  m + ) 1 (m − 7) > 0  m∈( ; −∞ − ) 1 ∪ (7; + ∞) 2m + 4 ≠ 0     ≠ − m +1 ⇔ m 2 − + ⇔  ⇔ m∈( ; −∞ − 2) ∪( 2; − − ) 2 > 0 1 .  < 2 m 3  m +1 m +1 2 ≥ 0  (ld)  − + 2 ≥ 0  2 2 Vậy m∈( ; −∞ − 2) ∪( 2; − − ) 1 .
Câu 4: Cho tam giác ABC đều cạnh 3a . Lấy các điểm M , N lần lượt trên các cạnh BC , CA
sao cho BM = a , CN = 2a .  
a. Tìm giá trị của tích vô hướng AM ⋅ BC theo a .
b. Gọi P là điểm nằm trên cạnh AB sao cho AM vuông góc với PN . Tính độ dài PN theo a . Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN N HÓM TOÁ N V D  
       – a. Ta có ⋅ = + ⋅ = ⋅ + ⋅ AM BC
(AB BM ) BC AB BC BM BC VDC 9 3
= 3a ⋅3a ⋅cos120° + a ⋅3a ⋅cos 0° 2 2 2
= − a + 3a = − a . 2 2  
    
   b. Ta có  
AM ⋅ PN = ( AB + BM )( AN − AP) 1 = AB + BC  ( AN − AP)  3 
    1   1   = 1 1 1 1  1 
AB ⋅ AN − AB ⋅ AP + BC ⋅ AN −
BC ⋅ AP = 3a ⋅ a ⋅
− 3a ⋅ x + ⋅ 3a ⋅ a ⋅ − ⋅ 3a ⋅ x −   3 3 2 3 2 3  2  5  5  2
= 2a − ax = a 2a − x   . 2  2    Theo đề, vì   AM ⊥ PN nên 5 4
AM ⋅ PN = 0 ⇔ a 2a − x = 0 ⇔ x = a   .  2  5
Câu 5: Cho hàm số f (x) 4 2
= x − 4x + 5 + m ( m là tham số). Tìm m để giá trị lớn nhất của hàm
số đã cho trên đoạn  2; − 5  
 đạt giá trị nhỏ nhất. Lời giải
Xét hàm số g (x) 4 2
= x − 4x + 5 + m trên đoạn  2; − 5    .
Ta có g (x) = (x − )2 2 2 + m +1. Do 2 2
− ≤ x ≤ 5 ⇒ 0 ≤ x ≤ 5 ⇒ − ≤ x − ≤ ⇒ ≤ (x − )2 2 2 2 2 3 0 2 ≤ 9
Suy ra m + ≤ (x − )2 2 1 2
+ m +1≤10 + m hay m +1≤ g (x) ≤ m +10, x ∀ ∈  2; − 5   
Suy ra g (x)∈[m +1;m +10], x ∀ ∈  2 − ; 5   .
 Trường hợp 1: 0 ≤ m +1 ⇔ m ≥ 1
− , suy ra max f (x) = m +10 .  2; − 5    m ≥ −  Trường hợp 2: 10
m +1 < 0 ≤ m +10 ⇔  ⇔ 10 − ≤ m < 1 − , m < 1 −
suy ra max f (x) = max{m +10;−m − } 1 .  2; − 5     Nếu 11  
m +10 > −m −1 ⇔ m > −
, suy ra max f (x) = m +10 khi 11 m ∈ − ; 1 −   . 2  2; − 5     2   Nếu 11  
m +10 < −m −1 ⇔ m < −
, suy ra max f (x) = −m −1 khi 11 m ∈ 1 − 0;−   . 2  2; − 5     2 
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD – VDC ĐỀ THI HSG TOÁN
 Trường hợp 3: m +10 < 0 ⇔ m < 10
− , suy ra max f (x) = −m −1.  2; − 5     11
−m −1, m < − N  2 HÓM
Tóm lại h(m) = max f (x) =  .  2; − 5    11
m +10,m ≥ −  2 TOÁ
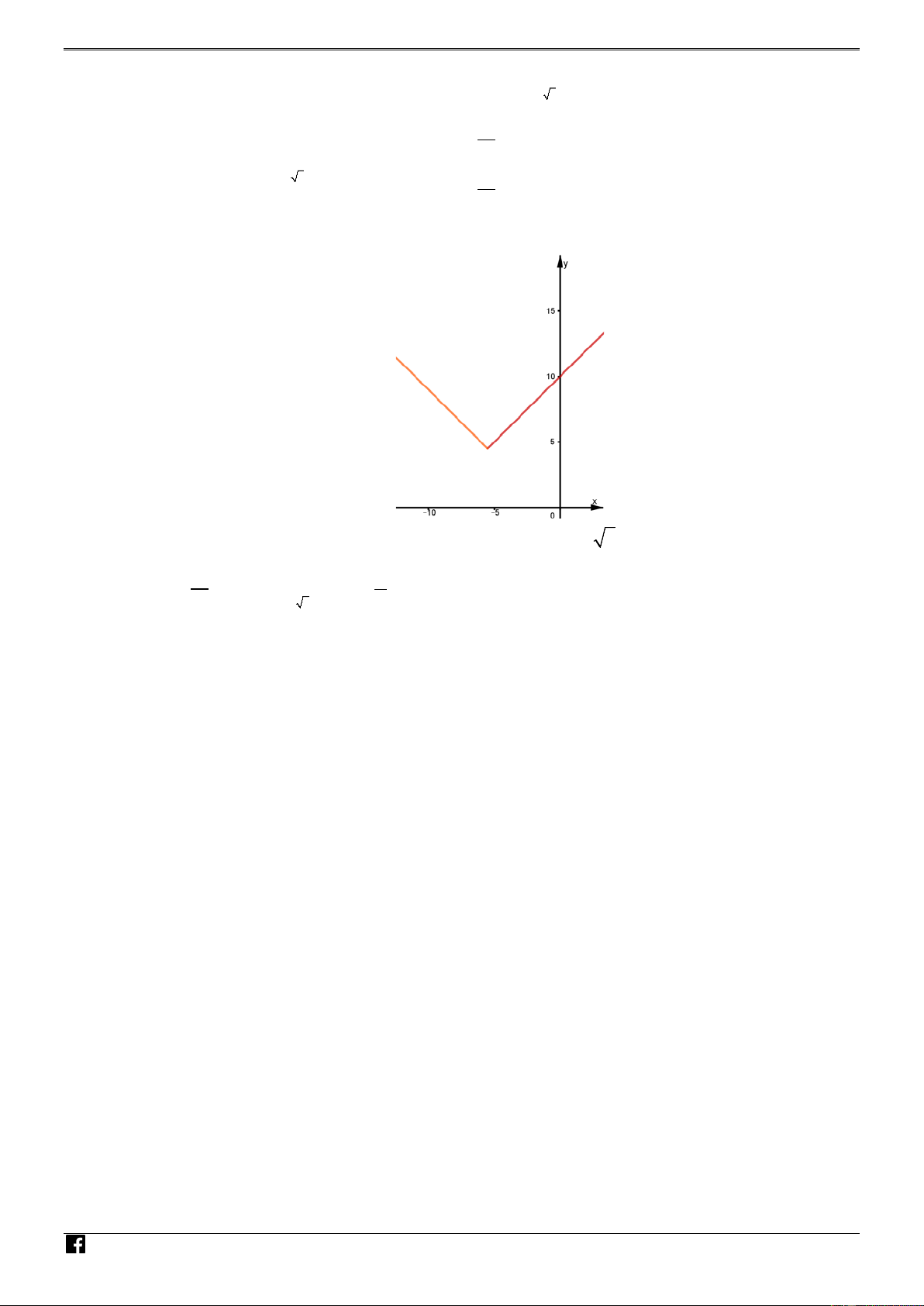
Suy ra được đồ thị của hàm số h(m) N V D – VDC
Vậy: Giá trị lớn nhất của hàm số đã cho trên đoạn  2; − 5  
 đạt giá trị nhỏ nhất khi 11 9 m = −
khi đó max f (x) = . 2  2; − 5    2
----------------HẾT----------------
https://www.facebook.com/groups/toanvd.vdc Trang 5
Document Outline

• ĐỀ BÀI
• HDG -HSG-Trần-Phú-lớp-10-năm-học-2019_2020