Đề thi chọn HSG Toán 10 năm 2023 – 2024 trường THPT Tiên Lãng – Hải Phòng

SỞ GD&ĐT HẢI PHÒNG
KỲ THI CHỌN HSG LỚP 10 THPT NĂM HỌC 2023-2024
TRƯỜNG THPT TIÊN LÃNG
ĐỀ THI MÔN: TOÁN HỌC
Thời gian làm bài: 150 phút, không kể thời gian phát đề. ĐỀ CHÍNH THỨC
Ngày thi: 20/04/2024
(Đề thi gồm 06 câu; 02 trang) Câu 1 (2,0 điểm). 1. Cho hàm số 2
y  x  2  mx  4 có đồ thị là P và điểm A5;5. Tìm m để đường
thẳng d : y  x
  m cắt đồ thị P tại hai điểm phân biệt M và N sao cho tứ giác OAMN
là hình bình hành (O là gốc tọa độ).
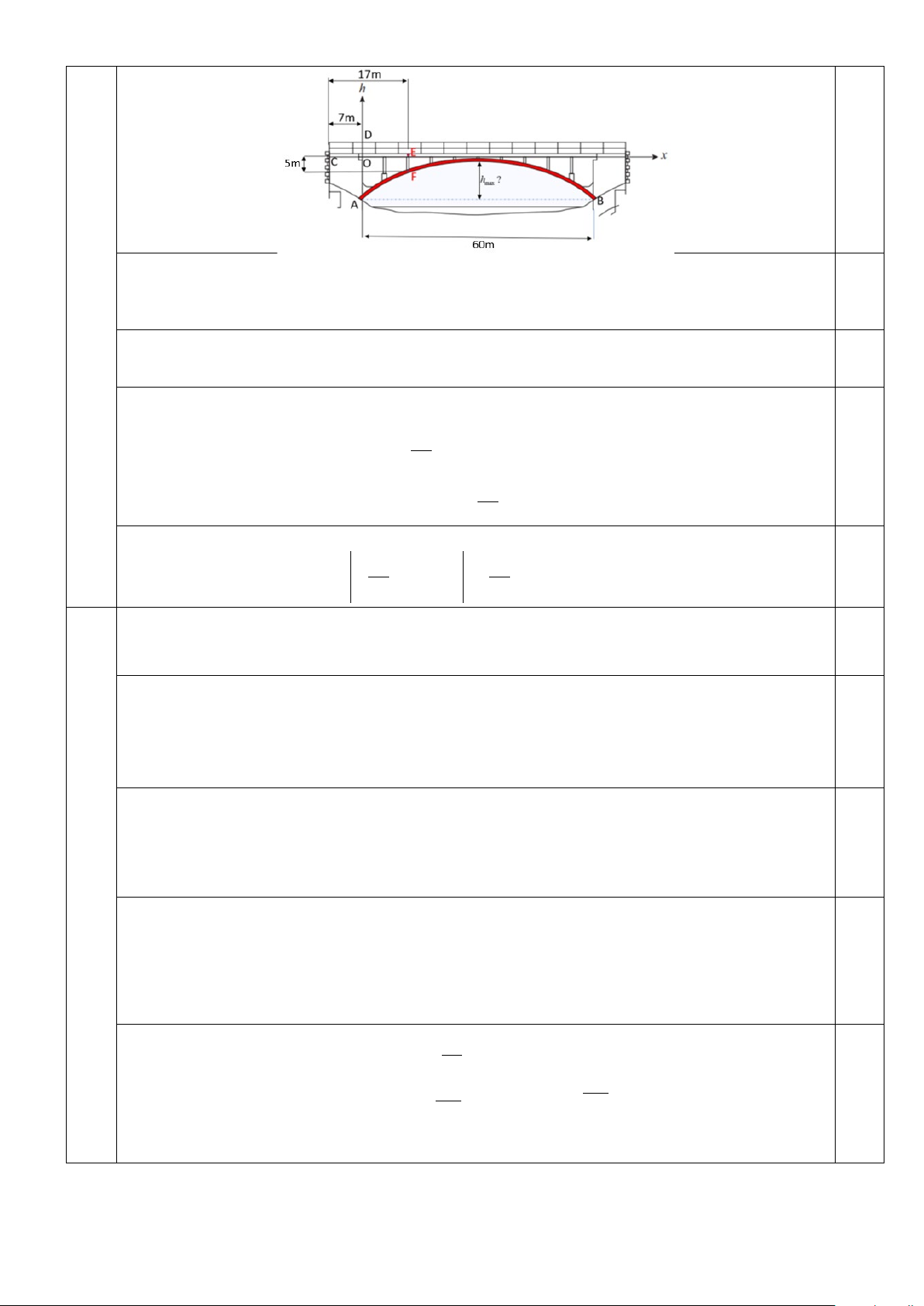
2. Một chiếc cầu được bắc qua sông. Để trợ lực cho cây cầu, người ta làm một vòm đỡ cong hình
parabol. Với hệ trục toạ độ xOh được gắn vào như hình vẽ, biết rằng khoảng cách giữa 2 chân
của vòm đỡ là AB  60m . Khoảng cách từ chân cầu (điểm C ) tới điểm O là 7m . Tại một
điểm cách chân cầu (điểm C )17m , người ta đo được khoảng cách từ mặt cầu xuống vòm đỡ là
5m .Tìm chiều cao tối đa h max của vòm đỡ (khoảng cách từ đỉnh vòm đến đường thẳngAB ) 4 2 2 3 x
  x y  x y  1
Câu 2 (1,5 điểm). Giải hệ phương trình  3 2 x
 y  xy  x  1  Câu 3 (2,5 điểm).
1. Trong mặt phẳng với hệ toạ độ Oxy , cho đường tròn C  2 2
: x  y  2x  8y  8  0 . Viết
phương trình đường thẳng song song với đường thẳng d : 3x  4y  2  0 và cắt đường tròn
theo một dây cung có độ dài bằng 6.
2.Trong mặt phẳng với hệ tọa độ Oxy , cho hình chữ nhật ABCD , có đỉnh A3  ;1 , đỉnh C
nằm trên đường thẳng  : x  y
2  5  0 . Trên tia đối của tia CD lấy điểm E sao cho
CE  CD , biết N 6; 
2 là hình chiếu vuông góc của D lên đường thẳng BE . Xác định tọa
độ các đỉnh còn lại của hình chữ nhật ABCD . 1 Câu 4 (1,0 điểm).
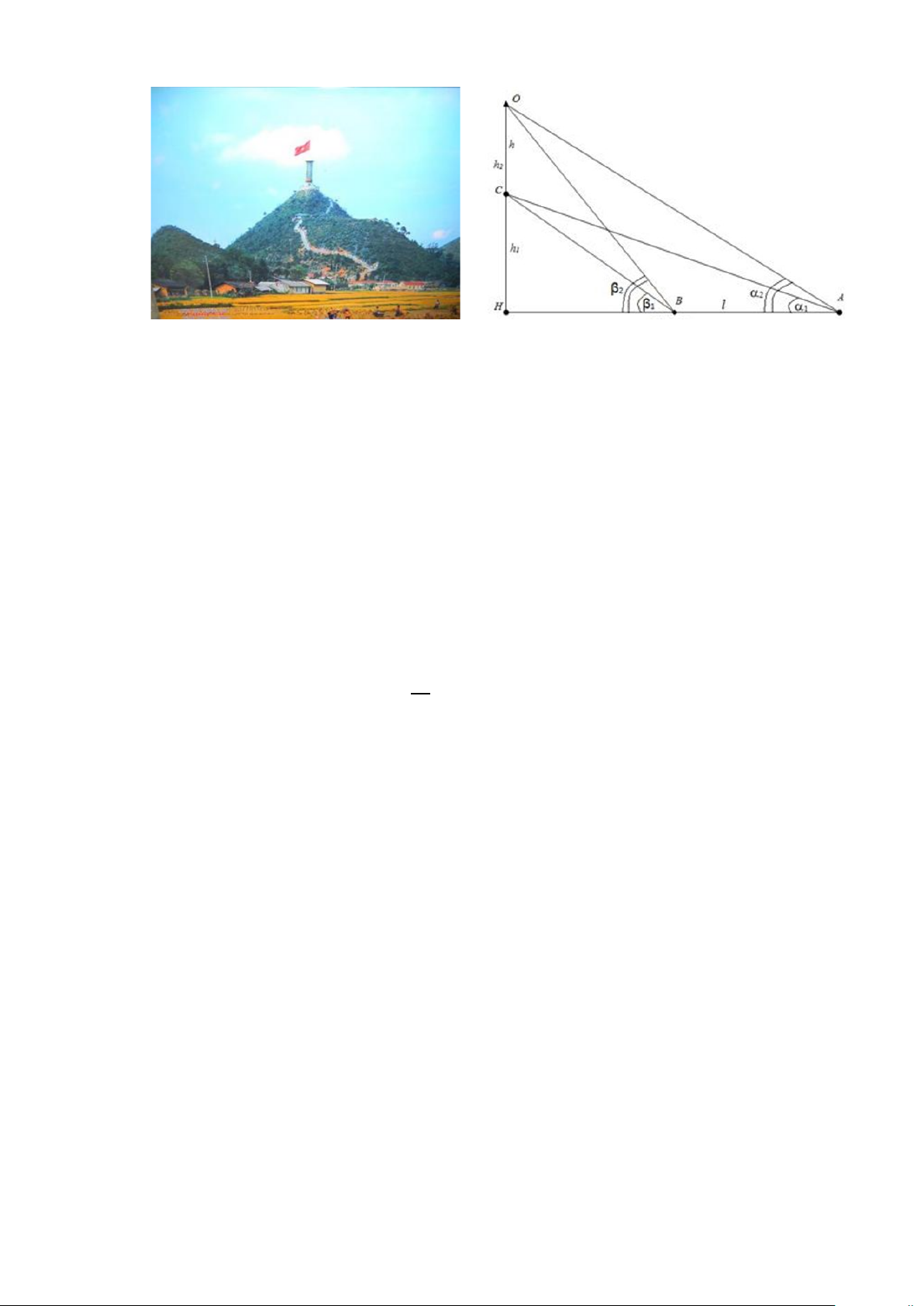
Cột cờ Lũng Cú là một cột cờ quốc gia nằm ở đỉnh Lũng Cú hay còn gọi là đỉnh núi Rồng (Long
Sơn) có độ cao khoảng 1.700m so với mực nước biển, thuộc xã Lũng Cú, huyện Đồng Văn,
tỉnh Hà Giang, nơi điểm cực Bắc của Việt Nam.
Để đo chiều cao của thân tháp cột cờ người ta đứng ở các vị trí ,
A B là hai điểm ở thung lũng
dưới núi cách nhau 15m (như hình vẽ) là hai vị trí được chọn để đặt giác kế nhìn đỉnh của thân
tháp O và đáy tháp C sao cho bốn điểm , A ,
B C,O đồng phẳng. Khi tiến hành quan sát người
đó đo được các góc  0  0
CAH  25,1 ,CBH  26,5 ;  0  0
OAH  28,5 ;OBH  30 (với H là hình
chiếu của O trên đường thẳng AB ). Tính chiều cao thân tháp cột cờ. Câu 5 (1,0 điểm).
Cho tam giác ABC đều, có cạnh bằng a . Tìm tập hợp các điểm M thoả mãn:       2 a .
MA MB  MB.MC  MC.MA  . 6 Câu 6 (2,0 điểm).
1. Đêm diễn văn nghệ chào mừng sinh nhật Đoàn 26 / 3năm học 2023  2024 tại một trường
trung học phổ thông X có 15 tiết mục gồm 7 tiết mục múa, 5 tiết mục tốp ca, 3 tiết mục đơn
ca. Có bao nhiêu cách sắp xếp thứ tự các tiết mục biểu diễn sao cho tiết mục đầu tiên và tiết mục
cuối cùng là tốp ca, đồng thời không có hai tiết mục nào cùng thể loại biểu diễn liên tiếp nhau? 2. Tính tổng: 2 2 2 3 k S  2 C  3 C
 ...    2 k 2 2025 1 k C  ...  2025 C . 2025 2025 2025 2025
---------------------------HẾT------------------------- 2
TRƯỜNG THPT TIÊN LÃNG
KỲ THI CHỌN HSG LỚP 10 THPT NĂM HỌC 2023-2024 TỔ TOÁN-VP
ĐỀ THI MÔN: TOÁN HỌC
Thời gian làm bài: 150 phút, không kể thời gian phát đề. HD ĐỀ CHÍNH THỨC
Ngày thi: 20/04/2024
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM MÔN TOÁN
(Hướng dẫn chấm có 06 trang) CÂU ĐÁP ÁN ĐIỂM Cho hàm số 2
y  x  2  mx  4 có đồ thị là P và điểm A5;5. Tìm m để đường
thẳng d : y  x
  m cắt đồ thị P tại hai điểm phân biệt M và N sao cho tứ giác OAMN 1,0
là hình bình hành (O là gốc tọa độ). Xét phương trình hoành độ giao điểm: 2
x    m 2 2 x  4  x
  m  x  3  mx  4 m  0(*)
Để d cắt P tại hai điểm phân biệt M và N thì phương trình (*) có hai nghiệm 0,25
phân biệt     m2   m 2 3 4 4
 0  m  2m  25  0, m .
Gọi x , x là hai nghiệm của phương trình (*). 1 2 x
  x  m  3 Theo Viet ta có:  1 2  ( 1) x
 .x  4  m 0,25  1 2  1.1
Ta có: M x ; x
  m , N x ; x   m 2 2  1 1   
5  x  x
Vì OAMN là hình bình hành nên  1 2
OA  NM  
 x  x  5 (2) 0,25 1 2 5   x  x  2 1 
Kết hợp (1) và ( 2) ta được:  m  8 x     1 x
  x  m  3  2  1 2    m  2 m   0   2 x  x 5 x  m 2m 0           1 2 2 2 m     2 x
 .x  4 m         0,25  1 2   m  8   m  2  .       4  m   2     2   m   0 Vậy  . m   2 
Một chiếc cầu được bắc qua sông. Để trợ lực cho cây cầu, người ta làm một vòm đỡ cong hình
parabol. Với hệ trục toạ độ xOh được gắn vào như hình vẽ, biết rằng khoảng cách giữa 2 chân
1.2 của vòm đỡ là AB  60m . Khoảng cách từ chân cầu (điểm C ) tới điểm O là 7m . Tại một
điểm cách chân cầu (điểm 1,0
C ) 17m , người ta đo được khoảng cách từ mặt cầu xuống vòm đỡ
là 5m . Tìm chiều cao tối đa h max của vòm đỡ (khoảng cách từ đỉnh vòm đến đường thẳng AB ). 1
Parabol h x có đỉnh nằm trên trục Ox và nằm hoàn toàn dưới trục Ox với hệ toạ độ 0,25
như hình vẽ nên suy ra phương trình của h xcó dạng      2 h x a x
k với a  0
Do AB  60 nên hoành độ của đỉnh parabol là 30 . Do đó k  30 .
Ta có OE  17  7  10 , suy ra toạ độ điểm F nằm trên parabol là F 10;5 0,25
Thay toạ độ F 10;5,k  30 vào phương trình parabol ta có:   a   2 1 5 10 30  a   80 0,25
Ta có phương trình parabol h x 1   x  302 80
Độ dài hmax của vòm đỡ cũng chính là độ dài đoạn OA .
Ta có OA  h   1     2 90 0 0 30   11,25m 0,25 80 8 4 2 2 3 x
  x y  x y  1
Giải hệ phương trình  1,5 3 2 x
 y  xy  x  1 
Ta có : x  x y  x xy2 4 2 2 2 3  2x y . 2 a
  x  xy 2 a  b  1 0,5 Đặt 
, hệ phương trình trở thành :  . 3 b   x y         a b 1  a   1 Suy ra 2
a  a  2  0   . a   2  0,25
Với a  1 ta tính được b  0 . 2
Với a  2 ta tính được b  3.  x   0      x   1    2 x   xy  1  2   x   xy  1 y   0 TH1:           . 0,5 3 x  y  0        x  1   x  1      y   0       y 0    2 3  4 2  2  x   xy  2 x    2
x  2x  3  0  TH2:  2     x     (vô nghiệm ). 3 x  y  3 3   3   y  y     0,25 3  3  x  x
Vậy hệ phương trình đã cho có hai nghiệm là: 1;0 và 1;0. 2
Trong mặt phẳng với hệ toạ độ Oxy , cho đường tròn C  2 2
: x  y  2x  8y  8  0 . Viết
phương trình đường thẳng song song với đường thẳng d : 3x  4y  2  0 và cắt đường tròn 1,0
theo một dây cung có độ dài bằng 6. I A H B 0,25
- Đường tròn C  2 2
: x  y  2x  8y  8  0 có tâm I 1;4 và bán kính R  5 3.1
- Đường thẳng d song song với đường thẳng d nên phương trình của d là:
3x  4y  m  0m  2
- Kẻ IH  d  HA  HB  3 và IH là khoảng cách từ I đến d : 3  4  m m  1 0,25 IH   5 5
Xét tam giác vuông IHA: 2 2 2
IH  IA  HA  25  9  16 m  2 1 0,25 
 16  m  1  20 . 25 m
  19  d ' : 3x  y  19  0   ( thỏa mãn ĐK) m
  21  d ' : 3x  y  21  0  0,25
Vậy có hai đường thẳng là: 3x  4y  19  0;3x  4y  21  0
Trong mặt phẳng với hệ tọa độ Oxy , cho hình chữ nhật ABCD , có đỉnh A3  ;1 , đỉnh C
nằm trên đường thẳng  : x  2y  5  0. Trên tia đối của tia CD lấy điểm E sao cho 1,5
CE  CD , biết N 6; 
2 là hình chiếu vuông góc của D lên đường thẳng BE . Xác định tọa
độ các đỉnh còn lại của hình chữ nhật ABCD . 3.2 0,5 Ta có   BAD BND 180  
, suy ra tứ giác ADBN nội tiếp  
 AND  ABD . Mà  
ABD  ACD (do ABCD là hình chữ nhật).
Suy ra tứ giác ANCD nội tiếp được một đường tròn. Mặt khác,  ADC 90  
 ANC  180  90 90  .
Do đó AN  CN . 3
Theo đề bài ta có điểm C nằm trên đường thẳng  : x  2y  5  0, suy ra
C 2c  5;c.  
Ta có AN  9; 
3 và CN  1 2c; 2 c. 0,25
Do AN  CN , suy ra  
AN CN  0  91 2c 32 c  0  c  1  C 7  ;1 . CE  AB  Ta có
  ACEB là hình bình hành, suy ra BE  AC .
CE  AB 0,25
Ta có BE qua N , song song AC nên có phương trình y  2  0 .   b   6
Gọi B b;  2 , ta có 2 AB CB 0 b 4b 12 0         . b   2 
Với b  6  B 6; 
2 , loại do trùng với N . 0,25
Với b  2  B 2;  2 .
Gọi D x ;y , ta có D D    x   0,25
AD  BC  x  y     6 3; 1 9;3  D    D . D D 6;4 y   4  D  1,0
Cột cờ Lũng Cú là một cột cờ quốc gia nằm ở đỉnh Lũng Cú hay còn gọi là đỉnh núi Rồng
(Long Sơn) có độ cao khoảng 1.700m so với mực nước biển, thuộc xã Lũng Cú, huyện Đồng
4 Văn, tỉnh Hà Giang, nơi điểm cực Bắc của Việt Nam.
Để đo chiều cao của thân tháp cột cờ người ta đứng ở các vị trí ,
A B là hai điểm ở
thung lũng dưới núi cách nhau 15m (như hình vẽ) là hai vị trí được chọn để đặt giác kế nhìn
đỉnh của thân tháp O và đáy tháp C sao cho bốn điểm , A ,
B C,O đồng phẳng. Khi tiến hành
quan sát người đó đo được các góc  0  0
CAH  25,1 ,CBH  26,5 ;  0  0
OAH  28,5 ;OBH  30
(với H là hình chiếu của O trên đường thẳng AB ). Tính chiều cao thân tháp cột cờ.
Gọi h là chiều cao của thân tháp cột cờ trên núi Lũng Cú cần đo.
Xét tam giác ABC, có AB=15m,  0  0  0
CAH  25,1 ,CBH  26,5  CBA  153,5 . Do đó ta có:  0 ACB  1, 4 . 0,25 Áp dụng định lí sin vào tam giác ABC, ta có 0 BC AB 15 sin 25.1     BC   260, 43m 0 sinCAH sin BCA sin1, 4 4
Xét tam giác HBC vuông tại H, có  0 BC  260, 43 ,
m CBH  26,5 , ta có 0,25 0
h  CH  260, 43.sin 26.5 hay h  116,2m (*) 1 1
Xét tam giác ABO, có  0  0  0 AB  15 ,
m OAH  28,5 ,OBH  30  OBA  1 0 5 . Do đó ta có  0 AOB  1,5 : .
Áp dụng định lí sin vào tam giác ABO, ta có: 0,25 0 BO AB 15 sin 28,5     BO   273, 42m 0 sinOAH sin AOB sin1,5
-Xét tam giác HBO vuông tại H, có BO  273,42m ,  0 OBH  30 , ta có: 0
h  OH  273, 42.sin 30  136,71m 2 0,25
+ Từ (*) và (**), ta có: h  h  h  20,51 2 1
Vậy chiều cao của thân tháp cột cờ trên đỉnh núi Lũng Cú là khoảng: 20,51m .
Cho tam giác ABC đều, có cạnh bằng a . Tìm tập hợp các điểm M thoả mãn:       2 a .
MA MB  MB.MC  MC.MA  1,0 6
Gọi G là trọng tâm tam giác ABC . Suy ra G là tâm đuòng tròn ngoại tiếp A
 BC và G cố định.        2  2
Ta có MA  MB  MC  3MG  MA  MB  MC  3MG 0,25 2 2 2       
 MA  MB  MC  MAMB  MB MC  MC  2 2 . . .MA  9MG 2 2 2   2   2   2
Ta lại có MA  MB  MC  MG G 
A  MG GB MG GC     2 2 2 2
 3MG GA GB GC  2MG GA GB GC 5  0,25 2 2 2 2
 3MG GA GB GC  2MG.0 2 2
 3MG  3GA 2     2 2 a 3 2 2  3MG  3  
  3MG  a 3 2    2       2 Ta có   2
*  3MG  a  2 .
MAMB  MB.MC  MC.  MA  9MG          a .
MA MB  MB.MC  MC.  2 2 MA  3MG  0,25 2 2 2 2 2 2 a a 2a a 2   3MG   MG   MG  6 2 9 3 Vậy tập hợp điểm a
M là đường tròn tâm G bán kính 2 R  0,25 3
Đêm diễn văn nghệ chào mừng sinh nhật Đoàn 26 / 3 năm học2023  2024 tại một trường
trung học phổ thông X có 15 tiết mục gồm 7 tiết mục múa, 5 tiết mục tốp ca, 3 tiết mục
6.1 đơn ca. Có bao nhiêu cách sắp xếp thứ tự các tiết mục biểu diễn sao cho tiết mục đầu tiên và 1,0
tiết mục cuối cùng là tốp ca, đồng thời không có hai tiết mục nào cùng thể loại biểu diễn liên tiếp nhau? 5 0,25
+ Chọn 2 tiết mục tốp ca (TC) và sắp xếp vào đầu và cuối để biểu diễn có: 2 C × 2! 5 cách.
+ Sắp xếp 7 tiết mục múa (hình vẽ) có 7! cách. 0,25
+ Sắp xếp 3 tiết mục tốp ca và 3 tiết mục đơn ca vào 6 vách ngăn (theo hình vẽ) có 6! cách. 0,25 Vậy có: 2
C × 2!×7!×6!= 72576000 cách sắp xếp 5 0,25 Tính tổng: 2 2 2 3 k S  2 C  3 C
 ...    2 k 2 2025 1 k C  ...  2025 C . 1,0 2025 2025 2025 2025
Trước hết ta chứng minh đẳng thức: 2 k
k C  n n  C   nC 
 k  n k n   . n   k 2 k 1 1 n n  1  * 2 , , 2 1  Thật vậy do 2 k
k C  k k   1 k k C  kC . n n n 2 Mà: n  n  k n  1!  1! ! k 1 kC  k.  n  n  nC  0,25 n
k !.n k . !
k  1!.n k . !
k  1!. n  1k  1 3 n 1    !
Áp dụng 3 hai lần ta được:
k  1.k. k
C  k  nC   n k  C   n n  C  n   k 1 1 . . . n   k 1 1 . n   k 2 1 4 1 1 n 2    6.2
Từ 2, 3, 4 ta được   1 . Áp dụng   1 ta được: 2025 S    2025 k 2 k 1 .k . k C    1 . k 2  k 1 2025.2024.C  2025.C  2025 2023 2024  0,25 k 2  k 2  2023 k k  2024.2025. k C .  2024 1  2025. k C . 1 2023 2024   k0 k 1  2023 Ta lại có : k k
C . 1 =  2023 1 1 =0 2023   k0 0,25 2024 k k
C . 1  1 2024 1  1  1 2024 k 1 
Nên S  2024.2025.0  2025.  1  2025. 0,25
------------------- Hết -------------------
Lưu ý khi chấm bài:
- Đáp án chỉ trình bày một cách giải bao gồm các ý bắt buộc phải có trong bài làm của học sinh. Khi chấm
nếu học sinh bỏ qua bước nào thì không cho điểm bước đó.
- Nếu học sinh giải cách khác, giám khảo căn cứ các ý trong đáp án để cho điểm.
- Trong bài làm, nếu ở một bước nào đó bị sai thì các phần sau có sử dụng kết quả sai đó không được điểm.
- Học sinh được sử dụng kết quả phần trước để làm phần sau.
- Trong lời giải bài hình, nếu học sinh không vẽ hình thì cho tối đa một nửa số điểm. Nếu học sinh vẽ sai hình
thì không cho điểm.
- Điểm toàn bài tính lẻ đến 0,25 và không làm tròn. 6
Document Outline

• ĐỀ HSG MÔN TOÁN LỚP 10 năm học 2023-2024
• HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM MÔN TOÁN 10-2024