Đề thi chọn HSG Toán 10 năm học 2019 – 2020 trường THPT thị xã Quảng Trị

SỞ GD&ĐT QUẢNG TRỊ KỲ THI CHỌN HSG VĂN HÓA LỚP 10, 11
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ Khóa thi ngày 12 tháng 6 năm 2020 Môn thi: Toán 10 ĐỀ THI CHÍN H TH ỨC (Đ ề có 01 t
rang) Thời gian làm bài: 180 phút, không kể thời gian giao đề
Câu 1 (2 điểm): Cho hàm số 2
y  x  4x  3 có đồ thị là (P) . Tìm giá trị của tham số m để
đường thẳng d : y  x  m cắt đồ thị (P) tại hai điểm phân biệt có hoành độ x , x thỏa mãn m 1 2 1 1   2. x x 1 2
Câu 2 (4 điểm):
a. Giải bất phương trình: 2 2
(x  3x) 2x  3x 1  0 . 2 3 2
x  x y  xy  xy  y 1
b. Giải hệ phương trình:  2 2
(x  y)  xy 1
Câu 3 (4 điểm): Cho phương trình: 2
x  4  5  x  20  x  x  m , (1), (với m là tham số).
a. Giải phương trình (1) khi m  3 .
b. Tìm tất cả các giá trị của m để phương trình (1) có nghiệm.
Câu 4 (4 điểm): 2sin  3cos
a. Cho cot  3 , tính giá trị biểu thức: P  . 3 3 cos   4sin 
b. Trong mặt phẳng tọa độ Oxy , cho hình chữ nhật ABCD có phương trình đường
thẳng AB là x  2y 1 0 . Biết phương trình đường thẳng BD là x  7y 14  0 và đường
thẳng AC đi qua điểm M (2;1) . Tìm tọa độ các đỉnh của hình chữ nhật ABCD .
Câu 5 (2 điểm): Cho tam giác ABC có trọng tâm G và điểm E thỏa mãn BE  3.EC  0.
Gọi I là giao điểm của AC và GE , tính tỉ số IA . IC
Câu 6 (2 điểm): Cho tam giác ABC có chu vi bằng 20, góc 0
BAC  60 , bán kính đường tròn
nội tiếp tam giác bằng 3 . Gọi A , B ,C là hình chiếu vuông góc của , A ,
B C lên BC,C , A AB 1 1 1
và M là điểm nằm trong tam giác ABC thỏa mãn ABM  BCM  CAM   . Tính cot và
bán kính đường tròn ngoại tiếp tam giác A B C . 1 1 1
Câu 7 (2 điểm): Cho x, y,z2019;202 
0 . Tìm giá trị lớn nhất của biểu thức: 2019.2020  xy 2019.2020  yz 2019.2020  zx f ( , x y, z)    .
(x  y)z
( y  z)x
(z  x) y
-----------------HẾT---------------------
Thí sinh không được sử dụng tài liệu và MTCT (đối với môn Toán).
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:……………………………….Số báo danh:……………….
ĐÁP ÁN THI CHỌN HSG VĂN HÓA LỚP 10, 11 – MÔN TOÁN Câu Lời giải Điểm
Phương trình hoành độ giao điểm của (P) và d     m: 2 x m x 4x 3 2 
x  5x  3  m  0 (*) 0,5đ
dm cắt đồ thị (P) tại hai điểm phân biệt khi (*) có 2 nghiệm phân biệt x , x 1 2     1) 2đ 13  x x 5
25 12  4m  0  m  . Khi đó 1 2  . 0,5đ 4 x x  3  m  1 2 1 1 1 0,5đ Mà 
 2  x  x  2x x  5  6  2m  m  thỏa mãn 1 2 1 2 x x 2 0,5đ 1 2
Giải bất phương trình: 2 2
(x  3x) 2x  3x 1  0 . (**) Điều kiện: 1 2
2x  3x 1  0  x  1 x  2 1 0,5đ + x  1 x  nghiệm đúng. 2.a) 2đ 2 1 + x  1 x  : 2
(**)  x  3x  0  x  3  x  0 , thỏa mãn 0,5đ 2 0,5đ Vậy (**) có nghiệm là: 1
x  3  x  0  x  1 x  2 0,5đ 2 3 2
x  x y  xy  xy  y 1
Giải hệ phương trình:  2 2
(x  y)  xy 1 2 2
xy(x  y)  xy  x  y 1 2     x y a  . Đặt  ta có hệ pt: 2 2
(x  y)  xy 1 xy  b 2 2
ab  a  b 1 b  1 a b  1 a      0,5đ 2 2 2 3 2 a  b 1
a(1 a )  a 1 a 1
a  a  2a  0 2 b  1 a
a 1 a  2  a  0 0,5đ 2.b) 2đ         3 2            a a 2a 0 b 0 b 3 b 1 a 1 2 x  y 1 x  0 x  1  +        b   0 xy  0 y  1  y  0 a  2  2 x  y  2  x  1  0,5đ +      b   3  xy  3  y  3  a  0 2 x  y  0 x 1 +      b  1 xy 1 y 1 0,5đ
Vậy nghiệm của hệ là : (1 ; 1) ; (0 ; -1) ; (-1 ; 3) ; (1 ; 0) ; (-1; 0) Khi m = 3 ta có pt: 2
x  4  5  x  20  x  x  3 : đk: x  4  ;  5 2  Đặt t 9 2
x  4  5  x  t  20  x  x  0,5đ 2 3a) 2đ 2 t  9 t  1  (l) Pttt: 2 t 
 3  t  2t  3  0   0,5đ 2 t  3 x  4  + 2 t  3 
x  4  5  x  3  20  x  x  0   0,5đ x  5 0,5đ 2  Đặt t 9 2
x  4  5  x  t  20  x  x  ;t  3  ;3 2   0,5đ 2 2 t  9 Pttt: 2 t 
 m  t  2t  2  m  9 0,5đ 3b) 2đ 2 Xét 2
f (t)  t  2t;t  3
 ;3 2  min f (t)  f (3)  3;max f (t)  f (3 2) 186 2   0,5đ  Vậy pt có nghiệm khi: 9 3  2
 m  9 18  6 2  3  m   3 2 0,5đ 2 2 2 2sin  3cos
2(1  cot x)  3cot x(1  cot x) 7  0 0,5đ    0,5đ 4a) 2đ P 3 3 3 cos   4sin  cot x  4 31 0,5đ 0,5đ
Do B  AB  D
B nên tọa độ B là nghiệm của hệ:  21 x 
x  2y 1  0  5  21 13      B ;    0,5đ
x  7 y  14  0 13  5 5  y   5 Gọi 2 2 n  ( ; a )
b ;(a  b  0) là VTPT của AC, AC ta có: 3 2 2 cos(n ;n
 cos(n ;n  2a  b  a  b AC AB D B AB 2 a  b  2 2 7a 8ab b 0       b   a   7 4b) 2đ
+ a= -b: Chọn a = 1; b = -1  AC: x – y – 1 = 0
A  AB  AC nên tọa độ A là nghiệm của hệ:
x  2y 1 0 x  3     A3;2 0,5đ
x  y 1 0 y  2
I  DB  AC nên tọa độ I là nghiệm của hệ:  7 x 
x  7y 14  0  2  7 5      I ;   0,5đ
x  y 1 0 5  2 2   y   2  
Do I là trung điểm của AC và BD nên   14 12 C 4;3 ;D ;    5 5  0,5đ
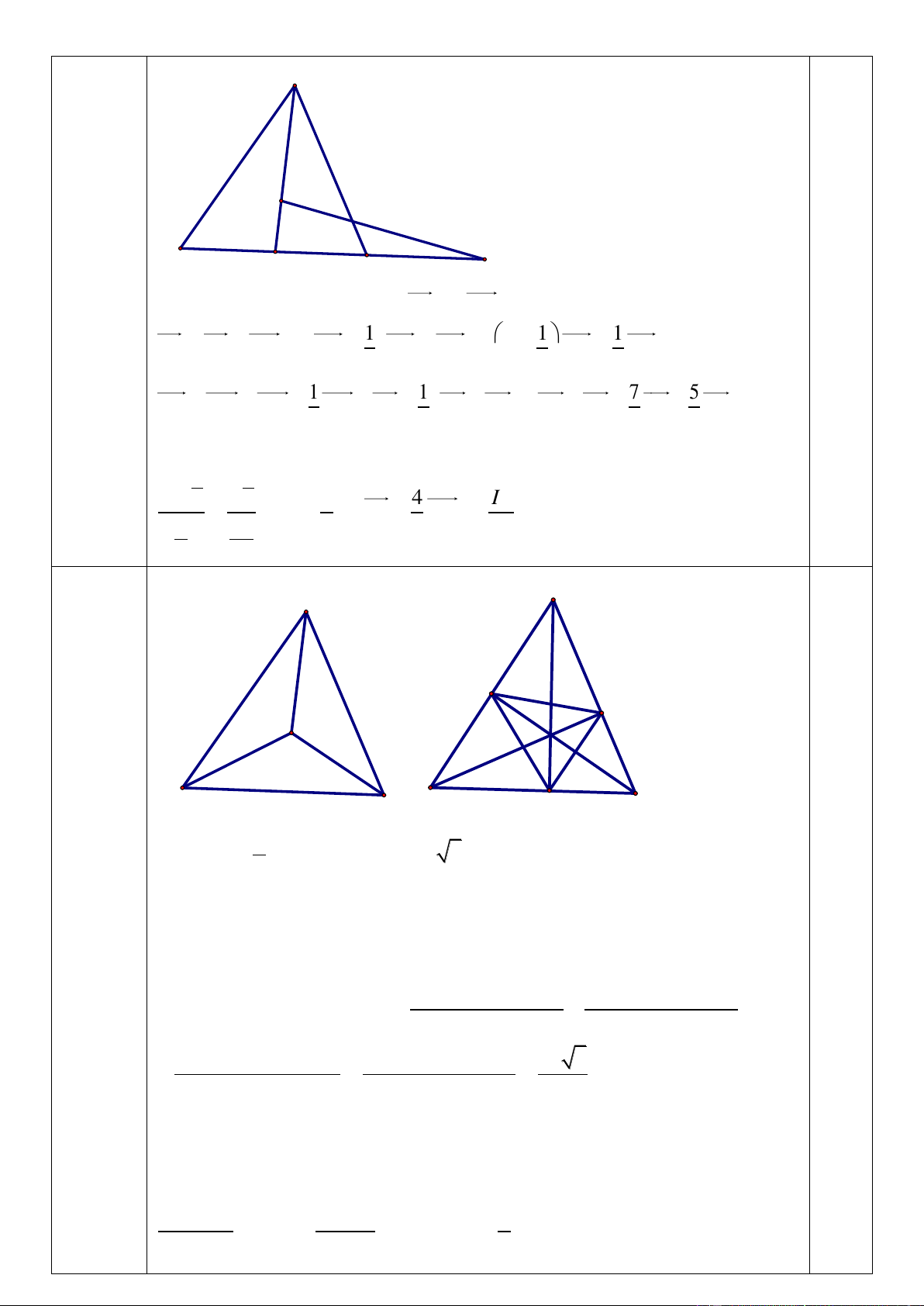
+ a = -b/7 (loại) vì AC//BD A G I B M C E 5) 2đ
Gọi M là trung điểm BC đặt  AI kAC 1  1  1
GI  AI  AG  k AC  (AB  AC)  k  AC  AB   0,5đ 3  3  3 1 1 N  GM        7 5 G MN AM BC
AB AC  AC  AB  AC  AB 0,5đ 3 6 6 6
Do G, I, N thẳng hàng nên ta có: 1 1 k   0,5đ 4 4 3 3 IA   k 
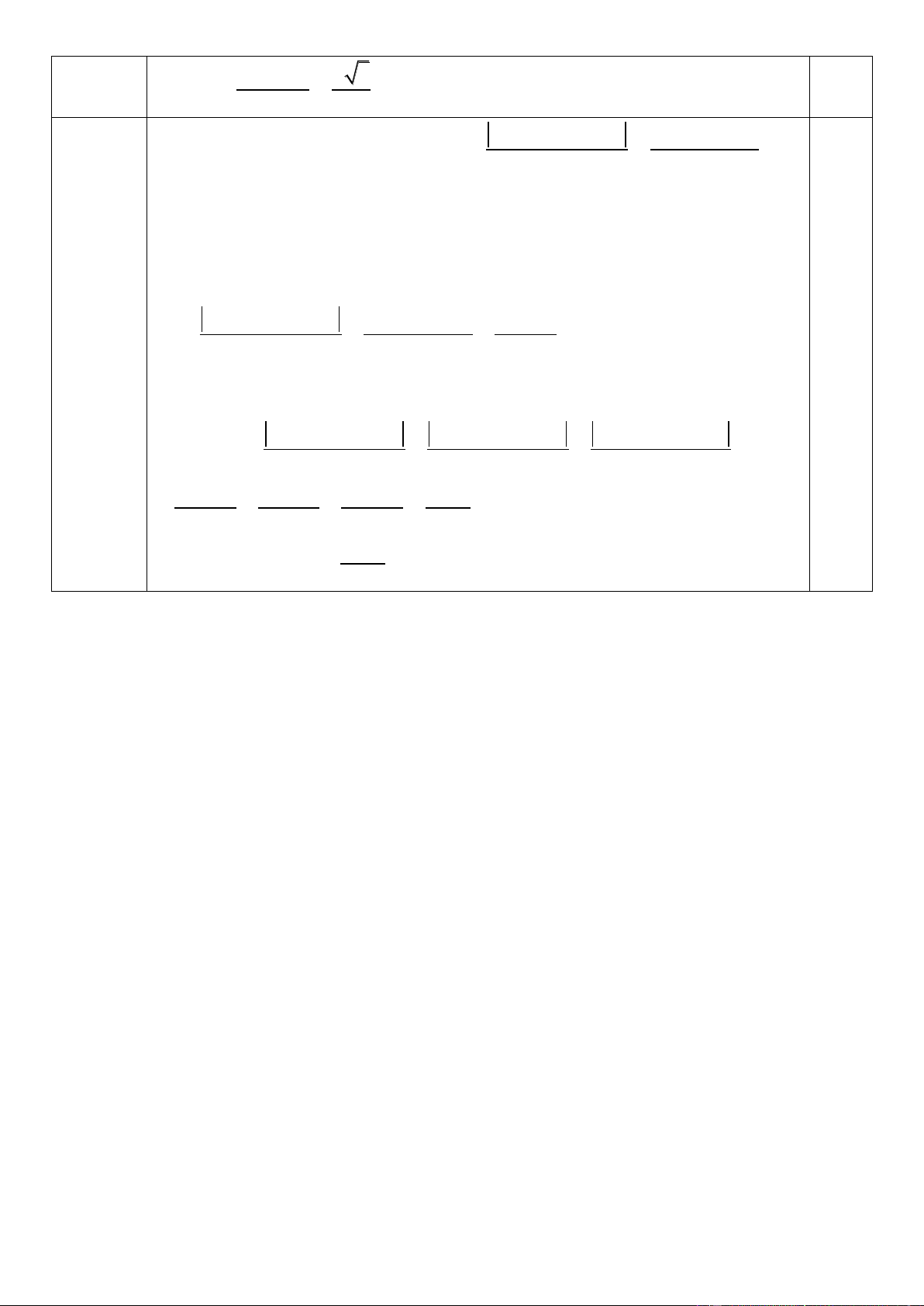
 AI  AC   4 7 5  5 5 IC 0,5đ 6 6 A A C1 c b B1 M B B a C A1 C Ta có: 1 0 S  b . c sin 60  r
p  10 3  bc  40 2 2 2 2 0 2 2 2 2
a  b  c  2b . c o
c s60  a  (b  c)  3bc  a  (10  a) 120  a  7 6) 2đ b   c 13 b   8 b   5 0,5đ      b  c  40 c   5 c   8 2 2 2 2 2 2 AB BM AM BC CM BM cot    
 ABM  BCM  CAM    4.S 4.S ABM CBM 2 2 2 2 2 2
CA  AM  CM
AB  BC  CA 23 3    0,5đ 4.S 4.S 20 CMA ABC Ta có 0 0
B BA  C CA  90  A  30 1 1 0
B A C  B A A  C A A  B BA  C CA  60 . Tam giác CC B nội tiếp 1 1 1 1 1 1 1 1 1 1 1
đường tròn đường kính BC nên ta có: B C B C 7 1 1 1 1  BC   7  B C  0 1 1 sin C CA sin 30 2 0,5đ 1 Mà B C 7 3 1 1 R   0,5đ 1 0 2sin 60 6 2019.2020  xy 2020  2019 Ta c/m: x
 , y2019;202  0 luôn có:  x  y 2 2 2 2
 4(2019.2020  xy)  (x  y) (2020  2019)
 (2.2019.2020  2xy (x  y)(2020  2019))(2.2019.2020  2xy  (x  y)(2020 2019))  0
 2020(2.2019  x  y)  (
x 2019  y)  y(2019  ) x . 
2019(2.2020  x  y)  (
x 2020  y)  y(2020  ) x   0 (đúng) 0,5đ 2019.2020  xy  Vậy 2020 2019 1   0,5đ 7) 2đ x  y z 2z 2.2019
Dấu « = » xảy ra khi x = y = z = 2019. Áp dụng ta có : 2019.2020  xy 2019.2020  yz 2019.2020  zx f ( , x y, z)   
(x  y)z
( y  z)x
(z  x) y 1 1 1 3     0,5đ 2.2019 2.2019 2.2019 4038 Vậy 3 max f ( , x y, z) 
;khi x  y  z  2019 0,5đ 4038