



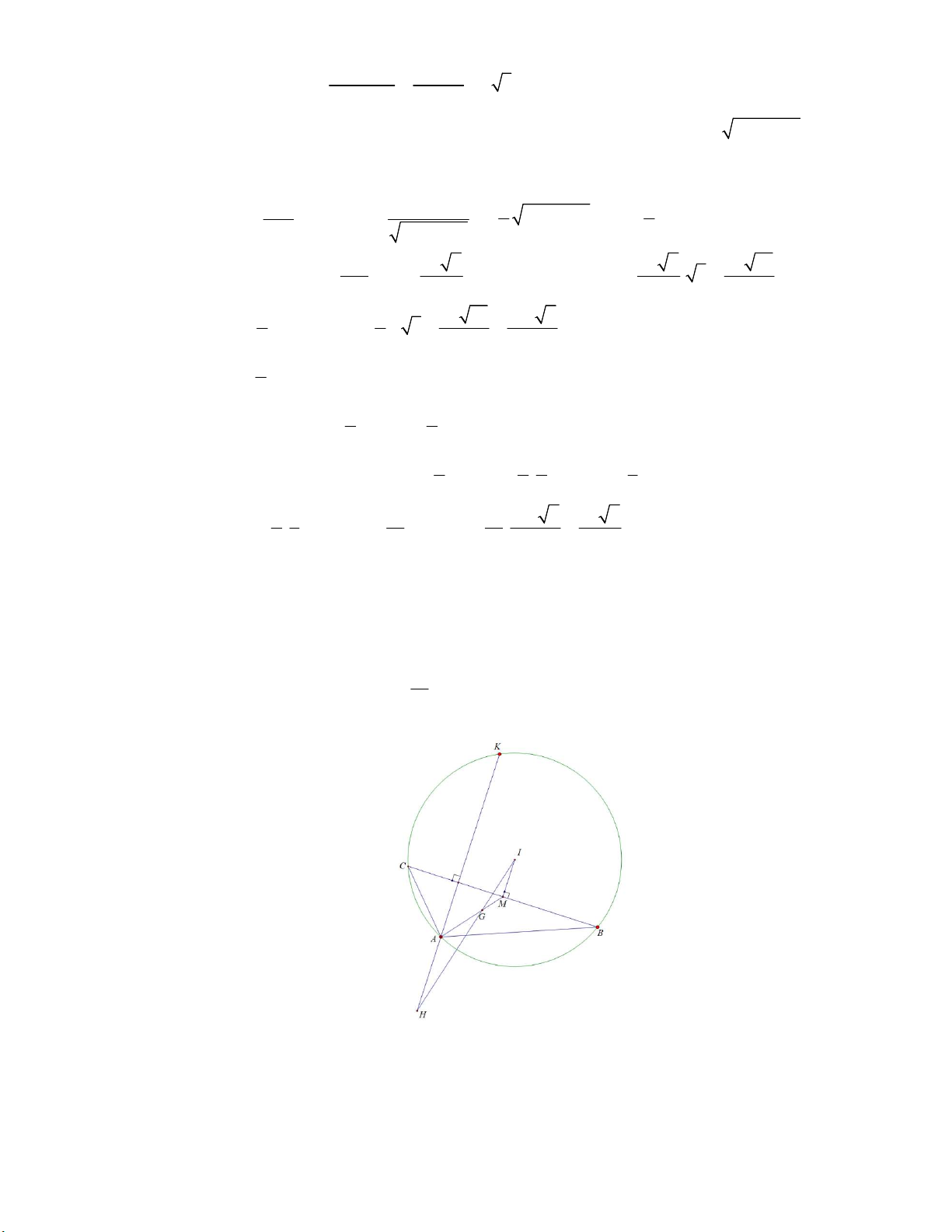


Preview text:
SỞ GD&ĐT VĨNH PHÚC
KỲ THI CHỌN HSG LỚP 12 THPT NĂM HỌC 2021 – 2022
ĐỀ THI MÔN: TOÁN – THPT
Thời gian: 180 phút, không kể thời gian giao đề. ĐỀ CHÍNH THỨC mx 25
Câu 1. Tìm tất cả các giá trị của tham số m để hàm số y
đồng biến trên khoảng 0;10 . x m Lời giải
Tập xác định: D \ m . 2 m 25 Ta có: y . x m2
Để hàm số đồng biến trên khoảng 0;10 thì m 5 y 0, x 0;10 2 m 25 0 m 5 m 10 m 0;10 m 0;10 m 0 m 5 m 10 Vậy m ;
105; là các giá trị cần tìm. 1 Câu 2. Cho hàm số 3 2 y x mx 2 m
1 x , với m là tham số. Tìm tất cả các giá trị của tham số m 3
để đồ thị hàm số đã cho có hai điểm cực trị , A B sao cho ,
A B cách đều đường thẳng d : y 5x 9 . Lời giải
Tập xác định D . a 1 0 y Ta có 2 2
y x 2mx m 1 có
suy ra hàm số đã cho luôn có 2 m m m y 2 1 1 0
hai điểm cực trị với mọi m . Cách 1. 1 1 2 1
Lấy y chia y ta được y x m y x m 2 m 1. 3 3 3 3
Đặt A x ; y , B x ; y là tọa độ hai điểm cực trị của đồ thị hàm số đã cho, ta có: 1 1 2 2 2 1 y x m 2 m 2 1 1 , y x m 2
m 1 . Do đó, đường thẳng đi qua hai điểm cực trị 1 1 2 2 3 3 3 3 2 1 ,
A B là : y x m 2 m 1 . 3 3 2 1
Vì đường thẳng : y x m 2 m
1 không song song với đường thẳng d : y 5x 9 3 3 nên ,
A B cách đều đường thẳng d : y 5x 9 khi và chỉ khi trung điểm I của đoạn thẳng AB
thuộc đường thẳng d : y 5x 9 . x x 2 1 1 1 Ta có 1 2 x
m, y x m m m m I m m m . I I I 2 3 3 1 ; 2 3 3 3 3 1 1 3 3 3 I ; m
m m d : y 5x 9 m m 5m 9 m 18m 27 0 3 3 m 3 m 3 2 m 3m 9 0 3 3 5 . m 2 m 3 Vậy 3 3 5
thỏa yêu cầu bài toán. m 2 Cách 2. 1
Đồ thị hàm số có điểm uốn 3 I ; m m m
. Để hai điểm cực trị cách đều đường thẳng 3 m 3 1
d : y 5x 9 thì I d hay 3 3
m m 5m 9 m 18m 27 0 . 3 3 3 5 m 2 m 3 Vậy 3 3 5
thỏa yêu cầu bài toán. m 2
Câu 3. Giải phương trình 3 1 cos 2x sin 2x 4cos x 8 4 3 1 sin x . Lời giải
Ta có 3 1 cos 2x sin 2x 4cos x 8 4 3 1 sin x 2
2 3 sin x 2sin x cos x 4cos x 4 3 sin x 4sin x 8 0
2sin x 3sin x cos x 2 4 3sin x cos x 2 0
2(sin x 2)( 3 sin x cos x 2) 0
3 sin x cos x 2 0
sin(x ) 1 x k2 , k . 6 3
Vậy phương trình có nghiệm: x k2 , k . 3 x 1 2 2019 2020 Câu 4. Cho f x log . Tính S f f ... f f . 2 1 x 2021 2021 2021 2021 Lời giải ĐK: 0 x 1. x Ta có f x log log x log 1 x . 2 2 2 1 x Xét: 1 1 2020 f log log . 2 2 2021 2021 2021 2 2 2019 f log log . 2 2 2021 2021 2021 3 3 2018 f log log . 2 2 2021 2021 2021 ………. 2019 2019 2 f log log . 2 2 2021 2021 2021 2020 2020 1 f log log . 2 2 2021 2021 2021 k 2021 k 1 2020 Ta thấy: f f
0, k ,1 k 2020 và từ f đến f có 2021 2021 2021 2021 2020 số hạng. 1 2 2019 2020 Do vậy tổng S f f ... f f 0 . 2021 2021 2021 2021 2 x x 2 1 y 1 y 1
Câu 5. Giải hệ phương trình: .
x 6x 2xy 1 4xy 6x 1 Lời giải 2 x x 2 1 y 1 y 1 1 .
x 6x 2xy 1 4xy 6x 1 2 1 Từ phương trình 1 ta có 2 x 1 x 2 2
x 1 x 1 y y 2 y 1 y x x y y2 2 1 1
f x f y * . Xét hàm số f t 2 t 1 t , t . 2 t 1 t t Ta có: f t 1 0, t . 2 2 1 t 1 t
Suy ra hàm số f liên tục và đồng biến trên .
Do đó * x y y x . Thay vào phương trình 2 ta được 2 2
x 2x 6x 1 4x 6x 1 2 2 2
2x 6x 1 x 2x 6x 1 6x 0 x 0 2 2x 6x 1 2 x 2 2x 6x 1 0 3 11 x 2 . 2 2x 6x 1 3x x 0 x 1 2 7x 6x 1 0 3 11 3 11
Vậy hệ phương trình đã cho có 2 nghiệm ; , 1; 1 . 2 2 Câu 6. Giả sử E 2 3 20
10;10 ;10 ;...;10 . Lấy ngẫu nhiên đồng thời 2 số từ tập hợp E , giả sử hai số được
lấy ra là x và y (với x y ). Tính xác suất sao cho log y là một số nguyên. x Lời giải n 2 C 190 . 20 x 10 ; y 10 . log y
; ; , 1;20 A . x
Nếu 1 n ; n 2;20 2;3;4;...;2
0 có 19 cách chọn.
Nếu 2 2n | n ; n 3;20 4;6;8;...;2 0 có 9 cách chọn.
Nếu 3 3n | n ; 2 n 6 6;9;12;15;1 8 có 5 cách chọn.
Nếu 4 4n | n ; 2 n 5 8;12;16;2 0 có 4 cách chọn.
Nếu 5 5n | n ; 2 n 4 10;15;2 0 có 3 cách chọn.
Nếu 6 6n | n ; 2 n 3 12;1 8 có 2 cách chọn.
Nếu 7 14 có 1 cách chọn.
Nếu 8 16 có 1 cách chọn.
Nếu 9 18 có 1 cách chọn.
Nếu 10 20 có 1 cách chọn.
Gọi A : “ log y là một số nguyên” x
n A 19 9 5 4 3 2 1111 46 . P A n A 46 23 . n 190 95
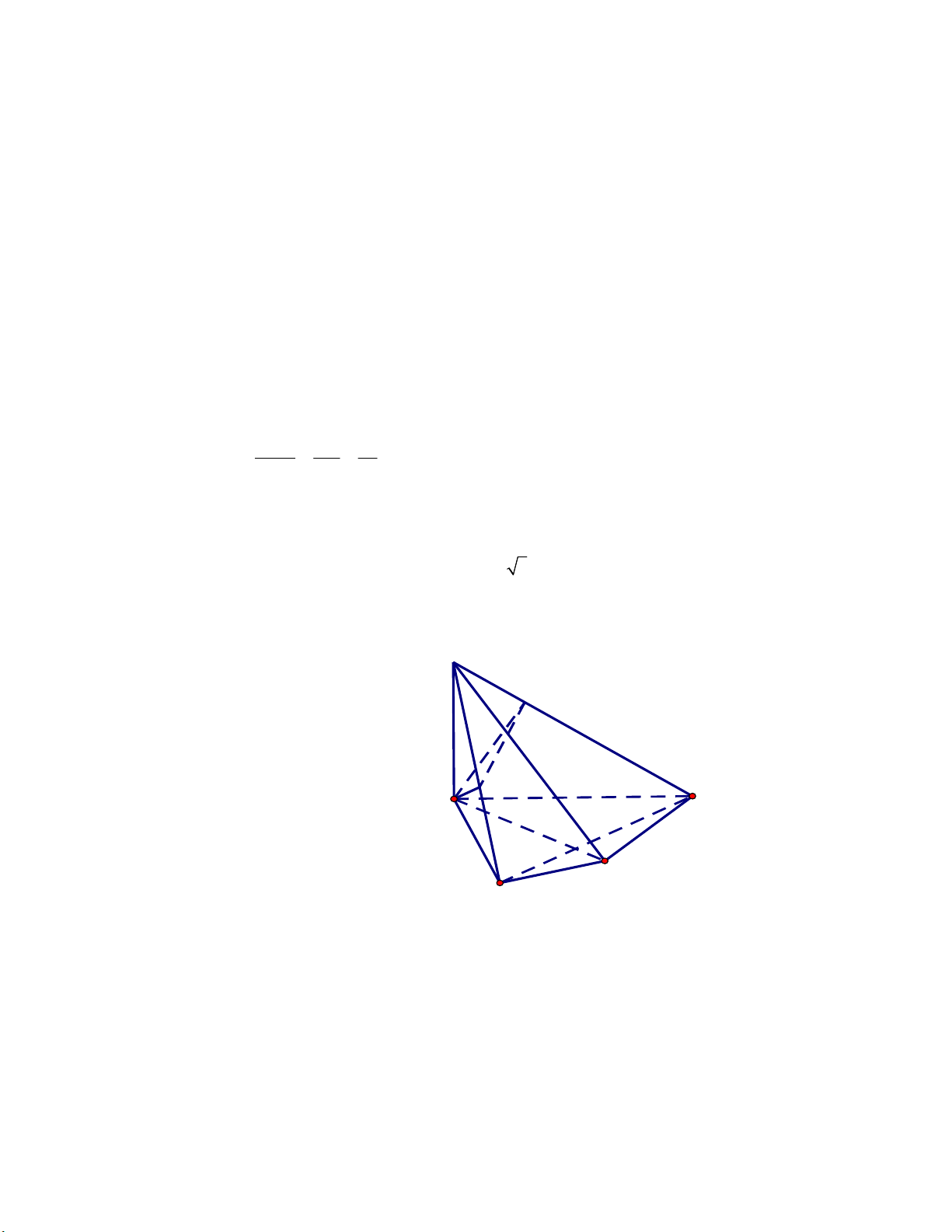
Câu 7. Cho hình chóp S.ABCD có SA vuông góc với mặt đáy, ABCD là tứ giác nội tiếp đường tròn
đường kính AC . Gọi hai điểm M , N tương ứng là hình chiếu vuông góc của điểm A lên hai
đường thẳng SB và SD . Biết SA a, BD a 3 và
BAD 60 . Tính côsin của góc giữa hai
mặt phẳng AMN và ABCD . Lời giải S N M A D C B
Do tứ giác ABCD là tứ giác nội tiếp đường tròn đường kính AC nên AB BC, AD DC . Ta có : BC BA +)
BC SAB BC AM BC SA AM SB +)
AM SBC AM SC AM BC C D AD +)
CD SAD CD AN C D SA AN SD +)
AN SCD AN SC AN CD SC AM +) SC AMN . SC AN SC AMN +)
AMN , ABCD SC, SA. SA ABCD
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABD . Khi đó ta có: BD a 3 R a . 2sin ABD 2sin 60
Mặt khác R cũng là bán kính đường tròn ngoại tiếp tứ giác ABCD AC 2R 2a.
Xét SAC vuông tại A , ta có: SC SA AC a a2 2 2 2 2 a 5. SA a 1 1 Khi đó: cos ASC 0 cosS , A SC cos ASC . SC a 5 5 5 1
Vậy côsin của góc giữa hai mặt phẳng AMN và ABCD là . 5
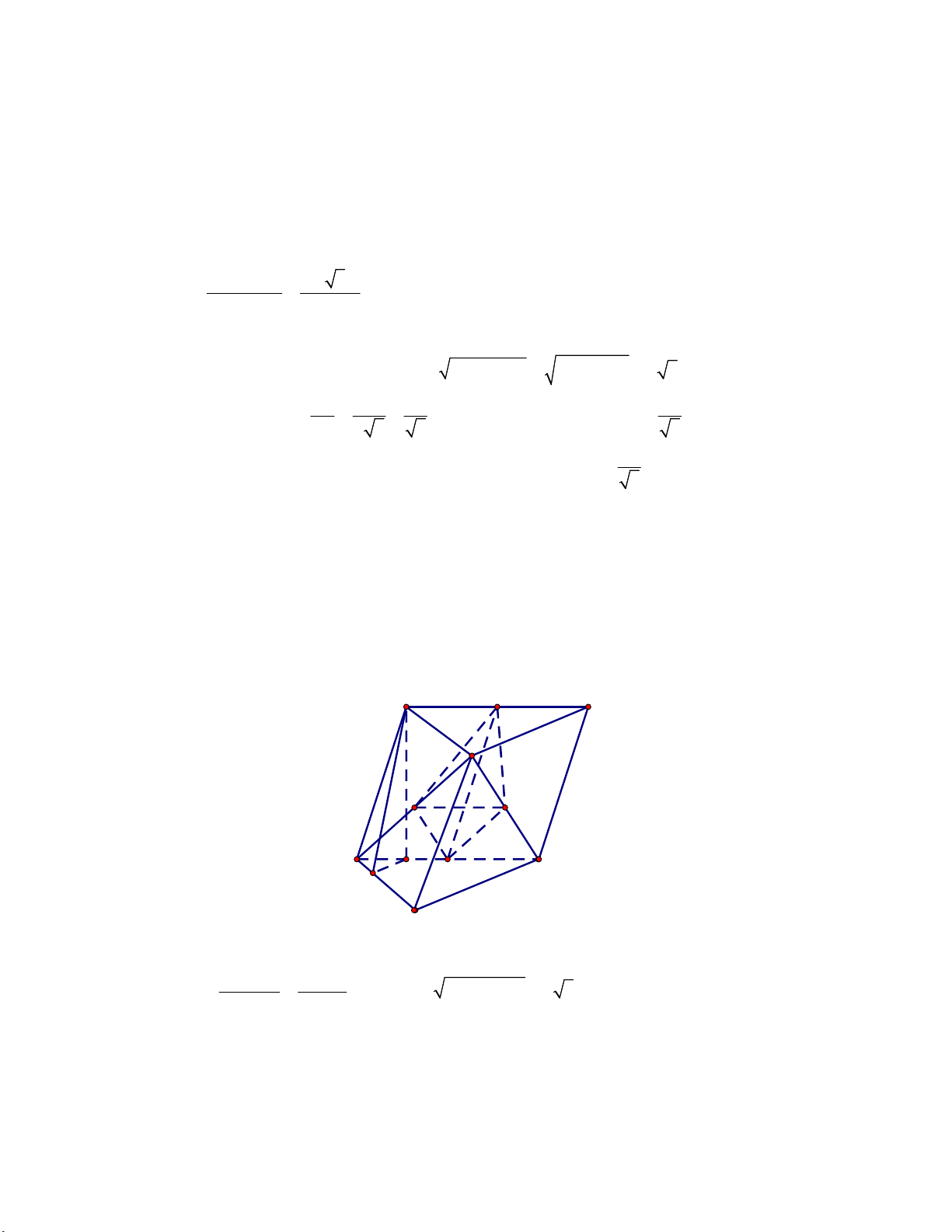
Câu 8. Cho hình lăng trụ ABC.A B C
có đáy ABC là tam giác vuông tại A , cạnh AC a và
ABC 30. Tứ giác BCC B là hình thoi có B B
C nhọn, mặt phẳng BCC B vuông góc với
mặt phẳng ABC , góc giữa mặt phẳng ABB A
và mặt phẳng ABC bằng 60. Gọi
M , N, P,Q lần lượt là trung điểm của các đoạn thẳng BC, B C , A B
và AC . Tính theo a thể
tích của khối tứ diện MNPQ . Lời giải B' N C' A' P Q B C H D M a A
Xét tam giác ABC vuông tại A ta có AC a 2 2 BC a AB BC AC a . sin 2 ; 3 ABC sin 30
Gọi H là hình chiếu của B lên BC . Khi đó B H (ABC) (do BCC B ABC ).
Gọi D là hình chiếu của H trên AB . AB DHB B D H ABB A , ABC 60. DH x Đặt DH x BD x . tan 3 DBH tan 30 Xét tam giác BB D vuông tại D có 2 2 2 2 2 B D B B BD 4a 3x 2 2 B D 4a 3x . Xét tam giác B D H vuông tại H ta có DH x 1 1 cos B D H cos60 2 2 4a 3x x 2 2 4a 3x 2 x . 2 2 B D 4a 3x 2 4 2 4a 2a 7 2a 7 2a 21 2 2 2 4a 7x x x B H DH.tan 60 . 3 . 7 7 7 7 3 1 1 2a 21 3a 7 V . .A . B AC.B H .a 3. . a ABC.A B C 2 2 7 7 1 Vì S S
và NC / / BC NC / / A B
C do đó d N, ABC d C , A B C . M PQ 4 A B C 1 1 Suy ra V V = V V MNPQ N .MPQ . 4 N A = BC . 4 C A B . C 1 1 2 1 Mặt khác ta lại có: V V V . V V . C .A BC A .C BC A .BCC B ABC.A B C ABC. 2 2 3 3 AB C 3 3 1 1 1 1 3a 7 a 7 Vậy V . V V . . MNPQ ABC.A B C ABC. 4 3 12 A B C 12 7 28
Câu 9. Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC có góc
BAC tù. Đường tròn C
ngoại tiếp tam giảc ABC có phương trình C x 2 y 2 : 2
2 25 . Đường thẳng đi qua A
và vuông góc với BC cắt đường tròn C tại điểm K 1;2 ( K không trùng với A ). Trọng 16
tâm của tam giác ABC là G 1;
. Tính diện tích tam giác ABC . 3 Lời giải
Gọi M là trung điểm BC . Khi đó IM BC với I 2;2 là tâm đường tròn C . Gọi H IG AK .
Do IM / / AH nên áp dụng định lý Talet ta có IM IG MG 1 G H 2.IG G H 2.IG 1 . AH GH GA 2 AH 2.IM AH 2.IM 2
Gọi tọa độ H x; y . 16 10
Ta có I 2;2 ; GH x 1; y ; IG 1; . 3 3 x 1 2 x 1 Từ (1) ta có 16 20 H 1;12 . y y 12 3 3
Đường thẳng AK đi qua điểm K 1;2 và H 1;12 có véctơ chỉ phương là 1 1
u KH 0;14 0;7 VTPT n 7;0 . 2 2
Phương trình đường thẳng AK là 7 x
1 0 y 2 0 x 1. Do ,
A K C AK , ta có x 1 x 1 x 1 y 2 . x 2
2 y 22 25 y 2 2 16 x 1 y 6
Suy ra tọa độ A1;6 .
Gọi tọa độ M a;b .
Ta có IM a 2;b 2 ; AH 0;6. 2 a 2 0 a 2 Từ (2) ta có M 2;5 . 2 b 2 6 b 5
Đường thẳng BC đi qua điểm M 2
;5 và vuông góc với AK nên có VTPT u 0; 7 có
phương trình là 7 y 5 0 y 5.
Do B , C là giao điểm của đường thẳng BC và đường tròn C nên tọa độ B , C là nghiệm hệ phương trình y 5 y 5 x 2
2 y 22 25 x 2 2 16
y 5 x 2 B 2;5 .
y 5 x 6 C 6 ;5 Khi đó BC 8 ;0 BC 8 . 1
Khoảng cách từ A đến BC là d , A BC 1. 2 1 1 1
Vậy diện tích ABC là S .d A BC BC . A BC , . .1.8 4 2 2 Câu 10. Cho ,
x y là các số thực thỏa mãn x y x 1 2 y 2 . Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
P x y 2 x 1 y 1 8 4 x y . Lời giải x 1
x y x 1 2 y 2 . Điều kiện x y 0 . y 1
Áp dụng bất đẳng thức Bunhiacopxki 2 2 2 2 ax by a b x y . x y x
y x y x y 2 2 1 2 2 1 2 1 3 x 1 y 1 3 x y
x y2 3x y 0 0 x y 3 .
P x y x y x y x y2 2 2 2 1 1 8 4
2x y 8 4 x y 2 .
Đặt t x y, 0 t 3. 4 2t 2 4t 4 2
P t 2t 8 4 t 2, 0 t 3, P 2t 2 . 4 t 4 t 0 t 3 P t 0 t 3 0 1 4 t 2 . t 2 1 4 t 3 2 4 t 2t 7t 0 0 t 3 0 t 3 t 0 P 0 18 t 0 t 0 . . t 1 2 2 P 3 25 2 t 2t 7 0 t 1 2 2 x 2 x 1
Vậy giá trị lớn nhất của P bằng 25 khi
và giá trị lớn nhất của P bằng 18 khi . y 1 y 1
Document Outline
- de-thi-chon-hsg-toan-12-thpt-nam-2021-2022-so-gddt-vinh-phuc-đã chuyển đổi
- HSG-VĨNH PHÚC NĂM 2021-2022




