Đề thi chuyên đề Toán 10 lần 2 năm 2019 – 2020 trường Ngô Gia Tự – Vĩnh Phúc

SỞ GD&ĐT VĨNH PHÚC
ĐỀ THI CHUYÊN ĐỀ LẦN II MÔN TOÁN LỚP 10
TRƯỜNG THPT NGÔ GIA TỰ
Năm học 2019 – 2020
--------------------------------
Thời gian làm bài: 120 phút
Đề thi gồm có 02 trang
(không kể thời gian phát đề) Mã đề: 132 I.
PHẦN TRẮC NGHIỆM (3,0 điểm)
Thí sinh kẻ ô theo mẫu sau vào giấy thi và điền phương án trả lời. 1 2 3 4 5 6 7 8 9 10 11 12
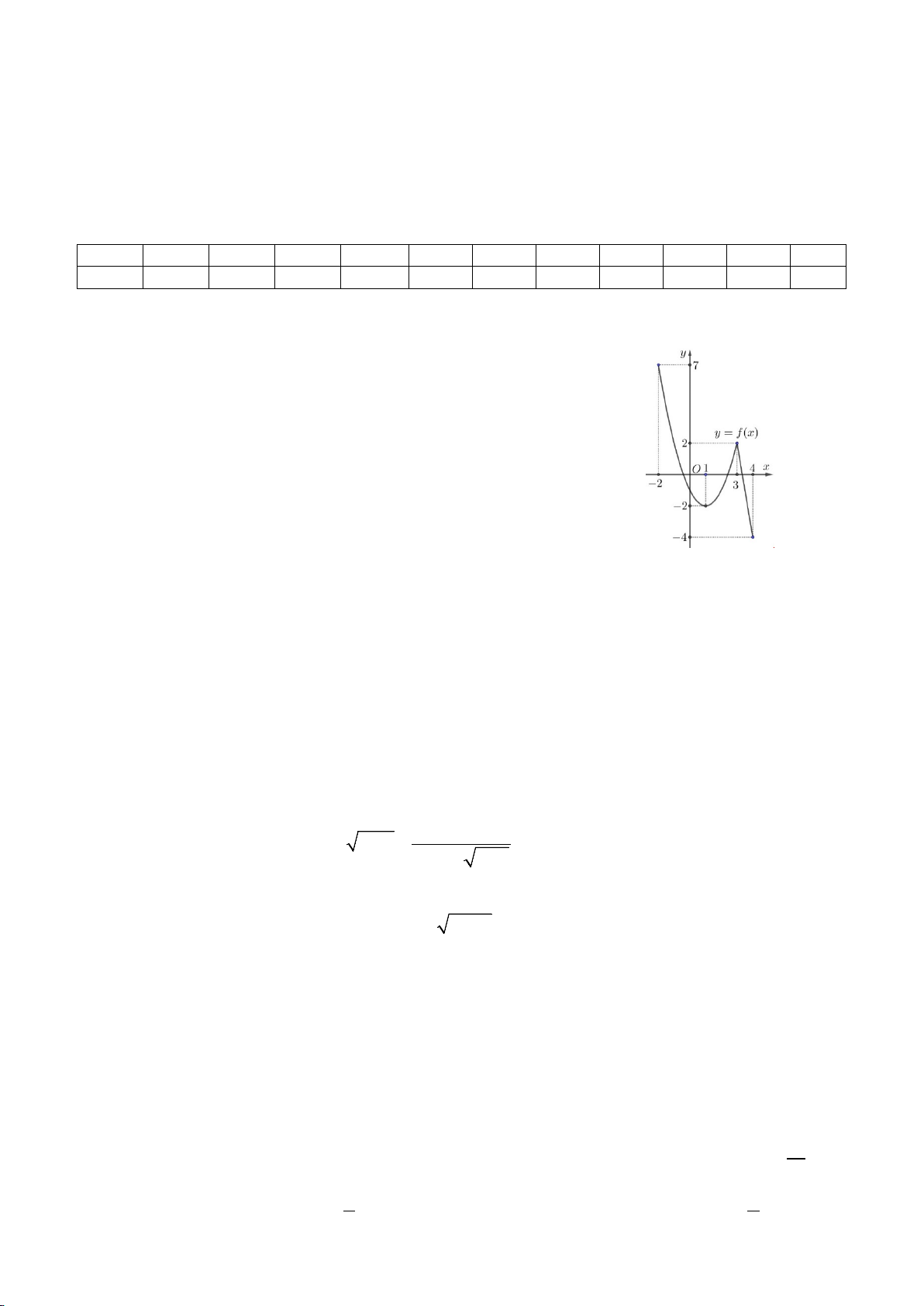
Câu 1: Cho hàm số y = f ( x) có đồ thị như hình vẽ bên. Trong các khẳng định sau, khẳng định nào sai?
A. Hàm số đồng biến trên khoảng (1;3) .
B. Hàm số nghịch biến trên khoảng (3; 4) .
C. Hàm số nghịch biến trên khoảng ( 2; − ) 1 .
D. Hàm số đồng biến trên khoảng (0;3) .
Câu 2: Tích tất cả các nghiệm của phương trình 2
x + x − 5 = 0 là A. 5 − B. 5 C. 1 D. 1 −
x − y + z = 2 
Câu 3: Số nghiệm của hệ phương trình x + y + z = 6 là
x + y − z = 4  A. 0 B. 1 C. 3 D. Vô số
Câu 4: Trong hệ trục tọa độ Oxy , cho tam giác ABC có A( 1 − ;3), B(2; ) 1 , C ( 1
− ;2). Tìm tọa độ trọng tâm
G của tam giác ABC . A. G (0;6) B. G (0; ) 1 C. G (0; 2) D. G (0;3) 3
Câu 5: Tập xác định của hàm số y = 6 − x + ( là x − 3) 1+ x A. D = ( 1 − ;6] \{ } 3 B. D = [ 1 − ;6] \{ } 3 C. D = ( 1 − ;6] D. D = [ 1 − ;6]
Câu 6: Tổng tất cả các nghiệm của phương trình 2x −1 = x − 2 là A. 6 B. 5 C. 1 D. 2 2
x = 3x − y Câu 7: Cho hệ 
có hai nghiệm ( x ; y , x ; y . Khi đó ( x + x + y y bằng 1 2 )2 1 1 ) ( 2 2 ) 2  1 2
y = 3y − x A. 3 B. 1 C. 4 D. 2 −
Câu 8: Trong hệ trục tọa độ Oxy cho bốn điểm A(0; ) 1 ; B ( 2; − 0);C (2; 2
− ); D(2;2) . Tìm ba điểm thẳng
hàng trong bốn điểm đã cho. A. , A B, C
B. B, C, D C. , A C, D D. , A B, D  13 
Câu 9: Tìm phương trình parabol ( P) 2
: y = ax − bx − 2 biết parabol ( P) có tọa độ đỉnh I 3 − ;−   .  2  1 1 A. 2
y = −x + 3x − 2 B. 2 y = x + 3x − 2 C. 2
y = x + 3x − 2 D. 2 y = − x + 3x − 2 2 2
Câu 10: Một công ty Taxi có 85 xe chở khách gồm hai loại: xe chở được 4 khách và xe chở được 7 khách.
Nếu dùng tất cả số xe đó, tối đa một lần công ty chở được 445 khách. Số lượng xe mỗi loại là
A. 35 xe 4 chỗ, 50 xe 7 chỗ;
B. 40 xe 4 chỗ, 45 xe 7 chỗ;
C. 50 xe 4 chỗ, 35 xe 7 chỗ;
D. 45 xe 4 chỗ, 40 xe 7 chỗ.
Câu 11: Có bao nhiêu số tự nhiên có 4 chữ số và chia hết cho ít nhất một trong ba số 3, 4, 5? A. 5100 B. 7050 C. 5250 D. 5400  1 
Câu 12: Cho tam giác ABC có trọng tâm G , H là chân đường cao kẻ từ A sao cho BH = HC . Điểm 3    
M di động trên BC sao cho BM = xBC . Tìm x để độ dài vectơ MA + GC đạt giá trị nhỏ nhất. 5 5 6 4 A. B. C. D. 6 4 5 5 II.
PHẦN TỰ LUẬN (7,0 điểm)
Câu 13: Cho phương trình 4 x − ( m + ) 2 3
1 x + 6m − 2 = 0 , với m là tham số thực.
a) Giải phương trình với m = 2 .
b) Tìm tất cả các giá trị của tham số m để phương trình có 4 nghiệm phân biệt x , x , x , x sao cho 1 2 3 4
x − x = x − x = x − x . 1 2 2 3 3 4
Câu 14: Giải các phương trình và hệ phương trình sau: 2
x − 2xy = 3 a)
2x −1 = 2 − x ; b)  . 2 2
2x + xy − y = 0
Câu 15: Trong hệ trục tọa độ Oxy cho tam giác ABC có A( 1 − ;3), B(2; ) 1 , C ( 3
− ;2). Tìm tọa độ điểm D
sao cho ABDC là hình bình hành.
Câu 16: Cho tam giác ABC , các điểm M , N lần lượt thuộc các cạnh AB, AC sao cho
AB = 3AM , 3AC = 4 AN . Gọi I là giao điểm của CM và BN .    
a) Phân tích các vectơ BN,CM theo hai vec tơ AB, AC .   
b) Tìm k, h ∈  sao cho IA = k IB + hIC . Câu 17: Cho hàm số 4 2
f (x) = x − 4x + 5 + m , m là tham số thực. Tìm tất cả các giá trị của tham số m để
giá trị lớn nhất của hàm số đã cho trên đoạn  2; − 5  
 đạt giá trị nhỏ nhất.
------------------- HẾT ------------------- https://toanmath.com/
Thí sinh không được sử dụng tài liệu; Cán bộ coi thi không giải thích gì thêm./.
ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ THI CHUYÊN ĐỀ MÔN TOÁN LỚP 10 LẦN II Năm học 2019 - 2020 I.
PHẦN TRẮC NGHIỆM (3,0 điểm) Mỗi câu 0,25 điểm. Mã đề 132 1 2 3 4 5 6 7 8 9 10 11 12 D A B C A B C D B C D A Mã đề 234 1 2 3 4 5 6 7 8 9 10 11 12 C D A B D A B C A B C D Mã đề 357 1 2 3 4 5 6 7 8 9 10 11 12 B C D A C D A B D A B C Mã đề 485 1 2 3 4 5 6 7 8 9 10 11 12 A B C D B C D A C D A B II.
PHẦN TỰ LUẬN (7,0 điểm) Câu Nội dung Thang điểm 13 Cho phương trình 4 x − ( m + ) 2 3
1 x + 6m − 2 = 0 , với m là tham số thực. 1,0
a) Giải phương trình với m = 2 .
Với m = 2 ta có phương trình 4 2
x − 7x +10 = 0 0,25 2 x = 2 0,25 ⇔  2 x = 5 x = ± 2 0,25 ⇔  x = ± 5
Vậy tập nghiệm của phương trình là S = {± 2;± 5} 0,25
b) Tìm tất cả các giá trị của tham số m để phương trình có 4 nghiệm 0,5
phân biệt x , x , x , x sao cho x − x = x − x = x − x . 1 2 3 4 1 2 2 3 3 4 2 x = 2 x = ± 2 0,25 Ta có 4 x − (3m + ) 2
1 x + 6m − 2 = 0 ⇔  ⇔  2 2 x = 3m −1
x = 3m −1  1  − >  > Phương trình có 4 nghiệ 3m 1 0 m m phân biệt khi  ⇔  3 3  m −1 ≠ 2 m ≠1
Khi đó phương trình có 4 nghiệm phân biệt 0,25
x = − 2, x = − 3m −1, x = 3m −1, x = 2 1 2 3 4 
x = − 3m −1; x = − 2; x = 2, x = 3m −1  1 2 3 4  11 m =  − =  Theo đề 3 3m 1 2 27 bài ta có  ⇔  (thỏa mãn điều kiện)  − = 19 3m 1 3 2 m =  3 11 19 Vậy m = hoặc m = . 27 3 1 14
Giải các phương trình và hệ phương trình sau: 1,5
a) 2x −1 = 2 − x ; ĐK: 1 ≤ 0,25 x ≤ 2 2
PT ⇒ x − = ( − x)2 2 1 2 0,25 2
⇔ x − 6x + 5 = 0 0,25 x = 1 0,25 ⇔  x = 5
Thử lại điều kiện ⇒ x = 1 0,25
Vậy phương trình có nghiệm duy nhất x = 1 . 0,25 2
x − 2xy = 3 1,0 b)  2 2
2x + xy − y = 0 2
x − 2xy = 3 0,25 ⇔ (  x + y  )(2x − y) = 0 2 x − 2xy = 3 0,25 
⇔ x + y = 0 
2x − y = 0 x = 1 ± 0,25 2  3  x = 3   y = −x y = −x ⇔ ⇔    15 2 5  x = 3 x = ±   5 y = 2x  y = 2x x = 1 ± 0,25  y = 1   15 ⇔ x = ±  5   2 15  y = ±   5
Vậy tập nghiệm của hệ phương trình là      S = (  − ) (− ) 15 2 15 15 2 15 1; 1 , 1;1 ,  ; , − ; −      5 5 5 5      15
Trong hệ trục tọa độ Oxy cho tam giác ABC có A( 1 − ;3), B(2; ) 1 , C ( 3 − ;2). 1,0
Tìm tọa độ điểm D sao cho ABDC là hình bình hành.  
ABDC là hình bình hành ⇔ AB = CD 0,25
Gọi D ( x ; y . Ta có 0,25 D D )   AB = (3; 2
− ),CD = (x + 3; y − 2 D D )   x + 3 = 3 0,25 D AB = CD ⇔  y − 2 = 2 −  D x = 0 0,25 D ⇔  y = 0  D 2 Vậy D(0;0) . 16
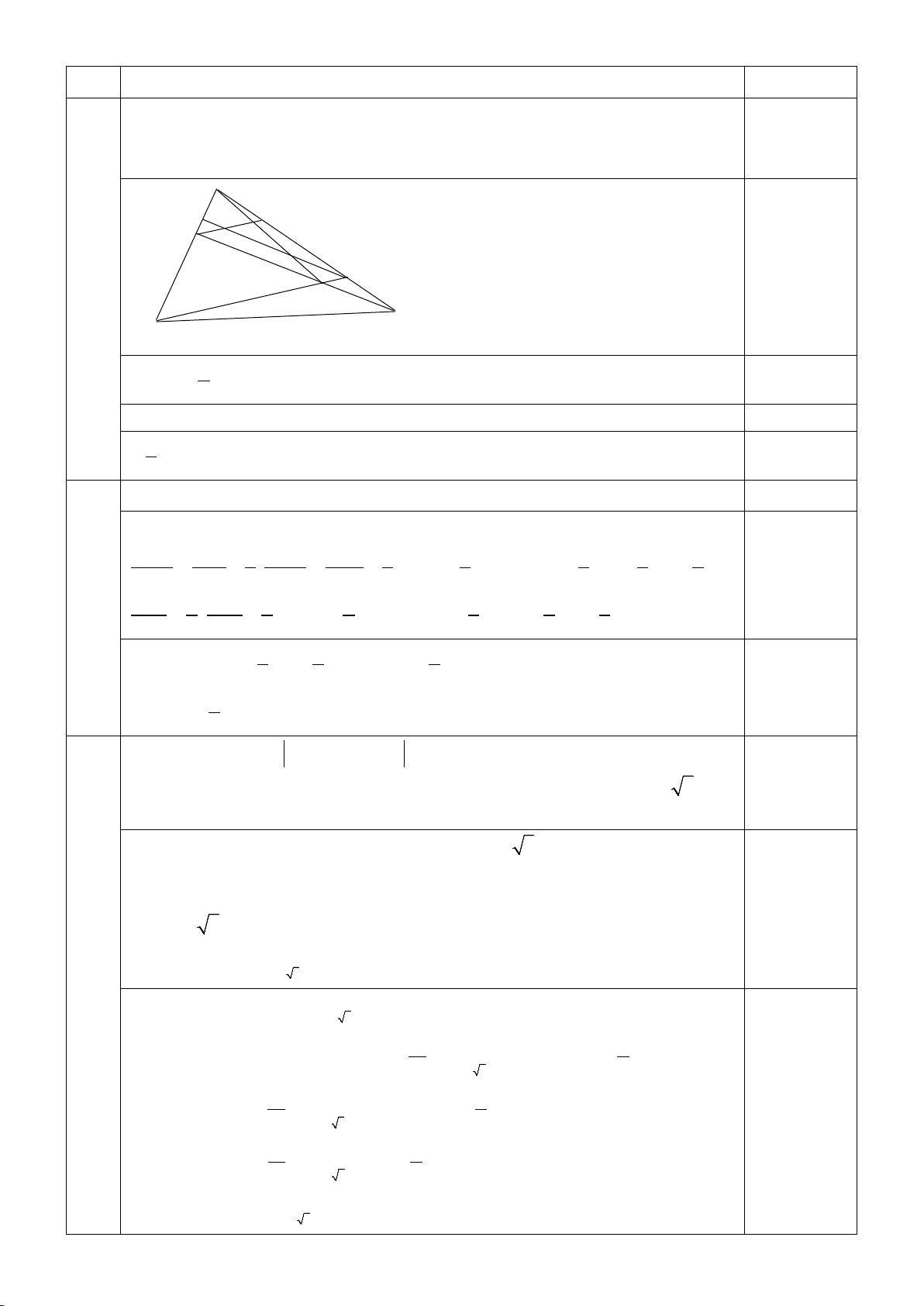
Cho tam giác ABC , các điểm M , N lần lượt thuộc các cạnh AB, AC sao cho 1,0
AB = 3AM , 3AC = 4 AN . Gọi I là giao điểm của CM và BN .    
a) Phân tích các vectơ BN,CM theo hai vec tơ AB, AC . A 0,25 N’ M’ M N I B C
  
Ta có: BN = BA + AN  3  = − 0,25 AB + AC 4
  
CM = CA + AM 0,25 1   = 0,25 AB − AC 3   
b) Tìm k, h ∈  sao cho IA = k IB + hIC . 0,5
Kẻ MM '/ /BN , NN '/ /CM ,(M '∈ AC, N '∈ AB) . Ta có 0,25 MM ' AM 1 IN CN 1  1   8  8  2  = = , =
= ⇒ IN = BN ⇔ IB = − BN = AB − AC BN AB 3 MM ' CM ' 3 9 9 9 3 NN ' 3 IM 8  2   1  1  1  = ,
= ⇒ IM = CM ⇔ IC = − CM = − AB + AC MC 4 NN ' 9 3 3 9 3
   1  2   1   0,25
IA = IB + BA = − AB − AC ⇒ IA = − IB − 3IC 9 3 2 1
Vậy k = − , h = 3 − . 2 17 Cho hàm số 4 2
f (x) = x − 4x + 5 + m , m là tham số thực. Tìm tất cả các giá trị 0,5
của tham số m để giá trị lớn nhất của hàm số đã cho trên đoạn  2; − 5    đạt giá trị nhỏ nhất.
Xét hàm số g ( x) 4 2
= x − 4x + 5 + m trên đoạn  2; − 5  0,25   .
g ( x) = ( x − 2)2 2 + m +1 2
− ≤ x ≤ 5 ⇒ 0 ≤ (x − 2)2 2
≤ 9 ⇒ m +1 ≤ g(x) ≤ m+10 + TH1: m ≥ 1
− ⇒ Max f (x) = m +10 ≥ 9  2; − 5    + TH2 : 10 − ≤ m < 1
− ⇒ Max = Max{m +10;−m − } 1 0,25  2; − 5    11 9
- Nếu m +10 > −m −1 ⇔ m > −
⇒ Max f (x) = m +10 >  2; − 5 2    2 11 9 - Nếu m < −
⇒ Max f (x) = −m −1 >  2; − 5 2    2 11 9 - Nếu m = − ⇒ Max f (x) =  2; − 5 2    2 + TH3: m < 10
− ⇒ Max f (x) = −m −1 > 9  2; − 5    3
Vậy giá trị lớn nhất của hàm số đã cho trên đoạn  2; − 5  
 đạt giá trị nhỏ nhất 9 11 bằng khi m = − . 2 2 4
Document Outline

• Mã 132-Đề thi chuyên đề môn Toán lớp 10 lần II năm học 2019 - 2020
• ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ THI CHUYÊN ĐỀ MÔN TOÁN LỚP 10 LẦN II