Đề thi cuối học kỳ 2 Toán 10 năm 2020 – 2021 sở GD&ĐT Quảng Nam

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2020-2021 QUẢNG NAM
Môn: TOÁN – Lớp 10
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC MÃ ĐỀ 101
(Đề gồm có 03 trang)
PHẦN TRẮC NGHIỆM: (7,0 điểm) 2x − 3 > 0
Câu 1: Tìm tập nghiệm S của hệ bất phương trình  . 1  − x ≤ 2 3
A. S = ( ;+∞). B. S = [ 1; − +∞). C. 3 S = [ 1; − ). D. S = . ∅ 2 2
Câu 2: Trên đường tròn lượng giác gốc A (hình vẽ bên), điểm nào y π B
dưới đây là điểm cuối của cung có số đo 7 ? N M 4 A. Điểm M. B. Điểm . Q A' O A x C. Điểm N. D. Điểm . P P Q B'
Câu 3: Cho tam giác ABC có diện tích bằng 24 và chu vi bằng 12. Bán kính đường tròn nội tiếp của tam giác ABC bằng A. 2. B. 1 ⋅ C. 1 ⋅ D. 4. 4 2
Câu 4: Gọi α là số đo của một cung lượng giác có điểm đầu là A, điểm cuối là B . Khi đó số đo của
cung lượng giác bất kỳ có điểm đầu A, điểm cuối B bằng
A. α + k2π , k ∈ Z .
B. α + kπ , k ∈ Z .
C. π −α + k2π , k ∈ Z . D. α
− + k2π , k ∈ Z .
Câu 5: Trong mặt phẳng Oxy, cho đường thẳng d : 3x − 2y +1 = 0. Vectơ nào sau đây là một vectơ
pháp tuyến của d ? A. n = 3;2 . B. n = 2; − 3 . C. n = 2;3 .
D. n = 3;− 2 . 1 ( ) 4 ( ) 3 ( ) 2 ( )
Câu 6: Cho tam giác ABC có bán kính đường tròn ngoại tiếp bằng 
25cm, BAC = 70°. Tính độ dài
cạnh BC (kết quả làm tròn đến hàng đơn vị). A. 39cm. B. 23cm. C. 47cm. D. 19cm. Trang 1/3 – Mã đề 101
Câu 7: Trong mặt phẳng Oxy, cho hai đường thẳng d :− x + y + 2 = 0 và d : 2 x − 3 = 0. Góc giữa hai 1 2
đường thẳng d và d bằng 1 2 A. 60 .° B. 30 .° C. 135 .° D. 45 .°
Câu 8: Giá trị x = 5 là nghiệm của bất phương trình nào sau đây? 1− x
A. x + 2 > 9. B. < 0. C. x + 4 ≤ 2.
D. 2x + 3 <15. x − 5
Câu 9: Cho tam giác ABC có BC = a, AC = b, AB = c . Diện tích của tam giác ABC bằng
A. 2absinC.
B. 1 abcosC.
C. 1 absinC.
D. abcosC. 2 2 Câu 10: α − α
Cho tanα = 3, giá trị biểu thức sin 2cos T = bằng sinα + cosα 5 1 5 − 1 − A. ⋅ B. ⋅ C. ⋅ D. ⋅ 4 4 4 4
Câu 11: Tìm điều kiện xác định của bất phương trình 2x −1 > 3. x + 2 A. x ≥ 2. − B. x > 2. − C. x ≠ 2. − D. x ≠ 2.
Câu 12: Trong mặt phẳng Oxy, cho hai điểm I ( 1; − )
1 và A(3;− 2). Đường tròn tâm I và đi qua A có phương trình là
A. (x + )2 + ( y − )2 1 1 = 5.
B. (x + )2 + ( y − )2 1 1 = 25.
C. (x − )2 + ( y + )2 1 1 = 25.
D. (x − )2 + ( y + )2 1 1 = 5.
Câu 13: Trong mặt phẳng Oxy, cho điểm I (1;− )
1 và đường thẳng d :4x − 3y + 3 = 0. Đường tròn tâm
I, tiếp xúc với đường thẳng d có phương trình là
A. (x − )2 + ( y + )2 1 1 = 2.
B. (x + )2 + ( y − )2 1 1 = 4.
C. (x − )2 + ( y + )2 1 1 = 4.
D. (x − )2 + ( y + )2 1 1 =10.
Câu 14: Cho tam thức bậc hai f ( x) 2
= ax + bx + c(a > 0). Tìm điều kiện để f (x) > 0, x ∀ ∈ .  A. ∆ ≤ 0. B. ∆ < 0. C. ∆ > 0. D. ∆ ≥ 0.
Câu 15: Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 2x + y − 7 > 0 ? A. N( 1; − 2).
B. P(2;3). C. Q(1;0). D. M (4;3).
Câu 16: Tìm số nghiệm nguyên của bất phương trình 2
x − 2x + 3 ≤ 2 . x A. 3. B. 1. C. 0. D. 2. Trang 2/3 – Mã đề 101
Câu 17: Trong mặt phẳng Oxy, cho đường tròn (C) (x − )2 + ( y + )2 : 2
3 = 25 . Tọa độ tâm I và bán
kính R của (C) là
A. I (2;− 3), R = 5.
B. I (2;− 3), R = 25. C. I ( 2; − 3), R = 5. D. I ( 2 − ;3), R = 25.
Câu 18: Cho α là một góc lượng giác bất kỳ, mệnh đề nào sau đây đúng?
A. cos(π −α) = cosα.
B. sin(π −α) = sinα.
C. cot(π −α) = − tanα.
D. tan(π −α) = cotα. 1 π
Câu 19: Cho α là một góc lượng giác thỏa mãn sinα = , với <α < π . Tính cosα ? 3 2 2 2 2 2 2 8 A. cosα − = ⋅ B. cosα = ⋅ C. cosα = ⋅ D. cosα = ⋅ 3 3 3 9
Câu 20: Cho biểu thức f (x) = x + 3. Mệnh đề nào sau đây đúng?
A. f ( x) < 0 khi x∈( 3 − ;+∞).
B. f ( x) > 0 khi x∈( ;3 −∞ ).
C. f ( x) < 0 khi x∈( ; −∞ 3 − ).
D. f ( x) > 0 khi x∈[ 3 − ;+∞).
Câu 21: Trong mặt phẳng Oxy, đường thẳng nào sau đây đi qua gốc tọa độ?
A. d :x + 2y = 0. d : y + 2 = 0.
C. d :x + y − 2 = 0.
D. d :4x − 3 = 0. 4 B. 1 2 3
PHẦN TỰ LUẬN: (3,0 điểm)
Bài 1. (2,0 điểm)
a) Giải bất phương trình 2
(x − 3)(−x + 4x + 5) ≥ 0. b) Cho biểu thức 2
f (x) = (m −1)x + 2(m −1)x + 2m − 3 , với m là tham số.
Tìm m để f (x) < 0, x ∀ ∈ .  Bài 2. (1,0 điểm)
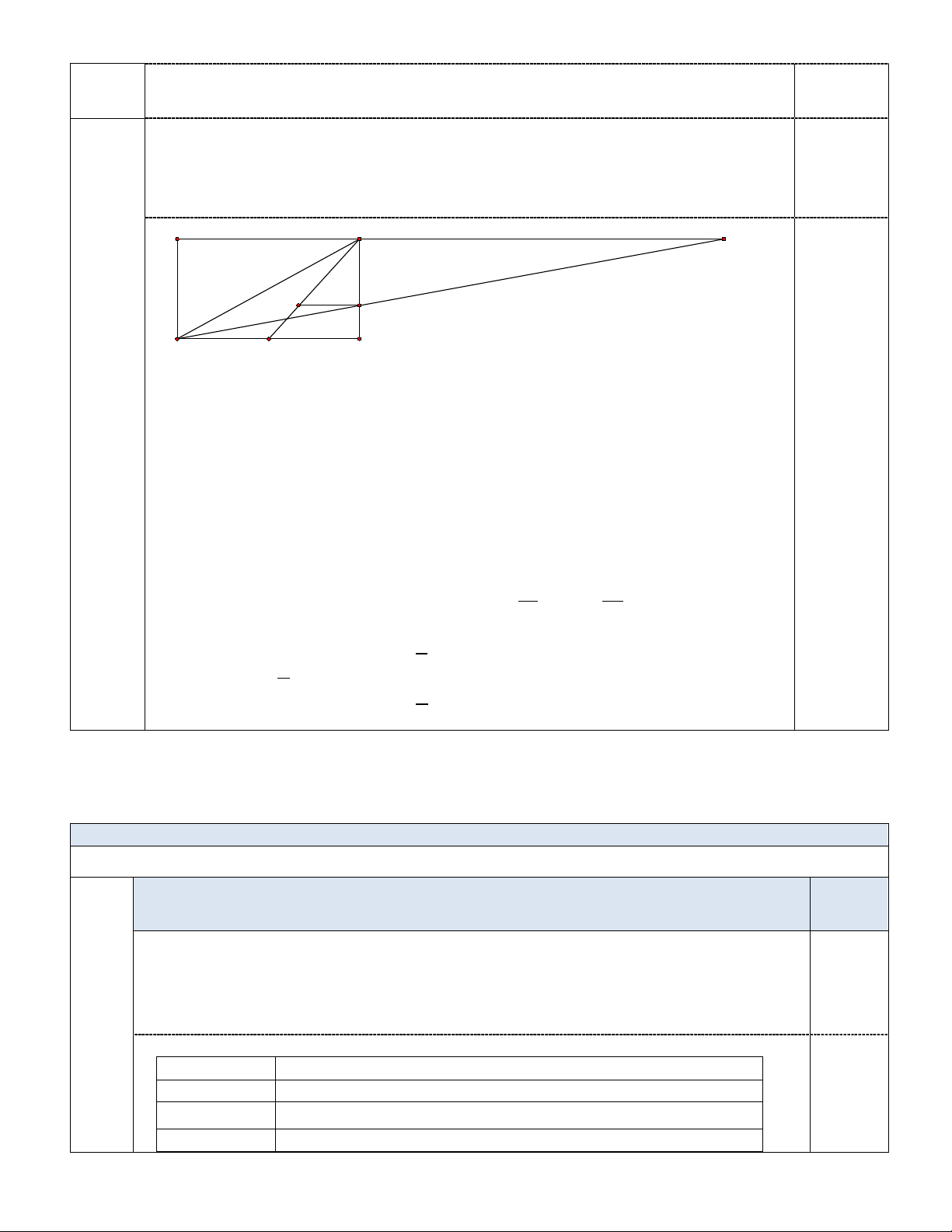
Trong mặt phẳng với hệ toạ độ Oxy, cho hình chữ nhật ABCD có điểm A(2;− ) 1 . Gọi G là
trọng tâm tam giác ABC , hình chiếu vuông góc của G lên cạnh BC là H (6;5), điểm D có hoành độ
âm và thuộc đường thẳng d : x + 2y − 3 = 0 . Viết phương trình tham số của đường thẳng d và tìm tọa độ điểm C.
………. HẾT ………. Trang 3/3 – Mã đề 101
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM BÀI KIỂM TRA CUỐI HỌC KỲ II QUẢNG NAM
NĂM HỌC 2020-2021–Môn: TOÁN – Lớp 10
(Hướng dẫn chấm gồm 05 trang)
A. PHẦN TRẮC NGHIỆM (7 điểm, 21 câu, mỗi câu 0,33 điểm) 101 102 103 104 105 106 107 108
Câu ĐA Câu ĐA Câu ĐA Câu ĐA Câu ĐA Câu ĐA Câu ĐA Câu ĐA 1 A 1 B 1 D
1 D 1 C 1 B 1 D 1 B 2 B 2 A 2 C 2 A 2 A
2 D 2 A 2 D 3 D
3 C 3 A 3 A 3 C 3 C 3 D 3 C 4 A
4 D 4 C 4 C 4 D 4 B 4 B 4 C 5 D 5 B 5 A 5 A 5 B 5 C 5 B 5 C 6 C
6 D 6 C 6 B 6 C 6 B 6 C 6 C 7 D 7 C 7 B 7 B 7 D 7 A 7 A 7 A 8 D
8 B 8 B 8 A 8 A 8 C 8 A 8 A 9 C 9 A 9 D 9 C 9 C
9 D 9 D 9 B
10 B 10 A 10 C 10 B 10 A 10 D 10 C 10 A
11 C 11 A 11 B 11 B 11 B 11 A 11 B 11 D
12 B 12 B 12 B 12 C 12 B 12 C 12 B 12 D
13 C 13 D 13 B 13 C 13 D 13 A 13 D 13 A
14 B 14 C 14 A 14 C 14 A 14 A 14 B 14 D
15 D 15 C 15 A 15 D 15 D 15 A 15 C 15 A
16 A 16 D 16 D 16 D 16 D 16 C 16 A 16 D
17 A 17 A 17 A 17 D 17 C 17 D 17 D 17 A
18 B 18 D 18 D 18 B 18 D 18 B 18 C 18 B
19 A 19 C 19 C 19 A 19 B 19 B 19 B 19 C
20 C 20 D 20 D 20 D 20 A 20 D 20 A 20 B
21 A 21 B 21 A 21 D 21 B 21 C 21 C 21 B
B. PHẦN TỰ LUẬN (3 điểm)
MÃ 101, 103, 105, 107: Câu Nội dung Điểm
a) Giải bất phương trình 2
(x − 3)(−x + 4x + 5) ≥ 0. (1,0 đ)
x − 3 = 0 ⇔ x = 3 2 x = 1 −
−x + 4x + 5 = 0 ⇔  x = 5 Bảng xét dấu: x  -1 3 5  1a x3  |  0 + | + 2 x
  4x  5  0 + | + 0  VT + 0  0 + 0  0,75
Nghiệm bậc nhất và xét dấu bậc nhất: 0,25đ
Nghiệm bậc hai và xét dấu bậc hai: 0,25đ Xét dấu tích: 0,25đ
KL tập nghiệm: S  (;1][3; 5] 0,25 Cho biểu thức 2
f (x) = (m −1)x + 2(m −1)x + 2m −3
Tìm m để f (x) < 0,∀x ∈R? (1,0 đ) TH1: m = 1 f (x) = 1 − < 0, x
∀ ∈ R nên m =1 thỏa YCBT 0,25 TH2: m ≠ 1 0,25 a < 0
f (x) < 0,∀x ∈R ⇔ 1b  ∆ ' < 0 m −1 < 0 ⇔  2
−m + 3m − 2 < 0 m <1 0,25 ⇔  ⇔ m <1
m <1 hoac m > 2 0,25 Kết luận: m ≤ 1
Trong mặt phẳng với hệ toạ độ Oxy cho hình chữ nhật ABCD có điểm 2 A(2;− )
1 . Gọi G là trọng tâm tam giác ABC , hình chiếu vuông góc của G
lên cạnh BC là H (6;5), điểm D có hoành độ âm và thuộc đường thẳng
d : x + 2y − 3 = 0 . Viết phương trình tham số của đường thẳng d và tìm tọa độ điểm C. 
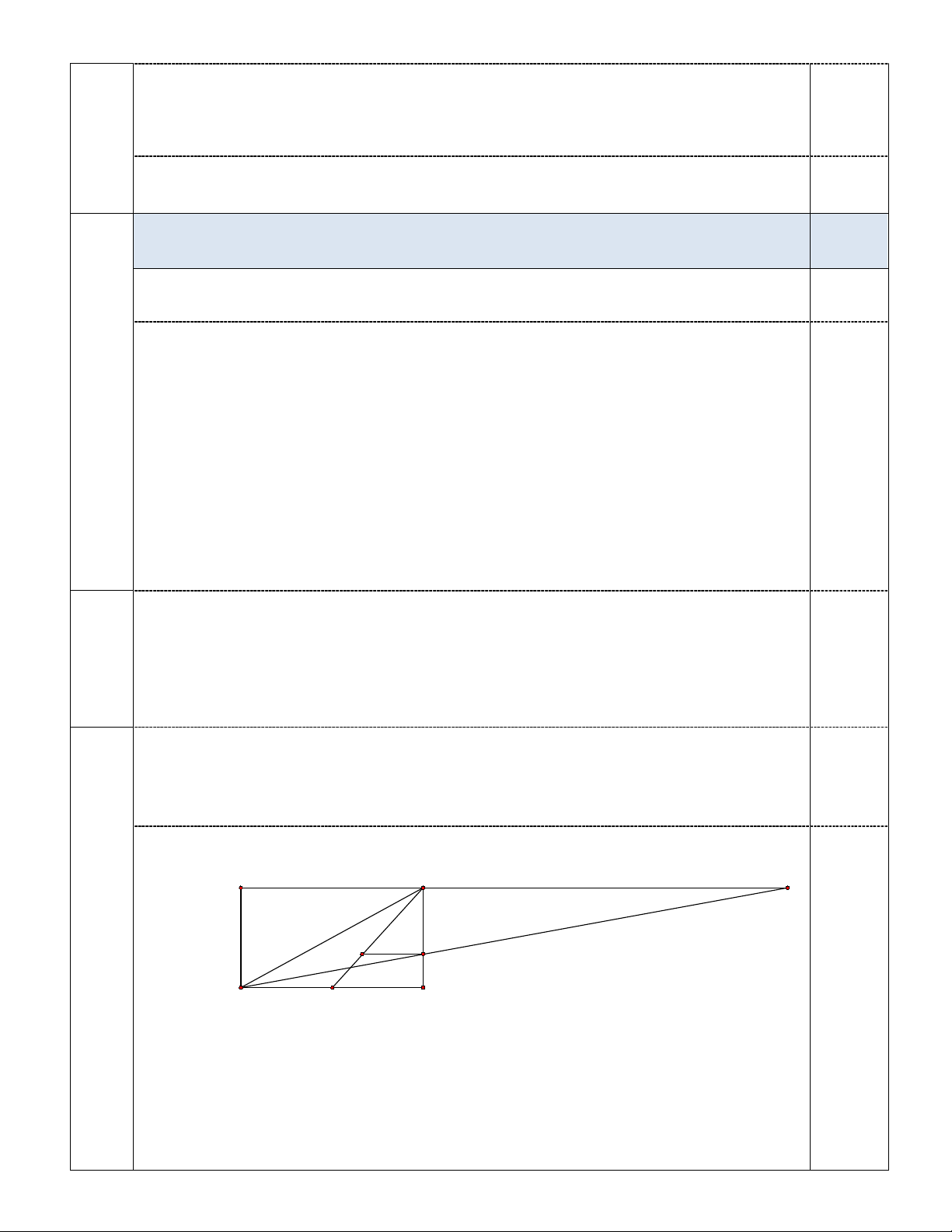
Đường thẳng d đi qua điểm có tọa độ (3;0) và có VTCP u = ( 2; − ) 1 nên có x = 3 − 2t 0,25 phương trình tham số  ; t ∈  y = t D C I H G A B    x − = − I 2 3(6 2)
Gọi I = AH ∩ DC ⇒ AI = 3AH ⇒  ⇒ I (14;17) 0,25 y + = +  I 1 3(5 )1  
D(3− 2t;t), ID = ( 2
− t −11;t −17), AD = (1− 2t;t + ) 1
t = 2 ⇒ D( 1; − 2) 2 ID AD 0,25 5t 4t 28 0  ⊥ ⇔ + − = ⇔  14 43 t = − ⇒ x = > loai D 0( )  5 5  2 6 − x = +    C (2 )1 2  3 CH = DA ⇒  ⇒ C (4;7) 0,25 3 2 5  − y = − − C ( 1 2)  3
MÃ 102, 104, 106, 108. Câu Nội dung Điểm
a) Giải bất phương trình 2
(1− x)(x + 5x + 6) ≤ 0 . (1,0 đ)
1− x = 0 ⇔ x =1 2 x = 3 −
x + 5x + 6 = 0 ⇔  1a x = 2 − Bảng xét dấu: x  3 2 1  1x + | + | + 0  0,75 2
x  5x 6 + 0  0 + | + VT + 0  0 + 0 
Nghiệm bậc nhất và xét dấu bậc nhất: 0,25đ
Nghiệm bậc hai và xét dấu bậc hai: 0,25đ Xét dấu tích: 0,25đ
KL tập nghiệm: S [3;2][1;) 0,25 b) Cho biểu thức 2
f (x) = (m −1)x + 2(m −1)x + 2m + 3 .
Tìm m để f (x) > 0,∀x ∈R? (1,0 đ) TH1: m = 1
f (x) = 5 > 0, x
∀ ∈ R nên m =1 thỏa YCBT 0,25 TH2: m ≠ 1 a > 0 0,25
f (x) > 0,∀x ∈R ⇔  ∆ ' < 0 1b m −1 > 0 ⇔  2
−m − 3m + 4 < 0 m >1 ⇔  ⇔ m >1 0,25 m < 4 − hoac m >1 Kết luận: m ≥ 1 0,25
Trong mặt phẳng với hệ toạ độ Oxy cho hình chữ nhật ABCD có điểm A( 1; − 2)
Gọi G là trọng tâm tam giác ABC , hình chiếu vuông góc của G lên cạnh BC là 2
H (5;6), điểm D có hoành độ dương và thuộc đường thẳng d : 2x + y − 3 = 0 . Viết
phương trình tham số của đường thẳng d và tìm tọa độ điểm C. 
Đường thẳng d đi qua điểm có tọa độ (0;3) và có VTCP u = (1; 2 − ) nên có phương x = t 0,25 trình tham số  ; t ∈  y = 3 − 2t D C I H G A B    0,25 x + = + I 1 3(5 ) 1
Gọi I = AH ∩ DC ⇒ AI = 3AH ⇒  ⇒ I (17;14) y − = −  I 2 3(6 2)  
D(t;3− 2t), ID = (t −17; 11
− − 2t), AD = (t +1;1− 2t) 0,25
t = 2 ⇒ D(2;− ) 1 2 ID AD 5t 4t 28 0  ⊥ ⇔ + − = ⇔  14 14 t = − ⇒ x = − < loai 0,25 D 0( )  5 5  2 5 − x = − −    C ( 1 2) 2  3 CH = DA ⇒  ⇒ C (7;4) 3 2 6− y = + C (2 )1  3
Ghi chú: - Học sinh giải cách khác đúng thì được điểm tối đa của câu đó.
- Tổ Toán mỗi trường cần thảo luận kỹ HDC trước khi tiến hành chấm.
--------------------------------Hết--------------------------------
Document Outline

• Mã_101
• HDC Toan 10