Đề thi cuối kỳ 2023 - 2024 môn Calculus 1 | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

VIETNAM NATIONAL UNIVERSITY - HCM INTERNATIONAL UNIVERSITY DEPARTMENT OF MATHEMATICS
CALCULUS 1 (MA001IU) – FINAL EXAMINATION Semester 1, 2023-2024
Duration: 120 minutes | Date: February 01, 2024
Lecturers: Pham Huu Anh Ngọc, N. Dinh, P.T. Duong, T.V. Khanh, N.M. Quan, M.D. Thanh, N.T.T. Van. INSTRUCTIONS
• Use of calculator is allowed. Each student is allowed one double-sided sheet of
reference material (size A4 or similar).
• All other documents and electronic devices are forbidden.
• You must explain your answers in detail; no points will be given for the answer alone.
• There is a total of 10 (ten) questions. Each one carries 10 points.
Question 1. Evaluate the following limit: sin x − ex + 1 lim x→0 1 − ex2
Question 2. A circle is inside a square (as Figure 1) and both are changing size. The
radius of the circle is decreasing at a rate of 3 cm per minute and the sides of the square
are increasing at a rate of 4 cm per minute. When the radius of the circle is 6 cm, and
the sides of the square are 15 cm, then how fast is the AREA outside the circle but inside the square changing? r x
Figure 1: A circle of radius r inside a square of side x √
Question 3. Use Newton’s method to approximate 7 1000 correct to seven decimal places
with the initial approximation x0 = 3.
Question 4. Evaluate the integral: Z 1 2 − 5x dx 2x2 + 11x + 5 0 1
Question 5. Evaluate the improper integral: Z ∞ dx x(ln x)3 e
Question 6. Use the trapezoidal rule to approximate the following integral by dividing
the interval [0, 1] into 5 equal subintervals: Z 1 √1 + x3 dx 0
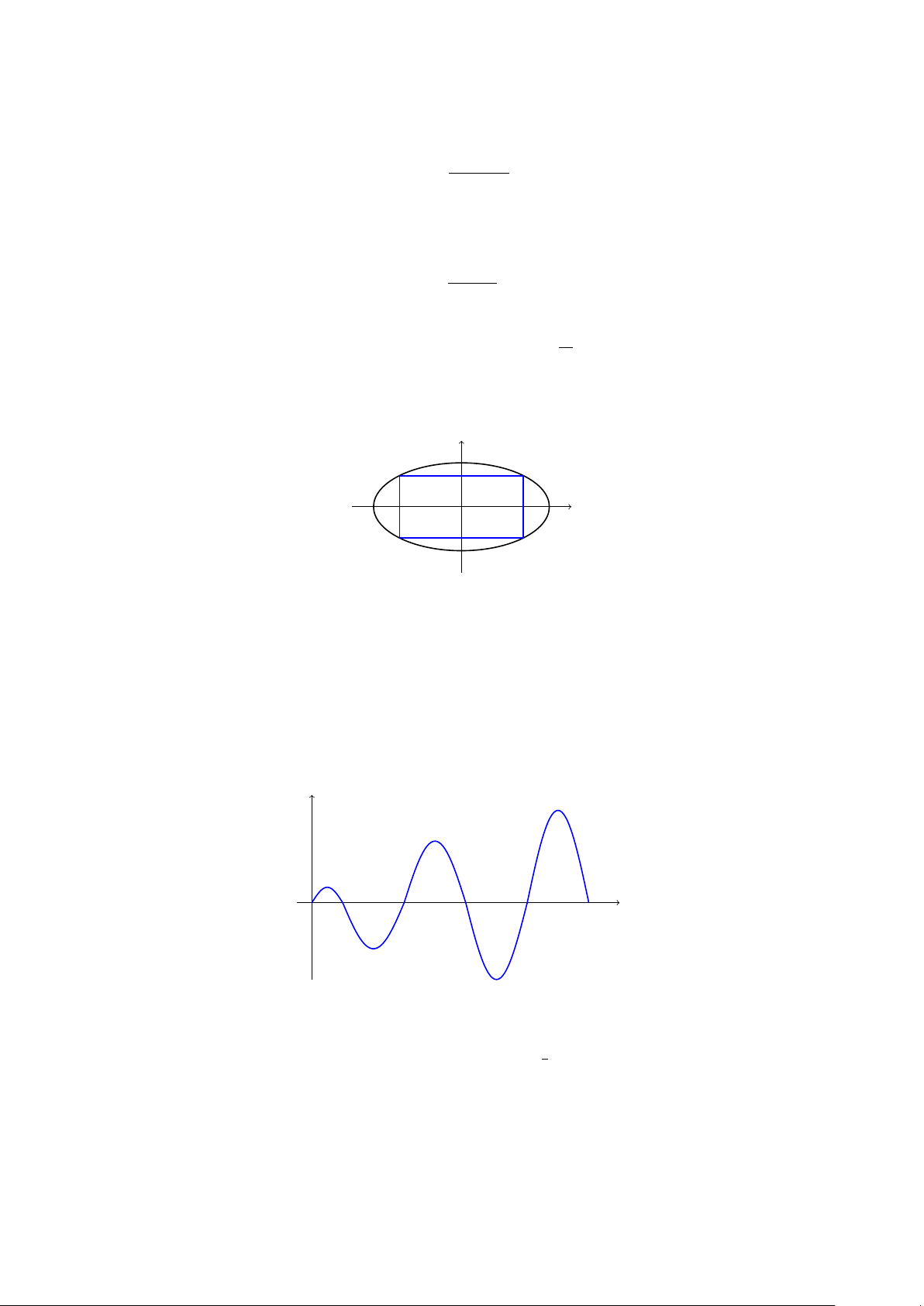
Question 7. A rectangle is to be inscribed in the ellipse x2 + y2 = 1 (see Figure 2). What 4
should the dimensions of the rectangle be to maximize its area? What is the maximum area? y Q(−x, y) P (x, y) x R(−x, −y) S(x, −y)
Figure 2: A rectangle inscribed in an ellipse
Question 8. Let g(x) = R x f (t) dt, where f is the function whose graph is shown in 0
Figure 3. The graph of y = f (t) intersects the t-axis at t = 0, 1, 3, 5, 7, 9.
(a) At which values of x do the local maximum and local minimum values of g occur?
(b) Where does g attain its absolute maximum value? y 3 2 1 t 0 2 4 6 8 -1 -2 Figure 3
Question 9. Find the arc length of the graph of y = 4 x3/2 between x = 0 and x = 1. 3
Question 10. Let R be the region enclosed by the graph of f (x) = 2x−x2 and the x-axis.
Find the volume of the solid of revolution formed by revolving R around the y-axis. - END OF THE QUESTION PAPER - 2