Note Calculus 1 Midterm - Calculus 1 | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố HCM
Note Calculus 1 Midterm - Calculus 1 | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố HCM được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Calculus 1 (MA001IU)
Trường: Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
Preview text:
Chapter 1 Straight line
Translation from f(x), c >0
Stretches and reflection 𝑦𝑦2−𝑦𝑦1 Left
𝑓𝑓(𝑥 𝑥 + 𝑐𝑐) Stretch vertically
𝑐𝑐𝑓𝑓(𝑥𝑥) • Slope: m = = tan α 𝑥𝑥2−𝑥𝑥1 Right
𝑓𝑓(𝑥𝑥 − 𝑐𝑐) Compress horizontally
𝑓𝑓(𝑐𝑐𝑥𝑥)
• Slope - intercept form: y = mx +b Up 𝑓𝑓(𝑥𝑥) + 𝑐𝑐 Reflect x – axis −𝑓𝑓(𝑥𝑥)
• Point - slope form: y – y1 = m (x – x1) Down
𝑓𝑓(𝑥𝑥) − 𝑐𝑐 Reflect y - axis 𝑓𝑓(−𝑥𝑥)
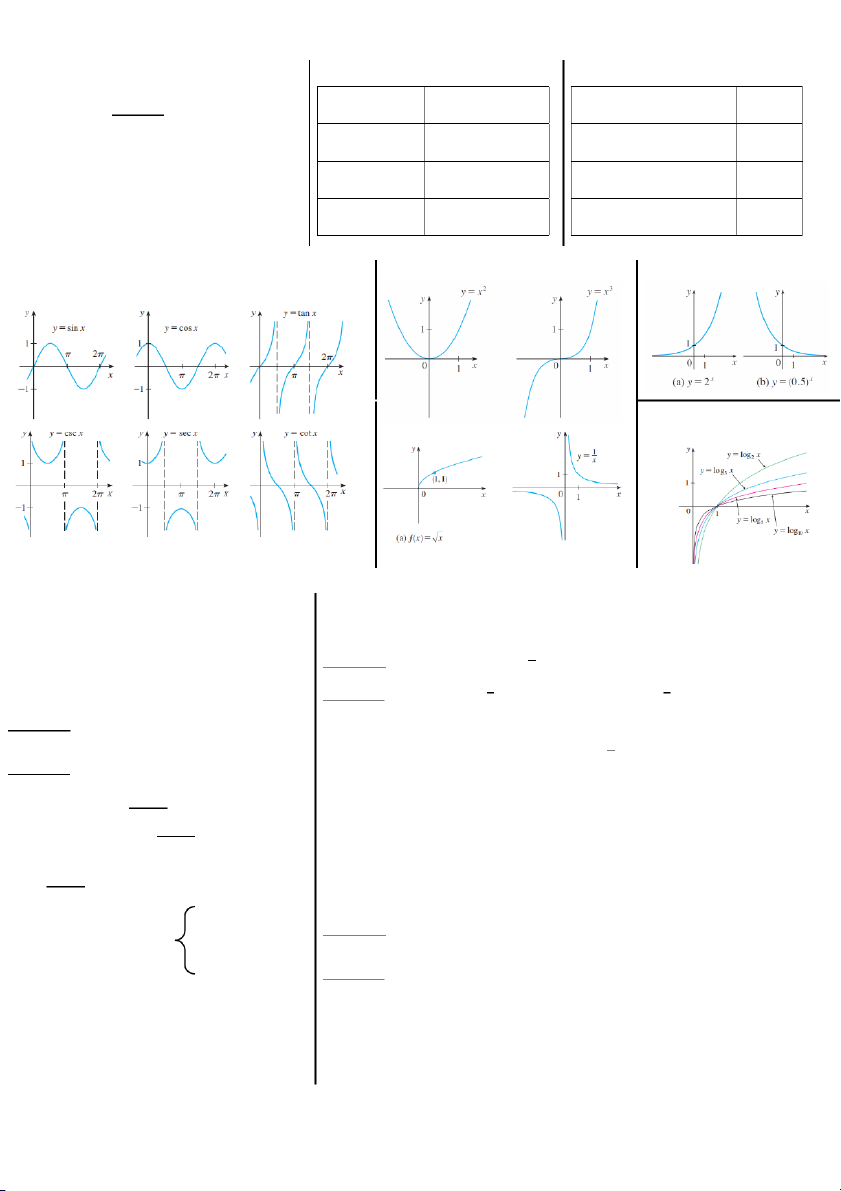
Graph of common function: • Power: • Exponential: • Trigonometric: • Logarithmic:
Composition: 𝑓𝑓𝑓𝑓𝑓𝑓 = 𝑓𝑓(𝑓𝑓(𝑥𝑥) )
Squeeze theorem: if f(x) ≤ g(x) ≤ h(x) ∀x in an open interval containing xo, One to one: f(x
𝑓𝑓 𝑥𝑥 = ℎ 𝑥𝑥 = L ⇒ 𝑓𝑓 1)≠ f(x2) whenever x1≠x2 and if lim ( ) lim( ) lim (𝑥𝑥) = L 𝑥𝑥 →𝑎𝑎 𝑥𝑥 →𝑎𝑎 𝑥𝑥 →𝑎𝑎
Inverse function: given f(x) is one to one 1
Example: Show that lim 𝑥 𝑥 cos = 0 𝑥𝑥 →0 𝑥𝑥
and defined in domain A and range B 1 1 ⇒ Solution:
�𝑥𝑥 cos � ≤ |𝑥𝑥| ⇔ −|𝑥𝑥| ≤ 𝑥 𝑥 co s ≤ |𝑥𝑥|
f -1(y) = x has domain B and range A 𝑥𝑥 𝑥 𝑥
Example: Let y = f(x) = x2 + 4x, x > 0. Find
and lim −|𝑥𝑥| = lim|𝑥𝑥| = 0 𝑥𝑥 →0 𝑥𝑥 →0 the inverse function of f(x) ⇒ 1 lim 𝑥 𝑥 cos = 0 𝑥𝑥 Solution: y = x2 + 4x 𝑥𝑥 →0 ⇔ Asymptote: y + 4 x = 2 + 4x + 4
𝑓𝑓(𝑥𝑥) = L1 and/or lim
𝑓𝑓(𝑥𝑥) = L2 then y = L and/or y = L is ⇔ • If lim 1 2 �𝑦 𝑦 + 4 = x + 2 𝑥𝑥 →∞ 𝑥𝑥 →−∞ horizontal asymptote
⇔ x = �𝑦 𝑦 + 4 – 2
• If lim 𝑓𝑓(𝑥𝑥) = ±∞ and/or lim
𝑓 𝑓(𝑥𝑥) = ±∞ then x = a is vertical asymp
Therefore, the inverse function of x2 + 4x is 𝑥𝑥→𝑎𝑎+ 𝑥𝑥→𝑎𝑎−
Intermediate value theorem: f(x) is continuous on [a,b], f(a) ≤ N ≤ f(b) y = √𝑥 𝑥 + 4 – 2
=> there is a number c, a ≤ c ≤ b such that f(c) = N Limit: lim 𝑓𝑓(𝑥𝑥) = L ⇔ li 𝑓 m𝑓(𝑥𝑥) = L 𝑥𝑥 →𝑎𝑎 𝑥𝑥→𝑎𝑎−
Example: Suppose f is continuous on [1, 5] and the only solutions of the
lim 𝑓𝑓(𝑥𝑥) = L e quation f(x) = 6 are x =
1 and x = 4. If f(2) = 8, explain why f(3) > 6. 𝑥𝑥→𝑎𝑎+ Solution:
Continuity: a function f(x) is continuous at
• f(3) = 6 ⇒ f(x) = 6 at x = 3 (invalid) ⇒ f(3) ≠ 6.
c if 𝑙𝑙𝑙𝑙𝑙𝑙 𝑓𝑓(𝑥𝑥) = 𝑓𝑓(𝑐𝑐)
• f(3) < 6 ⇒ f(3) < 6 < f(2) and f is continuous on [2,3]. Using IVF, there 𝑥𝑥→𝑐𝑐
Continuity from the left: 𝑙𝑙𝑙𝑙𝑙𝑙 𝑓𝑓(𝑥𝑥) = 𝑓𝑓(𝑐𝑐)
is at least c ∈ [2,3] at which f(c) = 6. Since c ≠ 1 and c ≠ 4, f(3) < 6 is 𝑥𝑥→𝑐𝑐− invalid.
Continuity from the right: 𝑙𝑙𝑙𝑙𝑙𝑙 𝑓𝑓(𝑥𝑥) = 𝑓𝑓(𝑐𝑐) 𝑥𝑥→𝑐𝑐+ • Therefore, f(3) > 6. Chapter 2 Derivative
Differentiable and continuous:
Logarithmic differentiation:
𝑓𝑓(𝑥𝑥+ℎ) −𝑓𝑓(𝑥𝑥) 𝑓𝑓′(𝑥𝑥) 𝑓𝑓(𝑥𝑥) = lim
• At c if 𝑓𝑓′(𝑐𝑐) exist
Method: 1. Take ln of both side of y = ℎ→0 ℎ
• On (a,b) if it is differentiable at any 2. Differentiate both side
Rule of differentiation: number in that interval 3. Solve for y’ 1 • (xn)’ = nxn-1
• f(x) is differentiable at a ⇒ f(x) is
Example: Find derivative of y = (1 + 𝑥𝑥) 𝑥𝑥 (1 ) continuous • (ax)’ = ax ln(a) Solution: 1 1
Chain rule: if y = f(u) and u = g(x) are
(1) ⇔ ln 𝑦𝑦 = ln(1 + 𝑥𝑥) • (log 𝑥𝑥 𝑎 𝑎 𝑥𝑥)’ =
𝑥 𝑥 𝑙𝑙𝑙𝑙(𝑎𝑎) both differentiable ⇔ 1 −1 1 y’ = 1
𝑑𝑑𝑦𝑦 𝑑𝑑𝑦𝑦𝑑𝑑𝑑𝑑 𝑦𝑦 𝑥𝑥2 ln(1 + 𝑥𝑥) + 𝑥𝑥(𝑥𝑥+1)
• (𝑙𝑙𝑙𝑙 𝑥𝑥)’ = = 𝑥𝑥
𝑑𝑑𝑥𝑥 𝑑𝑑𝑑𝑑𝑑𝑥𝑥 ⇔ 1 y’ = �−1 � 𝑦𝑦 𝑥𝑥2 ln(1 + 𝑥𝑥) + 𝑥𝑥(𝑥𝑥+1)
• (sin 𝑥𝑥)’ = cos 𝑥𝑥
Derivative of inverse function: 1 1 �
• (cos 𝑥𝑥)’ = − sin 𝑥𝑥
If f(x) is one to one and differentiable ⇔ y’ = �−1 (1 + 𝑥𝑥 𝑥𝑥 ) 𝑥𝑥2 ln(1 + 𝑥𝑥) + 𝑥𝑥(𝑥𝑥+1)
• (tan 𝑥𝑥)’ = 1 + 𝑡𝑡𝑡𝑡𝑙𝑙2 𝑥𝑥 1 (𝑓𝑓−1)′(𝑡𝑡) = Linear approximation:
𝑓𝑓′�𝑓𝑓−1(𝑡𝑡)� = sec2 𝑥𝑥
𝑓𝑓(𝑥𝑥) ≈ L(x) = 𝑓𝑓(𝑡𝑡) + 𝑓𝑓′(𝑡𝑡) (x-a)
• (cot 𝑥𝑥)’ = − (1 + 𝑐𝑐𝑓𝑓𝑡𝑡2 𝑥𝑥 E )
x ample: let f(x) = 2x + cos 𝑥𝑥, find Differentials: ′
= − 𝑐𝑐𝑐𝑐𝑐𝑐2 𝑥𝑥 (𝑓𝑓−1) (1) dy = 𝑓𝑓′(𝑥𝑥) dx Solution:
Example: The sphere has radius 21cm, with error
• (sec 𝑥𝑥)’ = sec 𝑥 𝑥 tan 𝑥𝑥
• 𝑓𝑓′(𝑥𝑥) = 2 - sin 𝑥𝑥 > 0 ∀x ⇒ 𝑓𝑓(𝑥𝑥) is io nn e
m easurement at most 0.05cm. Find maximum
• (csc 𝑥𝑥)’ = − csc 𝑥 𝑥 cot 𝑥𝑥 to one function error of volume of the sphere 1
• (𝑐𝑐𝑙𝑙𝑙𝑙−1 𝑥𝑥 )’ =
• 𝑓𝑓(𝑥𝑥) = 1 ⇒ x = 0 ⇒ 𝑓𝑓−1(1) = 0 Solution: 𝑎𝑎 √𝑎𝑎2−𝑥𝑥2 • 𝑓𝑓′(0) = 2
• We let the radius is r = 21cm, so the error is
• (cos−1 𝑥𝑥)’ = − 1 ⇒ 1 1 1 (𝑓𝑓−1)′(1) = = = 4 𝑎𝑎 √𝑎𝑎2−𝑥𝑥2
𝑓𝑓′�𝑓𝑓−1(1)� 𝑓𝑓′(0) 2
dr = 0.05cm, the volume is V = 𝜋𝜋r3 3 𝑎𝑎
• (𝑡𝑡𝑡𝑡𝑙𝑙−1 𝑥𝑥 )’ =
Implicit differentiation:
• The error of the volume is: 𝑎𝑎 𝑎𝑎2+𝑥𝑥2 ′
Example: Find y’ if sin(𝑥 𝑥 + 𝑦𝑦) = y2 (1 )
dV = �4 𝜋𝜋𝑟𝑟3� dr
• (𝑐𝑐𝑓𝑓𝑡𝑡−1 𝑥𝑥 )’ = − 𝑎𝑎 3 𝑎𝑎 𝑎𝑎2+𝑥𝑥2 Solution: 𝑎𝑎 ⇔ dV = 4 𝜋𝜋r2 dr
• (𝑐𝑐𝑠𝑠𝑐𝑐−1 𝑥𝑥 )’ = (1) ⇔ co (
s 𝑥 𝑥 + 𝑦𝑦) (1 + y’) = 2yy’ 𝑎𝑎
𝑥𝑥√𝑥𝑥2−𝑎𝑎2 ⇔
⇔ dV = 4𝜋𝜋 × 212×0.05 ≈ 277 (cm3)
cos(𝑥 𝑥 + 𝑦𝑦) = 2yy’ - cos(𝑥 𝑥 + 𝑦𝑦) 𝑦𝑦′
• (𝑐𝑐𝑐𝑐𝑐𝑐−1 𝑥𝑥 )’ = − 𝑎𝑎 𝑎𝑎 cos
• Therefore, the maximum error in the
𝑥𝑥√𝑥𝑥2−𝑎𝑎2 ⇔ (𝑥𝑥+𝑦𝑦) y’ =
2𝑦𝑦 − cos(𝑥𝑥+𝑦𝑦) calculated volume is 277 cm3 Chapter 3 Related rates
Solution: We called V, r, h is the volume, Method:
radius and height of the water at time t.
1. Assign variable. Restate the problem in terms of
Since the water is filled in the cone, its 𝑟𝑟 2 1 derivatives 1 volume is: V = 2 3 πr h. Also, ℎ = 4 = 2
2. Find an equation relating the variables and differentiate it 2 1
3. Use the known equations and data to find the unknown ⇒ 1 V = π�1ℎ� h = 3 2 12 πh3 derivative 𝑑𝑑𝑑𝑑 1 𝑑𝑑ℎ
Example: A water tank has the shape of an inverted circular ⇔ = πh2 𝑑𝑑𝑑𝑑 4 𝑑𝑑𝑑𝑑
cone with base radius 2 m and height 4 m. If water is being 1 𝑑𝑑ℎ 𝑑𝑑ℎ
pumped into the tank at a rate of 2 m3/min, find the rate at ⇔ 2 = π ⇔ ≈ 4 32 0.2 8 (m/min)
𝑑𝑑𝑑𝑑 𝑑𝑑𝑑𝑑
which the water level is rising when the water is 3 m deep.
Therefore, the water level rising at a rate of 0.28m/min