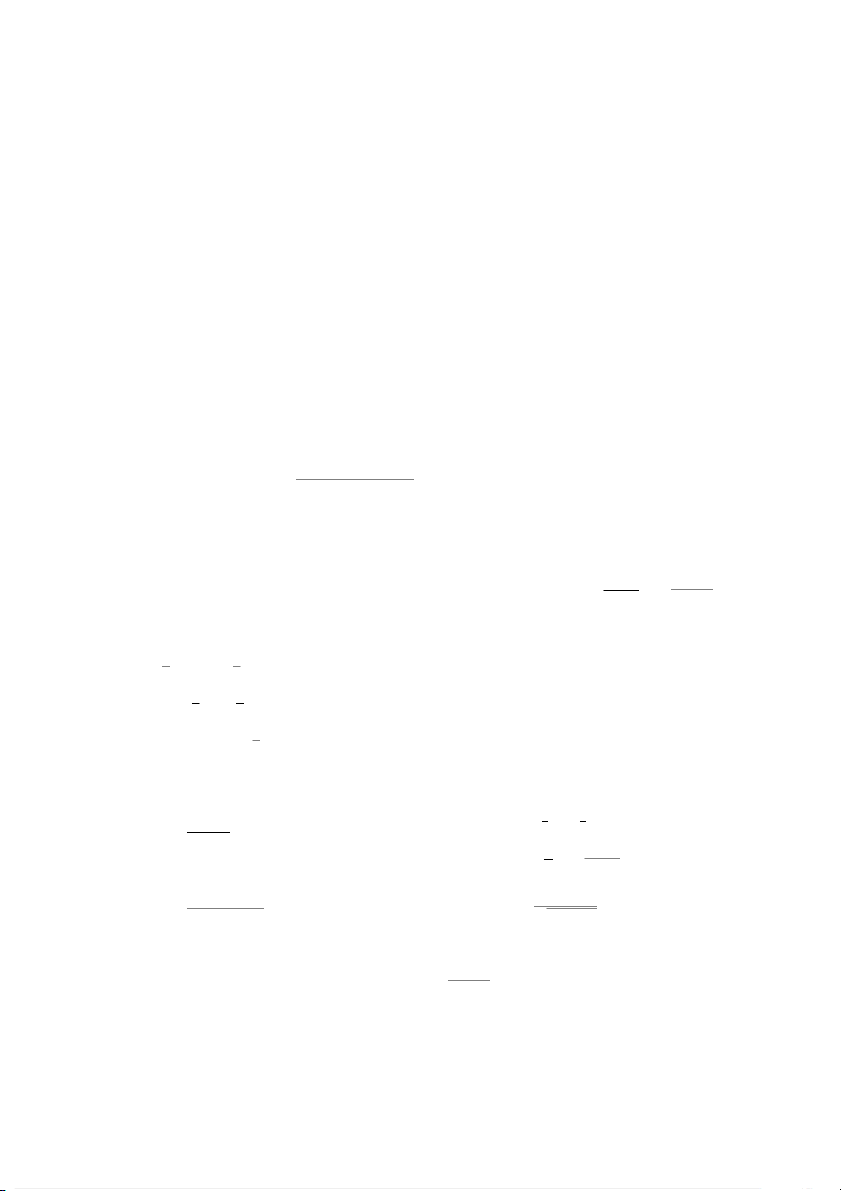


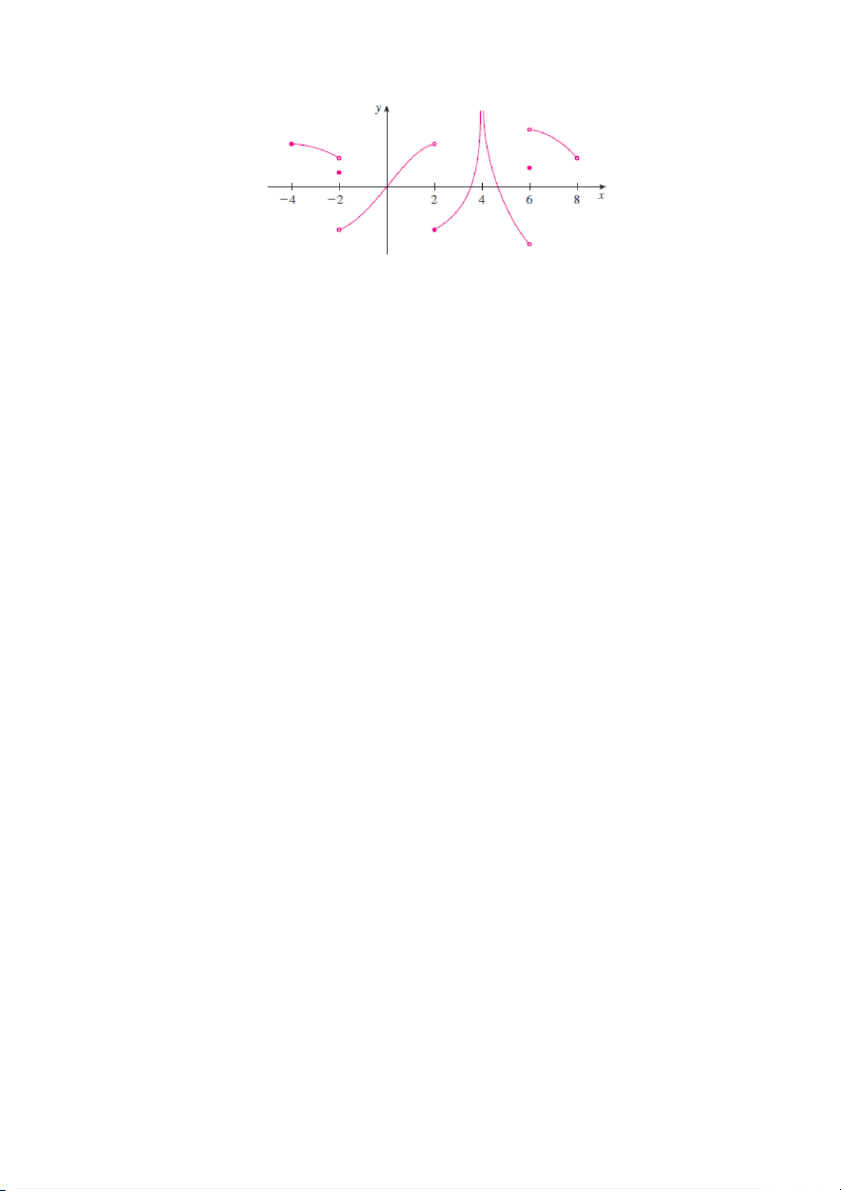



























Preview text:
Exercises: Calculus 1 Duong Thanh PHAM August 29, 2021 1
Functions, Limits and Continuity 1.1
Functions, domains, compositions
Exercise 1.1. Find a formula for the inverse of the function f (x) = x2 + 2x, x ≥ −1.
Exercise 1.2. Let f (x) = p2014 − cos(x + 1)
(i) Find the domain and the range of f .
(ii) Find functions g, h so that f (x) = g(h(x)), x ∈ (−∞, ∞). √ √
Exercise 1.3. Which of the following is the domain of the function y = 5 − x + x2 − 2? (A) {x ≤ 5} √ √ (B) {− 2 ≤ x ≤ 2} √ √ (C) {x ≤ − 2 or 2 ≤ x ≤ 5} √ (D) {x ≥ 5 or x ≤ − 2}
Exercise 1.4. Find the domains of the functions. x √ √ (i) f (x) = (iii) f (t) = t + 3 t 3x − 1 √ √ (iv) g(u) = u + 4 − u 5x + 4 1 (ii) f (x) = (v) h(x) = √ x2 + 3x + 2 x2 − 5x
Exercise 1.5. Find the domain of the range of the function p h(x) = 4 − x2.
Exercise 1.6. The graph below (Figure 1) shows a function f with domain [1, 4] and range [0, 2]. Let g(x) = 2f (x + 1). 1
Figure 1: This figure is used in Exercise 1.6
(i) State the domain and range of g(x). (ii) Sketch the graph of g(x).
Exercise 1.7. Let C be a circle with radius 2 centred at the point (2, 0).
(i) Write an equation for the circle C.
(ii) Is curve C the graph of a function of x? Explain your answer.
(iii) Write parametric equations to traverse C once, in a clockwise direction, starting from the origin.
Exercise 1.8. Let C be a circle centered at (0, 2) with radius 2. Which of the following is the
parametric equation of C, in the counter-clockwise direction, starting from the point (0, 4)? (A) x = 2 + 2 cos θ, y = 2 sin θ for θ ∈ [0, 2π], (B) x = 2 cos(θ + π ), y = 2 sin(θ + π ) for θ ∈ [0, 2π], 2 2 (C) x = 2 cos(θ + π ), y = 2 + 2 sin(θ + π) for θ ∈ [0, 2π], 2 2 (D) x = 2 cos(θ − π ), y = 2 + 2 sin(θ ) for θ , 2π 2 − π2 ∈ [0 ],
Exercise 1.9. Find an expression for the function whose graph is the given curve.
(i) The line segment joining the points (1, −3) and (5, 7).
(ii) The bottom half of the parabola x + (y − 1)2 = 0.
(iii) The top half of the circle x2 + (y − 2)2 = 4.
(iv) The two functions whose graphs are as in the following picture.
Exercise 1.10. Determine whether is even, odd, or neither. x x (i) (iii) (v) 1 + 3x2 − x4 x2 + 1 x + 1 x2 (ii) 3 5 x4 + 1 (iv) x |x| (vi) 1 + 3x − x 2
Exercise 1.11. Find the curve in the form y = f (x) whose parametric curve is
(x(t), y(t)) = (2t − 4, 3 + t2). 1.2 Limits 2x + 1 Exercise 1.12. The limit lim is x→−2+ x + 2 (A) −∞ (B) ∞ (C) 0 (D) undefined 4(0.5 + h)4 − 4(0.5)4 Exercise 1.13. What is lim ? h→0 h (A) 2 (C) 4 1 (B) 2 (D) the limit does not exist
Exercise 1.14. If bxc is the greatest integer that is not greater than x, then lim bxc is x 1 → 3 (A) 1 1 (C) 3 (B) 0 (D) the limit does not exist
Exercise 1.15. If bxc is the greatest integer that is not greater than x, then lim bxc is x→1 (A) 1 (C) 2 (B) 0 (D) the limit does not exist
Exercise 1.16. If dxe is the smallest integer that is not smaller than x, then lim dxe is x 1 → 3 3 (A) 1 1 (C) 3 (B) 0 (D) the limit does not exist
Exercise 1.17. If dxe is the smallest integer that is not smaller than x, then lim dxe is x→1 (A) 1 (C) 2 (B) 0 (D) the limit does not exist
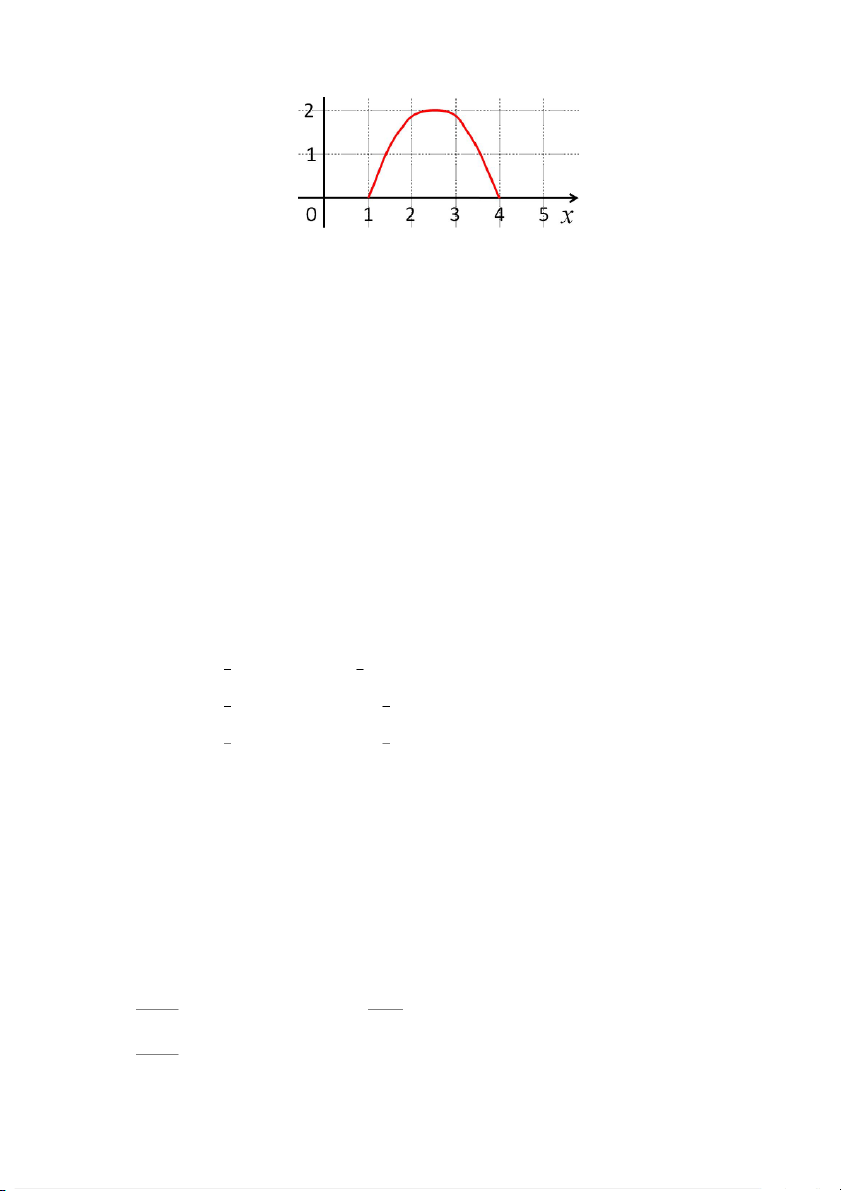
Exercise 1.18. For the function f whose graph is given, state the following. (i) lim f (x) (iv) lim f (x) x→2 x→∞ (ii) lim f (x) (v) lim f (x) x→−1 x→−∞ (iii) lim f (x)
(vi) The equations of asymptotes. x→−1+
Figure 2: This figure is used in Exercise 1.18 Exercise 1.19. Evaluate lim (cos x) cos(tan x). x→ 2 Exercise 1.20. (i) Evaluate the limit √6 − x − 2 lim √ . x→2 3 − x − 1
(ii) By using the Squeeze Theorem, or otherwise, evaluate the limit π lim (x − π) sin . x→π x − π 4 Exercise 1.21.
(i) Use Squeeze theorem to evaluate the limit lim x cos(ln |x|). x→0
(ii) Find F 0(1) where F (x) = xf (xf (x)), and f (1) = 1, f 0(1) = 2.
Exercise 1.22. Find the following limits: √3x + 4 − x (i) lim x→4 x − 4 2017 (ii) lim x2 sin + 2018 x→0 x (iii) lim esin 1 √x + sin x. x→0+ Exercise 1.23. Let sin x − 1 if x 6= π/2 f (x) = . 2 if x = π/2
Which of the following statements, I, II, and III, are true? (I) lim f (x) exists x→π/2 (II) f (π/2) exists
(III) f is continuous at x = π/2. (A) only I (C) I and II (B) only II (D) all of them x2 − 4x + 3 Exercise 1.24. Let f (x) =
. Choose the correct statement: x − 1 (A) lim f (x) = −2 x→1
(B) x = 1 is a vertical asymptote. (C) lim f (x) = −∞ x→1 (D) f (x) = x − 3 for all x. Exercise 1.25.
(i) A tank contains 5000 L of pure water. Brine that contains 30 g of salt per liter
of water is pumped into the tank at a rate of 25 L/min. Show that the concentration of salt
after t minutes (in grams per liter) is 30t C(t) = . 200 + t
(ii) What happens to the concentration as t → ∞? 5 1.3 Continuity
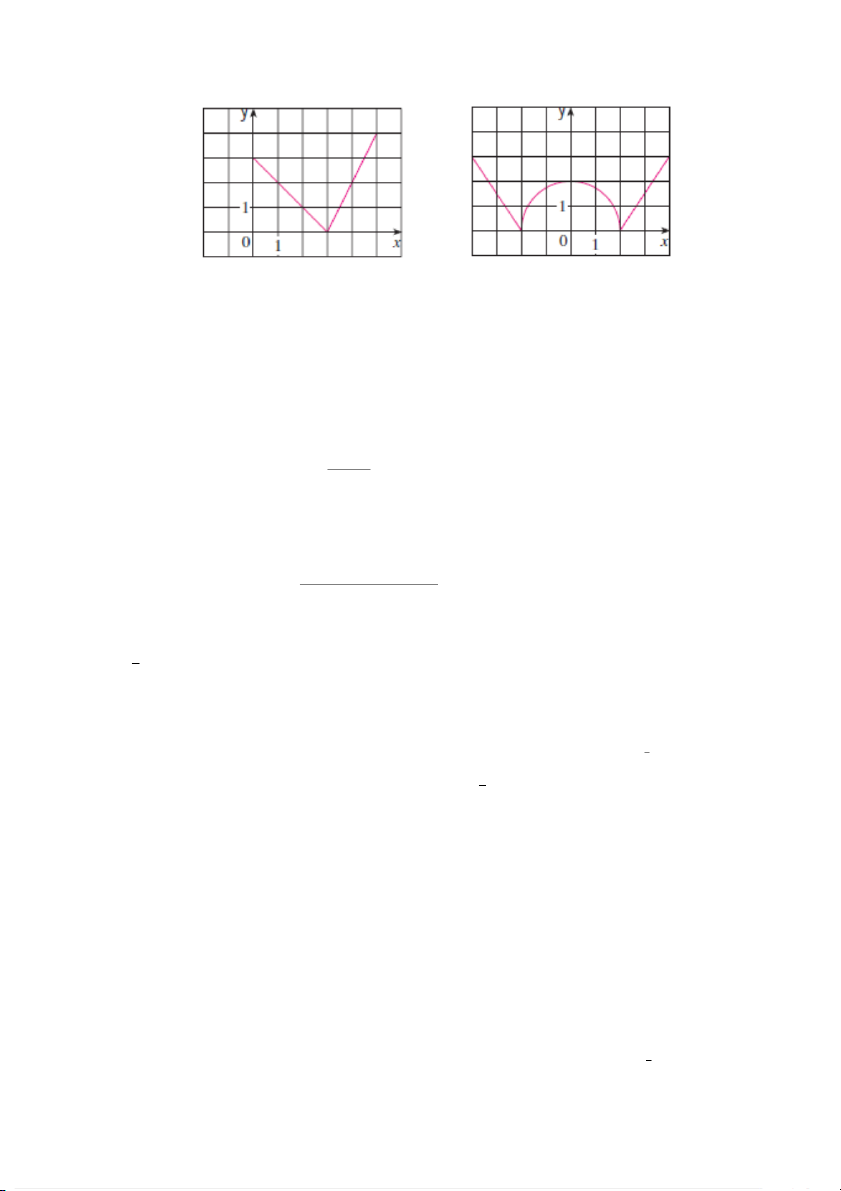
Exercise 1.26. Figure 3 shows the graph of a function f . At which numbers is f discontinuous? Why?
Figure 3: This figure is used in Exercise 1.26 Exercise 1.27.
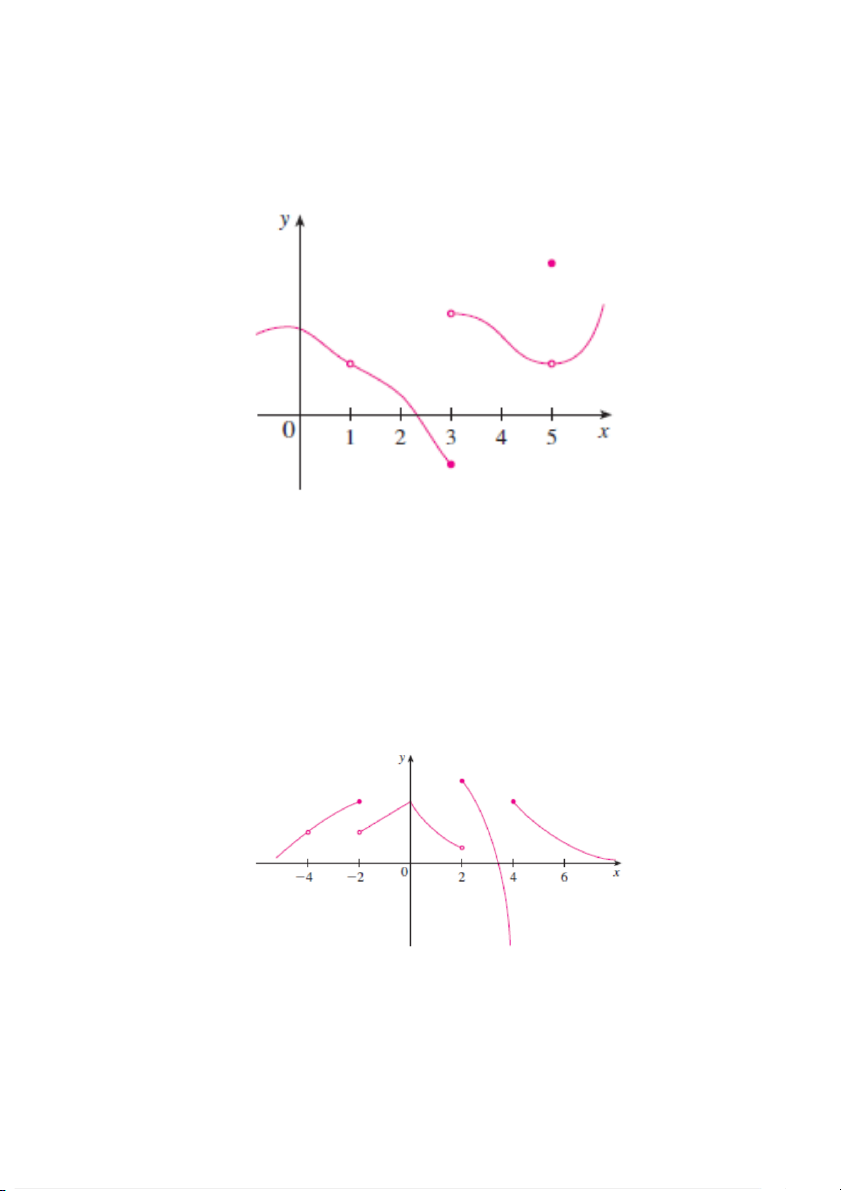
(i) From the graph of f (see Figure 4), state the numbers at which f is discontinuous and explain why.
(ii) For each of the numbers stated in part (i), determine whether is continuous from the right, or from the left, or neither.
Figure 4: This figure is used in Exercise 1.27 6
Figure 5: This figure is used in Exercise 1.28
Exercise 1.28. From the graph of g (see Figure 5), state the intervals on which g is continuous.
Exercise 1.29. Which of the following is true for the function f (x) given by 2x − 1 if x < −1 f (x) = x2 + 1 if − 1 ≤ x ≤ 1 x + 1 if x > 1.
(i) f is continuous everywhere,
(ii) f is continuous everywhere except at x = −1 and x = 1,
(iii) f is continuous everywhere except at x = −1,
(iv) f is continuous everywhere except at x = 1, (v) None of the above. Exercise 1.30. Let cos x if x < 0 g(x) = 0 if x = 0 1 − x2 if x > 0.
(i) Explain why g(x) is discontinuous at x = 0. (ii) Sketch the graph of g(x). Exercise 1.31.
(i) Find the value of the constant k so that the function kx2 if x ≤ 2 f (x) = x + k if x > 2
is continuous on (−∞, ∞). 7 √x − 1 (ii) Find lim . x→1 x2 − 1
Exercise 1.32. The radius of the earth is roughly 4000 miles, and an object located x miles from the
center of the earth weighs w(x) lb, where ax if 0 < x ≤ 4000 w(x) = b if x > 4000 x2
and a and b are positive constants.
(i) Show that w(x) is continuous on (0; ∞) if and only if b a = 40003
(ii) Find any horizontal asymptotes and sketch the graph of w(x). 1.4 The Intermediate Value Theorem
Exercise 1.33. Show that there are two positive real numbers c satisfying c + 1 sin c = . 3
Exercise 1.34. Prove that the equation ln x = e−x. has at least one root.
Exercise 1.35. Prove that the equation 84 x2016 + = 119, 1 + x2 + cos2 x has at least two roots.
Exercise 1.36. Show that the equation x3 − 2015x2 + 2x + 3 = 0 has three distinct real roots.
Exercise 1.37. Show that the equation √ x3 − x sin x − 1 = x x + 2
has a real root in the interval [0, 2]. 8
Exercise 1.38. Show that the equation 2012 2013 2014 + + = 0 x − 2012 x − 2013 x − 2014
has two real roots x1 ∈ (2012; 2013) and x2 ∈ (2013; 2014).
Exercise 1.39. If f (x) = x2 + 10 sin x, show that there is a number c such that f (c) = 1000.
Exercise 1.40. Suppose that f is continuous on [1, 5] and the only solutions of the equation f (x) = 6
are 1 and 4. If f (2) = 8, explain why f (3) > 6. 2 Differentiation 2.1 Definition of derivative
Exercise 2.1. Consider the function f defined by −x + a if x < 0 f (x) = x2 + 1 if 0 ≤ x ≤ 1 x − b if x > 1 where a and b are constants.
(i) Find values of a and b such that f is continuous on (−∞, ∞).
(ii) Sketch the graph of f with a and b found in (i). Is f differentiable at x = 1? Exercise 2.2. Let 2x + 1 if x < 0 f (x) = x2 + 1 if x ≥ 0.
(i) Show that f (x) is continuous at x = 0
(ii) Is f (x) differentiable at x = 0? Explain your answer. (iii) Find max f (x) and min f (x) x∈[−3,5] x∈[−3,5]
Exercise 2.3. Find the values of a and b that make x2 + 1 if x ≥ 0, f (x) = a sin x + b(x + 1) if x < 0, differentiable everywhere. Exercise 2.4. Let 1 if x < −1 x + a f (x) = x if − 1 ≤ x ≤ 1 (x − b)2 + 1 if x > 1, 9
(i) Find the values of a and b such that f (x) is defined and continuous everywhere.
(ii) With the values of a and b found in part (i), find any horizontal asymptotes, and sketch the graph of f (x).
(iii) Show that f (x) is not differentiable at x = 1.
Exercise 2.5. Show that the function f (x) = |x − 2| is continuous but not differentiable at x = 2.
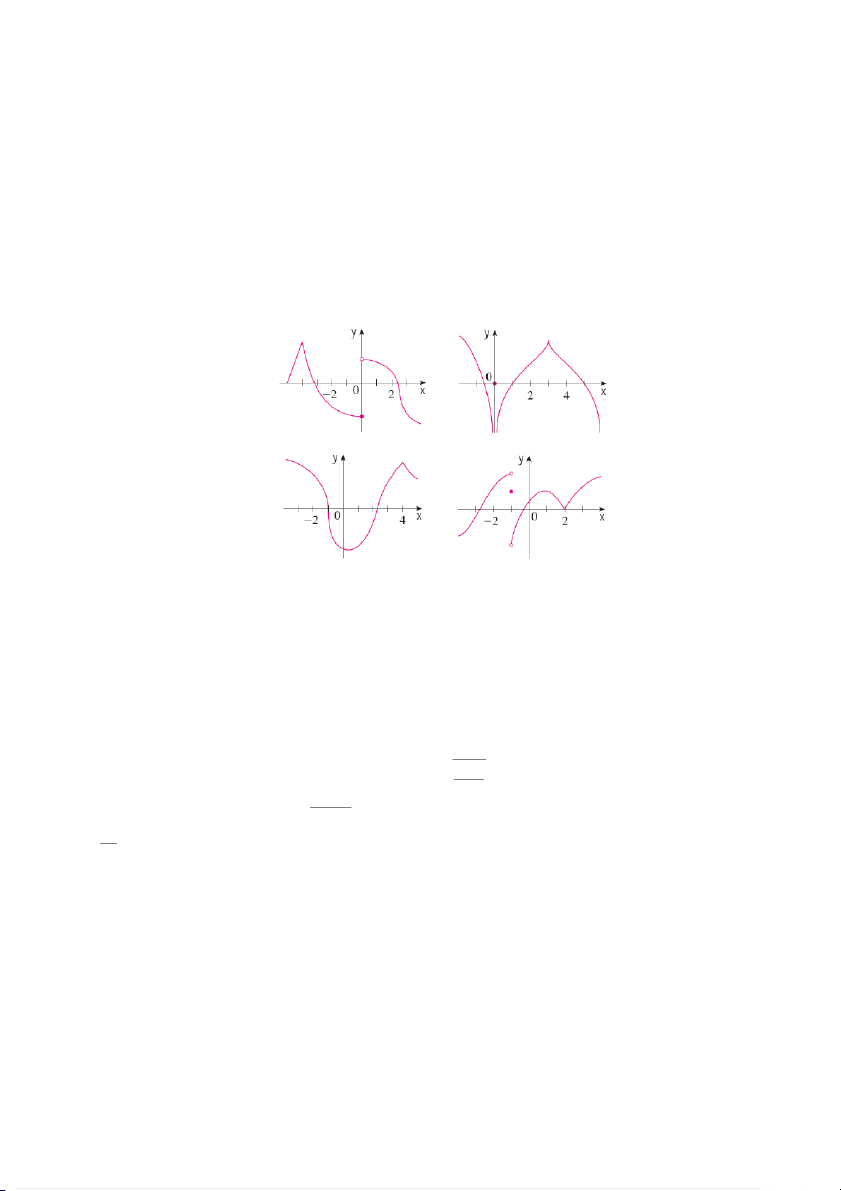
Exercise 2.6. The graph of f is given. State, with reasons, the numbers at which is not differentiable Figure 6: Exercise 2.6 2.2 Finding Derivatives 2.2.1 Direct differentiation
Exercise 2.7. Find the derivative of r sin x f (x) = . x √ Exercise 2.8. Let f (x) =
1 + x3; g(x) = e−2x+1. Evaluate the derivatives f 0(x), g0(x), and d (f(g(x))). dx
Exercise 2.9. Suppose f and g are two differentiable functions on (−∞, ∞) and f(1) = 5, f0(1) = −3,
g(1) = 1, g0(1) = −1. Find F 0(1) where F (x) = f (g(2x − 1)).
Exercise 2.10. Differentiate the function h(x) = e−x2 sin 2x. Exercise 2.11.
(i) Find an equation of the tangent line to the graph of y = g(x) at x = 5 if g(5) = −3 and g0(5) = 4. 10



