Calculus 1 (MA001IU) HW Assignment #4 HCMIU-2023
Deadline: 4:00 PM, April 04, 2023.
Submit your solution papers for Q1-Q15 into my mailbox in front of O2.610 by the deadline. Instructions:
Submit solutions (hard copy) for Questions 1-15. Others are for your practicing
only and are not graded. The solutions must be are in the order.
The submissions for HW Assignment 4 (in papers) are into my P.O. mailbox in front of
O2.610 (outside O2.610 and nearby the office door). Please mention your class (Wednes-
day or Thursday) on the first page. You should make a copy or take photos the assignment.
Exercises for chapter 4 and chapter 5.
1. Find the derivatives (a-b) and the limit (c): ! ! x4 x 1 √ (a) d R cos (t2) dt (b) d R et R 2+x dt (c) lim 1 + t3dt dx dx t x x 2 0 √x →0 2. Evaluate the integrals (a) R x sin 2xdx, (b) R (3x − 1) exdx, (c) R x3 ln xdx.
Hint: Use the Integration by Parts.
3. Find the average value of the function on the given interval. a. f (x) = 4x − x2, [0, 3] √ b. f (x) = x2 1 + x3, [0, 2].
c. f (x) = cos4 x sin x, [0, π] d. f (x) = xe−x2, [0, 5]. e. f (x) = |x2 − 4|, [0, 3]. sin x f. f (x) = , [−π, π]. x2 + 1
4. Calculate the definite integral 2 4 √ 4 √ π a. R xe9xdx, b. R x ln xdx, c. R x 4 − xdx, d. R x sin (2x) dx. 0 1 0 0
5. Alabama Instruments Company has set up a production line to manufacture a new cal-
culator. The rate of production of these calculators after t weeks is dx  100  = 5000 1 − (calculators/week). dt (t + 10)2
(Notice that production approaches 5000 per week as time goes on, but the initial pro-
duction is lower because of the workers’ unfamiliarity with the new techniques.) Find the
number of calculators produced from the beginning of the third week to the end of the fourth week. 1 Calculus 1 (MA001IU) HW Assignment #4 HCMIU-2023 6. Newton’s Law of Cooling
(a) A cup of coffee has temperature 95o C and takes 30 minutes to cool to 61o C in a room
with temperature 20o C. Use Newton’s Law of Cooling to show that the temperature of
the coffee after t minutes is T (t) = 20 + 75e−kt where k ≈ 0.02.
(b) What is the average temperature of the coffee during the first half hour? 7. Evaluate 3 4 1/2 √ 3 2 (a) R x−9 dx, (b) R dx , (c) R x −2x −4 dx, (d) R x2 1 − x2dx. (x+5)(x−2) x2−1 x3−2x2 2 3 0
Hint: (c) x3−2x2−4 = 1 + 1 + 2 − 1 . x3−2x2 x x2 x−2 1
8. Estimate R cos (x2) dx using (a) the Trapezoidal Rule and (b) the Midpoint Rule, each 0 with n = 4. Hint: (a) T4 ≈ 0.895759, (b) M4 ≈ 0.908907.
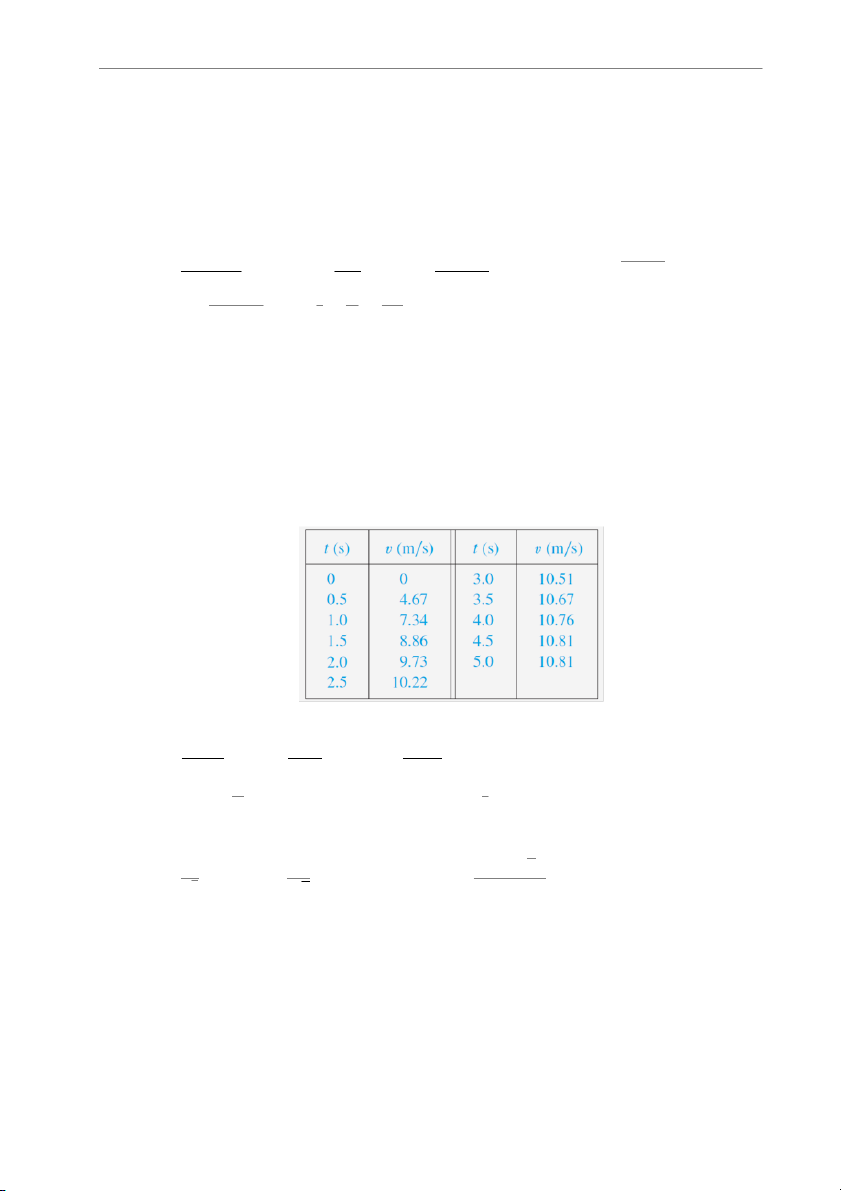
9. A radar gun was used to record the speed of a runner during the first 5 seconds of a race
(see the table). Use the Trapezoidal Rule to estimate the distance the runner covered during those 5 seconds.
10. Evaluate the integral or show that it is divergent ∞ ∞ ∞ (a) R dx , (b) R x+1 dx, (c) R 1 dx. (3x+1)2 x2+2x x(ln x)3 1 1 e
Answers: (a) 1 , convergent; (b) Divergent, (c) 1, convergent. 12 2
11. Evaluate the integral or show that it is divergent [(a)-(b)]. √ 4 ∞ 1 ∞ sin2 ( x) (a) R ln x R R √ dx, (b) √ dx, (c) Show that dx is convergent. x 3 x2 + x + 1 0 1 x 1
12. A radioactive substance decays exponentially: The mass at time is m (t) = m (0) ekt,
where m(0) is the initial mass and k is a negative constant. The mean life of an atom in the substance is ∞ Z M = −k tektdt 0 2 Calculus 1 (MA001IU) HW Assignment #4 HCMIU-2023
For the radioactive carbon isotope, 14C (Carbon-14), used in radiocarbon dating, the
value of k is −0.000121. Find the mean life of a 14C atom.
13. Sketch the region enclosed by the given curves. Then find the area of the region enclosed by the curves:
(a) y = x + 1, y = 9 − x2, x = −1, x = 2 (b) y = x, y = x2 (c) y = 1, y = 1 , x = 2 x x2 √ (d) y = x, y = x , x = 9 2 (e) x = 2y2, x = 4 + y2 (f) x = 1 − y2, x = y2 − 1
Answers (a) 39 , (b) 1, (c) ln 2 − 1, (d) 59 , (e) 32, (f) 8. 2 6 2 12 3 3
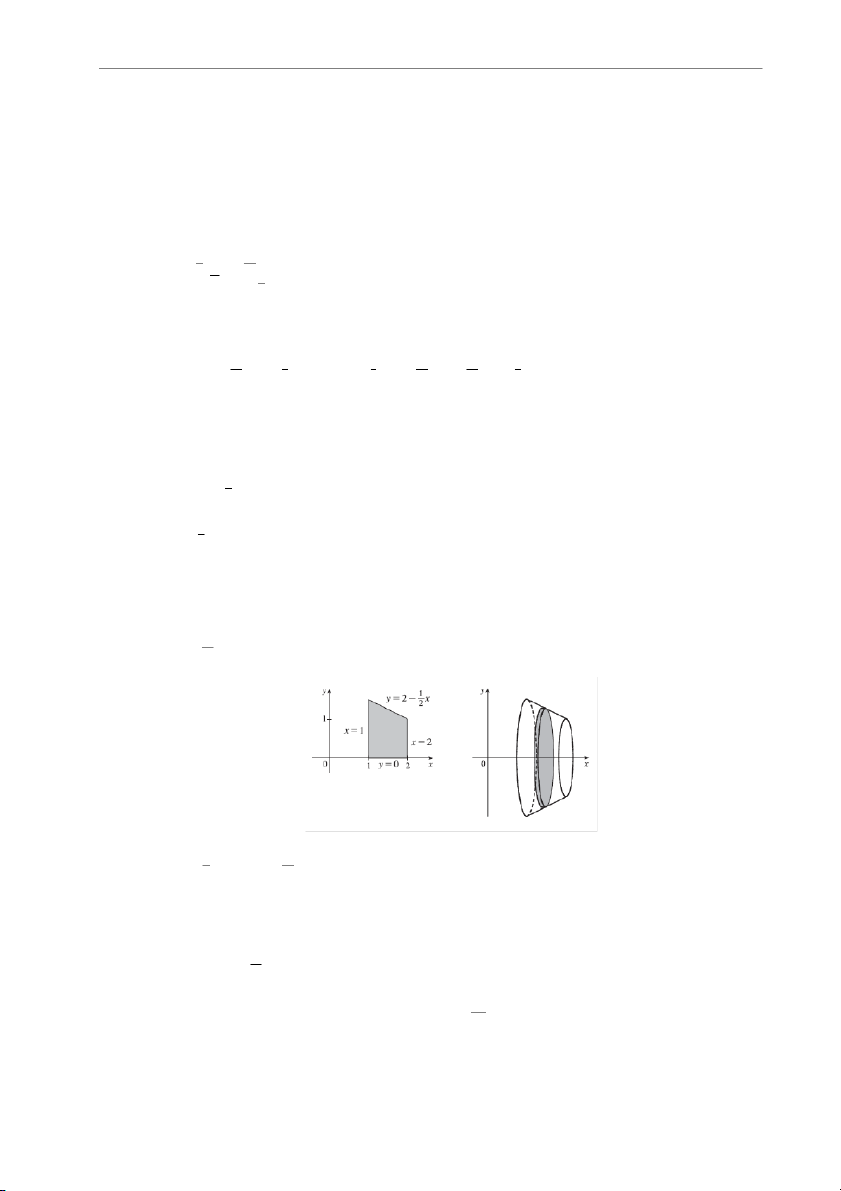
14. Find the volume of the solid obtained by rotating the region bounded by the given curves
about the specified line. Sketch the region, the solid, and a typical disk or washer.
(a) y = 2 − x , y = 0, x = 1, x = 2; about the x-axis 2
(b) y = 1 , x = 1, x = 2, y = 0; about the x-axis x
(c) y2 = x, x = 2y; about the y-axis Answers (a) V = 19π 12 (b) V = π , (c) V = 64π. 2 15
15. Calculate the arc length of the graph of
(a) y = f (x) = 1 x3 + x−1 over [1, 3]. 12 Hint:  x2 2 1 + (f ′ (x))2 = + x−2 4 3 Calculus 1 (MA001IU) HW Assignment #4 HCMIU-2023
(b) y = 1 + 6x3/2, over [0, 1].
The below suggested questions are for additional practicing. They are NOT for Assignment #4 submission: 16. Evaluate 1 (a) R x (x2 + 1)5dx, (b) R x+2 dx (d) R cos x x √ dx, (e) R cos(ln ) dx √ dx (c) R e x √x 1+sin x x 0 x2+4x Hint: Substitution
17. Express the following limit of the Riemann sum n lim X (x5i + x2i cos xi)∆x, n→∞ i=1 π where xi = i∆x, ∆x =
, as an integral on the interval [0, π]. n
18. Find the interval [a, b] for which the value of the integral R b(2 + x − x2)dx is a maximum. a
Hint: Sketch the function y = 2 + x − x2.
19. If f is continuous and R 2 f (x)dx = 6, evaluate R π/2 f (2 sin θ) cos θdθ. 0 0
20. If f is continuous on [0, 1], prove that R 1 f (x)dx = R 1 f (1 − x)dx. 0 0
21. The table (supplied by San Diego Gas and Electric) gives the power consumption P in
megawatts in San Diego County from midnight to 6:00 AM on December 8, 1999. Use
Trapezoidal Rule to estimate the energy used during that time period. (Use the fact that
power is the derivative of energy.)
22. Find the area of the shaded region 4 Calculus 1 (MA001IU) HW Assignment #4 HCMIU-2023
23. Consider the circle x2 + y2 = R2.
(a) Write down parametric equations to traverse the circle once.
(b) Show that the length of the circumference is 2πR.
24. Use the method of cylindrical shells to find the volume generated by rotating the region √
bounded by the curves y = 3 x, y = 0, and x = 1 about the y−axis. —END— 5