THE INTERNATIONAL UNIVERSITY (IU) Course: Stochastic Model
Department of Industrial System Engineering
FINAL E XAMINATION S T O C H A ST I C M O D E L Duration: 120 minutes Head of Department of Lecturer: Student ID: Date: Industrial & Systems 23 May 2016 , Engineering Name: Assoc Prof. Ho Thanh Phan Nguyen Ky Phuc Phong INSTRUCTIONS:
1. This is an open book examination. No laptops, PDA.
2. Use of calculator is allowed; discussion and material transfer are strictly prohibited. Total pages: 2 (including this page) PART I (100 %) Question 1: (20 pts) Given the network as follow:
Find the shortest path from node (1) to node (9) in term of expected cost. Given that if we choose
decision of going up (U), we will either go up with probability 0.7 or go down with probability 0.3. If we
choose decision of going down (D), we will either go – Final Exam 23, May, 2016 Stochastic Model 1
THE INTERNATIONAL UNIVERSITY (IU) Course: Stochastic Model
Department of Industrial System Engineering
up with probability 0.2 or go up with probability 0.8. If there is only one available decision, the
probability corresponding to the decision is 1. Question 2: (25pts)
An automobile maintenance center has two staffs A & B. This center offers two kinds of service for two
types of vehicles, i.e., type 1 & type 2. For type 1 vehicle, it can be served by either A or B. The service
rates for type 1 vehicle of A and B are 2 and 3 respectively. If both A and B are free, the type vehicle 1
will choose staff A with probability 0.4 and staff B with probability 0.6. The type 2 vehicle requires
simultaneous service of both staffs; hence, a type 2 vehicle will only enter the center if both staffs are
free. The time that it takes (the two staffs) to serve a type 2 vehicle is exponential with rate 3. Once a
service is completed on a vehicle, that vehicle departs the system. When a vehicle arrives the center and
know that it cannot be served immediately, it will leave the center. Given that the arrival rate of type 1
vehicle is 3 and type 2 vehicle is 2.
(a) Define state space (5pts)
(b) Draw the transition graph (5pts)
(c) Give the balance equations. (5pts)
(d) Calculate the average amount of time an entering vehicle spends in the system (5pts)
(e) The fraction of served vehicle that are type 1 (5pts) Question 3: (25pts)
An urn contains 2 Red balls and 1 Blue ball. Every time a ball is drawn from the urn another ball will be
refilled. The probabilities that the colors of refilled ball are Red and Blue are 0.6 and 0.4, respectively.
(a) Define state space (5pts)
(b) Find transition matrix (5pts)
(c) Find the long run proportion of time that the urn is in each state (5pts)
(d) Find the long-run average number of red ball in urn(5pts)
(e) Find the expected total number of Red ball in the next two draws (that is, in draws 1 and 2) (5pts)
Question 4: (10pts)
A doctor has scheduled two appointments, one at 1 P.M. and the other at 1:30 P.M. The amounts of time
that appointments last are independent exponential random variables with mean 30 minutes. Assuming
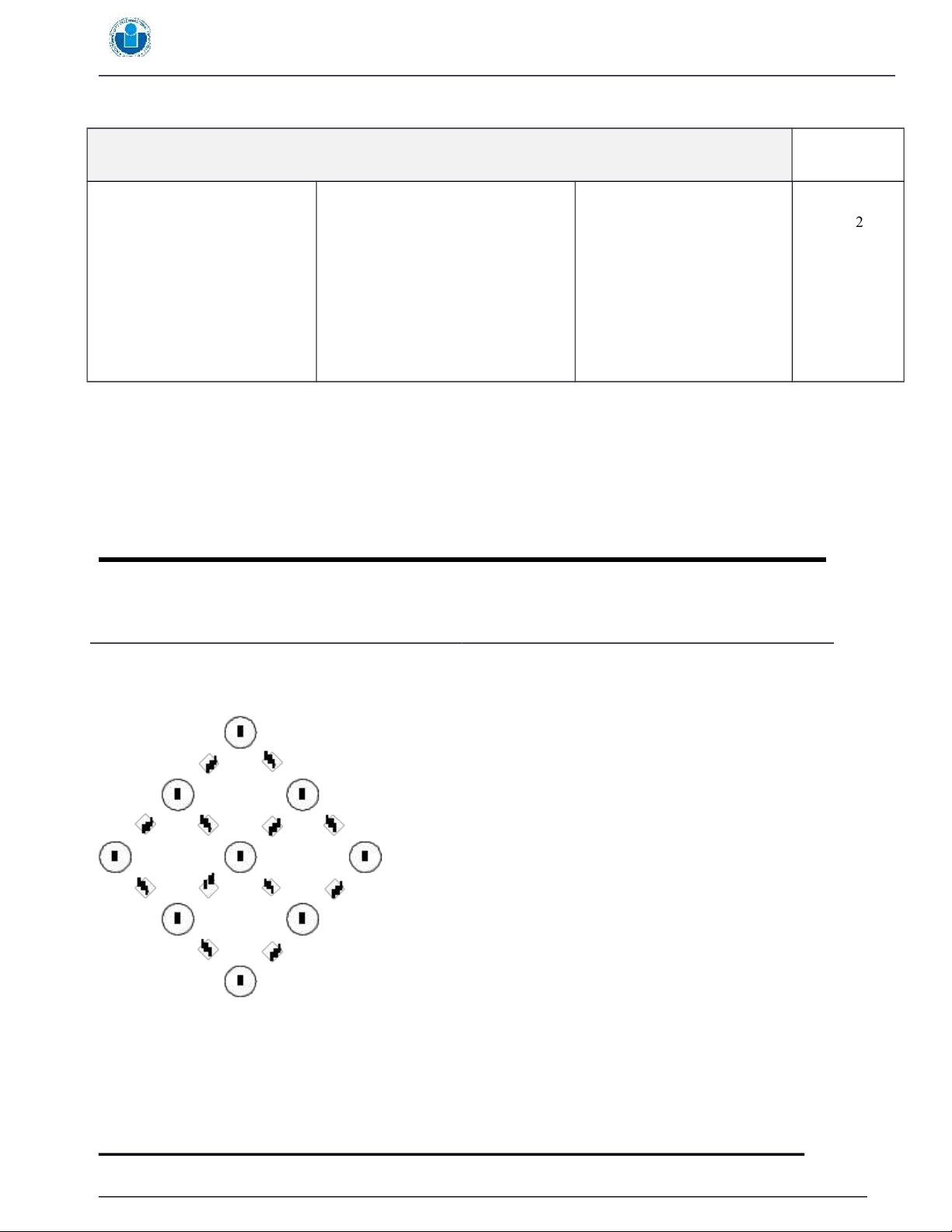
that both patients are on time, find the expected amount of time that the 1:30 appointment spends at the doctor’s office. Question 5: (20pts) Given the system below
a) Find the structural function of the system (5pts)
b) Find the minimal path set of the above system (5pts) Stochastic Model 2
THE INTERNATIONAL UNIVERSITY (IU) Course: Stochastic Model
Department of Industrial System Engineering – Final Exam 23, May, 2016
c) Give the probability that each component works well as follow: . Find the reliability of the system. (5pts)
d) If the component lifetimes of {4,5} are uniform distribution on (0, 10) and (0, 5) respectively .
Other components have the same probability of function. Find the expected life time of the system. (5pts)
GOOD LUCKS! 23, May, 2016 Stochastic Model 3