

























































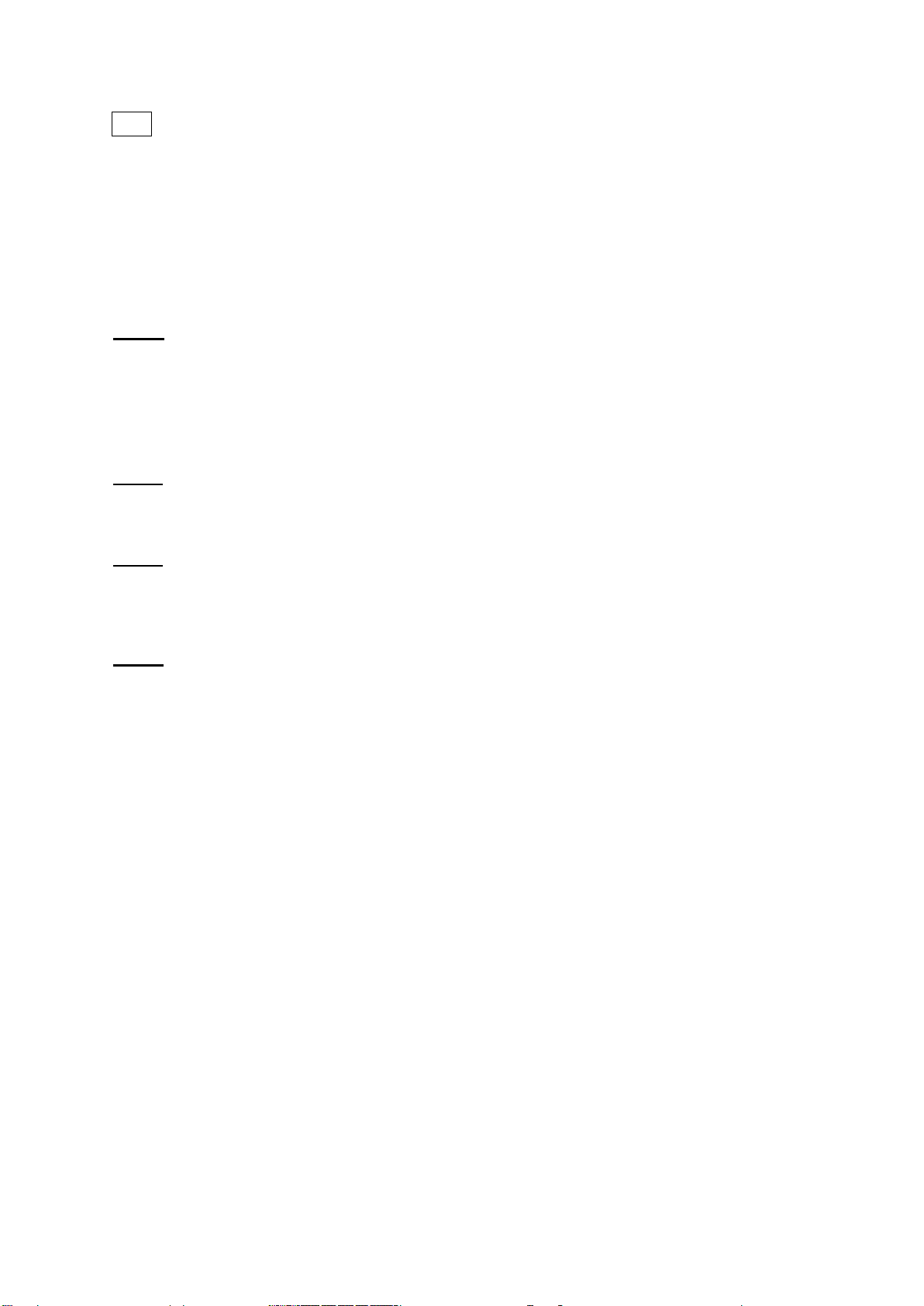










































































Preview text:
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 1
ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20153
Mã học phần: MI2020 Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tung ngẫu nhiên 8 lần một đồng xu (khả năng ra mặt sấp và ngửa là như nhau ở mỗi lần
tung). Tính xác suất để:
a. Được mặt sấp ở các lần gieo chẵn.
b. Chỉ được mặt sấp ở các lần gieo chẵn.
Câu 2. Một hộp có 20 sản phẩm, số chính phẩm có trong 20 sản phẩm đó là ngẫu nhiên và có
khả năng xảy ra như nhau. Người ta bỏ thêm vào hộp đó 1 chính phẩm, sau đó từ hộp này lại lấy
ngẫu nhiên ra một sản phẩm. Tính xác suất sản phẩm đó là chính phẩm.
Câu 3. Tuổi thọ của một loài côn trùng nào đó là biến ngẫu nhiên X (tháng tuổi) có hàm mật độ xác suất như sau: 2 ax (4 x) 0 x 4 f (x) 0 x [0; 4]
a. Xác định a, tìm tỷ lệ côn trùng sống không quá 1 tháng tuổi. b. Xác định mod(X).
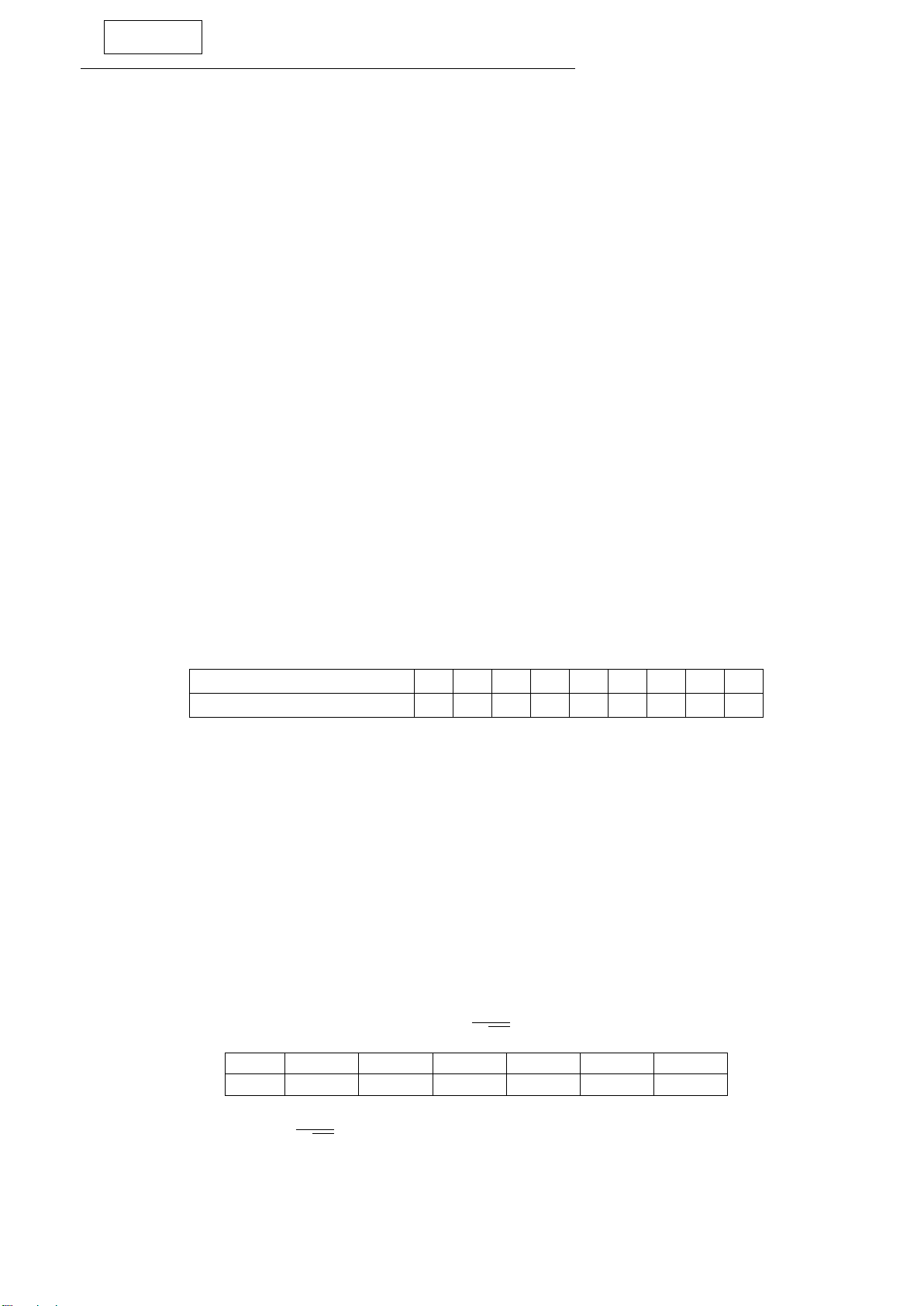
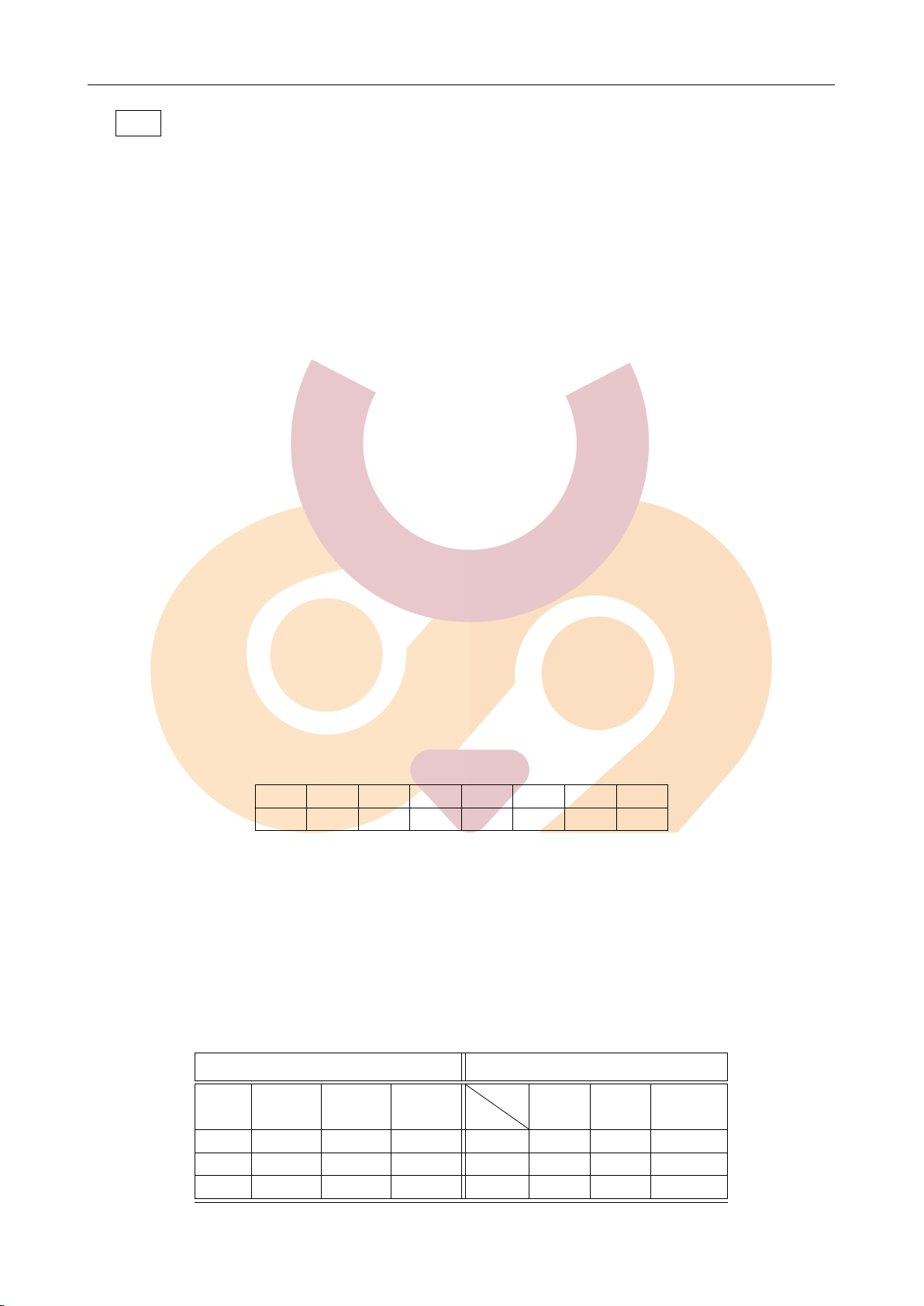
Câu 4. Nghiên cứu số vụ tai nạn giao thông xảy ra hàng ngày ở một khu vực ta có bảng số liệu sau: Số vụ tai nạn 0 1 2 3 4 5 6 7 Số ngày 229 211 93 35 7 0 0 1
Với độ tin cậy 90%, hãy ước lượng khoảng đối xứng cho số tai nạn trung bình hàng ngày trong khu vực trên.
Câu 5. Có người đưa ra ý kiến tỷ lệ ngày có xảy ra tai nạn bằng 60%. Với số liệu thu được ở
trên và với mức ý nghĩa 5%, hãy kết luận về ý kiến trên.
Chú ý: Không được sử dụng tài liệu x 2 1 Phụ lục
. Trích các số Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 3 0,9 0,95 0,975 0,9772 0,9987 x)
Hàm Laplace (x) = (x) – 0,5 1
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 2
ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20153
Mã học phần: MI2020 Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tung ngẫu nhiên 9 lần một đồng xu (khả năng ra mặt sấp và ngửa là như nhau ở mỗi lần
tung). Tính xác suất để:
a. Được mặt sấp ở 4 lần gieo đầu.
b. Chỉ được mặt sấp ở 4 lần gieo đầu.
Câu 2. Một hộp có 24 sản phẩm, số phế phẩm có trong 24 sản phẩm đó là ngẫu nhiên và có khả
năng xảy ra như nhau. Người ta bỏ thêm vào hộp đó một chính phẩm, sau đó từ hộp này lại lấy
ngẫu nhiên ra một sản phẩm. Tính xác suất sản phẩm đó là phế phẩm.
Câu 3. Tuổi thọ của một loài côn trùng nào đó là biến ngẫu nhiên X (tháng tuổi) có hàm mật độ xác suất như sau: 2 ax(4 x ) 0 x 2 f (x) 0 x [0; 2]
a. Xác định a, tìm tỷ lệ côn trùng sống không quá 1 tháng tuổi. b. Xác định mod(X).
Câu 4. Để xác định tốc độ của một phản ứng, người ta tiến hành 60 phép thử đo tốc độ phản ứng
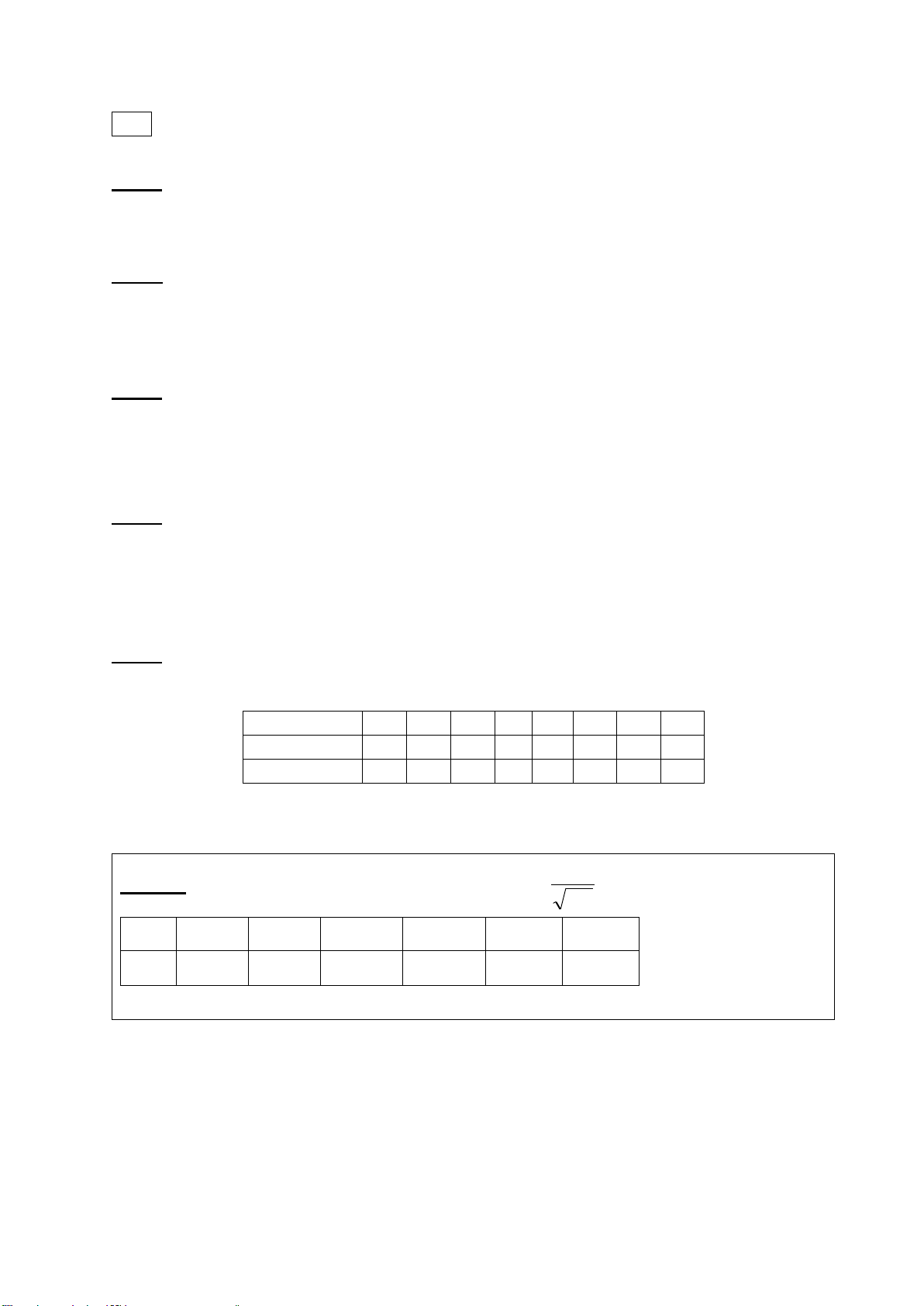
đó trong cùng điều kiện và bằng cùng một phương pháp đo. Kết quả thu được như sau: Tốc độ phản ứng 2,68 2,70 2,73 2,74 2,75 2,76 2,79 2,82 Số phép thử 1 4 12 18 17 5 2 1
Với độ tin cậy 90%, hãy ước lượng khoảng đối xứng cho tốc độ phản ứng trung bình theo cách trên.
Câu 5. Có người đưa ra ý kiến cho rằng xác suất để “tốc độ phản ứng nhỏ hơn 2,72” là thấp hơn
10%. Với số liệu thu được ở trên và với mức ý nghĩa 5%, hãy kết luận về ý kiến trên. x 2 1 Phụ lục
. Trích các số Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 3 (x) 0,9 0,95 0,975 0,9772 0,9987
Hàm Laplace (x) = (x) – 0,5 2
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐÁP ÁN ĐỀ 1 – XÁC SUẤT THỐNG KÊ
Câu 1.(2đ) Gọi A : “lần gieo thứ i được mặt sấp” , i 1, 2,...,8 i
a. Gọi A: “trong 8 lần gieo ta được mặt sấp ở các lần gieo chẵn”, 4 P( )
A P( A .A .A .A ) P( A ).P( A ).P( A ).P( A ) 0,5 0, 0625 (1đ) 2 4 6 8 2 4 6 8
b. Gọi B: “trong 8 lần gieo ta chỉ được mặt sấp ở các lần gieo chẵn”, 8 P( )
A P( A .A .A .A .A .A .A .A ) P( A ).P( A )...P( A ).P( A ) 0,5 0, 00391 (1đ) 1 2 3 4 5 6 7 8 1 2 7 8
Câu 2.(2đ) Gọi A : “trong hộp ban đầu có i chính phẩm”, i 0,1, 2,..., 20 i 1
P( A ) P( A ) ... P( A ) (0,5đ) 0 1 20 21
Gọi H: “sản phẩm lấy ra từ hộp là chính phẩm” i 1
P(H | A ) i 0,1,..., 20 (0,5đ) i 21 20 20 1 i 1
P(H ) P(A ).P(H | A ) (0,5đ) i i i i 21 21 0 0 1 1 21.22 11 (1 2 ... 21) (0,5đ) 21.21 21.21 2 21 Câu 3.(2đ) 3 4 4 x x 64 3 a. 2 4 1
ax (4 x)dx a(4 ) | . a a (0,5đ) 0 0 3 4 3 64 3 4 1 x x 3 4 1 13 2 1
ax (4 x)dx a(4 ) | ( ) 0,051 (0,5đ) 0 0 3 4 64 3 4 256 b. Xét x (0;4) x 0 2 f '(x) .
a (8x 3x ) 0 (0,5đ) x 8 / 3
Ta có hàm f’(x) dương trong khoảng (0; 8/3) và âm trong khoảng ( ; 0) (8 / 3; )
Do đó hàm số f(x) đạt cực đại tại x = 8/3 và đạt cực tiểu tại 0.
Do hàm mật độ chỉ khác 0 trong x(0;4) , nên mod(X) = 8/3 (0,5đ)
Câu 4.(2đ) Gọi X là số vụ tai nạn giao thông xảy ra trong một ngày, EX . Chọn thống kê X n ~ N(0;1) (0,5đ) s
Khoảng tin cậy đối xứng cho s s : x u ; x u (0,5đ) 1 1 n n 2 2
Với 1 0,9 0,1 u u 1,645 1 /2 0,95
Từ bảng số liệu ta tính được n 576 ; x 0,932 ; s 0,985 (0,5đ)
Thay số ta có khoảng tin cậy: (0,8645 ; 0,9995) (0,5đ) 3
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
Câu 5.(2đ) Gọi p là tỷ lệ số ngày có xảy ra tai nạn.
H : p p
Kiểm định cặp giả thuyết: 0 0 p 0,6 (0,5đ) 0
H : p p 1 0 Chọn thống kê f p0
n ~ N(0;1) khi H đúng 0 p (1 p ) 0 0 m
Từ bảng số liệu ta tính được 347
n 576 ; m 347 f 0,6024 n 576 suy ra giá trị quan sát f p 0,6024 0,6 0 k n 576 0 118 , (0,5đ) p (1 p ) 0,6.0,4 0 0
Với = 0,05 ta có miền bác bỏ H0: w ( ; u ) (u ; ) ( ; u ) (u ; ) ( ; 1 ,96) (1,96; ) (0,5đ) 1 /2 1 /2 0,975 0,975
Do k w nên ta không có cơ sở bác bỏ H . Vậy ý kiến đưa ra là đúng. (0,5đ) 0 4
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐÁP ÁN ĐỀ 2 – XÁC SUẤT THỐNG KÊ
Câu 1.(2đ) Gọi A : “lần gieo thứ i được mặt sấp” , i 1, 2,...,9 i
a. Gọi A: “trong 9 lần gieo ta được mặt sấp trong 4 lần gieo đầu”, 4 P( )
A P( A .A .A .A ) P( A ).P( A ).P( A ).P( A ) 0,5 0, 0625 (1đ) 1 2 3 4 1 2 3 4
b. Gọi B: “trong 9 lần gieo ta chỉ được mặt sấp trong 4 lần gieo đầu”, 4 5 P( )
A P( A .A .A .A .A .A .A .A .A ) P( A ).P( A )...P( A ).P( A ) 0,5 .0,5 0, 00195 (1đ) 1 2 3 4 5 6 7 8 9 1 2 8 9
Câu 2.(2đ) Gọi A : “trong hộp ban đầu có i phế phẩm”, i 0,1, 2,..., 24 i 1
P( A ) P( A ) ... P( A ) (0,5đ) 0 1 24 25
Gọi H: “sản phẩm lấy ra từ hộp là phế phẩm” i
P(H | A ) i 0,1,..., 24 (0,5đ) i 25 24 24 1 i
P(H ) P(A ).P(H | A ) (0,5đ) i i i i 25 25 0 0 1 1 24.25 12
(0 1 2 ... 24) (0,5đ) 25.25 25.25 2 25 Câu 3.(2đ) 4 2 x 1 a. 2 2 2 1
ax(4 x )dx a(2x
) | 4a a (0,5đ) 0 0 4 4 4 1 x 1 1 7 2 2 1
ax(4 x )dx a(2x ) | (2 ) 0,4375 (0,5đ) 0 0 4 4 4 16 b. Xét x (0;2)
x 4 / 3 2 3 / 3 2 f '(x) .
a (4 3x ) 0 (0,5đ)
x 4 / 3 2 3 / 3
Ta có hàm f’(x) dương trong khoảng ( 2 3 / 3 , 2 3 / 3) và âm trong khoảng ( ; 2 3 / 3) (2 3 / 3; )
Do đó hàm số f(x) đạt cực đại tại x 2 3 / 3 và đạt cực tiểu tại x 2 3 / 3.
Do hàm mật độ chỉ khác 0 trong x(0;2) , nên Mod(X ) 2 3 / 3 (0,5đ)
Câu 4.(2đ) Gọi X là tốc độ của phản ứng đang xét, EX . Chọn thống kê X n ~ N(0;1) (0,5đ) s
Khoảng tin cậy đối xứng cho s s : x u ; x u (0,5đ) 1 1 n n 2 2
Với 1 0,9 0,1 u u 1,645 1 /2 0,95
Từ bảng số liệu ta tính được n 60 ; x 2,742 ; s 0,021 (0,5đ) 5
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
Thay số ta có khoảng tin cậy: (2,738 ; 2,746) (0,5đ)
Câu 5.(2đ) Gọi p là xác suất để “tốc độ phản ứng nhỏ hơn 2,72”.
H : p p
Kiểm định cặp giả thuyết: 0 0 p 0,1 (0,5đ) 0
H : p p 1 0 Chọn thống kê f p0
n ~ N(0;1) khi H đúng 0 p (1 p ) 0 0 m
Từ bảng số liệu ta tính được 5
n 60 ; m 5 f n 60 suy ra giá trị quan sát f p 1 / 12 0 1 , 0 k n 60 0 ,43 (0,5đ) p (1 p ) 0 1 , .0,9 0 0
Với = 0,05 ta có miền bác bỏ H0: w ( ; u ) ( ; u ) ( ; 1 ,645) (0,5đ) 1 0,95
Do k w nên ta không có cơ sở bác bỏ H . Vậy ý kiến đưa ra là sai. (0,5đ) 0 6 ĐỀ 1
Đề thi môn XÁC SUẤT & THỐNG KÊ HK20171 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Xác suất làm việc của một hệ thống trong khoảng thời gian xác định nào đó được
gọi là xác suất tin cậy (XSTC) của hệ thống đó.
a/ Tính XSTC cùa một mạng gồm 2 linh kiện mắc nối tiếp cùng có XSTC là 0,95.
b/ Mắc song song với mạng trên một mạng dự phòng gồm 2 linh kiện mắc nối tiếp
cùng có XSTC là 0,94, tính XSTC cùa mạng mới đó.
Câu 2. Một lô hàng gồm 16 sản phẩm loại A và 12 loại B. Chọn ngẫu nhiên 3 sản phẩm.
a/ Tính xác suất để trong 3 sản phẩm đó có ít nhất 2 sản phẩm loại A.
b/ Chọn tiếp ngẫu nhiên ra 3 sản phẩm trong số còn lại, tính xác suất để trong số 3 sản
phẩm được chọn lần hai có ít nhất 1 sản phẩm loại A.
Câu 3. Theo điều tra cùa một hãng bảo hiểm ô tô tỷ lệ xe bị tai nạn trong năm là 0,15.
Trong số xe bị tai nạn: 80% được bồi thường tai nạn bằng 20% giá trị xe, 12% được bồi
thường 60% giá trị xe và 8% được bồi thường 100% giá trị xe.
a/ Hỏi trung bình phải bồi thường tai nạn bao nhiêu cho một xe có giá trị 600 triệu đồng?
b/ Đối với chiếc xe trên phải quy định phí bảo hiểm là bao nhiêu để hãng không bị lỗ
(chỉ kể chi phí bồi thường, không kể các chi phí khác)?
Câu 4. Thống kê ở một vùng trong 500 xe ô tô đăng ký có 68 xe thể thao. Với độ tin cậy
95% hãy xác định khoảng tin cậy đối xứng cho tỷ lệ xe thể thao ở vùng đó. Theo anh
(chị) có cách nào để nâng cao độ chính xác của khoảng tin cậy cho tỷ lệ trên?
Câu 5. Đo thời gian phản ứng (giây) đối với hai loại thuốc kích thích của 8 người tham
gia thí nghiệm (giả sử thời gian phản ứng đối với mỗi loại thuốc được coi là biến ngẫu
nhiên có phân phối chuẩn), ta có bộ số liệu cặp: Thuốc 3,1 1,5 2,9 2,6 1,7 2,3 3,8 2,4 1 Thuốc 4,1 2,2 3,5 1,8 2,7 2,5 3,4 3,2 Với mứ 2
c ý nghĩa =5%, có thể cho rằng thời gian phản ứng trung bình đối với 2 loại
thuốc là như nhau hay không?
ĐỀ 2 Đề thi môn XÁC SUẤT & THỐNG KÊ HK20171 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Xác suất làm việc của một hệ thống trong khoảng thời gian xác định nào đó được
gọi là xác suất tin cậy (XSTC) của hệ thống đó.
a/ Tính XSTC cùa một mạng gồm 2 linh kiện mắc nối tiếp cùng có XSTC là 0,94.
b/ Mắc song song với mạng trên một mạng dự phòng gồm 2 linh kiện mắc nối tiếp
cùng có XSTC là 0,92, tính XSTC cùa mạng mới đó.
Câu 2. Một lô hàng gồm 20 sản phẩm loại I và 16 loại II. Chọn ngẫu nhiên 3 sản phẩm.
a/ Tính xác suất để trong 3 sản phẩm đó có ít nhất 2 sản phẩm loại II.
b/ Chọn tiếp ngẫu nhiên ra 3 sản phẩm trong số còn lại, tính xác suất để trong số 3 sản
phẩm được chọn lần hai có ít nhất 1 sản phẩm loại I.
Câu 3. Theo điều tra cùa một hãng bảo hiểm bất động sản, tỷ lệ nhà ở bị hỏa hoạn trong
năm tại một vùng là 0,02. Trong số nhà bị cháy: 78% được bồi thường tai nạn bằng 20%
giá trị ngôi nhà, 14% được bồi thường 60% giá trị nhà và 8% được bồi thường 100% giá trị nhà.
a/ Hỏi trung bình phải bồi thường hỏa hoạn bao nhiêu cho một ngôi nhà có giá trị 5 tỷ đồng?
b/ Đối với ngôi nhà trên phải quy định phí bảo hiểm là bao nhiêu để hãng bảo hiểm
không bị lỗ (chỉ kể chi phí bồi thường, không kể các chi phí khác)?
Câu 4. Điều tra ở một vùng trong 800 người chọn ngẫu nhiên có 184 người tham gia tập
thể thao. Với độ tin cậy 90% hãy xác định khoảng tin cậy đối xứng cho tỷ lệ người có tập
thể thao ở vùng đó. Theo anh (chị) độ chính xác của khoảng tin cậy cho tỷ lệ trên có thể
phụ thuộc vào những yếu tố nào?
Câu 5. Để đánh giá trình độ của một người ứng viên người ta dựa vào 8 lần cho điểm
đồng thời của 2 chuyên gia (số liệu cặp và giả sử giá trị điểm số của mỗi chuyên gia
được coi là biến ngẫu nhiên có phân phối chuẩn): Ch/gia 1 76,3 88,4 80,2 94,7 68,7 82,8 76,1 79,0 Ch/gia 2 75,1 86,8 77,3 90,6 69,1 81,0 75,3 79,1
Với mức ý nghĩa =5%, có thể cho rằng điểm số trung bình của chuyên gia 1 là cao hơn
của chuyên gia 2 hay không? Đề 1
ĐỀ THI MÔN XÁC SUẤT & THỐNG KÊ HK20172 - MI2020
(Thời gian làm bài: 90phút)
Câu 1. Một hộp có n áo trắng và 2n áo xanh. Chia ngẫu nhiên các áo thành n nhóm mỗi nhóm 3 áo).
a/ Tính xác suất để trong mỗi nhóm đều có áo trắng.
b/ Áp dụng cho n = 5.
Câu 2. Một xí nghiệp có 4 chiếc máy tiện với xác suất bị sự cố trong ngày của mỗi máy
tương ứng là 0,01; 0,05; 0,1 và 0,1.
a/ Trong một ngày nào đó theo dõi một máy, tính xác suất để máy đó bị sự cố.
b/ Khi theo dõi 2 máy thì có đúng 1 máy bị sự cố, tính xác suất chiếc máy bị sự cố đó là máy thứ nhất.
Câu 3. Xét một phần tư hình tròn tâm 0(0,0) bán kính bằng a, kí hiệu OAB, với tọa độ
tương ứng A(a,0) và B(0,a).
a/ Trên đoạn OA lấy ngẫu nhiên một điểm c, tìm phân phối xác suất của độ dài đoạn OC.
b/ Dựng một đường thẳng đi qua c, vuông góc với OA và cắt cung tròn tại điểm D,
tính kỳ vọng và phương sai của độ dài đoạn CD.
Câu 4. Tiến hành 120 phép đo như nhau, độc lập, thì thấy sự kiện A xuất hiện 42 lần.
a/ Xác định khoảng tin cậy đối xứng 99% cho tỷ lệ xuất hiện A.
b/ Tính xác suất để sai số ước lượng của tỷ lệ trên bé hơn 10% tần suất mẫu.
Câu 5. Cân 150 con vịt người ta thu được bộ số liệu sau: Khối lượng 1,25 1,50 1,75 2,00 2,25 2,50 2,75 3.00 Số lượng 2 6 24 35 39 24 14 6
Với mức ý nghĩa 5% có thể cho rằng khối lượng trung bình của lứa vịt trên lớn hơn 2 kg được không?
ĐỂ 2 ĐỀ TIII MÔN XÁC SUẤT & THỐNG KÊ HK20172 - MI2020
(Thời gian ỉàm bài: 90 phút)
Câu 1. Một nhóm sinh viên có 2n nam và n nữ. Chia ngẫu nhiên nhóm này thành n nhóm con (mỗi nhóm 3 người).
a/ Tính xác suất để trong mỗi nhóm có cả nam và nữ.
b/ Áp dụng cho n = 4.
Câu 2. 4 xạ thủ được yêu cầu mỗi người bắn một phát đạn với xác suất trúng của mỗi
người tương ứng là 0,4; 0,5; 0,8 và 0,8.
a/ Chọn ngẫu nhiên một người, tính xác suất đêr người đó bắn trúng.
b/ Lấy ngẫu nhiên 2 người thì có đúng 1 người bắn trúng, tính xác suất người bắn
trúng đó là người thứ hai.
Câu 3. Xét một phần tư hình tròn tâm 0(0,0) bán kính bằng 1, kí hiệu OAB, với tọa độ
tương ứng A(l,0) và B(0,l).
a/ Trên cung tròn AB lấy ngẫu nhiên một điểm C, tìm phân phối xác suất của độ dài
cung AC (để ý độ dài cung tròn AB bằng /2).
b/ Dựng một đường thẳng đi qua C, vuông góc với OA và cắt OA tại điểm D, tính kỳ
vọng và phương sai của độ dài đoạn CD.
Câu 4. Tiến hành 100 phép đo như nhau, độc lập, thì thấy sự kiện B xuất hiện 35 lần.
a/ Xác định khoảng tin cậy đối xứng 95% cho tỷ lệ xuất hiện B.
b/ Tính xác suất để sai số ước lượng của tỷ lệ trên bé hơn 10% tần suất mẫu.
Câu 5. Đo chiều cao 300 trẻ 12 tuổi ở một trường học, người ta thu được bộ số liệu sau: Chiều cao 120 125 130 135 140 145 150 Số lượng 9 33 74 93 64 21 6
Với mức ý nghĩa 1% có thể cho rằng chiều cao trung bình của lứa trẻ trên nhỏ hơn 140 cm được không? ĐỀ 1
Đề thi môn XÁC SUẤT & THỐNG KÊ HK30173 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Một lô hàng có 15 sản phẩm gồm 6 loại A, 5 B và 4 C. Chọn ngẫu nhiên (không
hoàn lại) ra 4 sản phẩm.
a/ Tính xác suất trong 4 sản phẩm được chọn có đúng 2 sản phẩm loại B.
b/ Biết trong 4 sản phẩm được chọn có đúng 2 sản phẩm loại A, tính xác suất để trong
4 sản phẩm đó có đúng 1 sản phẩm loại C.
Câu 2. Một nhóm học sinh cỏ 5 loại giỏi, 4 khá và 2 trung bình. Chọn ngẫu nhiên ra một
nhóm gồm 2 học sinh.
a/ Tính giá trị trung bình của số học sinh giỏi trong nhóm đó.
b/ Biết trong nhóm 2 học sinh có ít nhất 1 loại khá, tính xác suất để trong nhóm đó có
đúng 1 học sinh giỏi.
Câu 3. Cho biến ngẫu nhiên X có hàm mật độ (phân phối Rayleigh) 0; x 0, f (x) 2 x /4 Ae ; x 0. a/ Tìm hằng số A.
b/ Tính các đặc trưng định vị: EX và modX (mốt của X).
Câu 4. Số liệu dưới đây cho tỷ lệ phần trăm một hóa chất trong 11 mẫu một loại xi
măng: 6 15 8 8 6 9 17 18 4 8 10.
Với độ tin cậy 95% hãy tìm ước lượng khoảng cho tỷ lệ phần trăm trung bình của loại hóa
chất trên (giả sử tỷ lệ đó là biến ngẫu nhiên tuân theo luật phân phối chuẩn).
Câu 5. Một mẫu gồm n = 64 sản phẩm có 4 sản phẩm lỗi. Có đủ bằng chứng để chấp nhận
giả thuyết “p > 5%” được không; cho mức ý nghĩa = 5%, p ký hiệu tỷ lệ sản phẩm lỗi? Đề 2
Đề thi môn XÁC SUẤT & THỐNG KÊ HK30173 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Trong hộp có 9 bút xanh, 4 bút tím và 2 bút đỏ. Chọn ngẫu nhiên (không hoàn lại) ra 4 bút.
a/ Tính xác suất trong 4 bút được chọn có đúng 2 bút tím.
b/ Biết trong 4 bút được chọn có đúng 2 bút xanh, tính xác suất để trong 4 bút đó có đúng 1 bút đỏ.
Câu 2. Một lô hàng gồm có 9 sản phẩm tốt, 2 sản phẩm lỗi ít và 1 sản phẩm lỗi nhiều.
Chọn ngẫu nhiên ra 2 sản phẩm.
a/ Hỏi trung bình trong 2 sản phẩm được chọn có bao nhiêu sản phẩm lỗi?
b/ Biết trong 2 sản phẩm được chọn có ít nhất 1 sản phẩm lỗi, tính xác suất để trong số
sản phẩm lỗi đó có đúng 1 sản phẩm lỗi ít. 0 ,1 ( ) t P T t e ,t 0.
Câu 3. Thời gian làm việc T của một thiết bị điện thỏa mãn
a/ Tìm hàm phân phối xác suất của T.
b/Tính P(15 < T < 20) và ET.
Cáu 4. Số liệu dưới đây cho nồng độ một hóa chất trong 16 mẫu nước ở một vùng
7 6 6 10 8 9 11 5 4 5 9 8 4 3 6 7
Với độ tin cậy 95% hãy tìm ước lượng khoảng cho nồng độ trung bình của loại hóa chất
trên (giả sử nồng độ đó là biến ngẫu nhiên tuân theo luật phân phối chuẩn).
Câu 5, Trong dãy n = 60 thí nghiệm Bernoulli quan sát có 15 thí nghiệm thành công. Có
thề bác bỏ giả thuyết “p < 30%” được không; cho mức ý nghĩa = 5%, p ký hiệu tỷ lệ thí nghiệm thành công? Đề 1
Đề thi môn XÁC SUẤT & THỐNG KÊ HK20181 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Ở một địa phương đàn ông chiếm 55% dân số. Theo thống kê tỷ lệ đàn ông bị bạch
tạng là 0,4%, còn tỷ lệ trên của đàn bà là 0,32%.
a. Tìm tỷ lệ người bị bệnh bạch tạng ở địa phương đó.
b. Gặp ngẫu nhiên một người bị bạch tạng, tính xác suất đó là đàn ông.
Câu 2. Một máy đếm người vào một siêu thị có tỷ lệ đếm sót là 0,018. Giả sử trọng vòng
1 giờ nào đó có 500 khách vào siêu thị.
a. Tính kỳ vọng và phương sai của số người được máy đếm trong số 500 người nói trên
b. Tính xác suất để máy này đếm sót từ 6 đến 10 người trong số 500 người đó.
Câu 3. Một linh kiện điện tử có thời gian hoạt động X là biến ngẫu nhiên có phân phối mũ x
với hàm mật độ của X là: f (x) .e , x 0.
a. Xác định phân phối xác suất cho thời gian hoạt động của một mạng gồm 2 linh kiện loại trên mắc song song.
b. Tính kỳ vọng và phương sai của thời gian hoạt động của mạng đó.
Câu 4. Ở một trung tâm giống cây trồng, theo dõi 3070 cây cà phê thì có 1135 cây cho thu hoạch thấp.
a. Với độ tin cậy 95% hãy xác định khoảng tin cậy cho tỷ lệ cây cà phê có thu hoạch thấp
b. Tần suất cà phê có thu hoạch thấp có là ước lượng không chệch của tỷ lệ cây cho
thu hoạch thấp không? Tại sao?
Câu 5. Theo dõi thời gian bắt đầu có tác dụng của một loại thuốc trên một nhóm bệnh nhân
trước và sau khi mổ dạ dày, ta thu được bộ số liệu (giả sử thời gian trên có phân phối chuẩn) Bệnh nhân 1 2 3 4 5 6 7 8 Trước mổ 44 51 52 55 66 68 70 71 Sau mổ 52 64 60 74 55 67 75 65
Hỏi thời gian tác dụng của thuốc trước và sau mổ có khác nhau không với mức ý nghĩa 1%? x 2 1 Phụ lục
. Trích Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 2,576 3 (x) 0,90 0,95 0,975 0,9772 0,995 0,9987
Hàm Laplace (x) = (x) – 0,5
Đề 2 Đề thi môn XÁC SUẤT & THỐNG KÊ HK20181 - MI2020
(Thời gian làm hài: 90 phủi)
Câu 1. Cho 3 con rô bốt chẩn đoán bệnh (một cách độc lập) cho một bệnh nhân và giả sử
biết xác suất chẩn đoán đúng của từng con tương ứng là 0,4; 0,7 và 0,9.
a/ Tính xác suất để có ít nhất 1 con rô bốt chẩn đoán đúng.
b/ Biết có đúng một con rô bốt chẩn đoán đúng (trong 3 con), tính xác suất đó là con thứ hai.
Câu 2. Giả sử cho biết xác suất một người mắc bệnh tim mạch là 0,01. Trên một tàu du
lịch có 1000 người và gọi X là số người mắc bệnh tim mạch trong nhóm người đó.
a/ Tính kỳ vọng và phương sai của X.
b/ Tính xác suất đế trong nhóm này có ít nhất 3 người mắc bệnh tim mạch.
Câu 3. Cho một loại bóng điện tử có thời gian hoạt động X là biến ngẫu nhiên có phân
phối mũ, với hàm mật độ của X là f (x) = e-.x, x > 0.
a/ Xác định phân phối xác suất cho thời gian hoạt động của một mạng gồm 2 bóng loại
trên được mắc nối tiếp.
b/ Tính kỳ vọng và phương sai của thời gian hoạt động của mạng đó.
Câu 4. Đo số lượng bạch cầu trong máu của 170 trẻ em, ta tính được các đặc trưng mẫu:
trung bình mẫu là 11250 và độ lệch chuẩn mẫu (chưa hiệu chỉnh) S = 2100.
a/ Với độ tin cậy 95% hãy xác định khoảng tin cậy cho số lượng bạch cầu trung bình của trẻ em.
b/ Tính ước lượng không chệch cho phương sai của số lượng bạch cầu đó.
Câu 5. Đo nồng độ một vi chất bằng hai phương pháp khác nhau, ta có kết quả (giả sử
nồng độ vi chất trên có phân phối chuẩn) Thứ tự mẫu 1 2 3 4 5 6 pp cũ
0,85 1,12 1,46 1,20 1,60 1,52 pp mới
1,09 1,24 1,20 1,25 1,65 1,48
Hỏi phương pháp mới có khác với phương pháp cũ hay không (cho mức ý nghĩa 1%)?
ĐỀ 1 ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20182 Mã HP: MI2020 Thời gian: 90 phút
Câu 1. Cho 3 sự kiện A, B, C độc lập từng đôi (2 sự kiện bất kỳ luôn độc lập với nhau)
thỏa mãn: P(A) = P(B) = P(C) = p và P(A.B.C) = 0. a. Tính ( P . A . B C), ( P . A . B C) .
b. Tìm giá trị p lớn nhất có thể có.
Câu 2. Một nhà máy có hai phân xưởng cùng sản xuất bóng đèn. Số bóng đèn do phân
xưởng 2 sản xuất gấp 2 lần số bóng đèn do phân xưởng 1 sản xuất. Tỷ lệ phế phẩm của 2
phân xưởng tương ứng là 0,005 và 0,008. Lấy ngẫu nhiên 1 bóng đèn của nhà máy để kiểm
tra thì thấy là phế phẩm. Tính xác suất bóng đèn đó do phân xưởng 2 sản xuất.
Câu 3. Có hai lô hàng I và II, mỗi lô chứa rất nhiều sản phẩm. Tỉ lệ sản phẩm loại A có
trong hai lô I và II lần lượt là 70% và 80%. Lấy ngẫu nhiên từ mỗi lô 2 sản phẩm.
a) Tính xác suất để số sản phẩm loại A lấy từ lô I lớn hơn số sản phẩm loại A lấy từ lô II.
b) Gọi X là số sản phẩm loại A có trong 4 sản phẩm được lấy ra. Tìm kỳ vọng và phương sai của X.
Câu 4. Khảo sát trọng lượng X(kg) của 200 con lợn xuất chuồng ta được bảng số liệu sau: X(kg) [85-95)
[95-105) [105-115) [115-125) [125-135) [135-145] Số lợn 10 30 45 80 30 5
Với độ tin cậy 90% hãy ước lượng khoảng cho trọng lượng trung bình của đàn lợn xuất chuồng.
Câu 5. Với số liệu ở câu 4 và mức ý nghĩa 5% liệu có thể khẳng định rằng tỷ lệ lợn xuất
chuồng có trọng lượng thấp hơn 115kg là ít hơn 50% hay không? x 2 1 Phụ lục
. Trích Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 2,576 3 (x) 0,90 0,95 0,975 0,9772 0,995 0,9987
Hàm Laplace (x) = (x) – 0,5
ĐỀ 2 ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20182 Mã HP: MI2020 Thời gian: 90 phút
Câu 1. Cho 3 sự kiện A, B, C độc lập từng đôi (2 sự kiện bất kỳ luôn độc lập với nhau) thỏa mãn:
P(A) = P(B) = P(C) = p và P(A.B.C) = 0. a. Tính ( P . A . B C), ( P . A . B C) .
b. Tìm giá trị p lớn nhất có thể có.
Câu 2. Một thùng có 20 sản phẩm trong đó có 15 chính phẩm và 5 phế phẩm. Trong quá
trình vận chuyển bị mất hai sản phẩm không rõ chất lượng. Lấy ngẫu nhiên 2 sản phẩm
trong 18 sản phẩm còn lại. Biết hai sản phẩm lấy ra đều là chính phẩm, tìm xác suất để hai
sản phẩm bị mất có một chính phẩm và một phế phẩm.
Câu 3. Khảo sát tình hình cung cấp thức ăn chăn nuôi tại một vùng, người ta điều tra các
cơ sở chế biến và bán thứ ăn gia súc tại vùng đó và mô hình hóa thức ăn gia súc bán theo
tuần X(nghìn tấn) bởi hàm mật độ xác suất:
ax(6 x) , x [0;6] f (x) 0 , x [0; 6].
a) Xác định a và E(X).
b) Xác định Med(X) và Mod(X).
Câu 4. Cân thử 100 quả trứng gà trong một trại chăn nuôi ta có kết quả sau: Trọng lượng (gam) 150 160 165 170 180 185 Số trứng 4 16 25 30 15 10
Với độ tin cậy 90%, hãy ước lượng khoảng cho trọng lượng trung bình của trứng gà trong trại chăn nuôi đó.
Câu 5. Với số liệu ở câu 4 và mức ý nghĩa 5% liệu có thể khẳng định rằng tỷ lệ trứng gà
nặng hơn 170 gam cao hơn 20% hay không? x 2 1 Phụ lục
. Trích Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 2,576 3 (x) 0,90 0,95 0,975 0,9772 0,995 0,9987
Hàm Laplace (x) = (x) – 0,5
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 1
ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20152
Mã học phần: MI2020 Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Hai người A và B chơi trò tung đồng xu (khả năng ra mặt sấp và ngửa là như nhau): mỗi
lần chơi ta tung đồng xu 1 lần, nếu ra mặt sấp thì A thắng, ra mặt ngửa thì B thắng. Hai người chơi 50 lần.
a. Tính xác suất A thắng 30 lần và B thắng 20 lần.
b. Số lần thắng của A lớn hơn số lần thắng của B.
Câu 2. Lô hàng xuất khẩu có 100 kiện hàng trong đó có 60 kiện loại A và 40 kiện loại B (số sản
phẩm có trong mỗi kiện hàng là rất lớn). Tỷ lệ phế phẩm của kiện loại A, B tương ứng là 10%
và 30%. Người ta lấy ngẫu nhiên 1 kiện hàng, từ kiện hàng đó lấy ngẫu nhiên 3 sản phẩm để
kiểm tra thì thấy có duy nhất 1 phế phẩm. Tính xác suất đó là kiện hàng loại A.
Câu 3. Tuổi thọ của người là biến ngẫu nhiên X (năm) có hàm mật độ xác suất: 0 x 0; f (x) . x e x 0.
Biết rằng trung bình trong 1000 người có 500 người sống quá 60 tuổi. a. Xác định .
b. Một cụ năm nay 60 tuổi. Tính xác suất để cụ sống hơn 70 tuổi.
Câu 4. Để tăng doanh số bán hàng, một siêu thị đã thực hiện một chương trình khuyến mãi. Số
liệu thu được (sau khi áp dụng chương trình khuyến mãi) về doanh số bán trong một ngày của siêu thị như sau:
Doanh số (triệu đồng/ngày) 24 30 36 42 48 54 60 65 70 Số ngày 5 12 25 35 24 15 12 10 6
Với độ tin cậy 90%, hãy ước lượng khoảng đối xứng cho doanh số bán trung bình trong một ngày của siêu thị đó.
Câu 5. Trước khi áp dụng khuyến mại, doanh số trung bình là 35 triệu đồng/ngày. Với số liệu ở
Câu 4 và với mức ý nghĩa 5% liệu có thể khẳng định doanh số bán trung bình trong một ngày
của siêu thị đó sau khi áp dụng khuyến mại tăng lớn hơn 9 triệu hay không?
Chú ý: Không được sử dụng tài liệu
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC x 2 1 Phụ lục
. Trích các số Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 3 0,9 0,95 0,975 0,9772 0,9987 x)
Hàm Laplace (x) = (x) – 0,5
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 2
ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20152
Mã học phần: MI2020 Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Hai người A và B chơi trò tung đồng xu (khả năng ra mặt sấp và ngửa là như nhau): mỗi
lần chơi ta tung đồng xu 1 lần, nếu ra mặt sấp thì A thắng, ra mặt ngửa thì B thắng. Hai người chơi 48 lần.
a. Tính xác suất A thắng 28 lần và B thắng 20 lần.
b. Số lần thắng của A lớn hơn số lần thắng của B.
Câu 2. Lô hàng xuất khẩu có 100 kiện hàng trong đó có 70 kiện loại A và 30 kiện loại B (số sản
phẩm có trong mỗi kiện hàng là rất lớn). Tỷ lệ phế phẩm của kiện loại A, B tương ứng là 10%
và 20%. Người ta lấy ngẫu nhiên 1 kiện hàng, từ kiện hàng đó lấy ngẫu nhiên 4 sản phẩm để
kiểm tra thì thấy có duy nhất 1 phế phẩm. Tính xác suất đó là kiện hàng loại B.
Câu 3. Tại một cơ sở sản xuất kẹo, số kẹo trong mỗi bao là X có bảng phân phối: X 18 19 20 21 22
Xác suất 0,14 0,24 0,32 0,21 0,09
Chi phí sản xuất mỗi bao kẹo là 3X + 16 (nghìn đồng). Tiền bán mỗi bao kẹo là 100 nghìn đồng.
Tìm lợi nhuận trung bình và độ lệch chuẩn của lợi nhuận cho mỗi bao kẹo.
Câu 4. Sau khi cải tiến kỹ thuật sản xuất bóng đèn, người ta thử nghiệm với 100 bóng, ta có kết quả như sau: Tuổi thọ (giờ) 1150 1160 1170 1180 1190 1200 Số bóng 10 15 20 30 15 10
Với độ tin cậy 90%, hãy ước lượng khoảng đối xứng cho tuổi thọ trung bình của bóng đèn sau
khi cải tiến kỹ thuật.
Câu 5. Tuổi thọ trung bình của bóng đèn trước cải tiến là 1100 giờ. Với số liệu ở Câu 4 và với
mức ý nghĩa 5% liệu có thể khẳng định tuổi thọ trung bình của bóng đèn sau khi cải tiến kỹ
thuật tăng ít nhất 100 giờ hay không? x 2 1 Phụ lục
. Trích các số Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 3 (x) 0,9 0,95 0,975 0,9772 0,9987
Hàm Laplace (x) = (x) – 0,5
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐÁP ÁN ĐỀ 1 – XÁC SUẤT THỐNG KÊ Câu 1.(2đ)
a. Gọi A: “A thắng 30 lần và B thắng 20 lần”, 30 30 20 P( ) A C * 0,5 * 0,5 0,0419 (0,5đ) 50
b. Gọi H: “Số lần thắng của A lớn hơn số lần thắng của B”
K: “Số lần thắng của A nhỏ hơn số lần thắng của B”
L: “Số lần thắng của A bằng số lần thắng của B”, 25 25 25
P(L) C * 0,5 * 0,5 0,1122 (0,5đ) 50
Do A và B khả năng thắng là như nhau trong mỗi lần chơi, do đó ta có P(H) P(K) (0,5đ) Lại do 1
P(H ) P(K ) P(L) 1 P(H ) P(K )
(1 P(L)) 0, 4439 (0,5đ) 2
Câu 2.(2đ) Gọi A: “kiện hàng lấy ra là loại A” và B: “kiện hàng lấy ra là loại B”
Gọi H: “3 sản phẩm kiểm tra thì thấy có duy nhất 1 phế phẩm” P( ) A 60 / 100 0.6 P(B) 0.4 (0,5đ) 1 2 1 2 P(H | )
A C * 0,1* 0,9 0, 243
P(H | B) C * 0,3* 0, 7 0, 441 (0,5đ) 3 3 ( P H ) ( P ) A * ( P H | ) A ( P ) B * ( P H | )
B 0,6*0, 243 0, 4*0, 441 0,3222 (0,5đ) P( )
A * P(H | ) A 0, 6 * 0, 243
P( A | H ) 0,453 (0,5đ) P(H ) 0,3222
Câu 3.(2đ) X(năm) là tuổi thọ của người 500
a. P( X 60) 0,5 (0,5đ) 1000 x x 60 ln 0,5 0,5 .e dx (e ) | e 0,01155 (0,5đ) 60 60 60 P( X 70)
b. P( X 70 | X 60) P(X (0,5đ) 60) . x e dx 70 e 70 10 e 0,891 (0,5đ) 60 e . x e dx 60
Câu 4.(2đ) Gọi X(triệu đồng/ngày) là doanh số bán trong ngày của siêu thị, EX . Chọn thống kê X n ~ N(0;1) (0,5đ) s
Khoảng tin cậy đối xứng cho s s : x u * ; x u * (0,5đ) 1 1 n n 2 2
Với 1 0,9 0,1 u u 1,645 1 /2 0,95
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
Từ bảng số liệu ta tính được n 144 ; x 45,85 ; s 11,53 (0,5đ)
Thay số ta có khoảng tin cậy: (44,27 ; 47,43) (0,5đ)
Câu 5.(2đ) X(triệu đồng/ngày) là doanh số bán trong ngày của siêu thị, EX . H :
Kiểm định cặp giả thuyết: 0 0 35 9 44 (0,5đ) 0 H : 1 0 Chọn thống kê X 0
n ~ N(0;1) khi H đúng s 0
Từ bảng số liệu ta tính được n 144 ; x 45,85 ; s 11,53 suy ra giá trị quan sát x - 45 8 , 5 - 44 0 k * n * 144 1 9 , 57 (0,5đ) s 11 5 , 3
Với = 0,05 ta có miền bác bỏ H 0: w (u ; ) (u ; ) (1,645; ) (0,5đ) 1 0,95
Do k w nên ta bác bỏ H và chấp nhận H , có thể khẳng định doanh số bán trung bình trong 0 1
một ngày của siêu thị đó sau khi áp dụng khuyến mại tăng lớn hơn 9 triệu. (0,5đ)
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐÁP ÁN ĐỀ 2 – XÁC SUẤT THỐNG KÊ Câu 1.(2đ)
a. Gọi A: “A thắng 28 lần và B thắng 20 lần”, 28 28 20 P( ) A C * 0,5 * 0,5 0,0595 (0,5đ) 48
b. Gọi H: “Số lần thắng của A lớn hơn số lần thắng của B”
K: “Số lần thắng của A nhỏ hơn số lần thắng của B”
L: “Số lần thắng của A bằng số lần thắng của B”, 24 24 24
P(L) C * 0,5 * 0,5 0,1146 (0,5đ) 48
Do A và B khả năng thắng là như nhau trong mỗi lần chơi, do đó ta có P(H) P(K) (0,5đ) Lại 1
do P(H ) P(K ) P(L) 1 P(H ) P(K )
(1 P(L)) 0, 4427 (0,5đ) 2
Câu 2.(2đ) Gọi A: “kiện hàng lấy ra là loại A” và B: “kiện hàng lấy ra là loại B”
Gọi H: “3 sản phẩm kiểm tra thì thấy có duy nhất 1 phế phẩm” P( ) A 70 / 100 0.7 P(B) 0.3 (0,5đ) 1 3 1 3 P(H | )
A C * 0,1* 0,9 0, 2916
P(H | B) C * 0, 2 * 0,8 0, 4096 (0,5đ) 4 4 ( P H) ( P ) A * ( P H | ) A ( P ) B * ( P H | )
B 0,7*0, 2916 0,3*0, 4096 0,327 (0,5đ)
P(B) * P(H | B) 0,3* 0, 4096
P(B | H ) 0,3758 (0,5đ) P(H ) 0,327
Câu 3.(2đ) Áp dụng công thức tính ta có: 5
EX x * p 18*0,14 19*0,24 20*0,32 21*0,21 22*0,09 19,87 i i i 1 5 2 2 2 2
VX E( X ) (EX ) x * p 19,87 1,353 (X ) VX 1,163 (0,5đ) i i i 1
Gọi Y(nghìn đồng) là lợi nhuận thu được trên mỗi bao kẹo.
Y 100 (3X 16) 84 3X (0,5đ)
EY E(84 3X ) 84 3EX 84 3*19,87 24,39 (0,5đ)
(Y) (84 3X) 3*(X) 3*1,163 3,489 (0,5đ)
Câu 4.(2đ) Gọi X(giờ) là tuổi thọ bóng đèn, EX . Chọn thống kê X n ~ N(0;1) (0,5đ) s s s
Khoảng tin cậy đối xứng cho : x u * ; x u * (0,5đ) 1 1 n n 2 2
Với 1 0,9 0,1 u u 1,645 1 /2 0,95
Từ bảng số liệu ta tính được n 100 ; x 1175,5 ; s 14,38 (0,5đ)
Thay số ta có khoảng tin cậy: (1173,13 ; 1177,87) (0,5đ)
Câu 5.(2đ) Gọi X(giờ) là tuổi thọ bóng đèn, EX .
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC H :
Kiểm định cặp giả thuyết: 0 0 1100 100 1200 (0,5đ) 0 H : 1 0 Chọn thống kê X 0
n ~ N(0;1) khi H đúng s 0
Từ bảng số liệu ta tính được n 100 ; x 1175,5 ; s 14,38 x - 1175 5 , -1200 suy ra giá trị quan sát 0 k * n * 100 1 7,04 (0,5đ) s 14 3 , 8
Với = 0,05 ta có miền bác bỏ H 0: w ( ; u ) ( ; u ) ( ; 1,645) (0,5đ) 1 0,95
Do k w nên ta bác bỏ H và chấp nhận H , có thể khẳng định tuổi thọ trung bình của bóng 0 1
đèn sau khi cải tiến kỹ thuật tăng ít hơn 100 giờ. (0,5đ)
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 1
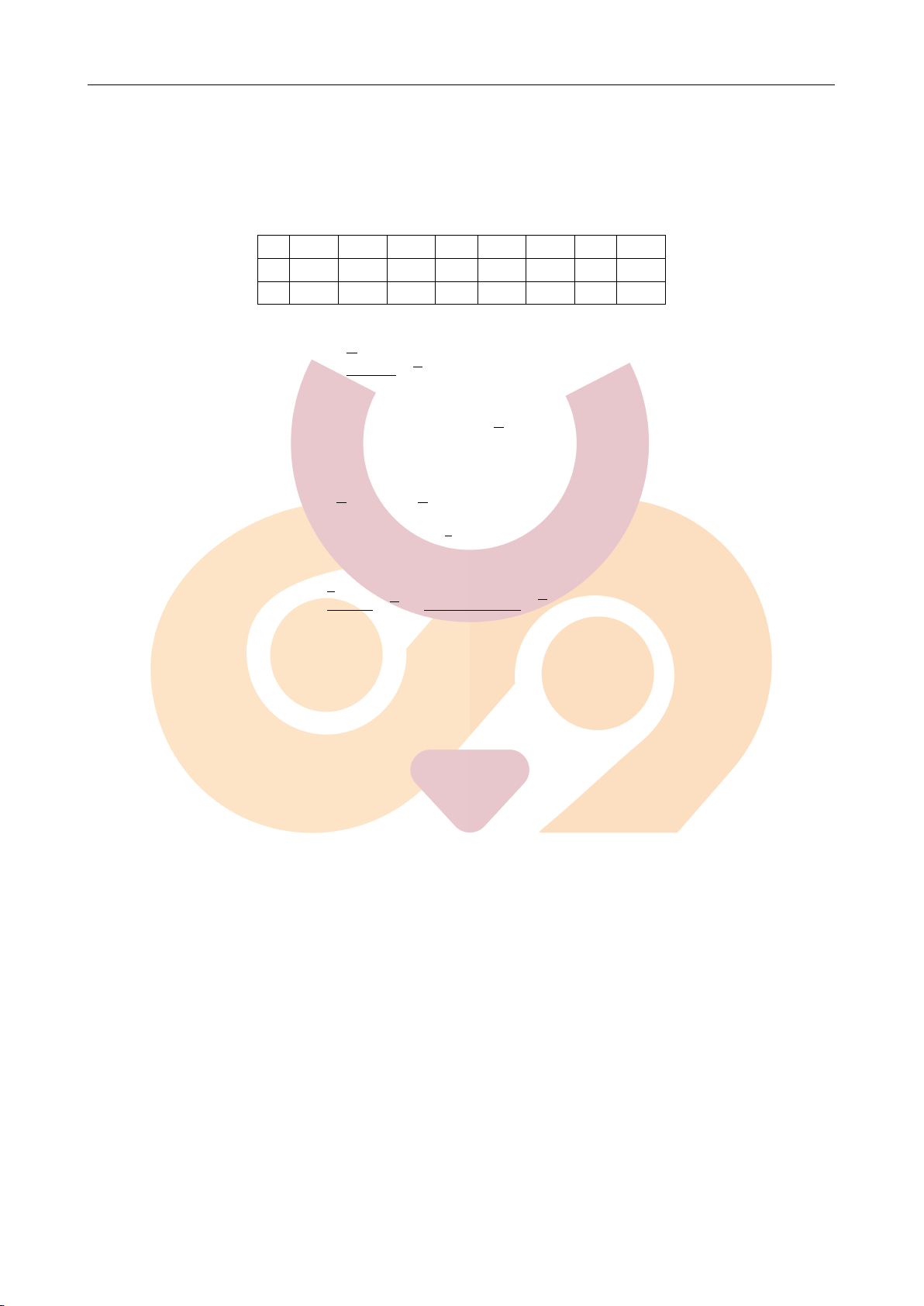
ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20153
Mã học phần: MI2020 Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tung ngẫu nhiên 8 lần một đồng xu (khả năng ra mặt sấp và ngửa là như nhau ở mỗi lần
tung). Tính xác suất để:
a. Được mặt sấp ở các lần gieo chẵn.
b. Chỉ được mặt sấp ở các lần gieo chẵn.
Câu 2. Một hộp có 20 sản phẩm, số chính phẩm có trong 20 sản phẩm đó là ngẫu nhiên và có
khả năng xảy ra như nhau. Người ta bỏ thêm vào hộp đó 1 chính phẩm, sau đó từ hộp này lại lấy
ngẫu nhiên ra một sản phẩm. Tính xác suất sản phẩm đó là chính phẩm.
Câu 3. Tuổi thọ của một loài côn trùng nào đó là biến ngẫu nhiên X (tháng tuổi) có hàm mật độ xác suất như sau: 2 ax (4 x) 0 x 4 f (x) 0 x [0; 4]
a. Xác định a, tìm tỷ lệ côn trùng sống không quá 1 tháng tuổi. b. Xác định mod(X).
Câu 4. Nghiên cứu số vụ tai nạn giao thông xảy ra hàng ngày ở một khu vực ta có bảng số liệu sau: Số vụ tai nạn 0 1 2 3 4 5 6 7 Số ngày 229 211 93 35 7 0 0 1
Với độ tin cậy 90%, hãy ước lượng khoảng đối xứng cho số tai nạn trung bình hàng ngày trong khu vực trên.
Câu 5. Có người đưa ra ý kiến tỷ lệ ngày có xảy ra tai nạn bằng 60%. Với số liệu thu được ở
trên và với mức ý nghĩa 5%, hãy kết luận về ý kiến trên.
Chú ý: Không được sử dụng tài liệu x 2 1 Phụ lục
. Trích các số Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 3 0,9 0,95 0,975 0,9772 0,9987 x)
Hàm Laplace (x) = (x) – 0,5 1
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 2
ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20153
Mã học phần: MI2020 Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tung ngẫu nhiên 9 lần một đồng xu (khả năng ra mặt sấp và ngửa là như nhau ở mỗi lần
tung). Tính xác suất để:
a. Được mặt sấp ở 4 lần gieo đầu.
b. Chỉ được mặt sấp ở 4 lần gieo đầu.
Câu 2. Một hộp có 24 sản phẩm, số phế phẩm có trong 24 sản phẩm đó là ngẫu nhiên và có khả
năng xảy ra như nhau. Người ta bỏ thêm vào hộp đó một chính phẩm, sau đó từ hộp này lại lấy
ngẫu nhiên ra một sản phẩm. Tính xác suất sản phẩm đó là phế phẩm.
Câu 3. Tuổi thọ của một loài côn trùng nào đó là biến ngẫu nhiên X (tháng tuổi) có hàm mật độ xác suất như sau: 2 ax(4 x ) 0 x 2 f (x) 0 x [0; 2]
a. Xác định a, tìm tỷ lệ côn trùng sống không quá 1 tháng tuổi. b. Xác định mod(X).
Câu 4. Để xác định tốc độ của một phản ứng, người ta tiến hành 60 phép thử đo tốc độ phản ứng
đó trong cùng điều kiện và bằng cùng một phương pháp đo. Kết quả thu được như sau: Tốc độ phản ứng 2,68 2,70 2,73 2,74 2,75 2,76 2,79 2,82 Số phép thử 1 4 12 18 17 5 2 1
Với độ tin cậy 90%, hãy ước lượng khoảng đối xứng cho tốc độ phản ứng trung bình theo cách trên.
Câu 5. Có người đưa ra ý kiến cho rằng xác suất để “tốc độ phản ứng nhỏ hơn 2,72” là thấp hơn
10%. Với số liệu thu được ở trên và với mức ý nghĩa 5%, hãy kết luận về ý kiến trên. x 2 1 Phụ lục
. Trích các số Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 3 (x) 0,9 0,95 0,975 0,9772 0,9987
Hàm Laplace (x) = (x) – 0,5 2
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐÁP ÁN ĐỀ 1 – XÁC SUẤT THỐNG KÊ
Câu 1.(2đ) Gọi A : “lần gieo thứ i được mặt sấp” , i 1, 2,...,8 i
a. Gọi A: “trong 8 lần gieo ta được mặt sấp ở các lần gieo chẵn”, 4 P( )
A P( A .A .A .A ) P( A ).P( A ).P( A ).P( A ) 0,5 0, 0625 (1đ) 2 4 6 8 2 4 6 8
b. Gọi B: “trong 8 lần gieo ta chỉ được mặt sấp ở các lần gieo chẵn”, 8 P( )
A P( A .A .A .A .A .A .A .A ) P( A ).P( A )...P( A ).P( A ) 0,5 0, 00391 (1đ) 1 2 3 4 5 6 7 8 1 2 7 8
Câu 2.(2đ) Gọi A : “trong hộp ban đầu có i chính phẩm”, i 0,1, 2,..., 20 i 1
P( A ) P( A ) ... P( A ) (0,5đ) 0 1 20 21
Gọi H: “sản phẩm lấy ra từ hộp là chính phẩm” i 1
P(H | A ) i 0,1,..., 20 (0,5đ) i 21 20 20 1 i 1
P(H ) P(A ).P(H | A ) (0,5đ) i i i i 21 21 0 0 1 1 21.22 11 (1 2 ... 21) (0,5đ) 21.21 21.21 2 21 Câu 3.(2đ) 3 4 4 x x 64 3 a. 2 4 1
ax (4 x)dx a(4 ) | . a a (0,5đ) 0 0 3 4 3 64 3 4 1 x x 3 4 1 13 2 1
ax (4 x)dx a(4 ) | ( ) 0,051 (0,5đ) 0 0 3 4 64 3 4 256 b. Xét x (0;4) x 0 2 f '(x) .
a (8x 3x ) 0 (0,5đ) x 8 / 3
Ta có hàm f’(x) dương trong khoảng (0; 8/3) và âm trong khoảng ( ; 0) (8 / 3; )
Do đó hàm số f(x) đạt cực đại tại x = 8/3 và đạt cực tiểu tại 0.
Do hàm mật độ chỉ khác 0 trong x(0;4) , nên mod(X) = 8/3 (0,5đ)
Câu 4.(2đ) Gọi X là số vụ tai nạn giao thông xảy ra trong một ngày, EX . Chọn thống kê X n ~ N(0;1) (0,5đ) s
Khoảng tin cậy đối xứng cho s s : x u ; x u (0,5đ) 1 1 n n 2 2
Với 1 0,9 0,1 u u 1,645 1 /2 0,95
Từ bảng số liệu ta tính được n 576 ; x 0,932 ; s 0,985 (0,5đ)
Thay số ta có khoảng tin cậy: (0,8645 ; 0,9995) (0,5đ) 3
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
Câu 5.(2đ) Gọi p là tỷ lệ số ngày có xảy ra tai nạn.
H : p p
Kiểm định cặp giả thuyết: 0 0 p 0,6 (0,5đ) 0
H : p p 1 0 Chọn thống kê f p0
n ~ N(0;1) khi H đúng 0 p (1 p ) 0 0 m
Từ bảng số liệu ta tính được 347
n 576 ; m 347 f 0,6024 n 576 suy ra giá trị quan sát f p 0,6024 0,6 0 k n 576 0 118 , (0,5đ) p (1 p ) 0,6.0,4 0 0
Với = 0,05 ta có miền bác bỏ H0: w ( ; u ) (u ; ) ( ; u ) (u ; ) ( ; 1 ,96) (1,96; ) (0,5đ) 1 /2 1 /2 0,975 0,975
Do k w nên ta không có cơ sở bác bỏ H . Vậy ý kiến đưa ra là đúng. (0,5đ) 0 4
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐÁP ÁN ĐỀ 2 – XÁC SUẤT THỐNG KÊ
Câu 1.(2đ) Gọi A : “lần gieo thứ i được mặt sấp” , i 1, 2,...,9 i
a. Gọi A: “trong 9 lần gieo ta được mặt sấp trong 4 lần gieo đầu”, 4 P( )
A P( A .A .A .A ) P( A ).P( A ).P( A ).P( A ) 0,5 0, 0625 (1đ) 1 2 3 4 1 2 3 4
b. Gọi B: “trong 9 lần gieo ta chỉ được mặt sấp trong 4 lần gieo đầu”, 4 5 P( )
A P( A .A .A .A .A .A .A .A .A ) P( A ).P( A )...P( A ).P( A ) 0,5 .0,5 0, 00195 (1đ) 1 2 3 4 5 6 7 8 9 1 2 8 9
Câu 2.(2đ) Gọi A : “trong hộp ban đầu có i phế phẩm”, i 0,1, 2,..., 24 i 1
P( A ) P( A ) ... P( A ) (0,5đ) 0 1 24 25
Gọi H: “sản phẩm lấy ra từ hộp là phế phẩm” i
P(H | A ) i 0,1,..., 24 (0,5đ) i 25 24 24 1 i
P(H ) P(A ).P(H | A ) (0,5đ) i i i i 25 25 0 0 1 1 24.25 12
(0 1 2 ... 24) (0,5đ) 25.25 25.25 2 25 Câu 3.(2đ) 4 2 x 1 a. 2 2 2 1
ax(4 x )dx a(2x
) | 4a a (0,5đ) 0 0 4 4 4 1 x 1 1 7 2 2 1
ax(4 x )dx a(2x ) | (2 ) 0,4375 (0,5đ) 0 0 4 4 4 16 b. Xét x (0;2)
x 4 / 3 2 3 / 3 2 f '(x) .
a (4 3x ) 0 (0,5đ)
x 4 / 3 2 3 / 3
Ta có hàm f’(x) dương trong khoảng ( 2 3 / 3 , 2 3 / 3) và âm trong khoảng ( ; 2 3 / 3) (2 3 / 3; )
Do đó hàm số f(x) đạt cực đại tại x 2 3 / 3 và đạt cực tiểu tại x 2 3 / 3.
Do hàm mật độ chỉ khác 0 trong x(0;2) , nên Mod(X ) 2 3 / 3 (0,5đ)
Câu 4.(2đ) Gọi X là tốc độ của phản ứng đang xét, EX . Chọn thống kê X n ~ N(0;1) (0,5đ) s
Khoảng tin cậy đối xứng cho s s : x u ; x u (0,5đ) 1 1 n n 2 2
Với 1 0,9 0,1 u u 1,645 1 /2 0,95
Từ bảng số liệu ta tính được n 60 ; x 2,742 ; s 0,021 (0,5đ) 5
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
Thay số ta có khoảng tin cậy: (2,738 ; 2,746) (0,5đ)
Câu 5.(2đ) Gọi p là xác suất để “tốc độ phản ứng nhỏ hơn 2,72”.
H : p p
Kiểm định cặp giả thuyết: 0 0 p 0,1 (0,5đ) 0
H : p p 1 0 Chọn thống kê f p0
n ~ N(0;1) khi H đúng 0 p (1 p ) 0 0 m
Từ bảng số liệu ta tính được 5
n 60 ; m 5 f n 60 suy ra giá trị quan sát f p 1 / 12 0 1 , 0 k n 60 0 ,43 (0,5đ) p (1 p ) 0 1 , .0,9 0 0
Với = 0,05 ta có miền bác bỏ H0: w ( ; u ) ( ; u ) ( ; 1 ,645) (0,5đ) 1 0,95
Do k w nên ta không có cơ sở bác bỏ H . Vậy ý kiến đưa ra là sai. (0,5đ) 0 6 ĐỀ 1
Đề thi môn XÁC SUẤT & THỐNG KÊ HK20171 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Xác suất làm việc của một hệ thống trong khoảng thời gian xác định nào đó được
gọi là xác suất tin cậy (XSTC) của hệ thống đó.
a/ Tính XSTC cùa một mạng gồm 2 linh kiện mắc nối tiếp cùng có XSTC là 0,95.
b/ Mắc song song với mạng trên một mạng dự phòng gồm 2 linh kiện mắc nối tiếp
cùng có XSTC là 0,94, tính XSTC cùa mạng mới đó.
Câu 2. Một lô hàng gồm 16 sản phẩm loại A và 12 loại B. Chọn ngẫu nhiên 3 sản phẩm.
a/ Tính xác suất để trong 3 sản phẩm đó có ít nhất 2 sản phẩm loại A.
b/ Chọn tiếp ngẫu nhiên ra 3 sản phẩm trong số còn lại, tính xác suất để trong số 3 sản
phẩm được chọn lần hai có ít nhất 1 sản phẩm loại A.
Câu 3. Theo điều tra cùa một hãng bảo hiểm ô tô tỷ lệ xe bị tai nạn trong năm là 0,15.
Trong số xe bị tai nạn: 80% được bồi thường tai nạn bằng 20% giá trị xe, 12% được bồi
thường 60% giá trị xe và 8% được bồi thường 100% giá trị xe.
a/ Hỏi trung bình phải bồi thường tai nạn bao nhiêu cho một xe có giá trị 600 triệu đồng?
b/ Đối với chiếc xe trên phải quy định phí bảo hiểm là bao nhiêu để hãng không bị lỗ
(chỉ kể chi phí bồi thường, không kể các chi phí khác)?
Câu 4. Thống kê ở một vùng trong 500 xe ô tô đăng ký có 68 xe thể thao. Với độ tin cậy
95% hãy xác định khoảng tin cậy đối xứng cho tỷ lệ xe thể thao ở vùng đó. Theo anh
(chị) có cách nào để nâng cao độ chính xác của khoảng tin cậy cho tỷ lệ trên?
Câu 5. Đo thời gian phản ứng (giây) đối với hai loại thuốc kích thích của 8 người tham
gia thí nghiệm (giả sử thời gian phản ứng đối với mỗi loại thuốc được coi là biến ngẫu
nhiên có phân phối chuẩn), ta có bộ số liệu cặp: Thuốc 3,1 1,5 2,9 2,6 1,7 2,3 3,8 2,4 1 Thuốc 4,1 2,2 3,5 1,8 2,7 2,5 3,4 3,2 Với mứ 2
c ý nghĩa =5%, có thể cho rằng thời gian phản ứng trung bình đối với 2 loại
thuốc là như nhau hay không?
ĐỀ 2 Đề thi môn XÁC SUẤT & THỐNG KÊ HK20171 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Xác suất làm việc của một hệ thống trong khoảng thời gian xác định nào đó được
gọi là xác suất tin cậy (XSTC) của hệ thống đó.
a/ Tính XSTC cùa một mạng gồm 2 linh kiện mắc nối tiếp cùng có XSTC là 0,94.
b/ Mắc song song với mạng trên một mạng dự phòng gồm 2 linh kiện mắc nối tiếp
cùng có XSTC là 0,92, tính XSTC cùa mạng mới đó.
Câu 2. Một lô hàng gồm 20 sản phẩm loại I và 16 loại II. Chọn ngẫu nhiên 3 sản phẩm.
a/ Tính xác suất để trong 3 sản phẩm đó có ít nhất 2 sản phẩm loại II.
b/ Chọn tiếp ngẫu nhiên ra 3 sản phẩm trong số còn lại, tính xác suất để trong số 3 sản
phẩm được chọn lần hai có ít nhất 1 sản phẩm loại I.
Câu 3. Theo điều tra cùa một hãng bảo hiểm bất động sản, tỷ lệ nhà ở bị hỏa hoạn trong
năm tại một vùng là 0,02. Trong số nhà bị cháy: 78% được bồi thường tai nạn bằng 20%
giá trị ngôi nhà, 14% được bồi thường 60% giá trị nhà và 8% được bồi thường 100% giá trị nhà.
a/ Hỏi trung bình phải bồi thường hỏa hoạn bao nhiêu cho một ngôi nhà có giá trị 5 tỷ đồng?
b/ Đối với ngôi nhà trên phải quy định phí bảo hiểm là bao nhiêu để hãng bảo hiểm
không bị lỗ (chỉ kể chi phí bồi thường, không kể các chi phí khác)?
Câu 4. Điều tra ở một vùng trong 800 người chọn ngẫu nhiên có 184 người tham gia tập
thể thao. Với độ tin cậy 90% hãy xác định khoảng tin cậy đối xứng cho tỷ lệ người có tập
thể thao ở vùng đó. Theo anh (chị) độ chính xác của khoảng tin cậy cho tỷ lệ trên có thể
phụ thuộc vào những yếu tố nào?
Câu 5. Để đánh giá trình độ của một người ứng viên người ta dựa vào 8 lần cho điểm
đồng thời của 2 chuyên gia (số liệu cặp và giả sử giá trị điểm số của mỗi chuyên gia
được coi là biến ngẫu nhiên có phân phối chuẩn): Ch/gia 1 76,3 88,4 80,2 94,7 68,7 82,8 76,1 79,0 Ch/gia 2 75,1 86,8 77,3 90,6 69,1 81,0 75,3 79,1
Với mức ý nghĩa =5%, có thể cho rằng điểm số trung bình của chuyên gia 1 là cao hơn
của chuyên gia 2 hay không? Đề 1
ĐỀ THI MÔN XÁC SUẤT & THỐNG KÊ HK20172 - MI2020
(Thời gian làm bài: 90phút)
Câu 1. Một hộp có n áo trắng và 2n áo xanh. Chia ngẫu nhiên các áo thành n nhóm mỗi nhóm 3 áo).
a/ Tính xác suất để trong mỗi nhóm đều có áo trắng.
b/ Áp dụng cho n = 5.
Câu 2. Một xí nghiệp có 4 chiếc máy tiện với xác suất bị sự cố trong ngày của mỗi máy
tương ứng là 0,01; 0,05; 0,1 và 0,1.
a/ Trong một ngày nào đó theo dõi một máy, tính xác suất để máy đó bị sự cố.
b/ Khi theo dõi 2 máy thì có đúng 1 máy bị sự cố, tính xác suất chiếc máy bị sự cố đó là máy thứ nhất.
Câu 3. Xét một phần tư hình tròn tâm 0(0,0) bán kính bằng a, kí hiệu OAB, với tọa độ
tương ứng A(a,0) và B(0,a).
a/ Trên đoạn OA lấy ngẫu nhiên một điểm c, tìm phân phối xác suất của độ dài đoạn OC.
b/ Dựng một đường thẳng đi qua c, vuông góc với OA và cắt cung tròn tại điểm D,
tính kỳ vọng và phương sai của độ dài đoạn CD.
Câu 4. Tiến hành 120 phép đo như nhau, độc lập, thì thấy sự kiện A xuất hiện 42 lần.
a/ Xác định khoảng tin cậy đối xứng 99% cho tỷ lệ xuất hiện A.
b/ Tính xác suất để sai số ước lượng của tỷ lệ trên bé hơn 10% tần suất mẫu.
Câu 5. Cân 150 con vịt người ta thu được bộ số liệu sau: Khối lượng 1,25 1,50 1,75 2,00 2,25 2,50 2,75 3.00 Số lượng 2 6 24 35 39 24 14 6
Với mức ý nghĩa 5% có thể cho rằng khối lượng trung bình của lứa vịt trên lớn hơn 2 kg được không?
ĐỂ 2 ĐỀ TIII MÔN XÁC SUẤT & THỐNG KÊ HK20172 - MI2020
(Thời gian ỉàm bài: 90 phút)
Câu 1. Một nhóm sinh viên có 2n nam và n nữ. Chia ngẫu nhiên nhóm này thành n nhóm con (mỗi nhóm 3 người).
a/ Tính xác suất để trong mỗi nhóm có cả nam và nữ.
b/ Áp dụng cho n = 4.
Câu 2. 4 xạ thủ được yêu cầu mỗi người bắn một phát đạn với xác suất trúng của mỗi
người tương ứng là 0,4; 0,5; 0,8 và 0,8.
a/ Chọn ngẫu nhiên một người, tính xác suất đêr người đó bắn trúng.
b/ Lấy ngẫu nhiên 2 người thì có đúng 1 người bắn trúng, tính xác suất người bắn
trúng đó là người thứ hai.
Câu 3. Xét một phần tư hình tròn tâm 0(0,0) bán kính bằng 1, kí hiệu OAB, với tọa độ
tương ứng A(l,0) và B(0,l).
a/ Trên cung tròn AB lấy ngẫu nhiên một điểm C, tìm phân phối xác suất của độ dài
cung AC (để ý độ dài cung tròn AB bằng /2).
b/ Dựng một đường thẳng đi qua C, vuông góc với OA và cắt OA tại điểm D, tính kỳ
vọng và phương sai của độ dài đoạn CD.
Câu 4. Tiến hành 100 phép đo như nhau, độc lập, thì thấy sự kiện B xuất hiện 35 lần.
a/ Xác định khoảng tin cậy đối xứng 95% cho tỷ lệ xuất hiện B.
b/ Tính xác suất để sai số ước lượng của tỷ lệ trên bé hơn 10% tần suất mẫu.
Câu 5. Đo chiều cao 300 trẻ 12 tuổi ở một trường học, người ta thu được bộ số liệu sau: Chiều cao 120 125 130 135 140 145 150 Số lượng 9 33 74 93 64 21 6
Với mức ý nghĩa 1% có thể cho rằng chiều cao trung bình của lứa trẻ trên nhỏ hơn 140 cm được không? ĐỀ 1
Đề thi môn XÁC SUẤT & THỐNG KÊ HK30173 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Một lô hàng có 15 sản phẩm gồm 6 loại A, 5 B và 4 C. Chọn ngẫu nhiên (không
hoàn lại) ra 4 sản phẩm.
a/ Tính xác suất trong 4 sản phẩm được chọn có đúng 2 sản phẩm loại B.
b/ Biết trong 4 sản phẩm được chọn có đúng 2 sản phẩm loại A, tính xác suất để trong
4 sản phẩm đó có đúng 1 sản phẩm loại C.
Câu 2. Một nhóm học sinh cỏ 5 loại giỏi, 4 khá và 2 trung bình. Chọn ngẫu nhiên ra một
nhóm gồm 2 học sinh.
a/ Tính giá trị trung bình của số học sinh giỏi trong nhóm đó.
b/ Biết trong nhóm 2 học sinh có ít nhất 1 loại khá, tính xác suất để trong nhóm đó có
đúng 1 học sinh giỏi.
Câu 3. Cho biến ngẫu nhiên X có hàm mật độ (phân phối Rayleigh) 0; x 0, f (x) 2 x /4 Ae ; x 0. a/ Tìm hằng số A.
b/ Tính các đặc trưng định vị: EX và modX (mốt của X).
Câu 4. Số liệu dưới đây cho tỷ lệ phần trăm một hóa chất trong 11 mẫu một loại xi
măng: 6 15 8 8 6 9 17 18 4 8 10.
Với độ tin cậy 95% hãy tìm ước lượng khoảng cho tỷ lệ phần trăm trung bình của loại hóa
chất trên (giả sử tỷ lệ đó là biến ngẫu nhiên tuân theo luật phân phối chuẩn).
Câu 5. Một mẫu gồm n = 64 sản phẩm có 4 sản phẩm lỗi. Có đủ bằng chứng để chấp nhận
giả thuyết “p > 5%” được không; cho mức ý nghĩa = 5%, p ký hiệu tỷ lệ sản phẩm lỗi? Đề 2
Đề thi môn XÁC SUẤT & THỐNG KÊ HK30173 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Trong hộp có 9 bút xanh, 4 bút tím và 2 bút đỏ. Chọn ngẫu nhiên (không hoàn lại) ra 4 bút.
a/ Tính xác suất trong 4 bút được chọn có đúng 2 bút tím.
b/ Biết trong 4 bút được chọn có đúng 2 bút xanh, tính xác suất để trong 4 bút đó có đúng 1 bút đỏ.
Câu 2. Một lô hàng gồm có 9 sản phẩm tốt, 2 sản phẩm lỗi ít và 1 sản phẩm lỗi nhiều.
Chọn ngẫu nhiên ra 2 sản phẩm.
a/ Hỏi trung bình trong 2 sản phẩm được chọn có bao nhiêu sản phẩm lỗi?
b/ Biết trong 2 sản phẩm được chọn có ít nhất 1 sản phẩm lỗi, tính xác suất để trong số
sản phẩm lỗi đó có đúng 1 sản phẩm lỗi ít. 0 ,1 ( ) t P T t e ,t 0.
Câu 3. Thời gian làm việc T của một thiết bị điện thỏa mãn
a/ Tìm hàm phân phối xác suất của T.
b/Tính P(15 < T < 20) và ET.
Cáu 4. Số liệu dưới đây cho nồng độ một hóa chất trong 16 mẫu nước ở một vùng
7 6 6 10 8 9 11 5 4 5 9 8 4 3 6 7
Với độ tin cậy 95% hãy tìm ước lượng khoảng cho nồng độ trung bình của loại hóa chất
trên (giả sử nồng độ đó là biến ngẫu nhiên tuân theo luật phân phối chuẩn).
Câu 5, Trong dãy n = 60 thí nghiệm Bernoulli quan sát có 15 thí nghiệm thành công. Có
thề bác bỏ giả thuyết “p < 30%” được không; cho mức ý nghĩa = 5%, p ký hiệu tỷ lệ thí nghiệm thành công? Đề 1
Đề thi môn XÁC SUẤT & THỐNG KÊ HK20181 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Ở một địa phương đàn ông chiếm 55% dân số. Theo thống kê tỷ lệ đàn ông bị bạch
tạng là 0,4%, còn tỷ lệ trên của đàn bà là 0,32%.
a. Tìm tỷ lệ người bị bệnh bạch tạng ở địa phương đó.
b. Gặp ngẫu nhiên một người bị bạch tạng, tính xác suất đó là đàn ông.
Câu 2. Một máy đếm người vào một siêu thị có tỷ lệ đếm sót là 0,018. Giả sử trọng vòng
1 giờ nào đó có 500 khách vào siêu thị.
a. Tính kỳ vọng và phương sai của số người được máy đếm trong số 500 người nói trên
b. Tính xác suất để máy này đếm sót từ 6 đến 10 người trong số 500 người đó.
Câu 3. Một linh kiện điện tử có thời gian hoạt động X là biến ngẫu nhiên có phân phối mũ x
với hàm mật độ của X là: f (x) .e , x 0.
a. Xác định phân phối xác suất cho thời gian hoạt động của một mạng gồm 2 linh kiện loại trên mắc song song.
b. Tính kỳ vọng và phương sai của thời gian hoạt động của mạng đó.
Câu 4. Ở một trung tâm giống cây trồng, theo dõi 3070 cây cà phê thì có 1135 cây cho thu hoạch thấp.
a. Với độ tin cậy 95% hãy xác định khoảng tin cậy cho tỷ lệ cây cà phê có thu hoạch thấp
b. Tần suất cà phê có thu hoạch thấp có là ước lượng không chệch của tỷ lệ cây cho
thu hoạch thấp không? Tại sao?
Câu 5. Theo dõi thời gian bắt đầu có tác dụng của một loại thuốc trên một nhóm bệnh nhân
trước và sau khi mổ dạ dày, ta thu được bộ số liệu (giả sử thời gian trên có phân phối chuẩn) Bệnh nhân 1 2 3 4 5 6 7 8 Trước mổ 44 51 52 55 66 68 70 71 Sau mổ 52 64 60 74 55 67 75 65
Hỏi thời gian tác dụng của thuốc trước và sau mổ có khác nhau không với mức ý nghĩa 1%? x 2 1 Phụ lục
. Trích Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 2,576 3 (x) 0,90 0,95 0,975 0,9772 0,995 0,9987
Hàm Laplace (x) = (x) – 0,5
Đề 2 Đề thi môn XÁC SUẤT & THỐNG KÊ HK20181 - MI2020
(Thời gian làm hài: 90 phủi)
Câu 1. Cho 3 con rô bốt chẩn đoán bệnh (một cách độc lập) cho một bệnh nhân và giả sử
biết xác suất chẩn đoán đúng của từng con tương ứng là 0,4; 0,7 và 0,9.
a/ Tính xác suất để có ít nhất 1 con rô bốt chẩn đoán đúng.
b/ Biết có đúng một con rô bốt chẩn đoán đúng (trong 3 con), tính xác suất đó là con thứ hai.
Câu 2. Giả sử cho biết xác suất một người mắc bệnh tim mạch là 0,01. Trên một tàu du
lịch có 1000 người và gọi X là số người mắc bệnh tim mạch trong nhóm người đó.
a/ Tính kỳ vọng và phương sai của X.
b/ Tính xác suất đế trong nhóm này có ít nhất 3 người mắc bệnh tim mạch.
Câu 3. Cho một loại bóng điện tử có thời gian hoạt động X là biến ngẫu nhiên có phân
phối mũ, với hàm mật độ của X là f (x) = e-.x, x > 0.
a/ Xác định phân phối xác suất cho thời gian hoạt động của một mạng gồm 2 bóng loại
trên được mắc nối tiếp.
b/ Tính kỳ vọng và phương sai của thời gian hoạt động của mạng đó.
Câu 4. Đo số lượng bạch cầu trong máu của 170 trẻ em, ta tính được các đặc trưng mẫu:
trung bình mẫu là 11250 và độ lệch chuẩn mẫu (chưa hiệu chỉnh) S = 2100.
a/ Với độ tin cậy 95% hãy xác định khoảng tin cậy cho số lượng bạch cầu trung bình của trẻ em.
b/ Tính ước lượng không chệch cho phương sai của số lượng bạch cầu đó.
Câu 5. Đo nồng độ một vi chất bằng hai phương pháp khác nhau, ta có kết quả (giả sử
nồng độ vi chất trên có phân phối chuẩn) Thứ tự mẫu 1 2 3 4 5 6 pp cũ
0,85 1,12 1,46 1,20 1,60 1,52 pp mới
1,09 1,24 1,20 1,25 1,65 1,48
Hỏi phương pháp mới có khác với phương pháp cũ hay không (cho mức ý nghĩa 1%)?
ĐỀ 1 ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20182 Mã HP: MI2020 Thời gian: 90 phút
Câu 1. Cho 3 sự kiện A, B, C độc lập từng đôi (2 sự kiện bất kỳ luôn độc lập với nhau)
thỏa mãn: P(A) = P(B) = P(C) = p và P(A.B.C) = 0. a. Tính ( P . A . B C), ( P . A . B C) .
b. Tìm giá trị p lớn nhất có thể có.
Câu 2. Một nhà máy có hai phân xưởng cùng sản xuất bóng đèn. Số bóng đèn do phân
xưởng 2 sản xuất gấp 2 lần số bóng đèn do phân xưởng 1 sản xuất. Tỷ lệ phế phẩm của 2
phân xưởng tương ứng là 0,005 và 0,008. Lấy ngẫu nhiên 1 bóng đèn của nhà máy để kiểm
tra thì thấy là phế phẩm. Tính xác suất bóng đèn đó do phân xưởng 2 sản xuất.
Câu 3. Có hai lô hàng I và II, mỗi lô chứa rất nhiều sản phẩm. Tỉ lệ sản phẩm loại A có
trong hai lô I và II lần lượt là 70% và 80%. Lấy ngẫu nhiên từ mỗi lô 2 sản phẩm.
a) Tính xác suất để số sản phẩm loại A lấy từ lô I lớn hơn số sản phẩm loại A lấy từ lô II.
b) Gọi X là số sản phẩm loại A có trong 4 sản phẩm được lấy ra. Tìm kỳ vọng và phương sai của X.
Câu 4. Khảo sát trọng lượng X(kg) của 200 con lợn xuất chuồng ta được bảng số liệu sau: X(kg) [85-95)
[95-105) [105-115) [115-125) [125-135) [135-145] Số lợn 10 30 45 80 30 5
Với độ tin cậy 90% hãy ước lượng khoảng cho trọng lượng trung bình của đàn lợn xuất chuồng.
Câu 5. Với số liệu ở câu 4 và mức ý nghĩa 5% liệu có thể khẳng định rằng tỷ lệ lợn xuất
chuồng có trọng lượng thấp hơn 115kg là ít hơn 50% hay không? x 2 1 Phụ lục
. Trích Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 2,576 3 (x) 0,90 0,95 0,975 0,9772 0,995 0,9987
Hàm Laplace (x) = (x) – 0,5
ĐỀ 2 ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20182 Mã HP: MI2020 Thời gian: 90 phút
Câu 1. Cho 3 sự kiện A, B, C độc lập từng đôi (2 sự kiện bất kỳ luôn độc lập với nhau) thỏa mãn:
P(A) = P(B) = P(C) = p và P(A.B.C) = 0. a. Tính ( P . A . B C), ( P . A . B C) .
b. Tìm giá trị p lớn nhất có thể có.
Câu 2. Một thùng có 20 sản phẩm trong đó có 15 chính phẩm và 5 phế phẩm. Trong quá
trình vận chuyển bị mất hai sản phẩm không rõ chất lượng. Lấy ngẫu nhiên 2 sản phẩm
trong 18 sản phẩm còn lại. Biết hai sản phẩm lấy ra đều là chính phẩm, tìm xác suất để hai
sản phẩm bị mất có một chính phẩm và một phế phẩm.
Câu 3. Khảo sát tình hình cung cấp thức ăn chăn nuôi tại một vùng, người ta điều tra các
cơ sở chế biến và bán thứ ăn gia súc tại vùng đó và mô hình hóa thức ăn gia súc bán theo
tuần X(nghìn tấn) bởi hàm mật độ xác suất:
ax(6 x) , x [0;6] f (x) 0 , x [0; 6].
a) Xác định a và E(X).
b) Xác định Med(X) và Mod(X).
Câu 4. Cân thử 100 quả trứng gà trong một trại chăn nuôi ta có kết quả sau: Trọng lượng (gam) 150 160 165 170 180 185 Số trứng 4 16 25 30 15 10
Với độ tin cậy 90%, hãy ước lượng khoảng cho trọng lượng trung bình của trứng gà trong trại chăn nuôi đó.
Câu 5. Với số liệu ở câu 4 và mức ý nghĩa 5% liệu có thể khẳng định rằng tỷ lệ trứng gà
nặng hơn 170 gam cao hơn 20% hay không? x 2 1 Phụ lục
. Trích Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 2,576 3 (x) 0,90 0,95 0,975 0,9772 0,995 0,9987
Hàm Laplace (x) = (x) – 0,5 ĐỀ SỐ 1
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN XÁC SUẤT THỐNG KÊ - Học kì 20183
Mã môn học: MI2020. Thời gian làm bài: 90 phút
Câu 1. (2,0 điểm) Có một nhóm 4 sinh viên, mỗi người có một chiếc mũ giống hệt nhau để
trên giá. Khi ra khỏi phòng, mỗi người lấy ngẫu nhiên một chiếc mũ để đội. Tính xác suất để:
(a) Sinh viên thứ nhất và sinh viên thứ ba lấy đúng mũ của mình.
(b) Có ít nhất một sinh viên lấy đúng mũ của mình.
Câu 2. (2,0 điểm) Một kiện hàng có 10 sản phẩm, trong đó có 7 sản phẩm loại I và 3 sản
phẩm loại II. Tiền lãi khi bán được mỗi sản phẩm loại I là 50 nghìn đồng, mỗi sản phẩm loại II là 20 nghìn đồng.
(a) Ngày thứ nhất lấy ngẫu nhiên từ kiện hàng ra 3 sản phẩm và đã bán hết cả 3 sản phẩm
đó. Tìm kỳ vọng của số tiền lãi thu được.
(b) Ngày thứ hai lấy ngẫu nhiên từ kiện hàng ra 2 sản phẩm. Tính xác suất để thu được 100
nghìn đồng tiền lãi khi bán 2 sản phẩm này.
Câu 3. (1,0 điểm) Cho biến ngẫu nhiên hai chiều liên tục (X, Y ) có hàm mật độ xác suất là
( k x2, nếu − 1 ≤ x ≤ 1, 0 ≤ y ≤ x2, fX,Y (x, y) = 2 0, nếu trái lại. (a) Tìm k. 1 (b) Tính P Y ≤ . 4
Câu 4. (3,0 điểm) Một công ty dự định mở một siêu thị tại khu dân cư A. Để đánh giá khả
năng mua hàng của khách hàng khu vực này, người ta đã điều tra ngẫu nhiên thu nhập trong
một tháng của 100 gia đình và thu được bảng số liệu sau: Thu nhập (triệu đồng) 34,0 34,5 35,0 35,5 36,0 36,5 37,0 37,5 Số gia đình 5 10 15 20 29 10 6 5
(a) Theo bộ phận tiếp thị thì chỉ nên mở siêu thị tại A nếu thu nhập trung bình của các gia
đình phải lớn hơn 35,5 triệu đồng/tháng. Với mức ý nghĩa 5% hãy cho biết có nên mở siêu
thị tại khu dân cư A hay không?
(b) Tìm khoảng tin cậy cho tỷ lệ các gia đình có thu nhập ≥ 35, 5 triệu đồng/tháng với độ tin cậy 95%.
Câu 5. (2,0 điểm) Điều tra ngẫu nhiên thu nhập của 100 gia đình ở khu dân cư B thấy thu
nhập bình quân là 35,8 triệu đồng/tháng và độ lệch chuẩn mẫu hiệu chỉnh là 1,1055 triệu
đồng. Với mức ý nghĩa 5% có thể kết luận thu nhập bình quân ở khu dân cư B cao hơn ở
khu dân cư A (với số liệu ở Câu 4) hay không? 1 x
Phụ lục: Trích Bảng phân vị chuẩn Φ(x) = √ R e−t2/2dt 2π −∞ x 1,000 1,585 1,645 1,960 2,377 2,575 Φ(x) 0,8413 0,9429 0,9500 0,9750 0,9933 0,9950 1 x Hàm Laplace φ(x) := √ R e−t2/2dt = Φ(x) − 0, 5. 2π 0
Chú ý: Thí sinh không được sử dụng tài liệu. Giám thị phải ký xác nhận số đề vào bài thi. ĐỀ SỐ 2
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN XÁC SUẤT THỐNG KÊ - Học kì 20183
Mã môn học: MI2020. Thời gian làm bài: 90 phút
Câu 1. (2,0 điểm) Có một nhóm 4 sinh viên, mỗi người có một chiếc mũ giống hệt nhau để
trên giá. Khi ra khỏi phòng, mỗi người lấy ngẫu nhiên một chiếc mũ để đội. Tính xác suất để:
(a) Sinh viên thứ nhất và sinh viên thứ hai lấy đúng mũ của mình.
(b) Có ít nhất một sinh viên lấy đúng mũ của mình.
Câu 2. (2,0 điểm) Một kiện hàng có 10 sản phẩm, trong đó có 7 sản phẩm loại I và 3 sản
phẩm loại II. Tiền lãi khi bán được mỗi sản phẩm loại I là 60 nghìn đồng, mỗi sản phẩm loại II là 30 nghìn đồng.
(a) Ngày thứ nhất lấy ngẫu nhiên từ kiện hàng ra 3 sản phẩm và đã bán hết cả 3 sản phẩm
đó. Tìm kỳ vọng của số tiền lãi thu được.
(b) Ngày thứ hai lấy ngẫu nhiên từ kiện hàng ra 2 sản phẩm. Tính xác suất để thu được 90
nghìn đồng tiền lãi khi bán 2 sản phẩm này.
Câu 3. (1,0 điểm) Cho biến ngẫu nhiên hai chiều liên tục (X, Y ) có hàm mật độ xác suất là ax2, nếu
− 1 ≤ x ≤ 1, 0 ≤ y ≤ x2, fX,Y (x, y) = 0, nếu trái lại. (a) Tìm hằng số a. 4 (b) Tính P Y ≤ . 9
Câu 4. (3,0 điểm) Một công ty dự định mở một siêu thị tại khu dân cư A. Để đánh giá khả
năng mua hàng của khách hàng khu vực này, người ta đã điều tra ngẫu nhiên thu nhập trong
một tháng của 100 gia đình và thu được bảng số liệu sau: Thu nhập (triệu đồng) 24,0 24,5 25,0 25,5 26,0 26,5 27,0 27,5 Số gia đình 5 10 15 20 29 10 6 5
(a) Theo bộ phận tiếp thị thì chỉ nên mở siêu thị tại A nếu thu nhập trung bình của các gia
đình phải lớn hơn 25,5 triệu đồng/tháng. Với mức ý nghĩa 5% hãy cho biết có nên mở siêu
thị tại khu dân cư A hay không?
(b) Tìm khoảng tin cậy cho tỷ lệ các gia đình có thu nhập ≥ 25, 5 triệu đồng/tháng với độ tin cậy 95%.
Câu 5. (2,0 điểm) Điều tra ngẫu nhiên thu nhập của 100 gia đình ở khu dân cư B thấy thu
nhập bình quân là 25,8 triệu đồng/tháng và độ lệch chuẩn mẫu hiệu chỉnh là 1,1055 triệu
đồng. Với mức ý nghĩa 5% có thể kết luận thu nhập bình quân ở khu dân cư A (với số liệu ở
Câu 4) thấp hơn ở khu dân cư B hay không? 1 x
Phụ lục: Trích Bảng phân vị chuẩn Φ(x) = √ R e−t2/2dt 2π −∞ x 1,000 1,585 1,645 1,960 2,377 2,575 Φ(x) 0,8413 0,9429 0,9500 0,9750 0,9933 0,9950 1 x Hàm Laplace φ(x) := √ R e−t2/2dt = Φ(x) − 0, 5. 2π 0
Chú ý: Thí sinh không được sử dụng tài liệu. Giám thị phải ký xác nhận số đề vào bài thi. ĐỀ SỐ 1
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN XÁC SUẤT THỐNG KÊ - Học kì 20191
Mã môn học: MI2020. Thời gian làm bài: 90 phút
Câu 1. (2,0 điểm) Có ba hộp I, II, III đựng bóng đèn. Hộp I có 8 bóng đèn màu đỏ, 2 bóng
đèn màu xanh; hộp II có 7 bóng đèn màu đỏ, 3 bóng đèn màu xanh; hộp III có 6 bóng đèn
màu đỏ, 4 bóng đèn màu xanh.
(a) Lấy ngẫu nhiên từ mỗi hộp ra một bóng đèn. Tính xác suất để được 3 bóng cùng màu.
(b) Lấy ngẫu nhiên ra một hộp rồi từ đó lấy ngẫu nhiên ra 3 bóng đèn thì được 2 bóng màu
đỏ, 1 bóng màu xanh. Tính xác suất để các bóng đèn này được lấy từ hộp I. 3e−3x, nếu x ≥ 0
Câu 2. (2,0 điểm) Cho hàm mật độ xác suất fX(x) = của biến ngẫu 0, nếu x < 0
nhiên liên tục X và định nghĩa Y = [X] là số nguyên lớn nhất không vượt quá X (nghĩa là
[x] = 0 nếu 0 ≤ x < 1, [x] = 1 nếu 1 ≤ x < 2. . . ). (a) Tính P (Y = 0). (b) Tính E(Y ).
Câu 3. (2,0 điểm) Cho U và V là hai biến ngẫu nhiên liên tục, độc lập với nhau và có cùng
phân phối đều trên [10; 30].
(a) Tìm hàm mật độ xác suất đồng thời fU,V (u, v) của biến ngẫu nhiên hai chiều (U, V ).
(b) Tính P (|U − V | < 10).
Câu 4. (2,0 điểm) Để điều tra doanh thu của các gia đình kinh doanh loại mặt hàng A tại
địa phương B, người ta khảo sát 100 gia đình kinh doanh loại mặt hàng này trong một tháng
của năm 2019 thu được bảng số liệu Doanh thu (triệu VNĐ) 25 30 35 40 45 50 55 60 65 Số gia đình 4 9 17 25 20 10 8 4 3
(a) Với độ tin cậy 95% hãy ước lượng doanh thu trung bình/tháng của các gia đình kinh
doanh loại mặt hàng A tại địa phương B.
(b) Một tài liệu thống kê cho biết doanh thu trung bình/tháng của các gia đình kinh doanh
loại mặt hàng A tại địa phương B là 40 triệu VNĐ. Hãy cho kết luận về tài liệu nói trên với mức ý nghĩa 5%.
Câu 5. (2,0 điểm) Điều tra doanh thu của 200 gia đình kinh doanh loại mặt hàng A ở địa
phương C người ta tính được doanh thu trung bình/tháng là 43 triệu VNĐ và độ lệch tiêu
chuẩn mẫu hiệu chỉnh là 8,912 triệu VNĐ. Doanh thu trung bình loại mặt hàng A ở địa
phương C và B (với số liệu ở Câu 4) có như nhau hay không? Hãy kết luận với mức ý nghĩa 1%. 1 x
Phụ lục: Trích Bảng phân vị chuẩn Φ(x) = √ R e−t2/2dt 2π −∞ x 1,000 1,585 1,645 1,960 2,377 2,575 Φ(x) 0,8413 0,9429 0,9500 0,9750 0,9933 0,9950 1 x Hàm Laplace φ(x) := √ R e−t2/2dt = Φ(x) − 0, 5. 2π 0
Chú ý: Thí sinh không được sử dụng tài liệu. Giám thị phải ký xác nhận số đề vào bài thi. ĐỀ SỐ 2
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐỀ THI CUỐI KÌ MÔN XÁC SUẤT THỐNG KÊ - Học kì 20191
Mã môn học: MI2020. Thời gian làm bài: 90 phút
Câu 1. (2,0 điểm) Có ba hộp I, II, III đựng bóng đèn. Hộp I có 7 bóng đèn màu đỏ, 3 bóng
đèn màu xanh; hộp II có 6 bóng đèn màu đỏ, 4 bóng đèn màu xanh; hộp III có 8 bóng đèn
màu đỏ, 2 bóng đèn màu xanh.
(a) Lấy ngẫu nhiên từ mỗi hộp ra một bóng đèn. Tính xác suất để được 3 bóng cùng màu.
(b) Lấy ngẫu nhiên ra một hộp rồi từ đó lấy ngẫu nhiên ra 3 bóng đèn thì được 2 bóng màu
đỏ, 1 bóng màu xanh. Tính xác suất để các bóng đèn này được lấy từ hộp II. 2e−2x, nếu x ≥ 0
Câu 2. (2,0 điểm) Cho hàm mật độ xác suất fX(x) = của biến ngẫu 0, nếu x < 0
nhiên liên tục X và định nghĩa Y = [X] là số nguyên lớn nhất không vượt quá X (nghĩa là
[x] = 0 nếu 0 ≤ x < 1, [x] = 1 nếu 1 ≤ x < 2. . . ). (a) Tính P (Y = 0). (b) Tính E(Y ).
Câu 3. (2,0 điểm) Cho U và V là hai biến ngẫu nhiên liên tục, độc lập với nhau và có cùng
phân phối đều trên [20; 60].
(a) Tìm hàm mật độ xác suất đồng thời fU,V (u, v) của biến ngẫu nhiên hai chiều (U, V ).
(b) Tính P (|V − U | < 20).
Câu 4. (2,0 điểm) Để điều tra doanh thu của các gia đình kinh doanh loại mặt hàng A tại
địa phương B, người ta khảo sát 100 gia đình kinh doanh loại mặt hàng này trong một tháng
của năm 2019 thu được bảng số liệu Doanh thu (triệu VNĐ) 28 33 38 43 48 53 58 63 68 Số gia đình 4 9 17 25 20 10 8 4 3
(a) Với độ tin cậy 95% hãy ước lượng doanh thu trung bình/tháng của các gia đình kinh
doanh loại mặt hàng A tại địa phương B.
(b) Một tài liệu thống kê cho biết doanh thu trung bình/tháng của các gia đình kinh doanh
loại mặt hàng A tại địa phương B là 40 triệu VNĐ. Hãy cho kết luận về tài liệu nói trên với mức ý nghĩa 5%.
Câu 5. (2,0 điểm) Điều tra doanh thu của 200 gia đình kinh doanh loại mặt hàng A ở địa
phương C người ta tính được doanh thu trung bình/tháng là 45 triệu VNĐ và độ lệch tiêu
chuẩn mẫu hiệu chỉnh là 8,912 triệu VNĐ. Doanh thu trung bình loại mặt hàng A ở địa
phương C và B (với số liệu ở Câu 4) có như nhau hay không? Hãy kết luận với mức ý nghĩa 1%. 1 x
Phụ lục: Trích Bảng phân vị chuẩn Φ(x) = √ R e−t2/2dt 2π −∞ x 1,000 1,585 1,645 1,960 2,377 2,575 Φ(x) 0,8413 0,9429 0,9500 0,9750 0,9933 0,9950 1 x Hàm Laplace φ(x) := √ R e−t2/2dt = Φ(x) − 0, 5. 2π 0
Chú ý: Thí sinh không được sử dụng tài liệu. Giám thị phải ký xác nhận số đề vào bài thi.
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 1
ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20152
Mã học phần: MI2020 Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Hai người A và B chơi trò tung đồng xu (khả năng ra mặt sấp và ngửa là như nhau): mỗi
lần chơi ta tung đồng xu 1 lần, nếu ra mặt sấp thì A thắng, ra mặt ngửa thì B thắng. Hai người chơi 50 lần.
a. Tính xác suất A thắng 30 lần và B thắng 20 lần.
b. Số lần thắng của A lớn hơn số lần thắng của B.
Câu 2. Lô hàng xuất khẩu có 100 kiện hàng trong đó có 60 kiện loại A và 40 kiện loại B (số sản
phẩm có trong mỗi kiện hàng là rất lớn). Tỷ lệ phế phẩm của kiện loại A, B tương ứng là 10%
và 30%. Người ta lấy ngẫu nhiên 1 kiện hàng, từ kiện hàng đó lấy ngẫu nhiên 3 sản phẩm để
kiểm tra thì thấy có duy nhất 1 phế phẩm. Tính xác suất đó là kiện hàng loại A.
Câu 3. Tuổi thọ của người là biến ngẫu nhiên X (năm) có hàm mật độ xác suất: 0 x 0; f (x) . x e x 0.
Biết rằng trung bình trong 1000 người có 500 người sống quá 60 tuổi. a. Xác định .
b. Một cụ năm nay 60 tuổi. Tính xác suất để cụ sống hơn 70 tuổi.
Câu 4. Để tăng doanh số bán hàng, một siêu thị đã thực hiện một chương trình khuyến mãi. Số
liệu thu được (sau khi áp dụng chương trình khuyến mãi) về doanh số bán trong một ngày của siêu thị như sau:
Doanh số (triệu đồng/ngày) 24 30 36 42 48 54 60 65 70 Số ngày 5 12 25 35 24 15 12 10 6
Với độ tin cậy 90%, hãy ước lượng khoảng đối xứng cho doanh số bán trung bình trong một ngày của siêu thị đó.
Câu 5. Trước khi áp dụng khuyến mại, doanh số trung bình là 35 triệu đồng/ngày. Với số liệu ở
Câu 4 và với mức ý nghĩa 5% liệu có thể khẳng định doanh số bán trung bình trong một ngày
của siêu thị đó sau khi áp dụng khuyến mại tăng lớn hơn 9 triệu hay không?
Chú ý: Không được sử dụng tài liệu
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC x 2 1 Phụ lục
. Trích các số Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 3 0,9 0,95 0,975 0,9772 0,9987 x)
Hàm Laplace (x) = (x) – 0,5
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 2
ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20152
Mã học phần: MI2020 Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Hai người A và B chơi trò tung đồng xu (khả năng ra mặt sấp và ngửa là như nhau): mỗi
lần chơi ta tung đồng xu 1 lần, nếu ra mặt sấp thì A thắng, ra mặt ngửa thì B thắng. Hai người chơi 48 lần.
a. Tính xác suất A thắng 28 lần và B thắng 20 lần.
b. Số lần thắng của A lớn hơn số lần thắng của B.
Câu 2. Lô hàng xuất khẩu có 100 kiện hàng trong đó có 70 kiện loại A và 30 kiện loại B (số sản
phẩm có trong mỗi kiện hàng là rất lớn). Tỷ lệ phế phẩm của kiện loại A, B tương ứng là 10%
và 20%. Người ta lấy ngẫu nhiên 1 kiện hàng, từ kiện hàng đó lấy ngẫu nhiên 4 sản phẩm để
kiểm tra thì thấy có duy nhất 1 phế phẩm. Tính xác suất đó là kiện hàng loại B.
Câu 3. Tại một cơ sở sản xuất kẹo, số kẹo trong mỗi bao là X có bảng phân phối: X 18 19 20 21 22
Xác suất 0,14 0,24 0,32 0,21 0,09
Chi phí sản xuất mỗi bao kẹo là 3X + 16 (nghìn đồng). Tiền bán mỗi bao kẹo là 100 nghìn đồng.
Tìm lợi nhuận trung bình và độ lệch chuẩn của lợi nhuận cho mỗi bao kẹo.
Câu 4. Sau khi cải tiến kỹ thuật sản xuất bóng đèn, người ta thử nghiệm với 100 bóng, ta có kết quả như sau: Tuổi thọ (giờ) 1150 1160 1170 1180 1190 1200 Số bóng 10 15 20 30 15 10
Với độ tin cậy 90%, hãy ước lượng khoảng đối xứng cho tuổi thọ trung bình của bóng đèn sau
khi cải tiến kỹ thuật.
Câu 5. Tuổi thọ trung bình của bóng đèn trước cải tiến là 1100 giờ. Với số liệu ở Câu 4 và với
mức ý nghĩa 5% liệu có thể khẳng định tuổi thọ trung bình của bóng đèn sau khi cải tiến kỹ
thuật tăng ít nhất 100 giờ hay không? x 2 1 Phụ lục
. Trích các số Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 3 (x) 0,9 0,95 0,975 0,9772 0,9987
Hàm Laplace (x) = (x) – 0,5
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐÁP ÁN ĐỀ 1 – XÁC SUẤT THỐNG KÊ Câu 1.(2đ)
a. Gọi A: “A thắng 30 lần và B thắng 20 lần”, 30 30 20 P( ) A C * 0,5 * 0,5 0,0419 (0,5đ) 50
b. Gọi H: “Số lần thắng của A lớn hơn số lần thắng của B”
K: “Số lần thắng của A nhỏ hơn số lần thắng của B”
L: “Số lần thắng của A bằng số lần thắng của B”, 25 25 25
P(L) C * 0,5 * 0,5 0,1122 (0,5đ) 50
Do A và B khả năng thắng là như nhau trong mỗi lần chơi, do đó ta có P(H) P(K) (0,5đ) Lại do 1
P(H ) P(K ) P(L) 1 P(H ) P(K )
(1 P(L)) 0, 4439 (0,5đ) 2
Câu 2.(2đ) Gọi A: “kiện hàng lấy ra là loại A” và B: “kiện hàng lấy ra là loại B”
Gọi H: “3 sản phẩm kiểm tra thì thấy có duy nhất 1 phế phẩm” P( ) A 60 / 100 0.6 P(B) 0.4 (0,5đ) 1 2 1 2 P(H | )
A C * 0,1* 0,9 0, 243
P(H | B) C * 0,3* 0, 7 0, 441 (0,5đ) 3 3 ( P H ) ( P ) A * ( P H | ) A ( P ) B * ( P H | )
B 0,6*0, 243 0, 4*0, 441 0,3222 (0,5đ) P( )
A * P(H | ) A 0, 6 * 0, 243
P( A | H ) 0,453 (0,5đ) P(H ) 0,3222
Câu 3.(2đ) X(năm) là tuổi thọ của người 500
a. P( X 60) 0,5 (0,5đ) 1000 x x 60 ln 0,5 0,5 .e dx (e ) | e 0,01155 (0,5đ) 60 60 60 P( X 70)
b. P( X 70 | X 60) P(X (0,5đ) 60) . x e dx 70 e 70 10 e 0,891 (0,5đ) 60 e . x e dx 60
Câu 4.(2đ) Gọi X(triệu đồng/ngày) là doanh số bán trong ngày của siêu thị, EX . Chọn thống kê X n ~ N(0;1) (0,5đ) s
Khoảng tin cậy đối xứng cho s s : x u * ; x u * (0,5đ) 1 1 n n 2 2
Với 1 0,9 0,1 u u 1,645 1 /2 0,95
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
Từ bảng số liệu ta tính được n 144 ; x 45,85 ; s 11,53 (0,5đ)
Thay số ta có khoảng tin cậy: (44,27 ; 47,43) (0,5đ)
Câu 5.(2đ) X(triệu đồng/ngày) là doanh số bán trong ngày của siêu thị, EX . H :
Kiểm định cặp giả thuyết: 0 0 35 9 44 (0,5đ) 0 H : 1 0 Chọn thống kê X 0
n ~ N(0;1) khi H đúng s 0
Từ bảng số liệu ta tính được n 144 ; x 45,85 ; s 11,53 suy ra giá trị quan sát x - 45 8 , 5 - 44 0 k * n * 144 1 9 , 57 (0,5đ) s 11 5 , 3
Với = 0,05 ta có miền bác bỏ H 0: w (u ; ) (u ; ) (1,645; ) (0,5đ) 1 0,95
Do k w nên ta bác bỏ H và chấp nhận H , có thể khẳng định doanh số bán trung bình trong 0 1
một ngày của siêu thị đó sau khi áp dụng khuyến mại tăng lớn hơn 9 triệu. (0,5đ)
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐÁP ÁN ĐỀ 2 – XÁC SUẤT THỐNG KÊ Câu 1.(2đ)
a. Gọi A: “A thắng 28 lần và B thắng 20 lần”, 28 28 20 P( ) A C * 0,5 * 0,5 0,0595 (0,5đ) 48
b. Gọi H: “Số lần thắng của A lớn hơn số lần thắng của B”
K: “Số lần thắng của A nhỏ hơn số lần thắng của B”
L: “Số lần thắng của A bằng số lần thắng của B”, 24 24 24
P(L) C * 0,5 * 0,5 0,1146 (0,5đ) 48
Do A và B khả năng thắng là như nhau trong mỗi lần chơi, do đó ta có P(H) P(K) (0,5đ) Lại 1
do P(H ) P(K ) P(L) 1 P(H ) P(K )
(1 P(L)) 0, 4427 (0,5đ) 2
Câu 2.(2đ) Gọi A: “kiện hàng lấy ra là loại A” và B: “kiện hàng lấy ra là loại B”
Gọi H: “3 sản phẩm kiểm tra thì thấy có duy nhất 1 phế phẩm” P( ) A 70 / 100 0.7 P(B) 0.3 (0,5đ) 1 3 1 3 P(H | )
A C * 0,1* 0,9 0, 2916
P(H | B) C * 0, 2 * 0,8 0, 4096 (0,5đ) 4 4 ( P H) ( P ) A * ( P H | ) A ( P ) B * ( P H | )
B 0,7*0, 2916 0,3*0, 4096 0,327 (0,5đ)
P(B) * P(H | B) 0,3* 0, 4096
P(B | H ) 0,3758 (0,5đ) P(H ) 0,327
Câu 3.(2đ) Áp dụng công thức tính ta có: 5
EX x * p 18*0,14 19*0,24 20*0,32 21*0,21 22*0,09 19,87 i i i 1 5 2 2 2 2
VX E( X ) (EX ) x * p 19,87 1,353 (X ) VX 1,163 (0,5đ) i i i 1
Gọi Y(nghìn đồng) là lợi nhuận thu được trên mỗi bao kẹo.
Y 100 (3X 16) 84 3X (0,5đ)
EY E(84 3X ) 84 3EX 84 3*19,87 24,39 (0,5đ)
(Y) (84 3X) 3*(X) 3*1,163 3,489 (0,5đ)
Câu 4.(2đ) Gọi X(giờ) là tuổi thọ bóng đèn, EX . Chọn thống kê X n ~ N(0;1) (0,5đ) s s s
Khoảng tin cậy đối xứng cho : x u * ; x u * (0,5đ) 1 1 n n 2 2
Với 1 0,9 0,1 u u 1,645 1 /2 0,95
Từ bảng số liệu ta tính được n 100 ; x 1175,5 ; s 14,38 (0,5đ)
Thay số ta có khoảng tin cậy: (1173,13 ; 1177,87) (0,5đ)
Câu 5.(2đ) Gọi X(giờ) là tuổi thọ bóng đèn, EX .
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC H :
Kiểm định cặp giả thuyết: 0 0 1100 100 1200 (0,5đ) 0 H : 1 0 Chọn thống kê X 0
n ~ N(0;1) khi H đúng s 0
Từ bảng số liệu ta tính được n 100 ; x 1175,5 ; s 14,38 x - 1175 5 , -1200 suy ra giá trị quan sát 0 k * n * 100 1 7,04 (0,5đ) s 14 3 , 8
Với = 0,05 ta có miền bác bỏ H 0: w ( ; u ) ( ; u ) ( ; 1,645) (0,5đ) 1 0,95
Do k w nên ta bác bỏ H và chấp nhận H , có thể khẳng định tuổi thọ trung bình của bóng 0 1
đèn sau khi cải tiến kỹ thuật tăng ít hơn 100 giờ. (0,5đ)
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 1
ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20153
Mã học phần: MI2020 Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tung ngẫu nhiên 8 lần một đồng xu (khả năng ra mặt sấp và ngửa là như nhau ở mỗi lần
tung). Tính xác suất để:
a. Được mặt sấp ở các lần gieo chẵn.
b. Chỉ được mặt sấp ở các lần gieo chẵn.
Câu 2. Một hộp có 20 sản phẩm, số chính phẩm có trong 20 sản phẩm đó là ngẫu nhiên và có
khả năng xảy ra như nhau. Người ta bỏ thêm vào hộp đó 1 chính phẩm, sau đó từ hộp này lại lấy
ngẫu nhiên ra một sản phẩm. Tính xác suất sản phẩm đó là chính phẩm.
Câu 3. Tuổi thọ của một loài côn trùng nào đó là biến ngẫu nhiên X (tháng tuổi) có hàm mật độ xác suất như sau: 2 ax (4 x) 0 x 4 f (x) 0 x [0; 4]
a. Xác định a, tìm tỷ lệ côn trùng sống không quá 1 tháng tuổi. b. Xác định mod(X).
Câu 4. Nghiên cứu số vụ tai nạn giao thông xảy ra hàng ngày ở một khu vực ta có bảng số liệu sau: Số vụ tai nạn 0 1 2 3 4 5 6 7 Số ngày 229 211 93 35 7 0 0 1
Với độ tin cậy 90%, hãy ước lượng khoảng đối xứng cho số tai nạn trung bình hàng ngày trong khu vực trên.
Câu 5. Có người đưa ra ý kiến tỷ lệ ngày có xảy ra tai nạn bằng 60%. Với số liệu thu được ở
trên và với mức ý nghĩa 5%, hãy kết luận về ý kiến trên.
Chú ý: Không được sử dụng tài liệu x 2 1 Phụ lục
. Trích các số Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 3 0,9 0,95 0,975 0,9772 0,9987 x)
Hàm Laplace (x) = (x) – 0,5 1
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 2
ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20153
Mã học phần: MI2020 Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Tung ngẫu nhiên 9 lần một đồng xu (khả năng ra mặt sấp và ngửa là như nhau ở mỗi lần
tung). Tính xác suất để:
a. Được mặt sấp ở 4 lần gieo đầu.
b. Chỉ được mặt sấp ở 4 lần gieo đầu.
Câu 2. Một hộp có 24 sản phẩm, số phế phẩm có trong 24 sản phẩm đó là ngẫu nhiên và có khả
năng xảy ra như nhau. Người ta bỏ thêm vào hộp đó một chính phẩm, sau đó từ hộp này lại lấy
ngẫu nhiên ra một sản phẩm. Tính xác suất sản phẩm đó là phế phẩm.
Câu 3. Tuổi thọ của một loài côn trùng nào đó là biến ngẫu nhiên X (tháng tuổi) có hàm mật độ xác suất như sau: 2 ax(4 x ) 0 x 2 f (x) 0 x [0; 2]
a. Xác định a, tìm tỷ lệ côn trùng sống không quá 1 tháng tuổi. b. Xác định mod(X).
Câu 4. Để xác định tốc độ của một phản ứng, người ta tiến hành 60 phép thử đo tốc độ phản ứng
đó trong cùng điều kiện và bằng cùng một phương pháp đo. Kết quả thu được như sau: Tốc độ phản ứng 2,68 2,70 2,73 2,74 2,75 2,76 2,79 2,82 Số phép thử 1 4 12 18 17 5 2 1
Với độ tin cậy 90%, hãy ước lượng khoảng đối xứng cho tốc độ phản ứng trung bình theo cách trên.
Câu 5. Có người đưa ra ý kiến cho rằng xác suất để “tốc độ phản ứng nhỏ hơn 2,72” là thấp hơn
10%. Với số liệu thu được ở trên và với mức ý nghĩa 5%, hãy kết luận về ý kiến trên. x 2 1 Phụ lục
. Trích các số Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 3 (x) 0,9 0,95 0,975 0,9772 0,9987
Hàm Laplace (x) = (x) – 0,5 2
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐÁP ÁN ĐỀ 1 – XÁC SUẤT THỐNG KÊ
Câu 1.(2đ) Gọi A : “lần gieo thứ i được mặt sấp” , i 1, 2,...,8 i
a. Gọi A: “trong 8 lần gieo ta được mặt sấp ở các lần gieo chẵn”, 4 P( )
A P( A .A .A .A ) P( A ).P( A ).P( A ).P( A ) 0,5 0, 0625 (1đ) 2 4 6 8 2 4 6 8
b. Gọi B: “trong 8 lần gieo ta chỉ được mặt sấp ở các lần gieo chẵn”, 8 P( )
A P( A .A .A .A .A .A .A .A ) P( A ).P( A )...P( A ).P( A ) 0,5 0, 00391 (1đ) 1 2 3 4 5 6 7 8 1 2 7 8
Câu 2.(2đ) Gọi A : “trong hộp ban đầu có i chính phẩm”, i 0,1, 2,..., 20 i 1
P( A ) P( A ) ... P( A ) (0,5đ) 0 1 20 21
Gọi H: “sản phẩm lấy ra từ hộp là chính phẩm” i 1
P(H | A ) i 0,1,..., 20 (0,5đ) i 21 20 20 1 i 1
P(H ) P(A ).P(H | A ) (0,5đ) i i i i 21 21 0 0 1 1 21.22 11 (1 2 ... 21) (0,5đ) 21.21 21.21 2 21 Câu 3.(2đ) 3 4 4 x x 64 3 a. 2 4 1
ax (4 x)dx a(4 ) | . a a (0,5đ) 0 0 3 4 3 64 3 4 1 x x 3 4 1 13 2 1
ax (4 x)dx a(4 ) | ( ) 0,051 (0,5đ) 0 0 3 4 64 3 4 256 b. Xét x (0;4) x 0 2 f '(x) .
a (8x 3x ) 0 (0,5đ) x 8 / 3
Ta có hàm f’(x) dương trong khoảng (0; 8/3) và âm trong khoảng ( ; 0) (8 / 3; )
Do đó hàm số f(x) đạt cực đại tại x = 8/3 và đạt cực tiểu tại 0.
Do hàm mật độ chỉ khác 0 trong x(0;4) , nên mod(X) = 8/3 (0,5đ)
Câu 4.(2đ) Gọi X là số vụ tai nạn giao thông xảy ra trong một ngày, EX . Chọn thống kê X n ~ N(0;1) (0,5đ) s
Khoảng tin cậy đối xứng cho s s : x u ; x u (0,5đ) 1 1 n n 2 2
Với 1 0,9 0,1 u u 1,645 1 /2 0,95
Từ bảng số liệu ta tính được n 576 ; x 0,932 ; s 0,985 (0,5đ)
Thay số ta có khoảng tin cậy: (0,8645 ; 0,9995) (0,5đ) 3
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
Câu 5.(2đ) Gọi p là tỷ lệ số ngày có xảy ra tai nạn.
H : p p
Kiểm định cặp giả thuyết: 0 0 p 0,6 (0,5đ) 0
H : p p 1 0 Chọn thống kê f p0
n ~ N(0;1) khi H đúng 0 p (1 p ) 0 0 m
Từ bảng số liệu ta tính được 347
n 576 ; m 347 f 0,6024 n 576 suy ra giá trị quan sát f p 0,6024 0,6 0 k n 576 0 118 , (0,5đ) p (1 p ) 0,6.0,4 0 0
Với = 0,05 ta có miền bác bỏ H0: w ( ; u ) (u ; ) ( ; u ) (u ; ) ( ; 1 ,96) (1,96; ) (0,5đ) 1 /2 1 /2 0,975 0,975
Do k w nên ta không có cơ sở bác bỏ H . Vậy ý kiến đưa ra là đúng. (0,5đ) 0 4
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐÁP ÁN ĐỀ 2 – XÁC SUẤT THỐNG KÊ
Câu 1.(2đ) Gọi A : “lần gieo thứ i được mặt sấp” , i 1, 2,...,9 i
a. Gọi A: “trong 9 lần gieo ta được mặt sấp trong 4 lần gieo đầu”, 4 P( )
A P( A .A .A .A ) P( A ).P( A ).P( A ).P( A ) 0,5 0, 0625 (1đ) 1 2 3 4 1 2 3 4
b. Gọi B: “trong 9 lần gieo ta chỉ được mặt sấp trong 4 lần gieo đầu”, 4 5 P( )
A P( A .A .A .A .A .A .A .A .A ) P( A ).P( A )...P( A ).P( A ) 0,5 .0,5 0, 00195 (1đ) 1 2 3 4 5 6 7 8 9 1 2 8 9
Câu 2.(2đ) Gọi A : “trong hộp ban đầu có i phế phẩm”, i 0,1, 2,..., 24 i 1
P( A ) P( A ) ... P( A ) (0,5đ) 0 1 24 25
Gọi H: “sản phẩm lấy ra từ hộp là phế phẩm” i
P(H | A ) i 0,1,..., 24 (0,5đ) i 25 24 24 1 i
P(H ) P(A ).P(H | A ) (0,5đ) i i i i 25 25 0 0 1 1 24.25 12
(0 1 2 ... 24) (0,5đ) 25.25 25.25 2 25 Câu 3.(2đ) 4 2 x 1 a. 2 2 2 1
ax(4 x )dx a(2x
) | 4a a (0,5đ) 0 0 4 4 4 1 x 1 1 7 2 2 1
ax(4 x )dx a(2x ) | (2 ) 0,4375 (0,5đ) 0 0 4 4 4 16 b. Xét x (0;2)
x 4 / 3 2 3 / 3 2 f '(x) .
a (4 3x ) 0 (0,5đ)
x 4 / 3 2 3 / 3
Ta có hàm f’(x) dương trong khoảng ( 2 3 / 3 , 2 3 / 3) và âm trong khoảng ( ; 2 3 / 3) (2 3 / 3; )
Do đó hàm số f(x) đạt cực đại tại x 2 3 / 3 và đạt cực tiểu tại x 2 3 / 3.
Do hàm mật độ chỉ khác 0 trong x(0;2) , nên Mod(X ) 2 3 / 3 (0,5đ)
Câu 4.(2đ) Gọi X là tốc độ của phản ứng đang xét, EX . Chọn thống kê X n ~ N(0;1) (0,5đ) s
Khoảng tin cậy đối xứng cho s s : x u ; x u (0,5đ) 1 1 n n 2 2
Với 1 0,9 0,1 u u 1,645 1 /2 0,95
Từ bảng số liệu ta tính được n 60 ; x 2,742 ; s 0,021 (0,5đ) 5
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
Thay số ta có khoảng tin cậy: (2,738 ; 2,746) (0,5đ)
Câu 5.(2đ) Gọi p là xác suất để “tốc độ phản ứng nhỏ hơn 2,72”.
H : p p
Kiểm định cặp giả thuyết: 0 0 p 0,1 (0,5đ) 0
H : p p 1 0 Chọn thống kê f p0
n ~ N(0;1) khi H đúng 0 p (1 p ) 0 0 m
Từ bảng số liệu ta tính được 5
n 60 ; m 5 f n 60 suy ra giá trị quan sát f p 1 / 12 0 1 , 0 k n 60 0 ,43 (0,5đ) p (1 p ) 0 1 , .0,9 0 0
Với = 0,05 ta có miền bác bỏ H0: w ( ; u ) ( ; u ) ( ; 1 ,645) (0,5đ) 1 0,95
Do k w nên ta không có cơ sở bác bỏ H . Vậy ý kiến đưa ra là sai. (0,5đ) 0 6
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 1
ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20152
Mã học phần: MI2020 Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Hai người A và B chơi trò tung đồng xu (khả năng ra mặt sấp và ngửa là như nhau): mỗi
lần chơi ta tung đồng xu 1 lần, nếu ra mặt sấp thì A thắng, ra mặt ngửa thì B thắng. Hai người chơi 50 lần.
a. Tính xác suất A thắng 30 lần và B thắng 20 lần.
b. Số lần thắng của A lớn hơn số lần thắng của B.
Câu 2. Lô hàng xuất khẩu có 100 kiện hàng trong đó có 60 kiện loại A và 40 kiện loại B (số sản
phẩm có trong mỗi kiện hàng là rất lớn). Tỷ lệ phế phẩm của kiện loại A, B tương ứng là 10%
và 30%. Người ta lấy ngẫu nhiên 1 kiện hàng, từ kiện hàng đó lấy ngẫu nhiên 3 sản phẩm để
kiểm tra thì thấy có duy nhất 1 phế phẩm. Tính xác suất đó là kiện hàng loại A.
Câu 3. Tuổi thọ của người là biến ngẫu nhiên X (năm) có hàm mật độ xác suất: 0 x 0; f (x) . x e x 0.
Biết rằng trung bình trong 1000 người có 500 người sống quá 60 tuổi. a. Xác định .
b. Một cụ năm nay 60 tuổi. Tính xác suất để cụ sống hơn 70 tuổi.
Câu 4. Để tăng doanh số bán hàng, một siêu thị đã thực hiện một chương trình khuyến mãi. Số
liệu thu được (sau khi áp dụng chương trình khuyến mãi) về doanh số bán trong một ngày của siêu thị như sau:
Doanh số (triệu đồng/ngày) 24 30 36 42 48 54 60 65 70 Số ngày 5 12 25 35 24 15 12 10 6
Với độ tin cậy 90%, hãy ước lượng khoảng đối xứng cho doanh số bán trung bình trong một ngày của siêu thị đó.
Câu 5. Trước khi áp dụng khuyến mại, doanh số trung bình là 35 triệu đồng/ngày. Với số liệu ở
Câu 4 và với mức ý nghĩa 5% liệu có thể khẳng định doanh số bán trung bình trong một ngày
của siêu thị đó sau khi áp dụng khuyến mại tăng lớn hơn 9 triệu hay không?
Chú ý: Không được sử dụng tài liệu
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC x 2 1 Phụ lục
. Trích các số Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 3 0,9 0,95 0,975 0,9772 0,9987 x)
Hàm Laplace (x) = (x) – 0,5
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC ĐỀ 2
ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20152
Mã học phần: MI2020 Thời gian: 90 phút
Chú ý: Thí sinh không được sử dụng tài liệu và giám thị phải ký xác nhận số đề vào bài thi
Câu 1. Hai người A và B chơi trò tung đồng xu (khả năng ra mặt sấp và ngửa là như nhau): mỗi
lần chơi ta tung đồng xu 1 lần, nếu ra mặt sấp thì A thắng, ra mặt ngửa thì B thắng. Hai người chơi 48 lần.
a. Tính xác suất A thắng 28 lần và B thắng 20 lần.
b. Số lần thắng của A lớn hơn số lần thắng của B.
Câu 2. Lô hàng xuất khẩu có 100 kiện hàng trong đó có 70 kiện loại A và 30 kiện loại B (số sản
phẩm có trong mỗi kiện hàng là rất lớn). Tỷ lệ phế phẩm của kiện loại A, B tương ứng là 10%
và 20%. Người ta lấy ngẫu nhiên 1 kiện hàng, từ kiện hàng đó lấy ngẫu nhiên 4 sản phẩm để
kiểm tra thì thấy có duy nhất 1 phế phẩm. Tính xác suất đó là kiện hàng loại B.
Câu 3. Tại một cơ sở sản xuất kẹo, số kẹo trong mỗi bao là X có bảng phân phối: X 18 19 20 21 22
Xác suất 0,14 0,24 0,32 0,21 0,09
Chi phí sản xuất mỗi bao kẹo là 3X + 16 (nghìn đồng). Tiền bán mỗi bao kẹo là 100 nghìn đồng.
Tìm lợi nhuận trung bình và độ lệch chuẩn của lợi nhuận cho mỗi bao kẹo.
Câu 4. Sau khi cải tiến kỹ thuật sản xuất bóng đèn, người ta thử nghiệm với 100 bóng, ta có kết quả như sau: Tuổi thọ (giờ) 1150 1160 1170 1180 1190 1200 Số bóng 10 15 20 30 15 10
Với độ tin cậy 90%, hãy ước lượng khoảng đối xứng cho tuổi thọ trung bình của bóng đèn sau
khi cải tiến kỹ thuật.
Câu 5. Tuổi thọ trung bình của bóng đèn trước cải tiến là 1100 giờ. Với số liệu ở Câu 4 và với
mức ý nghĩa 5% liệu có thể khẳng định tuổi thọ trung bình của bóng đèn sau khi cải tiến kỹ
thuật tăng ít nhất 100 giờ hay không? x 2 1 Phụ lục
. Trích các số Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 3 (x) 0,9 0,95 0,975 0,9772 0,9987
Hàm Laplace (x) = (x) – 0,5
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐÁP ÁN ĐỀ 1 – XÁC SUẤT THỐNG KÊ Câu 1.(2đ)
a. Gọi A: “A thắng 30 lần và B thắng 20 lần”, 30 30 20 P( ) A C * 0,5 * 0,5 0,0419 (0,5đ) 50
b. Gọi H: “Số lần thắng của A lớn hơn số lần thắng của B”
K: “Số lần thắng của A nhỏ hơn số lần thắng của B”
L: “Số lần thắng của A bằng số lần thắng của B”, 25 25 25
P(L) C * 0,5 * 0,5 0,1122 (0,5đ) 50
Do A và B khả năng thắng là như nhau trong mỗi lần chơi, do đó ta có P(H) P(K) (0,5đ) Lại do 1
P(H ) P(K ) P(L) 1 P(H ) P(K )
(1 P(L)) 0, 4439 (0,5đ) 2
Câu 2.(2đ) Gọi A: “kiện hàng lấy ra là loại A” và B: “kiện hàng lấy ra là loại B”
Gọi H: “3 sản phẩm kiểm tra thì thấy có duy nhất 1 phế phẩm” P( ) A 60 / 100 0.6 P(B) 0.4 (0,5đ) 1 2 1 2 P(H | )
A C * 0,1* 0,9 0, 243
P(H | B) C * 0,3* 0, 7 0, 441 (0,5đ) 3 3 ( P H ) ( P ) A * ( P H | ) A ( P ) B * ( P H | )
B 0,6*0, 243 0, 4*0, 441 0,3222 (0,5đ) P( )
A * P(H | ) A 0, 6 * 0, 243
P( A | H ) 0,453 (0,5đ) P(H ) 0,3222
Câu 3.(2đ) X(năm) là tuổi thọ của người 500
a. P( X 60) 0,5 (0,5đ) 1000 x x 60 ln 0,5 0,5 .e dx (e ) | e 0,01155 (0,5đ) 60 60 60 P( X 70)
b. P( X 70 | X 60) P(X (0,5đ) 60) . x e dx 70 e 70 10 e 0,891 (0,5đ) 60 e . x e dx 60
Câu 4.(2đ) Gọi X(triệu đồng/ngày) là doanh số bán trong ngày của siêu thị, EX . Chọn thống kê X n ~ N(0;1) (0,5đ) s
Khoảng tin cậy đối xứng cho s s : x u * ; x u * (0,5đ) 1 1 n n 2 2
Với 1 0,9 0,1 u u 1,645 1 /2 0,95
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
Từ bảng số liệu ta tính được n 144 ; x 45,85 ; s 11,53 (0,5đ)
Thay số ta có khoảng tin cậy: (44,27 ; 47,43) (0,5đ)
Câu 5.(2đ) X(triệu đồng/ngày) là doanh số bán trong ngày của siêu thị, EX . H :
Kiểm định cặp giả thuyết: 0 0 35 9 44 (0,5đ) 0 H : 1 0 Chọn thống kê X 0
n ~ N(0;1) khi H đúng s 0
Từ bảng số liệu ta tính được n 144 ; x 45,85 ; s 11,53 suy ra giá trị quan sát x - 45 8 , 5 - 44 0 k * n * 144 1 9 , 57 (0,5đ) s 11 5 , 3
Với = 0,05 ta có miền bác bỏ H 0: w (u ; ) (u ; ) (1,645; ) (0,5đ) 1 0,95
Do k w nên ta bác bỏ H và chấp nhận H , có thể khẳng định doanh số bán trung bình trong 0 1
một ngày của siêu thị đó sau khi áp dụng khuyến mại tăng lớn hơn 9 triệu. (0,5đ)
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC
ĐÁP ÁN ĐỀ 2 – XÁC SUẤT THỐNG KÊ Câu 1.(2đ)
a. Gọi A: “A thắng 28 lần và B thắng 20 lần”, 28 28 20 P( ) A C * 0,5 * 0,5 0,0595 (0,5đ) 48
b. Gọi H: “Số lần thắng của A lớn hơn số lần thắng của B”
K: “Số lần thắng của A nhỏ hơn số lần thắng của B”
L: “Số lần thắng của A bằng số lần thắng của B”, 24 24 24
P(L) C * 0,5 * 0,5 0,1146 (0,5đ) 48
Do A và B khả năng thắng là như nhau trong mỗi lần chơi, do đó ta có P(H) P(K) (0,5đ) Lại 1
do P(H ) P(K ) P(L) 1 P(H ) P(K )
(1 P(L)) 0, 4427 (0,5đ) 2
Câu 2.(2đ) Gọi A: “kiện hàng lấy ra là loại A” và B: “kiện hàng lấy ra là loại B”
Gọi H: “3 sản phẩm kiểm tra thì thấy có duy nhất 1 phế phẩm” P( ) A 70 / 100 0.7 P(B) 0.3 (0,5đ) 1 3 1 3 P(H | )
A C * 0,1* 0,9 0, 2916
P(H | B) C * 0, 2 * 0,8 0, 4096 (0,5đ) 4 4 ( P H) ( P ) A * ( P H | ) A ( P ) B * ( P H | )
B 0,7*0, 2916 0,3*0, 4096 0,327 (0,5đ)
P(B) * P(H | B) 0,3* 0, 4096
P(B | H ) 0,3758 (0,5đ) P(H ) 0,327
Câu 3.(2đ) Áp dụng công thức tính ta có: 5
EX x * p 18*0,14 19*0,24 20*0,32 21*0,21 22*0,09 19,87 i i i 1 5 2 2 2 2
VX E( X ) (EX ) x * p 19,87 1,353 (X ) VX 1,163 (0,5đ) i i i 1
Gọi Y(nghìn đồng) là lợi nhuận thu được trên mỗi bao kẹo.
Y 100 (3X 16) 84 3X (0,5đ)
EY E(84 3X ) 84 3EX 84 3*19,87 24,39 (0,5đ)
(Y) (84 3X) 3*(X) 3*1,163 3,489 (0,5đ)
Câu 4.(2đ) Gọi X(giờ) là tuổi thọ bóng đèn, EX . Chọn thống kê X n ~ N(0;1) (0,5đ) s s s
Khoảng tin cậy đối xứng cho : x u * ; x u * (0,5đ) 1 1 n n 2 2
Với 1 0,9 0,1 u u 1,645 1 /2 0,95
Từ bảng số liệu ta tính được n 100 ; x 1175,5 ; s 14,38 (0,5đ)
Thay số ta có khoảng tin cậy: (1173,13 ; 1177,87) (0,5đ)
Câu 5.(2đ) Gọi X(giờ) là tuổi thọ bóng đèn, EX .
VIỆN TOÁN ỨNG DỤNG VÀ TIN HỌC H :
Kiểm định cặp giả thuyết: 0 0 1100 100 1200 (0,5đ) 0 H : 1 0 Chọn thống kê X 0
n ~ N(0;1) khi H đúng s 0
Từ bảng số liệu ta tính được n 100 ; x 1175,5 ; s 14,38 x - 1175 5 , -1200 suy ra giá trị quan sát 0 k * n * 100 1 7,04 (0,5đ) s 14 3 , 8
Với = 0,05 ta có miền bác bỏ H 0: w ( ; u ) ( ; u ) ( ; 1,645) (0,5đ) 1 0,95
Do k w nên ta bác bỏ H và chấp nhận H , có thể khẳng định tuổi thọ trung bình của bóng 0 1
đèn sau khi cải tiến kỹ thuật tăng ít hơn 100 giờ. (0,5đ) ĐỀ 1
Đề thi môn XÁC SUẤT & THỐNG KÊ HK20171 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Xác suất làm việc của một hệ thống trong khoảng thời gian xác định nào đó được
gọi là xác suất tin cậy (XSTC) của hệ thống đó.
a/ Tính XSTC cùa một mạng gồm 2 linh kiện mắc nối tiếp cùng có XSTC là 0,95.
b/ Mắc song song với mạng trên một mạng dự phòng gồm 2 linh kiện mắc nối tiếp
cùng có XSTC là 0,94, tính XSTC cùa mạng mới đó.
Câu 2. Một lô hàng gồm 16 sản phẩm loại A và 12 loại B. Chọn ngẫu nhiên 3 sản phẩm.
a/ Tính xác suất để trong 3 sản phẩm đó có ít nhất 2 sản phẩm loại A.
b/ Chọn tiếp ngẫu nhiên ra 3 sản phẩm trong số còn lại, tính xác suất để trong số 3 sản
phẩm được chọn lần hai có ít nhất 1 sản phẩm loại A.
Câu 3. Theo điều tra cùa một hãng bảo hiểm ô tô tỷ lệ xe bị tai nạn trong năm là 0,15.
Trong số xe bị tai nạn: 80% được bồi thường tai nạn bằng 20% giá trị xe, 12% được bồi
thường 60% giá trị xe và 8% được bồi thường 100% giá trị xe.
a/ Hỏi trung bình phải bồi thường tai nạn bao nhiêu cho một xe có giá trị 600 triệu đồng?
b/ Đối với chiếc xe trên phải quy định phí bảo hiểm là bao nhiêu để hãng không bị lỗ
(chỉ kể chi phí bồi thường, không kể các chi phí khác)?
Câu 4. Thống kê ở một vùng trong 500 xe ô tô đăng ký có 68 xe thể thao. Với độ tin cậy
95% hãy xác định khoảng tin cậy đối xứng cho tỷ lệ xe thể thao ở vùng đó. Theo anh
(chị) có cách nào để nâng cao độ chính xác của khoảng tin cậy cho tỷ lệ trên?
Câu 5. Đo thời gian phản ứng (giây) đối với hai loại thuốc kích thích của 8 người tham
gia thí nghiệm (giả sử thời gian phản ứng đối với mỗi loại thuốc được coi là biến ngẫu
nhiên có phân phối chuẩn), ta có bộ số liệu cặp: Thuốc 3,1 1,5 2,9 2,6 1,7 2,3 3,8 2,4 1 Thuốc 4,1 2,2 3,5 1,8 2,7 2,5 3,4 3,2 Với mứ 2
c ý nghĩa =5%, có thể cho rằng thời gian phản ứng trung bình đối với 2 loại
thuốc là như nhau hay không?
ĐỀ 2 Đề thi môn XÁC SUẤT & THỐNG KÊ HK20171 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Xác suất làm việc của một hệ thống trong khoảng thời gian xác định nào đó được
gọi là xác suất tin cậy (XSTC) của hệ thống đó.
a/ Tính XSTC cùa một mạng gồm 2 linh kiện mắc nối tiếp cùng có XSTC là 0,94.
b/ Mắc song song với mạng trên một mạng dự phòng gồm 2 linh kiện mắc nối tiếp
cùng có XSTC là 0,92, tính XSTC cùa mạng mới đó.
Câu 2. Một lô hàng gồm 20 sản phẩm loại I và 16 loại II. Chọn ngẫu nhiên 3 sản phẩm.
a/ Tính xác suất để trong 3 sản phẩm đó có ít nhất 2 sản phẩm loại II.
b/ Chọn tiếp ngẫu nhiên ra 3 sản phẩm trong số còn lại, tính xác suất để trong số 3 sản
phẩm được chọn lần hai có ít nhất 1 sản phẩm loại I.
Câu 3. Theo điều tra cùa một hãng bảo hiểm bất động sản, tỷ lệ nhà ở bị hỏa hoạn trong
năm tại một vùng là 0,02. Trong số nhà bị cháy: 78% được bồi thường tai nạn bằng 20%
giá trị ngôi nhà, 14% được bồi thường 60% giá trị nhà và 8% được bồi thường 100% giá trị nhà.
a/ Hỏi trung bình phải bồi thường hỏa hoạn bao nhiêu cho một ngôi nhà có giá trị 5 tỷ đồng?
b/ Đối với ngôi nhà trên phải quy định phí bảo hiểm là bao nhiêu để hãng bảo hiểm
không bị lỗ (chỉ kể chi phí bồi thường, không kể các chi phí khác)?
Câu 4. Điều tra ở một vùng trong 800 người chọn ngẫu nhiên có 184 người tham gia tập
thể thao. Với độ tin cậy 90% hãy xác định khoảng tin cậy đối xứng cho tỷ lệ người có tập
thể thao ở vùng đó. Theo anh (chị) độ chính xác của khoảng tin cậy cho tỷ lệ trên có thể
phụ thuộc vào những yếu tố nào?
Câu 5. Để đánh giá trình độ của một người ứng viên người ta dựa vào 8 lần cho điểm
đồng thời của 2 chuyên gia (số liệu cặp và giả sử giá trị điểm số của mỗi chuyên gia
được coi là biến ngẫu nhiên có phân phối chuẩn): Ch/gia 1 76,3 88,4 80,2 94,7 68,7 82,8 76,1 79,0 Ch/gia 2 75,1 86,8 77,3 90,6 69,1 81,0 75,3 79,1
Với mức ý nghĩa =5%, có thể cho rằng điểm số trung bình của chuyên gia 1 là cao hơn
của chuyên gia 2 hay không? Đề 1
ĐỀ THI MÔN XÁC SUẤT & THỐNG KÊ HK20172 - MI2020
(Thời gian làm bài: 90phút)
Câu 1. Một hộp có n áo trắng và 2n áo xanh. Chia ngẫu nhiên các áo thành n nhóm mỗi nhóm 3 áo).
a/ Tính xác suất để trong mỗi nhóm đều có áo trắng.
b/ Áp dụng cho n = 5.
Câu 2. Một xí nghiệp có 4 chiếc máy tiện với xác suất bị sự cố trong ngày của mỗi máy
tương ứng là 0,01; 0,05; 0,1 và 0,1.
a/ Trong một ngày nào đó theo dõi một máy, tính xác suất để máy đó bị sự cố.
b/ Khi theo dõi 2 máy thì có đúng 1 máy bị sự cố, tính xác suất chiếc máy bị sự cố đó là máy thứ nhất.
Câu 3. Xét một phần tư hình tròn tâm 0(0,0) bán kính bằng a, kí hiệu OAB, với tọa độ
tương ứng A(a,0) và B(0,a).
a/ Trên đoạn OA lấy ngẫu nhiên một điểm c, tìm phân phối xác suất của độ dài đoạn OC.
b/ Dựng một đường thẳng đi qua c, vuông góc với OA và cắt cung tròn tại điểm D,
tính kỳ vọng và phương sai của độ dài đoạn CD.
Câu 4. Tiến hành 120 phép đo như nhau, độc lập, thì thấy sự kiện A xuất hiện 42 lần.
a/ Xác định khoảng tin cậy đối xứng 99% cho tỷ lệ xuất hiện A.
b/ Tính xác suất để sai số ước lượng của tỷ lệ trên bé hơn 10% tần suất mẫu.
Câu 5. Cân 150 con vịt người ta thu được bộ số liệu sau: Khối lượng 1,25 1,50 1,75 2,00 2,25 2,50 2,75 3.00 Số lượng 2 6 24 35 39 24 14 6
Với mức ý nghĩa 5% có thể cho rằng khối lượng trung bình của lứa vịt trên lớn hơn 2 kg được không?
ĐỂ 2 ĐỀ TIII MÔN XÁC SUẤT & THỐNG KÊ HK20172 - MI2020
(Thời gian ỉàm bài: 90 phút)
Câu 1. Một nhóm sinh viên có 2n nam và n nữ. Chia ngẫu nhiên nhóm này thành n nhóm con (mỗi nhóm 3 người).
a/ Tính xác suất để trong mỗi nhóm có cả nam và nữ.
b/ Áp dụng cho n = 4.
Câu 2. 4 xạ thủ được yêu cầu mỗi người bắn một phát đạn với xác suất trúng của mỗi
người tương ứng là 0,4; 0,5; 0,8 và 0,8.
a/ Chọn ngẫu nhiên một người, tính xác suất đêr người đó bắn trúng.
b/ Lấy ngẫu nhiên 2 người thì có đúng 1 người bắn trúng, tính xác suất người bắn
trúng đó là người thứ hai.
Câu 3. Xét một phần tư hình tròn tâm 0(0,0) bán kính bằng 1, kí hiệu OAB, với tọa độ
tương ứng A(l,0) và B(0,l).
a/ Trên cung tròn AB lấy ngẫu nhiên một điểm C, tìm phân phối xác suất của độ dài
cung AC (để ý độ dài cung tròn AB bằng /2).
b/ Dựng một đường thẳng đi qua C, vuông góc với OA và cắt OA tại điểm D, tính kỳ
vọng và phương sai của độ dài đoạn CD.
Câu 4. Tiến hành 100 phép đo như nhau, độc lập, thì thấy sự kiện B xuất hiện 35 lần.
a/ Xác định khoảng tin cậy đối xứng 95% cho tỷ lệ xuất hiện B.
b/ Tính xác suất để sai số ước lượng của tỷ lệ trên bé hơn 10% tần suất mẫu.
Câu 5. Đo chiều cao 300 trẻ 12 tuổi ở một trường học, người ta thu được bộ số liệu sau: Chiều cao 120 125 130 135 140 145 150 Số lượng 9 33 74 93 64 21 6
Với mức ý nghĩa 1% có thể cho rằng chiều cao trung bình của lứa trẻ trên nhỏ hơn 140 cm được không? ĐỀ 1
Đề thi môn XÁC SUẤT & THỐNG KÊ HK30173 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Một lô hàng có 15 sản phẩm gồm 6 loại A, 5 B và 4 C. Chọn ngẫu nhiên (không
hoàn lại) ra 4 sản phẩm.
a/ Tính xác suất trong 4 sản phẩm được chọn có đúng 2 sản phẩm loại B.
b/ Biết trong 4 sản phẩm được chọn có đúng 2 sản phẩm loại A, tính xác suất để trong
4 sản phẩm đó có đúng 1 sản phẩm loại C.
Câu 2. Một nhóm học sinh cỏ 5 loại giỏi, 4 khá và 2 trung bình. Chọn ngẫu nhiên ra một
nhóm gồm 2 học sinh.
a/ Tính giá trị trung bình của số học sinh giỏi trong nhóm đó.
b/ Biết trong nhóm 2 học sinh có ít nhất 1 loại khá, tính xác suất để trong nhóm đó có
đúng 1 học sinh giỏi.
Câu 3. Cho biến ngẫu nhiên X có hàm mật độ (phân phối Rayleigh) 0; x 0, f (x) 2 x /4 Ae ; x 0. a/ Tìm hằng số A.
b/ Tính các đặc trưng định vị: EX và modX (mốt của X).
Câu 4. Số liệu dưới đây cho tỷ lệ phần trăm một hóa chất trong 11 mẫu một loại xi
măng: 6 15 8 8 6 9 17 18 4 8 10.
Với độ tin cậy 95% hãy tìm ước lượng khoảng cho tỷ lệ phần trăm trung bình của loại hóa
chất trên (giả sử tỷ lệ đó là biến ngẫu nhiên tuân theo luật phân phối chuẩn).
Câu 5. Một mẫu gồm n = 64 sản phẩm có 4 sản phẩm lỗi. Có đủ bằng chứng để chấp nhận
giả thuyết “p > 5%” được không; cho mức ý nghĩa = 5%, p ký hiệu tỷ lệ sản phẩm lỗi? Đề 2
Đề thi môn XÁC SUẤT & THỐNG KÊ HK30173 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Trong hộp có 9 bút xanh, 4 bút tím và 2 bút đỏ. Chọn ngẫu nhiên (không hoàn lại) ra 4 bút.
a/ Tính xác suất trong 4 bút được chọn có đúng 2 bút tím.
b/ Biết trong 4 bút được chọn có đúng 2 bút xanh, tính xác suất để trong 4 bút đó có đúng 1 bút đỏ.
Câu 2. Một lô hàng gồm có 9 sản phẩm tốt, 2 sản phẩm lỗi ít và 1 sản phẩm lỗi nhiều.
Chọn ngẫu nhiên ra 2 sản phẩm.
a/ Hỏi trung bình trong 2 sản phẩm được chọn có bao nhiêu sản phẩm lỗi?
b/ Biết trong 2 sản phẩm được chọn có ít nhất 1 sản phẩm lỗi, tính xác suất để trong số
sản phẩm lỗi đó có đúng 1 sản phẩm lỗi ít. 0 ,1 ( ) t P T t e ,t 0.
Câu 3. Thời gian làm việc T của một thiết bị điện thỏa mãn
a/ Tìm hàm phân phối xác suất của T.
b/Tính P(15 < T < 20) và ET.
Cáu 4. Số liệu dưới đây cho nồng độ một hóa chất trong 16 mẫu nước ở một vùng
7 6 6 10 8 9 11 5 4 5 9 8 4 3 6 7
Với độ tin cậy 95% hãy tìm ước lượng khoảng cho nồng độ trung bình của loại hóa chất
trên (giả sử nồng độ đó là biến ngẫu nhiên tuân theo luật phân phối chuẩn).
Câu 5, Trong dãy n = 60 thí nghiệm Bernoulli quan sát có 15 thí nghiệm thành công. Có
thề bác bỏ giả thuyết “p < 30%” được không; cho mức ý nghĩa = 5%, p ký hiệu tỷ lệ thí nghiệm thành công? Đề 1
Đề thi môn XÁC SUẤT & THỐNG KÊ HK20181 - MI2020
(Thời gian làm bài: 90 phút)
Câu 1. Ở một địa phương đàn ông chiếm 55% dân số. Theo thống kê tỷ lệ đàn ông bị bạch
tạng là 0,4%, còn tỷ lệ trên của đàn bà là 0,32%.
a. Tìm tỷ lệ người bị bệnh bạch tạng ở địa phương đó.
b. Gặp ngẫu nhiên một người bị bạch tạng, tính xác suất đó là đàn ông.
Câu 2. Một máy đếm người vào một siêu thị có tỷ lệ đếm sót là 0,018. Giả sử trọng vòng
1 giờ nào đó có 500 khách vào siêu thị.
a. Tính kỳ vọng và phương sai của số người được máy đếm trong số 500 người nói trên
b. Tính xác suất để máy này đếm sót từ 6 đến 10 người trong số 500 người đó.
Câu 3. Một linh kiện điện tử có thời gian hoạt động X là biến ngẫu nhiên có phân phối mũ x
với hàm mật độ của X là: f (x) .e , x 0.
a. Xác định phân phối xác suất cho thời gian hoạt động của một mạng gồm 2 linh kiện loại trên mắc song song.
b. Tính kỳ vọng và phương sai của thời gian hoạt động của mạng đó.
Câu 4. Ở một trung tâm giống cây trồng, theo dõi 3070 cây cà phê thì có 1135 cây cho thu hoạch thấp.
a. Với độ tin cậy 95% hãy xác định khoảng tin cậy cho tỷ lệ cây cà phê có thu hoạch thấp
b. Tần suất cà phê có thu hoạch thấp có là ước lượng không chệch của tỷ lệ cây cho
thu hoạch thấp không? Tại sao?
Câu 5. Theo dõi thời gian bắt đầu có tác dụng của một loại thuốc trên một nhóm bệnh nhân
trước và sau khi mổ dạ dày, ta thu được bộ số liệu (giả sử thời gian trên có phân phối chuẩn) Bệnh nhân 1 2 3 4 5 6 7 8 Trước mổ 44 51 52 55 66 68 70 71 Sau mổ 52 64 60 74 55 67 75 65
Hỏi thời gian tác dụng của thuốc trước và sau mổ có khác nhau không với mức ý nghĩa 1%? x 2 1 Phụ lục
. Trích Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 2,576 3 (x) 0,90 0,95 0,975 0,9772 0,995 0,9987
Hàm Laplace (x) = (x) – 0,5
Đề 2 Đề thi môn XÁC SUẤT & THỐNG KÊ HK20181 - MI2020
(Thời gian làm hài: 90 phủi)
Câu 1. Cho 3 con rô bốt chẩn đoán bệnh (một cách độc lập) cho một bệnh nhân và giả sử
biết xác suất chẩn đoán đúng của từng con tương ứng là 0,4; 0,7 và 0,9.
a/ Tính xác suất để có ít nhất 1 con rô bốt chẩn đoán đúng.
b/ Biết có đúng một con rô bốt chẩn đoán đúng (trong 3 con), tính xác suất đó là con thứ hai.
Câu 2. Giả sử cho biết xác suất một người mắc bệnh tim mạch là 0,01. Trên một tàu du
lịch có 1000 người và gọi X là số người mắc bệnh tim mạch trong nhóm người đó.
a/ Tính kỳ vọng và phương sai của X.
b/ Tính xác suất đế trong nhóm này có ít nhất 3 người mắc bệnh tim mạch.
Câu 3. Cho một loại bóng điện tử có thời gian hoạt động X là biến ngẫu nhiên có phân
phối mũ, với hàm mật độ của X là f (x) = e-.x, x > 0.
a/ Xác định phân phối xác suất cho thời gian hoạt động của một mạng gồm 2 bóng loại
trên được mắc nối tiếp.
b/ Tính kỳ vọng và phương sai của thời gian hoạt động của mạng đó.
Câu 4. Đo số lượng bạch cầu trong máu của 170 trẻ em, ta tính được các đặc trưng mẫu:
trung bình mẫu là 11250 và độ lệch chuẩn mẫu (chưa hiệu chỉnh) S = 2100.
a/ Với độ tin cậy 95% hãy xác định khoảng tin cậy cho số lượng bạch cầu trung bình của trẻ em.
b/ Tính ước lượng không chệch cho phương sai của số lượng bạch cầu đó.
Câu 5. Đo nồng độ một vi chất bằng hai phương pháp khác nhau, ta có kết quả (giả sử
nồng độ vi chất trên có phân phối chuẩn) Thứ tự mẫu 1 2 3 4 5 6 pp cũ
0,85 1,12 1,46 1,20 1,60 1,52 pp mới
1,09 1,24 1,20 1,25 1,65 1,48
Hỏi phương pháp mới có khác với phương pháp cũ hay không (cho mức ý nghĩa 1%)?
ĐỀ 1 ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20182 Mã HP: MI2020 Thời gian: 90 phút
Câu 1. Cho 3 sự kiện A, B, C độc lập từng đôi (2 sự kiện bất kỳ luôn độc lập với nhau)
thỏa mãn: P(A) = P(B) = P(C) = p và P(A.B.C) = 0. a. Tính ( P . A . B C), ( P . A . B C) .
b. Tìm giá trị p lớn nhất có thể có.
Câu 2. Một nhà máy có hai phân xưởng cùng sản xuất bóng đèn. Số bóng đèn do phân
xưởng 2 sản xuất gấp 2 lần số bóng đèn do phân xưởng 1 sản xuất. Tỷ lệ phế phẩm của 2
phân xưởng tương ứng là 0,005 và 0,008. Lấy ngẫu nhiên 1 bóng đèn của nhà máy để kiểm
tra thì thấy là phế phẩm. Tính xác suất bóng đèn đó do phân xưởng 2 sản xuất.
Câu 3. Có hai lô hàng I và II, mỗi lô chứa rất nhiều sản phẩm. Tỉ lệ sản phẩm loại A có
trong hai lô I và II lần lượt là 70% và 80%. Lấy ngẫu nhiên từ mỗi lô 2 sản phẩm.
a) Tính xác suất để số sản phẩm loại A lấy từ lô I lớn hơn số sản phẩm loại A lấy từ lô II.
b) Gọi X là số sản phẩm loại A có trong 4 sản phẩm được lấy ra. Tìm kỳ vọng và phương sai của X.
Câu 4. Khảo sát trọng lượng X(kg) của 200 con lợn xuất chuồng ta được bảng số liệu sau: X(kg) [85-95)
[95-105) [105-115) [115-125) [125-135) [135-145] Số lợn 10 30 45 80 30 5
Với độ tin cậy 90% hãy ước lượng khoảng cho trọng lượng trung bình của đàn lợn xuất chuồng.
Câu 5. Với số liệu ở câu 4 và mức ý nghĩa 5% liệu có thể khẳng định rằng tỷ lệ lợn xuất
chuồng có trọng lượng thấp hơn 115kg là ít hơn 50% hay không? x 2 1 Phụ lục
. Trích Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 2,576 3 (x) 0,90 0,95 0,975 0,9772 0,995 0,9987
Hàm Laplace (x) = (x) – 0,5
ĐỀ 2 ĐỀ THI CUỐI KỲ MÔN XÁC SUẤT THỐNG KÊ – Học kì 20182 Mã HP: MI2020 Thời gian: 90 phút
Câu 1. Cho 3 sự kiện A, B, C độc lập từng đôi (2 sự kiện bất kỳ luôn độc lập với nhau) thỏa mãn:
P(A) = P(B) = P(C) = p và P(A.B.C) = 0. a. Tính ( P . A . B C), ( P . A . B C) .
b. Tìm giá trị p lớn nhất có thể có.
Câu 2. Một thùng có 20 sản phẩm trong đó có 15 chính phẩm và 5 phế phẩm. Trong quá
trình vận chuyển bị mất hai sản phẩm không rõ chất lượng. Lấy ngẫu nhiên 2 sản phẩm
trong 18 sản phẩm còn lại. Biết hai sản phẩm lấy ra đều là chính phẩm, tìm xác suất để hai
sản phẩm bị mất có một chính phẩm và một phế phẩm.
Câu 3. Khảo sát tình hình cung cấp thức ăn chăn nuôi tại một vùng, người ta điều tra các
cơ sở chế biến và bán thứ ăn gia súc tại vùng đó và mô hình hóa thức ăn gia súc bán theo
tuần X(nghìn tấn) bởi hàm mật độ xác suất:
ax(6 x) , x [0;6] f (x) 0 , x [0; 6].
a) Xác định a và E(X).
b) Xác định Med(X) và Mod(X).
Câu 4. Cân thử 100 quả trứng gà trong một trại chăn nuôi ta có kết quả sau: Trọng lượng (gam) 150 160 165 170 180 185 Số trứng 4 16 25 30 15 10
Với độ tin cậy 90%, hãy ước lượng khoảng cho trọng lượng trung bình của trứng gà trong trại chăn nuôi đó.
Câu 5. Với số liệu ở câu 4 và mức ý nghĩa 5% liệu có thể khẳng định rằng tỷ lệ trứng gà
nặng hơn 170 gam cao hơn 20% hay không? x 2 1 Phụ lục
. Trích Bảng hàm phân phối chuẩn (x) t e / 2 dt 2 x 1,282 1,645 1,96 2 2,576 3 (x) 0,90 0,95 0,975 0,9772 0,995 0,9987
Hàm Laplace (x) = (x) – 0,5
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Đề thi cuối kỳ môn Xác suất thống kê - Học kỳ: 20203 Thời gian: 90 phút
(Đề thi gồm 40 câu hỏi trắc nghiệm) Câu 01.
Một lớp học Triết học Mác – Lênin có 5 sinh viên. Xác suất có ít nhất 2 sinh viên trùng tháng sinh với nhau là. A 0.407 B 0.382 C 0.618 D 0.518 Câu 02.
Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập
hợp1, 2, 3, 4, 5, 6, 7. Chọn ngẫu nhiên một số thuộc S. Xác suất để số đó không có 2 chữ số liên tiếp nào cùng chẵn:. 9 22 19 16 A B C D 35 35 35 35 Câu 03.
Xác suất để một người tung một đồng xu đồng chất được mặt ngửa lần thứ ba ở lần tung thứ 7 là. A 0.2734 B 0.1172 C 0.1366 D 0.2598 Câu 04.
Điều tra mức thu nhập cá nhân trong một tháng (triệu đồng), ta có bảng số liệu mẫu sau: Thu nhập 1 − 2 2 − 3 3 − 4 4 − 5 5 − 6 6 − 7 Số người 10 8 5 7 3 2 Thu nhập bình quân là.
A 3.4256 triệu đồng B 3.243 triệu đồng C 3.014 triệu đồng D 3.512 triệu đồng Câu 05.
Một cửa hàng cho rằng xác suất bán được hàng trong 1 tuần là 0,4. Nếu bán được hàng thì lợi
nhuận là 10 triệu đồng. Nếu không bán được hàng thì lỗ 1 triệu đồng. Phương sai của lợi nhuận là. A 40,6 B 5,39 C 27,84 D 29,04 Câu 06.
Giả sử tuổi thọ của hai linh kiện của một thiết bị có hàm mật độ xác suất
(2e−x−2y, x > 0, y > 0 f (x, y) = 0, trái lại P (X < 1, Y < 1) =? A 0, 6321 B 0, 7358 C 0, 5466 D 0, 2707 Câu 07.
Biến ngẫu nhiên (X,Y) có hàm mật độ xác suất:
( k(2x + y), 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 f (x, y) = 0, ngược lại. Tính P(X + Y < 1) và E(X)
Life is not a problem to be solved, but a reality to experienced 1
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 3 7 1 7 1 11 1 11 A và B và C và D và 5 18 3 18 3 18 4 18 Câu 08.
Giả sử chiều cao của sinh viên có phân phối Chuẩn. Để kiểm định giả thuyết chiều cao trung
bình của sinh viên thấp hơn 163cm, đo chiều cao của 100 sinh viên thì tính được giá trị quan sát là (-1,68).
Với mức ý nghĩa 5%, kết luận nào đúng? Cho t99 = 1, 645; t99 = 1, 96 0,05 0,025
A H0 : µ = 163, H1 : µ < 163. Ý kiến đúng
B H0 : µ > 163, H1 : µ ≤ 163. Ý kiến đúng.
C H0 : µ = 163, H1 : µ < 163. Ý kiến sai.
D H0 : µ = 163, H1 : µ > 163. Ý kiến đúng. Câu 09.
Cân (kg) 9 con gà xuất chuồng, kết quả như sau: 2,1; 1,8; 2,0; 2,3; 1,7; 1,5; 2,0; 2,2; 1,8.
Với độ tin cậy 95%, ước lượng cân nặng trung bình của gà khi xuất chuồng: A (1, 675; 2, 191) B (1, 702; 2, 164) C (1, 768; 2, 098) D (1, 737; 2, 129) Câu 10.
Khảo sát năng suất của một giống lúa tại một tỉnh thành được kết quả sau: Năng suất (tạ/hecta) 60-65 65-70 70-75 75-80 Số hecta 5 12 21 9
Xác định độ lệch chuẩn mẫu hiệu chỉnh của năng suất giống lúa trên: A 4, 51 B 3, 25 C 6, 23 D 4, 16
Câu 11. Có hai cốc trà sữa. Mỗi cốc có 8 viên trân châu đen và 2 viên trân châu trắng. Bạn chuyển ngẫu
nhiên 1 viên trân châu từ cốc của bạn sang cốc của em mình, sau đó chuyển trả lại 1 viên từ cốc của em
mình về cốc của bạn. Cuối cùng bạn hút ở mỗi cốc 1 viên trân châu. Tính xác suất để cả 2 viên trân châu
bạn hút đều là trân châu đen. A 0, 6873 B 0, 7056 C 0, 7231 D 0, 6371 Câu 12.
Thời gian một người được phục vụ ở một quán cà phê là một biến ngẫu nhiên có phân phối
mũ với kì vọng là 4 phút. Tính xác suất một người được phục vụ ít hơn 3 phút vào ít nhất 4 ngày trong 6 ngày tiếp theo. A 0, 4621 B 0, 3968 C 0, 4723 D 0, 3454 Câu 13.
Một hãng sản xuất bóng đèn đã đưa vào thử nghiệm để xác định tuổi thọ trung bình. Chọn
một mẫu gồm 20 bóng đèn cùng loại để thử nghiệm. Tuổi thọ của 20 bóng đèn được cho trong bảng sau (đơn vị nghìn giờ): Thời gian Số bóng đèn (5; 5,5] 3 (5,5; 6] 6 (6; 6,5] 7 (6,5; 7] 4
Giả sử tuổi thọ của bóng đèn tuân theo luật phân phối chuẩn. Hãy xác định khoảng ước lượng tuổi thọ
trung bình của bóng đèn với độ tin cậy 95%
Life is not a problem to be solved, but a reality to experienced 2
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập A (5, 235; 6, 191) B (5, 817; 6, 283) C (5, 512; 6, 223) D (5, 643; 6, 201) 1 1 Câu 14.
X là biến ngẫu nhiên có hàm mật độ xác suất: f (x) = cx + d, 0 ≤ x ≤ 1 và P X > = . 2 3 Tính d − c 1 −1 A B C −3 D 3 3 3 Câu 15.
Miền được tô đen ở hình trên được biểu diễn bởi: A Không có đáp án B (A.B) + (A.B) C (A.B).(A.B) D (A + B).(A + B) đúng.
Câu 16. Cho A, B là hai sự kiện xung khắc. Nhóm sự kiện nào sau đây tạo thành một nhóm đầy đủ? A A, A + B, B B A, A + B, B C A, A + B, B D A, B Câu 17.
Trọng lượng (g) của một loại sản phẩm là biến ngẫu nhiên có phân phối chuẩn. Kiểm tra ngẫu
nhiên 36 sản phẩm tính được trung bình mẫu x = 100 (g) và độ lệch mẫu hiệu chỉnh s=5. Với độ tin cậy
95%, độ chính xác của ước lượng khoảng tin cậy đối xứng cho trọng lượng trung bình của sản phẩm này là: A ε = 5 B ε = 1, 96 C ε = 1, 633 D ε = 0, 95 Câu 18.
Cho ba biến ngẫu nhiên độc lập X, Y, Z biết: X ∼ N(5; 4),Y ∼ P(3), Z ∼ B(6; 0, 3). Tính
phương sai của T = 4X + 3Y + Z + 1 A 50, 26 B 92, 26 C 26, 26 D 8, 26
Câu 19. Bốc ngẫu nhiên 15 quân bài từ bộ bài 52 cây. Biết rằng quân Át cơ đã được bốc. Tính xác suất ít
nhất hai quân Át được bốc. 413 373 473 313 A B C D 595 595 1190 595
Life is not a problem to be solved, but a reality to experienced 3
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Câu 20.
Biến ngẫu nhiên liên tục X có hàm phân phối xác suất là: 0, x ≤ 2 F(x) = a(x − 2)2, 2 < x ≤ 4 1, x > 4
Gọi b = P(2 ≤ X < 3). Tính ab 1 1 1 A B 1 C D 2 4 16 Câu 21.
Một người có 10 đôi giày khác nhau và trong lúc đi du lịch vội vã lấy ngẫu nhiên 4 chiếc. Tính
xác suất để trong 4 chiếc giày lấy ra có ít nhất một đôi. 224 3 13 99 A B C D 323 7 64 223 Câu 22.
Trong một kỳ thi, mỗi sinh viên phải thi 2 môn. Một sinh viên A ước lượng rằng: xác suất đạt
môn thứ nhất là 0,8. Nếu đạt môn thứ nhất thì xác suất đạt môn thứ hai là 0,6; nếu không đạt môn thứ
nhất thì xác suất đạt môn thứ hai là 0,3. Biết rằng sinh viên A thi đạt một môn, xác suất để sinh viên A đạt môn thứ hai là: A 0, 8421 B 0, 54 C 0, 38 D 0, 1579 Câu 23.
Quan sát ngẫu nhiên 400 trẻ sơ sinh, ta thấy có 218 bé trai. Với mức ý nghĩa 5%, có thể khẳng
định tỉ lệ sinh con trai và gái như nhau không?
A Tỉ lệ sinh con trai lớn hơn gái
B Tỉ lệ sinh con trai nhỏ hơn gái
C Tỉ lệ sinh con trai và gái có thể coi là như
D Tỉ lệ sinh con trai và gái là khác nhau nhau Câu 24.
Một hộp chứa 3 bi trắng, 7 bi đỏ và 15 bi xanh. Một hộp khác chứa 10 bi trắng, 6 bi đỏ và 9 bi
xanh. Lấy ngẫu nhiên từ mỗi hộp một bi. Tính xác suất để 2 viên bi lấy ra cùng màu. A 0, 19 B 0.27 C 0, 33 D 0, 42 Câu 25.
Tại một cửa hàng bán sách, trung bình 5 phút có 2 người vào thăm cửa hàng. Tính xác suất
trong 10 phút không quá 3 người vào cửa hàng. A 0.567 B 0.219 C 0.265 D 0.433 Câu 26.
Ba xạ thủ, mỗi người bắn một viên đạn vào mục tiêu với xác suất trúng đích của mỗi người là
0.6; 0.7; 0.8. Tìm xác suất để có đúng 2 người bắn trúng. A 0.376 B 0.188 C 0.452 D 0.254 Câu 27.
Khảo sát 179 sinh viên thì tổng thu trung bình đi làm thêm hàng tháng là 2,18 triệu đồng với
độ lệch tiêu chuẩn mẫu hiệu chỉnh là 0,64 triệu. Tìm khoảng tin cậy thu trung bình hàng tháng của sinh viên với mức ý nghĩa 7% A (2, 101; 2, 259) B (2, 093; 2, 267) C (2, 086; 2, 274) D (2, 057; 2, 303)
Life is not a problem to be solved, but a reality to experienced 4
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Câu 28. Trong mặt phẳng tọa độ Oxy . Ở góc phần tư thứ nhất ta lấy 2 điểm phân biệt; cứ thế ở các góc
phần tư thứ hai, thứ ba, thứ tư ta lần lượt lấy 3, 4, 5 điểm phân biệt (các điểm không nằm trên các trục
tọa độ). Trong 14 điểm đó ta lấy 2 điểm bất kỳ. Tính xác suất để đoạn thẳng nối hai điểm đó cắt hai trục tọa độ. A 0.264 B 0.743 C 0.253 D 0.088 Câu 29.
Điều tra 260 sinh viên thì có đến 179 sinh viên đi làm thêm. Nếu muốn độ chính xác tỉ lệ
sinh viên làm thêm không quá 5% với độ tin cậy 95%, ta cần tiến hành điều tra ít nhất bao nhiên sinh viên? A 572 sinh viên B 70 sinh viên C 330 sinh viên D 312 sinh viên Câu 30.
Tìm kích thước mẫu tối thiểu phải điều tra thêm để xác định chiều cao trung bình sinh viên
trong trường với độ tin cậy 5% và độ chính xác không quá 1cm, biết rằng điều tra 100 sinh viên của năm
trước thì độ lệch chuẩn hiệu chỉnh là 7,4cm. A 211 sinh viên B 111 sinh viên C 11 sinh viên D 311 sinh viên Câu 31.
Trọng lượng X (tính bằng gram) một loại trái câu có phân phối chuẩn N( 2
µ, σ ), với µ =
500(gram) và σ = 4 gam, trong đó trái cây loại 3 là những quả có trọng lượng dưới 495 gram. Lấy 1 trái
cây bất kì, tính tỉ lệ đó là trái cây loại 3. A 0.894 B 0.378 C 0.106 D 0.622
Câu 32. Trong một cuộc khảo sát, có 22.5% người tham gia dùng sản phẩm loại X, 50% người dùng sản
phẩm loại Y và 36.5% trong số những người dùng sản phẩm loại Y có dùng sản phẩm loại X. Tính xác
suất một người dùng Y, biết người đó không dùng X. A 0.13 B 0.22 C 0.27 D 0.41 Câu 33.
Một nhà máy sản xuất với tỷ lệ phế phẩm là 3%. Phải kiểm tra ít nhất bao nhiêu sản phẩm để
tỉ lệ gặp được phế phẩm lớn hơn 80%. A 52 B 54 C 51 D 53 Câu 34.
Xác suất có bệnh của những người chờ khám tại 1 bệnh viện là 62%. Khám cho 20 người đang
chờ, hỏi xác suất có ít hơn 11 người bị bệnh là bao nhiêu? A 0.124 B 0.157 C 0.190 D 0.231 Câu 35.
Nhu cầu hàng năm về loại hàng A là biến ngẫu nhiên liên tục X có hàm mật độ xác suất như
sau (đơn vị: ngàn sản phẩm)
( k(30 − x), 0 < x < 30 f (x) = 0, ngược lại
Tính nhu cầu trung bình hằng năm của mặt hàng A. A 10 B 7 C 16 D 13 Câu 36.
Biến ngẫu nhiên liên tục X có hàm mật độ là f (x) = ae−|x|. Tính xác suất để sau ba lần lặp lại
phép thử một cách độc lập có 2 lần X nhận giá trị trong khoảng (0; ln 5).
Life is not a problem to be solved, but a reality to experienced 5
Hỗ trợ sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập A 0.576 B 0.144 C 0.432 D 0.288
Câu 37. Một bài thi 20 câu trắc nghiệm, mỗi câu hỏi 4 phương án trả lời, trong đó chỉ duy nhất 1 phương 1
án đúng. Một câu làm đúng được 1 điểm, ngược lại nếu chọn sai sẽ bị trừ
điểm. Nếu điểm tính ra dưới 3
hoặc bằng điểm 0 thì sẽ được ghi nhận bằng 0. Xác suất để một sinh viên làm bài bằng cách chọn hú họa
cả bài thi được 0 điểm. A 0.731 B 0.622 C 0.617 D 0.507 Câu 38.
Đo số lượng bạch cầu trong máu của 170 trẻ em, ta tính được các đặc trưng mẫu: Trung bình
mẫu 11250 và độ lệch chuẩn mẫu (chưa hiệu chỉnh) S=2100. Tính ước lượng không chệch cho phương
sai của số lượng bạch cầu đó. A 4436095 B 436081 C 4410000 D 2106 Câu 39.
Cho biến ngẫu nhiên X và Y có bảng phân bố xác suất đồng thời như sau: X|Y 1 2 3 1 0,12 0,15 0,03 2 0,28 0,35 0,07 Tính E(XY) A 3, 24 B 2, 89 C 2, 56 D 3, 61 Câu 40.
Cho hàm mật độ xác suất của biến ngẫu nhiên liên tục X: ( 5e−|5x|, x > 0 f (x) = 0, ngược lại
Y là số nguyên lớn nhất không vượt quá X. Tính E(Y) A 0.00723 B 0.00846 C 0.00678 D 0.00543
Life is not a problem to be solved, but a reality to experienced 6
HANOI UNIVERSITY OF SCIENCE AND TECHNOLOGY
GIẢI ĐỀ CUỐI KỲ XSTK MI2020 [20171-20201] Tác giả:
Tài liệu tham khảo: Made by Team XSTK
• Giáo trình XSTK - Tống Đình Quỳ
• Bài giảng XSTK - Nguyễn Thị Thu Thủy
Hà Nội, 31 tháng 5 năm 2021 Mục lục
Đề 20171 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Lời giải . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Đề 20172 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Lời giải . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Đề 20173 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Lời giải . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
Đề 20181 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
Lời giải . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Đề 20182 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Lời giải . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
Đề 20183 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
Lời giải . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
Đề 20191 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
Lời giải . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
Đề 20192 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
Lời giải . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
Đề 20193 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
Lời giải . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
Đề 20201 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
Lời giải . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
Hỗ trợ học tập đại cương Xác suất thống kê Đề 1
ĐỀ THI CUỐI KỲ - 20171
Mã học phần: MI2020
Câu 1. Xác suất làm việc của một hệ thống trong khoảng thời gian xác định nào đó được gọi là xác
suất tin cậy (XSTC) của hệ thống đó.
a) Tính XSTC của một mạng gồm 2 linh kiện mắc nối tiếp cùng có XSTC là 0,95.
b) Mắc song song với mạng trên một mạng dự phòng gồm 2 linh kiện mắc nối tiếp cùng có XSTC là
0,94. Tính XSTC của mạng mới đó.
Câu 2. Một lô hàng gồm 16 sản phẩm loại A và 12 sản phẩm loại B. Chọn ngẫu nhiên ra 3 sản phẩm.
a) Tính xác suất để trong 3 sản phẩm đó có ít nhất 2 sản phẩm loại A.
b) Chọn tiếp ngẫu nhiên ra 3 sản phẩm trong số sản phẩm còn lại. Tính xác suất để trong số 3 sản
phẩm được chọn lần hai có ít nhất 1 sản phẩm loại A.
Câu 3. Theo điều tra của một hãng bảo hiểm ô tô tỷ lệ xe bị tai nạn trong năm là 0,15. Trong số xe bị
tai nạn có: 80% được bồi thường tai nạn bằng 20% giá trị xe, 12% được bồi thường bằng 60% giá trị
xe và 8% được bồi thường bằng 100% giá trị xe.
a) Hỏi trung bình phải bồi thường tai nạn bằng bao nhiêu cho một xe có giá trị 600 triệu đồng?
b) Đối với chiếc xe trên phải quy định phí bảo hiểm là bao nhiêu để hãng không bị lỗ?
(Chỉ kể chi phí bồi thường, không kể các chi phí khác).
Câu 4. Thống kê ở một vùng trong 500 xe ô tô đăng ký có 68 xe thể thao. Với độ tin cậy 95% hãy
xác định khoảng tin cậy đối xứng cho tỷ lệ xe thể thao ở vùng đó. Theo anh (chị) có cách nào để nâng
cao độ chính xác của khoảng tin cậy cho tỷ lệ trên?
Câu 5. Đo thời gian phản ứng (giây) đối với hai loại thuốc kích thích của 8 người tham gia thí nghiệm
(giả sử thời gian phản ứng đối với mỗi loại thuốc được coi là biến ngẫu nhiên có phân phối chuẩn), ta có bộ số liệu cặp: Thuốc 3,1 1,5 2,9 2,6 1,7 2,3 3,8 2,4 Thuốc 4,1 2,2 3,5 1,8 2,7 2,5 3,4 3,2
Với mức ý nghĩa α = 5%, có thể cho rằng thời gian phản ứng trung bình đối với 2 loại thuốc là như nhau hay không?
Chúc các bạn qua môn! 1
Hỗ trợ học tập đại cương Xác suất thống kê
Giải đề cuối kì 20171
Câu 1. Gọi Ai = {Linh kiện i hoạt động tốt}, i = 1, 2
a) Gọi A ={Mạng làm việc tốt} ⇒ P(A) = A1A2
⇒ P(A) = P(A1A2) = P(A1)P(A2) = 0, 95.0, 95 = 0, 9025 (do tính độc lập) b)
* Gọi B ={Mạng dự phòng hoạt động tốt}
Bi = {Linh kiện i của mạng dự phòng hoạt động tốt}, i = 1, 2 ⇒ P(B) = B1B2
⇒ P(B) = P(B1B2) = P(B1)P(B2) = 0, 94.0, 94 = 0, 883
* Gọi C = {Mạng mới làm việc tốt} ⇒ C = A + B
⇒ P(C) = P(A + B) = P(A) + P(B) − P(AB) = P(A) + P(B) − P(A)P(B)
= 0, 9025 + 0, 8836 − 0, 9025.0, 8836 = 0, 9887 Câu 2.
Xét phép thử ngẫu nhiên chọn ra 3 sản phẩm
Số kết cục đồng khả năng là: n = C3 = 3276 cách 28
a) Gọi Ai={Trong 3 sản phẩm có ít nhất 2 sản phẩm loại A}
Số kết cục thuận lợi cho A là: m = C2 .12 +C3 = 2000 cách 16 16 2000 500 ⇒ P(A) = = = 0, 1605 3276 819
b) Gọi Bi = {Trong 3 sản phẩm lần đầu lấy ra có i sản phẩm loại B}, i = 0, 1, 2, 3
Hệ {Bi} tạo thành hệ đầy đủ với: C3 20 C2 .12 40 16.C2 88 C3 55 P(B 16 16 12 12 0) = = ; P(B1) = = ; P(B2) = = ; P(B3) = = C3 117 C3 91 C3 273 C3 819 28 28 28 28
Gọi B = {Trong 3 sản phẩm lần 2 có ít nhất 1 sản phẩm loại A}
⇒ B = {Trong 3 sản phẩm lần 2 có 0 sản phẩm loại A}
Áp dụng công thức xác suất đầy đủ:
P(B) = P(B0)P(B|B0) + P(B1)P(B|B1) + P(B2)P(B|B2) + P(B3)P(B|B3) trong đó: C3 11 C3 33 P(B 12 11 0)P(B|B0) = = ; P(B1)P(B|B1) = = ; C3 115 C3 460 25 25 C3 6 C3 21 P(B 10 9 2)P(B|B2) = = ; P(B3)P(B|B3) = = . C3 115 C3 575 25 25
Chúc các bạn qua môn! 2
Hỗ trợ học tập đại cương Xác suất thống kê 20 11 40 33 88 6 55 21 ⇒ P(B) = . + . + . + . = 0, 0672 117 115 91 460 273 115 819 575
⇒ P(B) = 1 − P(B) = 1 − 0, 0672 = 0, 9328 Câu 3:
a) Gọi X là biến ngẫu nhiên chỉ chi phí bồi thường cho chiếc xe 600 triệu. X = {120, 360, 600} P(X = 120) = 0, 8 P(X = 360) = 0, 12 P(X = 600) = 0, 08
Ta có bảng phân phối xác suất: X 120 360 600 P 0,8 0,12 0,08
⇒ E(X) = 120.0, 8 + 360.0, 12 + 600.0, 08 = 187, 2
Vậy trung bình phải bồi thường tai nạn cho một xe có giá trị 600 triệu đồng là 187,2 triệu đồng.
b) Gọi x là phí bảo hiểm. Để không lỗ thì:
x − 0, 15.E(X ) ≥ 0 ⇔ x − 0, 15.187, 2 ≥ 0 ⇔ x ≥ 28, 08 triệu đồng Câu 4:
Gọi p là tỷ lệ xe thể thao ở vùng đó. Kiểm tra điều kiện:
n f = 500.0, 136 = 68 > 5; n(1 − f ) = 500.864 = 432 > 5. f − p √ - Chọn thống kê: Z = n.Z ∼ N(0, 1) p f (1 − f )
- Khoảng tin vậy đối xứng của xác suất p là: r r ! f (1 − f ) f (1 − f ) f − u ; f + u 1− α 1− α 2 n 2 n trong đó u = u 1− α
0,975 = 1, 96 được tra từ bảng phân phối chuẩn tắc. 2 m - Với n = 500; m = 68; f =
= 0, 136 suy ra khoảng tin cậy đối xứng của p là: n r r ! 0, 136(1 − 0, 136) 0, 136(1 − 0, 136) 0, 136 − 1, 96. ; 0, 136 + 1, 96. = (0, 1060; 0, 1660) 500 500
- Vậy với mức ý nghĩa 5% tỷ lệ xe thể thao ở vùng đó từ 10, 6% đến 16, 6%
Để nâng cao độ chính xác của khoảng tin cậy cho tỷ lệ trên cần tăng cỡ mẫu hoặc giảm độ tin cậy
(hoặc đồng thời cả hai). Câu 5:
Gọi X, Y lần lượt là thời gian phản ứng (giây) đối với hai loại thuốc kích thích, Ta có:
Chúc các bạn qua môn! 3
Hỗ trợ học tập đại cương Xác suất thống kê X ∼ N( 2 2 µ1; σ ); Y ∼ N( ) 2 µ2; σ2 n1 = n2 = 8
Đặt Z = X - Y, thiết lập hiệu zi = xi − yi, i = 1, 2, ..., 8: X 3,1 1,5 2,9 2,6 1,7 2,3 3,8 2,4 P 4,1 2,2 3,5 1,8 2,7 2,5 3,4 3,2 Z -1,0 -0,7 -0,6 0,8 -1,0 -0,2 0,4 -0,8
- Đặt giả thuyết H0 : µ = µ0;
đối thuyết H1 : µ 6= µ0 với µ0 = 0. Z − µ0 √
- Chọn tiêu chuẩn kiểm định: T =
n nếu H0 đúng. T ∼ (n − 1) S
- Với α = 0, 05, tra bảng phân phối Student ta được tn−1 = t7
= 2, 365. Miền bác bỏ giả thuyết H0 1− α 0,975 2 là: W = − ∪ tn−1 ; + = (− α ∞; −tn−1 ∞
∞; −2, 365) ∪ (2, 365; +∞) 1− α 1− α 2 2
- Từ số liệu đầu bài, tính toán ta được: n = 8; z = −0, 3875; s = 0, 6686 với µ0 = 0 suy ra giá trị quan sát là: z − µ √ 0 √ −0, 3875 − 0 tqs = n = 8 = −1, 6393 s 0, 6686 - Vì tqs = −1, 6393 /
∈ Wqs nên chưa có cơ sở bác bỏ giả thuyết H0, nghĩa là với số liệu này có thể cho
rằng thời gian phản ứng trung bình đối với 2 loại thuốc là như nhau hay với mức ý nghĩa 5%
Chúc các bạn qua môn! 4
Hỗ trợ học tập đại cương Xác suất thống kê Đề 1
ĐỀ THI CUỐI KỲ - 20172
Mã học phần: MI2020
Câu 1. Một hộp có n áo trắng và 2n áo xanh. Chia ngẫu nhiên các áo thành n nhóm (mỗi nhóm 3 áo).
a) Tính xác suất để trong mỗi nhóm đều có áo trắng. b) Áp dụng có n = 5.
Câu 2. Một xí nghiệp có 4 chiếc máy tiện với xác suất bị sự cố trong ngày của mỗi máy tương ứng là 0,01; 0,05; 0,1 và 0,1.
a) Trong một ngày nào đó theo dõi một máy. Tính xác suất để máy đó bị sự cố.
b) Khi theo dõi 2 máy thì có đúng 1 máy bị sự cố. Tính xác suất chiếc máy bị sự cố đó là máy thứ nhất.
Câu 3. Xét một phần tư hình tròn tâm O(0; 0) bán kính bằng a, kí hiệu OAB, với tọa độ tương ứng là A(a; 0) và B(0; a).
a) Trên đoạn OA lấy ngẫu nhiên một điểm C. Tìm phân phối xác suất của độ dài đoạn OC.
b) Dựng một đường đi qua C, vuông góc với OA và cắt cung tròn tại điểm D. Tính kỳ vọng và phương
sai của độ dài đoạn CD.
Câu 4. Tiến hành 120 phép đo như nhau, độc lập, thì thấy sự kiện A xuất hiện 42 lần.
a) Xác định khoảng tin cậy đối xứng 99% cho tỷ lệ xuất hiện A.
b) Tính xác suất để sai số ước lượng của tỷ lệ trên bé hơn 10% tần suất mẫu.
Câu 5. Cân 150 con vịt người ta thu được bộ số liệu sau: Khối lượng 1,25 1,50 1,75 2,00 2,25 2,50 2,75 3,00 Số lượng 2 6 24 35 39 24 14 6
Với mức ý nghĩa 5% có thể cho rằng khối lượng trung bình của lứa vịt trên lớn hơn 2 kg được không?
Chúc các bạn qua môn! 5
Hỗ trợ học tập đại cương Xác suất thống kê
Giải đề cuối kì 20172 Câu 1.
Xét phép thử chia ngẫu nhiên các áo thành n nhóm (mỗi nhóm 3 áo).
Tổng số kết cục đồng khả năng là: n = C3 .C3 ...C3 3n 3n−3 3
a) Gọi A= {Trong mỗi nhóm đều có áo trắng}
Số kết cục thuận lợi cho A là: m = n.C2 .(n − 1).C2 ...1.C2 2n 2n−2 2 (2n)! (2n − 2)! 2! n. .(n − 1). ...1. m n.C2 .(n − 1).C2 ...1.C2 2!(2n − 2)! 2!(2n − 4)! 2! ⇒ P(A) = = 2n 2n−2 2 = n C3 .C3 ...C3 (3n)! (3n − 3)! 3! 3n 3n−3 3 . ... 3!(3n − 3)! 3!(3n − 6)! 3! n!.(2n)! (2!)n n!(2n)! 3n = = 3n. = (3n)! (3n)! Cn3n (3!)n 35 81 b) Với n = 5: P(A) = = C5 1001 15 Câu 2.
a) Gọi Ai = {Máy theo dõi là máy i}, i = 1, 2, 3, 4
Hệ {Ai} tạo thành hệ đầy đủ với: 1
P(A1) = P(A2) = P(A3) = P(A4) = 4
Gọi H = {Máy bị sự cố}
Áp dụng công thức xác suất đầy đủ:
P(H) = P(A1)P(H|A1) + P(A2)P(H|A2) + P(A3)P(H|A3) + P(A4)P(H|A4) trong đó: P(H|A1) = 0, 01; P(H|A2) = 0, 05; P(H|A3) = 0, 1; P(H|A4) = 0, 1. 1 1 1 1 13
⇒ P(H) = .0, 01 + .0, 05 + .0, 1 + .0, 1 = = 0, 065 4 4 4 4 200
b) Hệ {A1A2, A1A3, A1A,A2A3, A2A4, A3A4} tạo thành hệ đầy đủ với: 1
P(A1A2) = P(A1A3) = P(A1A4) = P(A2A3) = P(A2A4) = P(A3A4) = 6
Chúc các bạn qua môn! 6
Hỗ trợ học tập đại cương Xác suất thống kê
Gọi K = {Có đúng 1 máy bị sự cố khi theo dõi 2 máy}
Áp dụng công thức xác suất đầy đủ:
P(K) = P(A1A2)P(k|A1A2) + P(A1A3)P(k|A1A3) + P(A1A4)P(k|A1A4) + P(A2A3)P(k|A2A3) +
P(A2A4)P(k|A2A4) + P(A3A4)P(k|A3A4) trong đó:
P(K|A1A2) = 0, 01.0, 95 + 0, 99.0, 05 = 0, 059
P(K|A1A3) = 0, 01.0, 90 + 0, 99.0, 1 = 0, 108
P(K|A1A4) = 0, 01.0, 90 + 0, 99.0, 1 = 0, 108
P(K|A2A3) = 0, 05.0, 9 + 0, 95.0, 1 = 0, 14
P(K|A2A4) = 0, 05.0, 9 + 0, 95.0, 1 = 0, 14
P(K|A3A4) = 0, 1.0, 9 + 0, 9.0, 1 = 0, 18 ⇒ P(K) = 0, 1225
Gọi C = {Trong 2 máy thì máy bị sự cố là máy thứ nhất}
⇒ CK = {Có đúng máy thứ nhất bị sự cố khi theo dõi 2 máy}
Áp dụng công thức xác suất đầy đủ:
P(CK) = P(A1A2)P(CK|A1A2) + P(A1A3)P(CK|A1A3) + P(A1A4)P(CK|A1A4) +
P(A2A3)P(CK|A2A3) + P(A2A4)P(CK|A2A4) + P(A3A4)P(CK|A3A4) trong đó:
P(CK)|A1A2) = 0, 01.0, 95 = 0, 0095
P(CK)|A1A3) = 0, 01.0, 90 = 0, 009
P(CK)|A1A4) = 0, 01.0, 90 = 0, 009 P(CK)|A2A3) = 0 P(CK)|A2A4) = 0 P(CK)|A3A4) = 0 11 ⇒ P(CK) = 2400 11 P(CK)
Xác suất cần tính là: P(C|K) = = 2400 = 0, 0374 P(K) 0, 1225 Câu 3.
a) Gọi X là độ dài đoạn OC thì X là biến ngẫu nhiên có phân phối đều, X ∼ U [0, a], Hàm mật độ xác suất của X: 1 , x ∈ [0, a] fX (x) = a 0, x / ∈ [0, a]
Chúc các bạn qua môn! 7
Hỗ trợ học tập đại cương Xác suất thống kê
b) Gọi Y là độ dài đoạn CD thì Y là biến ngẫu nhiên thỏa mãn điều kiện: √ ( a2 − x2, x ∈ [0, a] Y = 0, x / ∈ [0, a] +∞ a Z Z 1 p Kì vọng của Y: E(Y ) = Y fX (x)dx = a2 − x2dx a −∞ 0
Đặt x = a sint ⇒ dx = a costdt π π π 2 2 2 Z 1 Z 1 + cos 2t t sin 2t aπ E(Y ) = .a2. cos2 tdt = a dt = a + = a 2 2 4 4 0 0 0 +∞ a a Z Z 1 1 x3 2a2 Có: E(Y 2) = Y 2 f X (x)dx = (a2 − x2)dx = . a2x − = a a 3 3 − ∞ 0 0 2a2 a2 2 2 π 2 π
⇒ V (Y ) = E(Y 2) − E(Y 2) = − = − a2 3 16 3 16 Câu 4. 42
a) Gọi p là tỷ lệ cây cà phê có thu hoạch thấp. f =
= 0, 35. Kiểm tra điều kiện: 120 n f = 42 > 5; n(1 − f ) = 78 > 5 f − p √ - Chọn thống kê Z = n.Z ∼ N(0, 1) p f (1 − p)
- Khoảng tin vậy đối xứng của xác suất p là: r r ! f (1 − f ) f (1 − f ) f − u ; f + u 1− α 1− α 2 n 2 n trong đó α = 0, 01; u = u 1− α
0,995 = 2, 575 được tra từ bảng phân phối chuẩn. 2
- Với n = 120; m = 42; f = 0, 35 suy ra khoảng tin cậy đối xứng của p là: r ! 0, 35.0, 65 r 0,35.0,65 0, 35 − 2, 575. ; 0, 35 + 2, 575. = (0, 2379; 0, 4621) 120 120
Vậy với độ tin cậy 95%, tỷ lệ cây cà phê có thu hoạch thấp từ 23,79% đến 46,21% ε
b) Xác suất cần tính là: P(|p − p| < ε) = 2φ σ c p trong đó:
Chúc các bạn qua môn! 8
Hỗ trợ học tập đại cương Xác suất thống kê r 0,35.0,65 ε = 0, 1.0, 35 = 0, 035; σ = 0, 0435 c p = 120
⇒ P(|p − p| < ε) = 2φ (0, 8046) = 0, 602 Câu 5.
Gọi X là biến ngẫu nhiên chỉ khối lượng trung bình của lứa vịt trên. E(X ) = µ
- Đặt giả thuyết H0 : µ = µ0. Đối thuyết H1 : µ > µ0 với µ0 = 2 X − µ0 √
- Chọn tiêu chuẩn kiểm định: U =
n nếu H0 đúng. U ∼ N(0, 1) s
- Với α = 0, 05 tra bảng phân phối chuẩn tắc có u1− = u α
0,95 = 1, 65. Miền bác bỏ H0 là: Ws = (u1− ; + α ∞) = (1, 65; +∞)
- Từ số liệu đã cho, có: µ0 = 2; n = 150; x = 2, 185; s = 0, 3781 suy ra giá trị quan sát: x − µ √ 0 √ 2, 185 − 2 uqs = n = 150 = 5, 9925 s 0, 3781
- Vì uqs ∈ Ws nên bác bỏ H0, chấp nhận H1, nghĩa là có thể cho rằng khối lượng trung bình của lứa vịt
trên lớn hơn 2kg với mức ý nghĩa 5%.
Chúc các bạn qua môn! 9
Hỗ trợ học tập đại cương Xác suất thống kê Đề 1
ĐỀ THI CUỐI KỲ - 20173
Mã học phần: MI2020
Câu 1. Một lô hàng có 15 sản phẩm gồm 6 loại A, 5 loại B và 4 loại C. Chọn ngẫu nhiên (không hoàn lại) ra 4 sản phẩm.
a) Tính xác suất trong 4 sản phẩm đươc chọn có đúng 2 sản phẩm loại B.
b) Biết trong 4 sản phẩm được chọn có đúng 2 sản phẩm loại A. Tính xác suất để trong 4 sản phẩm
đó có đúng 1 sản phẩm loại C.
Câu 2. Một nhóm học sinh có 5 loại giỏi, 4 khá và 2 trung bình. Chọn ngẫu nhiên ra một nhóm gồm 2 học sinh.
a) Tính giá trị trung bình của số học sinh giỏi trong nhóm đó.
b) Biết trong nhóm 2 học sinh có ít nhất 1 loại khá. Tính xác suất để trong nhóm đó có đúng 1 học sinh giỏi.
Câu 3. Cho biến ngẫu nhiên X có hàm mật độ (phân phối Rayleigh) ( −x2 f (x) = A.e 4 x ≥ 0 0 x < 0 a) Tìm hằng số A.
b) Tính các đặc trưng định vị: E(X) và mod(X).
Câu 4. Số liệu dưới đây cho tỷ lệ phần trăm một hóa chất trong 11 mẫu một loại xi măng: Tỷ lệ (%) 6 15 8 8 6 9 17 18 4 8 10
Với độ tin cậy 95% hãy tìm ước lượng khoảng cho tỷ lệ phần trăm trung bình của loại hóa chất trên
(giả sử tỷ lệ đó là biến ngẫu nhiên tuân theo luật phân phối chuẩn).
Câu 5. Một mẫ gồm n = 64 sản phẩm có 4 sản phẩm lỗi. Có đủ bằng chứng để chấp nhận giá thuyết "p > 5%" được không?
Cho mức ý nghĩa α = 5%, p ký hiệu tỷ lệ sản phẩm lỗi.
Chúc các bạn qua môn! 10
Hỗ trợ học tập đại cương Xác suất thống kê
Giải đề cuối kỳ 20173 Câu 1.
Xét phép thử chọn ngẫu nhiên (không hoàn lại) ra 4 sản phẩm.
Số kết cục đồng khả năng là: n = C4 = 1365 cách 15
a) Gọi B ={Trong 4 sản phẩm được chọn có đúng 2 sản phẩm loại B}
Số kết cục thuận lợi cho B là: m = C2.C2 = 450 cách 5 10 m 450 30 ⇒ P(B) = = = n 1365 91
b) Gọi A ={Trong 4 sản phẩm được chọn có đúng 2 sản phẩm loại A}
Số kết cục thuận lợi cho A là: p = C2.C2 = 540 cách 6 9 p 540 36 ⇒ P(A) = = = n 1365 91
Gọi H ={Trong 4 sản phẩm đó có đúng 1 sản phẩm loại C} Xác suất cần tính là: P(AH) P(H|A) = P(A) trong đó: C2.C1.C1 20 P(AH) = 6 4 5 = C4 91 15 P(AH) 20 5 ⇒ P(H|A) = = 91 = P(A) 36 9 91 Câu 2.
a) Gọi X là biến ngẫu nhiên chỉ số học sinh giỏi trong số 2 người được chọn.
Gọi Ai ={Trong 2 người được chọn có i học sinh giỏi}, i={0,1,2} C2 3 P(X = 0) = P(A 6 0) = = C2 11 11 5.6 6 P(X = 1) = P(A1) = = C2 11 11 C2 2 P(X = 2) = P(A 5 2) = = C2 11 11
Chúc các bạn qua môn! 11
Hỗ trợ học tập đại cương Xác suất thống kê
Ta có bảng phân phối xác suất: X 0 1 2 P 3/11 6/11 2/11 3 6 2 10 ⇒ E(X) = 0. + 1. + 2. = 11 11 11 11
b) Gọi H ={Trong 2 người được chọn có ít nhất 1 học sinh khá} Xác suất cần tính là: P(A1H) P(A1|H) = P(H) trong đó: 5.4 4 P(A1H) = = C2 11 11 C2 34 P(H) = 1 − P(H) = 1 − 7 = C2 35 11 P(A 4 10 ⇒ 1H ) P(A 11 1|H ) = = = P(H) 34 17 35 Câu 3.
a) Vì f (x) là hàm mật độ xác suất nên: f (x) ≥ 0 ∀x (1) Z +∞ f (x)dx = 1 (2) −∞ −x2
(1) ⇔ A.e 4 ≥ 0 ⇔ A ≥ 0 (2): x2 1 − √ Đặt g(x) = √ √
e 2( 2)2 là hàm mật độ xác suất của BNN X có phân phối chuẩn. 2 2π √ X ∼ N(0; ( 2)2) x2 Z +∞ Z +∞ 1 − √ Z +∞ 1 −x2 ⇒ g(x)dx = √ √ e 2( 2)2 dx = √ e 4 dx = 1 −∞ −∞ 2 2π −∞ 2 π Z +∞ Z +∞ −x2 Z +∞ √ 1 −x2 √ Z +∞ 1 −x2 Có: f (x)dx = A.e 4 dx = A.2 π. √ e 4 dx = A π 2. √ e 4 dx −∞ 0 0 2 π 0 2 π 1 −x2
Do √ e 4 là hàm chẵn nên: 2 π Z +∞ 1 −x2 Z +∞ 1 −x2 2 √ e 4 dx = √ e 4 dx 0 2 π −∞ 2 π
Chúc các bạn qua môn! 12
Hỗ trợ học tập đại cương Xác suất thống kê Z +∞ Z +∞ 1 −x2 √ Z +∞ 1 −x2 √ ⇒ f (x)dx = √ e 4 dx = A π √ e 4 dx = A π −∞ 0 2 π −∞ 2 π Z +∞ √ 1 ⇒
f (x)dx = 1 ⇔ A π = 1 ⇔ A = √ (TM) −∞ π Vậy: 1 −x2 √ e 4 , x ≥ 0 f (x) = π 0, trái lại Z +∞ Z +∞ 1 −x2 Z +∞ −2 −x −x2 −2 Z +∞ −x2 2 b) E(X ) = x f (x)dx = √ xxe 4 dx = √ e 4 dx = √ d(e 4 ) = √ −∞ 0 π 0 π 2 π 0 π
Hàm mật độ xác suất có: −x −x2 √ e 4 , x ≥ 0 f 0(x) = 2 π 0, trái lại
đổi dấu sang âm khi đi qua x = 0, do đó đạt cực đại tại điểm này, nên modX = 0
Câu 4. Gọi X là biến ngẫu nhiên chỉ tỷ lệ phần trăm một hóa chất trong các mẫu xi măng. X ∼ N( 2 µ ; σ ).E(X ) = µ X − µ √ - Chọn thống kê T =
n. Vì n = 11 < 30 nên T có phân phối Student với n − 1 bậc tự do s
- Sử dụng khoảng tin cậy đối xứng cho E(X ) = µ s s
x − tn−1 . √ ; x + tn−1 . √ 1− α 1− α 2 n 2 n trong đó tn−1 = t10
= 2, 228 được xác định từ bảng phân phối Student. 1− α 0,975 2
- Tính toán ta được: x = 9, 9091; s = 4, 6788; n = 11. Khoảng tin cậy đối xứng là: 4, 6788 4, 6788 9, 9091 − 2, 228 √ ; 9, 9091 + 2, 228 √ = (6, 77; 13, 05) 11 11
- Vậy với độ tin cậy 95%, tỷ lệ phần trăm trung bình một hóa chất trong các mẫu xi măng từ 6, 77% đến 13, 05%.
Chúc các bạn qua môn! 13
Hỗ trợ học tập đại cương Xác suất thống kê Câu 5.
Gọi p là tỷ lệ sản phẩm lỗi
- Đặt giả thuyết H0 : p = p0. Đối thuyết H1 : p > p0 với p0 = 0, 05 f − p0 √
- Chọn tiêu chuẩn kiểm định: U = n nếu H p 0 đúng. U ∼ N(0; 1) p0(1 − p0) - Với α = 0, 05, u1− = u α
0,95 = 1, 645 tra từ bảng phân phối chuẩn tắc. Miền bác bỏ H0 là: Ws = (u1− ; + α ∞) = (1, 645; +∞) m 4
- Từ số liệu đề bài, ta có: n = 64; m = 4 ⇒ f = =
= 0, 0625 suy ra giá trị quan sát: n 64 f − p √ 0 √ 0, 0625 − 0, 05 uqs = n = 64 = 0, 4588 p p p0(1 − p0) 0, 05(1 − 0, 05) - Vì uqs /
∈ Ws nên chưa đủ cơ sở bác bỏ giả thuyết H0, nghĩa là có đủ bằng chứng để chấp nhận giả thuyết "p > 5%".
Chúc các bạn qua môn! 14
Hỗ trợ học tập đại cương Xác suất thống kê Đề 1
ĐỀ THI CUỐI KỲ - 20181
Mã học phần: MI2020
Câu 1. Ở một địa phương đàn ông chiếm 55% dân số. Theo thống kê tỷ lệ đàn ông bị bạch tạng là
0,4%, còn tỷ lệ trên của đàn bà là 0,32%.
a) Tìm tỷ lệ người bị bệnh bạch tạng ở địa phương đó.
b) Gặp ngẫu nhiên một người bị bạch tạng, tính xác suất đó là đàn ông.
Câu 2. Một máy đếm người vào một siêu thị có tỷ lệ đếm sót là 0,018. Giả sử trong vòng 1 giờ nào
đó có 500 khách vào siêu thị.
a) Tính kỳ vọng và phương sai của số người được máy đếm trong số 500 người nói trên.
b) Tính xác suất để máy này đếm sót từ 6 đến 10 người trong số 500 người đó.
Câu 3. Một linh kiện điện tử có thời gian hoạt động X là biến ngẫu nhiên có phân phối mũ với hàm
mật độ của X là: f (x) = λ .e−λ.x, x > 0.
a) Xác định phân phối xác suất cho thời gian hoạt động của một mạng gồm 2 linh kiện loại trên mắc song song.
b) Tính kỳ vọng và phương sai của thời gian hoạt động của mạng đó.
Câu 4. Ở một trung tâm giống cây trồng, theo dõi 3070 cây cà phê thì có 1135 cây cho thu hoạch thấp.
a) Với độ tin cậy 95% hãy xác định khoảng tin cậy cho tỷ lệ cây cà phê có thu hoạch thấp.
b) Tần suất cà phê có thu hoạch thấp có là ước lượng không chệch của tỷ lệ cây cho thu hoạch thấp không? Tại sao?
Câu 5. Theo dõi thời gian bắt đầu có tác dụng của một loại thuốc trên một nhóm bệnh nhân trước và
sau khi mổ dạ dày, ta thu được bộ số liệu (giả sử thời gian trên có phân phối chuẩn): Bệnh nhân 1 2 3 4 5 6 7 8 Trước mổ 44 51 52 55 66 68 70 71 Sau mổ 52 64 60 74 55 67 75 65
Hỏi thời gian tác dụng của thuốc trước và sau mổ có khác nhau không với mức ý nghĩa 1%?
Phụ lục: trích Bảng hàm phân phối chuẩn x 1,282 1,645 1,96 2 2,576 3 Φ(x) 0,90 0,95 0,975 0,9772 0,995 0,9987
Hàm Laplace φ (x) = Φ(x) - 0,5.
Chúc các bạn qua môn! 15
Hỗ trợ học tập đại cương Xác suất thống kê
Giải đề cuối kỳ 20181 Câu 1.
Gọi A1 ={Gặp được đàn ông}; A2 ={Gặp được đàn bà}
Hệ A1; A2 tạo thành hệ đầy đủ với: P(A1) = 0, 55; P(A2) = 0, 45
a) Gọi A ={Gặp được người bị bạch tạng}
Áp dụng công thức xác suất đầy đủ:
P(A) = P(A1)P(A|A1) + P(A2)P(A|A2) trong đó:
P(A|A1) = 0, 4; P(A|A2) = 0, 32
⇒ P(A) = 0, 55.0, 4 + 0, 45.0, 32 = 0, 364
b) Xác suất cần tính là: P(A1A) P(A1)P(A|A1) 0, 55.0, 4 P(A1|A) = = = = 0, 6044 P(A) P(A) 0, 364 Câu 2.
Gọi X là biến ngẫu nhiên chỉ số người do máy đếm được. X ∼ B(n; p) với n = 500; p = 0, 982
a) E(X ) = np = 500.0, 982 = 491 người
V (X ) = np(1 − p) = 500.0, 982 = 0, 018 = 8, 838
b) Sự kiện Máy này đếm sót từ 6 đến 10 người trong số 500 người tương đương với máy đếm được
490 đến 494người trong số 500 người đó. Xác suất cần tính là: 494 P(490 ≤ X ≤ 494) = ∑ Ck .
500 0, 982k.0, 018500−k = 0, 5936 k=490 Câu 3.
a) Gọi X1, X2 lần lượt là biến ngẫu nhiên chỉ thời gian hoạt động của 2 linh kiện trong mạch.
Gọi Y là biến ngẫu nhiên chỉ thời gian hoạt động của mạng lắp song song. Khi đó ta có: Y = max(X1, X2) > 0
Chúc các bạn qua môn! 16
Hỗ trợ học tập đại cương Xác suất thống kê Có:
FY (y) = P(Y < y) = P(X1 < y; X2 < y) = P(X1 < y)P(X2 < y) (do tính độc lập) Z y 2 Z y 2 = fX (x)dx = λ e−λ xdx = (1 − e−λ y)2 −∞ −∞
Vậy ta có hàm phân phối xác suất: ( (1 − e−λy)2, y > 0 FY (y) = 0, trái lại
b) Từ hàm phân phối xác suất, ta có hàm mật độ:
( 2λe−λy (1 − e−λy), y > 0 fY (y) = 0, trái lại Z +∞ Có: Hàm Gamma: Γ(z) = xz−1e−xdx 0 Z +∞ Z +∞ Z +∞ 2 1 3 E(Y ) = y fY (y)dy = 2λ ye−λ ydy − 2λ ye−2λ ydy = Γ(2) − Γ(2) = −∞ 0 0 λ 2λ 2λ Z +∞ Z +∞ Z +∞ 2 1 7 E(Y 2) = y2 fY (y)dy = 2λ y2e−λ ydy − 2λ y2e−2λ ydy = Γ(3) − Γ(3) = −∞ 0 0 λ 2 4λ 2 2λ 2 7 9 5
⇒ V (Y ) = E(Y 2) − [E(Y )]2 = − = 2λ 2 4λ 2 4λ 2 Câu 4. 1135
a) Gọi p là tỷ lệ cây cà phê có thu hoạch thấp. f =
= 0, 3697. Kiểm tra điều kiện: 3070
n f = 1135; n(1 − f ) = 1935 > 5 f − p √ - Chọn thống kê Z = n. Z ∼ N(0; 1) p f (1 − f )
- Khoảng tin cậy đối xứng của xác suất p là: r r f (1 − f ) f (1 − f ) ( f − u ; f + u ) 1− α 1− α 2 n 2 n trong đó α = 0, 05, u = u 1− α
0,975 = 1, 96 được tra từ bảng phân phối chuẩn. 2
- Với n = 3070, m = 1135, f = 0, 3697 suy ra khoảng tin cậy đối xứng của p là: r 0,3697.0,6303 r 0,3697.0,6303 0, 3697 − 1, 96. ; 0, 3697 + 1, 96. = (0, 3526; 0, 3868) 3070 3070
Vậy với độ tin cậy 95% tỷ lệ cây cà phê có thu hoạch thấp từ 35, 26% đến 38, 68% m b) Có: f = mà m ∼ B(n; p) n E(m) ⇒ E( f ) =
= p nên f là ước lượng không chệch của p. n
Chúc các bạn qua môn! 17
Hỗ trợ học tập đại cương Xác suất thống kê Câu 5.
Gọi X , Y lần lượt là thời gian bắt đầu có tác dụng của một loại thuốc trước và sau khi mổ dạ dày. Ta có: X ∼ N( 2 2 µ1; σ ); Y ∼ N( ).n 1 µ2; σ2 1 = n2 = 8
Đặt Z = X −Y , thiết lập hiệu zi = xi − yi, i = 1, 2, ..., 8: X 44 51 52 55 66 68 70 71 Y 52 64 60 74 55 67 75 65 Z -8 -13 -8 -19 11 1 -5 6
- Đặt giả thuyết H0: µ = µ0; đối thuyết H1: µ 6= µ0 với µ0 = 0. Z − µ0 √
- Chọn tiêu chuẩn kiểm định: T =
n nếu H0 đúng. T ∼ T (n − 1) s
- Với α = 0, 01 Tra bảng phân phối Student ta được tn−1 = t7
= 3, 499. Miền bác bỏ giả thuyết H0 1− α 0,995 2 là: W = − ∪ tn−1 ; + = (− α ∞; −tn−1 ∞
∞; −3, 499) ∪ (3, 499; +∞) 1− α 1− α 2 2
- Từ số liệu đầu bài, tính toán ta được: n = 8; z = −4, 375; s = 9, 913 với µ0 = 0 suy ra giá trị quan sát: z − µ √ √ 0 −4, 375 − 0 tqs = n = 8 = −1, 2483 s 9, 913 - Vì tqs = −1, 2483 /
∈ Wqs nên chưa có cơ sở bác bỏ giả thuyết H0, nghĩa là số liệu này có thể cho rằng
thời gian tác dụng của thuốc trước và sau mổ là như nhau với mức ý nghĩa 1%.
Chúc các bạn qua môn! 18
Hỗ trợ học tập đại cương Xác suất thống kê Đề 1
ĐỀ THI CUỐI KỲ - 20182
Mã học phần: MI2020
Câu 1. Cho 3 sự kiện A, B, C độc lập từng đôi (2 sự kiện bất kỳ luôn độc lập với nhau) thỏa mãn:
P(A) = P(B) = P(C) = p và P(ABC) = 0. a) Tính P(A.B.C), P(A.B.C).
b) Tìm giá trị p lớn nhất có thể có.
Câu 2. Một nhà máy có hai phân xưởng cùng sản xuất bóng đèn. Số bóng đèn do phân xưởng 2 sản
xuất gấp 2 lần số bóng đèn do phân xưởng 1 sản xuất. Tỷ lệ phế phẩm của 2 phân xưởng tương ứng là
0,005 và 0,008. Lấy ngẫu nhiên 1 bóng đèn của nhà máy để kiểm tra thì thấy là phế phẩm. Tính xác
suất bóng đèn đó do phân xưởng 2 sản xuất.
Câu 3. Có hai lô hàng I và II, mỗi lô chứa rất nhiều sản phẩm. Tỉ lệ sản phẩm loại A có trong hai lô
I và II lần lượt là 70% và 80%. Lấy ngẫu nhiên từ mỗi lô 2 sản phẩm.
a) Tính xác suất để số sản phẩm loại A lấy từ lô I lớn hơn số sản phẩm loại A lấy từ lô II.
b) Gọi X là số sản phẩm loại A có trong 4 sản phẩm được lấy ra. Tìm kỳ vọng và phương sai của X.
Câu 4. Khảo sát trọng lượng X(kg) của 200 con lợn xuất chuồng ta được bảng số liệu sau: X(kg) [85-95) [95-105) [105-115) [115-125) [125-135) [135-145) Số lợn 10 30 45 80 30 5
Với độ tin cậy 90% hãy ước lượng khoảng cho trọng lượng trung bình của đàn lợn xuất chuồng.
Câu 5. Với số liệu ở câu 4 và mức ý nghĩa 5%, liệu có thể khẳng định rằng tỷ lệ lợn xuất chuồng có
trọng lượng thấp hơn 115kg là ít hơn 50% hay không?
Phụ lục: trích Bảng phân phối chuẩn x 1,282 1,645 1,96 2 2,576 3 Φ(x) 0,90 0,95 0,975 0,9772 0,995 0,9987
Hàm Laplace φ (x) = Φ(x) − 0, 5.
Chúc các bạn qua môn! 19
Hỗ trợ học tập đại cương Xác suất thống kê
Giải đề cuối kì 20182 Câu 1: a,
• P(ABC) = P(AB) − P(ABC) = P(AB) = P(A).P(B) = p2
• P(A B C) = 1 − P(A + B +C)
= 1 − [P(A) + P(B) + P(C) − P(AB) − P(AC) − P(BC) + P(ABC)] = 1 − 3p + 3p2 b,
• P(AB C) = P(A) − P(ABC) − P(ABC) − P(ABC) = p − 2p2 Vậy: • P(ABC) = 0
• P(ABC) = P(ABC) = P(ABC) = p2
• P(AB C) = P(ABC) = P(A BC) = p − 2p2 • P(A B C) = 1 − 3p + 3p2 0 ≤ p2 ≤ 1 1 1
Điều kiện: Các xác suất thuộc [0;1] ⇔ 0 ≤ p − 2p2 ≤ 1 ⇔ 0 ≤ p ≤ ⇒ pmax = 2 2
0 ≤ 1 − 3p − 3p2 ≤ 1 Câu 2:
Gọi H = {Sản phẩm đó là phế phẩm}
Gọi Ai = {Sản phẩm đó do phân xưởng i sản xuất}, i = {1, 2}
Hệ {Ai} tạo thành hệ đầy đủ với: 1 ( 2P(A P(A 1) = P(A2) 1) = ⇔ 3 P(A 2 1) + P(A2) = 1 P(A 2) = 3
Áp dụng công thức xác suất đầy đủ:
P(H) = P(A1)P(H|A1) + P(A2)P(H|A2) với: P(H|A1) = 0, 005; P(H|A2) = 0, 008 1 2
⇒ P(H) = .0, 005 + .0, 008 = 0, 007 3 3 Xác suất cần tính là: 2 P(A .0, 008 2H ) P(A2)P(H|A2) 16 P(A 3 2|H ) = = = = P(H) P(H) 0, 007 21
Chúc các bạn qua môn! 20
Hỗ trợ học tập đại cương Xác suất thống kê Câu 3:
Gọi X1, X2 lần lượt là số sản phẩm loại A được lấy từ lô hàng I và II. X1 ∼ B(2; 0, 7); X2 ∼ B(2; 0, 8)
a, Xác suất cần tính là:
P(X1 > X2) = P(X1 = 1, X2 = 0) + P(X1 = 2, X2 = 0) + P(X1 = 2, X2 = 1)
= P(X1 = 1)P(X2 = 0) + P(X1 = 2)P(X2 = 0) + P(X1 = 2)P(X2 = 1) (Do tính độc lập) = C12.0,71.0,31.C0. . . 2 0, 80.0, 22 + C2 2 .0, 72.0, 30.C0 2 0, 80.0, 22 + C2 2 .0, 72.0, 30.C0 2 0, 81.0, 21 = 0, 1932
b, X là số sản phẩm loại A có trong 4 sản phẩm được lấy ra. ⇒ X = X1 + X2 Do tính độc lập nên:
• E(X ) = E(X1 + X2) = E(X1) + E(X2) = 2.0, 7 + 2.0, 8 = 3
• V (X ) = V (X1 + X2) = V (X1) +V (X2) = 2.0, 7.0, 3 + 2.0, 8.0, 2 = 0, 74 Câu 4:
- Gọi X là trọng lượng lợn trong trại nuôi. X 2 ∼ N(µ , σ ); E(X ) = µ X − µ √ - Chọn thống kê: U =
n. Vì n = 200 > 30 nên thống kê U ∼ N(0; 1) s
- Khoảng tin cậy đối xứng cho E(X ) = µ là: s 1 s1
x − u1−α .√ ; x + u1−α .√ 2 n1 2 n1
trong đó, α = 0, 1; u1−α = u0,95 = 1, 645 được tra từ bảng phân phối chuẩn tắc. 2
- Tính toán ta được: x = 115, 25; s1 = 11, 4276; n1 = 200. Khoảng tin cậy đối xứng: 11, 4276 11, 4276 115, 25 − 1, 645. √ ; 115, 25 + 1, 645. √ = (113, 9208; 116, 5792) 200 200
- Với độ tin cậy 90%, trọng lượng trung bình của đàn lợn xuất chuồng từ 113,9208 đến 116,5792 kg. Câu 5:
- Gọi p là tỷ lệ lợn xuất chuồng có trọng lượng thấp hơn 115kg.
- Đặt giả thuyết H0 : p = p0. Đối thuyết H1 : p < p0 với p0 = 0, 5. f − p0 √
- Chọn tiêu chuẩn kiểm định: U = n nếu H p
0 đúng. Vì n. p0 = n(1 − p0) = 200.0, 5 = p0(1 − p0)
100 khá lớn nên U ∼ N(0; 1) - Với α = 0, 05; u1− = u α
0,95 = 1, 645 tra từ bảng phân phối chuẩn tắc. Miền bác bỏ H0 là: Ws = (∞; −u1− ) = ( α ∞; −1, 645) m 85
- Từ số liệu đề bài ta có: n = 200; m = 85 ⇒ f = =
= 0, 425 suy ra giá trị quan sát: n 200 f − p √ √ 0 0, 425 − 0, 5 uqs = n = 200 = −2, 21 p p 0, 5(1 − 0, 5) 0(1 − p0)
- Vì uqs ∈ Ws nên bác bỏ giá thuyết H0, nghĩa là có thể khẳng định rằng tỷ lệ lợn xuất chuồng có trọng
lượng thấp hơn 115kg là ít hơn 50% với mức ý nghĩa 5
Chúc các bạn qua môn! 21
Hỗ trợ học tập đại cương Xác suất thống kê Đề 1
ĐỀ THI CUỐI KỲ - 20183
Mã học phần: MI2020
Câu 1. Có một nhóm 4 sinh viên, mỗi người có một chiếc mũ giống hệt nhau để trên giá. Khi ra khỏi
phòng, mỗi người lấy ngẫu nhiên một chiếc mũ để đội. Tính xác suất để:
a) Sinh viên thứ nhất và sinh viên thứ ba lấy đúng mũ của mình.
b) Có ít nhất một sinh viên lấy đúng mũ của mình.
Câu 2. Một kiện hàng có 10 sản phẩm, trong đó có 7 sản phẩm loại I và 3 sản phẩm loại II. Tiền lãi
khi bán được mỗi sản phẩm loại I là 50 nghìn đồng, mỗi sản phẩm loại II là 20 nghìn đồng.
a) Ngày thứ nhất lấy ngẫu nhiên từ kiện hàng ra 3 sản phẩm và đã bán hết cả 3 sản phẩm đó. Tìm kỳ
vọng của số lãi thu được.
b) Ngày thứ hai lấy ngẫu nhiên từ kiện hàng ra 2 sản phẩm. Tính xác suất để thu được 100 nghìn đồng
tiền lãi khi bán 2 sản phẩm này.
Câu 3. Cho biến ngẫu nhiên hai chiều liên tục (X .Y ) có hàm mật độ xác suất là: (
k x2, nếu−1 ≤ x ≤ 1,0 ≤ y ≤ x2, fX,Y (x, y) = 2 0, nếu trái lại. 1 a) Tìm k. b) Tính P Y ≤ 4
Câu 4. Một công ty dự định mở một siêu thị tại khu dân cư A. Để đánh giá khả năng mua hàng của
khách hàng tại khu vực này, người ta đã điều tra ngẫu nhiên thu nhập trong một tháng của 100 gia
đình và thu được bảng số liệu sau: Thu nhập (triệu đồng) 34,0 34,5 35,0 35,5 36,0 36,5 37,0 37,5 Số gia đình 5 10 15 20 29 10 6 5
a) Theo bộ phận tiếp thị thì chỉ nên mở siêu thị tại A nếu thu nhập trung bình của các gia đình phải
lớn hơn 35,5 triệu đồng/tháng. Với mức ý nghĩa 5%, hãy cho biết có nên mở siêu thị tại khu dân cư A hay không?
b) Tìm khoảng tin cậy cho tỷ lệ các gia đình có thu nhập ≥ 35,5 triệu đồng/tháng với độ tin cậy 95%.
Câu 5. Điều tra ngẫu nhiên thu nhập của 100 hộ gia đình ở khu dân cư B thấy thu nhập bình quân là
35,8 triệu đồng/tháng và độ lệch chuẩn mẫu hiệu chỉnh là 1,1055 triệu đồng. Với mức ý nghĩa 5%, có
thể kết luận thu nhập bình quân ở khu dân cư B cao hơn ở khu dân cư A (với số liệu câu 4) hay không?
Phụ lục: trích Bảng phân phối chuẩn x 1,000 1,585 1,645 1,960 2,377 2,575 Φ(x) 0,8413 0,9429 0,9500 0,9750 0,9933 0,9950
Chúc các bạn qua môn! 22
Hỗ trợ học tập đại cương Xác suất thống kê
Giải đề cuối kì 20183 Câu 1:
a, Xét phép thử mỗi người lấy ngẫu nhiên một chiếc mũ để đội.
• Số kết cục đồng khả năng là: n = 4! = 24 cách
• Gọi A = {Sinh viên thứ nhất và thứ ba lấy đúng mũ của mình}
• Số kết cục thuận lợi cho A là: m = 1.1.2.1 = 2 cách m 2 1 ⇒ P(A) = = = n 24 12
b, Gọi B = {Có ít nhất một sinh viên lấy đúng mũ của mình}
Gọi Ai = {Sinh viên thứ i lấy đúng mũ của mình}, i = {1,2,3,4} Xác suất cần tính là: P(B) = P(A1 + A2 + A3 + A4) 4
= ∑ P(Ai) − P(A1A2) − P(A1A3) − P(A1A4) − P(A2A3) − P(A2A4) − P(A3A4) i=1
+ P(A1A2A3) + P(A1A2A4) + P(A1A3A4) + P(A2A3A4) − P(A1A2A3A4) Trong đó: 1
• P(A1) = P(A2) = P(A3) = P(A4) = 4 1.1.2.1 1
• P(A1A2) = P(A1A3) = P(A1A4) = P(A2A3) = P(A2A4) = P(A3A4) = = 24 12 1.1.1.1 1
• P(A1A2A3) = P(A1A2A4) = P(A1A3A4) = P(A2A3A4) = = 24 24 1.1.1.1 1 • P(A1A2A3A4) = = 24 24 1 1 1 1 5 ⇒ P(B) = 4. − 6. + 4. − = 4 12 24 24 8 Câu 2:
a, Gọi X là biến ngẫu nhiên chỉ số tiền lãi thu được. X = {60, 90, 120, 150}
Gọi Ai = {Trong ngày đầu bán được i sản phẩm loại I}, i = {0, 1, 2, 3} C3 1 • P(X = 60) = P(A 3 0) = = C3 120 10 7.C2 7 • P(X = 90) = P(A 3 1) = = C3 40 10 C2.3 21 • P(X = 120) = P(A 7 2) = = C3 40 10 C3 7 • P(X = 150) = P(A 7 3) = = C3 24 10
Chúc các bạn qua môn! 23
Hỗ trợ học tập đại cương Xác suất thống kê
Ta có bảng phân phối xác suất: X 60 90 120 150 P 1/120 7/40 21/40 7/24 1 21 7 ⇒ E(X) = 60. + 120. + 150. = 123 120 40 24
b, Gọi A = {Ngày thứ hai thu được 100 nghìn đồng tiền lãi khi bán 2 sản phẩm}
Hệ {Ai} tạo thành hệ đầy đủ.
P(A) = P(A0)P(A|A0) + P(A1)P(A|A1) + P(A2)P(A|A2) + P(A3)P(A|A3) 1 C2 7 C2 21 C2 7 C2 = . 7 + . 6 + . 5 + . 4 120 C2 40 C2 40 C2 24 C2 7 7 7 7 7 = 15 = 0, 4667 Câu 3:
a, Ta giải hệ phương trình: ( k −1 ≤ x ≤ 1 k ≥ .x2 ≥ 0, với 0 2 0 ≤ y ≤ x2 1 x2 ∞ ∞ ⇒ Z Z k ⇒ k = 5 (Thoả mãn) Z Z k dx .x2 dy = 1 .x2 dx dy = 1 2 2 −1 0 −∞ −∞ ( 5 −1 ≤ x ≤ 1 .x2, với ⇒ fX,Y (x, y) = 2 0 ≤ y ≤ x2 0, trái lại
b, Ký hiệu D là miền trên đó fX,Y (x, y) 6= 0 D = {(x, y) ∈ 2
R | − 1 ≤ x ≤ 1; 0 ≤ y ≤ x2} 1 1 2 x2 1 4 1 ZZ Z Z 5 Z Z 5 ⇒ P Y ≤ = fX,Y (x, y) = 2. dx .x2 dy + 2. dx .x2 dy 4 2 2 D∩(y≤ 1 ) 0 0 1 0 4 2 1 2 1 Z 5 Z 5 = 2. .x4 dx + 2. .x2 dx 2 8 0 1 2 = 0, 3958
Chúc các bạn qua môn! 24
Hỗ trợ học tập đại cương Xác suất thống kê Câu 4:
a, Gọi X là biến ngẫu nhiên chỉ thu nhập trong một tháng của các hộ gia đình tại A. E(X ) = µ1
- Đặt giả thuyết H0 : µ1 = µ0. Đối thuyết H1 : µ1 > µ0 với µ0 = 35, 5 X − µ0 √
- Chọn tiêu chuẩn kiểm định: U =
n nếu H0 đúng. U ∼ N(0; 1) s
- Với α = 0, 05 tra bảng phân phối chuẩn tắc, có u1− = u α
0,95 = 1, 65. Miền bác bỏ H0 là: Ws = (u1− ; + α ∞) = (1, 65; +∞)
- Từ số liệu đã cho, có: µ0 = 35, 5; n1 = 100; x1 = 35, 685; s1 = 0, 8547 suy ra giá trị quan sát: x √ 1 = µ0 √ 35, 685 − 35, 5 uqs = n1 = 100 = 2, 1645 s1 0, 8547
- Vì uqs ∈ Ws nên bác bỏ H0, chấp nhận H1, nghĩa là có nên mở siêu thị tại khu dân cư A với mức ý nghĩa 5%.
b, Gọi p là tỷ lệ các gia đình có thu nhập ≥ 35,5 triệu đồng/tháng ở khu A. Kiểm tra điều kiện:
n1 f = 100.0, 7 = 70 > 5; n1(1 − f ) = 100.0, 3 = 30 > 5 f − p √ - Chọn thống kê: Z = n. Z p ∼ N(0; 1) f (1 − f )
- Khoảng tin cậy đối xứng của xác suất p là: r r ! f (1 − f ) f (1 − f ) f − u1−α ; f + u1−α 2 n 2 n
trong đó u1−α = u0,975 = 1, 96 được tra từ bảng phân phối chuẩn tắc. 2 m - Với n1 = 100; m = 70; f =
= 0, 7 suy ra khoảng tin cậy đối xứng của p là: n1 r r ! 0, 7(1 − 0, 7) 0, 7(1 − 0, 7) 0, 7 − 1, 96. ; 0, 7 + 1, 96. = (0, 6102; 0, 7898) 100 100
- Vậy với mức ý nghĩa 5%, tỷ lệ các gia đình có thu nhập ≥ 35,5 triệu đồng/tháng ở khu A từ 61,02% đến 78,98%
Chúc các bạn qua môn! 25
Hỗ trợ học tập đại cương Xác suất thống kê Câu 5:
- Gọi Y là biến ngẫu nhiên chỉ thu nhập trong một tháng của các hộ gia đình tại B. E(Y ) = µ2. Giả sử 2 2 σ = 1 σ2
- Đặt giả thuyết H0 : µ1 = µ2. Đối thuyết H1 : µ1 < µ2 X − Y
- Chọn tiêu chuẩn kiểm định: U = nếu giả thuyết H s 0 đúng. U ∼ N(0; 1) s2 s2 1 + 2 n1 n2
- Với α = 0, 05 tra bảng phân phối chuẩn tắc được u1− = u α
0,95 = 1, 645. Miền bác bỏ H0 là:
Ws = (−∞; −u1− ) = (− α ∞; −1, 645)
- Từ số liệu đã cho, có: n1 = 100; n2 = 100; x = 35, 685; s1 = 0, 8547; y = 35, 8; s2 = 1, 1055 x − y 35, 685 − 35, 8 ⇒ uqs = = = −0, 8230 s r s2 s2 0, 85472 1, 10552 1 + 2 + n 100 100 1 n2 - Vì uqs /
∈ Ws nên chưa có cơ sở bác bỏ H0, nghĩa là chưa thể kết luận thu nhập bình quân ở khu dân
cư B cao hơn ở khu dân cư A với mức ý nghĩa 5%.
Chúc các bạn qua môn! 26
Hỗ trợ học tập đại cương Xác suất thống kê Đề 1
ĐỀ THI CUỐI KỲ - 20191
Mã học phần: MI2020
Câu 1. Có ba hộp I, II, III đựng bóng đèn. Hộp I có 8 bóng đèn màu đỏ, 2 bóng đèn màu xanh; hộp
II có 7 bóng đèn màu đỏ, 3 bóng đèn màu xanh; hộp III có 6 bóng đèn màu đỏ, 4 bóng đèn màu xanh.
a) Lấy ngẫu nhiên từ mỗi hộp ra một bóng đèn. Tính xác suất để được 3 bóng cùng màu.
b) Lấy ngẫu nhiên ra một hộp rồi từ đó lấy ngẫu nhiên ra 3 bóng đèn thì được 2 bóng màu đỏ, 1 bóng
màu xanh. Tính xác suất để các bóng đèn này được lấy từ hộp I. 3e−3x, nếu x ≥ 0
Câu 2. Cho hàm mật độ xác suất fX (x) =
của biến ngẫu nhiên liên tục X và 0, nếu x < 0
định nghĩa Y = [X ] là số nguyên lớn nhất không vượt quá X (nghĩa là [x] = 0 nếu 0 ≤ x < 1, [x] = 1 nếu 1 ≤ x < 2...). a) Tính P(Y = 0) b) Tính E(Y )
Câu 3. Cho U và V là hai biến ngẫu nhiên liên tục, độc lập với nhau và có cùng phân phối đều trên [10;30].
a) Tìm hàm mật độ xác suất đồng thời fU,V (u, v) của biến ngẫu nhiên hai chiều (U,V ). b) Tính P (|U −V | < 10)
Câu 4. Để điều tra doanh thu của các gia đình kinh doanh loại mặt hàng A tại địa phương B, người ta
khảo sát 100 gia đình kinh doanh loại mặt hàng này trong một tháng của năm 2019 thu được bảng số liệu: Doanh thu (triệu VNĐ) 25 30 35 40 45 50 55 60 65 Số gia đình 4 9 17 25 20 10 8 4 3
a) Với độ tin cậy 95%, hãy ước lượng doanh thu trung bình/tháng của các gia đình kinh doanh loại
mặt hàng A tại địa phương B.
b) Một tài liệu thống kê cho biết doanh thu trung bình/tháng của các gia đình kinh doanh loại mặt
hàng A tại địa phương B là 40 triệu VND. Hãy cho kết luận về tài liệu nói trên với mức ý nghĩa 5%.
Câu 5. Điều tra doanh thu của 200 gia đình kinh doanh loại mặt hàng A ở địa phương C, người ta tính
được doanh thu trung bình/tháng là 43 triệu VNĐ và độ lệch tiêu chuẩn của mẫu hiệu chỉnh là 8,912
triệu VNĐ. Doanh thu trung bình loại mặt hàng A ở địa phương C và B (với số liệu ở câu 4) có như
nhau hay không? Hãy kết luận với mức ý nghĩa 1%.
Phụ lục: trích Bảng phân phối chuẩn x 1,000 1,585 1,645 1,960 2,377 2,575 Φ(x) 0,8413 0,9429 0,9500 0,9750 0,9933 0,9950
Chúc các bạn qua môn! 27
Hỗ trợ học tập đại cương Xác suất thống kê
Giải đề cuối kì 20191 Câu 1: a,
Xét phép thử lấy ngẫu nhiên từ mỗi hộp ra một bóng đèn.
Tổng số kết cục đồng khả năng là: n = 10.10.10 = 1000 cách.
Gọi A = {Lấy được 3 bóng cùng màu}.
Số kết cục thuận lợi cho A là: m = 8.7.6 + 2.3.4 = 360 cách m 360 ⇒ P (A) = = = 0, 36 n 1000 b,
Gọi Ai = {Số bóng lấy ra được lấy từ hộp i}, i = 1, 2, 3.
Hệ {Ai} tạo thành hệ đầy đủ với: 1 P (A1) = P (A2) = P (A3) = 3
Gọi B = {Lấy ra được 2 bóng màu đỏ, 1 bóng màu xanh}
Áp dụng công thức xác suất đầy đủ:
P (B) = P (A1) P ( B| A1) + P (A2) P ( B| A2) + P (A3) P ( B| A3) với: C2.2 7 C2.3 21 C2.4 1 P ( B| A 8 7 6 1) = = P ( B| A2) = = P ( B| A3) = = C3 15 C3 40 C3 2 10 10 10 1 7 1 21 1 1 P (B) = . + . + . = 0, 4972 3 15 3 40 3 2 Xác suất cần tính là: 1 7 P (A . 1B) P (A1) P ( B| A1) P ( A 3 15 1| B) = = = = 0, 3129 P (B) P (B) 0, 4972 Câu 2: a, Y = 0 xảy ra khi 0 ≤ X < 1 1 Z
P (Y = 0) = P (0 ≤ X < 1) =
3.e−3xdx = 1 − e−3 = 0, 9502 0 b, Ta có: y+1 Z
P (Y = y) = P (y ≤ X < y + 1) =
3.e−3xdx = 1 − e−3 e−3y, y = 0, 1, 2 . . . y ∞
⇒ E (Y ) = 1 − e−3 ∑ ye−3y y=0 Có: !0 !0 ∞ ∞ ∞ ∞ 0 0 0 1 x 1 ∑ kxk−1 = ∑ xk = ∑ xk = ∑ xk − 1 = − 1 = = 1 − x 1 − x y=0 y=0 y=0 y=0 (1 − x)2
Chúc các bạn qua môn! 28
Hỗ trợ học tập đại cương Xác suất thống kê ∞ ∞ ∞
⇒ E (Y ) = 1 − e−3 ∑ ye−3y = 1 − e−3 ∑ ye−3y = e−3 1 − e−3 ∑ ye−3(y−1) y=0 y=1 y=1 1 1 = e−3 1 − e−3 . = = 0, 0524 (1 − e−3)2 e3 − 1 Câu 3: a,
Vì U và V là hai biến ngẫu nhiên liên tục, có phân phối đều trên [10; 30] nên: ( 1 ( 1 , u ∈ [10; 30] , u ∈ [10; 30] fU (u) = 20 fV (v) = 20 0,trai lai 0,trai lai
Mặt khác vì U và V độc lập nên: 2 ( 1 ,(u,v) ∈ [10;30] fU,V (u, v) = 400 0,trai lai b, ZZ P (|U − V | < 10) =
fU,V (u, v) dudv, D = (u, v) ∈ R2 : |u − v| < 10 D∩SU,V
Sử dụng tính chất của tích phân hai lớp ta được: 1 3 P (|U − V | < 10) = . 202 − 102 = = 0, 75 400 4 Câu 4: a,
Gọi X là biến ngẫu nhiên chỉ doanh thu của các gia đình kinh doanh loại mặt hàng A tại địa phương B. X ∼ N 2 µ1, σ . E (X ) = 1 µ1. X − µ √ • Chọn thống kê U =
n. Vì n = 100 > 30 nên U ∼ N (0, 1) S
• Sử dụng khoảng tin cậy đối xứng cho E (X ) = µ1: s 1 s1 x − u √ √ 1− α . ; x + u1−α . 2 n 2 n
Trong đó u1−α = u0,975 = 1, 96 được xác định từ bảng phân phối chuẩn tắc. 2
• Từ số liệu vừa tính toán ta có khoảng tin cậy đối xứng là: 9, 2245 9, 2245 42, 4 − 1, 96. √ ; 42, 4 + 1, 96. √ = (40, 5920; 44, 2080) 100 100
Vậy với độ tin cậy 95%, doanh thu trung bình của các hộ gia đình từ 40,5920 đến 44,2080.
Chúc các bạn qua môn! 29
Hỗ trợ học tập đại cương Xác suất thống kê b, • Đặt giả thuyết H0 : µ = µ0; đối thuyết H1 : µ 6= µ0 với µ0 = 40 X − µ √ 0
• Chọn tiêu chuẩn kiểm định U =
n nếu H0 đúng.U ∼ N (0; 1) s
• Với α = 0, 05, tra bảng phân phối chuẩn tắc ta có
u1−α = u0,975 = 1, 96, miền bác bỏ giả 2 thuyết H0 là: W = − ∪ u ; + = (− α ∞; −u1− α 1− α ∞
∞; −1, 96) ∪ (1, 96; +∞) 2 2
• Từ số liệu đầu bài, tính toán ta được:n1 = 100; x = 42, 4; s1 = 9, 2245 với µ0 = 40: x − µ √ √ 0 42, 4 − 40 uqs = n = . 100 = 2, 6018 s 9, 2245
Vì uqs ∈ Ws nên bác bỏ giả thuyết H0 nghĩa là tài liệu kia không đúng với mức ý nghĩa 5%. Câu 5:
Gọi Y là biến ngẫu nhiên chỉ doanh thu của các gia đình kinh doanh loại mặt hàng A tại địa phương C.Y ∼ N 2 µ2, σ . E (Y ) = 2 µ2 • Đặt giả thuyết H0 : µ = µ0; đối thuyết H1 : µ 6= µ0 X − Y
• Chọn tiêu chuẩn kiểm định U = nếu H s 0 đúng. U ∼ N (0; 1) s2 s2 1 + 2 n1 n2
• Với α = 0, 01, tra bảng phân phối chuẩn tắc ta có
u1−α = u0,995 = 2, 58, miền bác bỏ giả 2 thuyết H0 là: W = − ∪ u ; + = (− α ∞; −u1− α 1− α ∞
∞; −2, 58) ∪ (2, 58; +∞) 2 2
• Từ số liệu đầu bài, tính toán ta được:n1 = 100; x = 42, 4, y = 43 s1 = 9, 2245, s2 = 8, 912 với µ0 = 40: x − y 42, 4 − 43 uqs = = = −0, 5371 s r s2 s2 9, 22452 8, 9122 1 + 2 + n 100 100 1 n2 Vì uqs /
∈ Ws nên chưa có cơ sở bác bỏ H0, nghĩa là có thể kết luận doanh thu trung bình loạimặt hàng
A ở địa phương C và B là như nhau.
Chúc các bạn qua môn! 30
Hỗ trợ học tập đại cương Xác suất thống kê Đề 1
ĐỀ THI CUỐI KỲ - 20192
Mã học phần: MI2020
Câu 1. Cho biết xác suất để một sinh viên mượn một cuốn sách Kỹ thuật ở thư viện là 0,8; còn xác
suất mượn một cuốn sách Văn học là 0,2. Một ngày có 5 sinh viên đến mượn sách tại thư viện, mỗi
người mượn 2 cuốn sách.
a) Tính xác suất để trong 5 người đó có đúng 2 người, mỗi người mượn một cuốn sách Kỹ thuật và một cuốn sách Văn học.
b) Biết trong 5 người có ít nhất 2 người, mỗi người mượn 2 cuốn sách Kỹ thuật. Tính xác suất để
trong 5 người đó có đúng 2 người, mỗi người mượn 1 cuốn sách Kỹ thuật và 1 cuốn sách Văn học.
Câu 2. Có hai nhóm sinh viên. Nhóm I có 5 sinh viên nam và 3 sinh viên nữ; nhóm II có 4 sinh viên
nam và 2 sinh viên nữ. Từ nhóm I chọn ngẫu nhiên ra 2 sinh viên, từ nhóm II chọn ra 1 sinh viên.
a) Hỏi trung bình chọn được bao nhiêu sinh viên nữ trong 3 sinh viên được chọn.
b) Biết trong 3 sinh viên được chọn có ít nhất 1 sinh viên nữ. Tính xác suất để trong 3 sinh viên đó có đúng 1 sinh viên nam.
Câu 3. Thời gian hoạt động Xi, i = 1, 2, 3 của linh kiện điện tử I, II, II là các biến ngẫu nhiên độc lập,
tuân theo luật phân phối mũ với hàm mật độ xác suất tương ứng là fX (x) = λ e−λix, x > 0, λi > 0.
a) Tìm hàm phân phối xác suất của biến ngẫu nhiên chỉ thời gian hoạt động của một hệ thống gồm 3
linh kiện trên mắc nối tiếp.
b) Tìm kỳ vọng và phương sai của biến ngẫu nhiên chỉ thời gian hoạt động của hệ thống đó.
Câu 4. Đo độ xa X (đơn vị đo là mm) từ điểm trúng bia đến tâm bia của 16 lần bắn ta thu được số liệu sau: 2,10 1,95 2,07 2,03 1,91 2,08 1,98 2,10 2,06 1,92 1,95 2,11 2,00 1,96 2,08 1,91
a) Hãy ước lượng độ xa trung bình với độ tin cậy 95%. Giả sử độ xa X là biến ngẫu nhiên có phân phối chuẩn.
b) Tính xác suất để độ xa X lớn hơn 2mm.
Câu 5. Số lượng người mắc bệnh sốt xuất huyết ở địa phương A là 15 người trên một mẫu 200 người;
số lượng này ở địa phương B là 20 người trên một mẫu 250 người. Hỏi tỷ lệ mắc bệnh sốt xuất huyết
ở 2 địa phương trên có được coi là như nhau hay không? Hãy kết luận với mức ý nghĩa α = 0, 05.
Phụ lục: trích các bảng số (n) Phân vị chuẩn Φ(x) Phân vị Student P(X < t ) = α α α x 0,178 1,165 1,645 0,950 0,975 0,995 n Φ(x) 0,5695 0,8780 0,9500 8 1,860 2,306 3,355 x 1,960 2,377 2,575 14 1,761 2,145 2,977 Φ(x) 0,9750 0,9933 0,9950 15 1,753 2,131 2,947
Chúc các bạn qua môn! 31
Hỗ trợ học tập đại cương Xác suất thống kê
Giải đề cuối kì 20192 Câu 1:
Xác suất để một người mượn một cuốn sách Kỹ thuật và một cuốn sách Văn học: p = 2.0, 2.0, 8 = 0, 32 a,
Gọi A = {Trong 5 người đó có đúng 2 người, mỗi người mượn một cuốn sách Kỹ thuật và một cuốn sách Văn học}
Bài toán thoả lược đồ Bernoulli với:
n = 5; p = 0, 32; q = 1 − p = 0, 68 ⇒ P (A) = P5 (2) = C2. 5 0, 322.0, 683 = 0, 3220 b,
Gọi B = {Trong 5 người có ít nhất 2 người, mỗi người mượn 2 cuốn sách Kỹ thuật}
Bài toán thoả lược đồ Bernoulli với: n = 5; p = 0, 82 = 0, 64; q = 1 − p = 0, 36; k1 = 2; k2 = 5 ⇒ P (B) = P5 (2; 5) = C2. . . . 5 0, 642.0, 363 +C3 5 0, 643.0, 362 +C4 5 0, 644.0, 361 +C5 5 0, 645.0, 360 = 0, 9402 P (AB)
Xác suất cần tính là: P ( A| B) = P(B)
Trong đó: AB = { Trong 5 người đó có đúng 2 người, mỗi người mượn một cuốn sách Kỹ thuật và một
cuốn sách Văn học, ít nhất 2 người, mỗi người mượn 2 cuốn sách Kỹ thuật} • Trường hợp 1:
2 người, mỗi người mượn một cuốn sách Kỹ thuật và một cuốn sách Văn học;
2 người, mỗi người mượn 2 cuốn sách Kỹ thuật; 1 người mượn 2 cuốn Văn học. PTH1 = C2. 5 0, 322.C2 3 0, 642.C1 1 .0, 04 = 0, 0503 • Trường hợp 2:
2 người, mỗi người mượn một cuốn sách Kỹ thuật và một cuốn sách Văn học;
3 người, mỗi người mượn 2 cuốn sách Kỹ thuật. PTH2 = C2. 5 0, 322.C3 3 0, 643 = 0, 2684
⇒ P (AB) = 0, 0503 + 0, 2684 = 0, 3187 P (AB) 0, 3187 ⇒ P ( A| B) = = = 0, 3390 P (B) 0, 9402 Câu 2: a,
Gọi X là biến ngẫu nhiên chỉ số sinh viên nữ được chọn .X = {0, 1, 2, 3}
Gọi Ai = {Chọn được i sinh viên nữ từ nhóm I}.
Gọi Bi = {Chọn được i sinh viên nữ từ nhóm II}. C2 C1 5 P (X = 0) = P (A 5 4 0B0) = P (A0) .P (B0) = . = C2 C1 21 8 6 5.3 C1 C2 C1 10 P (X = 1) = P (A 4 5 2
1B0 + A0B1) = P (A1) .P (B0) + P (A01) .P (B1) = . + . = C2 C1 C2 C1 21 8 6 8 6 C2 C1 5.3 C1 1 P (X = 2) = P (A 3 4 2
2B0 + A1B1) = P (A2) .P (B0) + P (A1) .P (B1) = . + . = C2 C1 C2 C1 4 8 6 8 6 C2 C1 1 P (X = 3) = P (A 3 2 2B1) = P (A2) .P (B1) = . = C2 C1 28 8 6
Chúc các bạn qua môn! 32
Hỗ trợ học tập đại cương Xác suất thống kê X 0 1 2 3
Ta có bảng phân phối xác suất: 5 10 1 1 Y 21 21 4 2 5 10 1 1 13 ⇒ E (X) = 0. + 1. + 2. + 3. = 21 21 4 28 12 13 Vậy trung bình có
sinh viên nữ được chọn trong số 3 sinh viên. 12 b,
Gọi A = {Trong 3 sinh viên được chọn có ít nhất 1 sinh viên nữ}. 5 16
⇒ P (A) = 1 − P A = 1 − P (X = 0) = 1 − = 21 21
Gọi B = {Trong 3 sinh viên đó có đúng 1 sinh viên nam}. 1 ⇒ P (B) = P (X = 2) = 4 Xác suất cần tính là: 1 P (AB) P (B) 21 ⇒ P ( B| A) = = = 4 = P (A) P (A) 16 64 21 Câu 3: a,
Gọi X1, X2, X3 lần lượt là biến ngẫu nhiên chỉ thời gian hoạt động của 3 linh kiện trong mạch.
Gọi Y là biến ngẫu nhiên chỉ thời gian hoạt động của mạng lắp nối tiếp. Ta có: Y = min (X1, X2) > 0
FY (y) = P (Y < y) = 1 − P (Y > y) = 1 − P (X1 > y) P (X2 > y) P (X3 > y) + ∞ +∞ +∞ Z Z Z = 1 − fX (x) dx f (x) dx f (x) dx 1 X2 X3 = 1 − e−(λ1+λ2+λ3)y y y y Vậy:
(1 − e−(λ1+λ2+λ3)y,y > 0 FY (y) = 0, trai lai b,
Từ hàm phân phối, ta tìm được hàm mật độ xác suất: (λ f
1 + λ2 + λ3) e−(λ1+λ2+λ3)y, y > 0 Y (y) = 0, trai lai
• Cách 1: Dễ thấy Y là biến ngẫu nhiên có phân phối mũ. Y ∼ Exp (λ1 + λ2 + λ3) Suy ra: 1 1 E (Y ) = V (Y ) = λ1 + λ2 + λ3 (λ1 + λ2 + λ3)2
Chúc các bạn qua môn! 33
Hỗ trợ học tập đại cương Xác suất thống kê +∞
• Cách 2: Ta có hàm Gamma: R Γ (y) = xy−1e−xdx 0 +∞ +∞ E (Y ) = R yf R Y (y)dy =
y (λ1 + λ2 + λ3) e−(λ1+λ2+λ3)ydy −∞ 0 1 1 = .Γ (2) = λ1 + λ2 + λ3 λ1 + λ2 + λ3 +∞ +∞ E Y 2 = R y2f R Y (y)dy =
y2 (λ1 + λ2 + λ3) e−(λ1+λ2+λ3)ydy −∞ 0 1 2 = .Γ (3) = (λ1 + λ2 + λ3)2 (λ1 + λ2 + λ3)2 2 1 1
⇒ V (Y ) = E Y 2 − [E (Y )]2 = − = (λ1 + λ2 + λ3)2 (λ1 + λ2 + λ3)2 (λ1 + λ2 + λ3)2 Câu 4:
Gọi X là biến ngẫu nhiên chỉ độ xa từ điểm trúng bia đến tâm bia. X ∼ N 2 µ , σ , E (X ) = µ Ta tính toán được:
n = 16; x = 2, 0131; s = 0, 0735 a, X − µ √ • Chọn thống kê T =
n. Vì n = 16 < 30 nên T có phân phối Student với n − 1 bậc tự do. S
• Sử dụng khoảng tin cậy đối xứng cho E (X ) = µ: s s
x − tn−1 . √ ; x + tn−1 . √ 1− α 1− α 2 n 2 n Trong đó tn−1 = t1
5 = 2, 131 được xác định từ bảng phân phối Student. 1− α 0,975 2
• Từ số liệu vừa tính toán ta có khoảng tin cậy đối xứng là: 0, 0735 0, 0735 2, 0131 − 2, 131. √ ; 2, 0131 + 2, 131. √ = (1, 9739; 2, 0522) 16 16
Vậy với độ tin cậy 95%, tuổi thọ trung bình của ắc quy của công ty A từ 1,9739 đến 2,0522. b,
x là ước lượng không chệch của µ và s là ước lượng không chệch của σ . Xác suất cần tính là: 2 − x 2 − 2, 0131
P (X > 2) = P (2 < X < +∞) = 0, 5 − φ = 0, 5 − φ s 0, 0735
= 0, 5 − φ (−0, 178) = 0, 5 + φ (0, 178) = 0, 5 + Φ (0, 178) − 0, 5 = Φ (0, 178) = 0, 5695 Câu 5:
Gọi p1, p2 lần lượt là tỷ lệ người mắc bệnh sốt xuất huyết ở địa phương A và B. • Đặt giả thuyết H0 : p1 = p2; đối thuyết H1 : p1 6= p2 f1 − f2
• Chọn tiêu chuẩn kiểm định Z = nếu H s 0 đúng. U ∼ N(0, 1) 1 1 f 1 − f + n1 n2
Chúc các bạn qua môn! 34
Hỗ trợ học tập đại cương Xác suất thống kê
• Với α = 0, 05, tra bảng phân phối chuẩn tắc ta có z1−α = z0,975 = 1, 96, miền bác bỏ giả thuyết 2 H0 là: W = − ∪ z ; + = (− α ∞; −z1− α 1− α ∞
∞; −1, 96) ∪ (1, 96; +∞) 2 2 • Theo bài ra 15 3 20 2
n1 = 200, n2 = 250, m1 = 15, m2 = 20, f1 = = , f2 = = 200 40 250 25 n1 f1 + n2 f2 15 + 20 7 f = = = n1 + n2 450 90 f ⇒ 1 − f2 zqs = = −0, 1968 s 1 1 f 1 − f + n1 n2
Vì zqs ∈ Ws nên bác bỏ H0 nghĩa là không thể chấp nhận tỷ lệ mắc sốt xuất huyết ở hai địa phương là
như nhau với mức ý nghĩa 5%.
Chúc các bạn qua môn! 35
Hỗ trợ học tập đại cương Xác suất thống kê Đề 1
ĐỀ THI CUỐI KỲ - 20193
Mã học phần: MI2020
Câu 1. Từ kinh nghiệm quá khứ biết rằng có 20% khách đến cửa hàng có quyết định mua ô tô. Tìm
xác suất để số khách hàng mua xe không vượt quá 2 nếu trong một lần:
a) có 5 khách hàng đến cửa hàng.
b) có 5 khách hàng đến cửa hàng và biết có không quá 4 người mua xe.
Câu 2. Một phân xưởng có hai lô hàng: lô I có 9 chính phẩm và 2 phế phẩm; lô II có 8 chính phẩm
và 1 phế phẩm. Chọn ngẫu nhiên 2 sản phẩm từ lô I chuyển sang lô II.
a) Tính xác suất để trong lô II có đúng 2 phế phẩm.
b) Tìm số phế phẩm trung bình của lô II.
Câu 3. Cho thời gian làm việc (hoạt động) T của một con chíp máy tính tuân theo luật phân phối mũ
với hàm mật độ có dạng f (x) = 1 e− xλ , x > 0, E(T ) = 800 giờ. λ
a) Tìm tham số λ và hàm phân phối xác suất của T .
b) Tìm tỷ lệ các con chíp có thời gian hoạt động lớn hơn 1600 giờ.
Câu 4. Một nhà bán lẻ kiểm tra tuổi thọ (đơn vị tháng) của 10 ắc quy ô tô của công ty A và thu được bộ số liệu là: 27,6 28,7 34,7 29,0 22,9 29,6 29,4 30,3 36,5 34,7
a) Tìm ước lượng không chệch của độ lệch chuẩn của tuổi thọ trên.
b) Với độ tin cậy 95%, xác định khoảng tin cậy cho tuổi thọ trung bình của loại ắc quy đó, biết tuổi
thọ trên là biến ngẫu tuân theo luật phân phối chuẩn.
Câu 5. Cho một nhóm sinh viên gồm 11 người thi tiếng Anh trong hai vòng thi, kết quả như sau: Sinh viên 1 2 3 4 5 6 7 8 9 10 11 Lần 1 45 64 86 96 40 57 73 32 28 89 66 Lần 2 56 68 84 97 36 60 70 39 27 92 75
a) Có thể cho rằng kết quả hai vòng thi là giống nhau, biết rằng điểm thi tuân theo luật phân phối chuẩn (α = 0, 05)?
b) Có thể kết luận vòng thi 2 cho kết quả tốt hơn (α = 0, 01)?
Phụ lục: trích các bảng số Phân vị chuẩn Φ(x)
Phân vị Student P(X < p) = t(n; p) p x 1,000 1,645 1,880 0,95 0,975 0,99 n Φ(x) 0,8413 0,950 0,970 9 1,833 2,262 2,821 x 1,960 2,326 2,575 10 1,812 2,228 2,764 Φ(x) 0,975 0,990 0,995 11 1,796 2,201 2,718 20 1,725 2,086 2,528 21 1,721 2,080 2,518
Chúc các bạn qua môn! 36
Hỗ trợ học tập đại cương Xác suất thống kê
Giải đề cuối kì 20193 Câu 1:
Gọi X là biến ngẫu nhiên chỉ số khách đến mua ô tô. X ∼ B(n, p)
a)Gọi A ={Số khách mua xe không vượt quá 2 nếu trong một lần có 5 khách đến cửa hàng}.
⇒ P (A) = P (X ≤ 2) = P (X = 0) + P (X = 1) + P (X = 2)
= C0.0, 20.(1 − 0, 2)5 +C1.0, 21.(1 − 0, 2)4 +C2.0, 22.(1 − 0, 2)3 = 0, 9421 5 5 5
b) Gọi B ={Số khách mua xe không vượt quá 4 nếu trong một lần có 5 khách đến cửa hàng }.
⇒ P (B) = P (X ≤ 4) = 1 − P (X > 4) = 1 − P (X = 5) = 1 −C5.
5 0, 25.(1 − 0, 2)0 = 0, 9997 P (AB) P (A) 0, 9421
⇒Xác suất cần tính là: P ( A| B) = = = = 0, 9424 P (B) P (B) 0, 9997 Câu 2:
Gọi Ai = {Trong 2 sản phẩm lấy được từ lô I có i chính phẩm},i = 0, 1, 2.
Hệ {Ai} tạo thành một hệ đầy đủ với: C2 1 2.9 18 C2 36 P(A 2 9 0) = = , P(A1) = = , P(A2) = = C2 55 C2 55 C2 55 11 11 11
a) Gọi A = {Trong lô II có đúng 2 phế phẩm}. 18 ⇒ P (A) = P (A1) = 55
b) Gọi X là biến ngẫu nhiên chỉ số phế phẩm của lô II.X = 1, 2, 3. 36 P (X = 1) = P (A2) = 55 18 P (X = 2) = P (A1) = 551 P (X = 3) = P (A0) = 55 Ta có bảng: X 1 2 3 36 18 1 P 55 55 55 36 18 1 15 ⇒ E (X) = 1. + 2. + 3. = = 1, 3636 55 55 55 11
Vậy trung bình có 1,3636 phế phẩm trong lô II. Câu 3:
a, T là biến ngẫu nhiên liên tục tuân theo phân phối mũ với: 1 −x f (x) = .e λ , x > 0 λ
Có: E (T ) = 800 mà E (T ) = 1 = 1 λ ⇒ λ = 800 λ 1 −x ⇒ f (x) = .e 800 , x > 0 800
Chúc các bạn qua môn! 37
Hỗ trợ học tập đại cương Xác suất thống kê Với x > 0: x x x Z Z Z 1 −t −t x −x F (x) = f (t)dt = f (t)dt =
.e 800 dt = − e 800 = 1 − e 800 800 0 −∞ 0 0 Với x ≤ 0: F (x) = 0 −x 1 − e 800 , x > 0 ⇒ F (x) = 0, x ≤ 0
b, Gọi A = {Các con chíp có thời gian hoạt động lớn hơn 1600 giờ} −1600
⇒ P (A) = P (T > 1600) = 1 − P (T ≤ 1600) = 1 − 1 − e 800 = 0, 1353 Câu 4:
Gọi X là biến ngẫu nhiên chỉ tuổi thọ của ắc quy ô tô của công ty A. X ∼ N 2 µ , σ , E (X ) = µ Ta tính toán được:
n = 10; x = 30, 34; s = 4, 0103
a, Ước lượng không chệch của độ lệch chuẩn của tuổi thọ trên là: s = 4, 0103. b, X − µ √ • Chọn thống kê T =
n. Vì n = 10 < 30 nên T có phân phối Student với n − 1 bậc tự do. S
• Sử dụng khoảng tin cậy đối xứng cho E (X ) = µ: s s
x − tn−1 . √ ; x + tn−1 . √ 1− α 1− α 2 n 2 n Trong đó tn−1 = t9
= 2, 262 được xác định từ bảng phân phối Student. 1− α 0,975 2
• Từ số liệu vừa tính toán ta có khoảng tin cậy đối xứng là: 4, 0103 4, 0103 30, 34 − 2, 262. √ ; 30, 34 + 2, 262. √ = (27, 4714; 33, 2086) 10 10
Vậy với độ tin cậy 95%, tuổi thọ trung bình của ắc quy của công ty A từ 27,4714 đến 33,2086. Câu 5:
Gọi X, Y lần lượt là kết quả thi của người thi tiếng Anh trong vòng thi thứ nhất, thứ hai. Ta có: X ∼ N 2 2 µ1, σ1 ; Y ∼ N µ2, σ2 ; n1 = n2 = 11
Đặt Z = X −Y , thiết lập hiệu zi = xi − yi, i = 1, 2, ...11 : X 45 64 86 96 40 57 73 32 28 89 66 Y 56 68 84 97 36 60 70 39 27 92 75 Z −11 −4 2 −1 4 −3 3 −7 1 −3 −6 a, • Đặt giả thuyết H0 : µ = µ0; đối thuyết H1 : µ 6= µ0 với µ0 z − µ √ 0
• Chọn tiêu chuẩn kiểm địnhT = n nếu H0 đúng. T ∼ T (n − 1) S
Chúc các bạn qua môn! 38
Hỗ trợ học tập đại cương Xác suất thống kê
• Với α = 0, 05, tra bảng phân phối Student ta có tn−1 = t10
= 2, 228, miền bác bỏ giả thuyết 1− α 0,975 2 H0 là: W = − ∪ tn−1 ; + = (− α ∞; tn−1 ∞
∞; −2, 228) ∪ (2, 228; +∞) 1− α 1− α 2 2
• Từ số liệu đầu bài, tính toán ta được:n = 11; z = −2, 5455; s = 4, 9470 với µ0 = 0: z − µ √ √ 0 −2, 5455 − 0 tqs = n = . 11 = −1, 7066 s 4, 9470 Vì tqs = −1, 7066 /
∈ Wqs nên chưa có cơ sở bác bỏ giả thuyết H0, nghĩa là với số liệu này có thể cho
rằng kết quả hai vòng thi là giống nhau với mức ý nghĩa 5%. b, • Đặt giả thuyết H0 : µ = µ0; đối thuyết H1 : µ < µ0 với µ0 z − µ √ 0
• Chọn tiêu chuẩn kiểm địnhT = n nếu H0 đúng. T ∼ T (n − 1) S
• Với α = 0, 05, tra bảng phân phối Student ta có tn−1 = t10 = 2, 764, miền bác bỏ giả thuyết 1−α 0,99 H0 là: W = − = (− α ∞; tn−1 1− ∞; −2, 764) α Vì tqs = −1, 7066 /
∈ Wqs nên bác bỏ giả thuyết H1, nghĩa là chưa thể kết luận vòng thi 2 cho kết quả
tốt hơn với mức ý nghĩa 5%
Chúc các bạn qua môn! 39
Hỗ trợ học tập đại cương Xác suất thống kê Đề 2
ĐỀ THI CUỐI KỲ - 20201
Mã học phần: MI2020
Câu 1. Điểm thi của 100 sinh viên (thi độc lập nhau) được cho ở bảng dưới: Điểm 3,0 3,5 4,0 4,5 5,0 5,5 6,0 6,5 Số sinh viên 2 4 12 21 28 20 9 4
Lấy ngẫu nhiên điểm thi của 6 sinh viên để khảo sát. Tính xác suất trong 6 điểm thi đó:
a) Có hai điểm thi cao hơn 5,5 và một điểm thi thấp hơn 4,0.
b) Có cả điểm 6 và điểm 6,5.
Câu 2. Một lô hàng với số lượng sản phẩm lớn có ba loại 1, 2 và 3 chiếm tỷ lệ tương ứng là 50%,
20% và 30%. Lấy nhiên 6 sản phẩm để kiểm tra và gọi X và Y tương ứng chỉ số sản phẩm loại 1 và
loại 2 có trong 6 sản phẩm được lấy ra.
a) Tính trung bình của Z = X +Y
b) Tính phương sai và mốt của Y .
Câu 3. Cho biến ngẫu nhiên hai chiều liên tục (U,V ) có hàm mật độ xác suất là:
ku2v, nếu 0 ≤ u ≤ 1, 0 ≤ v ≤ 1, f (u, v) = 0, nếu trái lại. 2 a) Tìm hằng số k. b) Tính P max(U,V ) ≤ . 3
Câu 4. Để kiểm tra trọng lượng loại sản phẩm S do nhà máy Q sản xuất trong quý IV năm 2020,
người ta cần thử 100 sản phẩm loại này thu được bảng số liệu: Trọng lượng (gam) 5 - 6 6 - 7 7 - 8 8 - 9 9 - 10 10 - 11 11 - 12 12 - 13 Số sản phẩm 5 10 15 20 29 10 6 5
a) Với độ tin cậy 95% hãy ước lượng trọng lượng trung bình của loại sản phẩm S do nhà máy Q sản
xuất tại thời điểm kiểm tra.
b) Nếu yêu cầu sai số của ước lượng ở ý a) là 0,24 thì cần phải cân thêm bao nhiêu sản phẩm nữa?
Câu 5. Một công ty có hai phân xưởng I và II sản xuất cùng loại sản phẩm. Kiểm tra ngẫu nhiên 1000
sản phẩm do phân xưởng I sản xuất thấy 35 sản phẩm loại B; kiểm tra 900 sản phẩm do phân xưởng
II sản xuất thấy 20 sản phẩm loại B. Có thể xem tỷ lệ sản phẩm loại B do phân xưởng I sản xuất cao
hơn tỷ lệ sản phẩm loại B do phân xưởng II sản xuất hay không với mức ý nghĩa 1%?
Phụ lục: trích các bảng số (n) Phân vị chuẩn Φ(x) Phân vị Student P(X < t ) = p α p x 1,645 1,960 2,330 2,575 0,950 0,990 0,995 n Φ(x) 0,9500 0,9750 0,9900 0,9950 15 1,753 2,602 2,947
Chúc các bạn qua môn! 40
Hỗ trợ học tập đại cương Xác suất thống kê
Giải đề cuối kì 20201 Câu 1:
Xét phép thử chọn ngẫu nhiên 6 sinh viên để khảo sát.
Số kết cục đồng khả năng là: n = C6 cách. 100 a,
Gọi A = {Có hai điểm thi cao hơn 5,5 và một điểm thi thấp hơn 4,0}
Số kết cục thuận lợi cho A là: m = C2 .C1.C3 13 6 81 m C2 .C1.C3 ⇒ P (A) = = 13 6 81 = 0.0335 n C6100 b,
Gọi B = {Có cả điểm 6 và điểm 6,5}
Gọi C = {Không có điểm 6}
Gọi D = {Không có điểm 6,5}
⇒ B = C.D ⇒ P (B) = P C.D = P C + D = 1 − P (C + D) = 1 − P (C) − P (D) + P (DC) c C6
Số kết cục thuận lợi cho C là: c = C6 ⇒ P (C) = = 91 91 n C6100 d C6
Số kết cục thuận lợi cho D là: d = C6 ⇒ P (D) = = 96 96 n C6100 e C6
Số kết cục thuận lợi cho CD là: e = C6 ⇒ P (CD) = = 87 96 n C6100 C6 C6 C6 ⇒ P (B) = 1 − 91 − 96 + 87 = 0,0868 C6 C6 C6 100 100 100 Câu 2: a,
Gọi T là biến ngẫu nhiên chỉ số sản phẩm loại 3 trong 6 sản phẩm được lấy ra. T ∼ B (n, p) với n = 6; p = 0, 3 ⇒ X +Y + T = 6
⇒ E (X +Y ) = E (6 − T ) = 6 − E (T ) = 6 − np = 6 − 6.0, 3 = 4, 2 b,
Y ∼ B (n, p) với n = 6; p = 0, 2
⇒ V (Y ) = npq = 6.0, 2.0, 8 = 0, 96 Theo bài ra ta có:
np − q = 6.0, 2 − 0, 8 = 0, 4 / ∈ Z
Vậy số sản phẩm loại 2 có khả năng nhất trong 6 sản phẩm là:y0 = [np − q] + 1 = 1.
Vậy modY = y0 = 1. Câu 3:
a, Ta giải hệ phương trình 0 ≤ u ≤ 1 ku2v ≥ 0, k ≥ 0 ( 0 ≤ v ≤ 1 k ≥ 0 1 1 +∞ +∞ ⇔ Z Z ⇔ k ⇔ k = 6(T M) Z Z k u2du vdv = 1 = 1 ku2vdudv = 1 6 0 0 −∞ −∞
Chúc các bạn qua môn! 41
Hỗ trợ học tập đại cương Xác suất thống kê Vậy:
6u2v, 0 ≤ u ≤ 1, 0 ≤ v ≤ 1 f (u, v) = 0, trai lai b,
P max (U,V ) ≤ 2 = P U ≤ 2 ,V ≤ 2 3 3 3 2 2 2 2 3 3 3 3 Z Z Z Z 8 2 = 6u2vdudv = 6 u2du vdv = 6. . = 0, 1317 81 9 0 0 0 0 Câu 4: a,
Gọi X là biến ngẫu nhiên chỉ trọng lượng loại sản phẩm S do nhà máy Q sản xuất trong quý IV năm 2020. X ∼ N 2 µ , σ , E (X ) = µ X − µ √ • Chọn thống kê U =
n. Vì n = 100 > 30 nên U ∼ N (0, 1) S
• Sử dụng khoảng tin cậy đối xứng cho E (X ) = µ: s s x − u √ √ 1− α . ; x + u1−α . 2 n 2 n
Trong đó u1−α = u0,975 = 1, 96 được xác định từ bảng phân phối chuẩn tắc. 2
• Từ số liệu vừa tính toán ta có khoảng tin cậy đối xứng là: 1, 7095 1, 7095 8, 87 − 1, 96. √ ; 8, 87 + 1, 96. √ = (8, 5349; 9, 2051) 100 100
Vậy với độ tin cậy 95%, trọng lượng trung bình của loại sản phẩm S do nhà máy Q sản xuất tại thời
điểm kiểm tra từ 8,5349g đến 9,2051g. b,
Sai số của ước lượng là s1 ε = u √ 1− α . 2 n 2 u1−α .s2 1, 962.1, 70952 ⇒ 2 n = ≥ = 194, 9 ε 2 0, 242
Vậy nếu yêu cầu sai số của ước lượng ở ý a) là 0,24 thì cần phải cân thêm 195 – 100 = 95 sản phẩm nữa. Câu 5:
Gọi p1, p2 lần lượt là tỷ lệ sản phẩm loại B do phân xưởng I và II sản xuất. • Đặt giả thuyết H0 : p1 = p2; đối thuyết H1 : p1 > p2 f1 − f2
• Chọn tiêu chuẩn kiểm định Z = nếu H s 0 đúng. U ∼ N(0, 1) 1 1 f 1 − f + n1 n2
• Với α = 0, 05, tra bảng phân phối chuẩn tắc ta có z1− = z α
0,95 = 1, 645, miền bác bỏ giả thuyết H0 là: W = (z ; + α 1−α ∞) = (1, 645; +∞)
Chúc các bạn qua môn! 42
Hỗ trợ học tập đại cương Xác suất thống kê • Theo bài ra 35 7 20 1
n1 = 1000, n2 = 900, m1 = 35, m2 = 20, f1 = = , f2 = = 1000 200 900 45 n1 f1 + n2 f2 35 + 20 11 f = = = n1 + n2 1900 380 f ⇒ 1 − f2 zqs = = 1, 6587 r f 1 − f 1 + 1 n1 n2
Vì zqs ∈ Ws nên bác bỏ H0 nghĩa là có thể xem tỷ lệ sản phẩm loại B do phân xưởng I sản xuất cao
hơn tỷ lệ sản phẩm loại B do phân xưởng II sản xuất với mức ý nghĩa 5%.
Chúc các bạn qua môn! 43

