Đề thi cuối ký môn Cấu trúc dữ liệu và giải thuật năm 2011 | Đại học Bách Khoa Hà Nội
Đề thi cuối ký môn Cấu trúc dữ liệu và giải thuật năm 2011 | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!
Môn: Cấu trúc dữ liệu và giải thuật (ET2100) 133 tài liệu
Trường: Đại học Bách Khoa Hà Nội 2.8 K tài liệu
Tác giả:
Preview text:
ĐẠI HỌC BÁCH KHOA HÀ NỘI
ĐỀ THI MÔN: CTDL & GT
Trường Điện – Điện tử
Lần thi: Cuối kỳ Ngày thi: 24/2/2022 --------
Thời gian làm bài: 80 phút
Mã đề: Tổng số trang: 1
(Được sử dụng tài liệu) Ký duyệt Trưởng nhóm môn học: Trưởng Khoa: Họ tên sinh viên: MSSV: K = ( … )
Dãy khóa K được tạo ra gồm 8 số trích ra từ MSSV.
Ví dụ: MSSV = 20211234 thì K = (2, 0, 2, 1, 1, 2, 3, 4)
(Sinh viên không nhập đúng theo MSSV của mình sẽ được điểm 0)
1. Trình bày sự thay đổi của dãy K trong quá trình thực hiện các thuật toán sắp xếp:
a. Chèn (Insert sort). (1,5 đ)
b. Phân đoạn (Partition sort) (1,5 đ) 2. Từ dãy K yêu cầu:
a. Dựng cây nhị phân tìm kiếm (1đ), sau đó hãy:
b. Duyệt cây theo thứ tự trước (1đ)
c. Duyệt cây theo từng mức (1đ)
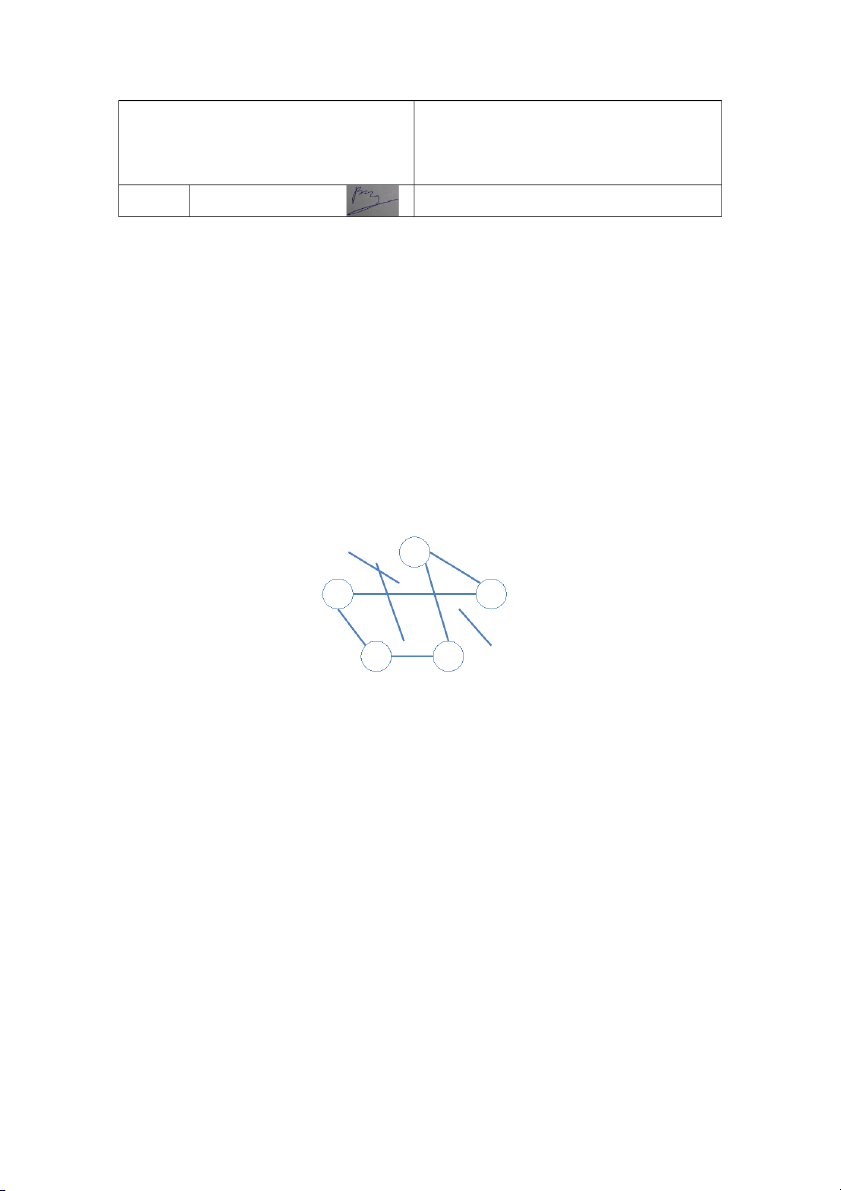
3. Cho đồ thị có trọng số G(V, E) như sau:
Trong đó: V = {A, B, C, D, F}; E = {d0, d1, d2, d3, d4, d5, d6, d7} = K A d0 d1 d5 F B d6 d7 d4 d2 D C d3
+ 1, với K cho ở trên (theo K ở trên ta có E = {3, 1, 3, 2, 2, 3, 4, 5}). Yêu cầu:
a. Vẽ lại đồ thị theo các giá trị K (0,5đ)
b. Biểu diễn cách cài đặt đồ thị bằng ma trận đỉnh kề (1,5đ).
c. Nêu thứ tự duyệt đồ thị theo chiều sâu bắt đầu từ F (các nút
kề được duyệt theo thứ tự bảng chữ cái) (1đ).
d. Tìm đường đi ngắn nhất từ đỉnh A đến tất cả các đỉnh còn lại (1đ)