


Preview text:
ĐỀ THAM KHẢO GIỮA KÌ 1
I. PHẦN TRẮC NGHIỆM (3,0 ĐIỂM)
Câu 1. Trong những biểu thức sau, biểu thức nào là đơn thức nhiều biến?.
A. 3x(x - 2) B. 4xy x C. D. 2x - 1 y
Câu 2. Biểu thức nào sau đây là không là đa thức nhiều biến?. 4
A. 3xy - 10x B. + 2x 5 y
C. 3yz + x D.10 + 2xy
Câu 3: Chọn đáp án đúng, với đa thức B khác đa thức 0 . A . A M A. =
, M là một đa thức khác đa thức 0 . B . B M A A + M B. = . B B + M A A − M C. = . B B − M A . A M D. = . B . B M
Câu 4. Khai triển biểu thức sau (x + )2 3 = ? A. 2
x + 3x + 9 B. 2
x + 6x + 3 C. 2
x + 2x + 9 D. 2
x + 6x + 9
Câu 5. Kết quả của phép tính (x + )3 2 là A. 3 2
x + 3x + 3x + 8 B. 3 2
x + 6x + 12x + 8 C. 3 2
x + 12x + 3x + 8 D. 3 2
x + 12x + 6x + 8 x - 21
Câu 6. Điều kiện xác định của phân thức là: 2x + 2023
A. x + 21¹ 0 B. x + 21= 0
C. 2x + 2023 ¹ 0 D. 2x + 2023 = 0 xy + 1 Câu 7. Cho P =
. Giá trị của phân thức P tại x = - 1, y = 1là xy - 2023 A. 1 B. 0 C. 5 D. - 5 x 3y
Câu 8. Hai phân thức và
bằng nhau thì ( xem phân thức đã xác định). 2 y x A. . x 3y = 2 . y x B. . x 2 y = 3 . y x C. . x x = 2 .
y 3y D. 3 . x x = 2 . y y
Câu 9. Hình chóp tam giác đều là hình chóp có đáy là hình gì? A. Tam giác nhọn.
B. Tam giác vuông. C. Tam giác cân. D. Tam giác đều.
Câu 10. Các mặt bên của hình chóp tứ giác đều ở hình sau là: A. SC ;
D SCB; SBM ; SMD .
B. SCD; SCB; SBM .
C. SCD; SC; SMD .
D. SCD; SCB; SBM ; SBD .
Câu 11. Cho hình chóp tam giác đều S.ABC có AB = 6cm , SH = 9cm . Độ dài các cạnh đáy
của hình chóp tam giác đều là:
A. AB = BC = SC = 6cm .
B. AB = BC = SA = 6cm .
C. AB = BC = AC = 6cm .
D. Các cạnh đáy tam giác đều là 9cm .
Câu 12. Cho ∆DEF vuông tại D. Em hãy chọn khẳng định
đúng trong các khẳng định sau theo định lý Pythagore.
A. EF = 13. B. 2 EF = 13 . C. 2 EF = 119 . D. EF= 119 .
II. PHẦN TỰ LUẬN (7,0 ĐIỂM)
Bài 1. (1,0 đ): Cho hai đa thức: 3 2
M = 2a - 12ab + 5b và 3 2
N = a + 12ab + 5b a) Tính M + N b)
Tính M - N
Bài 2. (2,0đ): Thực hiện phép tính a) x xy + - y( 2 2 .(2 3) 4 x + 5x)
b) (x + 2)(1+ 2 y) - 2(xy + 1) c) 3 2 2
(8x y - 12x y - 4xy) : 4xy d) (x - )2
3 + (5 - x).(5 + x)
Bài 3. (1,0đ): Phân tích các đa thức sau thành nhân tử a) 2
x + 12x + 36 b) 2 2
x + 1- y + 2x
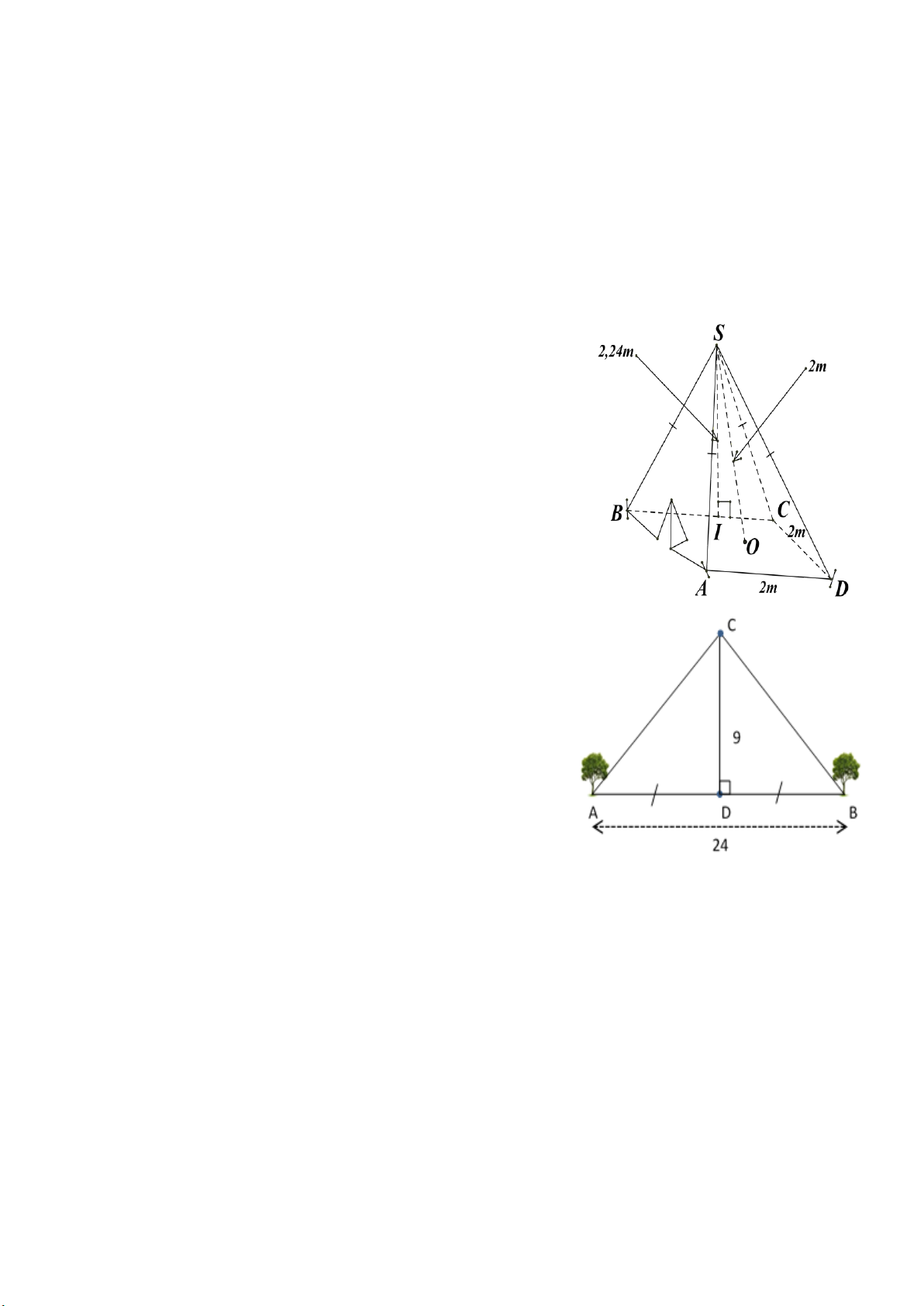
Bài 4.(1,0đ): Hình bên là một cái lều ở một trại hè của học sinh
tham gia cắm trại có dạng hình chóp tứ giác đều theo các kích thước như hình vẽ:
a/ Thể tích không khí bên trong lều là bao nhiêu ?
b/ Xác định số vải bạt cần thiết để dựng lều ( không tính
đến đường viền, nếp gấp, đáy…) là bao nhiêu ? Biết độ dài trung
đoạn của lều trại là 2,24 m.
( Kết quả làm tròn đến chữ số thập phân thứ hai).
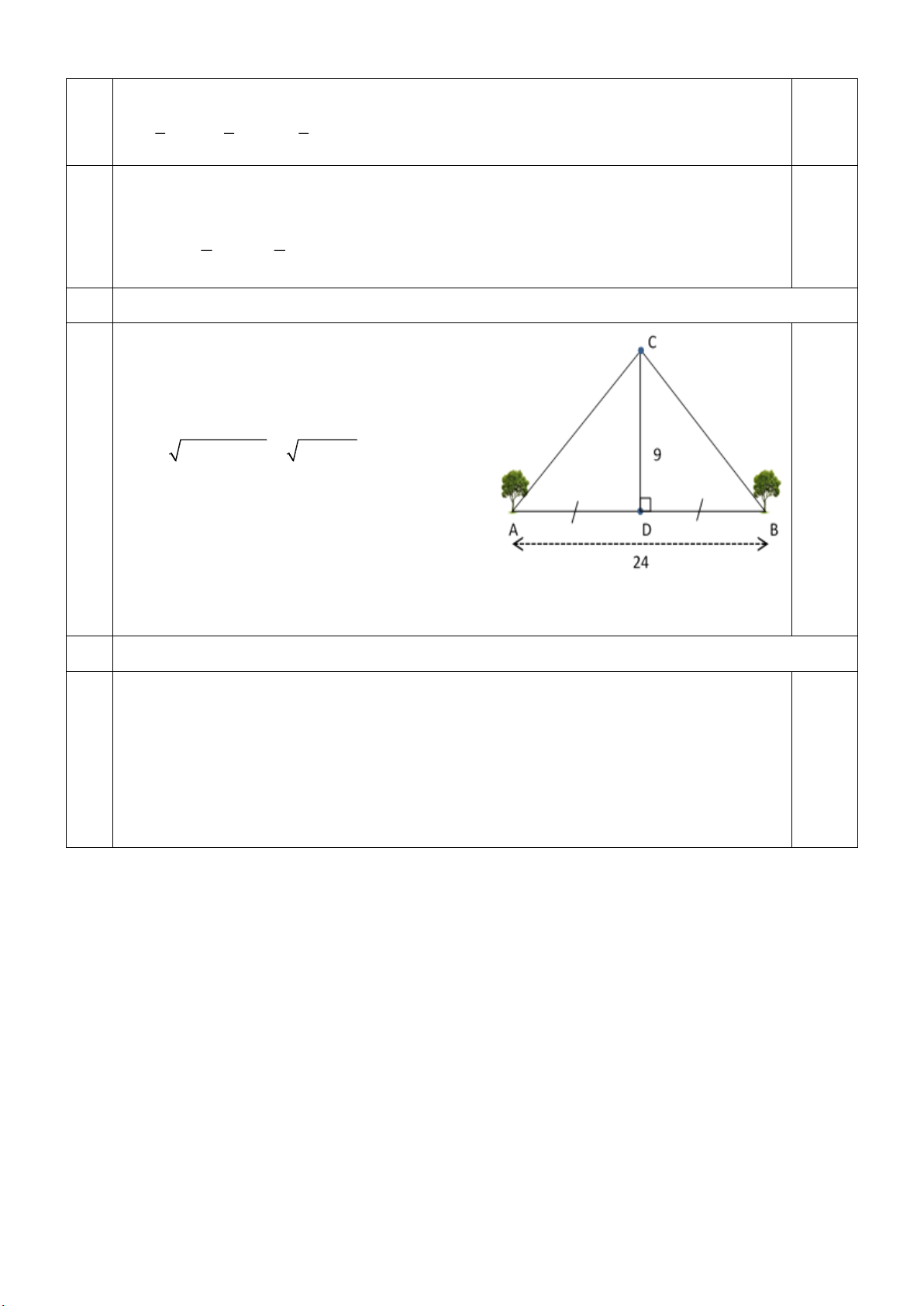
Bài 5. (1,0đ): Hai cây A và B được trồng dọc trên đường,
cách nhau 24m và cách đều cột đèn D . Ngôi trường C cách
cột đèn D là 9m theo hướng vuông góc với đường ( xem hình
vẽ). Tính khoảng cách từ mỗi cây đến ngôi trường.
Bài 6. (1,0đ): Cho các số x, y thoả mãn đẳng thức 2 2
5x + 5y + 8xy − 2x + 2y + 2 = 0 . Tính giá trị của 2023 2024 2025 biểu thức M = (x + y) + (x −2) +(y + ) 1 ___ HẾT ___ ỦY BAN NHÂN DÂN
ĐỀ THAM KHẢO HỌC KỲ I NĂM HỌC 2023 - 2024 HUYỆN HÓC MÔN ĐÁP ÁN TRƯỜNG THCS …….
MÔN: TOÁN - KHỐI LỚP: 8
PHẦN TRẮC NGHIỆM (3,0 ĐIỂM) 1 2 3 4 5 6 7 8 9 10 11 12 B B A D B C B C D A C A
PHẦN TỰ LUẬN (7,0 ĐIỂM) Bài Đáp án Điểm 1 (1,0 điểm) 3 2 3 2
M + N = M = 2a - 12ab + 5b + a + 12ab + 5b a) 0.5 3 = 3a + 10b 3 2
M - N = a - ab + b - ( 3 2 2 12 5
a + 12ab + 5b ) b) 3 2 3 2
= 2a - 12ab + 5b - a - 12ab - 5b 0.5 3 = a - 24ab 2 (2 điểm) x xy + - y( 2 2 .(2 3) 4 x + 5x) a) 0.5 2 2
= 4x y + 6x - 4x y - 20xy = 6x - 20xy b)
(x + 2)(1+ 2 y) - 2(xy + 1) = x + 2xy + 2 + 4 y - 2xy - 2 = x + 4 y 0.5 3 2 2 2 c)
(8x y - 12x y - 4xy) : 4xy = 2x y - 3x - 1 0.5 2 2 d) (x - )2
3 + (5 - x).(5 + x) = x - 6x + 9 + 25- x = - 6x + 34 0.5 3 (1 điểm) 2 a)
x + 12x + 36 = (x + )2 6 0.5 2 2
x + 1- y + 2x b) 2 2 2 2
= (x + 2x + 1) - y = (x + 1) - y 0.5
= (x + 1+ y)(x + 1- y) 4 (1 điểm)
Thể tích không khí bên trong lều chính là thể tích hình chóp tứ giác đều a) 1 1 8 0.5 2 3 V =
S h = 2 2 = 2,67(m ) 3 3 3
Số vải bạt cần thiết để dựng lều chính là diện tích xung quanh hình chóp tứ giác đều. b) 0.5 1 1 2 S
= C d = (2 4) 2, 24 8,96(m ) xq 2 2 5 (1 điểm)
Vì D là trung điểm của AB ( gt)
AD = DB = AB : 2 = 24: 2 =12m
Theo định lý Pythagore trong A CD vuông tại D ta có: 2 2 2 2 AC =
AD + CD = 12 + 9 = 15( ) m 1đ
CD vừa là đường cao đồng thời là đường trung tuyến ABC cân tại C
CA = CB =15m
Vậy khoảng cách từ mỗi cây đến ngôi trường khoảng 15m . 6 (1 điểm) 2 5x + 2 5y + 8xy − 2x + 2y + 2 = 0 2 (x − 2x +1) + 2 (y + 2y +1) + 2 (4x + 8xy + 2 4y ) = 0 (x − 2 1) + (y + 2 1) + 4(x + 2 y) = 0 1đ x =1; y = 1 − ; x + y = 0 2023 2024 2025
Vậy M = (1− ) 1 + (1− 2) + ( 1 − + ) 1 =1




