



Preview text:
UBND HUYỆN ..............
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
TRƯỜNG THCS .............. NĂM 2023 – 2024 MÔN: TOÁN 8
Thời gian kiểm tra: 90 phút (không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (3,0 ĐIỂM)
Câu 1. Trong những biểu thức sau, biểu thức nào là đơn thức nhiều biến? A. 3 8x + 3 .
B. xy − 2 y .
C. 4xyz . D. 2 2x + 3x +1 5 x + y
Câu 2. Cho các biểu thức 2 2
2x + 3x + y;4x + 8x + 4; xyz;
. Có báo nhiêu đa thức nhiều 3 5
biến trong các biểu thức trên? A. 1. B. 2 C. 3 D. 4
Câu 3. Nếu hai biểu thức P và Q nhận giá trị như nhau với … của biến thì ta nói P = Q là một
… Hãy điền vào chỗ để được khẳng định đúng.
A. một giá trị; hằng đẳng thức
B. mọi giá trị; hằng đẳng thức
C. vài giá trị; đồng nhất thức
D. một số giá trị; đồng nhất thức
Câu 4. Tìm hằng đẳng thức là bình phương của một tổng: A. 2 2 2 (a + ) b
= a + 2ab + b B. 2 2 2 (a + ) b
= a − 2ab − b C. 2 2 2 (a − ) b
= a − 2ab + b D. 2 (a − ) b = (a − ) b (a + ) b
Câu 5. Tìm hằng đẳng thức là tổng hai lập phương: A. 3 3 2 2
a + b = (a − )
b (a + 2ab + b ) B. 3 3 2 2
a + b = (a + )
b (a − 2ab + b ) C. 3 3 2 2
a + b = (a − )
b (a + ab + b ) D. 3 3 2 2
a + b = (a + )
b (a − ab + b ) A
Câu 6. Điều kiện xác định của phân thức là: B
A. A = 0 B. A 0
C. B = 0 D. B 0
Câu 7. Chọn câu sai. Với đa thức B ≠ 0, ta có: A . A M A. =
(Với M là đa thức khác đa thức 0) B . B M A A : M B. B. =
(Với M là 1 nhân tử chung, M khác đa thức 0) B B : M A A − M C. = B B − M A −A D. = − B B x − 2
Câu 8. Với điều kiện nào của x thì phân thức có nghĩa: x + 1 A. x = 1 B. x ≠ 1
C. x ≠ 2
D. x ≠ 1 và x ≠ 2
Câu 9. Cho hình chóp tam giác đều như hình sau, mặt đáy của hình chóp là : A. Mặt SAB B. Mặt ABC C. Mặt SAC D. Mặt SBC
Câu 10. Cho hình chóp tam giác đều S.MNP có SM = 4cm, MN = 5cm. So sánh độ dài SN và SP:
A. SN ≠ SP B. SN > SP
C. SN = SP D. SN < SP
Câu 11. Hình chóp tứ giác đều có mấy cạnh bên: A. 1. B. 2 C. 3 D. 4
Câu 12. Cho tam giác ABC vuông tại C, áp dụng định lý Pythagoreta có: A. 2 2 2
AB = CA + CB B. 2 2 2
BC = AB + AC C. 2 2 2
AB = CA − CB D. 2 2 2
BC = AB − AC
II. PHẦN TỰ LUẬN (7,0 ĐIỂM)
Bài 1. (1 điểm). Cho 2 đa thức: 2 2
M = 2x − 5xy + 4 y + 7 2 2
N = x −10xy + 8y − 6 a)
Tìm đa thức P = M + N
b) Tìm đa thức Q = M − N
Bài 2. (2 điểm). Thực hiện phép tính: a) 2 3 2
x (x − y) + (10x y ) : (2xy) b) 2
x (x + y) + xy(2x −1) c) 2 2 2
(4x y − 2xy + 6x y ) : (xy) d) 2
(x −1)(x + x +1) − (x +1)(x −1)
Bài 3. (1 điểm). Phân tích các đa thức sau thành nhân tử: a) 2 2
x − 6xy + 9y b) 2 2
25x − y + 4y − 4
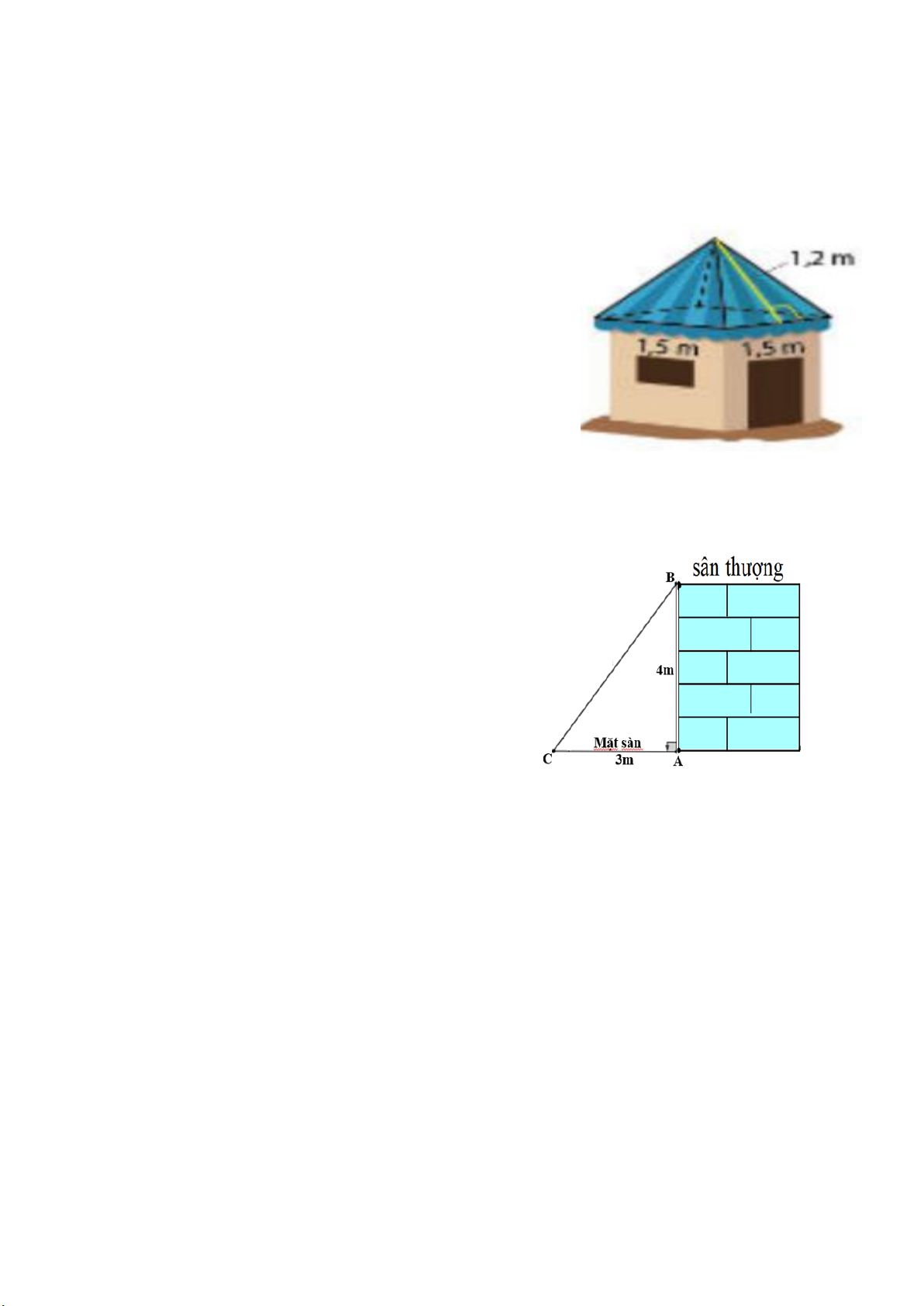
Bài 4. (1 điểm). Mái của một chòi trên bãi biển có dạng
hình chóp tứ giác đều như hình bên. a)
Tính diện tích vải bạc cần dùng để phủ mái
chòi, biết rằng người ta chỉ dùng một lớp bạt
(không tính phần viền xung quanh). b)
Biết rằng cứ mỗi mét vuông bạc cần trả chi
phí khoảng 100 000 đồng. Hỏi cần phải trả bao
nhiêu tiền để hoàn thành mái chòi?
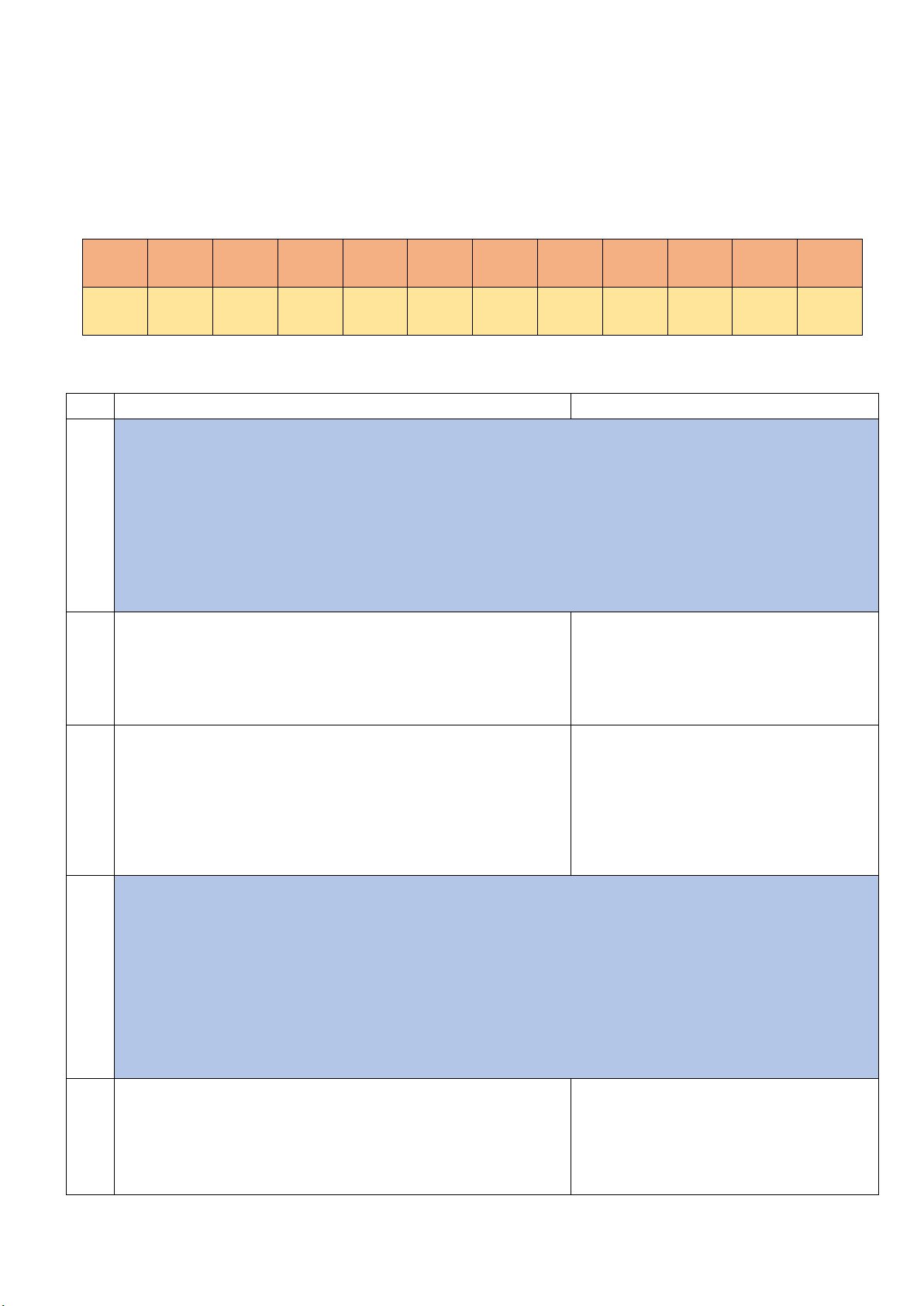
Bài 5. (1 điểm). Bác thợ muốn xây một chiếc cầu
thang bắc từ mặt sàn lên sân thượng. Biết rằng
bức tường từ sàn lên sân thượng cao 4m, chân
cầu thang cách bức tường 3m. Hỏi chiều dài
của cầu thang là bao nhiêu mét?
Bài 6. (1 điểm) Cho x và y thỏa: 2 2
x − 2xy + 2y + 2y +1 = 0 .
Tính giá trị biểu thức B = 2023x + 2024 y . ____HẾT____ ỦY BAN NHÂN DÂN
KIỂM TRA GIỮA KỲ I NĂM HỌC 2023 - HUYỆN ………….. 2024
PHÒNG GIÁO DỤC VÀ ĐÀO ĐÁP ÁN TẠO
MÔN: TOÁN - KHỐI LỚP: 8
PHẦN TRẮC NGHIỆM (3,0 ĐIỂM) 1 2 3 4 5 6 7 8 9 10 11 12 C C C A D D C B B C D A
PHẦN TỰ LUẬN (7,0 ĐIỂM) Bài Đáp án Điểm
(1,0 điểm) Cho 2 đa thức: 2 2
M = 2x − 5xy + 4 y + 7 1 2 2
N = x −10xy + 8y − 6 a)
Tìm đa thức P = M + N b)
Tìm đa thức Q = M − N
a)P = M + N 0.25 2 2 2 2 a)
= 2x − 5xy + 4y + 7 + x −10xy + 8y − 6 2 2 = 0.25
3x −15xy + 12 y + 1
b)Q = M − N 2 2 2 2
= 2x − 5xy + 4y + 7 − (x −10xy + 8y − 6) 0.2 b) 2 2 2 2
= 2x − 5xy + 4y + 7 − x +10xy − 8y + 6 0.25 2 2
= x + 5xy − 4y +13
(2 điểm). Thực hiện phép tính: 2 3 2
a) x (x − y) + (10x y ) : (2xy) 2 2 )
b x (x + y) + xy(2x −1) 2 2 2
c) (4x y − 2xy + 6x y ) : (xy) 2
d) (x −1)(x + x +1) − (x +1)(x −1) 2 3 2
a)x (x − y) + (10x y ) : (2xy) 0.25 a) 3 2 2
= x − x y + 5x y 0.25 3 2 = x + 4x y 2
b)x (x + y) + xy(2x −1) 0.25 b) 3 2 2
= x + x y + 2x y − xy 0.25 3 2
= x + 3x y − xy c) 2 2 2
c)(4x y − 2x y + 6xy) : (xy) = 4xy − 2x + 6 0.5 2
d )(x −1)(x + x + 1) − (x + 1)(x −1) 3 2 2 2
= x + x + x − x − x −1− (x −1) 0.25 d 3 2 2 2 =
x + x + x − x − x −1 − x + 1 0.25 3 2 = x − x
(1 điểm). Phân tích các đa thức sau thành nhân tử: 2 2
a)x − 6xy + 9y 3 2 2 )
b 25x − y + 4y − 4 2 2 2 − + = − a) a)x 6xy 9y (x 3y) 0.5 2 2
b)25x − y + 4 y − 4 2 2
= 25x − (y − 4y + 4) 0.25 b) 2 2 =
25x − ( y − 2) 0.25
= (5x + y − 2)(5x − y + 2)
(1 điểm) Mái của một chòi trên bãi biển có dạng hình chóp tứ giác đều như hình bên. 4
a) Tính diện tích vải bạc cần dùng để phủ mái chòi, biết rằng người ta chỉ dùng một
lớp bạt (không tính phần viền xung quanh).
b) Biết rằng cứ mỗi mét vuông bạc cần trả chi phí khoảng 100000 đồng. Hỏi cần phải
trả bao nhiêu tiền để hoàn thành mái chòi? a)
Diện tích vải bạc cần dùng để phủ mái chòi: 0.5 1 2
.(1,5.4).1, 2 = 3,6(m ) 2
Số tiền cần phải trả để hoàn thành mái chòi: b) 3,6.100000 = 360000 (đồng) 0.5
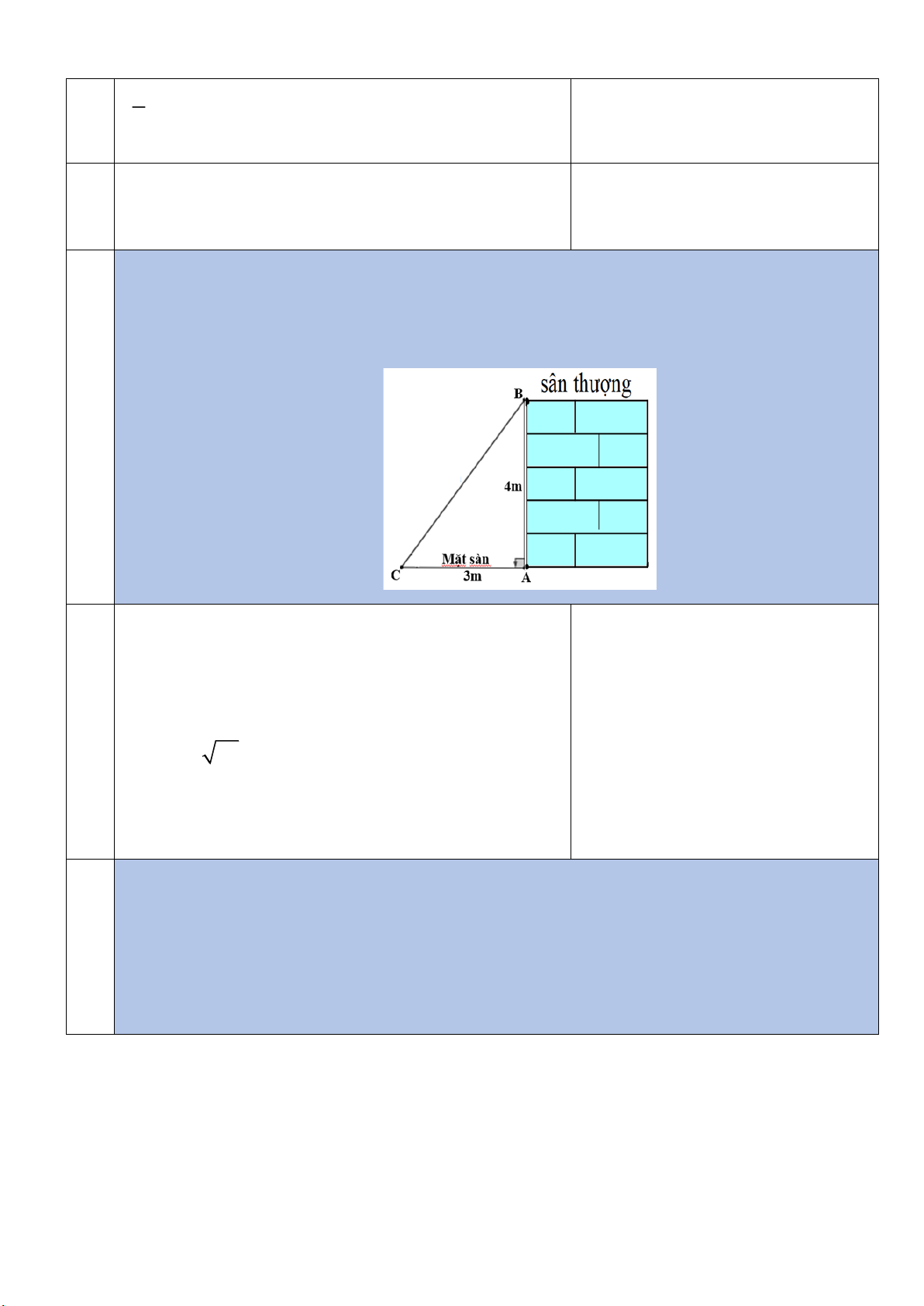
(1 điểm) Bác thợ muốn xây một chiếc cầu thang bắc từ mặt sàn lên sân thượng. Biết
rằng bức tường từ sàn lên sân thượng cao 4m, chân cầu thang cách bức tường 3m. Hỏi
chiều dài của cầu thang là bao nhiêu mét? 5
Áp dụng định lý Pytago cho tam giác ABC vuông tại A ta được: 0.5 2 2 2 2 2 = + = + = BC AB AC 4 3 25 0.25
BC = 25 = 5(m) 0.25
Vậy chiều dài của cầu thang là 5m.
(1 điểm) Cho x và y thỏa: 2 2
x − 2xy + 2y + 2y +1 = 0 . 6
Tính giá trị biểu thức B = 2023x + 2024 y . Ta có: 2 2
x − 2xy + 2y + 2y +1 = 0 2 2 2
x − 2xy + y + y + 2y +1= 0 0.25 x − + ( y + )2 2 ( 1) 1 = 0 0.25
x −1 = 0 và y +1= 0
x =1 và y = 1 −
Thế x = 1 và y = 1
− vào B = 2023x + 2024y ta 0.5
được: B = 2023.1+ 2024.( 1 − ) = 2023 − 2024 = 1 − https://www.vnteach.com




