





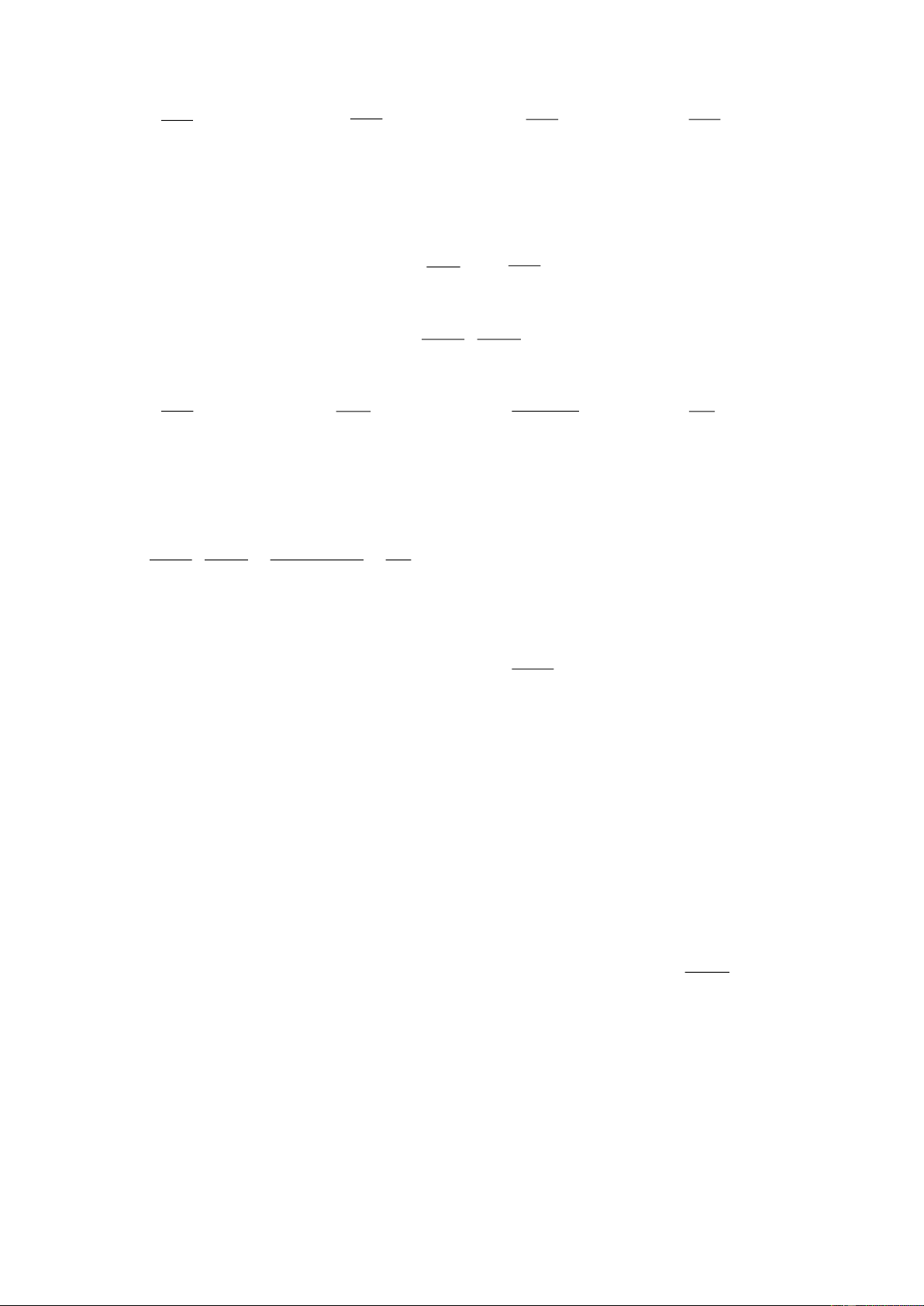



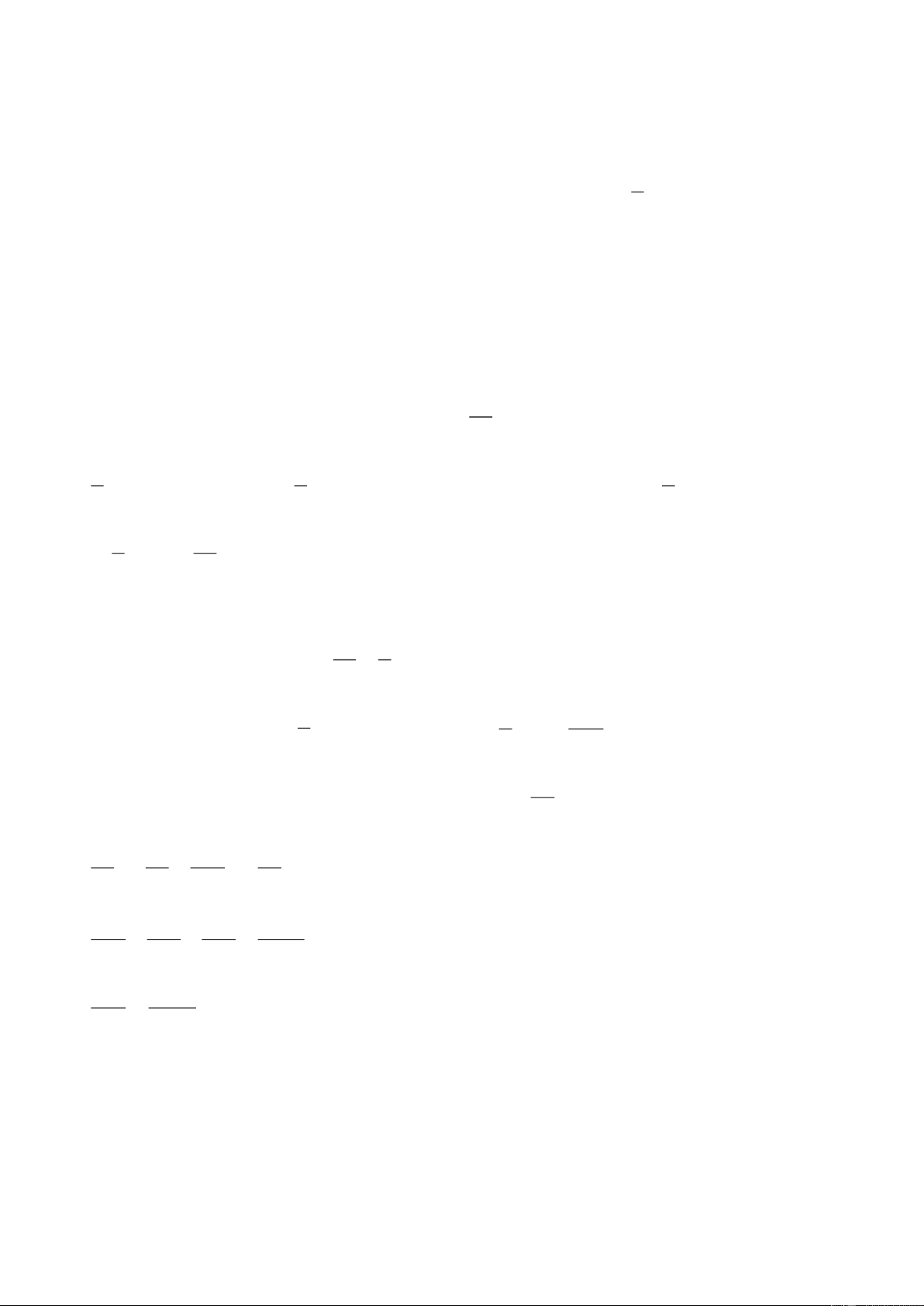
Preview text:
BỘ SÁCH: KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2
MÔN: TOÁN – LỚP 8
A. KHUNG MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 – TOÁN 8 – KẾT NỐI TRI THỨC
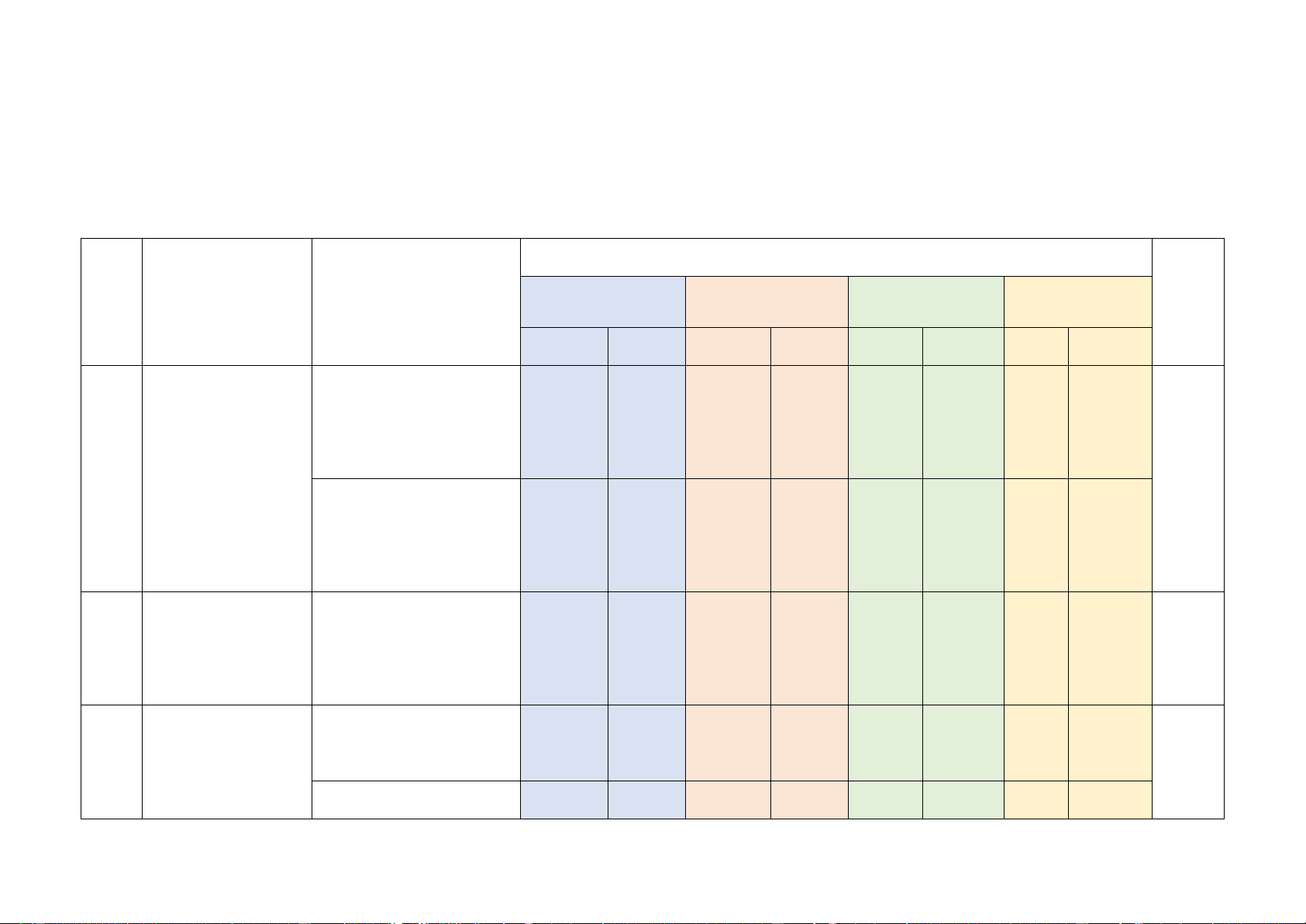
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Tổng Chương/ Chủ STT
Nội dung kiến thức Nhận biết Thông hiểu Vận dụng
Vận dụng cao % đề điểm TN TL TN TL TN TL TN TL
Phân thức đại số. 1 1
Tính chất cơ bản của (0,25đ) (0,5đ)
phân thức đại số. 1
Phân thức đại số 35%
Các phép toán cộng, 2 1 1 1 1
trừ, nhân, chia các (0,5đ) (0,25đ) (0,5đ) (1,0đ) (0,5đ)
phân thức đại số Phương trình Phương trình bậc 1 1 1 2 2
bậc nhất và hàm 30% nhất (0,25đ) (0,25đ) (0,5đ) (2,0đ)
số bậc nhất
Tam giác đồng 2 1 2 1
Tam giác đồng dạng 3 dạng (0,5đ) (0,25đ) (1,5đ) (0,5đ) 35% Định lí Pythagore 1 1 (0,25đ) (0,5đ)
Tổng: Số câu 6 1 4 5 4 1 21 Điểm
(1,5đ) (0,5đ) (1,0đ) (3,0đ) (3,5đ) (0,5đ) (10đ) Tỉ lệ 20% 40% 35% 5% 100% Tỉ lệ chung 60% 40% 100% Lưu ý:
– Các câu hỏi trắc nghiệm khách quan là các câu hỏi ở mức độ nhận biết và thông hiểu, mỗi câu hỏi có 4 lựa chọn, trong đó có
duy nhất 1 lựa chọn đúng.
– Các câu hỏi tự luận là các câu hỏi ở mức độ nhận biết, thông hiểu, vận dụng và vận dụng cao.
– Số điểm tính cho 1 câu trắc nghiệm là 0,25 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải
tương ứng với tỉ lệ điểm được quy định trong ma trận.
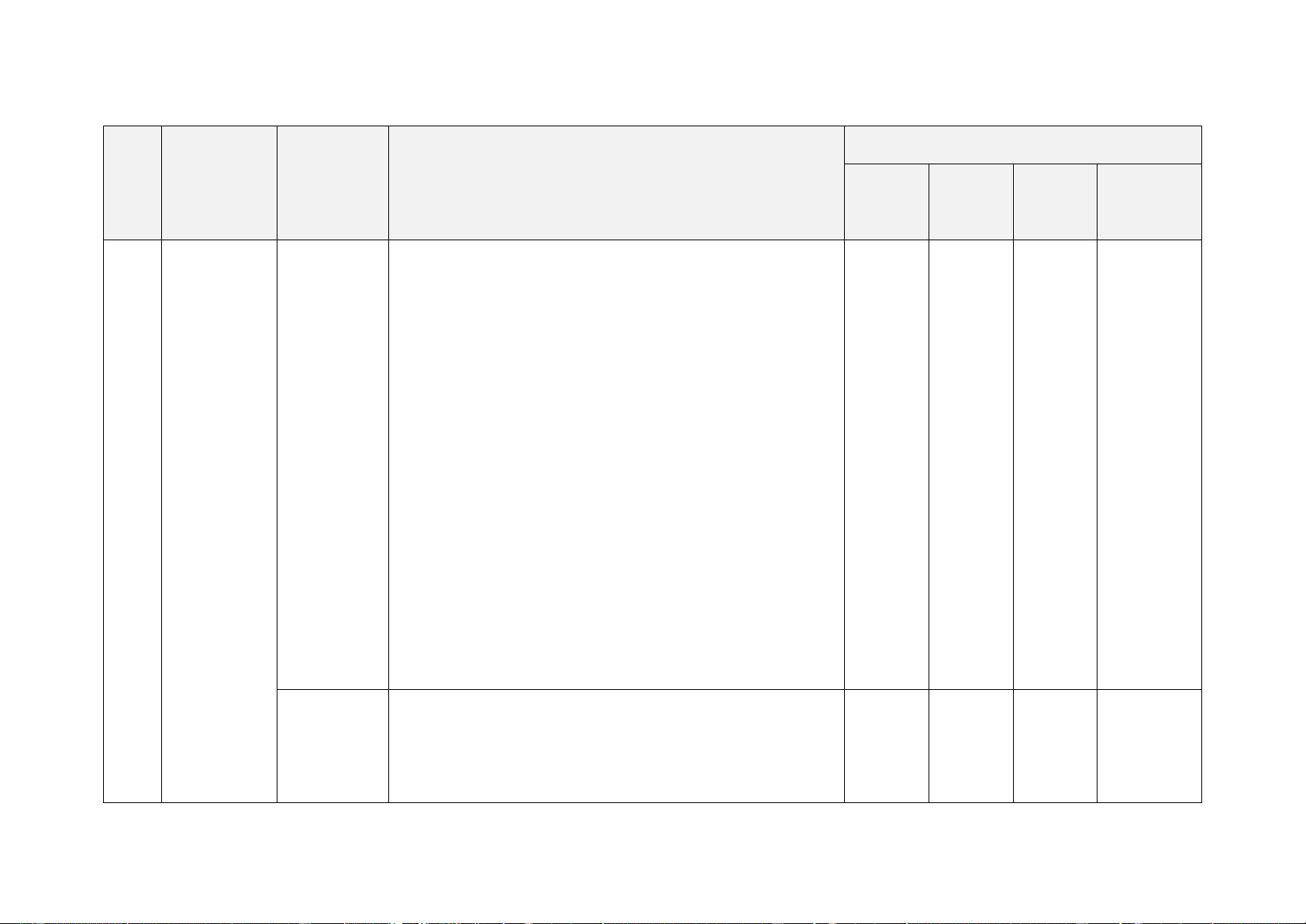
B. BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 – TOÁN 8 – KẾT NỐI TRI THỨC
Số câu hỏi theo mức độ Chương/ Nội dung STT
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Nhận Thông Vận Vận Chủ đề kiến thức biết hiểu dụng dụng cao 1
Phân thức Phân thức Nhận biết: 1TN, đại số đại
số. – Nhận biết được các khái niệm cơ bản về phân 1TL
Tính chất thức đại số: định nghĩa; điều kiện xác định; giá trị
cơ bản của của phân thức đại số; hai phân thức bằng nhau.
phân thức – Nhận biết được mẫu thức chung của các phân đại số. thức. Thông hiểu:
– Mô tả được những tính chất cơ bản của phân thức đại số. Vận dụng:
– Sử dụng các tính chất cơ bản của phân thức để xét
sự bằng nhau của hai phân thức, rút gọn phân thức.
Các phép Nhận biết: 2TN 1TN, 1TL 1TL
toán cộng, – Nhận biết được phân thức đối, phân thức nghịch 1TL
trừ, nhân, đảo của một phân thức.
chia các Thông hiểu:
phân thức – Thực hiện được các phép tính: phép cộng, phép trừ, đại số
phép nhân, phép chia đối với hai phân thức đại số. Vận dụng:
– Vận dụng được các tính chất giao hoán, kết hợp,
phân phối của phép nhân đối với phép cộng, quy
tắc dấu ngoặc với phân thức đại số trong tính toán.
Vận dụng cao:
– Tìm được giá trị lớn nhất, giá trị nhỏ nhất của phân thức đại số.
– Tìm được giá trị nguyên của x để phân thức đạt giá trị nguyên.
– Rút gọn, tính giá trị của một phân thức phức tạp. 2 Phương Phương Nhận biết: 1TN 1TN, 2TL
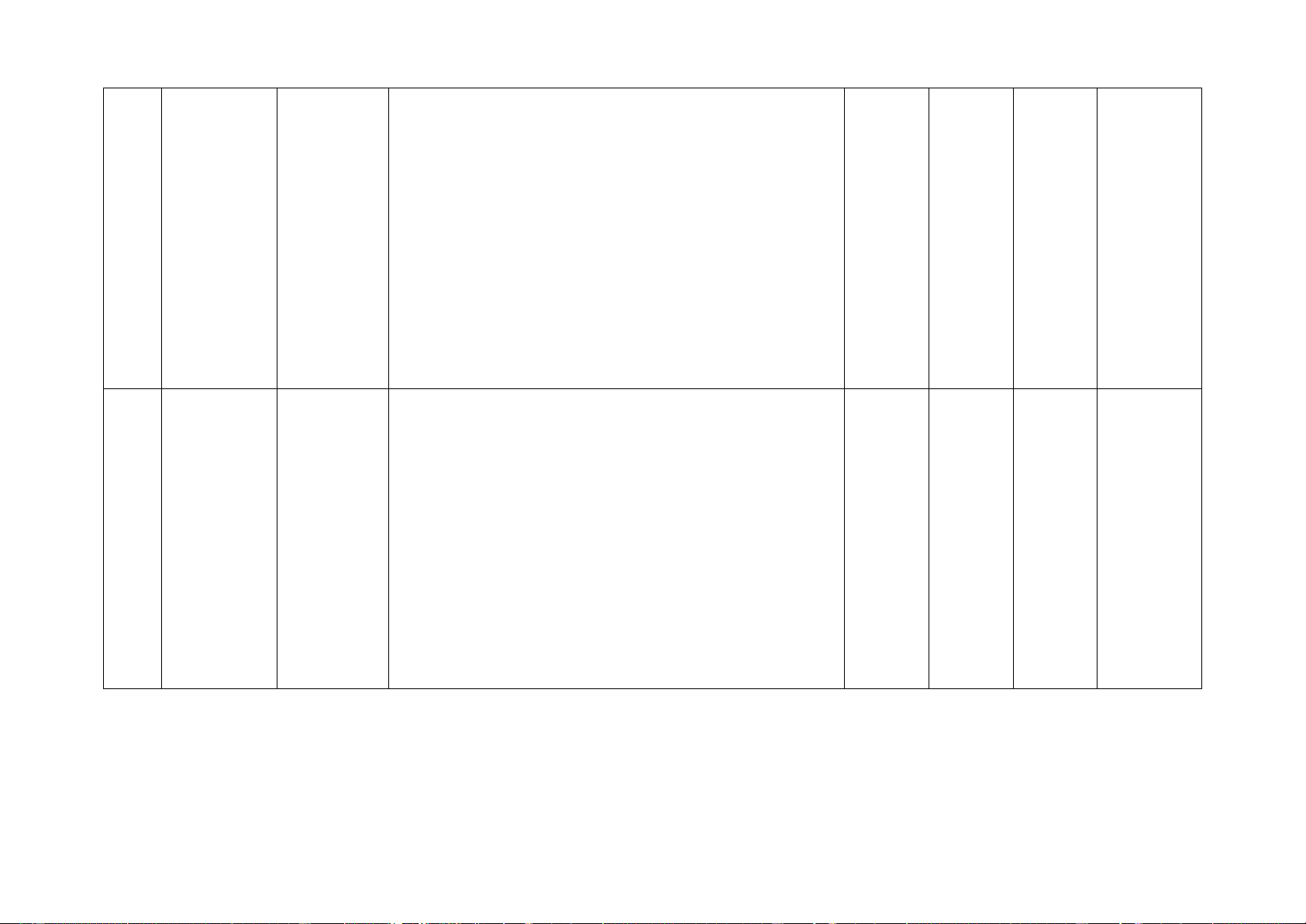
trình bậc trình bậc – Nhận biết được phương trình bậc nhất một ẩn. 1TL nhất và nhất
– Nhận biết được một số là nghiệm của phương hàm số
trình bậc nhất một ẩn. bậc nhất Thông hiểu:
– Hiểu được cách giải phương trình bậc nhất một ẩn.
– Giải được phương trình bậc nhất một ẩn. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn với
phương trình bậc nhất (ví dụ: các bài toán liên quan
đến chuyển động trong Vật lí, các bài toán liên quan đến Hóa học, …). 3
Tam giác Tam giác Nhận biết: 2TN 1TN, 1TL
đồng dạng đồng dạng – Nhận biết được cách viết kí hiệu hai tam giác 2TL đồng dạng.
– Từ kí hiệu hai tam giác đồng dạng viết được hai
góc tương ứng bằng nhau và tỉ số hai cạnh tương ứng. Thông hiểu:
– Mô tả được định nghĩa của hai tam giác đồng dạng.
– Giải thích được các trường hợp đồng dạng của
hai tam giác, của hai tam giác vuông. Vận dụng:
– Chứng minh được hai tam giác đồng dạng, hai
tam giác vuông đồng dạng.
– Giải quyết được một số vấn đề thực tiễn gắn với
việc vận dụng kiến thức về hai tam giác đồng dạng
(ví dụ: tính độ dài đường cao hạ xuống cạnh huyền
trong tam giác vuông bằng cách sử dụng mối quan
hệ giữa đường cao đó với tích hai hình chiếu của
hai cạnh góc vuông lên cạnh huyền; đo gián tiếp
chiều cao của vật; tính khoảng cách giữa hai vị trí
trong đó có một vị trí không thể tới được, …). Định
lí Thông hiểu: 1TN,
Pythagore – Giải thích được định lí Pythagore. 1TL
– Tính được độ dài cạnh trong tam giác vuông bằng
cách sử dụng định lí Pythagore. Vận dụng:
– Giải quyết được một số vấn đề thực tiễn gắn với
việc vận dụng định lí Pythagore (ví dụ: tính khoảng cách giữa hai vị trí).
C. ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 – TOÁN 8 – KẾT NỐI TRI THỨC
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 TRƯỜNG …
MÔN: TOÁN – LỚP 8
NĂM HỌC: … – … Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1. Biểu thức nào sau đây không phải là phân thức? − 2 x − 2x + 4 2 − + A. 5xy 7 2x x 1 . B. 2 5xy − 2. C. . . 2 y 3x − D. 1 1 x − y
Câu 2. Phân thức đối của phân thức 3x là x + y x x + y x x A. 3 . B. . C. 3 − . D. 3 − . x − y 3x x + y x − y 2 3y
Câu 3. Phân thức nghịch đảo của phân thức − là 2x 2 3y 2 2x 2x 2x A. . B. − . C. − . D. . 2x 3y 2 3y 2 3y 2 5 15x 34 y
Câu 4. Với x 0 và y 0, phép tính có kết quả là 4 3 17 y 15x + A. 10x y x y y . B. 10 . C. 10 . D. 2 . 3y 3x 3xy x
Câu 5. Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn? A. 2 1 – x = 0. B. 2x – 5 = 0. C. 2 +1 = 0. D. 3
x – x + 2 = 0. x − 3
Câu 6. Với m = −1 thì phương trình ( 2
2m − 2) x = m +1 A. Vô nghiệm. B. Vô số nghiệm.
C. Có nghiệm duy nhất là x = m −1. D. Có 1 nghiệm là 1 x = . m −1
Câu 7. Cho tam giác ABC đồng dạng với tam giác A B C
. Khẳng định nào sau đây là đúng? A. B = B . B. A = B . C. C = B . D. B = C . Câu 8. Nếu A BC ∽ D
EF theo tỉ số k thì D EF ∽ A
BC theo tỉ số bằng A. 1 k. B. 1 . C. 2 k . D. . k 2 k
Câu 9. Cho tam giác ABC vuông tại ,
A kẻ AH ⊥ BC ( H BC). Khẳng định nào sau đây là đúng? A. AB C ∽ H AC. B. AB C ∽ AH C. C. ABC ∽ AH . B D. AB C ∽ AB H .
Câu 10. Bộ ba độ dài nào sau đây là độ dài ba cạnh của một tam giác vuông? A. 9 cm, 12 cm, 15 cm. B. 7 cm, 8 cm, 10 cm. C. 6 dm, 7 dm, 9 dm. D. 10 m, 13 m, 15 m.
PHẦN II. TỰ LUẬN (7,5 điểm) 2 − +
Bài 1. (2,0 điểm) Cho biểu thức x 2 x 1 x 5 A = − + : 2 − . 2
x + 3 x − 3 9 − x 3 + x
a) Tìm điều kiện xác định của biểu thức . A b) Rút gọn biểu thức . A
c) Tính giá trị của biểu thức A biết 2
x − x − 2 = 0.
Bài 2. (1,0 điểm) Giải các phương trình sau: a) 2 3
5 − 2x = x + 11.
b) x(x + 3) − 3x = (x + 2) +1.
Bài 3. (1,5 điểm) Giải bài toán sau bằng cách lập phương trình:
Một xe tải và một xe con cùng khởi hành, từ tỉnh A đến tỉnh B. Xe tải đi với vận 3
tốc 30 km/h, xe con đi với vận tốc 45 km/h. Sau khi đi được quãng đường AB, xe 4
con tăng vận tốc 5 km/h trên quãng đường còn lại thì đến B sớm hơn xe tải là 2 giờ 27
phút. Tính quãng đường AB.
Bài 4. (2,5 điểm) Cho tam giác ABC vuông tại A có AB = 6 cm và AC = 8 cm. Đường
phân giác của góc ABC cắt cạnh AC tại .
D Từ C kẻ CE ⊥ BD tại E. a) Tính độ dài AD BC và tỉ số . DC b) Chứng minh A BD∽ E
BC. Từ đó suy ra BD EC = AD BC. c) Chứng minh CD CE = . BC BE
d) Gọi EH là đường cao EBC
. Chứng minh CH HB = ED . EB
Bài 5. (0,5 điểm) Rút gọn biểu thức sau:
B = (ab + bc + ca) 1 1 1 1 1 1 + + − abc + + . 2 2 2 a b c a b c -----HẾT-----
D. ĐÁP ÁN & HƯỚNG DẪN ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 – TOÁN 8 – KẾT NỐI TRI THỨC
PHÒNG GIÁO DỤC & ĐÀO TẠO …
ĐÁP ÁN & HƯỚNG DẪN GIẢI TRƯỜNG …
KIỂM TRA GIỮA HỌC KÌ 2 MÃ ĐỀ MT101
MÔN: TOÁN – LỚP 8
NĂM HỌC: … – …
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2,5 điểm)
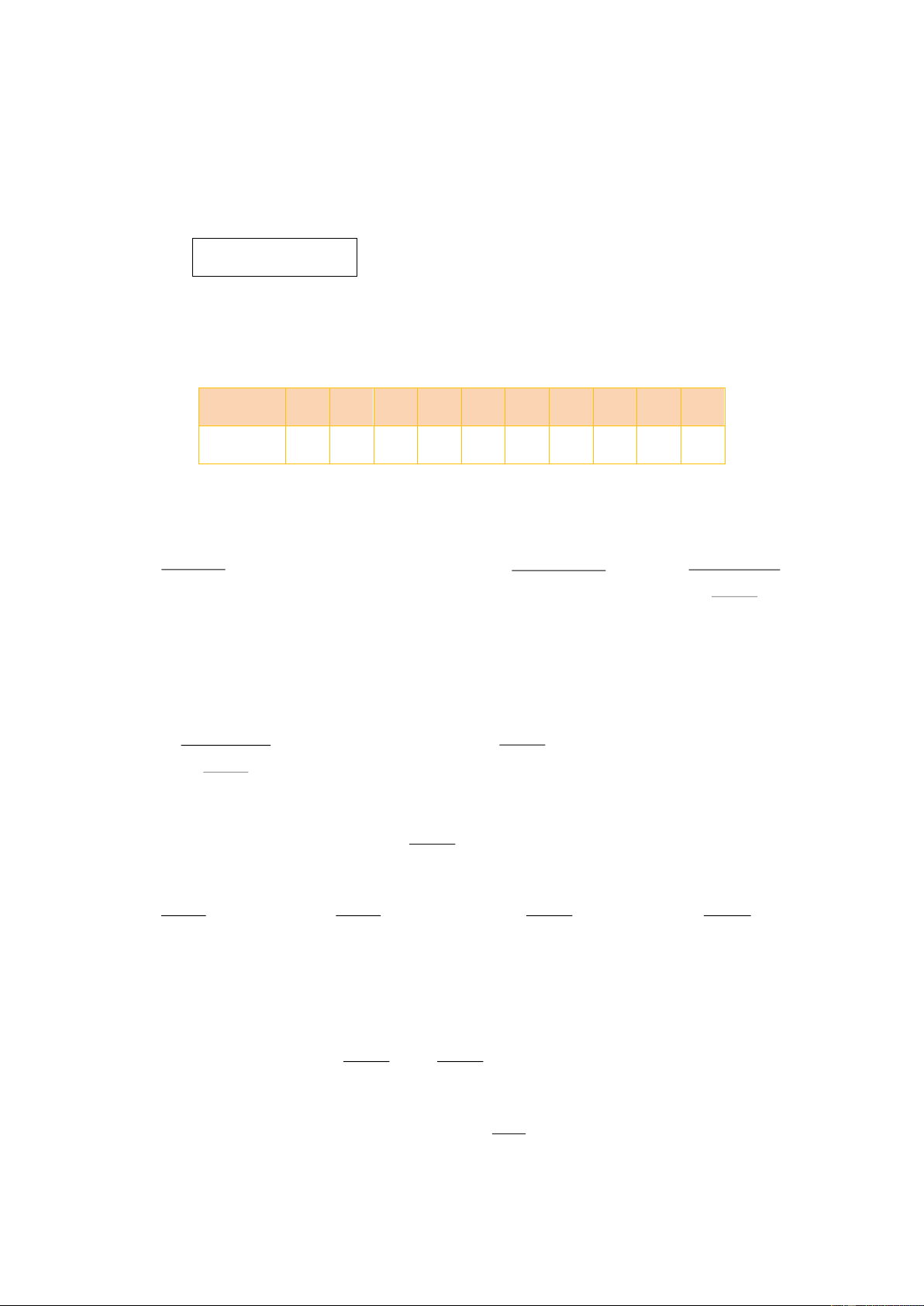
Bảng đáp án trắc nghiệm: Câu 1 2 3 4 5 6 7 8 9 10
Đáp án D C C D B B A B A A
Hướng dẫn giải phần trắc nghiệm
Câu 1. Biểu thức nào sau đây không phải là phân thức? − 2 − + 2 − + A. 5xy 7 x 2x 4 2x x 1 . B. 2 5xy − 2. C. . D. . 2 y 3x −1 1 x − y Hướng dẫn giải
Đáp án đúng là: D 2 − + Biểu thức 2x
x 1 không phải phân thức vì 1 không phải là đa thức. 1 x − y x − y
Câu 2. Phân thức đối của phân thức 3x là x + y x x + y x x A. 3 . B. . C. 3 − . D. 3 − . x − y 3x x + y x − y Hướng dẫn giải
Đáp án đúng là: C
Phân thức đối của phân thức 3x là 3x − . x + y x + y 2
Câu 3. Phân thức nghịch đảo của phân thức 3y − là 2x 2 2 3y 2x 2x 2x A. . B. − . C. − . D. . 2x 3y 2 3y 2 3y Hướng dẫn giải
Đáp án đúng là: C 2
Phân thức nghịch đảo của phân thức 3y − là 2x − . 2x 2 3y 2 5 15x 34 y
Câu 4. Với x 0 và y 0, phép tính có kết quả là 4 3 17 y 15x + A. 10x y x y y . B. 10 . C. 10 . D. 2 . 3y 3x 3xy x Hướng dẫn giải
Đáp án đúng là: D 2 5 2 5 15x 34 y 15x 34 y 2 y Ta có: = = . 4 3 4 3 17 y 15x 17 y 15x x
Câu 5. Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn? A. 2 1 – x = 0. B. 2x – 5 = 0. C. 2 +1 = 0. D. 3
x – x + 2 = 0. x − 3 Hướng dẫn giải
Đáp án đúng là: B
Phương trình bậc nhất một ẩn có dạng ax + b = 0 với a 0.
Vậy ta chọn phương án B.
Câu 6. Với m = −1 thì phương trình ( 2
2m − 2) x = m +1 A. Vô nghiệm. B. Vô số nghiệm.
C. Có nghiệm duy nhất là x = m −1. D. Có 1 nghiệm là 1 x = . m −1 Hướng dẫn giải
Đáp án đúng là: B
Thay m = −1 vào phương trình ( 2
2m − 2) x = m +1 ta có: (− )2 2 1 − 2 x = 1 − +1 0x = 0 (luôn đúng).
Vậy phương trình có vô số nghiệm.
Câu 7. Cho tam giác ABC đồng dạng với tam giác A B C
. Khẳng định nào sau đây là đúng? A. B = B . B. A = B . C. C = B . D. B = C . Hướng dẫn giải
Đáp án đúng là: A Vì ABC ∽ A B C
nên ta có A = A ; B = B ; C = C .
Vậy phương án A là khẳng định đúng. Câu 8. Nếu A BC ∽ D
EF theo tỉ số k thì D EF ∽ A
BC theo tỉ số bằng A. 1 k. B. 1 . C. 2 k . D. . k 2 k Hướng dẫn giải
Đáp án đúng là: B Nếu A BC ∽ D
EF theo tỉ số k thì D EF ∽ A
BC theo tỉ số bằng 1 . k
Câu 9. Cho tam giác ABC vuông tại ,
A kẻ AH ⊥ BC ( H BC). Khẳng định nào sau đây là đúng? A. AB C ∽ H AC. B. AB C ∽ AH C. C. ABC ∽ AH . B D. AB C ∽ AB H . Hướng dẫn giải
Đáp án đúng là: A
Xét ABC (vuông tại )
A và HAC (vuông tại H ) có B H
C là góc chung nên AB C ∽ H AC.
Tương tự, ta cũng có ABC ∽ H . BA A C
Vậy ta chọn phương án A.
Câu 10. Bộ ba độ dài nào sau đây là độ dài ba cạnh của một tam giác vuông? A. 9 cm, 12 cm, 15 cm. B. 7 cm, 8 cm, 10 cm. C. 6 dm, 7 dm, 9 dm. D. 10 m, 13 m, 15 m. Hướng dẫn giải
Đáp án đúng là: A Ta có: ⦁ 2 2 2
9 +12 = 225 =15 , do đó bộ ba độ dài 9 cm, 12 cm, 15 cm là độ dài ba cạnh của một tam giác vuông. ⦁ 2 2 2
7 + 8 =113 10 , do đó bộ ba độ dài 7 cm, 8 cm, 10 cm không là độ dài ba cạnh của một tam giác vuông. ⦁ 2 2 2
6 + 7 = 85 9 , do đó bộ ba độ dài 6 dm, 7 dm, 9 dm không là độ dài ba cạnh của một tam giác vuông. ⦁ 2 2 2
10 +13 = 269 15 , do đó bộ ba độ dài 10 m, 13 m, 15 m không là độ dài ba cạnh của một tam giác vuông.
Vậy ta chọn phương án A.
PHẦN II. TỰ LUẬN (7,5 điểm) 2 − +
Bài 1. (2,0 điểm) Cho biểu thức x 2 x 1 x 5 A = − + : 2 − . 2
x + 3 x − 3 9 − x 3 + x
a) Tìm điều kiện xác định của biểu thức . A b) Rút gọn biểu thức . A
c) Tính giá trị của biểu thức A biết 2
x − x − 2 = 0. Hướng dẫn giải a) Ta có 2
9 − x = (3 − x)(3 + x). x + 5
2(3 + x) − ( x + 5)
6 + 2x − x − 5 x + 1 2 − = = = . 3 + x 3 + x 3 + x x + 3 x + 3 0 x −3 0 + − x 3 0 x 3
Điều kiện xác định của biểu thức A là 2 9 − x 0
hay x − 3 0, tức là x 3 . x + 5 + − x 1 0 x 1 2 − 0 3 + x
Vậy điều kiện xác định của biểu thức A là x 3
− , x 3 và x 1. − b) Với x 3
− , x 3 và x 1 − ta có: 2 x 2 x −1 x + 5 A = − + : 2 − 2
x + 3 x − 3 9 − x 3 + x 2 x 2 x −1 x +1 = − − x + x − (x − )(x + ) : 3 3 3 3 x + 3
x( x − ) − ( x + ) − ( 2 3 2 3 x − ) 1 x +1 = ( x − )( x + ) : 3 3 x + 3 2 2
x − 3x − 2x − 6 − x +1 x + 3 = (x − )(x + ) . 3 3 x + 1 5 − x − 5 x + 3 −5( x + ) − = 1 5 ( = = . x − )( x + ) . 3 3 x + 1 (x − 3)(x + ) 1 x − 3 − Vậy với x 3
− , x 3 và x 1 − thì 5 A = . x − 3 c) Với 2
x − x − 2 = 0 ta có 2
x − 2x + x − 2 = 0
x( x − 2) + ( x − 2) = 0 (x − 2)(x + ) 1 = 0
Suy ra x − 2 = 0 hoặc x +1 = 0
x = 2 (thỏa mãn điều kiện) hoặc x = 1
− (không thỏa mãn điều kiện) − − −
Thay x = 2 vào biểu thức 5 A = ta được: 5 5 A = = = 5. x − 3 2 − 3 1 − Vậy nếu 2
x − x − 2 = 0 thì A = 5.
Bài 2. (1,0 điểm) Giải các phương trình sau: a) 2 3
5 − 2x = x + 11.
b) x(x + 3) − 3x = (x + 2) +1. Hướng dẫn giải
a) 5 − 2x = x +11
b) x(x + )2 − x = (x + )3 3 3 2 +1 2
− x − x =11− 5 x( 2 x + x + ) 3 2 6
9 − 3x = x + 6x +12x + 8 +1 −3x = 6 3 2 3 2
x + 6x + 9x − 3x = x + 6x + 12x + 9 x = 2. − −6x = 9
Vậy phương trình đã cho có nghiệm x = 1 − ,5 là x = 2. −
Vậy phương trình đã cho có nghiệm là x = −1,5.
Bài 3. (1,5 điểm) Giải bài toán sau bằng cách lập phương trình:
Một xe tải và một xe con cùng khởi hành, từ tỉnh A đến tỉnh B. Xe tải đi với vận 3
tốc 30 km/h, xe con đi với vận tốc 45 km/h. Sau khi đi được quãng đường AB, xe 4
con tăng vận tốc 5 km/h trên quãng đường còn lại thì đến B sớm hơn xe tải là 2 giờ 27
phút. Tính quãng đường AB. Hướng dẫn giải
Gọi quãng đường AB dài x (km) (x 0).
Thời gian xe tải đi hết quãng đường AB là: x (giờ). 30 3 3 3
quãng đường AB là x (km), khi đó thời gian ô tô con đi hết quãng đường AB 4 4 4 là 3 x x : 45 = (giờ). 4 60
Vận tốc xe con sau khi tăng thêm 5 km/h là: 45 + 5 = 50 (km/h). 3x x
Quãng đường còn lại là: 1− = (km). 4 4 1
Thời gian xe con đi hết quãng đường AB là x x : 50 = (giờ). 4 4 200
Vì xe con đến B sớm hơn xe tải là 2 giờ 27 phút 49 =
giờ nên ta có phương trình: 20 x x x 49 − + = 30 60 200 20 20x 10x 3x 1 470 − − = 600 600 600 600 7x 1 470 = 600 600 7x =1 470 x = 210 (thỏa mãn).
Vậy quãng đường AB dài 210 km.
Bài 4. (2,5 điểm) Cho tam giác ABC vuông tại A có AB = 6 cm và AC = 8 cm. Đường
phân giác của góc ABC cắt cạnh AC tại .
D Từ C kẻ CE ⊥ BD tại E. a) Tính độ dài AD BC và tỉ số . DC b) Chứng minh A BD∽ E
BC. Từ đó suy ra BD EC = AD BC. c) Chứng minh CD CE = . BC BE
d) Gọi EH là đường cao EBC
. Chứng minh CH HB = ED . EB Hướng dẫn giải
a) Xét ABC vuông tại ,
A theo định lí Pytagore ta B có: 2 2 2 2 2
BC = AB + AC = 8 + 6 = 64 + 36 = 100 2 1
Suy ra BC = 100 =10 cm.
Vì BD là tia phân giác của góc ABC nên suy ra: DA BA 6 3 = = = . A C D DC BC 10 5
b) Theo đề bài, CE ⊥ BD tại E nên BEC = 90 . E Xét ABD và EBC có:
BAD = BEC = 90 và B = B (vì BD là tia phân giác của góc ABC) 1 2 Do đó AB D∽ EB C (g.g). Suy ra: BD BC =
(tỉ số cạnh tương ứng). AD EC
Do đó BD EC = AD BC. c) Từ DA AB = suy ra CD AD = ( ) 1 DC BC BC AB AD EC Vì AD AB AB D∽ EB C (câu b) nên = , suy ra = (2) EC EB AB EB Từ ( ) CD CE 1 và (2) suy ra: = . BC BE
d) Tương tự câu b ta chứng minh được: B CH CE 2 ⦁ CH E∽ CE B (g.g) nên = . 1 CE CB Suy ra 2
CH CB = CE ( ) 3 H ED CE ⦁ CD E ∽ B CE (g.g) nên = . A C D EC BE Suy ra 2
ED EB = CE (4) E
Từ (3) và (4) suy ra: CH HB = ED . EB
Bài 5. (0,5 điểm) Rút gọn biểu thức sau:
B = (ab + bc + ca) 1 1 1 1 1 1 + + − abc + + . 2 2 2 a b c a b c Hướng dẫn giải Với a, , b c 0, ta có = ( + + ) 1 1 1 1 1 1 B ab bc ca + + − abc + + 2 2 2 a b c a b c 1 1 1 1 1 1
1 1 1 abc abc abc = ab + + + bc + + + ca + + − + + 2 2 2 a b c a b c
a b c a b c ab bc ca bc ac ab = b + a + +
+ c + b + c + + a − − − c a b a b c
= 2(a + b + c).
Vậy B = 2(a + b + c). -----HẾT-----




