Đề thi giữa học kì 2 Toán 8 năm 2023 – 2024 phòng GD&ĐT Hiệp Hòa – Bắc Giang
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề kiểm tra chất lượng giữa học kì 2 môn Toán 8 năm học 2023 – 2024 phòng Giáo dục và Đào tạo huyện Hiệp Hòa, tỉnh Bắc Giang; đề thi gồm 02 trang, cấu trúc 50% trắc nghiệm (20 câu) + 50% tự luận (04 câu), thời gian làm bài 90 phút (không kể thời gian giao đề); đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA GIỮA HỌC KÌ II HIỆP HÒA NĂM HỌC 2023 - 2024 MÔN: TOÁN LỚP 8
( Đề thi giồm 02 trang )
Thời gian làm bài: 90 phút, không kể thời gian giao đề
I. TRẮC NGHIỆM (5,0 điểm). Chọn phương án trả lời đúng của mỗi câu hỏi sau:
Câu 1. Cách viết nào sau đây không cho một phân thức? A. 0 . B. xy . C. x + y . D. x - xy . x -1 -5 0
Câu 2. Phân thức: x −1 rút gọn thành: 2 x −1 A. 1 B. 1 C. x +1. D. 1 . x +1 x x −1
Câu 3. Giá trị x = - 4 là nghiệm của phương trình:
A. -2,5x + 1 = 11. B. -2,5x = -10. C. 3x – 8 = 0. D. 3x – 1 = x + 7.
Câu 4. Trang x tuổi, anh trai Trang hơn Trang 3 tuổi, tuổi anh trai Trang được tính theo tuổi Trang là:
A. 15 B. x+3. C. 3x. D. 12.
Câu 5. Điều kiện của biến x để phân thức x − 2 được xác định là 2 x − 4 A. x ≠ 2 ± .
B. x ≠ 2 . C. x ≠ 2 − .
D. x ≠ 0 và x ≠ 2 ± . 2
Câu 6. Giá trị của phân thức x +1 tại x = -1 là x −1 A.0. B. 2 . C. 1 − . D. 1. 0
Câu 7. Phân thức nghịch đảo của phân thức x − y là x + y
A. x − y B. x + y + − − C. x y D. x y − x + y x − y x − y x + y
Câu 8. Cho ∆ ABC có Â = 400; B = 600 và ∆ DEF có E = 800; D = 600. Khẳng định nào sau đây đúng? A. ∆ABC ∆DEF.
B. ∆ABC ∆ EFD. C. ∆ABC ∆DFE. D. ∆ABC ∆FDE.
Câu 9. Nếu ∆ABC ∆DEF thì ta có: AB AC A. AB BC = . B. AB AC = . C. = AB BC D. = . DE DF DE EF DE ED DE EF
Câu 10. Cho tam giác ABC có AC= 5cm, biết D, E thứ tự là trung điểm của AB, BC. Độ dài đoạn thẳng DE bằng: A. 1cm B. 2,5cm C. 2cm D. 1,5cm
Câu 11. Giá trị của m để phương trình x2 +(2m-1)x-5= 2x-3 có nghiệm x = -1 là A. 2 B. -1 C. 0 D. 1
Câu 12. Phương trình x2 -3x + 2 = 0 nhận số nào sau đây là nghiệm ? A. 1 B. -2 C. 3 D. 4
Câu 13. Phân thức đối của phân thức x + y là x − y
A. y + x
B. x − y
C. x + y D. x − y − x − y x + y y − x x + y B
Câu 14. Một người cắm một cái cọc vuông góc với mặt đất sao
cho bóng của đỉnh cọc trùng với bóng của ngọn cây (như hình vẽ).
Biết cọc cao 1, 5 m so với mặt đất, chân cọc cách gốc cây 8m và
cách bóng của đỉnh cọc2m . Khi đó, chiều cao AB của cây là: D A. 3m B. 7, 5m 1,5m C. 6m D. 13, 3m A 8m
C 2m E Câu 15. Cho BD A
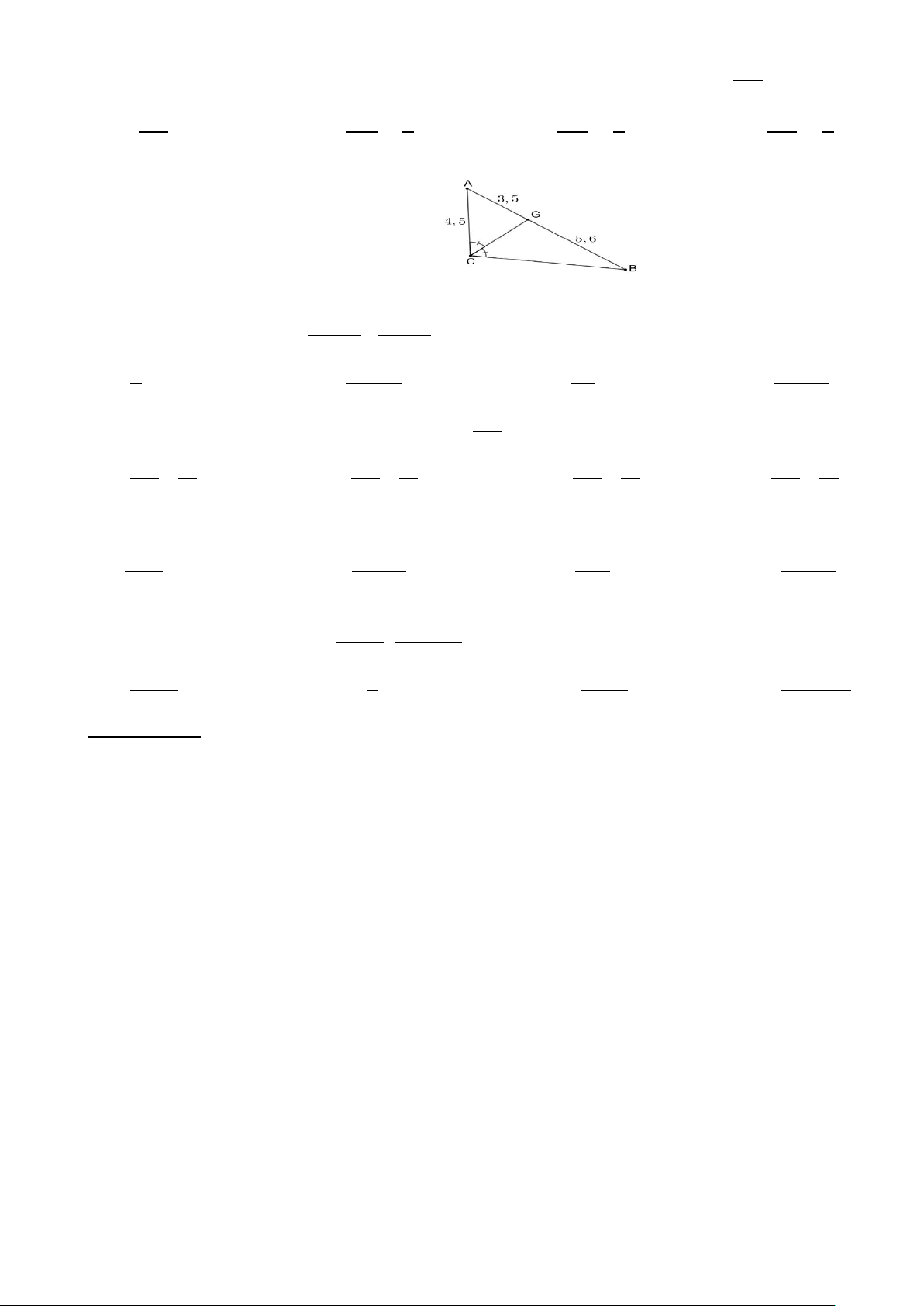
BC , AC 2AB , AD là đường phân giác của A BC , khi đó ? CD A. BD BD BD BD 1 B. 1 C. 1 D. 1 CD CD 2 CD 4 CD 3
Câu 16. Độ dài BC trên hình vẽ là: A. 4,4 B. 2,8 C. 5,6 D. 7,2
Câu 17. Kết quả phép tính: 3xy −3 3xy −5 − 7 7 A. 2 . B. 6xy −8 . C. −8 . D. 6xy +8 . 7 7 7 7
Câu 18. Cho AB = 16cm; CD = 3dm. Tính tỉ số: AB là: CD A. AB 16 = B. AB 8 = C. AB 3 = D. AB 15 = CD 3 CD 15 CD 16 CD 8
Câu 19. Một ngân hàng huy động vốn với mức lãi suất 1 năm là x%. Để sau 1 năm người gửi được
lãi a đồng thì người đó phải gửi vào ngân hàng số tiền là :
A.100a (đồng) B. a (đồng) C. a (đồng) D. 100a x x +100 x +1 x +100 (đồng)
Câu 20. Kết quả của phép chia: a − 2b 2 − a + 4 : b bằng: 16 12 A. 6 B. 3 3 −
C. a − 2b D. a − b 2 8 8 ( 4 a − 2b)
II. TỰ LUẬN (5,0 điểm): Bài 1 (2,0 điểm ):
1. Giải phương trình sau: a) 2x-3=x+5 b) 5x − 3(3x − 7) = 35 2
2. Rút gọn biểu thức: x 2 2 M = + +
(với x ≠ 0 và x ≠ 2 − ) 2
x + 2x x + 2 x
Bài 2 (1,0 điểm): Tháng 1 năm 2024, tổng giá của hai sản phẩm A và B là 600000 đồng. Tháng 3
2024 do nhu cầu mua cao nên giá của sản phẩm A tăng 10%, giá sản phẩm B tăng 15% so với tháng
1 năm 2024. Do đó người mua phải trả cho 2 sản phẩm A và B vào tháng 3 năm 2024 là 677500
đồng. Hỏi vào tháng 1 năm 2024 mỗi sản phẩm A và B có giá bao nhiêu tiền?
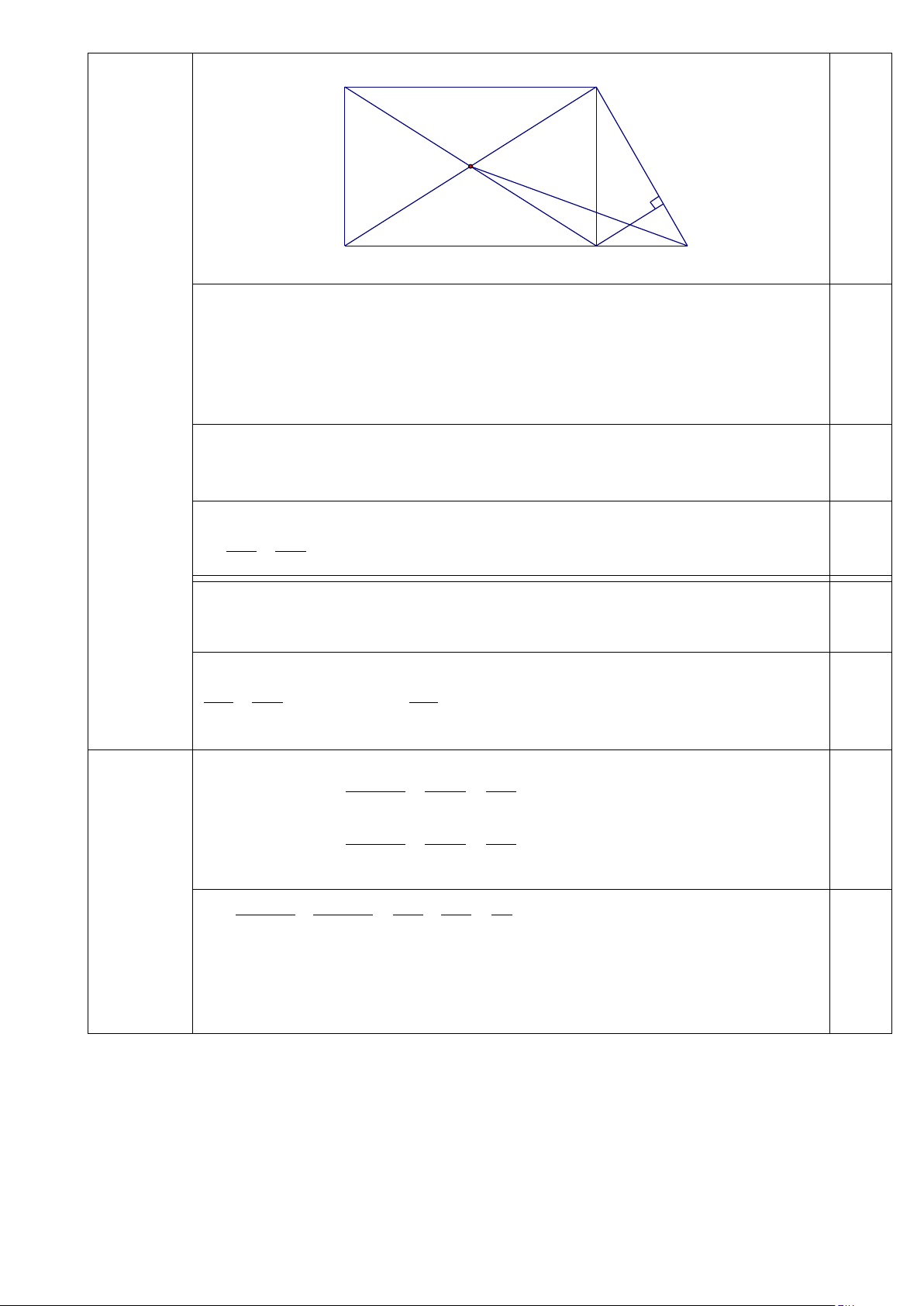
Bài 3 (1,5 điểm ): Cho hình chữ nhật ABCD, hai đường chéo AC và BD cắt nhau tại O. Qua D kẻ
đường thẳng d vuông góc với BD, d cắt BC tại E
a) Chứng minh ∆BDE ∽ ∆DCE.
b) Kẻ đường cao CH ⊥ DE. Chứng minh DC2 = CH.BD.
c) Gọi K là giao điểm của CH và OE. Chứng minh K là trung điểm của CH.
Bài 4. Cho x, y là hai số dương thoả x.y = 1. Tìm giá trị lớn nhất của biểu thức x y A = + 4 2 4 2 x + y y + x
--------------- Hết ---------------
PHÒNG GD-ĐT HIỆP HOÀ
KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2023-2024
HƯỚNG DẪN CHẤM MÔN TOÁN LỚP 8
I. TRẮC NGHIỆM: (5,0 điểm) mỗi câu đúng 0,25 điểm
Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Đ/A C A A B A C C D D B D A C B B D A B A B
II. TỰ LUẬN: (5,0 điểm)
Dưới đây chỉ là sơ lược các bước giải và thang điểm. Bài giải của học sinh cần chặt chẽ,
hợp logic toán học. Nếu học sinh làm bài theo cách khác hướng dẫn chấm mà đúng thì chấm và
cho điểm tối đa của bài đó. Đối với bài hình học (bài 4), nếu học sinh vẽ sai hình hoặc không vẽ
hình thì không được tính điểm. Bài Nội dung Điểm Bài 1 2x-3=x+5 1a 2x-x=5+3 0.25 (0.75đ) x=8 0.25 KL 0.25
Ta có: 5x − 3(3x − 7) = 35 ⇔ 5x − 9x + 21 = 35 0.25 ⇔ 4 − x = 35 − 21 ⇔ 4 − x = 14 1b (0.5đ) 7 x − ⇔ = 0.25 2 KL:…. 0.25 Ta có: 2 2 x 2 2 x 2 2 M = + + = + + 2
x + 2x x + 2 x x(x + 2) x + 2 x 2
x + 2x + 2(x + 2) 2 x + 4x + 4 0.25 2 = = (0,75đ) x(x + 2) x(x + 2) 2 (x + 2) x + 2 0.25 = = x(x + 2) x Vậy + 2 M x =
với x ≠ 0 và x ≠ 2 − . 0.25 x
Gọi giá sản phẩm A vào tháng 1 năm 2024 là x (nghìn đồng), ĐK: 0
Giá sản phẩm B vào tháng 1 năm 2024 là 600-x( nghìn đồng) 0.25 Bài 2
Giá sản phẩm A vào tháng 3 năm 2024 là 1,1x (nghìn đồng)
(1,0đ) Giá sản phẩm B vào tháng 3 năm 2024 là 1,15(600-x) (nghìn đồng), 0.25
Từ đó ta có phương trình: 1,1x+1,15(600-x)=677,5
Giải PT được: x = 250 từ đó tính được giá mỗi sản phẩm A và B 0.25 KL:... 0.25 D A O K H B C E
a) - Chứng minh ∆BDE ∽ ∆DCE Xét ∆HAE và ∆HBF có: = AHE BHF (dd) Bài 3 = 0 AEH BFH = 90 (1,5 điểm) 0.25
Do đó ∆HAE đồng dạng ∆HBF (g-g) 0.25
b) Kẻ đường cao CH ⊥ DE. Chứng minh DC2 = CH.BD 0.25
- Vì ∆BCD ∽ ∆DCE ⇒ CBD = CDE
- Chứng minh ∆BCD ∽ ∆DHC (g.g) 0.25 ⇒ CD BD = ⇒ đpcm HC DC
c) Gọi K là giao điểm của CH và OE. Chứng minh K là trung điểm của CH
- Chỉ ra CH // BD (cùng ⊥ DE) ⇒ CK // BO; KH // OD 0.25
- Áp dụng hệ quả của định lí Talets chỉ ra được CK KH = (vì cùng bằng EK ) BO OD EO
Mà OB = OD ⇒ CK = KH ⇒ K là trung điểm của CH 0.25 4 2 2 x x
x + y ≥ 2x y 1 ⇒ ≤ = (x, y là các số dương) x4 + y2 2x2 y 2xy 0.25 4 2 2 y y
y + x ≥ 2y x 1 ⇒ ≤ = (x, y là các số dương) y4 + x2 2y2x 2xy Bài 4 (0,5 điểm) x y 1 1 1 A = + ≤ + = = 1 0.25 4 2 4 2 x + y y + x 2xy 2xy xy 4 x = 2 y 6 x = 6 y x = 1 Dấu “=” xảy ra khi 2 x = 4 y ⇔ ⇔ (x, y là các số dương) xy = 1 y = 1 xy = 1