Đề Thi Giữa Học Kỳ 1 Toán 12 Cánh Diều Giải Chi Tiết-Đề 1

ĐỀ 1
ĐỀ KIỂM TRA GIỮA HỌC KỲ I NĂM HỌC 2024-2025 t MÔN: TOÁN 12
Thời gian làm bài: 90 phút
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số 3 2
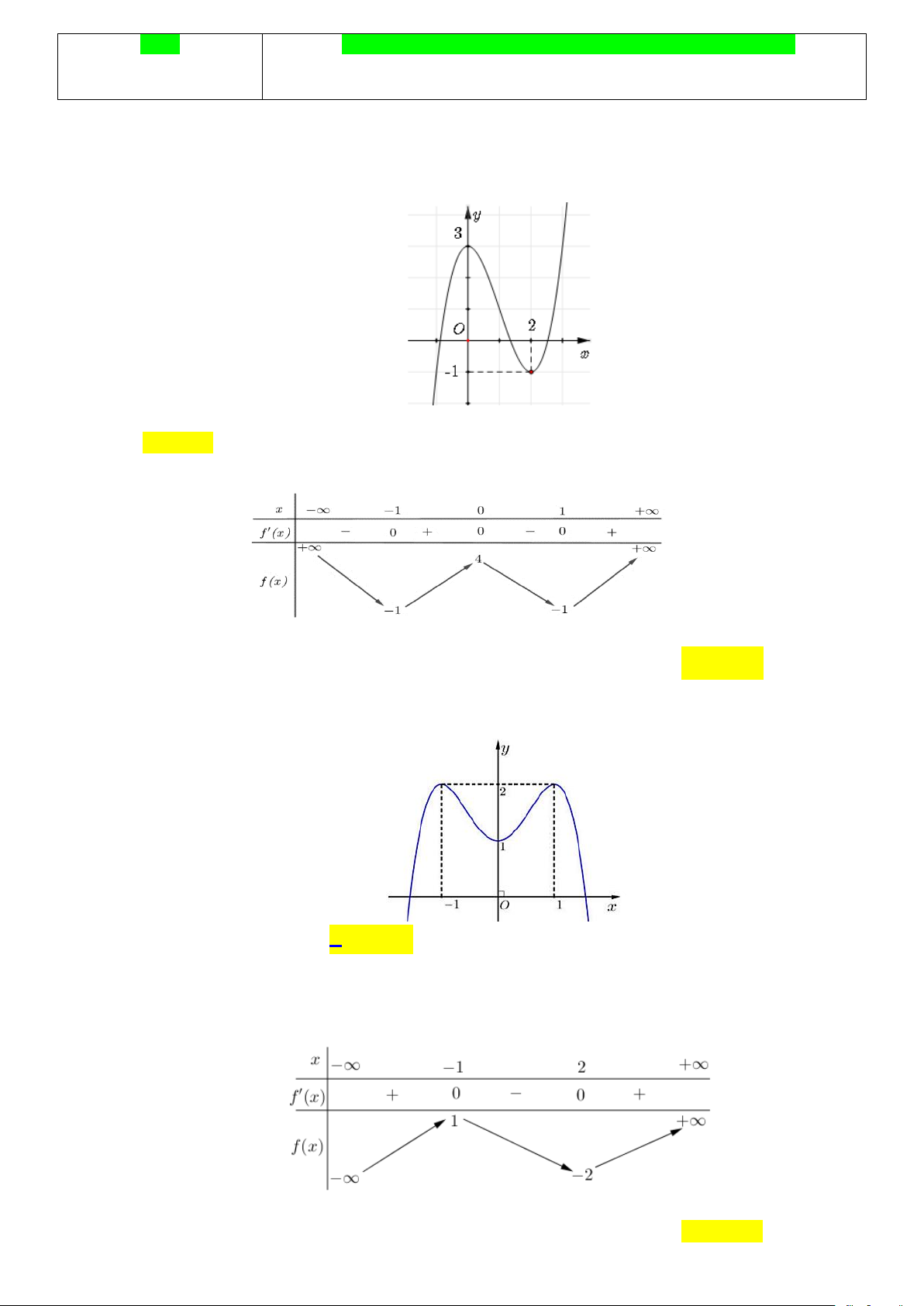
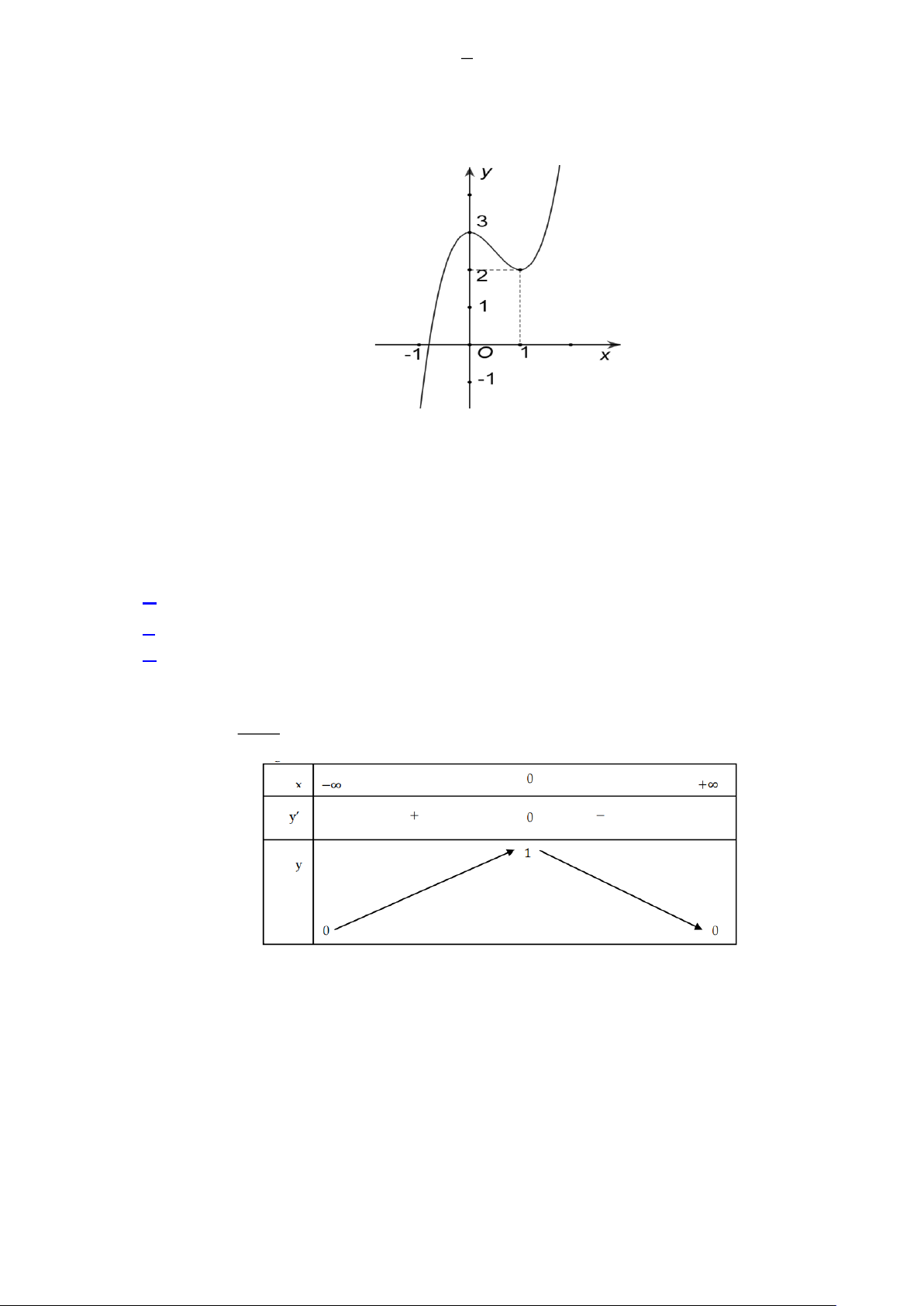
y = ax + bx + cx + d có đồ thị là đường cong trong hình bên dưới.
Điểm cực đại của hàm số đã cho là A. x = 0 . B. x = 3. C. x = 1 − . D. x = 2 .
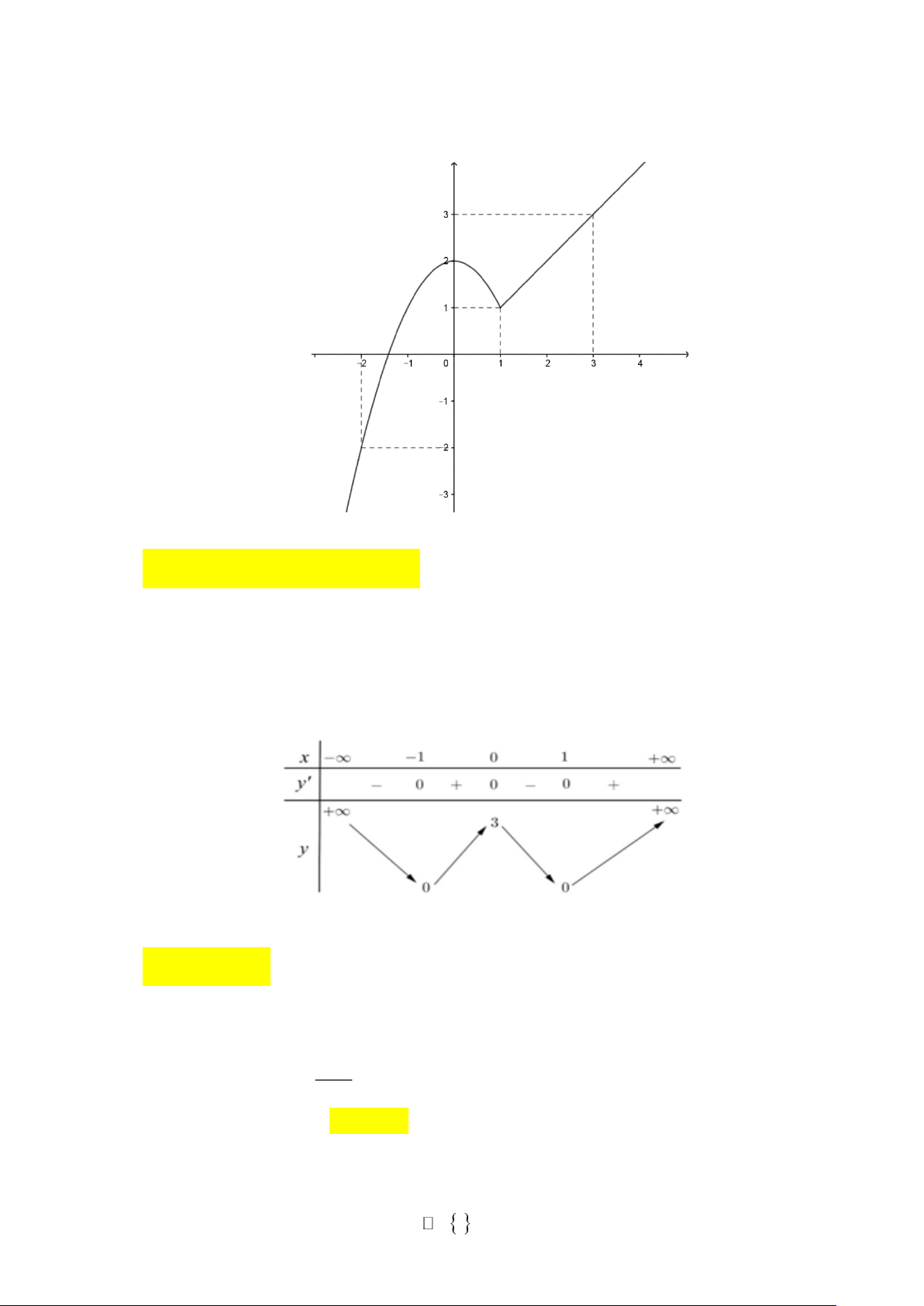
Câu 2. Cho hàm số f ( x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (− ;  − ) 1 . B. (0; ) 1 . C. ( 1 − ; ) 1 . D. ( 1 − ;0) .
Câu 3. Cho hàm số y = f (x) có đồ thị là đường cong hình bên dưới. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. ( 1 − ; ) 1 . B. (1;+). C. (0; ) 1 . D. ( 1 − ;+). Lời giải
Hàm số y = f (x) nghịch biến trên khoảng ( 1 − ;0) và (1;+).
Câu 4. Cho hàm số f ( x) có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại A. x = 2 − . B. x = 2 . C. x =1. D. x = 1 − . Trang 1 Lời giải Chọn D
Hàm số đạt cực đại tại điểm mà đạo hàm đổi dấu từ dương sang âm.
Từ bảng biến thiên hàm số đạt cực đại tại x = 1 − .
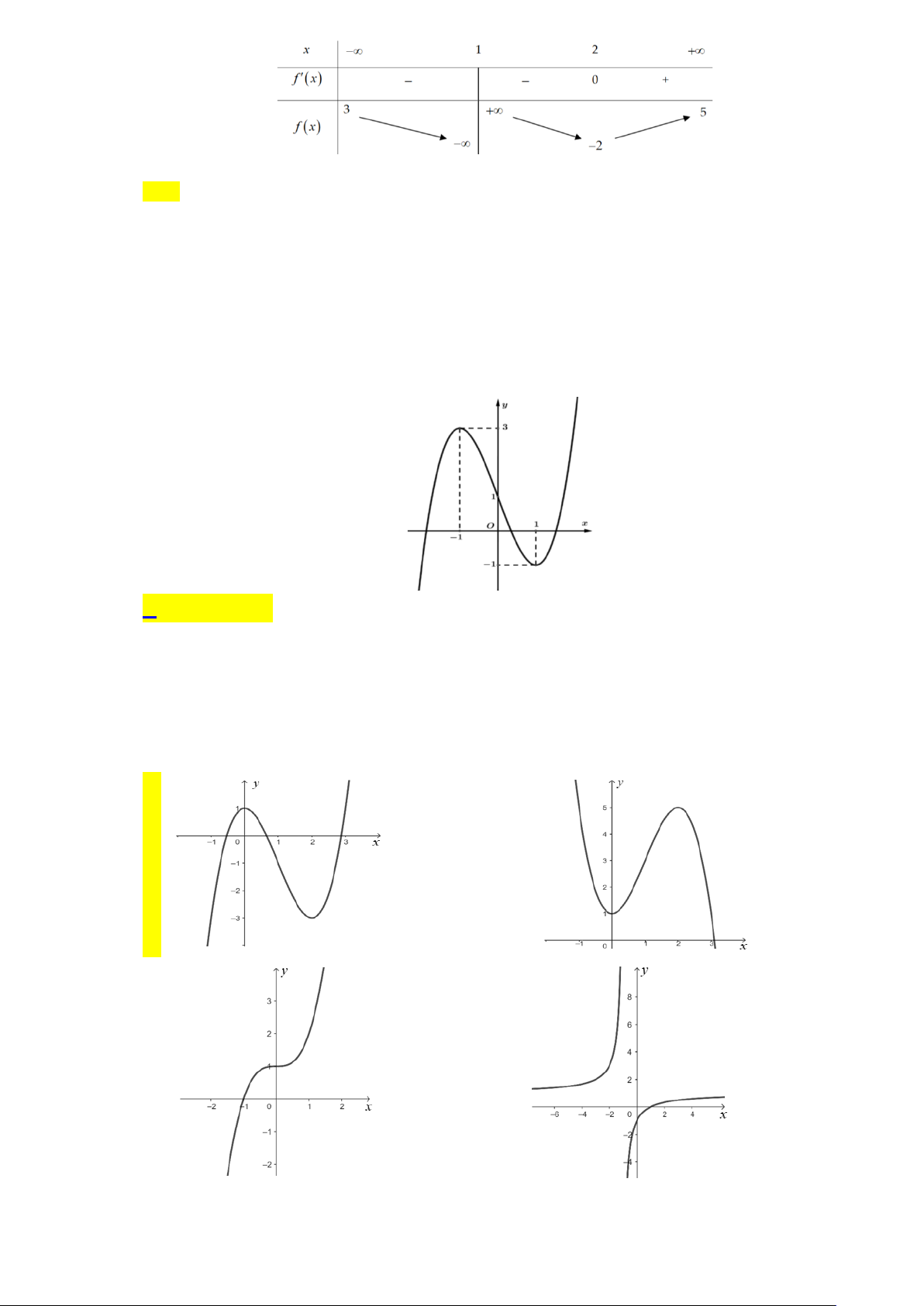
Câu 5. Cho hàm số y = f (x) có đồ thị như hình dưới đây:
Tìm giá trị lớn nhất và nhỏ nhất của hàm số f ( x) trên đoạn  2 − ,  3 ?
A. min f ( x) = −2 và max f ( x) = 3 .
B. min f ( x) = −2 và max f ( x) = 2 .  2 − ,  3  2 − ,  3  2 − ,  3  2 − ,  3
C. min f ( x) = 1 và max f ( x) = 3 .
D. min f ( x) = −2 và max f ( x) = 4 .  2 − ,  3  2 − ,  3  2 − ,  3  2 − ,  3 Lời giải
Dựa vào đồ thị ta có min f ( x) = −2 và max f ( x) = 3 .  2 − ,  3  2 − ,  3
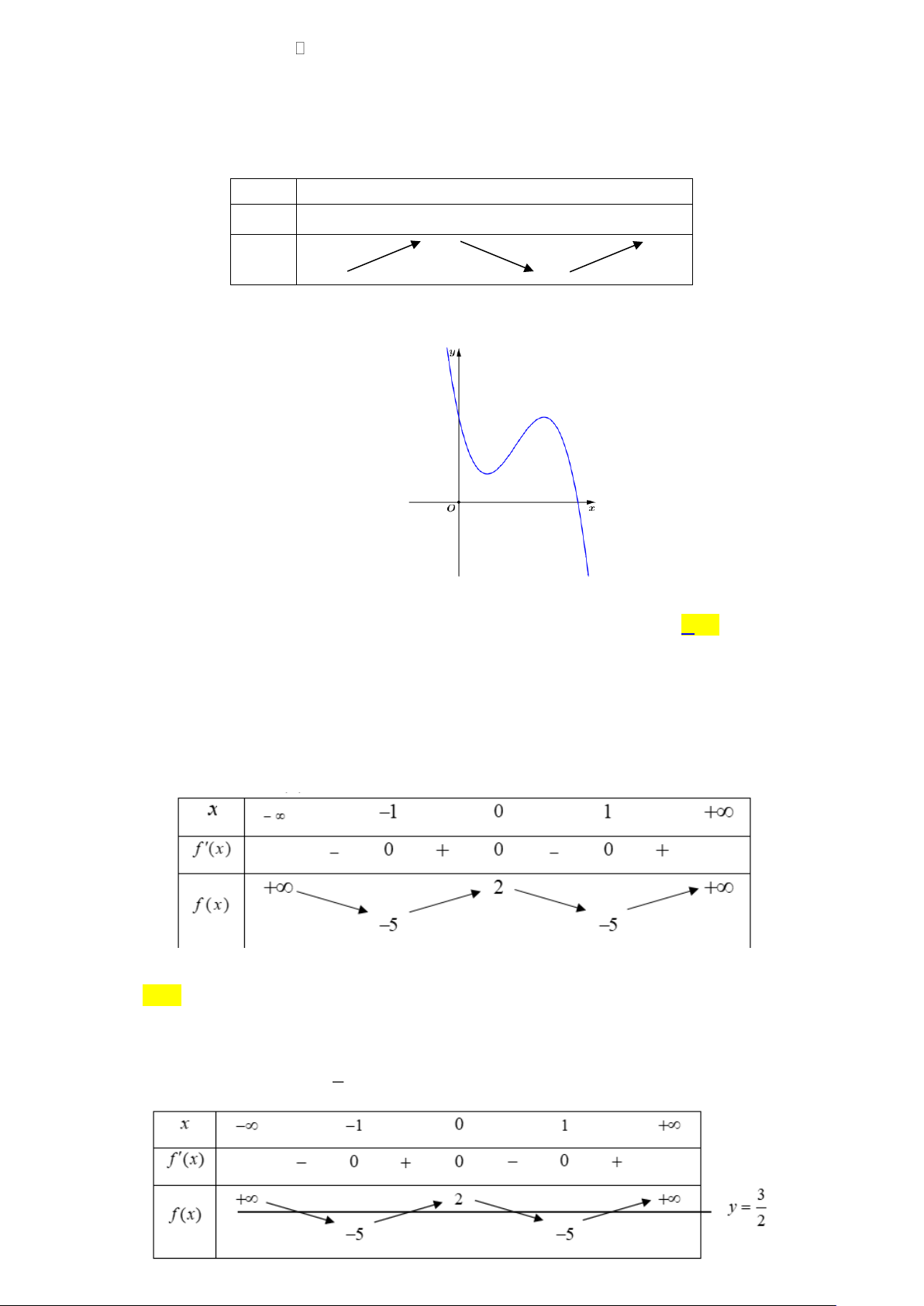
Câu 6. Cho hàm số y = f (x) có bảng biến thiên như sau
Cho biết giá trị nhỏ nhất của hàm số trên đoạn  1 − ;  1 là bao nhiêu?
A. min f ( x) = 0
B. min f ( x) = 3
C. min f ( x) = 1
D. min f ( x) = 1 − −  1;1 −  1;1  1 − ;  1 −  1;1 Lời giải
Từ BBT suy ra min f ( x) = 0 tại x = 1  . −  1;1 x − 2
Câu 7. Đồ thị của hàm số y =
có đường tiệm cận đứng là x +1 A. y = −1. B. x = 1. − C. x =1. D. y = 1. Lời giải Chọn B
Ta có tiệm cận đứng x = 1 − .
Câu 8. Cho hàm số y = f (x) xác định trên  \ 
1 liên tục trên mỗi khoảng xác định và có bảng biến thiên sau. Trang 2
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? A. 3. B. 4. C. 5. D. 2. Lời giải Chọn A
Dựa vào đồ thị hàm số ta thấy lim y = 3, lim y = 5  y = 3, y = 5 là 2 đường tiệm cận ngang x→− x→+ của đồ thị hàm số.
Mặt khác lim y =   x = 1 là tiệm cận đứng của đồ thị hàm số. x 1 →
Do đó đồ thị hàm số có 3 đường tiệm cận.
Câu 9. Đồ thị sau đây là của hàm số nào? A. 3
y = x − 3x +1. B. 3
y = x − 3x −1. C. 3
y = −x − 3x −1. D. 3
y = −x + 3x +1. Lời giải
Đồ thị hàm số trên là đồ thị hàm số bậc ba 3 2
y = ax + bx + cx + d (a  0) .
Nhìn vào nhánh phải của đồ thị ta thấy đồ thị có hướng đi lên suy ra a  0 .
Đồ thị hàm số cắt trục tung tại điểm có tung độ y = 1. Vậy hàm số thỏa đề là 3
y = x − 3x +1.
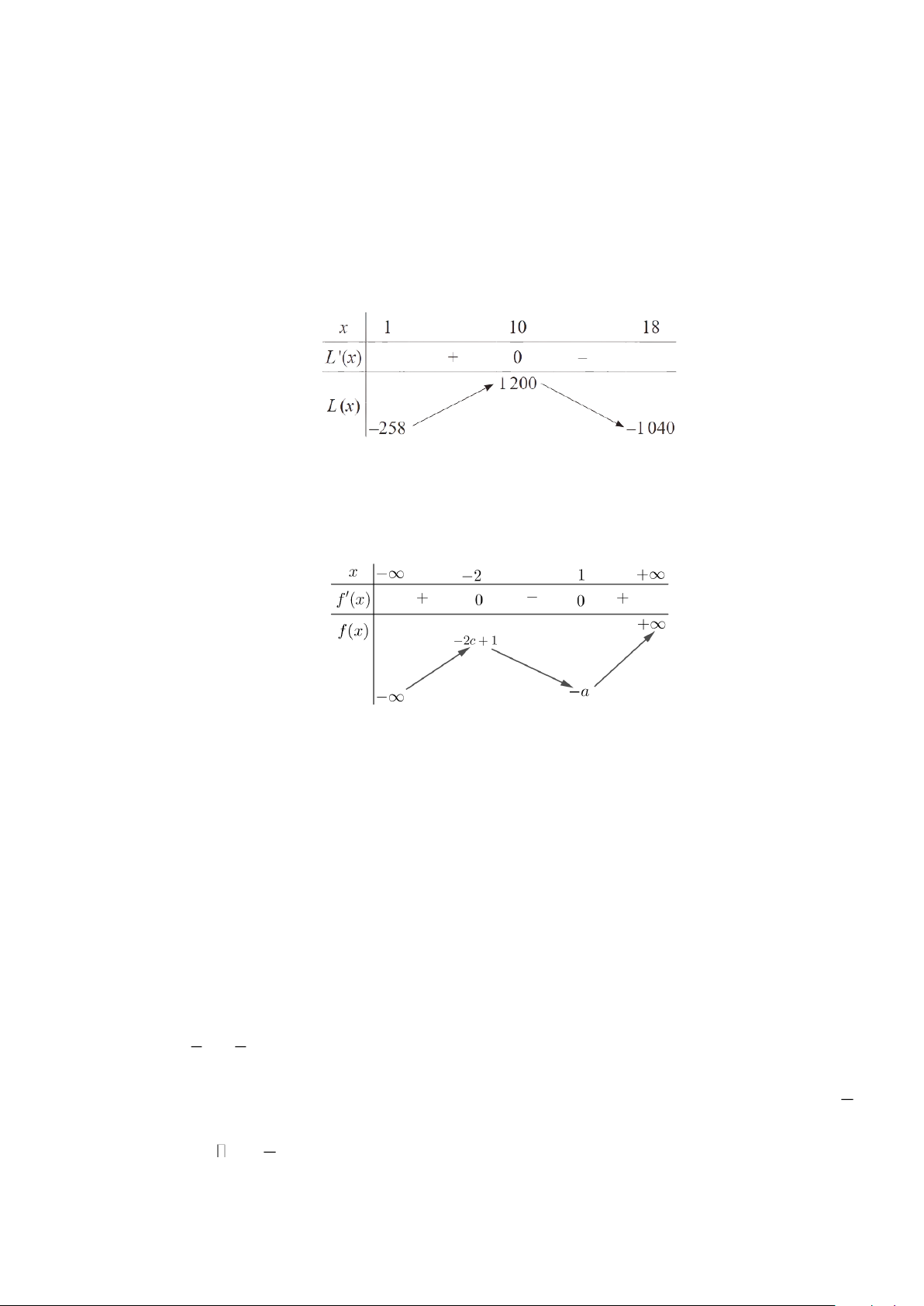
Câu 10. Đường cong nào dưới đây là đồ thị của hàm số 3 2
y = x − 3x +1 A. . B. . C. . D. . Lời giải Chọn A Trang 3 3 2
y = x − 3x +1; D =  2
y ' = 3x − 6x
x = 0  y = 1 2
y ' = 0  3x − 6x = 0  x = 2 y = −3 Bảng biến thiên: x − 0 2 + f (x) + 0 − 0 + f (x) 1 + − 3 − .
Câu 11. Cho hàm số ( ) 4 3 2
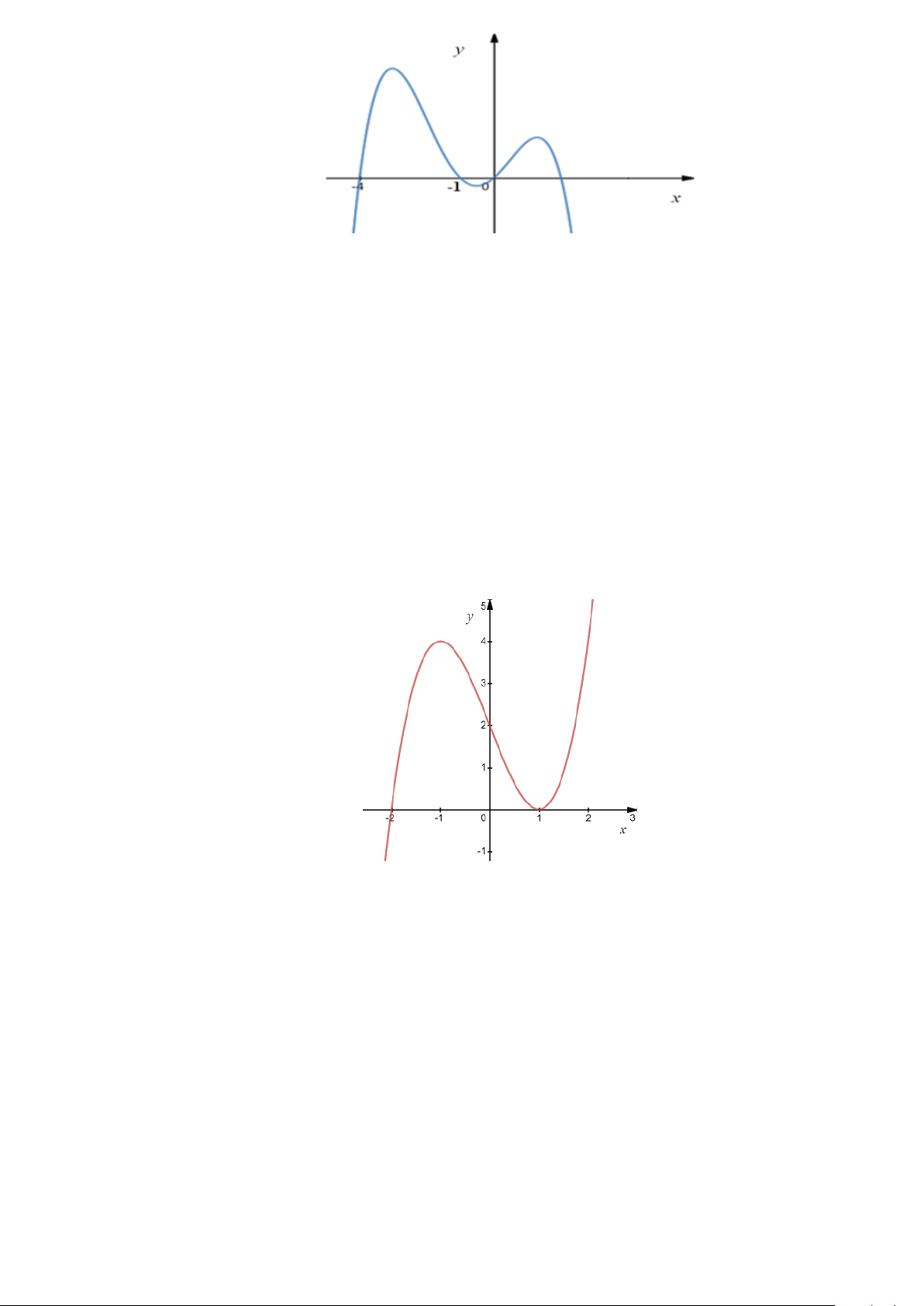
f x = ax + bx + cx + dx + e . Hàm số y = f (x) có đồ thị như hình vẽ sau.
Đồ thị hàm số y = f (x) có tất cả bao nhiêu điểm cực trị? A. 4 . B. 2 . C. 3 . D. 1. Lời giải
Ta có y = f (x)  y = f (x)
Ta thấy đồ thị hàm số y = f (x) cắt đường thẳng y = 0 tại 1 điểm suy ra phương trình
f (x) = 0 có 1 nghiệm đơn. Vậy hàm số y = f (x) có 1 điểm cực trị.
Câu 12. Cho hàm số f ( x) có bảng biến thiên như sau:
Số nghiệm của phương trình 2 f (x) −3 = 0 là? A. 4 . B. 1. C. 2 . D. 3 . Lời giải Chọn A
f ( x) − =  f (x) 3 2 3 0 = . 2 Trang 4 3
Từ bảng biến thiên, thấy đường thẳng y =
cắt đồ thị tại 4 điểm. 2
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý A), B), C), D) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13. Cho hàm số y = f (x) có đồ thị như hình vẽ bên.
A. Hàm số nghịch biến trên khoảng (0; ) 1 .
B. Hàm số đạt cực trị tại các điểm x = 0 và x =1.
C. Hàm số đồng biến trên khoảng ( ;0 − ) và (1;+).
D. Hàm số đồng biến trên khoảng ( ;3 − ) và (1;+) Lời giải
Từ đồ thị, ta thấy
A. Hàm số nghịch biến trên khoảng (0; ) 1 ĐÚNG.
B. Hàm số đạt cực trị tại các điểm x = 0 và x =1 ĐÚNG.
C. Hàm số đồng biến trên khoảng ( ;0
− ) và (1;+) ĐÚNG.
D. Hàm số đồng biến trên khoảng ( ;3
− ) và (1;+) SAI. 1
Câu 14. Hàm số y =
có bảng biến thiên như hình vẽ. 2 x +1
Xét trên tập xác định của hàm số.
A. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0.
B. Hàm số có giá trị lớn nhất bằng 0.
C. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
D. Hàm số đạt giá trị lớn nhất bằng 1. Lời giải
A. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0. SAI.
B. Hàm số có giá trị lớn nhất bằng 0. SAI.
C. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số. SAI.
D. Hàm số đạt giá trị lớn nhất bằng 1.. ĐÚNG.
Câu 15. Cho hàm số y = f (x) liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽ sau: Trang 5
A. Số đường tiệm cận đứng của đồ thị hàm số đã cho là 2.
B. Đồ thị hàm số y = f ( x) có ba đường tiệm cận ngang y = 1; y = 2; y = 3 .
C. Đồ thị hàm số y = f ( x) có đường tiệm cận đứng là x = 2 − ; x = 0 .
D. Tổng số đường tiệm cận của đồ thị hàm số y = f ( x) bằng 3. Lời giải
Dựa vào bảng biến thiên, ta có
A. Số đường tiệm cận đứng của đồ thị hàm số đã cho là 2 ĐÚNG.
B. Đồ thị hàm số y = f ( x) có ba đường tiệm cận ngang y = 1; y = 2; y = 3 SAI
C. Đồ thị hàm số y = f ( x) có đường tiệm cận đứng là x = 2 − ; x = 0 . ĐÚNG
D. Tổng số đường tiệm cận của đồ thị hàm số y = f ( x) bằng 3. SAI
Câu 16. Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho tọa
độ của hạt (đơn vị: mét) tại thời điểm t (giây) là 3
y = t −12t + 3, (t  0)
A.Hàm vận tốc là: v(t) 2
= y ' = 3t −12, (t  0) và hàm gia tốc là a(t) = 6t, (t  0).
B. Hạt chuyển động lên trên khi t  2 và hạt chuyển động xuống dưới khi t  2 .
C. Quãng đường hạt chuyển động trong khoảng thời gian 0  t  3 là 9 m.
D.Hạt tăng tốc khi t  2 và hạt giảm tốc 0  t  2 . Lời giải a) b) c) d) ĐÚNG SAI ĐÚNG SAI
a) Hàm vận tốc là: v(t) 2
= y ' = 3t −12, (t  0)
Hàm gia tốc là a(t) = v'(t) = 6t, (t  0)
b) Hạt chuyển động lên trên khi v(t) 2
 0  3t −12  0  t  2, (do t  0)
Hạt chuyển động xuống dưới khi v(t) 2
 0  3t −12  0  0  t  2
c) Quãng đường hạt đi được trong khoảng thời gian 0  t  3. Ta có y( ) 3 − y (0) = 9 −
Quãng đường hạt chuyển động trong khoảng thời gian 0  t  3 là 9m
d) Hạt tăng tốc khi v'(t)  0  6t  0  t  0
Hạt giảm tốc khi v'(t)  0  6t  0  t  0 loại vì t  0
Vậy hạt tăng tốc khi t  0 và hạt không giảm tốc
PHẦN III. Câu trắc nghiệm trả lời ngắn. Mỗi câu hỏi thí sinh chỉ trả lời đáp án.
Câu 17. Cho hàm số y = f (x) liên tục trên R và đồ thị có ba điểm cực trị như hình dưới đây Trang 6
Số điểm cực trị của hàm số 3
g(x) = f (x − 3x + 2) là bao nhiêu?
Trả lời:………………….. Lời giải
Đáp án: hàm số đã cho có 7 cực trị. Cách 1: Tự luận Ta có: 2 3
g '(x) = (3x − 3). f '(x − 3x + 2) x =1 x = 1 − 2 3x 3 0   − = 3 g '(x) 0  =  
 x − 3x + 2 = a (1) 3
 f '(x − 3x + 2) = 0  3
x − 3x + 2 = b (2)  3
x − 3x + 2 = c (3)
Dựa vào đồ thị hàm số 3
y = x − 3x + 2 , suy ra:
Phương trình (1) có 1 nghiệm khác 1, vì 4 −  a  1 −
Phương trình (2) có 1 nghiệm khác 1, vì 1 −  b  0
Phương trình (3) có 3 nghiệm phân biệt khác 1, vì 0  c  4
Như vậy phương trình g '(x) = 0 có 7 nghiệm phân biệt, tức là hàm số 3
g(x) = f (x − 3x + 2) có
7 điểm cực trị. Chọn B.
Câu 18. Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được x mét vải lụa ( 1 x 18) . Tổng
chi phí sản xuất x mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí: 3 2
C(x) = x − 3x − 20x + 500.
Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá 220 nghìn đồng/mét. Gọi ( B ) x
là số tiền bán được và ( L )
x là lợi nhuận thu được khi bán x mét vải lụa. Hộ làm nghề dệt này
cần sản xuất và bán ra mỗi ngày bao nhiêu mét vải lụa để thu được lợi nhuận tối đa. Hãy tính lợi nhuận tối đa đó.
 Lời giải
✓ Trả lời: 1200
Khi bán x mét vải lụa: Trang 7
- Số tiền thu được là: (
B x) = 220x (nghìn đồng).
- Lợi nhuận thu được là: 3 2 ( L x) = (
B x) −C(x) = −x + 3x + 240x − 500 (nghìn đồng). Hàm số (
L x) xác định trên 1  ;18   . - Sự biến thiên: + Chiều biến thiên:
- Đạo hàm L(x) 2 = 3
− x + 6x + 240; L(x) = 0  x =10 hoặc x = 8 − (loại).
- Trên khoảng (1;10) , L (x)  0 nên hàm số đồng biến trên khoảng này.
- Trên khoảng (1;10) , L (x)  0 nên hàm số nghịch biến trên khoảng này. + Cực trị: Hàm số (
L x) đạt cực đại tại x =10 và L = L 1 ( 0) =1200 . CÐ + Bảng biến thiên:
Từ bảng biến thiên, ta nhận thấy khi x =10 thì hàm số đạt giá trị lớn nhất là 1200 . Như vậy,
hộ làm nghề dệt cần sản xuất và bán ra mỗi ngày 10 mét vải lụa để thu được lợi nhuận tối đa.
Lợi nhuận tối đa này là 1200 nghìn đồng. Câu 19. Cho hàm số 3 2
y = ax + bx + cx + d có bảng biến thiên như sau:
Tìm S = a + b + c + . d
 Lời giải ✓ Trả lời: -2 Ta có: 2
y' = 3ax + 2bx + c
Dựa vào bảng biến thiên ta có:  f '( 2 − ) = 0 1
 2a − 4b + c = 0 a = 2   f '( ) 1 0   = 3
 a + 2b + c = 0 b = 3       f ( 2 − ) = 2 − c +1 8
− a + 4b − 2c + d = 2 − c +1 c = 1 − 2    f  ( )  = −
a + b + c + d = −a d = 5 1 a S = 2+3−12+5 = 2 − .
Câu 20. Một chất điểm chuyển động có quãng đường được cho bởi phương trình 1 4 4 3 2
s(t) = t − t + 5t − 7 , trong đó t  0 với t tính bằng giây (s), s(t) tính bằng mét (m) . Vận 6 3 a
tốc chuyển động của chất điểm tại thời điểm chất điểm có gia tốc chuyển động nhỏ nhất là b a
với a,b  và là phân số tối giản. Tính T = 2a −3b .Biết hàm vận tốc v(t) = s (  t) b
Trả lời:………………….. Lời giải Trang 8 2 Ta có vận tốc 3 2
v(t) = s (t) = t − 4t +10t . 3 Gia tốc 2 2
a(t) = v (
 t) = 2t −8t +10 = 2(t − 2) + 2  2 . 28
Gia tốc nhỏ nhất bằng 2 khi t = 2. Khi đó v(2) = 3
T = 2a −3b = 228−33 = 47.
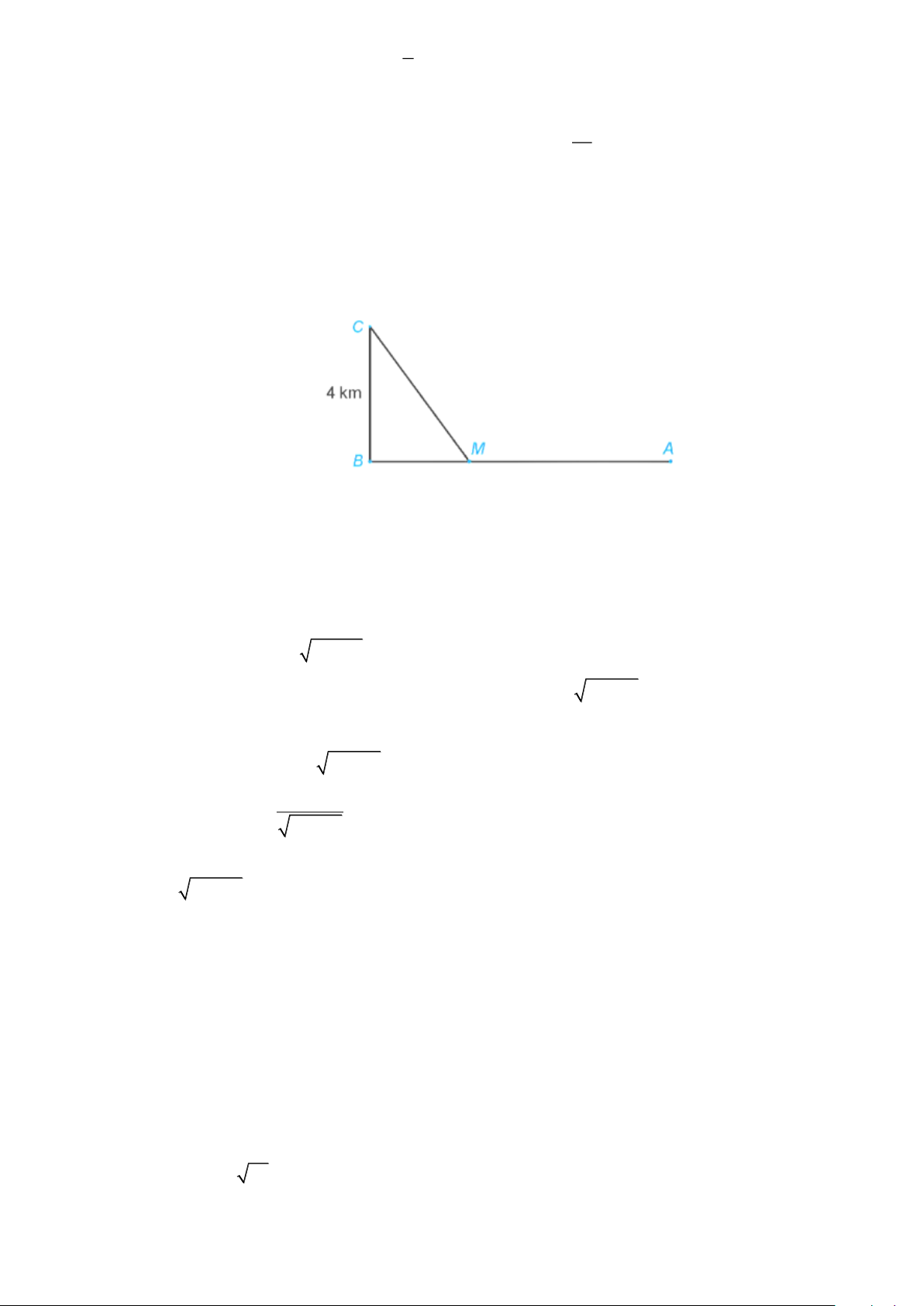
Câu 21. Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như Hình vẽ.
Khoảng cách từ C đến B là 4 km. Bờ biển chạy thẳng từ A đến B với khoảng cách là 10 km.
Tổng chi phí lắp đặt cho 1 km dây điện trên biển là 50 triệu đồng, còn trên đất liền là 30 triệu
đồng. Xác định vị trí điểm M(đoạn MB) trên đoạn AB (điểm nối dây từ đất liền ra đảo) để tổng
chi phí lắp đặt là nhỏ nhất.
Trả lời: ………………. Lời giải
Đáp án: chi phí nhỏ nhất để lắp dây điện là 460 triệu đồng khi M cách B một đoạn 3 km trên đoạn AB.
Gọi khoảng cách BM là x (km), ( 0  x 10).
Khi đó khoảng cách AM là 10 − x(km) (km). Khoảng cách CM là 2 16 + x (km) .
Khi đó chi phí lắp đặt dây điện là: f (x) = ( − x) 2 30 10
+ 50 16 + x (triệu đồng).
Bài toán trở thành tìm x để f ( x) đạt giá trị nhỏ nhất.
f (x) = ( − x) 2 30 10
+ 50 16 + x với 0  x 10  (x) 50x f ' = −30 + 2 16 + x  f '(x) = 0 2
 3 16 + x = 5x x  0   9  ( 2 16 + x ) 2 = 25x x  0   x = −3  (loai)  x = 3  (nhan) Ta có f (0) = 500 f (3) = 460 f (10) = 100 29
Do đó chi phí nhỏ nhất để lắp dây điện là 460 triệu đồng khi M cách B một đoạn 3 km trên đoạn AB. Trang 9
Câu 22. Một công ty kinh doanh bất động sản có 20 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ
với giá 2 triệu đồng/1 tháng thì tất cả các căn hộ đều có người thuê. Nhưng cứ mỗi lần tăng giá
cho thuê mỗi căn hộ thêm 200 nghìn đồng/1 tháng thì có thêm một căn hộ bị bỏ trống. Hỏi
công ty nên cho thuê mỗi căn hộ bao nhiêu tiền một tháng để tổng số tiền thu được là lớn nhất?
Trả lời: ………………. Lời giải
Đáp án: công ty nên cho thuê mỗi căn hộ 3 triệu đồng/1 tháng thì tổng số tiền thu được là lớn nhất.
Cứ tăng thêm 200 nghìn đồng vào giá thuê một căn hộ trên một tháng thì có một căn hộ bị bỏ trống.
Gọi số lần tăng 200 nghìn đồng vào giá thuê một căn hộ trên một tháng là ( * x x   ) .
Khi đó x cũng là số căn hộ bị bỏ trống.
Tổng số tiền công ty thu được lúc này là T (x) = ( + x)( − x) 2 2000 200 20 = 2
− 00x + 2000x + 40000 (nghìn đồng).
Xét hàm số T (x) 2 = 2
− 00x + 2000x + 40000 với * x    T '(x) 2 = 400 − x + 2000  T '(x) = 0 2  400 − x + 2000 = 0  x = 5(nhan)
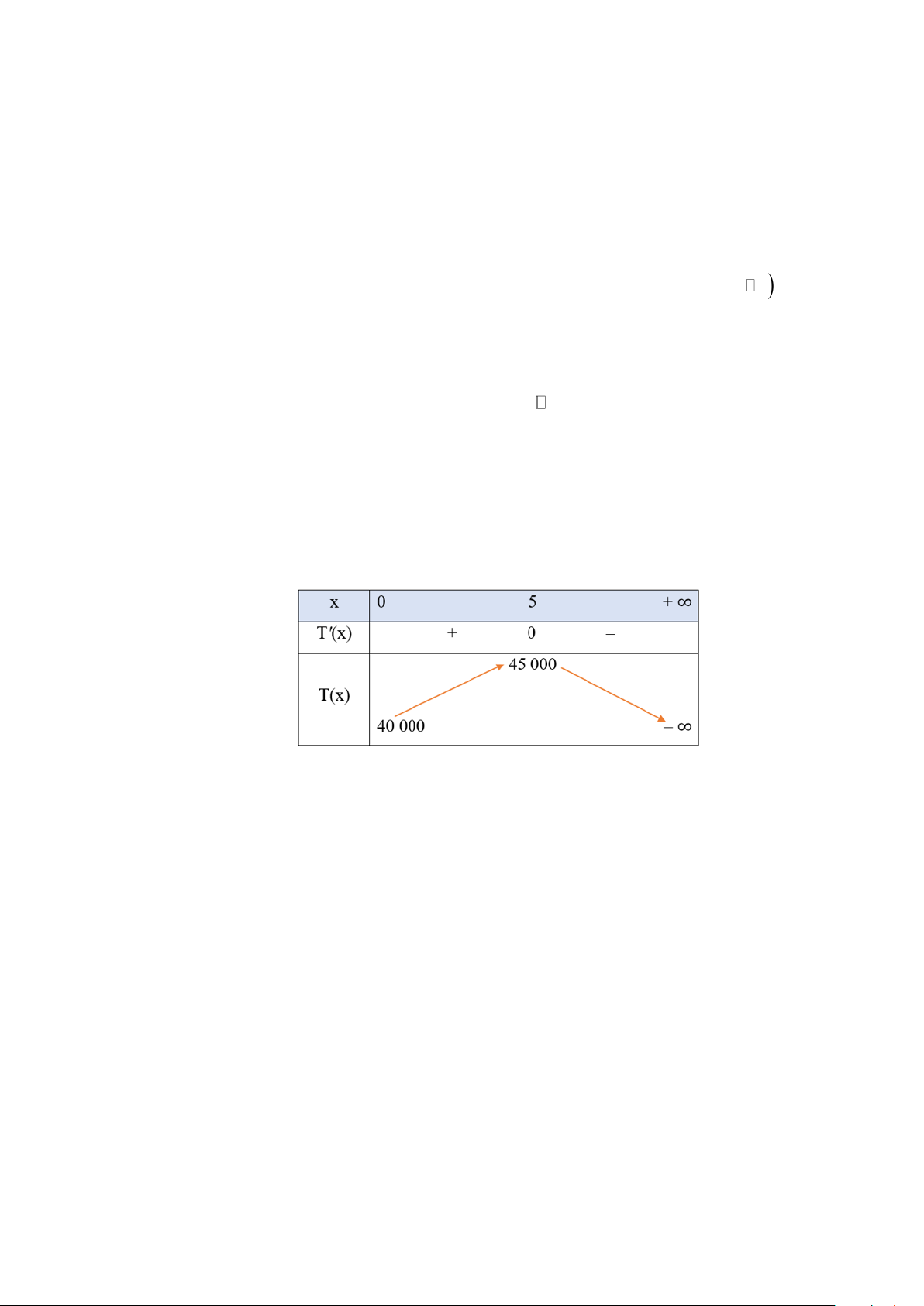
Bảng biến thiên của hàm số T (x) như sau:
Căn cứ vào bảng biến thiên trên, ta thấy hàm số T (x) đạt giá trị lớn nhất bằng 45 000 khi x = 5.
Khi đó, số tiền tăng lên khi cho thuê một căn hộ là 200 ∙ 5 = 1 000 nghìn đồng = 1 triệu đồng.
Vậy công ty nên cho thuê mỗi căn hộ 3 triệu đồng/1 tháng thì tổng số tiền thu được là lớn nhất. Trang 10
Document Outline

• Câu 21. Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như Hình vẽ. Khoảng cách từ C đến B là 4 km. Bờ biển chạy thẳng từ A đến B với khoảng cách là 10 km. Tổng chi phí lắp đặt cho 1 km dây điện trên biển là 50 triệu đồng, còn...