



Preview text:
PHÒNG GD&ĐT QUẬN NAM TỪ LIÊM
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
TRƯỜNG THCS NAM TỪ LIÊM NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Bài 1: (2,0 điểm ). Rút gọn các biểu thức sau
a) 2 27 − 3 12 + 98 − 18 . b) 14 + 6 5 + 14 − 6 5 . 3 + 2 3 2 + 2 c) + − (2+ 3). 3 1+ 2 Bài 2: (2,5 điểm ). a +1 a + 3 a + 2 a + a 1 1 Cho : P = và Q = − : − với a − 2
( a + 2)( a + )1 a −1 a +1 a −1
a > 0; a ≠ 1; 4
a) Tính giá trị của P tại a thỏa mãn a − 5 a + 6 = 0 . b) Rút gọn Q . 4Q
c) Tìm a nguyên để nhận giá trị nguyên. P Bài 3:
( 1,5 điểm) . Giải các phương trình vô tỉ sau x − 5 1 a) 4x − 20 + 3 −
9x − 45 = 3x −12 . 9 3
b) 2x + 27 − 6 = x . Bài 4: ( 3,5 điểm )
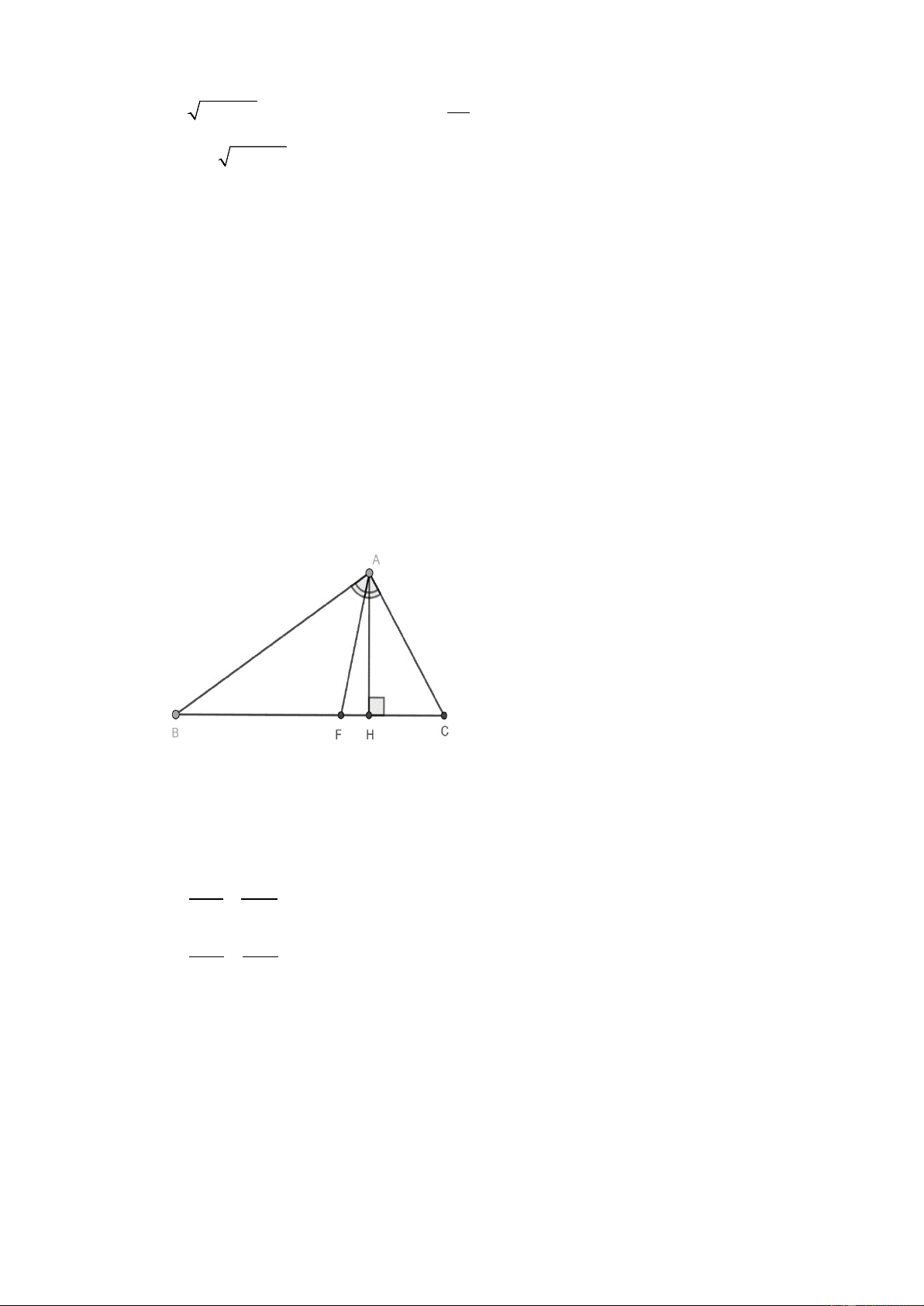
1. Cho tam giác vuông ABC ( AB > AC) , có đường cao AH . 2 2 AB AC a) Chứng minh rằng = . BH CH b) Biết
C = 60° , AC = 8 cm, AB = 12 cm. Giải tam giác vuông HAB . 1 =
c) Kẻ AF là phân giác của
BAC . Chứng minh rằng S
.CF.AC.sin ACH . ACF 2 2 1 1 Từ đó suy ra = + . AF AB AC
2. Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng
30° và bóng của một tháp trên mặt đất dài 92 m. Tính chiều
cao của tháp. (Kết quả làm tròn đến số thập phân thứ 2). Bài 5: ( 0,5 điểm ) 1
Giải phương trình x − 2 + y + 2009 + z − 2010 = ( x + y + z) 2 HẾT
PHÒNG GD&ĐT QUẬN NAM TỪ LIÊM
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
TRƯỜNG THCS NAM TỪ LIÊM NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. − + − a) 2 27 3 12 98 18 .
= 2 9.3 − 3 4.3 + 49.2 − 9.2 = 6 3 − 6 3 + 7 2 − 3 2 = 4 2 . b) 14 + 6 5 + 14 − 6 5 = 9 + 6 5 + 5 + 9 − 6 5 + 5 = ( + )2 + ( − )2 3 5 3 5 = 3+ 5 + 3− 5 = 3+ 5 + 3− 5 . = 6 3 + 2 3 2 + 2 c) + − (2+ 3) 3 1+ 2 3 ( 3 + 2) 2 ( 2 + ) 1 = + − (2+ 3) 3 1+ 2 = 3 + 2 + 2 − 2 − 3 = 2 . Câu 2.
a) Ta có a − 5 a + 6 = 0
⇔ a − 2 a − 3 a + 6 = 0
⇔ a ( a − 2)−3( a − 2) = 0
⇔ ( a − 2)( a −3) = 0 a − 2 = 0 ⇔ a −3=0
⇔ a = 4 (loại) hoặc a = 9 (thỏa mãn).
Thay a = 9 vào biểu thức P , ta được 9 +1 P = = 4 . 9 −1
Vậy P = 4 tại a − 5 a + 6 = 0 .
b) Với a > 0; a ≠ 1; 4 a + 3 a + 2 a + a 1 1 Q = ( − −
a + 2)( a + ) : 1
a −1 a +1 a −1
( a + )1( a + 2) a ( a + ) 1 a −1+ a +1 = ( −
a + )( a + ) ( a + )( a − ) : 2 1 1 1 ( a + ) 1 ( a − )1 a +1 a 2 a = − : a −1 a −1 ( a + ) 1 ( a − ) 1 ( a − )1( a+1 1 ) = . a −1 2 a a +1 = 2 a a +1 Vậy Q =
với a > 0; a ≠ 1; 4 . 2 a
c) Với a > 0; a ≠ 1; 4 4 ( a + Q )1 4 a +1 Ta có = : P 2 a a − 2 4Q 2 a − 4 4 ⇒ = = 2 − P a a 4Q 4 ∈ ⇔
∈ ⇔ a ∈U (4) = { 1 ± , ± 2, ± } 4 . P a Vì a > 0 ⇒ a ∈{1, 2, } 4 ⇒ a ∈{1, 4,1 } 6
Mà a > 0; a ≠ 1; 4 ⇒ a = 16 (TM) x − 5 1 Câu 3. a) 4x − 20 + 3 −
9x − 45 = 3x −12 . Điều kiện x ≥ 5 . 9 3
⇔ 2 x − 5 + x − 5 − x − 5 = 3x −12
⇔ 2 x − 5 = 3x −12
⇔ 4(x −5) = 3x −12 ⇔ x = 8 (t/m)
Vậy tập nghiệm của phương trình S = { } 8 . 27 b)
2x + 27 − 6 = x . Điều kiện x ≥ − . 2 PT ⇔ 2x + 27 = x + 6 x ≥ 6 − ⇔ 2x + 27 = (x + 6)2 (*) (*) 2
⇔ 2x + 27 = x +12x + 36 2
⇔ x +10x + 9 = 0 2
⇔ x + x + 9x + 9 = 0 ⇔ x(x + ) 1 + 9 ( x + ) 1 = 0 ⇔ (x + ) 1 ( x + 9) = 0 x +1 = 0 x = 1( − tm) ⇔ ⇔ x + 9 = 0 x = 9 − (ktm)
Vậy tập nghiệm của phương trình S = {− } 1 . Câu 4. a) Ta có A
∆ BC vuông tại A có AH là đường cao của tam giác 2
AC = CH.BC
.( Áp dụng hệ thức lượng trong tam giác vuông) 2
AB = BH.BC 2 2 AB AC ⇒ = = BC . BH CH 2 2 AB AC ⇒ =
(Điều phải chứng minh) BH CH
b) Tam giác ABC vuông tại A ta có: + ABC ACB = 90° ⇒ ABC + 60° = 90° ⇒
ABC = 90° − 60° = 30°
Tam giác ABH vuông tại H ta có: + = ° ⇒ ABH HAB 90
HAB = 90° − 30° = 60° AH AH sin ABC = 1 ⇒ sin 30° = = ⇒ AH = 6 cm AB 12 2 BH AH cos ABC = 3 ⇒ cos30° = = ⇒ BH = 6 3 cm AB 12 2 1 c) S = .AH.CF ACF (1) 2 =
Tam giác ACH vuông tại H ta có: AH AC.sin ACH (2) 1 =
Từ (1) và (2) suy ra S
.CF.AC.sin ACH ACF 2 Ta có: = + S S S ACB AFB AFC 1 ⇒ 1 = 1 + A . B AC.sin BAC A . B AF.sin BAF
AC.AF.sin CAF 2 2 2 1 1 1 ⇒ A . B AC.sin 90° = A . B AF.sin 45° + AC.AF.sin 45° 2 2 2 1 1 2 1 2 ⇒ A . B AC = A . B AF. + AC.AF. 2 2 2 2 2 ⇒ 2A . B AC = A .
B AF. 2 + AC.AF. 2 . 2 1 1
Chia cả 2 vế của đẳng thức cuối cùng cho 2.A .
B AC.AF ta được: = + . AF AB AC 2.
Gọi chiều cao của tháp là h (m)
Bóng của tháp trên mặt đất là b (m) ⇒ b = 92 m h ⇒ t 30 an ° = b 1 h 92 ⇒ = ⇒ h = ≈ 53,12 3 92 3
Vậy chiều cao của tháp là 53,12 cm Câu 5. ( 0,5 điểm ) 1
Giải phương trình: x − 2 + y + 2009 + z − 2010 = ( x + y + z) 2 Lời giải 1
Giải phương trình: x − 2 + y + 2009 + z − 2010 = ( x + y + z) ( )1 2 x ≥ 2
ĐKXĐ: y ≥ 2009 − z ≥ 2010 ( )
1 ⇔ 2 ( x − 2 + y + 2009 + z − 2010 ) = x + y + z
⇔ (x − 2− 2 x − 2 + )
1 + ( y + 2009 − 2 y + 2009 + )
1 + ( z − 2010 − 2 z − 2010 + ) 1 = 0
⇔ ( x − − )2 +( y + − )2 +( z − − )2 2 1 2009 1 2010 1 = 0 (2) ( x−2 − )2 1 ≥ 0 2 Vì ( y + 2009 − ) 1 ≥ 0 nên ( z−2010 − )2 1 ≥ 0 ( x−2 − )2 1 = 0 x = 3 ( 2 2) ⇔ ( y + 2009 − ) 1 = 0 ⇔ y = 2008 − (tmđk). ( = z − − )2 z 2011 2010 1 = 0
Vậy ( x, y, z) = (3; − 2008; ) 2011 . HẾT




