Đề thi giữa kì 1 Toán 9 năm 2020 – 2021 trường THCS Nguyễn Công Trứ – Hà Nội
Nhằm kiểm tra đánh giá chất lượng dạy và học môn Toán lớp 9 định kỳ, ngày … tháng 11 năm 2020, trường THCS Nguyễn Công Trứ, Ba Đình, thành phố Hà Nội tổ chức kỳ thi kiểm tra chất lượng giữa học kỳ 1 môn Toán 9 năm học 2020 – 2021. Mời bạn đọc đón xem.
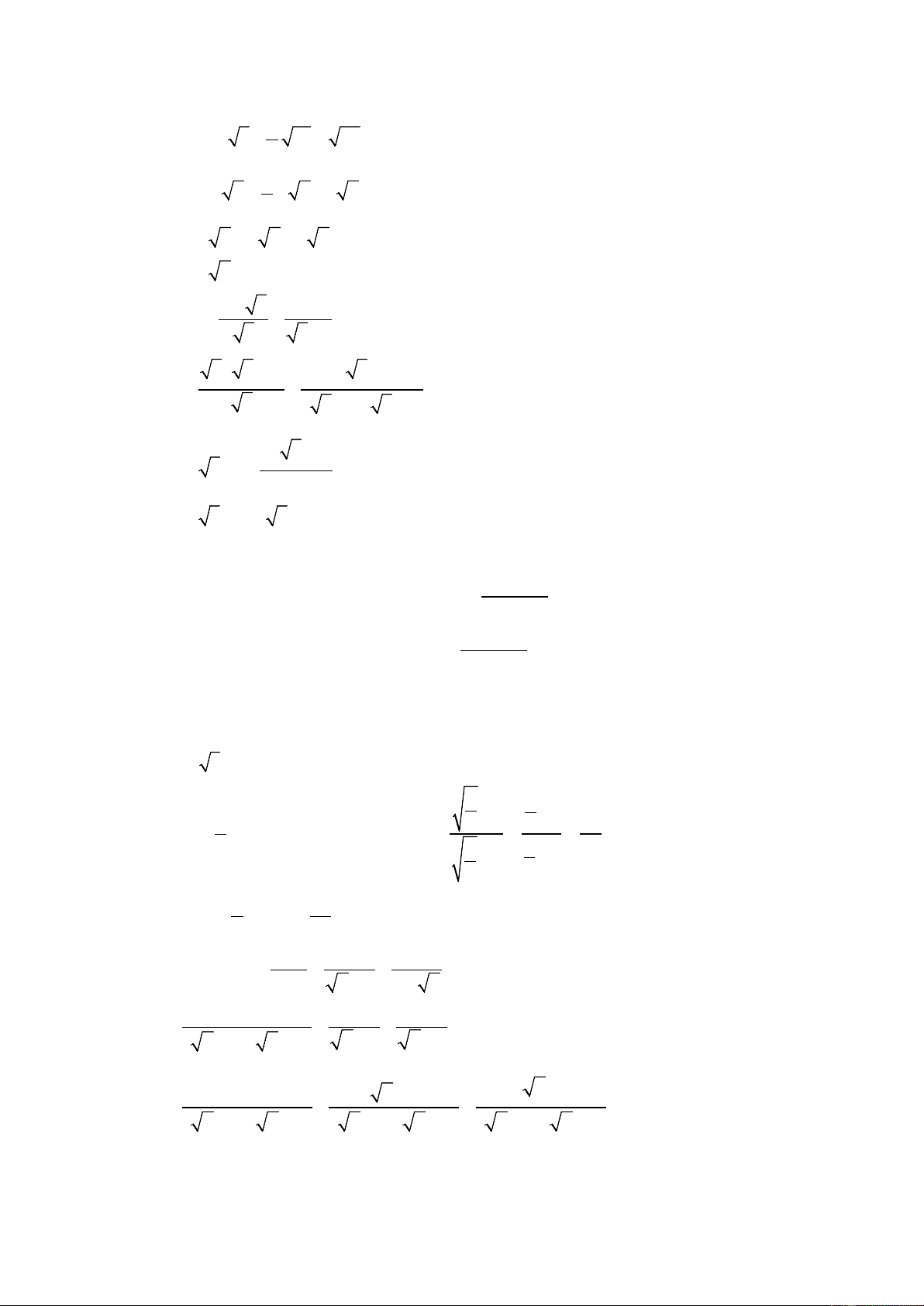
Preview text:
PHÒNG GD VÀ ĐT QUẬN BA ĐÌNH
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
TRƯỜNG THCS NGUYỄN CÔNG TRỨ NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Bài 1:
(1,5 điểm) Thực hiện phép tính: 2 a) A = 2 8 − 18 + 50 3 3 + 3 2 b) B = − 3 3 −1 2 cos 39° c) 2 2 C = cot 30 . ° sin 65° + tan 60 . ° sin 25° − sin51° x +1 x − 3 1 2 Bài 2:
(3 điểm) Cho hai biểu thức A = và B = + −
với x ≥ 0 ; x ≠ 9 x − 3 x − 9 x + 3 3 − x 1
a) Tính giá trị của biểu thức A với x = 4
b) Rút gọn biểu thức B
c) Cho P = B : A . Tìm x để 5 P = 2
d) Tìm x để P nhận giá trị nguyên. Bài 3:
(1,5 điểm) Giải phương trình:
a) 9x − 5 x = 6 − 4 x b) 2
x + x + 5 = x +1 Bài 4:
(0,5 điểm) Tại một thời điểm trong ngày, một cái cây có bóng trên mặt đất dài 4,5m .
Tính chiều cao của cây biết tia nắng mặt trời hợp với phương thẳng đứng một góc 50° . Bài 5:
(3 điểm) Cho A
∆ BC vuông tại A , đường cao AD . Biết AB = 6cm , BC =10cm .
a) Tính AC , góc B và góc C .
b) Kẻ DE vuông góc với AB ở E và DF vuông góc với AC ở F . Tính độ dài EF . c) Chứng minh 3 3
AB .CF = AC .BE . HẾT
HƯỚNG DẪN GIẢI CHI TIẾT 2 Bài 1: a) A = 2 8 − 18 + 50 3 2
A = 2.2 2 − .3 2 + 5 2 3 A = 4 2 − 2 2 + 5 2 A = 7 2 . 3 + 3 2 b) B = − 3 3 −1 3 ( 3 + ) 1 2 ( 3 + ) 1 B = − 3 ( 3− )1( 3+ )1 2 ( 3 + ) 1 B = 3 +1− 2 B = 3 +1− ( 3 + ) 1 B = 0 2 cos 39° c) 2 2 C = cot 30 . ° sin 65° + tan 60 . ° sin 25° − sin51° 2 cos 39° 2 2 C = cot 30 . ° sin 65° + cot 30 . ° os c 65° − co 39 s ° C = ° ( 2 2 cot 30 . sin 65° + os c 65°) − 2 C = cot 30 .1 ° − 2 C = 3 − 2 1 1 +1 +1 1 4 3 − Bài 2: a) x = (thoả mãn điều kiện) 2 ⇒ A = = = 4 1 1 5 − − 3 3 2 4 1 3 − Vậy x = thì A = 4 5 x − 3 1 2 b) Ta có: B = + −
với x ≥ 0 ; x ≠ 9 x − 9 x + 3 3 − x x − 3 1 2 = ( + + x + 3)( x − 3) x + 3 x − 3 2 + x − x − ( x 3 3 3 ) = ( + +
x + 3)( x − 3) ( x + 3)( x − 3) ( x + 3)( x − 3)
x − 3 + x − 3 + 2 x + 6 = ( x +3)( x −3) x + 3 x
= ( x +3)( x −3) x ( x + 3)
= ( x +3)( x −3) x = x −3 x Vậy B =
với x ≥ 0 ; x ≠ 9 x − 3 x x + x x − 3 x c) Ta có: P = 1 B : A = : = . = x − 3 x − 3 x − 3 x +1 x +1 − − − − Để 5 x x 5 2 x 5 x 5 3 x 5 P = 5 ⇔ = ⇔ − = 0 ⇔ = 0 ⇔ = 0 2 x +1 2 x +1 2 x +1 x +1 ⇒ − 3 − x − 5 = 5 0 ⇔ x = 3 5 − 5 Vì x ≥ 0 , x
∀ ≥ 0 ; x ≠ 9 mà
< 0 ⇒ không có x thỏa mãn P = 3 2 x
d) Với x ≥ 0 ; x ≠ 9 ⇒ ≥ 0 ⇒ P ≥ 0 ( ) 1 x +1 x 1 − Ta có P −1 = −1 = < 0 ⇒ P < 1 (2) x +1 x +1 x Từ ( ) 1
và (2) ⇒ 0 ≤ P < 1 P ∈⇒ P = ⇔
= 0 ⇔ x = 0 ⇔ x = 0 (thoả mà 0 x +1 mãn)
Vậy x = 0 thì P nhận giá trị nguyên. Bài 3:
a) 9x − 5 x = 6 − 4 x (*)
Điều kiện xác định: x ≥ 0
(*) ⇔ 3 x −5 x = 6− 4 x
⇔ 3 x − 5 x + 4 x = 6 ⇔ 2 x = 6 ⇔ x = 3
⇔ x = 9 (thoả mãn) Vậy x = 9 b) 2
x + x + 5 = x +1 x ≥ 1 −
⇔ x + x+5 = (x + )2 2 1 x ≥ 1 − ⇔ 2 2
x + x + 5 = x + 2x +1 x ≥ 1 − ⇔
⇔ x = 4(thoaû maõn) x = 4 Vậy x = 4 Bài 4: B 500 A C
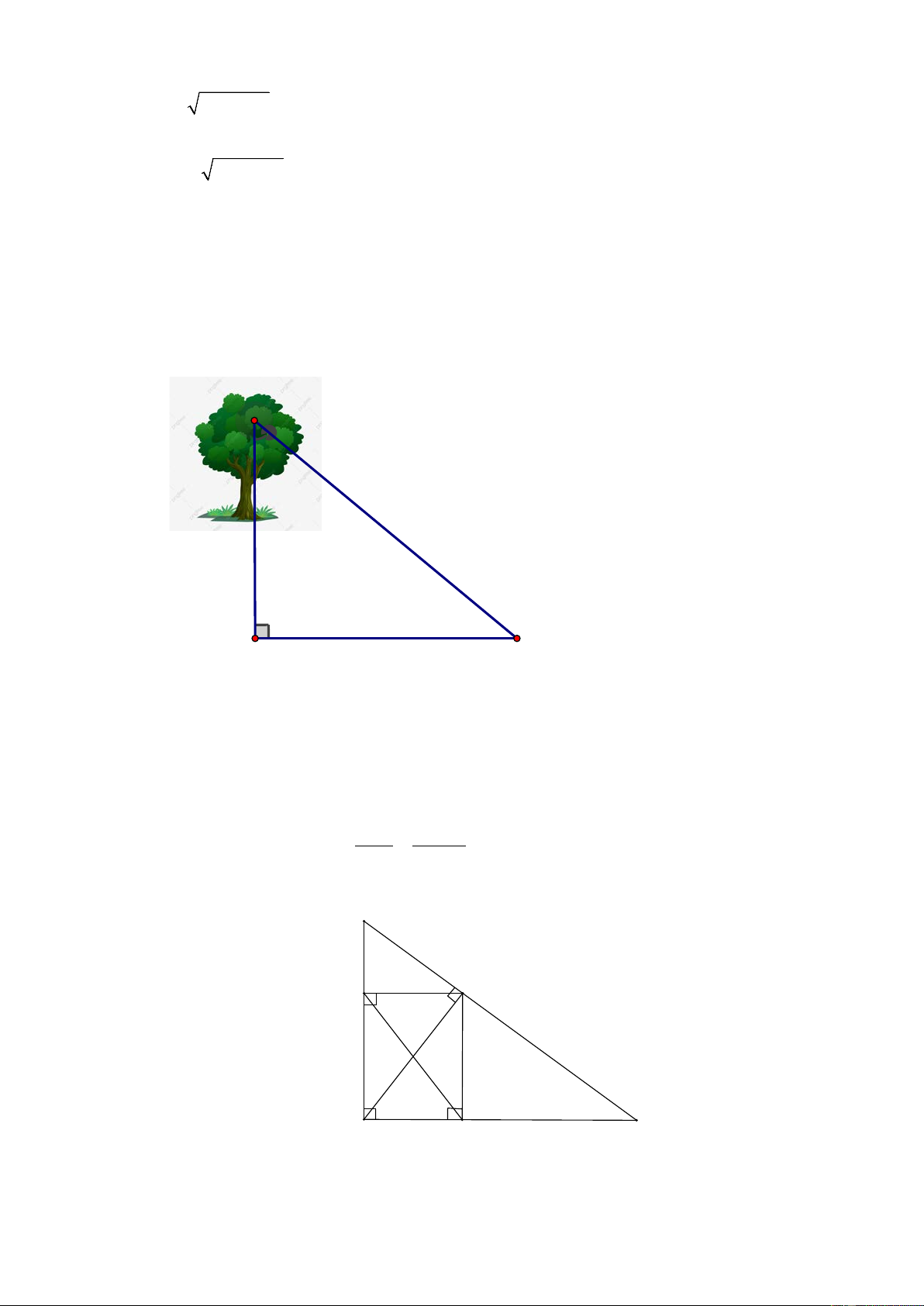
Ta có hình minh họa, trong đó:
AB : là chiều cao của cây
AC : độ dài bóng cây, AC = 4, 5 m
ABC là góc hợp bởi tia nắng mặt trời với phương thẳng đứng, ABC = 50° . Xét A
∆ BC vuông tại A , áp dụng hệ thức về cạnh và góc trong tam giác vuông ta có: 4, 5 = . tanB ⇒ = = ≈ 3.8( m AC AC AB AB ) tanB tan 50° Bài 5: B D E A C F a) Xét A
∆ BC vuông tại A , theo định lý Pytago ta có: 2 2 2 2 2 2
BC = AB + AC ⇔ AC = BC − AB 2 2 2 ⇔ AC =10 − 6 = 64 ⇔ AC = 8(cm). AC 8 4 Ta có: sin B = = = ⇒ B ≈ 53° . BC 10 5 Vì A
∆ BC vuông tại A nên
C = 90° − B = 90° − 53° = 37° . b) Xét A
∆ BC vuông tại A , đường cao AD , ta có: A . B AC = A .
D BC (hệ thức lượng trong tam giác vuông) A . B AC 6.8 ⇔ AD = = = 4,8( cm) . BC 10
Xét tứ giác AEDF có
EAF = AED = AFD = 90° , suy ra AEDF là hình chữ nhật.
⇒ EF = AD (hai đường chéo của hình chữ nhật bằng nhau) Mà AD = 4,8 cm ⇒ EF = 4,8cm . 3 AB BE c) Ta có 3 3
AB .CF = AC .BE ⇔ = AC CF 4 AB BE AB ⇔ = . AC CF AC 2 2 AB BE.AB ⇔ = . ( ) 1 2 AC CF.AC
Xét các tam giác vuông ABC , ADB , ACD ta có: 2 AB = B . D BC ; 2 AC = C . D BC ; 2
BE.BA = BD ; 2
CF.CA = CD . 2 2 2 2 B . D BC BD BD BD Khi đó ( ) 1 ⇔ = ⇔ = (luôn đúng). 2 . CD BC CD CD CD Vậy 3 3
AB .CF = AC .BE . HẾT