


Preview text:
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
ĐỀ THI MÔN: Xử lý số tín hiệu
VIỆN ĐIỆN TỬ - VIỄN THÔNG
Lần thi: giữa kỳ Ngày thi: 22/05/2020
Thời gian làm bài: 60 phút Đề số: 1 Tổng số trang: 2
(Được sử dụng tài liệu duy nhất là 01 tờ A4.
Không được sử dụng điện thoại và máy vi tính) Họ và tên: Mã số sinh viên Lớp: Số thứ tự:
Câu 1: Cho hai tín hiệu x(n) và h(n) như sau:
x(n) = {2, 3, -1, 0, 2} và h(n) = {2, -1, 1}
a) (2 điểm) Tính y(n) = x(n) * h(n).
……………………………………………………………………………………….
……………………………………………………………………………………….
b) (1 điểm) Tính y1(n) = x(n-2) * h(n+1).
……………………………………………………………………………………….
……………………………………………………………………………………….
Câu 2: Cho dãy x(n) = u(n+1) – u(n-4).
a) (1 điểm) Tìm miền hội tụ của X(z).
……………………………………………………………………………………….
……………………………………………………………………………………….
b) (1 điểm) Vẽ các điểm không của X(z) lên mặt phẳng phức.
Câu 3: Cho hệ thống LTI được biểu diễn bởi phương trình sai phân:
y(n) = -x(n+3) - 2x(n+1) + x(n) – x(n-1) + 2x(n-2) + x(n-4)
a) (2 điểm) Tính đáp ứng pha arg {H (ejω)}.
………………………………………………………………………………………. 2π
b) (1 điểm) Tính∫¿ H(e jω)∨¿2dω¿. 0
……………………………………………………………………………………….
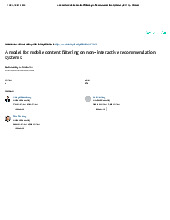
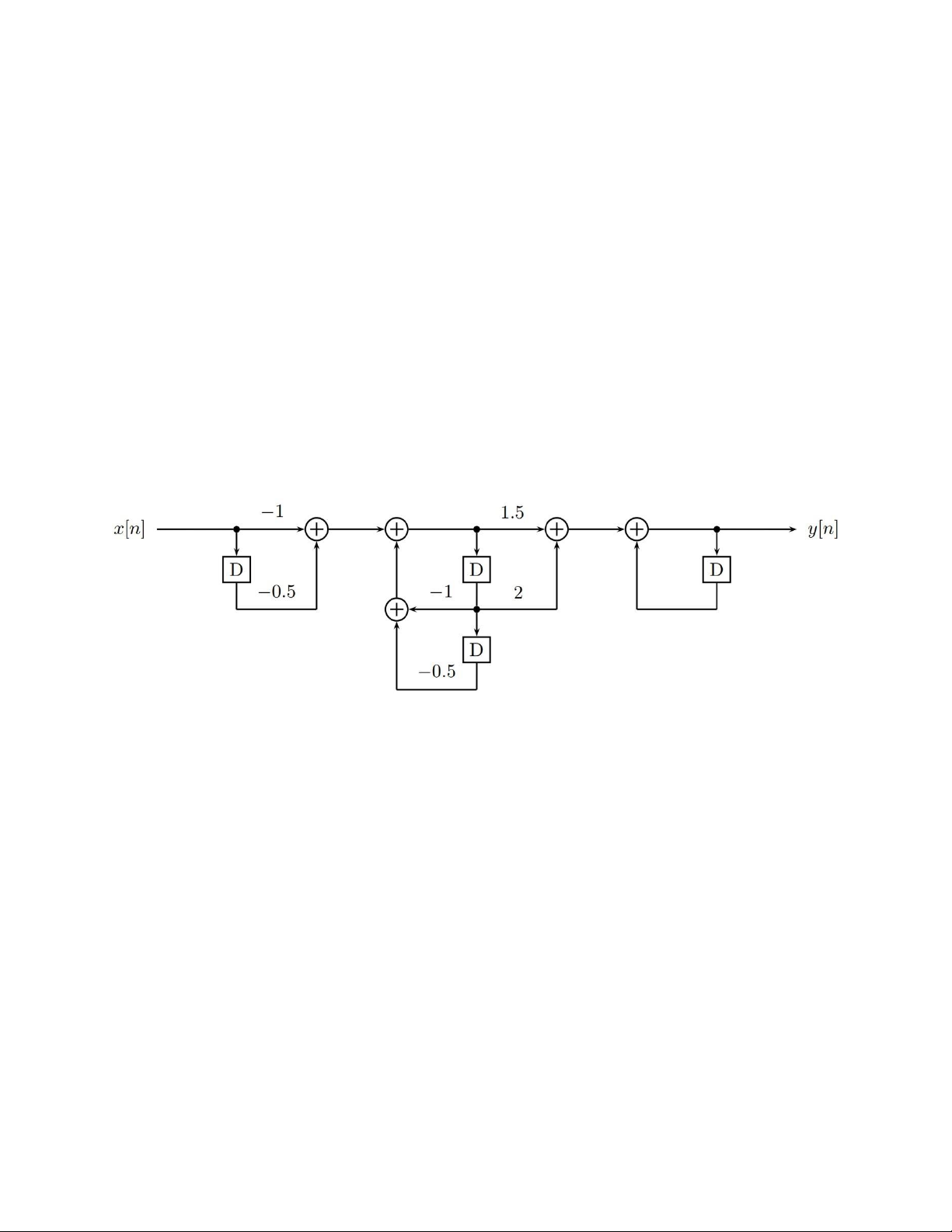
Câu 4: (2 điểm)Cho hê tḥ ống LTI với sơ đồ thực hiên như sau:̣
Viết phương trình sai phân của hệ thống.
……………………………………………………………………………………….
Câu 1: Cho hai tín hiệu x(n) và h(n) như sau:
x(n) = {-2, 3, -1, 0, 2} và h(n) = {-2, -1, 1}
c) (2 điểm) Tính y(n) = x(n) * h(n).
……………………………………………………………………………………….
……………………………………………………………………………………….
d) (1 điểm) Tính y1(n) = x(n-1) * h(n+2).
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
ĐỀ THI MÔN: Xử lý số tín hiệu
VIỆN ĐIỆN TỬ - VIỄN THÔNG
Lần thi: giữa kỳ Ngày thi: 22/05/2020
Thời gian làm bài: 60 phút Đề số: 2 Tổng số trang: 2
(Được sử dụng tài liệu duy nhất là 01 tờ A4.
Không được sử dụng điện thoại và máy vi tính) Họ và tên: Mã số sinh viên Lớp: Số thứ tự:
……………………………………………………………………………………….
……………………………………………………………………………………….
Câu 2: Cho dãy x(n) = u(n+2) – u(n-1).
c) (1 điểm) Tìm miền hội tụ của X(z).
……………………………………………………………………………………….
……………………………………………………………………………………….
d) (1 điểm) Vẽ các điểm không của X(z) lên mặt phẳng phức.
Câu 3: Cho hệ thống LTI được biểu diễn bởi phương trình sai phân:
y(n) = x(n+3) - 2x(n+1) + x(n) – x(n-1) + 2x(n-2) - x(n-4)
c) (2 điểm) Tính đáp ứng pha arg {H (ejω)}.
………………………………………………………………………………………. 2π
d) (1 điểm) Tính∫¿ H(e jω)∨¿2dω¿. 0
……………………………………………………………………………………….
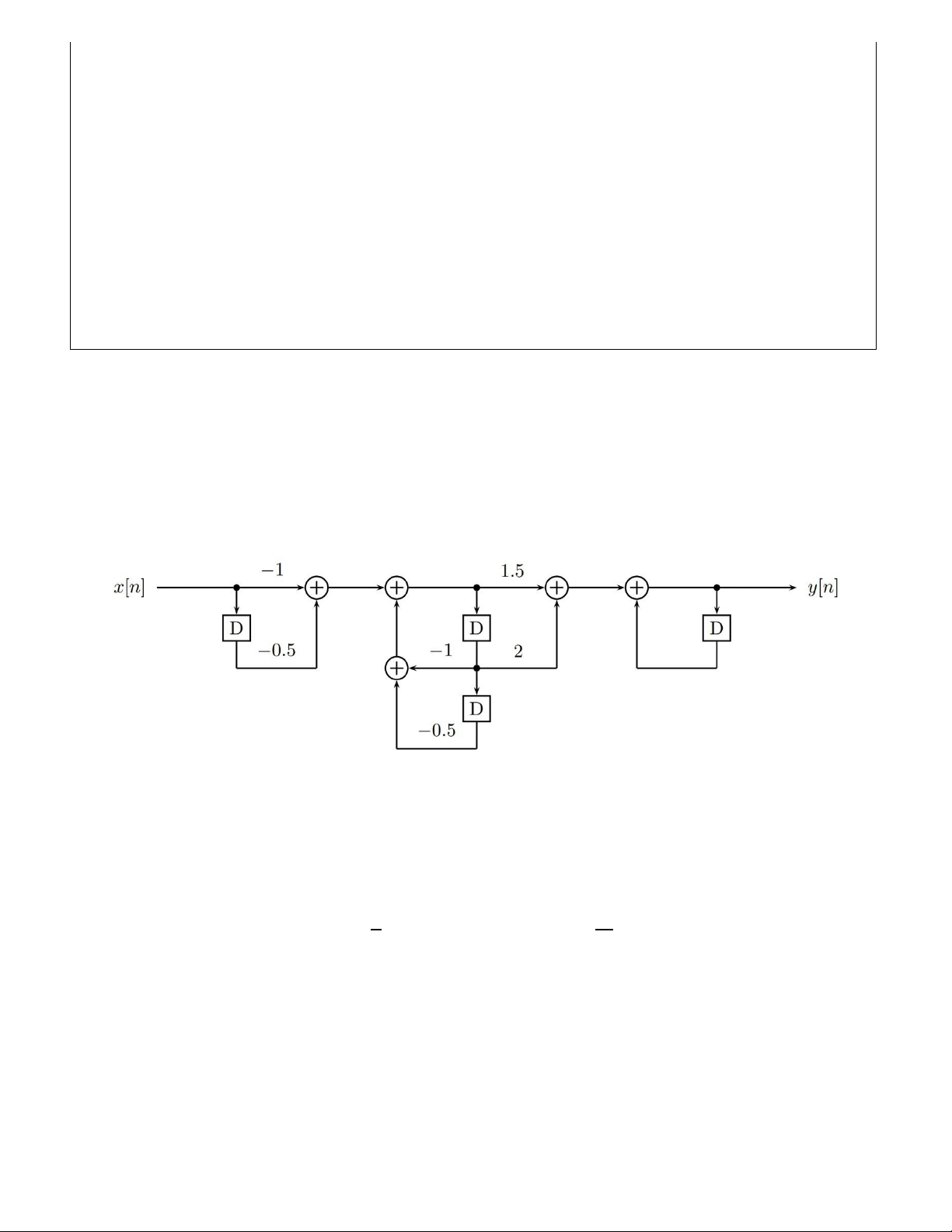
Câu 4: (2 điểm)Cho hê tḥ ống LTI với sơ đồ thực hiên như sau:̣
Viết phương trình sai phân của hệ thống.
……………………………………………………………………………………….
Câu 1: Cho hai tín hiệu x(n) và h(n) như sau:
x(n) = {2, 3, 1, 0, 2} và h(n) = {2, -1, -1}
e) (2 điểm) Tính y(n) = x(n) * h(n).
……………………………………………………………………………………….
……………………………………………………………………………………….
f) (1 điểm) Tính y1(n) = x(n+1) * h(n-2).
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
ĐỀ THI MÔN: Xử lý số tín hiệu
VIỆN ĐIỆN TỬ - VIỄN THÔNG
Lần thi: giữa kỳ Ngày thi: 22/05/2020
Thời gian làm bài: 60 phút Đề số: 3 Tổng số trang: 2
(Được sử dụng tài liệu duy nhất là 01 tờ A4.
Không được sử dụng điện thoại và máy vi tính) Họ và tên: Mã số sinh viên Lớp: Số thứ tự:
……………………………………………………………………………………….
……………………………………………………………………………………….
Câu 2: Cho dãy x(n) = u(n+2) – u(n-3).
e) (1 điểm) Tìm miền hội tụ của X(z).
……………………………………………………………………………………….
……………………………………………………………………………………….
f) (1 điểm) Vẽ các điểm không của X(z) lên mặt phẳng phức.
Câu 3: Cho hệ thống LTI được biểu diễn bởi phương trình sai phân:
y(n) = 2x(n+3) - 2x(n+1) + x(n) – x(n-1) + 2x(n-2) + -2x(n-4)
e) (2 điểm) Tính đáp ứng pha arg {H (ejω)}.
………………………………………………………………………………………. 2π
f) (1 điểm) Tính∫¿ H(e jω)∨¿2dω¿. 0
……………………………………………………………………………………….
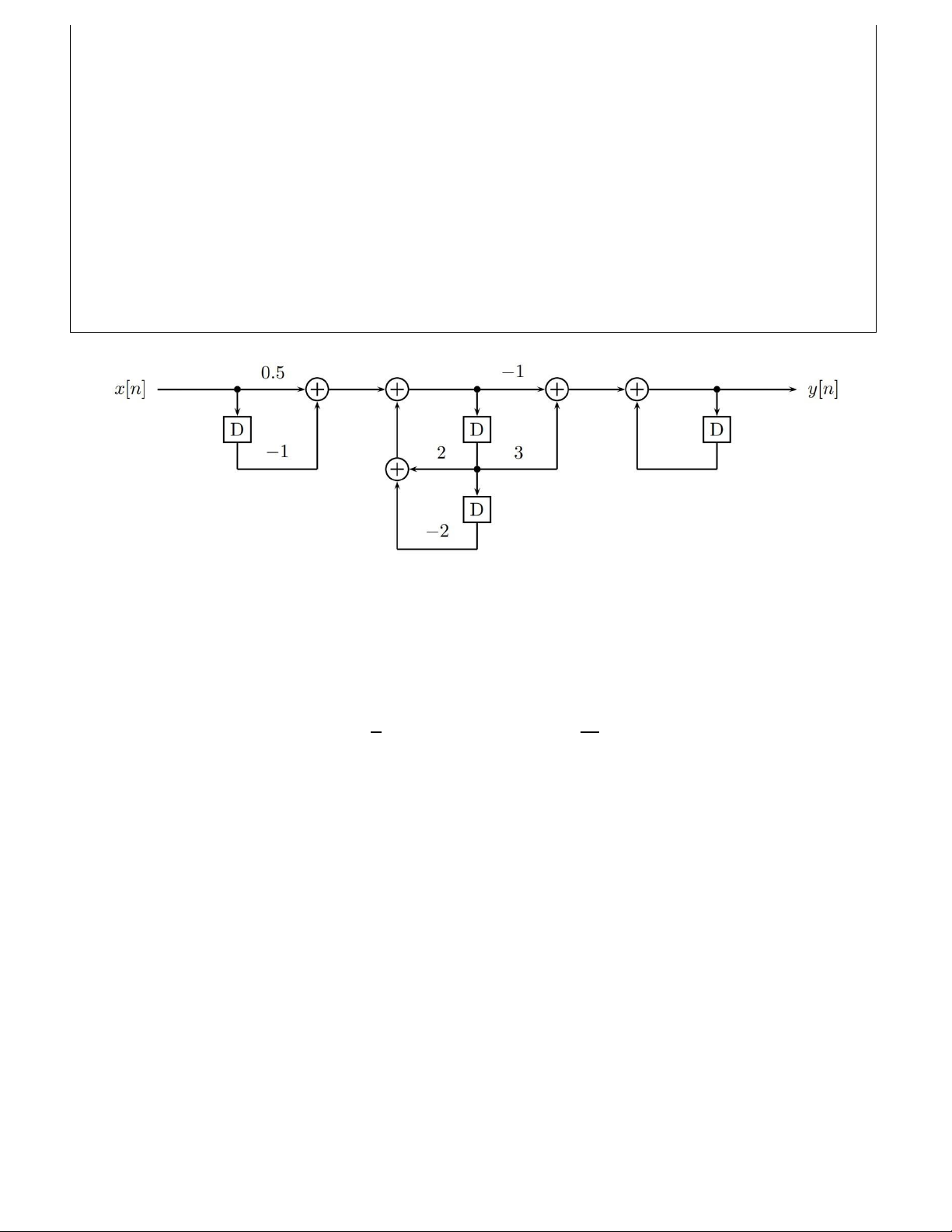
Câu 4: (2 điểm)Cho hê tḥ ống LTI với sơ đồ thực hiên như sau:̣
Viết phương trình sai phân của hệ thống.
……………………………………………………………………………………….
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
ĐỀ THI MÔN: Xử lý số tín hiệu
VIỆN ĐIỆN TỬ - VIỄN THÔNG
Lần thi: giữa kỳ Ngày thi: 22/05/2020
Thời gian làm bài: 60 phút Đề số: 4 Tổng số trang: 2
(Được sử dụng tài liệu duy nhất là 01 tờ A4.
Không được sử dụng điện thoại và máy vi tính) Họ và tên: Mã số sinh viên Lớp: Số thứ tự:
Câu 1: Cho hai tín hiệu x(n) và h(n) như sau:
x(n) = {2, -3, -1, 0, 2} và h(n) = {2, 1, -1}
g) (2 điểm) Tính y(n) = x(n) * h(n).
……………………………………………………………………………………….
……………………………………………………………………………………….
e) (1 điểm) Tính y1(n) = x(n+2) * h(n-1).
……………………………………………………………………………………….
……………………………………………………………………………………….
Câu 2: Cho dãy x(n) = u(n+2) – u(n-2).
g) (1 điểm) Tìm miền hội tụ của X(z).
……………………………………………………………………………………….
……………………………………………………………………………………….
h) (1 điểm) Vẽ các điểm không của X(z) lên mặt phẳng phức.
Câu 3: Cho hệ thống LTI được biểu diễn bởi phương trình sai phân:
y(n) = -x(n+3) + 2x(n+1) + 2x(n) – 2x(n-1) - 2x(n-2) + x(n-4)
g) (2 điểm) Tính đáp ứng pha arg {H (ejω)}.
………………………………………………………………………………………. 2π
h) (1 điểm) Tính∫¿ H(e jω)∨¿2dω¿. 0
……………………………………………………………………………………….
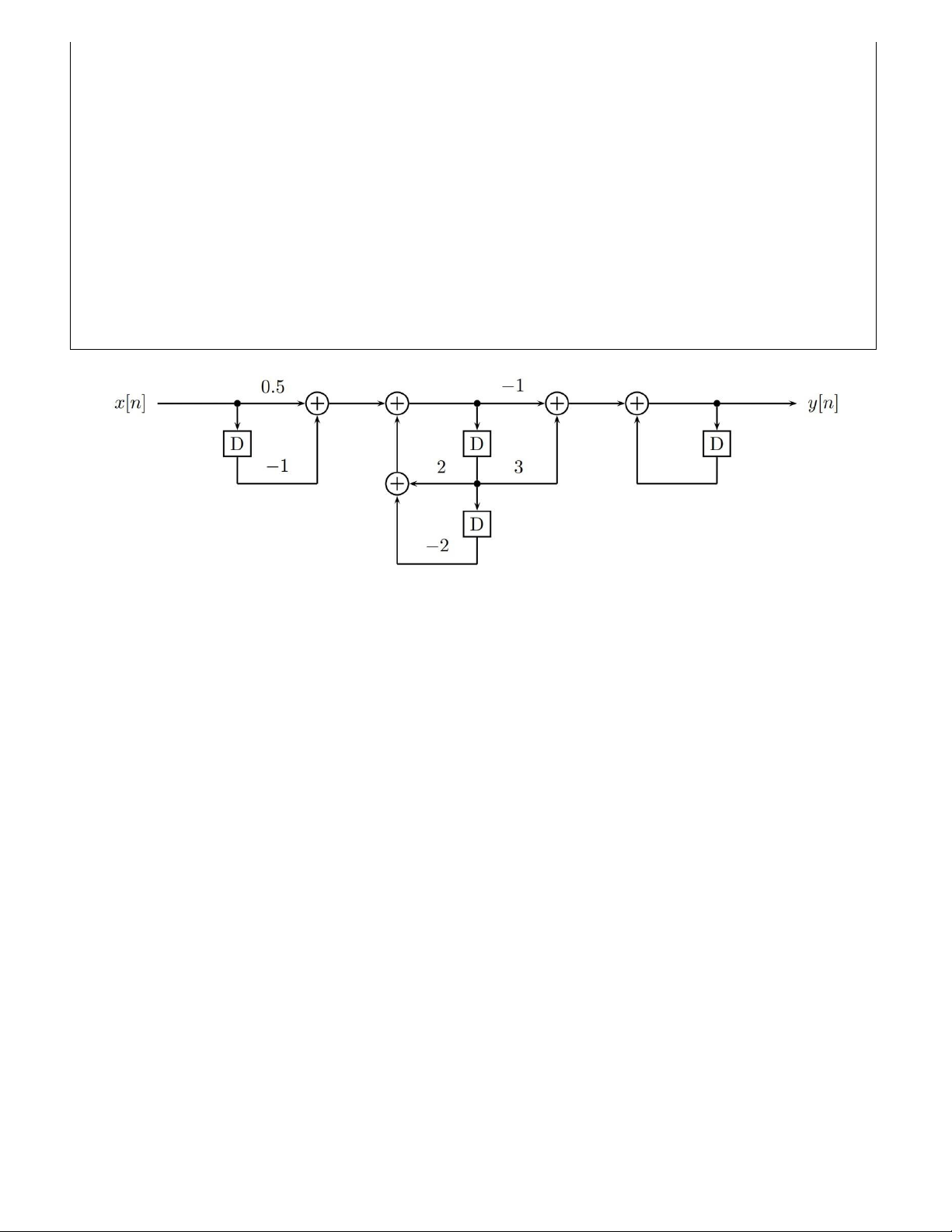
Câu 4: (2 điểm) Cho hê tḥ ống LTI với sơ đồ thực hiên như sau:̣
Viết phương trình sai phân của hệ thống.
……………………………………………………………………………………….
……………………………………………………………………………………….
……………………………………………………………………………………….