Trường ĐH Duy Tân
Đề kiểm tra giữa kỳ Trường ĐH Duy Tân
Đề kiểm tra giữa kỳ Khoa KHTN Năm học 2013 – 2014 Khoa KHTN Năm học 2013 – 2014 = = = = = Khối lớp MTH 203 = = = = = Khối lớp MTH 203
MÔN TOÁN CAO CẤP A3
MÔN TOÁN CAO CẤP A3 (Thời gian 50 phút) (Thời gian 50 phút) (Đề số 1) (Đề số 1)
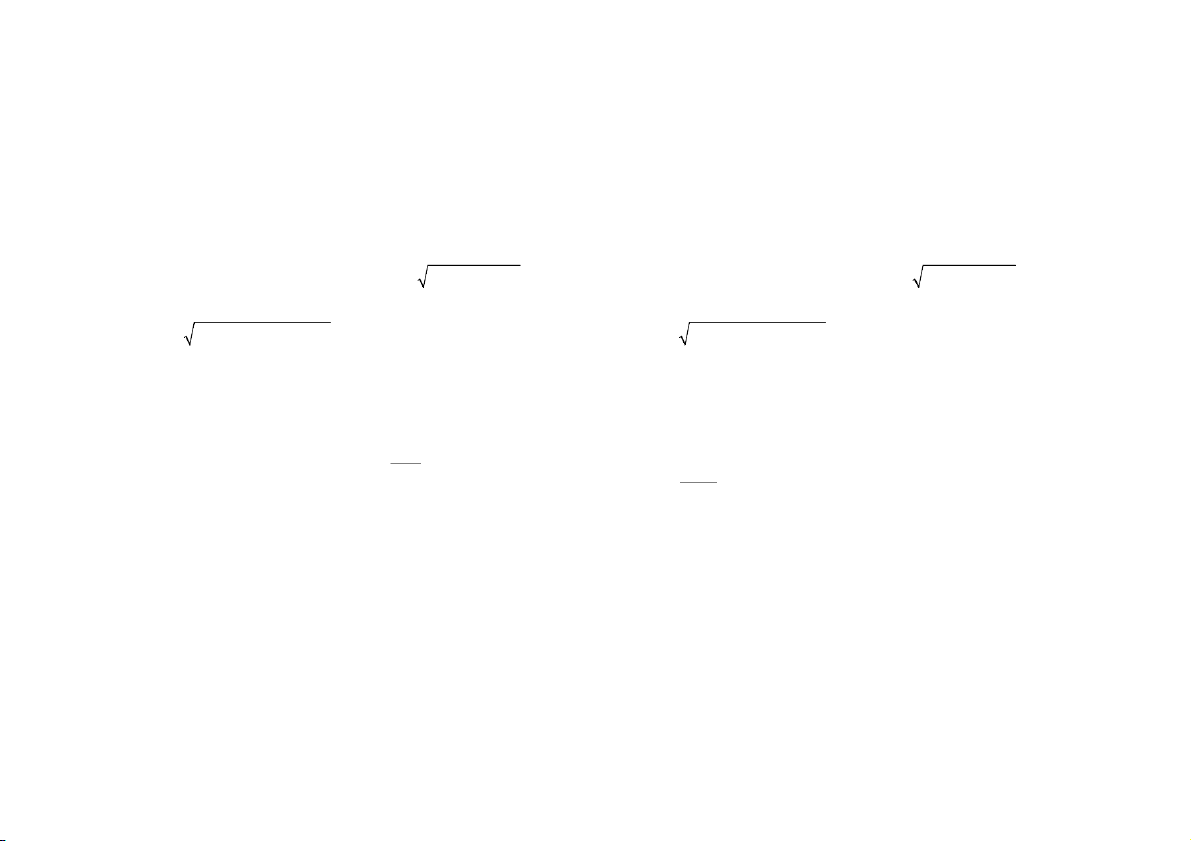
Câu 2: Tìm xấp xỉ tuyến tính của hàm 2 3 3
(f ,x )y = 26 +3 x − 2 y tại
Câu 2: Tìm xấp xỉ tuyến tính của hàm 2 3 3
(f ,x )y = 26 +3 x − 2 y tại
điểm (1;1) và sử dụng xấp xỉ tuyến tính để xấp xỉ
điểm (1;1) và sử dụng xấp xỉ tuyến tính để xấp xỉ 2 3 3 (0, 9 f ;1, 3) 2 = 6 3( +0, 9) 2
− (1, bằng một phân số. 2 3 3 (0, 9 f ;1, 3) 2 = 6 3( +0, 9) 2
− (1, bằng một phân số.
Câu 3: Tìm cực trị địa phương của hàm hai biến
Câu 3: Tìm cực trị địa phương của hàm hai biến 2 / y 2 f ( ,x ) y = (x + ) y e . 2 / y 2 f x y x y e . Câu 4: ( , ) = ( + )
a) Cho mãnh kim loại D là miền tam giác tạo bởi các đỉnh Câu 4: 1
(0; 0), (1;1), (0; với hàm mật độ ρ( , x y )= Tính khối lượng 1+ x 1 a) Tính ∫∫
dA với D là miền tam giác tạo bởi các đỉnh của D. D 2 1+ x b) Tính ∫∫ ydA (0;0), (1;1), (0;1
với D là miền bị chặn bởi hai parabol 2 x = y và D 2 x =8 − y .
b) Tính ∫∫ ydA với D là miền bị chặn bởi hai parabol 2 x = y và D
Chú ý: Sinh viên được sử dụng tài liệu, không trao đổi trong lúc làm 2 x =8 − y . bài.
Chú ý: Sinh viên được sử dụng tài liệu, không trao đổi trong lúc làm Đặng Văn Cường bài. Đặng Văn Cường Trường ĐH Duy Tân
Đề kiểm tra giữa kỳ Trường ĐH Duy Tân
Đề kiểm tra giữa kỳ Khoa KHTN Năm học 2013 – 2014 Khoa KHTN Năm học 2013 – 2014 = = = = = Khối lớp MTH 203 = = = = = Khối lớp MTH 203
MÔN TOÁN CAO CẤP A3
MÔN TOÁN CAO CẤP A3 (Thời gian 50 phút) (Thời gian 50 phút) (Đề số 2) (Đề số 2)
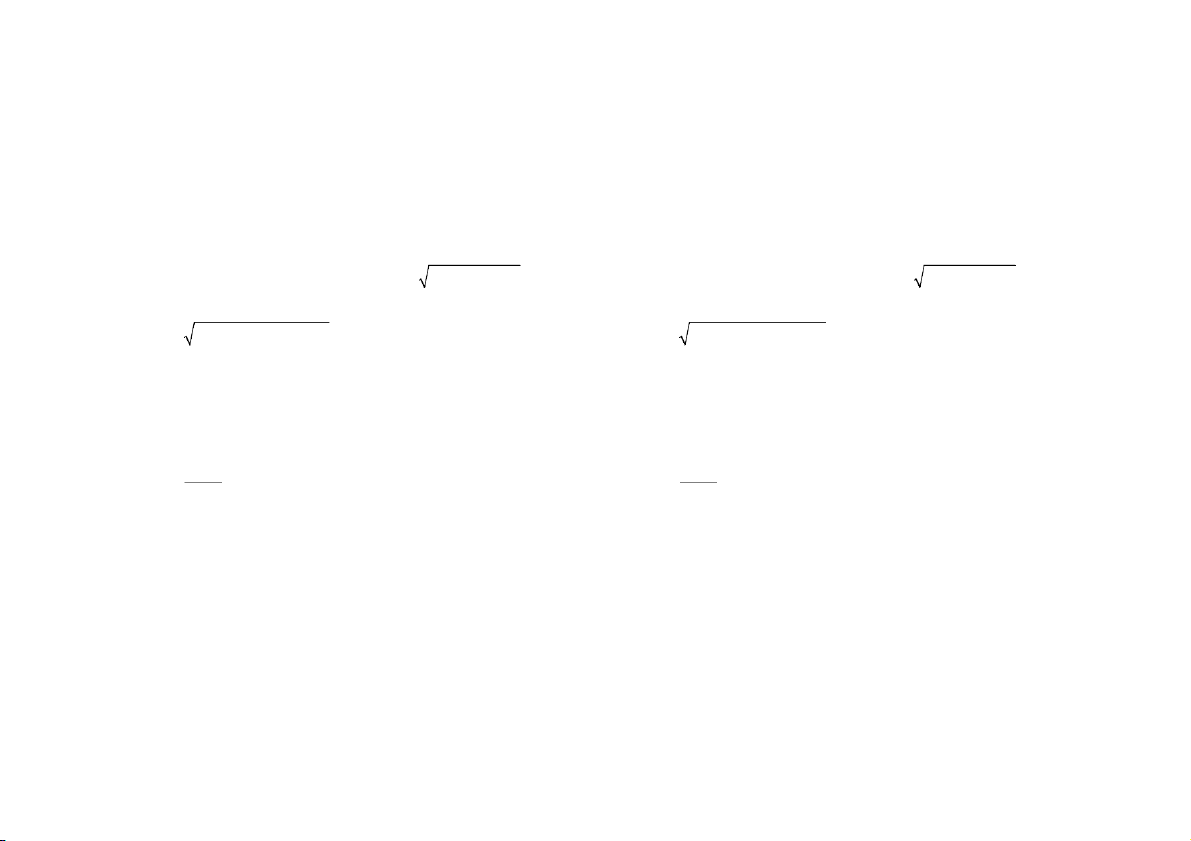
Câu 1: Tìm xấp xỉ tuyến tính của hàm 3 2 4 f ( x, y)= 17− 3x + 2y tại
Câu 1: Tìm xấp xỉ tuyến tính của hàm 3 2 4
(f ,x )y = 17 −3 x + 2 y tại
điểm (1;1) và sử dụng xấp xỉ tuyến tính để xấp xỉ
điểm (1;1) và sử dụng xấp xỉ tuyến tính để xấp xỉ 3 2 4 f (0, 9;1, 3) 1 = 7 3(1 − , 3) 2
+ (0, bằng một phân số. 3 2 4 (0, 9 f ;1, 3) 2 = 7 3(1 − , 3) 2
+ (0, bằng một phân số.
Câu 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm
Câu 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm (f ,x ,
y )z = xy với điều kiện ràng buộc 2 2 2 x + y + z = 3. (f ,x ,
y )z = xy với điều kiện ràng buộc 2 2 2 x + y + z = 3. Câu 3: Câu 3: x+ y x+ y a) Tính ∫∫
dA với D là miền tam giác tạo bởi các đỉnh a) Tính ∫∫
dA với D là miền tam giác tạo bởi các đỉnh D 2 1+ x D 2 1+ x (0;0), (1;1), (1; 0 (0;0), (1;1), (1;
b) Tính ∫∫ xydA với D là miền bị chặn bởi hai parabol 2 x = − y và
b) Tính ∫∫ xydA với D là miền bị chặn bởi hai parabol 2 x = − y và D D 2 x = y −4. 2 x = y −4.
Chú ý: Sinh viên được sử dụng tài liệu, không trao đổi trong lúc làm
Chú ý: Sinh viên được sử dụng tài liệu, không trao đổi trong lúc làm bài. bài. Đặng Văn Cường Đặng Văn Cường