Đề thi HK1 Toán 8 năm học 2017 – 2018 phòng GD và ĐT Vĩnh Bảo – Hải Phòng
Đề thi HK1 Toán 8 năm học 2017 – 2018 phòng GD và ĐT Vĩnh Bảo – Hải Phòng gồm 5 bài toán tự luận, thời gian làm bài 90 phút, đề thi có lời giải chi tiết.
Preview text:
UBND HUYỆN VĨNH BẢO
ĐỀ KHẢO SÁT HỌC KỲ I
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC 2017 – 2018 MÔN: TOÁN 8 Đề chính thức
(Đề thi gồm 01 trang)
(Thời gian:120 phút không kể giao đề)
Bài 1. (1,5 điểm) 1 1. Tính: 2 2
x y(15xy − 5y + 3xy) 5
2. Phân tích các đa thức sau thành nhân tử. a) 5x3 - 5x b) 3x2 + 5y - 3xy - 5x x + 2 x − 2 8 − 4
Bài 2. (2,0 điểm) Cho P = + + : 2
2x − 4 2x + 4 x − 4 x − 2
a) Tìm điều kiện của x để P xác định ?
b) Rút gọn biểu thức P. 1
c) Tính giá trị của biểu thức P khi x = 1 − . 3
Bài 3. (2,0 điểm) Cho hai đa thức A = 2x3 + 5x2 - 2x + a và B = 2x2 - x + 1
a) Tính giá trị đa thức B tại x = - 1
b) Tìm a để đa thức A chia hết cho đa thức B
c) Tìm x để giá trị đa thức B = 1
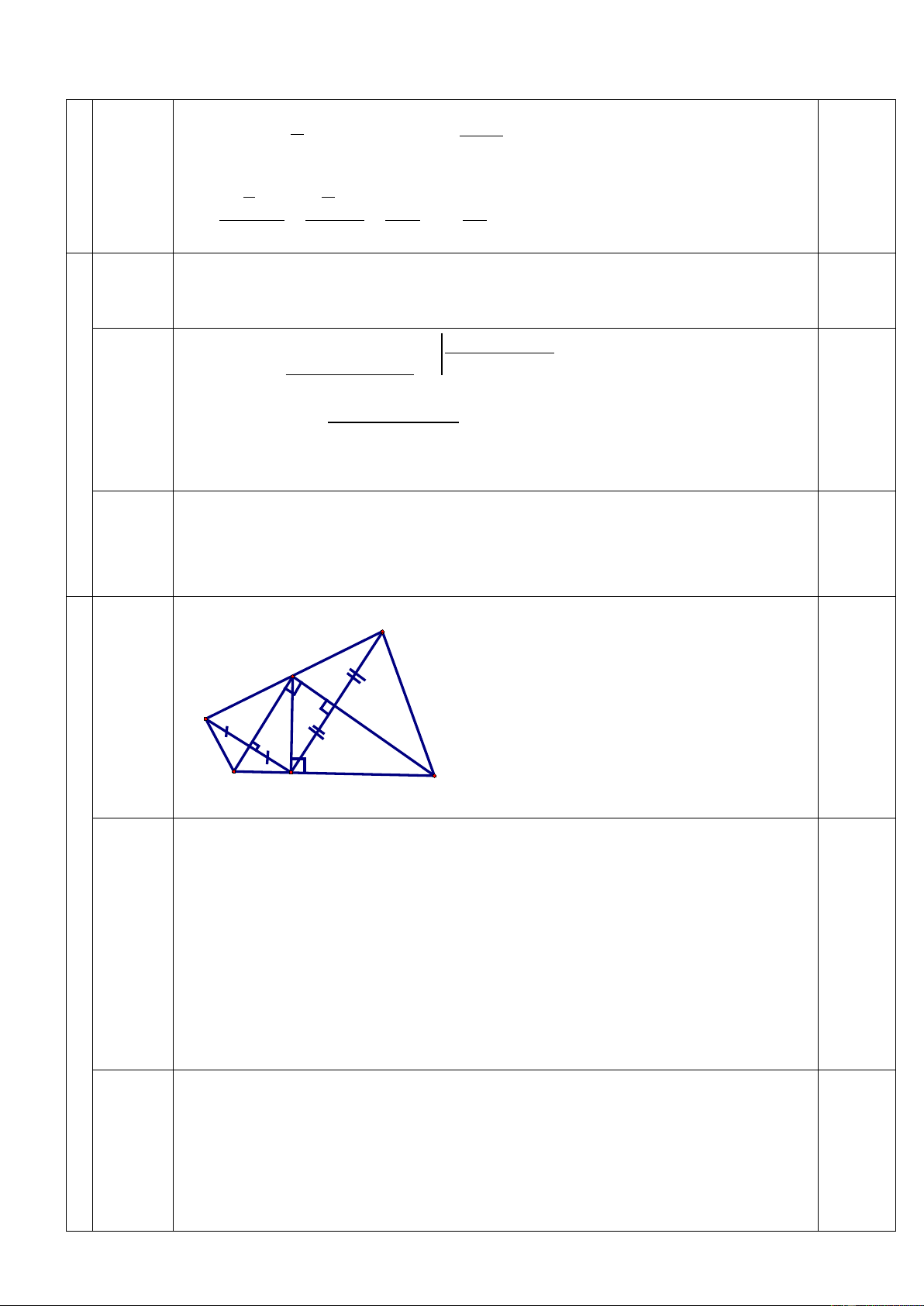
Bài 4. (3,5điểm) Cho ΔABC có 0
A = 90 và AH là đường cao. Gọi D là điểm đối xứng
với H qua AB, E là điểm đối xứng với H qua AC. Gọi I là giao điểm của AB và DH,
K là giao điểm của AC và HE.
a) Tứ giác AIHK là hình gì? Vì sao ?
b) Chứng minh 3 điểm D, A, E thẳng hàng.
c) Chứng minh CB = BD + CE.
d) Biết diện tích tứ giác AIHK là a(đvdt). Tính diện tích ΔDHE theo a.
Bài 5. (1,0 điểm)
a) Tìm các số x, y thoả mãn đẳng thức: 2 + 2 3x
3y + 4xy + 2x − 2y + 2 = 0 . a b c d
b) Với a,b,c,d dương, chứng minh rằng: F = + + + ≥ 2 b + c c + d d + a a + b ----------- Hết -----------
(Cán bộ coi thi không giải thích gì thêm)
1. Họ, tên thí sinh:.................................
1. Giám thị 1:.......................................
2. SBD:............Phòng thi số:................
2. Giám thị 2:.........................................
UBND HUYỆN VĨNH BẢO
ĐÁP ÁN, BIỂU ĐIỂM CHẤ ĐỀ HỌC KY I
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN 8
(Đáp án gồm 03 trang) Bài Nội dung - đáp án Điểm 1 2 2
x y(15xy − 5y + 3xy) 5 = 1 1 1 2 2 x y.15xy + 2 x y(−5y) + 2 x y.3xy 0,25 1 5 5 5 (0,5đ) = 3 3 3 3x y − 2 2 x y + 3 3 x y 5 1 0,25 = 18 3 3 x y − 2 2 x y 5 2a 5x3 - 5x = 5x.( x2 - 1) 0,25
(0,5đ) = 5x.( x - 1)(x + 1) 0,25 3x2 + 5y - 3xy - 5x = ( 2 3x − 3 y x ) + (5y − 5x) 2b 0,25
(0,5đ) = 3x(x − y) − 5(x − y) = (x − y)(3x − 5) 0,25 a P xác đị 2
nh khi 2x − 4 ≠ 0 ; 2x + 4 ≠ 0 ; x − 4 ≠ 0 ; x − 2 ≠ 0 0,25x2
(0,5đ) => …Điều kiện của x là: x ≠ 2 và x ≠ 2 − x + 2 x − 2 8 − 4 P = ( + +
x ) (x ) (x )(x ) : 2 2 2 2 2 2 − + − + x − 2 0,25
(x + 2)2 +(x − 2)2 −16 x − 2 = 2 ( . 2 x − 4) 4 0,25 2 2 b 2 2
x + 4x + 4 + x − 4x + 4 −16 x − 2 2x − 8 x − 2 . = . (0,75đ) = 2 ( 2 x − 4) 4 2 ( 2 x − 4) 4 2 ( 2 x − 4) x − 2 = 2 ( . 2 x − 4) 4 0,25 x − 2 = 4 c 1 0.25 Với x = 1 −
thỏa mãn điều kiện bài toán. (0,5đ) 3 1 x − 2 Thay x = 1 − vào biểu thức P = ta được: 3 4 1 4 0,25x2 1 − − 2 − − 2 10 − 5 3 3 − P = = = : 4 = 4 4 3 6 a
Tại x = - 1 ta có B = 2.(-1)2 - (-1) + 1 = 2 + 1 + 1 = 4 0,25x2 (0,5đ) Xét: 2x3+5x2- 2x+a 2x2- x+1 2x3- x2+ x x + 3 0,25 b 6x2 - 3x + a 0,25 6x2 - 3x + 3 3 (1,0đ) a - 3 0,25
Để đa thức 2x3 + 5x2 - 2x + a chia hết cho đa thức 2x2- x +1 thì đa thức dư 0,25
phải bằng 0 nên => a - 3 = 0 => a = 3 Ta có: 2x2 - x + 1 = 1 c 0,25 <=> x(2x - 1) = 0 (0,5đ) 0,25 có x = 0 hoặc x = 1/2 E A K (0,5đ) D 0,5 I B H C Vẽ hình đúng cho câu a Xét tứ giác AIHK có IAK = 0 90 (gt) 0,25 4 a 0
AKH = 90 (D ®èi xøng víi H qua AC) 0,25 (1,0đ) 0,25 AIH = 0
90 (E ®èi xøng víi H qua AB) 0,25
⇒ Tø gi¸c AIHK lµ h×nh ch÷ nhËt
Có ∆ADH cân tại A (Vì AB là đường cao đồng thời là đường trung tuyến) 0,25 b
=> AB là phân giác của DAH hay DAB = HAB 0,25
(0,75đ) Có ∆AEH cân tại A(AC là đường cao đồng thời là đường trung tuyến) 0,25
=> AC là phân giác của EAH hay DAC = HAC . Mà + = 0 BAH HAC 90 nên + = 0 BAD EAC 90 => = 0 DAE 180
=> 3 điểm D, A, E thẳng hàng (đpcm). 0,25 c
Có BC = BH + HC (H thuộc BC).
Mà ∆BDH cân tại B => BD = BH; ∆CEH cân tại C => CE = CH. 0,25
(0,75đ) Vậy BH + CH = BD + CE => BC = BH + HC = BD + CE. (đpcm) 0,25 1
Có: ∆AHI = ∆ADI (c. c. c) suy ra S∆AHI = S∆ADI ⇒ S∆AHI = S∆ 2 ADH 0,25 ⇒ 1 d
Có: ∆AHK = ∆AEK (c. c. c) suy ra S∆AHK = S∆AEK S∆AHK = S∆ 2 AEH (0,5đ) 1 1 1 0,25 => S∆AHI + S∆AHK = S∆ S∆ S∆ 2 ADH + 2 AEH = 2 DHE
hay S∆DHE = 2 SAIHK = 2a (đvdt) 2 2
Biến đổi: 3x + 3y + 4xy + 2x − 2y + 2 = 0 ⇔ 2( 2 x + 2xy + 2 y )+( 2 x + 2x + ) 1 + ( 2 y − 2y + ) 1 = 0 2 2 2 a ⇔ 2(x + y) + (x + ) 1 + (y − ) 1 = 0 0,25 (0,25đ) x = −y
Đẳng thức chỉ có khi: x = −1 y = 1 a b c d 0,25 F = + + + b + c c + d d + a a + b a c b d
a(d + a) + c(b + c) b(a + b) + d(c + d) = + + + = + ≥ 5
b + c d + a c + d a + b
(b + c)(d + a)
(c + d )(a + b) 2 2 2 2 2 2 2 2
a + c + ad + bc
b + d + ab + cd
4(a + b + c + d + ab + ad + bc + cd + = 2 1 1
(a + b + c + d ) 0,25 b 2 2
(b + c + d + a)
(c + d + a + b) 4 4 (0,75đ) 1
(Theo bất đẳng thức xy ≤ 2 (x + y) ) 4
Mặt khác: 2(a2 + b2 + c2 + d2 + ab + ad + bc + cd) – (a + b + c + d)2 0,25
= a2 + b2 + c2 + d2 – 2ac – 2bd = (a - c)2 + (b - d)2 ≥ 0
Suy ra F ≥ 2 và đẳng thức xảy ra a = c; b = d. Tổng 10đ Chú ý:
- Học sinh làm cách khác đúng vẫn cho điểm tối đa;
- Vẽ hình sai không chấm, không vẽ hình làm đúng phần nào cho nửa số điểm phần đó;
- Trong một câu nếu phần trên sai thì không chấm phần dưới, đúng đến đâu cho điểm đến đó;
- Trong một bài có nhiều câu, nếu HS công nhận KQ câu trên làm câu dưới mà đúng vẫn chấm điểm./.
--------------------- Hết------------------