Đề thi HK1 Toán 8 năm học 2018 – 2019 trường THCS Dịch Vọng – Hà Nội

Đề thi HK1 Toán 8 năm học 2018 – 2019 trường THCS Dịch Vọng – Hà Nội gồm 5 bài toán tự luận, thời gian dành cho học sinh để hoàn thành bài thi là 90 phút, đề thi có lời giải chi tiết.

Trích dẫn đề thi HK1 Toán 8 năm học 2018 – 2019 trường THCS Dịch Vọng – Hà Nội:
+Cho tam giác ABC vuông tại A, AB < AC, đường cao AH. Gọi I là trung điểm của AB. Lấy điểm K đối xứng với B qua H. Qua A dựng đường thẳng song song với BC cắt HI tại D.
a) Tứ giác AKHD là hình gì? Chứng minh?
b) Chứng minh tứ giác AHBD là hình chữ nhật. Từ đó tính diện tích của tứ giác AHBD nếu AH = 6cm, AB = 10cm.
c) Tam giác vuông ABC phải có thêm điều kiện gì để tứ giác AHBD là hình vuông?
d) M là điểm đối xứng với A qua H. Chứng minh AK vuông góc với CM.

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 8

Môn: Toán 8

Thông tin:

12 trang 4 tháng trước

Tác giả:

Profile Mai Nguyệt
1/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
TRƯỜNG THCS DỊCH VỌNG
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2018 − 2019
MÔN: TOÁN 8
Thời gian làm bài: 90 phút.
Bài 1. (2,0 điểm) Phân tích các đa thức sau thành nhân tử:
a)
+
2
5 10x y xy
b)
− + −
2 2
2 25x xy y
c)
− + −
3
8 2 ( 2)x x x
d)
+ +
4 2 2 4
x x y y
Bài 2. (2,0 điểm)
1) Tìm
x
biết:
a)
− + = −
2
( 3) 5 8x x x x
b)
+ − − =
2
3( 4) 4 0x x x
c)
+ − =
3 2
7 12 4 0x x x
2) Tìm
a
sao cho đa thức
− + − +
4 3 2
6x x x x a
chia hết cho đa thức
− +
2
5x x
Bài 3. (2,0 điểm) Thực hiện phép tính
a)
+ +
− ≠
2
3 3
2 2 2
( , 0)
2 2
x x
x y
xy xy
b)
−
− + ≠ ±
− +
−
2
2
4 1 13
( 5)
5 5
25
x x
x
x x
x
2/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 4. (3,5 điểm)
Cho tam giác ABC vuông tại A, <AB AC , đường cao AH . Gọi
I
là
trung điểm của AB . Lấy điểm
K
đối xứng với
B
qua
H
. Qua A dựng
đường thẳng song song với
BC
cắt
HI
tại
D
a) Tứ giác AKHD là hình gì? Chứng minh?
b) Chứng minh tứ giác AHBD là hình chữ nhật. Từ đó tính diện tích
của tứ giác AHBD nếu
= =6 ; 10AH cm AB cm
c) Tam giác vuông ABC phải có thêm điều kiện gì để tứ giác AHBD là
hình vuông?
d)
M
là điểm đối xứng với A qua
H
. Chứng minh ⊥AK CM
Bài 5. (0,5 điểm) Cho các số thực
,x y
thỏa mãn đẳng thức
+ + + − + =
2 2
5 8 5 4 4 8 0x xy y x y
Tính giá trị của biểu thức:
= + + + + −
8 11 2018
( ) ( 1) ( 1)P x y x y
3/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
HƯỚNG DẪN GIẢI
Bài 1. (2,0 điểm) Phân tích các đa thức sau thành nhân tử:
a)
+
2
5 10x y xy
= +
5 ( 2)xy x
b)
− + −
2 2
2 25x xy y
= − + −
2 2
( 2 ) 25x xy y
= − −
2 2
( ) 5x y
= − − − +
( 5)( 5)x y x y
c)
− + −
3
8 2 ( 2)x x x
= − + −
3
( 8) 2 ( 2)x x x
= − + −
3 3
( 2 ) 2 ( 2)x x x
= − + + + −
2
( 2)( 2 4) 2 ( 2)x x x x x
= − + + +
2
( 2)( 2 4 2 )x x x x
= − + +
2
( 2)( 4 4)x x x
= − +
2
( 2)( 2)x x
d)
+ +
4 2 2 4
x x y y
= + + −
4 2 2 4 2 2
2x x y y x y
= + + −
4 2 2 4 2 2
( 2 )x x y y x y
= + −
2 2 2 2
( ) ( )x y xy
= + − + +
2 2 2 2
( )( )x y xy x y xy
4/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 2. (2,0 điểm)
1) Tìm
x
biết:
a)
− + = −
2
( 3) 5 8x x x x
− + − + =
2
( 3) 5 8 0x x x x
− + − + =
2 2
3 5 8 0x x x x
+ =
2 8 0x
= −
2 8x
= −
= −
8 : 2
4
x
x
b) + − − =
2
3( 4) 4 0x x x
+ − + =
2
3( 4) ( 4 ) 0x x x
+ − + =3( 4) ( 4) 0x x x
+ − =( 4)(3 ) 0x x
⇒ + =4 0x hoặc − =3 0x
⇒ = −4x hoặc = 3x
c) + − =
3 2
7 12 4 0x x x
+ − =
2
.(7 12 4) 0x x x
− + =(7 2)( 2) 0x x x
= 0x hoặc − =7 2 0x hoặc + =2 0x
= 0x hoặc =
2
7
x hoặc = −2x
5/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
2) Tìm a sao cho đa thức − + − +
4 3 2
6x x x x a chia hết cho đa thức
− +
2
5x x
− + − +
− +
− +
+
− +
− +
−
4 3 2
2
4 3 2
2
2
2
6
5
5
1
5
5
x x x x a
x x
x x x
x
x x a
x x
a
Suy ra:
− + − +
4 3 2
6x x x x a
chia hết cho
− +
2
5x x
khi
− = ⇒ =5 0 5a a
Vậy
= 5a
thì đa thức
− + − +
4 3 2
6x x x x a
chia hết cho đa thức
− +
2
5x x
−
−
6/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 3. (2,0 điểm) Thực hiện phép tính
a)
+ +
− ≠
2
3 3
2 2 2
( , 0)
2 2
x x
x y
xy xy
+ − +
= +
2
3 3
2 (2 2)
2 2
x x
xy xy
+ − − + − −
= + =
− − −
= = =
2 2
3 3 3
2
3 3 3
2 2 2 2 2 2
2 2 2
2 ( 2) 2
2 2 2
x x x x
xy xy xy
x x x x x
xy xy y
b)
−
− + ≠ ±
− +
−
2
2
4 1 13
( 5)
5 5
25
x x
x
x x
x
− −
= + +
− +
−
2
2
4 1 13
5 5
25
x x
x x
x
− −
= + +
− + − +
2
4 1 13
5 5 ( 5)( 5)
x x
x x x x
+ − − −
= + +
− + + − − +
2
4( 5) 1( 5) 13
( 5)( 5) ( 5)( 5) ( 5)( 5)
x x x x
x x x x x x
+ − + −
= + +
− + + − − +
2
4 20 1 5 13
( 5)( 5) ( 5)( 5) ( 5)( 5)
x x x x
x x x x x x
+ − + + −
=
− +
2
4 20 5 13
( 5)( 5)
x x x x
x x
− +
=
− +
2
10 25
( 5)( 5)
x x
x x
− −
= =
− + +
2
( 5) 5
( 5)( 5) 5
x x
x x x
7/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 4. (3,5 điểm)
Cho tam giác ABC vuông tại A, <AB AC , đường cao AH . Gọi I là
trung điểm của AB . Lấy điểm K đối xứng với B qua H . Qua A dựng
đường thẳng song song với BC cắt HI tại D
a) Tứ giác AKHD là hình gì? Chứng minh?
b) Chứng minh tứ giác AHBD là hình chữ nhật. Từ đó tính diện tích
của tứ giác AHBD nếu = =6 ; 10AH cm AB cm
c) Tam giác vuông ABC phải có thêm điều kiện gì để tứ giác AHBD là
hình vuông?
d) M là điểm đối xứng với A qua H . Chứng minh ⊥AK CM
Lời giải
a) Tứ giác AKHD là hình gì? Chứng minh?
Xét ∆IAD và ∆IBH có:
=IAD IBH (Hai góc so le trong, / /AD BC )
= ( )IA IB gt
=AID BIH (Hai góc đối đỉnh)
Do đó: ∆ = ∆ ( . . )IAD IBH g c g
⇒ =AD BH
(Hai cạnh tương ứng)
Mà
=BH HK
(vì
K
đối xứng với
B
qua
H
)
⇒ =AD HK
(1)
K
H
I
D
C
B
A
8/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
Ta lại có: / /
AD HK
(vì / /
AD BC
và
∈
,
H K BC
) (2)
Từ (1) và (2) suy ra tứ giác AKHD là bình bình hành (tứ giác có 2 cạnh
đối song song và bằng nhau)
b) Chứng minh tứ giác AHBD là hình chữ nhật. Từ đó tính diện tích
của tứ giác AHBD nếu
= =
6 ; 10
AH cm AB cm
Xét tứ giác AHBD có:
/ /
AD BH
(vì
∈
/ / ,
AD BC H BC
)
=
( )
AD BH cmt
Suy ra tứ giác AHBD là hình bình hành (tứ giác có 2 cạnh đối song song
và bằng nhau)
Mà
=
0
90
AHB
(vì ⊥AH BC )
Do đó: AHBD là hình chữ nhật (Hình bình hành có 1 góc vuông)
Xét ∆AHB vuông tại
H
, theo định lí Pitago ta có:
= +
2 2 2
AB AH HB
⇒ = − = − = − =
2 2 2 2 2
10 6 100 36 64
HB AB AH
⇒ = 8HB cm
Diện tích hình chữ nhật AHBD là:
= = =
2
. 6.8 48( )
AHBD
S AH BH cm
K
H
I
D
C
B
A
9/1
2
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
c) Tam giác vuông ABC phải có thêm điều kiện gì để tứ giác AHBD là
hình vuông?
Hình chữ nhật AHBD là hình vuông khi =AH BH
⇒ ∆AHB
cân tại
H
. Mà
=
0
90AHB
⇒ ∆AHB
vuông cân tại
H
⇒ = =
0
45ABH BAH
(vì
=ABH BAH
và
+ =
0
90ABH BAH
)
Ta có:
+ =
0
90ABH ACB
(∆ABC vuông tại A, hai góc nhọn phụ
nhau)
= − = − =
0 0 0 0
90 90 45 45ACB ABH
⇒ = =
0
45ABC ACB
⇒ ∆ABC
vuông cân tại A
Vậy∆ABC vuông cân tại A thì tứ giác AHBD là hình vuông
K
H
I
D
C
B
A
10/
12
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
d)
M
là điểm đối xứng với A qua
H
. Chứng minh ⊥AK CM
Gọi
N
là giao điểm của AK và
CM
. Ta chứng minh
=
0
90KNC
Xét ∆ABK có AH là đường cao đồng thời là đường trung tuyến nên
∆ABK cân tại A
⇒ =ABK AKB
Mà
=AKB CKN
(Hai góc đối đỉnh)
⇒ =ABK CKN
(3)
Xét ∆AHC và
∆MHC
có:
HC
là cạnh chung
= =
0
90AHC MHC
= ( )HA HM gt
Do đó:
∆ = ∆ ( . . )AHC MHC c g c
⇒ =ACH MCH
(Hai góc tương ứng) (4)
Từ (3) và (4) suy ra:
+ = +CKN NCK ABK ACH
Mà
+ =
0
90ABK ACH
(∆ABC vuông tại A, hai góc nhọn phụ nhau)
⇒ + =
0
90CKN NCK
N
M
K
H
I
D
C
B
A
11/
12
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
Xét
∆CKN
có:
+ =
0
90CKN NCK
⇒ =
0
90KNC
⇒ ⊥AK CM
12/
12
Thầy Phúc Toán – GV dạy Toán Online
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017
Bài 5. (0,5 điểm) Cho các số thực
,x y
thỏa mãn đẳng thức
+ + + − + =
2 2
5 8 5 4 4 8 0x xy y x y
Tính giá trị của biểu thức:
= + + + + −
8 11 2018
( ) ( 1) ( 1)P x y x y
Lời giải
+ + + − + =
2 2
5 8 5 4 4 8 0x xy y x y
⇒ + + + + + − + + =
2 2 2 2
4 8 4 4 4 4 4 0x x xy y y x y
⇒ + + + − + + + + =
2 2 2 2
( 4 4) ( 4 4) (4 8 4 ) 0x x y y x xy y
⇒ + + − + + + =
2 2 2 2
( 2) ( 2) 4( 2 ) 0x y x xy y
⇒ + + − + + =
2 2 2
( 2) ( 2) 4( ) 0x y x y
Ta có:
+ ≥
− ≥ ⇒ + + − + + ≥
+ ≥
2
2 2 2 2
2
( 2) 0
( 2) 0 ( 2) ( 2) 4( ) 0
4( ) 0
x
y x y x y
x y
với mọi
∈
ℝ
,x y
Dấu “=” xảy ra khi
+ =
+ =
= −
− = ⇒ − = ⇒
=
+ =
+ =
2
2
2
( 2) 0
2 0
2
( 2) 0 2 0
2
0
4( ) 0
x
x
x
y y
y
x y
x y
Thay
= − =2; 2x y
vào biểu thức
= + + + + −
8 11 2018
( ) ( 1) ( 1)P x y x y
= − + + − + + −
8 11 2018
( 2 2) ( 2 1) (2 1)P
= + − +
= + − +
=
11 2018
0 ( 1) 1
0 ( 1) 1
0
P
P
P
| 1/12
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

1/1 2
Thầy Phúc Toán – GV dạy Toán Online
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2018 − 2019
TRƯỜNG THCS DỊCH VỌNG MÔN: TOÁN 8
Thời gian làm bài: 90 phút.
Bài 1. (2,0 điểm) Phân tích các đa thức sau thành nhân tử: a) 2 5x y + 10xy b) 2 x − xy + 2 2 y − 25 c) 3
x − 8 + 2x(x − 2) d) 4 + 2 2 + 4 x x y y Bài 2. (2,0 điểm) 1) Tìm x biết: a) x x − + x = 2 ( 3) 5 x − 8 b) x + − 2 3( 4) x − 4x = 0 c) 3 x + 2 7 12x − 4x = 0
2) Tìm a sao cho đa thức 4 x − 3 x + 2
6x − x + a chia hết cho đa thức 2 x − x + 5
Bài 3. (2,0 điểm) Thực hiện phép tính 2 x + 2 2x + 2 a) − (x,y ≠ 0) 3 3 2xy 2xy 4 1 13x − 2 x b) − + (x ≠ ±5) x − 5 x + 5 25 − 2 x
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 2/1 2
Thầy Phúc Toán – GV dạy Toán Online Bài 4. (3,5 điểm)
Cho tam giác ABC vuông tại A, AB < AC , đường cao AH . Gọi I là
trung điểm của AB . Lấy điểm K đối xứng với B qua H . Qua A dựng
đường thẳng song song với BC cắt HI tại D
a) Tứ giác AKHD là hình gì? Chứng minh?
b) Chứng minh tứ giác AHBD là hình chữ nhật. Từ đó tính diện tích
của tứ giác AHBD nếu AH = 6cm; AB = 10cm
c) Tam giác vuông ABC phải có thêm điều kiện gì để tứ giác AHBD là hình vuông?
d) M là điểm đối xứng với A qua H . Chứng minh AK ⊥ CM
Bài 5. (0,5 điểm) Cho các số thực x,y thỏa mãn đẳng thức 2 x + xy + 2 5 8
5y + 4x − 4y + 8 = 0
Tính giá trị của biểu thức: P = x + 8 y
+ x + 11 + y − 2018 ( ) ( 1) ( 1)
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 3/1 2
Thầy Phúc Toán – GV dạy Toán Online HƯỚNG DẪN GIẢI
Bài 1. (2,0 điểm) Phân tích các đa thức sau thành nhân tử: a) 2 5x y + 10xy = 5xy(x + 2) b) 2 x − xy + 2 2 y − 25 = 2 x − xy + 2 ( 2 y ) − 25 = x − 2 y − 2 ( ) 5
= (x − y − 5)(x − y + 5) c) 3
x − 8 + 2x(x − 2) = 3
(x − 8) + 2x(x − 2) = 3 x − 3 (
2 ) + 2x(x − 2) = x − 2 (
2)(x + 2x + 4) + 2x(x − 2) = x − 2 (
2)(x + 2x + 4 + 2x) = x − 2 ( 2)(x + 4x + 4) = x − x + 2 ( 2)( 2) d) 4 + 2 2 + 4 x x y y = 4 x + 2 2 x y + 4 y − 2 2 2 x y = 4 x + 2 2 x y + 4 y − 2 2 ( 2 ) x y = 2 x + 2 2 y − 2 ( ) (xy) = 2 x + 2 y − 2 xy x + 2 ( )( y + xy)
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 4/1 2
Thầy Phúc Toán – GV dạy Toán Online Bài 2. (2,0 điểm) 1) Tìm x biết: a) x x − + x = 2 ( 3) 5 x − 8 x x − + x − 2 ( 3) 5 x + 8 = 0 2
x − x + x − 2 3 5 x + 8 = 0 2x + 8 = 0 2x = −8 x = −8 : 2 x = −4 b) x + − 2 3( 4) x − 4x = 0 x + − 2 3( 4) (x + 4x) = 0
3(x + 4) − x(x + 4) = 0
(x + 4)(3 − x) = 0
⇒ x + 4 = 0 hoặc 3 − x = 0
⇒ x = −4 hoặc x = 3 c) 3 x + 2 7 12x − 4x = 0 2
x.(7x + 12x − 4) = 0
x(7x − 2)(x + 2) = 0
x = 0 hoặc 7x − 2 = 0 hoặc x + 2 = 0
x = 0 hoặc x = 2 hoặc x = −2 7
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 5/1 2
Thầy Phúc Toán – GV dạy Toán Online
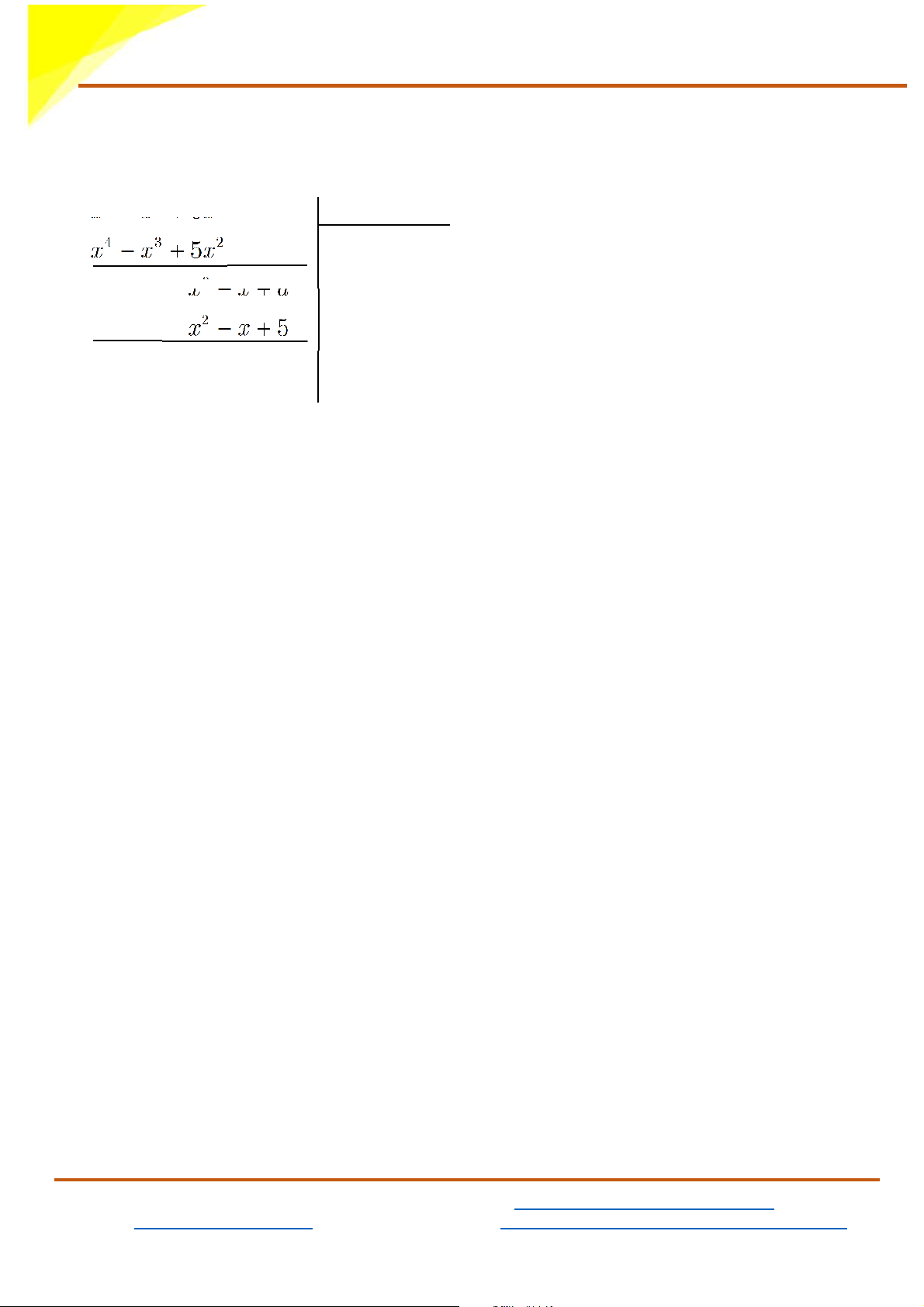
2) Tìm a sao cho đa thức 4 x − 3 x + 2
6x − x + a chia hết cho đa thức 2 x − x + 5 4 x − 3 x + 2 6x − x + 2 a x − x + 5 − 4 x − 3 x + 2 2 5x x + 1 2
x − x + a − 2 x − x + 5 a − 5 Suy ra: 4 x − 3 x + 2
6x − x + a chia hết cho 2 x − x + 5 khi
a − 5 = 0 ⇒ a = 5
Vậy a = 5 thì đa thức 4 x − 3 x + 2
6x − x + a chia hết cho đa thức 2 x − x + 5
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 6/1 2
Thầy Phúc Toán – GV dạy Toán Online
Bài 3. (2,0 điểm) Thực hiện phép tính 2 x + 2 2x + 2 a) − (x,y ≠ 0) 3 3 2xy 2xy 2 x + 2 −(2x + = + 2) 3 3 2xy 2xy 2 x + 2 −2x − 2 2 x + 2 − 2x − = + = 2 3 3 3 2xy 2xy 2xy 2 x − 2x x(x − 2) x − = = = 2 3 3 3 2xy 2xy 2y 4 1 13x − 2 x b) − + (x ≠ ±5) x − 5 x + 5 25 − 2 x 4 − 2 1 x − 13x = + + x − 5 x + 2 5 x − 25 − 2 4 1 x − = + + 13x x − 5 x + 5 (x − 5)(x + 5) x + − x − 2 4( 5) 1( 5) x − = + + 13x (x − 5)(x + 5) (x + 5)(x − 5) (x − 5)(x + 5) x + − x + 2 4 20 1 5 x − = + + 13x (x − 5)(x + 5) (x + 5)(x − 5) (x − 5)(x + 5) x + − x + + 2 4 20 5 x − = 13x (x − 5)(x + 5) 2 x − 10x + = 25 (x − 5)(x + 5) x − 2 ( 5) x − = = 5 (x − 5)(x + 5) x + 5
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 7/1 2
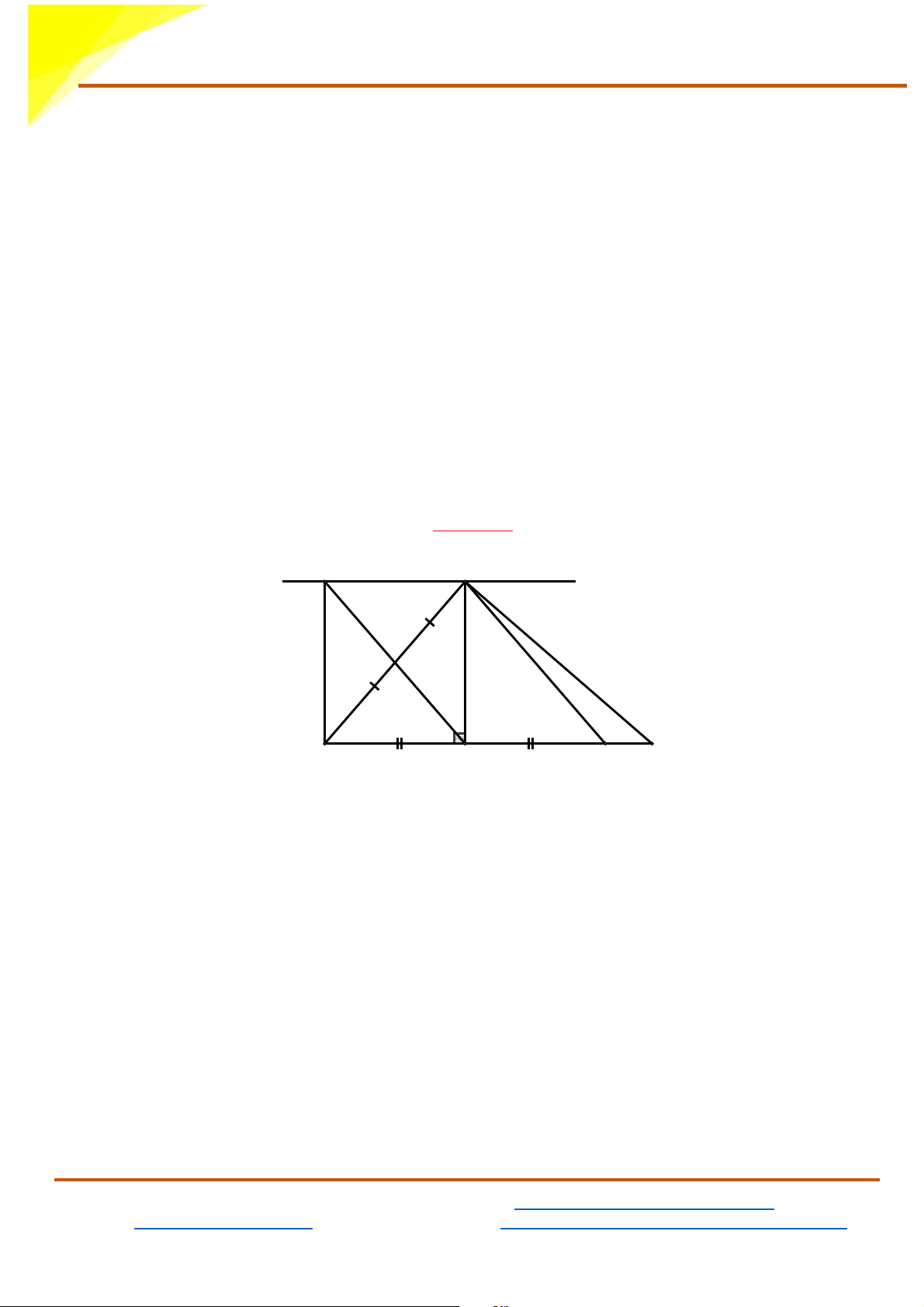
Thầy Phúc Toán – GV dạy Toán Online Bài 4. (3,5 điểm)
Cho tam giác ABC vuông tại A, AB < AC , đường cao AH . Gọi I là
trung điểm của AB . Lấy điểm K đối xứng với B qua H . Qua A dựng
đường thẳng song song với BC cắt HI tại D
a) Tứ giác AKHD là hình gì? Chứng minh?
b) Chứng minh tứ giác AHBD là hình chữ nhật. Từ đó tính diện tích
của tứ giác AHBD nếu AH = 6cm; AB = 10cm
c) Tam giác vuông ABC phải có thêm điều kiện gì để tứ giác AHBD là hình vuông?
d) M là điểm đối xứng với A qua H . Chứng minh AK ⊥ CM Lời giải D A I H K C B
a) Tứ giác AKHD là hình gì? Chứng minh?
Xét ∆IAD và ∆IBH có:
IAD = IBH (Hai góc so le trong, AD / /BC )
IA = IB(gt)
AID = BIH (Hai góc đối đỉnh)
Do đó: ∆IAD = ∆IBH(g. . c g)
⇒ AD = BH (Hai cạnh tương ứng)
Mà BH = HK (vì K đối xứng với B qua H ) ⇒ AD = HK (1)
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 8/1 2
Thầy Phúc Toán – GV dạy Toán Online
Ta lại có: AD / /HK (vì AD / /BC và H,K ∈ BC ) (2)
Từ (1) và (2) suy ra tứ giác AKHD là bình bình hành (tứ giác có 2 cạnh
đối song song và bằng nhau)
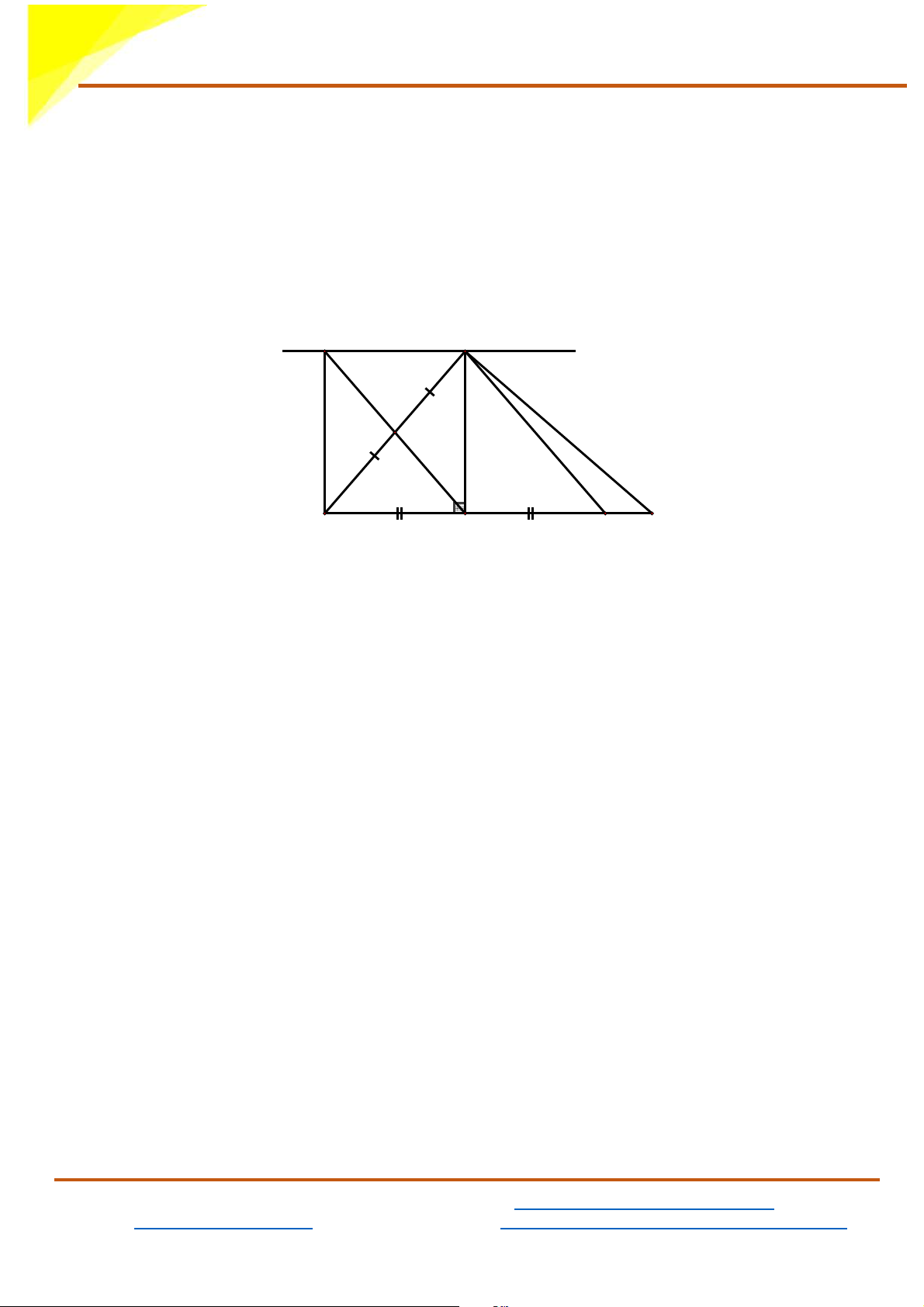
b) Chứng minh tứ giác AHBD là hình chữ nhật. Từ đó tính diện tích
của tứ giác AHBD nếu AH = 6cm; AB = 10cm D A I H K C B
Xét tứ giác AHBD có:
AD / /BH (vì AD / /BC, H ∈ BC )
AD = BH (cmt)
Suy ra tứ giác AHBD là hình bình hành (tứ giác có 2 cạnh đối song song và bằng nhau) Mà AHB = 0
90 (vì AH ⊥ BC )
Do đó: AHBD là hình chữ nhật (Hình bình hành có 1 góc vuông)
Xét ∆AHB vuông tại H , theo định lí Pitago ta có: 2 = 2 + 2 AB AH HB ⇒ 2 HB = 2 AB − 2 AH = 2 − 2 10 6 = 100 − 36 = 64 ⇒ HB = 8cm
Diện tích hình chữ nhật AHBD là: S = AH BH = = 2 . 6.8 48(cm ) AHBD
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 9/1 2
Thầy Phúc Toán – GV dạy Toán Online
c) Tam giác vuông ABC phải có thêm điều kiện gì để tứ giác AHBD là hình vuông? D A I H K C B
Hình chữ nhật AHBD là hình vuông khi AH = BH
⇒ ∆AHB cân tại H . Mà AHB = 0 90
⇒ ∆AHB vuông cân tại H ⇒ ABH = BAH = 0
45 (vì ABH = BAH và ABH + BAH = 0 90 )
Ta có: ABH + ACB = 0
90 ( ∆ABC vuông tại A, hai góc nhọn phụ nhau) ACB = 0 − ABH = 0 − 0 = 0 90 90 45 45 ⇒ ABC = ACB = 0 45
⇒ ∆ABC vuông cân tại A
Vậy ∆ABC vuông cân tại A thì tứ giác AHBD là hình vuông
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 10/ 12
Thầy Phúc Toán – GV dạy Toán Online
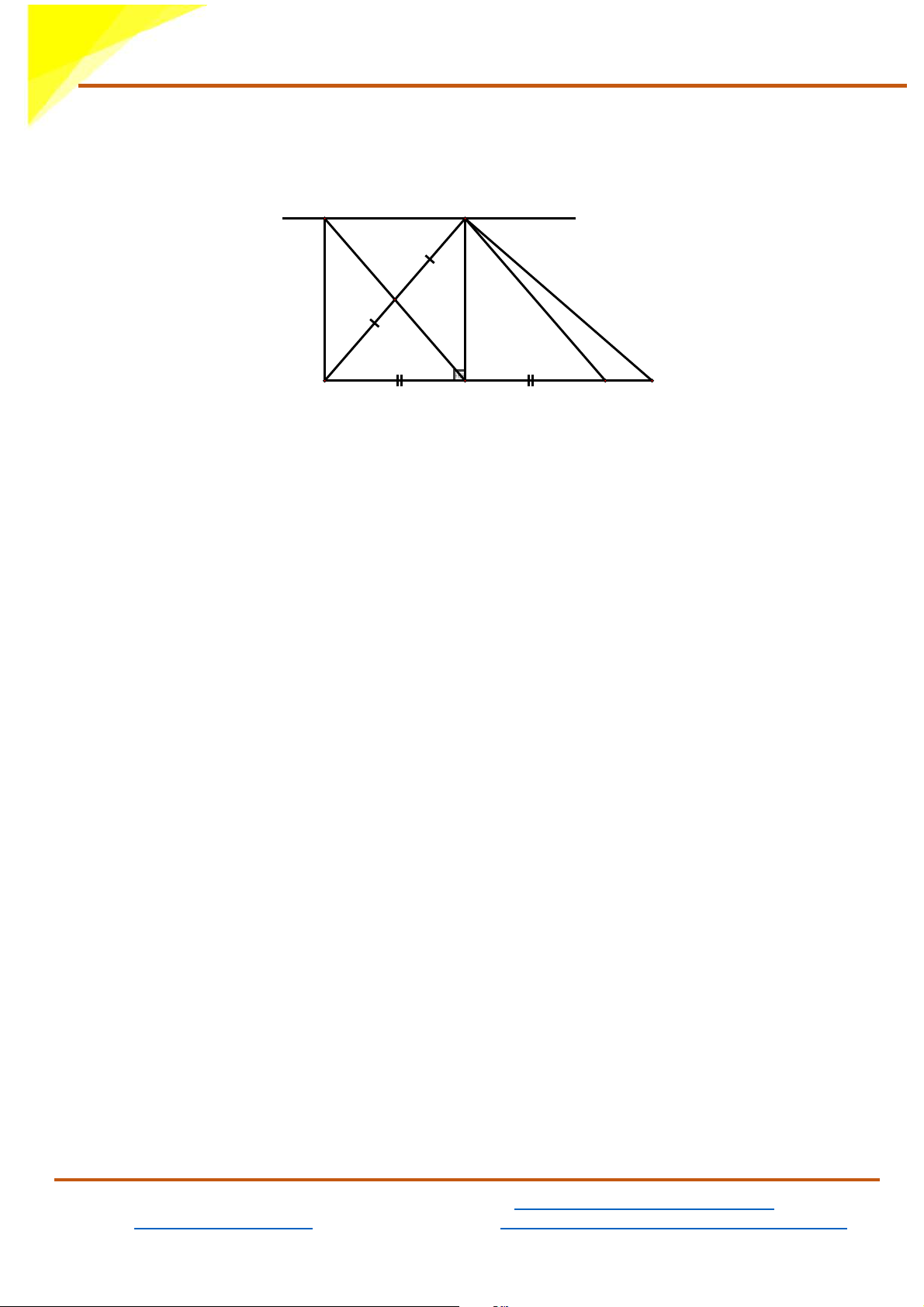
d) M là điểm đối xứng với A qua H . Chứng minh AK ⊥ CM D A I C B K H N M
Gọi N là giao điểm của AK và CM . Ta chứng minh KNC = 0 90
Xét ∆ABK có AH là đường cao đồng thời là đường trung tuyến nên
∆ABK cân tại A ⇒ ABK = AKB
Mà AKB = CKN (Hai góc đối đỉnh)
⇒ ABK = CKN (3)
Xét ∆AHC và ∆MHC có: HC là cạnh chung AHC = MHC = 0 90
HA = HM(gt)
Do đó: ∆AHC = ∆MHC( . c g.c)
⇒ ACH = MCH (Hai góc tương ứng) (4)
Từ (3) và (4) suy ra: CKN + NCK = ABK + ACH Mà ABK + ACH = 0
90 ( ∆ABC vuông tại A, hai góc nhọn phụ nhau) ⇒ CKN + NCK = 0 90
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 11/ 12
Thầy Phúc Toán – GV dạy Toán Online
Xét ∆CKN có: CKN + NCK = 0 90 ⇒ KNC = 0 90 ⇒ AK ⊥ CM
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017 12/ 12
Thầy Phúc Toán – GV dạy Toán Online
Bài 5. (0,5 điểm) Cho các số thực x,y thỏa mãn đẳng thức 2 x + xy + 2 5 8
5y + 4x − 4y + 8 = 0
Tính giá trị của biểu thức: P = x + 8 y
+ x + 11 + y − 2018 ( ) ( 1) ( 1) Lời giải 2 x + xy + 2 5 8
5y + 4x − 4y + 8 = 0 ⇒ 2 x + 2 x + xy + 2 y + 2 4 8
4y + 4x − 4y + 4 + 4 = 0 ⇒ 2 x + x + + 2 y − y + + 2 x + xy + 2 ( 4 4) ( 4 4) (4 8 4y ) = 0
⇒ x + 2 + y − 2 + 2 x + xy + 2 ( 2) ( 2) 4( 2 y ) = 0
⇒ x + 2 + y − 2 + x + 2 ( 2) ( 2) 4( y) = 0 Ta có: (x + 2 2) ≥  0  (y − 2 2) ≥ 0  ⇒ (x + 2 2) + (y − 2 2) + 4(x + 2
y) ≥ 0 với mọi x,y ∈ ℝ 2 
4(x + y) ≥ 0 (x + 2 2) =  0 x + 2 = 0   x = −  2
Dấu “=” xảy ra khi (y − 2
2) = 0 ⇒ y − 2 = 0 ⇒  y =  2 2   4(x + y) = x + y =  0  0
Thay x = −2;y = 2 vào biểu thức P = x + 8 y
+ x + 11 + y − 2018 ( ) ( 1) ( 1) P = − + 8 + − + 11 + − 2018 ( 2 2) ( 2 1) (2 1) P = + − 11 + 2018 0 ( 1) 1 P = 0 + (−1) + 1 P = 0
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Website: https://chiasefull.com Youtube:https://youtube.com/nguyenhuuphuc2017