












Preview text:
TRƢỜNG LƢƠNG THẾ VINH HÀ NỘI
ĐỀ THI HỌC KỲ II MÔN TOÁN LỚP 10
NĂM HỌC 2018 – 2019
Đề thi gồm 50 câu Trắc nghiệm
Thời gian: 90 phút (Không kể thời gian phát đề) ĐỀ CHÍNH THỨC Mã đề thi
Họ và tên:………………………………….Lớp:…………….............……..…… 162 1 3
Câu 1. Cho góc lƣợng giác thỏa mãn sin và . Tính sin 2 . 3 2 7 4 2 4 2 2 A. . B. . C. . D. . 9 9 9 3
Câu 2. Tìm m để phƣơng trình 2
(m 3)x 2mx 3 m 0 có 2 nghiệm trái dấu.
A. m 3 .
B. m 3.
C. m 3 .
D. m 3 .
Câu 3. Trong mặt phẳng với hệ trục tọa độ Oxy , phƣơng trình tham số của đƣờng thẳng đi qua M 2 ;3 và
song song với đƣờng thẳng x 7 y 5 là 1 5
x 5 2t x t x 2 t
x 3 5t A. . B. . C. . D. . y 1 3t y 5t y 3 5t y 2 t
Câu 4. Trong mặt phẳng với hệ trục tọa độ Oxy , cho đƣờng tròn C 2 2
: x y 2x 10y 1 0 . Trong các điểm M 1
;3, N 4; 1 , P 2; 1 ,Q 3; 2
, điểm nào thuộc C?
A. Điểm P .
B. Điểm Q .
C. Điểm N .
D. Điểm M .
Câu 5. Gọi m và M lần lƣợt là nghiệm nguyên nhỏ nhất và lớn nhất của hệ bất phƣơng trình 2 2
(2 x) 7 3x x
. Tổng m M bằng 3 3 2
(x 2) x 3x 3x 20 A. 3 . B. 2 . C. 6 . D. 7 .
Câu 6. Góc có số đo 0
120 đổi sang rađian là: 3 2 A. . B. . C. . D. . 2 3 4 10
Câu 7. Trong mặt phẳng với hệ trục tọa độ Oxy , tính góc giữa đƣờng thẳng 3x y 1 0 và trục hoành. A. 0 45 . B. 0 135 . C. 0 60 . D. 0 120 .
Câu 8. Mệnh đề nào sau đây sai? A. 2
cos 2a 1 2sin a .
B. cos 2a 2sin a cos a . C. 2 2
cos 2a cos a sin a . D. 2
cos 2a 2cos a 1. 1 Câu 9. Cho cos
. Khi đó cos 3 bằng 3 1 1 2 2 A. . B. . C. . D. . 3 3 3 3 x y
Câu 10. Trong mặt phẳng với hệ trục tọa độ Oxy , cho elip E 2 2 :
1. Tính tiêu cự của elip E. 9 4 A. 6 . B. 4 . C. 2 5 . D. 5 .
Câu 11. Số nghiệm nguyên của bất phƣơng trình 2
x 2x 3 là A. 5. B. 3. C. 2. D. 4.
Câu 12. Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC có A2;
1 , B 4;5,C 3 ;2 . Viết
phƣơng trình đƣờng thẳng chứa đƣờng cao của tam giác ABC đi qua đỉnh C . Trang 1/5 - Mã đề thi 162
A. x 3y 3 0 .
B. 3x y 11 0 .
C. x 3y 3 0 .
D. x y 1 0 .
Câu 13. Phƣơng trình x 3 3 x có tập nghiệm là A. ;3 . B. ;3 .
C. 3; . D. 3 .
Câu 14. Trong mặt phẳng với hệ trục tọa độ Oxy , cho đƣờng thẳng : 2x 3y 1 0 . Một vec tơ chỉ
phƣơng của đƣờng thẳng là
A. u 3; 2 . B. u 2; 3 .
C. u 2;3 . D. u 3; 2 .
Câu 15. Cho tam giác ABC . Mệnh đề nào sau đây đúng? A B C A B C A. sin sin . B. cos cos . 2 2 2 2
C. sin A B sin C .
D. cos A B cosC .
Câu 16. Cho hàm số y ax ,
b trong đó a, b là tham số, a 0 . Mệnh đề nào sau đây đúng?
A. Hàm số y ax b nhận giá trị dƣơng trên R . b
B. Hàm số y ax b nhận giá trị âm trên ; . a
C. Hàm số y ax b nhận giá trị âm trên R . b
D. Hàm số y ax b nhận giá trị dƣơng trên ; . a
Câu 17. Cho góc lƣợng giác thỏa mãn
. Khẳng định nào sau đây đúng? 2
A. cot 0 .
B. cos 0 .
C. tan 0.
D. sin 0.
Câu 18. Trong mặt phẳng với hệ trục tọa độ Oxy , phƣơng trình nào sau đây là phƣơng trình đƣờng tròn? A. 2 2
x y 2x 4y 9 0 . B. 2 2
2x 2y 4x 8y 19 0 . C. 2 2
x y 2x 6y 15 0 . D. 2 2
x y 4y 6y 13 0 .
Câu 19. Cho hàm số f x 2
ax bx ca 0 . Biết rằng 2
a 0; b 4ac 0 . Mệnh đề nào sau đây đúng? A. x
, x : f x 0, x
x ; x .
B. f x 0, x R . 1 2 1 2 C. x
, x : f x . f x 0 .
D. f x 0, x R . 1 2 1 2
Câu 20. Trong mặt phẳng với hệ trục tọa độ Oxy , cho đƣờng tròn C 2 2
: x y 25 . Phƣơng trình tiếp tuyến
của đƣờng tròn tại điểm A3;4 là
A. 4x 3y 0 .
B. 4x 3y 24 0 .
C. 3x 4y 25 0 .
D. 3x 4y 25 0 .
Câu 21. Trong mặt phẳng với hệ trục tọa độ Oxy , cho đƣờng tròn C 2 2
: x y 4x 2y 1 0 . Bán kính R
của đƣờng tròn C là
A. R 6 .
B. R 2 .
C. R 1 .
D. R 6 .
Câu 22. Tập nghiệm của bất phƣơng trình 2
2x x 1 0 là 1 1 A. ; . B. .
C. R | . D. R . 4 4
Câu 23. Cho các góc lƣợng giác a, b và T cos a bcosa b sin a bsin a b . Mệnh đề nào sau đây đúng?
A. T sin 2b . B. T cos 2 . a
C. T sin 2a .
D. T cos 2b . 1
Câu 24. Biết rằng tập xác định của hàm số 2 y
x x 2 là D ;
a . Khẳng định nào sau đây x đúng?
A. a 0 .
B. a 0 . C. 3
a 0 . D. a 3 .
Câu 25. Cho các số a 0,b 0 thỏa mãn ab 1. Mệnh đề nào sau đây đúng? Trang 2/5 - Mã đề thi 162
A. 1 a b 2 .
B. a b 2 .
C. 0 a b 1.
D. a b 2 .
Câu 26. Với mọi góc lƣợng giác và số nguyên k , mệnh đề nào sau đây sai?
A. sin k2 sin .
B. cos k cos .
C. tan k tan .
D. cot k cot .
Câu 27. Tập nghiệm của bất phƣơng trình 2 1 là x A. 2 ;0 . B. ; 2 . C. ; 2
0; . D. 2; .
Câu 28. Trong mặt phẳng với hệ trục tọa độ Oxy , viết phƣơng trình chính tắc của elip E biết rằng với mọi điểm 3
M thuộc E thì MF MF 10 ( F , F là hai tiêu điểm của E ) và tâm sai của E là e . 1 2 1 2 5 2 2 x y 2 2 x y 2 2 x y 2 2 x y A. 1. B. 1. C. 1. D. 1. 100 36 25 16 100 64 25 9
Câu 29. Cho hai góc lƣợng giác a,b 0 a,b a b
. Tính a b . 2 thỏa mãn 1 3 tan ; tan 7 4 5 A. . B. . C. . D. . 4 4 4 3
Câu 30. Tập nghiệm của bất phƣơng trình 2x 1 x 2 là
A. 0; .
B. 1; . C. ; 1 . D. 1 ;1 .
Câu 31. Có bao nhiêu giá trị nguyên thuộc 1
0;10 của m để bất phƣơng trình 2
mx 4x m 0 vô nghiệm? A. 9. B. 10. C. 8. D. 11. 1 Câu 32. Biết rằng cos 2x cos 2x sin .cos 2x sin
ax b với mọi giá trị của 2 3 2 12 12
góc lƣợng giác x ; trong đó a là số tự nhiên, b là số hữu tỉ thuộc 1 0;
. Mệnh đề nào sau đây đúng? 2 1 3 5
A. a b .
B. a b .
C. a b .
D. a b 2 . 2 2 2 Câu 33. Trong mặt phẳng với hệ trục tọa độ Oxy , cho đƣờng tròn C 2 2
: x y 2mx 4m 2 y 6m 5 0 ( m là tham số). Tập hợp các điểm I là tâm của đƣờng tròn m m
C khi m thay đổi là m
A. Parabol P 2 : y 2 x 1.
B. Đƣờng thẳng d ' : y 2x 1.
C. Parabol P 2
: y 2x 1.
D. Đƣờng thẳng d : y 2 x 1. x
Câu 34. Cho 0 x 1. Giá trị nhỏ nhất của biểu thức 4 f (x) 1 bằng x 1 x A. 9. B. 7. C. 5. D. 3.
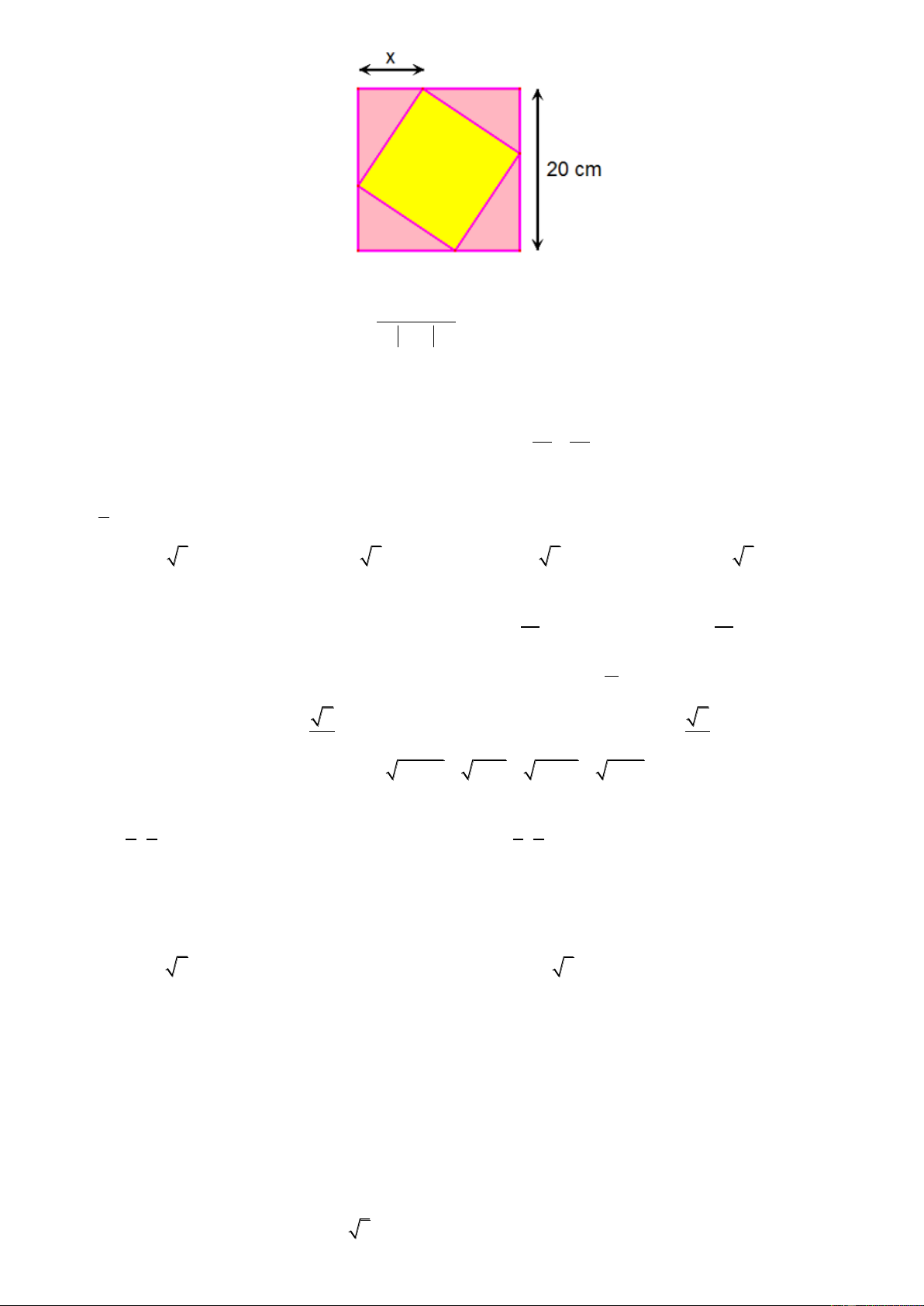
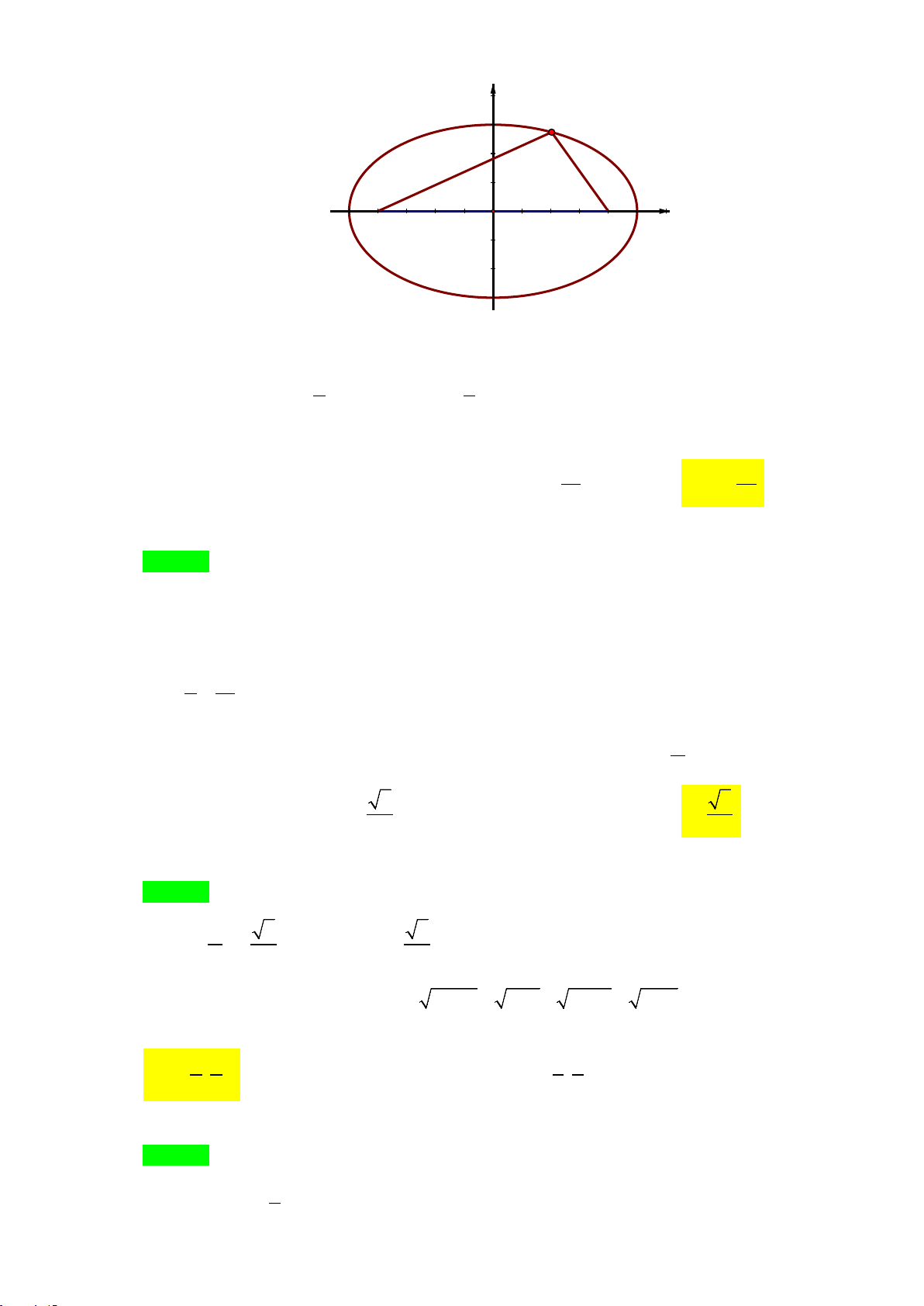
Câu 35. Một viên gạch hình vuông có cạnh thay đổi đƣợc đặt nội tiếp trong một hình vuông có cạnh bằng
20cm , tạo thành bốn tam giác xung quanh nhƣ hình vẽ. Tìm tập hợp các giá trị của x để diện tích viên gạch không vƣợt quá 2 208cm . Trang 3/5 - Mã đề thi 162
A. 8 x 12.
B. 6 x 14 .
C. 12 x 14 .
D. 12 x 18 . 2 x 2x 8
Câu 36. Tập nghiệm của bất phƣơng trình 0 là x 1 A. 4 ; 1 1 ;2. B. 4 ;2 . C. 1 ;2 . D. 2 ; 1 1 ;2. 2 2 x y
Câu 37. Trong mặt phẳng với hệ trục tọa độ Oxy , cho elip (E):
1 có hai tiêu điểm F , F . Biết rằng, 25 9 1 2
điểm M là điểm có tung độ y dƣơng thuộc elip (E) sao cho bán kính đƣờng tròn nội tiếp tam giác MF F M 1 2
bằng 4 . Khẳng định nào sau đây đúng? 3
A. y 0; 3 .
B. y 2; 8 .
C. y 8;5 .
D. y 3;2 . M M M M Câu 38. Tính tổng 2 0 2 0 2 0 2 0
S sin 5 sin 10 sin 15 ... sin 85 . 19 17
A. S 9 .
B. S 8 . C. S . D. S . 2 2
Câu 39. Cho góc lƣợng giác thỏa mãn sin cos 1. Tính sin . 4 2 2 A. 1 . B. . C. 1. D. . 2 2
Câu 40. Tập nghiệm của bất phƣơng trình 2x 4 x 1 2x 1 x 4 x 3 là tập con của tập hợp nào sau đây? 2 1 1 2 A. ; . B. 1 ;0 . C. ; . D. 0 ;1 . 3 2 3 3 2 2
Câu 41. Trong mặt phẳng với hệ trục tọa độ Oxy , cho đƣờng tròn C x a y b 2 : R và đƣờng
thẳng : x y a b 0. Biết rằng đƣờng thẳng cắt đƣờng tròn C tại 2 điểm M , N phân biệt. Tính độ dài MN .
A. MN R 2 .
B. MN 2R .
C. MN R 3 .
D. MN R .
Câu 42. Trong mặt phẳng với hệ trục tọa độ Oxy , cho đƣờng thẳng d : 3x 4y 12 0 . Phƣơng trình
đƣờng thẳng đi qua M 2;
1 và tạo với d một góc 0
45 có dạng ax by 5 0, trong đó a, b cùng
dấu. Khẳng định nào sau đây đúng?
A. a b 6 .
B. a b 8 .
C. a b 8 .
D. a b 6 .
Câu 43. Cho tam giác ABC có các góc thỏa mãn sin A sin B cos A cos B . Tính số đo góc C của tam giác ABC . A. 0 90 . B. 0 120 . C. 0 60 . D. 0 45 .
Câu 44. Trong mặt phẳng với hệ trục tọa độ Oxy , cho đƣờng tròn 2 2
(C) : (x 2) ( y 2) 9 . Phƣơng trình
các tiếp tuyến của đƣờng tròn đi qua điểm A5; 1 là
A. x 2y 3 0 hoặc 2x y 2 3 5 0 .
B. x y 4 0 hoặc x y 6 0 . Trang 4/5 - Mã đề thi 162
C. 3x 4y 1 0 hoặc 4x 3y 13 0 .
D. x 5 hoặc y 1 .
Câu 45. Có bao nhiêu giá trị của x để hàm số y
x x x 2 2 2 2 32 1 2
1 đạt giá trị lớn nhất trên 1 ;1 tại 0
x x ? o A. 4. B. 8. C. 6. D. 10.
Câu 46. Tìm tập hợp tất cả các giá trị của m để bất phƣơng trình 2
x 2x m 0 nghiệm đúng với mọi x 0; 3 . A. ; 1 .
B. 3; . C. 1 ;. D. 1 ; 3 .
Câu 47. Có bao nhiêu giá trị thực của m để bất phƣơng trình 2 m
1 x m 0 vô nghiệm? A. 0 . B. 3 . C. 1. D. 2 .
sin 2a sin 5a sin 3a
Câu 48. Cho góc lƣợng giác a thỏa mãn 2
. Tính sin a . 2
2 cos 2a cos a 1 1 1 A. . B. 1 . C. 1. D. . 4 4
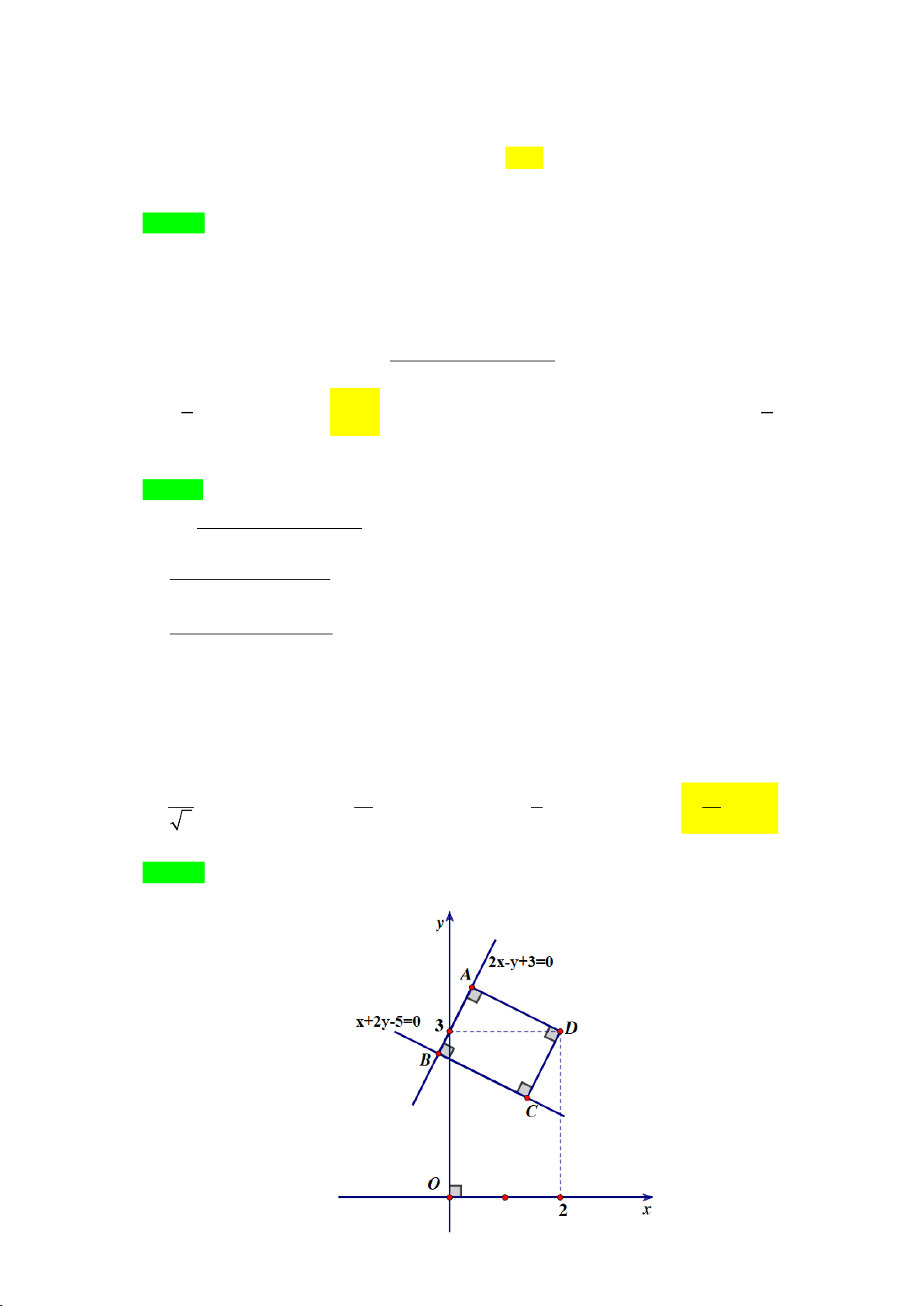
Câu 49. Trong mặt phẳng với hệ trục tọa độ Oxy , cho hình chữ nhật có hai cạnh nằm trên hai đƣờng thẳng có
phƣơng trình lần lƣợt là 2x y 3 0; x 2y 5 0 và tọa độ một đỉnh là 2;3. Diện tích hình chữ nhật đó là 12 16 9 12 A. (đvdt). B. (đvdt). C. (đvdt). D. (đvdt). 5 5 5 5
Câu 50. Trong mặt phẳng với hệ trục tọa độ Oxy , viết phƣơng trình đƣờng tròn tâm O 0;0 cắt đƣờng thẳng
: x 2y 5 0 tại hai điểm M, N sao cho MN 4. A. 2 2
x y 9 . B. 2 2
x y 1. C. 2 2
x y 21. D. 2 2
x y 3 .
------------- HẾT ------------- Trang 5/5 - Mã đề thi 162
ĐÁP ÁN CÁC MÃ ĐỀ [TEST_de hk2 toan 10 ltv cuoi]
------------------------ Mã đề [162] 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B B C C A B C B A C D C B A C D D C D C A D B A B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B C B B D A D D B A A C D D A B C A D A B C B D A Mã đề [251] 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C A C B C C B B D A A D A A B D D B C A D C C D A
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B B B B C D A C A A D C D B A D D C B B D B A A C Mã đề [336] 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C B B D D A D A B B A D A B D A D D D A B B D C C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C A B A B D B A A C B B C C A D C B A C C C D A C Mã đề [465] 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C B B D D B C C B C D B B D C A A C C B A B B B C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A D A D D D A D D A C B A A A A C A D C B A B C D Mã đề [567] 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B A B C D B A D D B C C B D D C B C A B C C B A C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A A D B B D D A A B B A D D A A C A D C D A C C B Mã đề [633] 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C D B A C C A B A C D D A D B B C A A A B D C A B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C B C A A B C C A B D A A D D B D D D C C B D B B BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 11 12 13B 14 15 B B C C A B C B A C D C A C 16 17 18 19 20 21 22 23B 24 25B 26B 27 28B 29B 30 D D C D C A D A C D 31 32 33 34B 35 36 37 38 39 40 41B 42 43 44 45 A D D A A C D D A C A D A 46B 47 48B 49 50 C D A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho góc lượng giác α thỏa mãn 1 π sinα = − , và 3 π < α < . Tính sin 2α 3 2 A. 7 . B. 4 2 . C. 4 2 − . D. 2 − . 9 9 9 3 Lời giải Chọn B Ta có: 1 2 2 2
sinα = − ⇒ cosα = ± 1− sin α = ± 3 3 Theo giả thiết: 3π 2 2 π < α < ⇒ cosα = − 2 3 1 2 2 4 2
sin 2α = 2sinα.cosα = 2. − − = . 3 3 9
Câu 2: Tìm m phương trình (m − ) 2
3 x + 2mx + 3− m = 0 có hai nghiệm trái dấu. A. m = 3 . B. m ≠ 3. C. m > 3 . D. m < 3 . Lời giải Chọn B
Điều kiện để phương trình (m − ) 2
3 x + 2mx + 3− m = 0 có hai nghiệm trái dấu:
(m −3)(3− m) < 0
⇔ −(m − 3)2 < 0 ⇔ m ≠ 3
Câu 3: Trong mặt phẳng với hệ tọa độ Oxy , phương trình tham số của đường thẳng đi qua M ( 2; − 3)
và song song với đường thẳng x − 7 y + 5 = là 1 − 5 x = 5 − 2t x = −t x = 2 − − t x = 3 + 5t A. . B. . C. D. . y = 1 − + 3t y = 5t y = 3 + 5t y = 2 − − t Lời giải Chọn C
Do hai đường thẳng song song nên đường thẳng cần tìm nhận u = ( 1;
− 5) là vectơ chỉ phương. x = 2 − − t
Do đó phương trình tham số là . y = 3 + 5t
Câu 4: Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn (C) 2 2
: x + y − 2x +10y +1 = 0 . Trong các điểm M ( 1 − ;3), N (4;− ) 1 , P(2; ) 1 ,Q(3; 2
− ), điểm nào thuộc (C) ? A. Điểm P . B. Điểm Q . C. Điểm N . D. Điểm M . Lời giải Chọn C
Thay tọa độ các điểm vào phương trình của (C) thì chỉ có điểm N thỏa mãn phương trình
đường tròn. Vậy điểm N ∈(C) . Câu 5: Gọi ,
m M lần lượt là nghiệm nguyên nhỏ nhất và lớn nhất của hệ bất phương trình ( 2 − x)2 2 ≤ 7 − 3x + x
. Tổng m + M bằng ( x + 2 )3 3 2
< x + 3x + 3x + 20 A. 3 − . B. 2 − . C. 6 − . D. 7 − . Lời giải
Chọn A (2−x)2 2 2 2 ≤ 7 − 3x + x
4 − 4x + x ≤ 7 −3x + x Ta có hệ ⇔ ( x + 2 )3 3 2 3 2 3 2
< x + 3x + 3x + 20
x + 6x +12x + 8 < x + 3x + 3x + 20 x ≥ 3 − x ≥ 3 − ⇔ ⇔ ⇔ 3
− ≤ x <1. Do đó nghiệm nguyên nhỏ nhất là x = 3 − và 2 3
x + 9x −12 < 0 4 − < x <1
nghiệm nguyên lớn nhất là x = 0 . Vậy m + M = 3 − .
Câu 6: Góc có số đo 120° đổi sang rađian là: A. 3π . B. 2π . C. π . D. π . 2 3 4 10 Lời giải Chọn B Ta có: π 2π 120° = .120 = rad. 180 3
Câu 7: Trong mặt phẳng với hệ trục tọa độ Oxy , tính góc giữa đường thẳng 3x − y +1= 0 và trục hoành. A. 45°. B. 135° C. 60°. D. 120°. Lời giải Chọn C
Đường thẳng 3x − y +1 = 0 có vectơ pháp tuyến là n = ( 3;− )1.
Trục Ox có vectơ pháp tuyến là j = (0 ) ;1 .
Gọi α là góc giữa đường thẳng 3x − y +1 = 0 và trục hoành. . n j Khi đó ta có 1 cosα = = ⇒ α = 60° . n . j 2
Câu 8: Mệnh đề nào sau đây sai? A. 2
cos 2a =1− 2sin a .
B. cos 2a = 2sin a cos a C. 2 2
cos 2a = cos a − sin a . D. 2
cos 2a = 2cos a −1. Lời giải Chọn B Câu 9: Cho 1
cosα = . Khi đó cos(3π +α ) bằng 3 A. 1 − . B. 1 . C. 2 . D. 2 − . 3 3 3 3 Lời giải Chọn A cos(3π +α ) = −cosα 1 = − . 3 2 2
Câu 10: Trong mặt phẳng với hệ trục tọa độ Oxy , cho elip ( ) : x y E +
= 1. Tính tiêu cự của elip (E). 9 4 A. 6 . B. 4 C. 2 5 . D. 5 . Lời giải Chọn C Ta có 2 a = 9 , 2 b = 4 2 2 2
⇒ c = a − b = 5 ⇒ c = 5 .
Tiêu cự 2c = 2 5 .
Câu 11: Số nghiệm nguyên của bất phương trình 2
x − 2x ≤ 3 là A. 5. B. 3. C. 2 . D. 4 . Lời giải Chọn D x ≤ 0
Điều kiện xác định của bất phương trình . x ≥ 2 2 x − 2x ≤ 3 2
⇔ x − 2x ≤ 3 2
⇔ x − 2x − 3 ≤ 0 ⇔ 1 − ≤ x ≤ 3.
Kết hợp với điều kiện ở trên suy ra tập các nghiệm nguyên của bất phương trình là T = { 1 − ;0;2; } 3 .
Câu 12: Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC có A(2;− )
1 , B(4;5) , C ( 3 − ;2).
Viết phương trình đường thẳng chứa đường cao của tam giác ABC đi qua đỉnh C .
A. x + 3y + 3 = 0 .
B. 3x − y +11 = 0 .
C. x + 3y − 3 = 0 .
D. x + y +1 = 0 . Lời giải Chọn C
Đường cao đi qua đỉnh C ( 3
− ;2) nhận vectơ AB = (2;6) làm véctơ pháp tuyến, sẽ có phương
trình là 2(x + 3) + 6( y − 2) = 0 ⇔ x + 3y −3 = 0 .
Câu 13: Phương trình x −3 = 3− x có tập nghiệm là: A. ( ; −∞ 3) . B. ( ; −∞ ] 3 . C. [3;+∞) . D. { } 3 . Lời giải Chọn B 3 − x ≥ 0 x ≤ 3 x 3 3 x x − 3 = 3 − = − ⇔
− x ⇔ x = 0 ⇔ x ≤ 3
x − 3 = x − 3 x ∈
Tập nghiệm của phương trình là: ( ; −∞ ] 3 . Cách 2
Áp dụng định nghĩa A = −A ⇔ A ≤ 0 .
x − 3 = 3− x ⇔ x − 3 ≤ 0 ⇔ x ≤ 3 . Tập nghiệm của phương trình là: ( ; −∞ ] 3 .
Câu 14: Trong mặt phẳng với hệ trục tọa độ Oxy , cho đường thẳng (∆) : 2x −3y +1= 0 . Một vec tơ chỉ
phương của đường thẳng (∆) là :
A. u = (3;2) . B. u = (2; 3) − .
C. u = (2;3) . D. u = (3; 2 − ) . Lời giải Chọn A
(∆) : 2x − 3y +1 = 0 ⇒ n∆ = (2; 3
− ) là một véctơ pháp tuyến.
Suy ra một vectơ chỉ phương của (∆) là : u∆ = (3;2) .
Câu 15: Cho tam giác ABC . Mệnh đề nào sau đây đúng?
A. sin A + B A + = sin C . B. cos B = cosC . 2 2 2 2
C. sin(A + B) = sin C .
D. cos(A + B) = cosC . Lời giải Chọn C
A + B + C = π ⇒ sin ( A+ B) = sin (π − C) = sin C .
Câu 16: Cho hàm số y = ax + ,
b a > 0,a,b là tham số. Mệnh đề nào sau đây đúng?
A. Hàm số y = ax + b nhận giá trị dương trên . B. Hàm số b
y = ax + b nhận giá trị âm trên ; − +∞ . a
C. Hàm số y = ax + b nhận giá trị âm trên .
D. Hàm số y b
= ax + b nhận giá trị dương trên ; − +∞ . a Lời giải Chọn D. π
Câu 17: Cho góc lượng giác α thỏa mãn < α < π . Khẳng định nào sau đây đúng? 2 A. cotα > 0 . B. cosα > 0 . C. tanα > 0. D. sinα > 0. Lời giải Chọn D.
Câu 18: Trong mặt phẳng tọa độ Oxy , phương trình nào sau đây là phương trình đường tròn? A. 2 2
x + y − 2x + 4y + 9 = 0 . B. 2 2
2x + 2y + 4x −8y +19 = 0 . C. 2 2
x + y − 2x + 6y −15 = 0 . D. 2 2
x + y + 4x − 6y +13 = 0 . Lời giải Chọn C.
Phương trình đường tròn có dạng 2 2
x + y − 2ax − 2by + c = 0 với 2 2
a + b − c > 0 .
Như vậy với c < 0 thì với mọi a , b phương trình trên luôn là phương trình đường tròn. Phương trình : 2 2
x + y − 2x + 6y −15 = 0 là phương trình đường tròn.
Câu 19: Cho hàm số ( ) 2
f x = ax + bx + c với a ≠ 0 . Biết rằng a < 0 , 2
∆ = b − 4ac < 0. Mệnh đề nào sau đây đúng? A. x
∃ , x : f (x) > , x
∀ ∈(x ; x .
B. f x > , x ∀ ∈ 1 2 ) 1 2 0 ( ) 0 . C. x
∃ , x : f (x . f x < 0 .
D. f (x) < 0 , x ∀ ∈ 1 ) ( 2) 1 2 . Lời giải Chọn D. Khi 2
∆ = b − 4ac < 0 thì ( ) 2
f x = ax + bx + c cùng dấu với a với mọi x ∈ .
Vì a < 0 nên f (x) < 0 với x ∀ ∈ .
Câu 20: Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn (C): 2 2
x + y = 25 . Phương trình tiếp
tuyến của đường tròn tại điểm A(3;4) là
A. 4x − 3y = 0 .
B. 4x−3y −24 = 0. C. 3x+4y −25 = 0. D. 3x+4y +25 = 0 . Lời giải Chọn C.
Đường tròn(C) có tâm O và có bán kính bằng 5.
Tiếp tuyến của đường tròn tại A(3;4) và có vtpt là OA = (3;4) .
Phương trình của tiếp tuyến 3(x −3) + 4( y − 4) = 0 hay 3x + 4y − 25 = 0.
Câu 21: Trong mặt phẳng với hệ trục tọa độ Oxy , cho đường tròn 2 2
(C) : x + y − 4x + 2y −1 = 0 . Bán
kính đường tròn (C)là A. R = 6 . B. R = 2 . C. R =1. D. R = 6 . Lời giải Chọn A Có 2 2 a = 2;b = 1, − c = 1
− ⇒ R = a + b − c = 6 .
Câu 22: Tập nghiệm của bất phương trình 2
2x + x +1 > 0 là A. 1 ; − +∞ . B. ∅. C. 1 \ − . D. . 4 4 Lời giải Chọn D ∆ = 7 − < 0 Có 2
⇒ 2x + x +1 > 0, x ∀ ∈ . a = 2 > 0
Câu 23: Cho các góc lượng giác a,b và T = cos(a + b)cos(a −b) −sin(a + b)sin(a −b) . Mệnh đề sau đây đúng?
A. T = sin 2b .
B. T = cos2a .
C. T = sin 2a .
D. T = cos2b. Lời giải Chọn B
Ta có T = cos(a + b)cos(a − b) − sin(a + b)sin(a − b) = cos (a +b)+(a −b) = cos2a .
Câu 24: Biết rằng tập xác định của hàm số 2 1
y = x + x − 2 + là D = [ ;
a +∞) . Khẳng định nào sau x đây đúng? A. a > 0 . B. a = 0 . C. 3 − < a < 0 . D. a = 3 − . Lời giải Chọn A 2
x + x − 2 ≥ 0 x ≤ 2 − ∨ x ≥1 Hàm số 2 1
y = x + x − 2 + xác định khi ⇔ ⇒ x ≥1. x x > 0 x > 0
Vậy D = [1;+∞) ⇒ a > 0.
Câu 25: Cho các số a ≥ 0,b ≥ 0 thỏa mãn ab =1. Mệnh đề nào sau đây đúng?
A. 1≤ a + b ≤ 2 .
B. a + b ≥ 2.
C. 0 < a + b <1.
D. a + b > 2 . Lời giải Chọn B
Với hai số a ≥ 0,b ≥ 0, ta có: a + b ≥ 2 ab = 2 . Dấu “=” xảy ra khi và chỉ khi a = b .
Câu 26: Với mọi góc lượng giác αvà số nguyên k , mệnh đề nào sau đây sai ?
A.sin(α + k2π) = sin α .
B. cos(α + kπ) = cosα .
C. tan(α + kπ) = tan α .
D. cot (α + kπ) = cot α . Lời giải Chọn B α k = l Vì (α + kπ) cos khi 2 cos = , k,l ∈ .
− cosα khi k = 2l +1
Câu 27: Tập nghiệm của bất phương trình 2 > −1 là x A.(−2;0) . B.(− ; ∞ −2) . C. (− ; ∞ −2) ∪ (0;+∞) . D.(−2;+∞) . Lời giải Chọn C 2 2 x + 2 x > 0
Bất phương trình > −1 ⇔ +1 > 0 ⇔ > 0 ⇔ . x x x x < −2
Vậy tập nghiệm của bất phương trình là: S = (− ; ∞ −2) ∪ (0;+∞)
Câu 28: Trong mặt phẳng với hệ tọa độ Oxy , viết phương trình chính tắc của elip (E) biết rằng với mọi
điểm M thuộc (E) thì MF + MF = 10 ( F , F là hai tiêu điểm của (E) )và tâm sai của (E) là 1 2 1 2 3 e = 5 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 100 36 25 16 100 64 25 9 Lời giải Chọn B 2 2
Gọi phương trình chính tắc của (E) có dạng x y +
= 1, a > b > 0 . 2 2 a b
Vì MF + MF = 10 ⇒ 2a = 10 ⇔ a = 5. 1 2 Tâm sai của (E) là 3 e = c 3
⇒ = ⇒ c = 3. Do đó 2 2 2 2
b = a − c = 5 − 3 = 4 . 5 a 5 2 2
Vậy phương trình chính tắc của (E) là x y + = 1. 25 16
Câu 29: Cho hai góc lượng giác a,b0 a,b π < < thỏa mãn 1 3
tan a = ;tanb = . Tính a + b . 2 7 4 A. 5π . B. π . C. π π − . D. . 4 4 4 3 Lời giải Chọn B 1 3 + Ta có
(a + b) tana + tanb 7 4 tan = = = 1. 1− tan a.tanb 1 3 1− . 7 4 Mà 0 a,b π <
< nên 0 < a + b < π a b π ⇒ + = . 2 4
Câu 30: Tập nghiệm của bất phương trình 2x +1 < x + 2 là A.(0;+∞) . B.(1;+∞) . C. (− ; ∞ − ) 1 . D.(−1; ) 1 . Lời giải Chọn D x > −2 x > −2 x + 2 > 0
Ta có 2x +1 < x + 2 3x 3 ⇔ ⇔
> − ⇔ x > −1 ⇔ −1< x < 1.
−x − 2 < 2x +1 < x + 2 x 1 < x < 1
Vậy tập nghiệm của bất phương trình là S = (−1; ) 1 .
Câu 31: Có bao nhiêu giá trị nguyên thuộc [ 10
− ;10] của m để bất phương trình 2
mx − 4x + m < 0 vô nghiệm? A. 9. B. 10. C. 8 . D. 11. Lời giải Chọn A. Ta có 2
mx − 4x + m < 0 vô nghiệm 2
⇔ mx − 4x + m ≥ 0 , x ∀ ∈ . (I )
Trường hợp : m = 0, bất phương trình (I ) thành 4
− x ≥ 0 ⇔ x ≤ 0 ⇒ m = 0 không thỏa yêu cầu bài toán. m > 0 m > 0
Trường hợp : m ≠ 0 , 2
mx − 4x + m ≥ 0 , x ∀ ∈ ⇔ ⇔ ⇔ m ≥ 2 . 2 ∆′ ≤ 0 4 − m ≤ 0
Mà m nguyên và m∈[ 10
− ;10] nên m∈{2;3;4;5;6;7;8;9;1 } 0 .
Vậy có 9 giá trị của m thỏa yêu cầu bài toán.
Câu 32: Biết rằng 1 π π π π cos 2x cos 2x sin cos 2x − − + − ⋅ + = sin (ax +
bπ ) với mọi giá trị 2 3 2 12 12
của góc lượng giác x ; trong đó a là số tự nhiên, b là số hữu tỉ thuộc 1 0; . Mệnh đề nào 2 sau đây đúng? A. 1
a + b = . B. 3
a + b = . C. 5
a + b = .
D. a + b = 2 . 2 2 2 Lời giải Chọn D. Ta có: 1 π π π π cos 2x cos 2x sin cos 2x − − + − ⋅ + 2 3 2 12 12 1 π π π π cos 2x cos 2x sin cos 2x = − + − − − ⋅ + 2 2 3 12 12 5π π π π sin sin 2x sin cos 2x = + − ⋅ + 12 12 12 12 π π π π = sin + 2x cos − cos + 2x sin = sin 2x 12 12 12 12
Suy ra a = 2,b = 0 . Vậy a + b = 2 . Câu 33: Trong mặt phẳng với hệ trục tọa độ
Oxy , cho đường tròn
(C x + y − mx + m + y − m − = ( m là tham số). Tập hợp các điểm I là tâm của m ) 2 2 : 2 (4 2) 6 5 0 m
đường tròn khi m thay đổi là A. Parabol (P) 2 : y = 2 − x +1.
B. Đường thẳng (d′) : y = 2x +1. C. Parabol (P) 2 : y = 2x +1.
D. Đường thẳng (d′) : y = 2 − x −1. Lời giải Chọn D.
Đường tròn (C có tâm I ( ; m 2 − m − ) 1 và bán kính 2
R = 5m +10m + 6 . m ) x = m Ta có: I
⇒ y = − x − . Suy ra tập hợp các điểm I là tâm của đường tròn khi I 2 I 1 y = − m − m I 2 1
m thay đổi là đường thẳng (d′) : y = 2 − x −1.
Câu 34: Cho 0 < x <1. Giá trị nhỏ nhất của biểu thức ( ) 4 x f x = + −1 bằng x 1− x A. 9. B. 7 . C. 5. D. 3. Lời giải Chọn B. 4 x 4 x 4 1− x Ta có: ( ) ( ) = + −1 = − 4 + + 3 x f x = + + 3 x 1− x x 1− x x 1− x 4(1− x)
Vì 0 < x <1 nên x x
> 0 . Áp dụng bất đẳng thức Cô si cho hai số ; ta 1− x x 1− x 4(1− x) 4(1− x) được: x +
≥ 2 4 = 4 , đẳng thức xảy ra khi x 2 = ⇔ x = . x 1− x x 1− x 3
Khi đó f (x) ≥ 4 + 3 = 7 . Vậy giá trị nhỏ nhất của biểu thức f (x) là 7 .
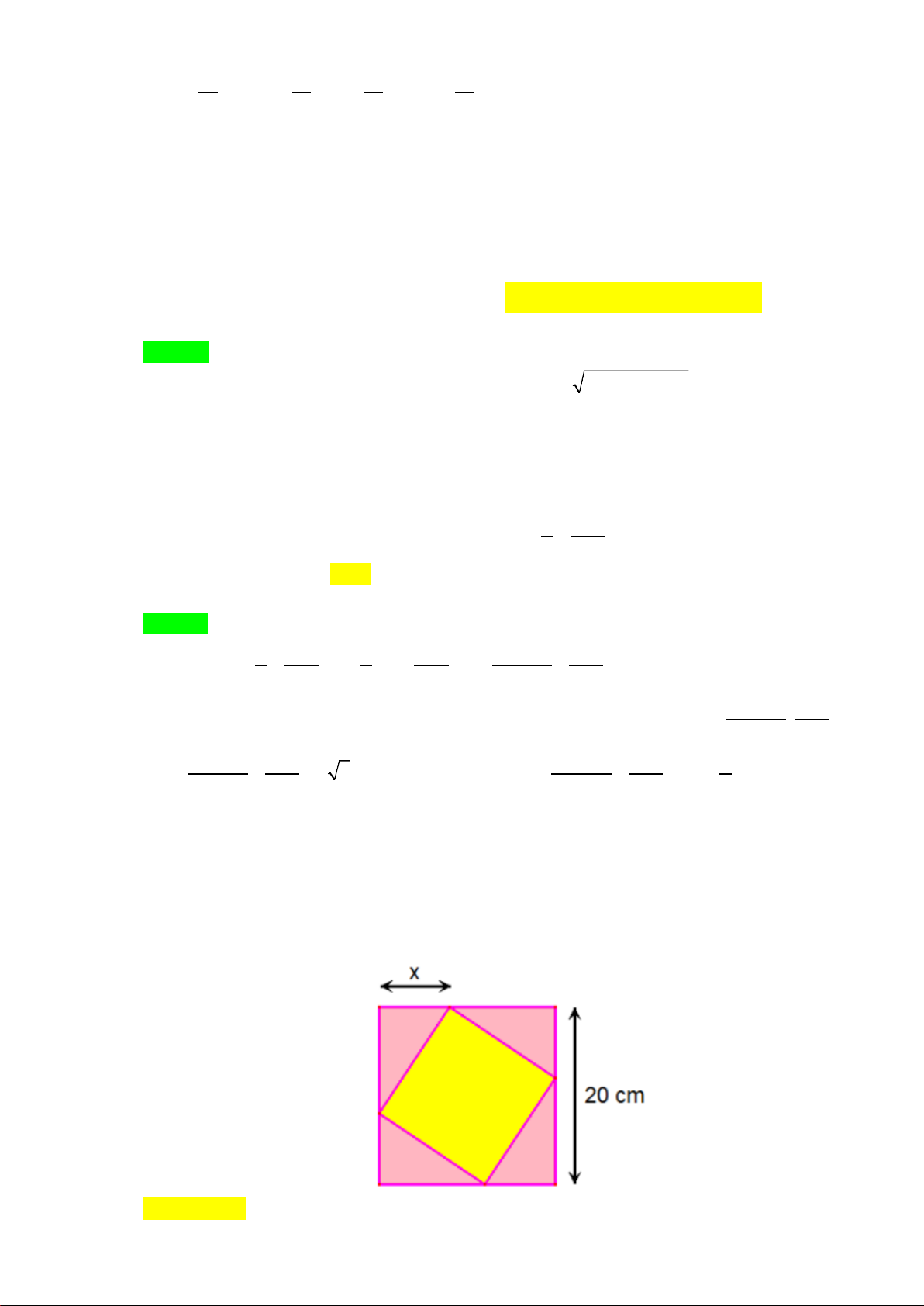
Câu 35: Một viên gạch hình vuông có cạnh thay đổi được đặt nội tiếp trong một hình vuông có cạnh bằng
20cm , tạo thành bốn tam giác xung quanh như hình vẽ. Tìm tất cả các giá trị của x để diện
tích viên gạch không vượt quá 2 208cm .
A. 8 ≤ x ≤12.
B. 6 ≤ x ≤14 .
C. 12 ≤ x ≤14 .
D. 12 ≤ x ≤18 . Lời giải Chọn A.
Gọi E, F ,G , H là bốn đỉnh của viên gạch hình vuông nội tiếp trong hình vuông ABCD có
cạnh 20cm như hình vẽ x E 20-x D A F H C B G
Ta có cạnh viên gạch là 2
EF = x + ( − x)2 2 20
= 2x − 40x + 400 .
Diện tích của viên gạch là: 2 2
EF = 2x − 40x + 400 .
Theo đề ta có diện tích viên gạch không vượt quá 2 208cm 2 2
⇔ 2x − 40x + 400 ≤ 208 ⇔ 2x − 40x +192 ≤ 0 ⇔ 8 ≤ x ≤12. 2
Câu 36: Tập nghiệm của bất phương trình x + 2x −8 < 0 là x +1 A. ( 4 − ;− ) 1 ∪( 1; − 2) . B. ( 4; − 2) . C. ( 1; − 2) . D. ( 2 − ;− ) 1 ∪( 1; − 2) . Lời giải Chọn A.
Điều kiện xác định x ≠ 1 − . Bất phương trình 2
⇔ x + 2x −8 < 0 ⇔ (x + 4)(x − 2) < 0 ⇔ 4 − < x < 2.
Vậy tập nghiệm của bất phương trình là ( 4 − ;− ) 1 ∪( 1; − 2) . 2 2
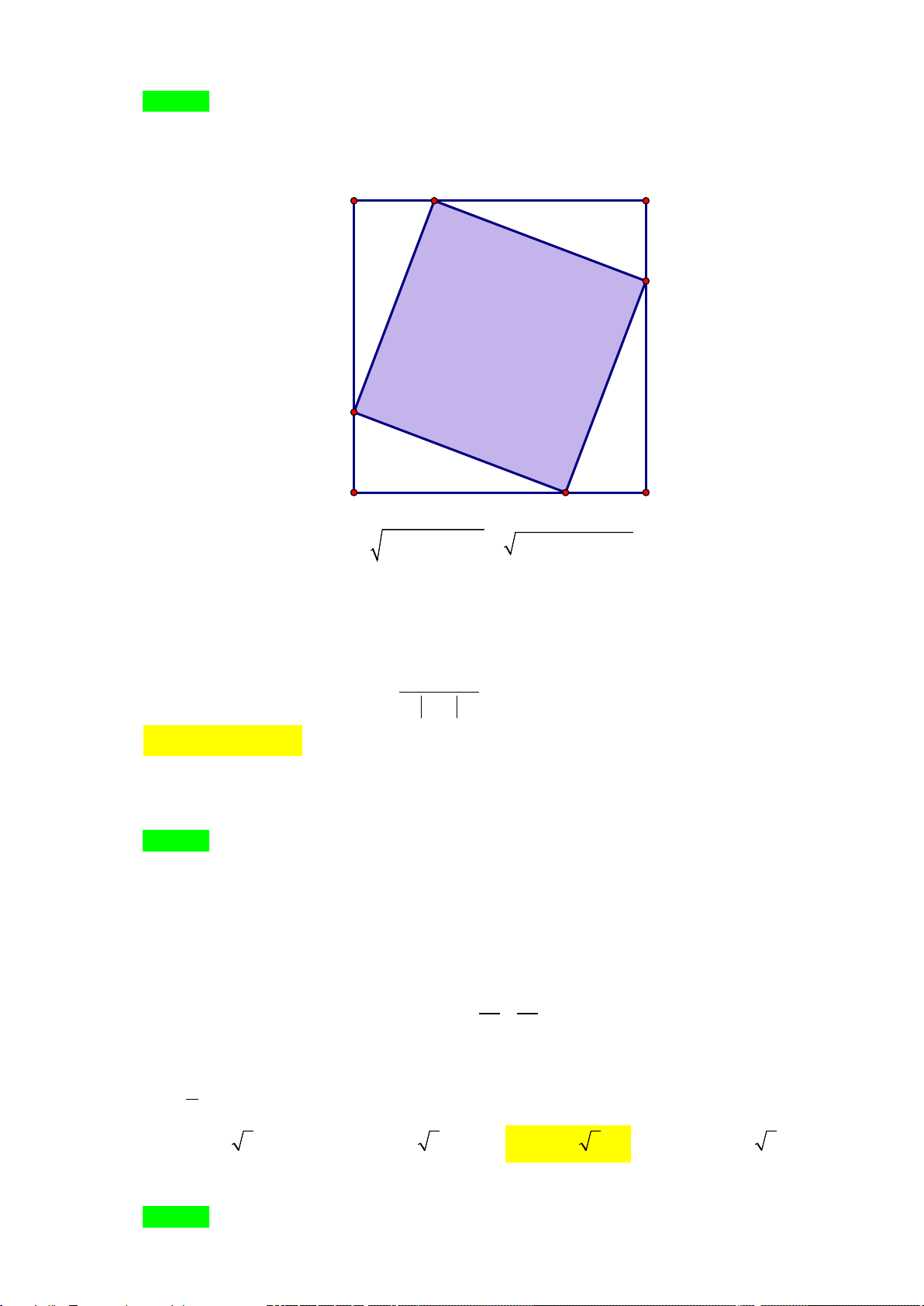
Câu 37: Trong mặt phẳng tọa độ Oxy , cho Elip ( ) : x y E +
= 1 có hai tiêu điểm F , F . Biết điểm M 25 9 1 2
có tung độ y dương thuộc Elip (E) sao cho bán kính đường tròn nội tiếp tam giác MF F M 1 2
bằng 4 . Mệnh đề nào sau đây là đúng? 3 A. y ∈ . B. y ∈ . C. y ∈ . D. y ∈ . M ( 3;2) M ( 8;5) M (2; 8) M (0; 3) Lời giải Chọn C. y M 2 1 F1 F2 -4 -3 -2 -1O 1 2 3 4 x -1 -2
Ta có: MF + MF + F F = 2a + 2c =18. 1 2 1 2 Suy ra: 4 S = p r = = . Suy ra 1
12 = y .F F ⇒ y = 3. MAB . 9. 12 3 1 2 2 M M Câu 38: Tính tổng 2 2 2 2
S = sin 5° + sin 10° + sin 15° +...+ sin 85° . A. S = 9 . B. S = 8. C. 19 S = . D. 17 S = . 2 2 Lời giải Chọn D. 2 2 2 2
S = sin 5° + sin 10° + sin 15° +...+ sin 85° = ( 2 2 ° + °) + ( 2 2 ° + °) + + ( 2 2 ° + °) 2 sin 5 sin 85 sin 10 sin 80 ... sin 40 sin 50 + sin 45° 1 17 = 8 + = . 2 2
Câu 39: Cho góc lượng giác α thỏa mãn π
sinα + cosα =1. Giá trị của sin α + bằng 4 A. 1 − . B. 2 − . C. 1. D. 2 . 2 2 Lời giải Chọn D. π 2 α + = ( α + α ) 2 sin sin cos = . 4 2 2
Câu 40: Tập nghiệm của bất phương trình ( 2x + 4 − x +1)( 2x +1+ x + 4) ≤ x +3 là tập con của tập hợp nào sau đây? A. 2 1 ; − . B. ( 1; − 0). C. 1 2 − ; . D. (0; ) 1 . 3 2 3 3 Lời giải Chọn A. Điều kiện: 1 x ≥ − . 2
( 2x+4 − x+1)( 2x+1+ x+4)≤ x+3
⇔ ( 2x + 4 − x +1)( 2x + 4 + x +1)( 2x +1+ x + 4) ≤ (x +3)( 2x + 4 + x +1) ⇔ x + + x + ≤
x + + x + ⇔ ( x + + x + )2 ≤ ( x + + x + )2 2 1 4 2 4 1 2 1 4 2 4 1 ⇔ (2x + )
1 (x + 4) ≤ (2x + 4)(x + )
1 ⇔ 9x ≤ 6x ⇔ x ≤ 0 .
Vậy tập nghiệm của bất phương trình là 1 ;0 − . 2
Câu 41: Trong mặt phẳng tọa độ với hệ trục tọa độ Oxy , cho đường tròn (C): ( − )2 + ( − )2 2 x a y b = R và đường thẳng (∆) :
x + y − a − b = 0 . Biết đường thẳng (∆) cắt đường tròn (C) tại 2 điểm
M , N phân biệt. Tính độ dài MN .
A. MN = R 2 .
B. MN = 2R .
C. MN = R 3 .
D. MN = R . Lời giải Chọn B
Từ (C): ( − )2 + ( − )2 2 x a
y b = R ta có tâm I ( ;
a b) , bán kính R . Ta có I ∈(∆) nên MN là
đường kính của đường tròn (C) ⇒ MN = 2R .
Câu 42: Trong mặt phẳng tọa độ với hệ trục tọa độ Oxy , cho đường thẳng (d ) : 3x − 4y −12 = 0.
Phương trình đường thẳng (∆) đi qua điểm M (2;− )
1 và tạo với (d ) một góc 0 45 có dạng
ax + by + 5 = 0, trong đó a, b cùng dấu. Khẳng định nào sau đây đúng?
A. a + b = 6.
B. a + b = 8 − .
C. a + b = 8 .
D. a + b = 6 − . Lời giải Chọn C
Từ (d ) : 3x − 4y −12 = 0 có vecto pháp tuyến n = 3; 4
− , (∆) : ax + by + 5 = 0 có vecto pháp 1 ( ) tuyến n = a;b . 2 ( ) 3a − 4b Khi đó 0 2 2 cos45 =
⇔ 7a + 48ab − 7b = 0 b
⇔ a = hoặc ⇔ a = 7 − b ( loại) 2 2 5 a + b 7
Mà (∆) đi qua điểm M (2;− )
1 nên ta có 2a − b + 5 = 0 (*) Với b
a = kết hợp (*) suy ra a =1, 7
b = ⇒ a + b = 8 . 7
Câu 43: Cho tam giác ABC có các góc thỏa mãn sin A+ sin B = cos A+ cos B . Tính số đo góc C của tam giác ABC . A. 0 90 . B. 0 120 . C. 0 60 . D. 0 45 . Lời giải Chọn A Từ sin + − + −
A + sin B = cos A + cos B ⇔ 2sin A B A B 2 A B A B cos cos cos = 2 2 2 2
sin A + B sin C ⇔ = ⇒ A + B = C . 2 2 Mà 0 0 0
A + B + C =180 ⇔ 2C =180 ⇒ C = 90 .
Câu 44: Trong mặt phẳng tọa độ với hệ trục tọa độ Oxy , cho đường tròn (C) (x − )2 + ( y − )2 : 2 2 = 9 .
Phương trình các tiếp tuyến của đường tròn đi qua điểm A(5;− ) 1 là
A. x + 2y − 3 = 0 hoặc 2x − y − 2 + 3 5 = 0 .
B. x + y − 4 = 0 hoặc x − y − 6 = 0.
C. 3x + 4y +1 = 0 hoặc 4x − 3y +13 = 0 .
D. x = 5 hoặc y = 1 − . Lời giải Chọn D
Từ (C) (x − )2 + ( y − )2 : 2
2 = 9 có tâm I (2;2) bán kính R = 3 . Từ điểm A(5;− )
1 ta kiểm tra đường thẳng (d ) : x = 5 ta có d (I;(d )) = R
⇒ x = 5 là tiếp tuyến.
Câu 45: Có bao nhiêu giá trị của x để hàm số y = x ( − x )( x − )2 2 2 2 32 1 2
1 đạt giá trị lớn nhất trên ( 1; − ) 1 0 tại x = x ? 0 A. 4 . B. 8 . C. 6 . D. 10. Lời giải Chọn A
Đặt x = cosα với α ∈(0;π ) , ta có y = cos α ( − cos α )( cos α − )2 2 2 2 32 1 2 1 2 2 2 2 2
⇔ y = 32cos α.sin α.cos 2α = 8sin 2α.cos 2α 2
⇔ y = 2sin 4α ⇒ 0 < y ≤ 2 Suy ra π π π π max y = 2 khi 2
sin 4α =1 ⇔ cos4α = 0 với α ∈(0;π ) 3 5 7 α ; ; ; ⇒ ∈ 8 8 8 8
Câu 46: Tìm tập hợp các giá trị của m để bất phương tình 2
x − 2x − m ≤ 0 nghiệm đúng với mọi x ∈[0; ] 3 A. ( ; −∞ − ] 1 .
B. [3;+∞) . C. [ 1; − +∞). D. [ 1; − ]3. Lời giải Chọn B 2 2
x − 2x − m ≤ 0 ⇔ m ≥ x − 2x . Đặt f (x) 2
= x − 2x ⇒ m ≥ f (x), x ∀ ∈[0; ]
3 ⇔ m ≥ max f (x). [0; ]3
Ta có bảng biến thiên của f (x) x ∞ 0 1 3 + ∞ y 0 3 -1
Vậy m ≥ 3 ⇒ m∈[3;+∞) .
Câu 47: Có bao nhiêu giá trị của m để bất phương trình ( 2 m − )
1 x + m > 0 vô nghiệm? A. 0 . B. 3. C. 1. D. 2 . Lời giải Chọn C m =1 2 − =
Bất phương rình vô nghiệm khi và chỉ khi m 1 0 ⇔ m = 1 − ⇔ m = 1 − . m ≤ 0 m ≤ 0
Câu 48: Cho góc lượng giác a thỏa mãn sin 2a + sin5a −sin3a = 2 − . Tính sin a 2
2cos 2a + cos a −1 A. 1 − . B. 1 − . C. 1. D. 1 . 4 4 Lời giải Chọn B
Ta có sin 2a + sin 5a − sin 3a = 2 − 2
2cos 2a + cos a −1 sin 2a + 2cos 4 . a sin a ⇔ = 2 − os
c 4a + cos a
2sin a(cos a + os c 4a) ⇔ = 2 − os
c 4a + cos a ⇔ sin a = 1 − .
Câu 49: Trong mặt phẳng với hệ trục tọa độ Oxy , cho hình chữ nhật có hai cạnh nằm trên hai đường
thẳng có phương trình lần lượt là 2x − y + 3 = 0; x + 2y − 5 = 0 và tọa độ một đỉnh là (2;3).
Diện tích hình chữ nhật đó là: A. 12 (đvdt). B. 16 (đvdt). C. 9 (đvdt). D.12 (đvdt). 5 5 5 5 Lời giải Chọn D
Vì hai phương trình đã cho là phương trình của hai đường thẳng cắt nhau nên giả sử
AB : 2x − y + 3 = 0 ; BC : x + 2y − 5 = 0
2x − y + 3 = 0
Tọa độ đỉnh B là nghiệm của hpt 1 − 13 B ; ⇒ x 2y 5 0 5 5 + − =
Ta thấy tọa độ đỉnh còn lại đều không thỏa hai phương trình đã cho nên đó chính là đỉnh D(2;3).
AD//BC, AD đi qua D(2;3) ⇒ AD : x + 2y −8 = 0
2x − y + 3 = 0 Tọa độ đỉnh 2 19
A là nghiệm của hpt A ; ⇒ .
x + 2y − 8 = 0 5 5 2 2 1 2 13 19 3 2 2 AB − = − + − = 2 19 4 , AD = 2 − + 3− = 5 5 5 5 5 5 5 5 3 4 12 ⇒ S = AB AD = = . Vậy 12 S = (đvdt). ABCD . . 5 5 5 ABCD 5
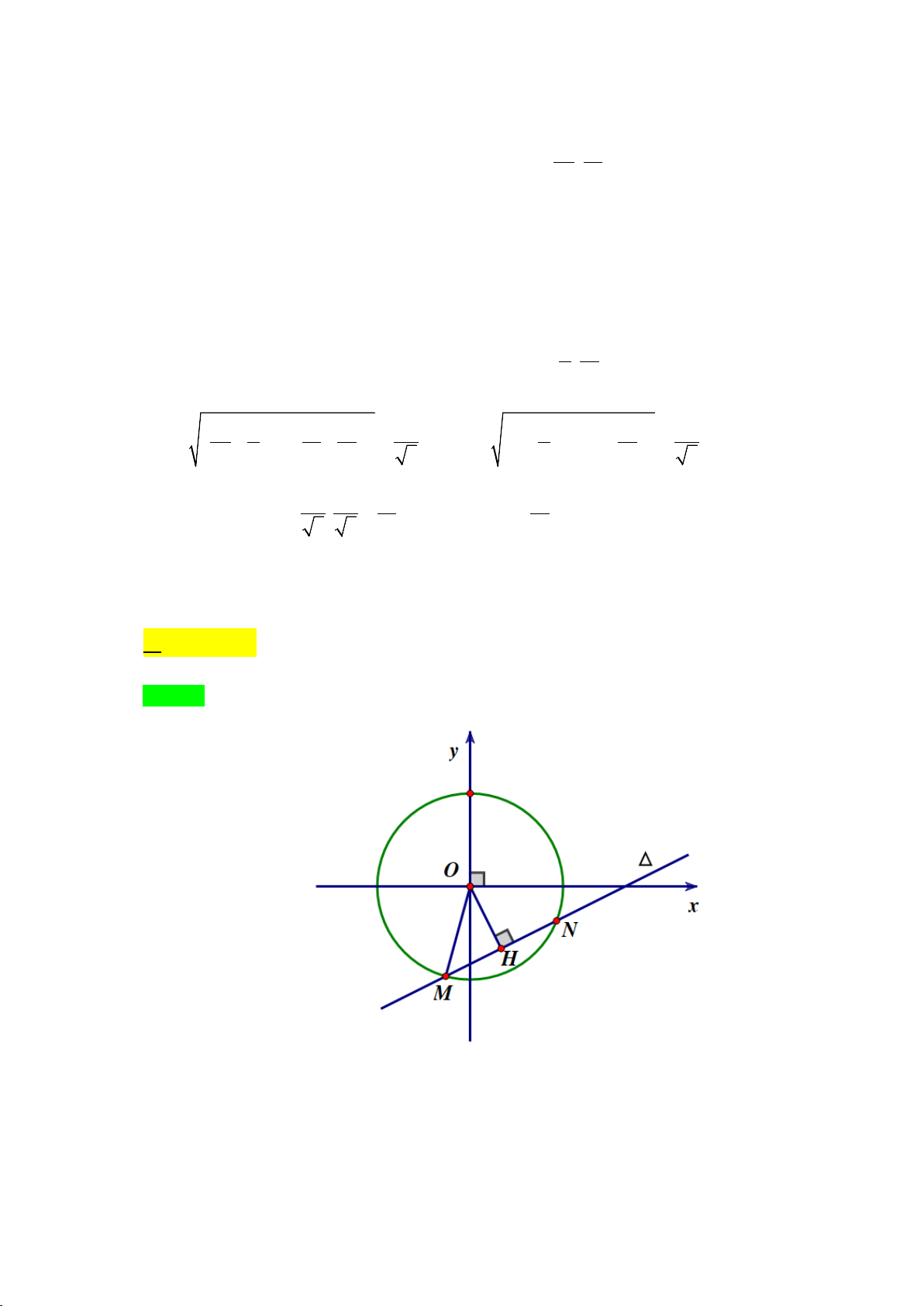
Câu 50: Trong mặt phẳng với hệ trục tọa độ Oxy , viết phương trình đường tròn tâm O(0;0) cắt đường
thẳng (∆) : x + 2y −5 = 0 tại hai điểm M; N sao cho MN = 4. A. 2 2 x + y = 9. B. 2 2
x + y =1. C. 2 2 x + y = 21. D. 2 2 x + y = 3. Lời giải Chọn A
Gọi R là bán kính của đường tròn (C) thỏa đề bài.
∆ không qua O(0;0) nên MN không phải là đường kính của (C).
Gọi H là hình chiếu của O trên ∆ thì H là trung điểm của MN 1 MH = MN = 2. 2 −
OH = d (O ∆) 5 ; = = 5 2 2 1 + 2 2 2
R = MO = OH + MH = 5 + 4 = 3. Vậy (C) 2 2 : x + y = 9.
---------------- HẾT ----------------
Document Outline
- de-thi-hk2-toan-10-nam-2018-2019-truong-luong-the-vinh-ha-noi
- TEST_de-hk2-toan-10-ltv-cuoi-Made-162
- TEST_de-hk2-toan-10-ltv-cuoi-Dap-an
- Tổ-7-góp-đề-L10-Lương-Thế-Vinh-Hà-Nội-HK2-1819




