Đề thi HK2 Toán 10 năm 2018 – 2019 trường Phạm Văn Đồng – Quảng Ngãi

Giới thiệu đến quý thầy, cô giáo cùng các em học sinh lớp 10 đề thi HK2 Toán 10 năm 2018 – 2019 trường Phạm Văn Đồng – Quảng Ngãi, kỳ thi nhằm kiểm tra chất lượng môn Toán lớp 10 trong học kỳ vừa qua, mời các bạn đón xem

13 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 10

Môn: Toán 10

Thông tin:

14 trang 6 tháng trước

Tác giả:

Profile Thanh Tâm
Trang 1/4 - Mã đề 158
TRƯỜNG THPT PHẠM VĂN ĐỒNG
TỔ TOÁN
KIỂM TRA CHẤT LƯỢNG HỌC KỲ II
NĂM HỌC 2018 – 2019
Môn: Toán - Lớp 10 - Chương trình chuẩn
ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề)
Mã đề thi
158
Họ và tên: ……………………………………………. Lớp: ……………........
I. PHẦN TRẮC NGHIỆM (7 ĐIỂM)
Câu 1. Trong mặt phẳng
Oxy
, cho đường tròn
( ) ( ) ( )
22
: 3 1 10Cx y− +− =
. Phương trình tiếp tuyến
của
( )
C
tại điểm
( )
4; 4A
là
A.
3 50xy− +=
. B.
3 16 0
xy+−=
. C.
3 40xy+ −=
. D.
3 16 0xy−+=
.
Câu 2. Cho ΔABC có
12, 15BC AC= =
,góc
0
60C =
.Khi đó độ dài cạnh AB là:
A.
6 21AB =
B.
3 21
AB =
C.
67AB =
D.
37AB =
Câu 3. Giải hệ bất phương trình
( )( )
56 0
2 13
xx
x
+ −>
+<
.
A.
51
x
−< <
. B.
5x >−
. C.
5x <−
. D.
1x <
.
Câu 4. Cho đường tròn
( ) ( ) ( )
22
: 1 3 10Cx y− ++ =
và đường thẳng
: 10xy∆ + +=
biết đường thẳng
∆
cắt
( )
C
tại hai điểm phân biệt
A
,
B
. Độ dài đoạn thẳng
AB
bằng
A.
19
2
. B.
19
2
. C.
38
2
. D.
38
.
Câu 5. Chọn khẳng định đúng?
A.
( )
sin sin
πα α
−=−
. B.
( )
tan tan
πα α
−=
.
C.
( )
cot cot
πα α
−=
. D.
( )
cos cos
πα α
−=−
.
Câu 6. Phương trình nào sau đây là phương trình đường tròn?
A.
22
4 10 4 2 0
xy xy+ − + −=
. B.
22
4810xy xy
+−−+=
.
C.
22
2 4 6 10x y xy+ − + −=
. D.
22
2 8 20 0
xy xy+−−+=
.
Câu 7. Đường thẳng đi qua
( 1; 2 ),A −
nhận
(2; 4)n = −
làm vec tơ pháp tuyến có phương trình là:
A.
2 4 0.xy−+ − =
B.
2 4 0.xy− −=
C.
2 5 0.xy− +=
D.
4 0.xy++=
Câu 8. Phương trình chính tắc của
( )
E
có
54ca=
, độ dài trục nhỏ bằng
12
là
A.
22
1
100 36
xy
+=
. B.
22
1
36 25
xy
+=
. C.
22
1
64 36
xy
+=
. D.
22
1
25 36
xy
+=
.
Câu 9. Cung có số đo
250°
thì có số đo theo đơn vị là radian là
A.
35
18
π
. B.
25
18
π
. C.
25
12
π
. D.
25
9
π
.
Câu 10. Giải bất phương trình
210x − ≥
. Kết quả tập nghiệm nào sau đây là đúng?
A. B. C. D.

−∞

1
S = ;
2

+∞

1
S = ;
2

−∞


1
S = ;
2

− +∞

1
S = ;
2
Trang 2/4 - Mã đề 158
Câu 11. Cho
3
sin
4
α
=
. Khi đó,
cos 2
α
bằng
A.
1
8
. B.
7
4
. C.
1
8
−
. D.
7
4
−
.
Câu 12. Tam thức bậc hai
( )
2
12 13
fx x x=−−
nhận giá trị không âm khi và chỉ khi
A.
( )
1;1 3x ∈−
. B.
[ ]
\ 1;1 3x ∈−
.
C.
[
]
1;1 3
x
∈−
. D.
(
] [
)
; 1 13;x ∈ −∞ − ∪ +∞
.
Câu 13. Đường thẳng
:3 2 7 0xy∆ − −=
cắt đường thẳng nào sau đây?
A.
1
:3 2 0dxy+=
. B.
4
: 6 4 14 0dxy− −=
.
C.
3
:3 2 7 0d xy− + −=
. D.
2
:3 2 0dxy−=
.
Câu 14. Trong tam giác
ABC
, đẳng thức nào dưới đây luôn đúng?
A.
cos sinAB=
. B.
tan cot
2
AB
π

= +


.
C.
cos sin
22
AB C
+
=
. D.
( )
sin cosAB C+=
.
Câu 15. Chọn điểm
( )
1; 0
A
làm điểm đầu của cung lượng giác trên đường tròn lượng giác. Tìm điểm
cuối
M
của cung lượng giác có số đo
25
4
π
.
A.
M
là điểm chính giữa của cung phần tư thứ
I
.
B.
M
là điểm chính giữa của cung phần tư thứ
IV
.
C.
M
là điểm chính giữa của cung phần tư thứ
III
.
D.
M
là điểm chính giữa của cung phần tư thứ
II
.
Câu 16. Cho đường thẳng
: 2 30
dx y
− −=
. Tìm tọa độ hình chiếu vuông góc
H
của điểm
( )
0;1M
trên đường thẳng.
A.
(
)
5;1
H
. B.
( )
1; 1H
−
. C.
( )
1; 2H −
. D.
( )
3; 0H
.
Câu 17. Cho
3
sin
5
α
=
và
2
π
απ
<<
. Tính giá trị
cos
α
.
A.
4
5
. B.
16
25
. C.
4
5
±
. D.
4
5
−
.
Câu 18. Trên đường tròn bán kính
6R
=
, cung
60°
có độ dài bằng bao nhiêu?
A.
2l
π
=
. B.
4l
π
=
. C.
2
l
π
=
. D.
l
π
=
.
Câu 19. Cho hai đường thẳng
1
: 20dxy
−−=
và
2
:2 3 3 0d xy+ +=
. Góc tạo bởi đường thẳng
1
d
và
2
d
là ( chọn kết quả gần đúng nhất)
A.
101 19
′
°
. B.
78 41
′
°
. C.
11 19
′
°
. D.
78 31
′
°
.
Câu 20. Cho tam giác
ABC
có độ dài ba cạnh là
2AB =
,
3BC =
,
4CA =
. Tính độ dài đường trung
tuyến
MA
, với
M
là trung điểm của
BC
.
A.
31
4
. B.
23
2
. C.
31
2
. D.
5
2
.
Trang 3/4 - Mã đề 158
Câu 21. Tìm một vectơ chỉ phương của đường thẳng
12
:
35
xt
d
yt
=−+
= −
.
A.
( )
3;1u = −
. B.
( )
5; 2u =
. C.
( )
2; 5u = −
. D.
(
)
1; 3u = −
.
Câu 22. Cung nào sau đây có điểm cuối trùng với B’.
A. B. C. D.
Câu 23. Trong mặt phẳng với hệ tọa độ
Oxy
cho đường thẳng
: 2 10dx y− +=
và điểm
( )
2;3
M
.
Phương trình đường thẳng
∆
đi qua điểm
M
và vuông góc với đường thẳng
d
là
A.
2 80xy+ −=
. B.
2 70
xy
+−=
. C.
2 10
xy
− −=
. D.
2 40xy− +=
.
Câu 24. Miền nghiệm của hệ bất phương trình:
34120
50
10
xy
xy
x
−+≥
+−≥
+>
Là miền chứa điểm nào trong các điểm sau?
A. B. C. D.
Câu 25. Phương trình chính tắc của
( )
E
có độ dài trục lớn bằng
8
, trục nhỏ bằng
6
là
A.
22
1
16 9
xy
+=
. B.
22
9 16 1xy+=
. C.
22
1
9 16
xy
+=
. D.
22
1
64 36
xy
+=
.
Câu 26. Cho góc
α
thỏa mãn và
2
π
απ
<<
. Tính
sin 2cos 1
αα
+=−
. Tính giá trị
sin 2
α
.
A.
26
5
. B.
24
25
. C.
26
5
−
. D.
24
25
−
.
Câu 27. Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9kg chất
B
. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6kg
chất
B
. Từ mỗi tấn nguyên liệu loại II giá 3,5 triệu đồng, có thể chiết suất được 10kg chất
A
và 1,5kg
chất
B
. Hỏi chi phí mua nguyên vật liệu ít nhất bằng bao nhiêu, biết rằng cơ sở cung cấp nguyên
liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II?
A. 47 triệu đồng. B. 34 triệu đồng. C. 31,5 triệu đồng D. 31 triệu đồng.
Câu 28. Cho tam giác
ABC
thỏa mãn
2
2
tan sin
tan sin
BB
CC
=
thì:
A. Tam giác
ABC
vuông. B. Tam giác
ABC
cân.
C. Tam giác
ABC
đều. D. Tam giác
ABC
vuông hoặc cân.
Câu 29. Cho các góc
α
,
β
thỏa mãn
2
π
α
<
,
βπ
<
,
1
sin
3
α
=
,
2
cos
3
β
= −
. Tính
( )
sin
αβ
+
.
A.
( )
5 42
sin
9
αβ
+
+=
. B.
( )
5 42
sin
9
αβ
−
+=
.
C.
( )
2 10 2
sin
9
αβ
−
+=
. D.
( )
2 2 10
sin
9
αβ
+
+=−
.
2
k
π
2
2
k
π
π
−+
k
ππ
+
2
2
k
π
π
+
( )
−
1; 3
M
( )
4; 3N
( )
1; 5
P
−
( )
2; 3Q
−−
Trang 4/4 - Mã đề 158
Câu 30. Biết
d
là đường thẳng đi qua điểm
(1; 2)A
và cắt tia
,x OyO
thứ tự tại
( ; 0), (0; )Mm N n
sao
cho tam giác
OMN
có diện tích nhỏ nhất. Khi đó tổng
?mn+=
A. 1. B. 3. C. 4. D. 6.
Câu 31. Biểu thức:
( ) ( )
( ) ( )
2003
cos 26 2sin 7 cos1,5 cos cos 1,5 .cot 8
2
A
π
α π απ π α α π απ

= + − −− − + + − −


có kết quả thu gọn bằng:
A.
cos
α
−
. B.
sin
α
−
. C.
sin
α
. D.
cos
α
.
Câu 32. Bất phương trình
27
1
4
x
x
+
<
−
có bao nhiêu nghiệm nguyên dương?
A.
4
. B.
3
. C.
14
. D.
0
.
Câu 33. Điều kiện của bất phương trình
2
23
2 3 10
5
x
xx
x
+
+ − +>
−
là:
A.
1
2
1x
x
≥
≤
B.
1
2
5
1
x
x
≤≤
≤
C.
1
2
5
1
x
x
≤
≤
<
D.
1
1
2
5
x
x
≤
<
≤
Câu 34. Tìm
m
để
( )
2
1 0;m x mx m x+ + + < ∀∈
?
A.
1
m >−
. B.
4
3
m >
. C.
4
3
m <−
. D.
1m <−
.
Câu 35. Tìm tất cả các giá trị thực của tham số
m
để phương trình
( )
2
2 1 9 50x m xm+ + + −=
có hai
nghiệm âm phân biệt?
A.
6m
<
. B.
5
1
9
m
<<
hoặc
6m >
.
C.
16
m<<
. D.
1m >
.
II. PHẦN TỰ LUẬN (3 ĐIỂM)
Câu 36. (1đ) a) Giải bất phương trình sau
13 7x
−≤
;
b) Bằng cách lập bảng xét dấu, giải bất phương trình
2
(2 1)(3 )
0
54
xx
xx
−−
>
−+
.
Câu 37. (1đ) a) Cho
2
cos , .
32
a
π
πα

=− <<


Tính
sin
α
.
b)
Trong mặt phẳng với hệ tọa độ
Oxy
, viết phương trình của đường thẳng
d
biết
d
vuông góc
với đường thẳng
:2 1 0xy∆ − +=
và cắt đường tròn
22
: 24 0( 4
)Cx y x y+ + − −=
theo một dây cung
có độ dài bằng 6.
Câu 38. (1đ) Giải phương trình:
1
4
10 9
14 1
x
xx
x
−
−=
−
+−
.
-------------- HẾT --------------
1
ĐÁP ÁN CÁC MÃ ĐỀ
------------------------
Mã đề [158]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
B
A
D
D
B
C
A
B
B
C
D
A
C
A
B
D
A
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
B
C
C
B
B
B
A
D
B
D
D
D
C
B
C
C
B
Mã đề [291]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
C
D
A
A
B
A
B
B
C
B
B
B
B
D
A
C
B
B
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
D
B
D
C
C
C
C
C
D
D
D
D
D
A
D
D
A
Mã đề [348]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
C
C
D
C
A
B
B
C
A
D
B
C
D
A
B
C
D
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
A
A
A
C
D
A
D
D
A
C
D
C
B
B
B
C
A
Mã đề [470]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
C
C
A
D
B
D
B
D
D
D
B
B
C
C
A
D
D
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
B
D
B
A
B
C
A
C
A
C
C
B
A
A
D
B
D
Lời giải phần tự luận
Câu 36.
a) Gii bsau
1 3 7x
;

1 3 7 7 1 3 7x x 

36
8
28
3
xx

b) Bp bu, gii b
2
(2 1)(3 )
0
54
xx
xx


.
Bu:
Lc b
Vy tp nghim ca b
1
;1 3; 4
2
S





Câu 37. (1đ)
a) Cho
2
cos , .
32
a




sin
.
x

1
2
1
3 4

21x
0
|
|
|
3 x
|
|
0
-
| -
0
2
54xx
+
|
+
0 - | - 0 +
VT
0
|| -
0
+ || -
2

2
2
25
sin 1 sin .
39
5
3






2


sin sin
5
0
3
.


b)
Trong mt phng vi h t
Oxy
, ving thng
d
bit
d
i
ng thng
:2 1 0xy
 ct ng 
22
: 2 4 0( 4)C x y x y
theo mt 
ng 6.
Hướng dẫn giải:

1;2 ,I

3R

2 2 2 2 2
3 3 0IH R HB I H
.
ng thng
d
i
ng
20x y c
.
d
m I. Suy ra
1 2.2 0 3cc
. Vy
: 2 3 0d x y
. 
Câu 38. (1đ) Gi
1
4
10 9
14 1
x
xx
x


.
Hướng dẫn giải

9
10
x
(0,25đ)

2
4 1 014 1 10 9xxx x x
3) ( 1) 0( 14 1 10 9xxx x x x
3) ( 1) 0( 14 1 10 9xx x x x


(0,25đ)
22
6 9 14 1 2 1 10 9
0
3114 1 10 9
x x x x x
x
x
x
x x x





2
1
8 10 0
3114 1 10 9
x
x
x
x
x x x




(0,25đ)

9
10
x

0
3 14 1
x
xx


1
0
1 10 9x x

)
2
8 10 0xx 
64x
(th

6; 644S 
(0,25đ).
CÂU HỎI TRẮC NGHIỆM
Câu 1. t  cng thng
12
:
35
xt
d
yt

2; 5u 
22
1
9 16
xy

.
A. . B.
5;2u
. C.
1;3u 
. D.
3;1u 
.
Hướng dẫn giải
Chọn A.
M ng thng
d

2; 5u 
.
Câu 2. Hướng dẫn giải b
210x
. Kt qu tp nghi
d
A
I
B
H
3
A. B. C. D.
Câu 3. c ca
E
 c ln bng
8
, trc nh bng
6

A.
22
1
64 36
xy

. B. . C.
22
9 16 1xy
. D.
22
1
16 9
xy

.
Hướng dẫn giải
Chọn B.

28
26
a
b
4
3
a
b
.
Vc ca
E
:
22
1
16 9
xy

Câu 4. 
1;0A


M

25
4
.
A.
M

I
.
B.
M

II
.
C.
M

III
.
D.
M

IV
.
Hướng dẫn giải
Chọn A.
Theo gi thi
25
6
44
AM
m
M
a ca cung ph
Câu 5. Min nghim ca h b:
3 4 12 0
50
10
xy
xy
x

n chm sau?
A. B. C. D.
Câu 6. 
2
12 13f x x x
không âm 
A.
\ 1;13x
. B.
1;13x
. C.
; 1 13;x 
. D.
1;13x
.
Câu 7. 
250

A.
25
12
. B.
25
18
. C.
25
9
. D.
35
18
.
Hướng dẫn giải
Chọn B.

25
250 .250
180 18

.
Câu 8. m cu
A. B. C. D.
Câu 9. 
6R
, cung
60

A.
2
l
. B.
4l
. C.
2l
. D.
l
.
Hướng dẫn giải
Chọn C.
60
3

rad.


R

lR
.




1
S = ;
2



1
S = ;
2



1
S = ;
2



1
S = ;
2
1;5P
4;3N
2; 3Q 
1; 3M
2
2
k

2k
2
2
k
k

4

60

6.
3
l
2
.
Câu 10. Chn kh
A.
tan tan

.
B.
sin sin
.
C.
cot cot

. D.
cos cos
.
Hướng dẫn giải
Chọn D.
tan tan


tan tan
;
sin sin

sin sin

;
cot cot


cot cot
.
Câu 11. Trong tam g
ABC

A.
sin cosA B C
. B.
cos sinAB
.
C.
tan cot
2
AB




. D.
cos sin
22
A B C
.
Hướng dẫn giải
Chọn D.

cos cos sin
2 2 2 2
A B C C



.
Câu 12. Cho
3
sin
5

2


. 
cos
.
A.
16
25
. B.
4
5
. C.
4
5
. D.
4
5
.
Hướng dẫn giải
Chọn D.

2



2
4
cos 1 sin .
5

Câu 13. Cho
3
sin
4

cos2
bng
A.
1
8
. B.
7
4
. C.
7
4
. D.
1
8
.
Hướng dẫn giải
Chọn A.
2
2
31
cos2 1 2sin 1 2.
48




.
Câu 14. c ca
E

54ca
 c nh bng
12

A.
22
1
25 36
xy

. B.
22
1
64 36
xy

. C.
22
1
100 36
xy

. D.
22
1
36 25
xy

.
Hướng dẫn giải
Chọn C.

4
5
2 12
e
b
54
6
ca
b
22
25 16
6
ca
b
2 2 2
25 16
6
a b a
b

10
6
a
b
.
Va
E
:
22
1
100 36
xy

.
Câu 15. Cho 
12, 15BC AC

0
60C
.
A.
67AB
B.
37AB
C.
3 21AB
D.
6 21AB
5
Câu 16. 
ABC

2AB
,
3BC
,
4CA


MA
, v
M

BC
.
A.
5
2
. B.
31
2
. C.
23
2
. D.
31
4
.
Câu 17. ng th
( 1;2),A
nhn
(2; 4)n 

A.
2 4 0.xy
B.
2 4 0.xy
C.
2 5 0.xy
D.
4 0.xy
Hướng dẫn giải.
Chọn C.
ng thng c
2( 1) 4( 2) 0xy
2 4 10 0xy
2 5 0.xy
Câu 18. Trong mt phng vi h t
Oxy
ng thng
: 2 1 0d x y
m
2;3M
.
ng thng

M

d

A.
2 8 0xy
. B.
2 4 0xy
. C.
2 1 0xy
. D.
2 7 0xy
.
Hướng dẫn giải
Chọn D.

: 2 1 0d x y


2;1n
.
qua
2;3M

2 2 3 0xy
2 7 0xy
.
Câu 19. 
:3 2 7 0xy

A.
1
:3 2 0d x y
. B.
2
:3 2 0d x y
.
C.
3
: 3 2 7 0d x y
. D.
4
:6 4 14 0d x y
.
Hướng dẫn giải
Chọn A.
X
:3 2 7 0xy

1
:3 2 0d x y

32
32


1
d
.
Câu 20. ng thng
1
: 2 0d x y

2
:2 3 3 0d x y
c to bng thng
1
d

2
d
n kt qu gt)
A.
11 19
. B.
78 41
. C.
101 19
. D.
78 31
.
Hướng dẫn giải
Chọn B.
1
: 2 0d x y

1

1
1; 1n 
.
2
:2 3 3 0d x y

1

2
2;3n
.

1
d

2
d

.

12
12
.
cos
.
nn
nn
2
2 2 2
23
1 1 . 2 3
26
26
78 41
.
Câu 21. 
A.
22
4 8 1 0x y x y
. B.
22
4 10 4 2 0x y x y
.
C.
22
2 8 20 0x y x y
. D.
22
2 4 6 1 0x y x y
.
Hướng dẫn giải
Chọn A.

C
:
22
4 8 1 0x y x y

2 2 2 2
2 4 1 19 0a b c
.
Vy
C

Câu 22. ng thng
: 2 3 0d x y
 
H
cm
0;1M

ng thng.
A.
1;2H
. B.
5;1H
. C.
3;0H
. D.
1; 1H
.
Hướng dẫn giải
6
Chọn D.
:2 0d x y m

0;1 :M 
2.0 1 0m
1m
:2 1 0xy
.
Ta  m
H
m ca h:
2 1 0
2 3 0
xy
xy
1
1
x
y

. Vy
1; 1H
.
Câu 23. Trong mt phng
Oxy
, c
22
: 3 1 10C x y
p tuyn ca
C
tm
4;4A

A.
3 16 0xy
. B.
3 4 0xy
.
C.
3 5 0xy
. D.
3 16 0xy
.
Hướng dẫn giải
Chọn A.

C

3;1I
m
4;4A

Tip tuyn ca
C
tm
4;4A

1;3IA
p tuyn
d

ng
30x y c
.
d

4;4A

4 3.4 0 16cc
.
Va
d
:
3 16 0xy
.
Câu 24. 
22
: 1 3 10C x y

: 1 0xy


C

A
,
B

AB

A.
19
2
. B.
38
. C.
19
2
. D.
38
2
.
Hướng dẫn giải
Chọn B.

C

1; 3I

10R IA
.

H
B.

;
1 3 1
1
1 1 2
I
IH d

.

AIH

H

1 38
10
22
AH
.

2 38AB AH
.
Câu 25. Hướng dẫn giải 
5 6 0
2 1 3
xx
x

.
A.
51x
. B.
1x
. C.
5x 
. D.
5x 
.
Hướng dẫn giải
Chọn A.
5 6 0 1
2 1 3 2
xx
x

.
+) 
1

1
5;6S 
.
+) 
2
:
1x 

2

2
;1S
.

12
5;1S S S
.
Câu 26. 
27
1
4
x
x
nghiệm nguyên dương?
A.
14
. B.
3
. C.
0
. D.
4
.
Hướng dẫn giải
Chọn B.
2 7 11
1 0 11 4
44
xx
x
xx


.
7

3

1;2;3
.
Câu 27. 
m

2
1 0;m x mx m x
?
A.
4
3
m
. B.
1m 
. C.
4
3
m 
. D.
1m 
.
Hướng dẫn giải
Chọn C.
t
2
1f x m x mx m

1 0 1mm

1 0 1f x x x


1 0 1mm

0,f x x
2
10
4 1 0
m
m m m

10
3 4 0
m
mm


1
4
3
0
m
m
m


4
3
m
.
Câu 28. t c  thc ca tham s
m
 
2
2 1 9 5 0x m x m

nghit?
A.
5
1
9
m
hoc
6m
. B.
16m
.
C.
6m
. D.
1m
.
Hướng dẫn giải
Chọn A.
t khi
2
0
7 6 0
0 1 0
9 5 0
0
mm
b
m
a
m
c
a





6
1
5
1
1
9
6
5
9
m
m
m
m
m
m


.
Câu 29. 
th
2



sin 2cos 1


sin2
.
A.
24
25
. B.
26
5
. C.
24
25
. D.
26
5
.
Hướng dẫn giải
Chọn A.
sin 2cos 1 sin 1 2cos
.

2
2 2 2 2
0
sin 1 1 2cos 1 5 4 0
4
5
cos
cos cos cos cos
cos


th
2



43
sin
55
cos

.

sin2 2sin .cos

24
25
Câu 30. 
2
23
2 3 1 0
5
x
xx
x

8
A.
1
2
5
1
x
x
B.
1
2
1x
x
C.
1
2
5
1
x
x

D.
1
1
2
5x
x
Hướng dẫn giải:

2
5
50
1
2 0
1
2
31
x
x
x
xx
x



15
1
2
x
x
.
Câu 31. Biu thc:
2003
cos 26 2sin 7 cos1,5 cos cos 1,5 .cot 8
2
A



t qu thu gn bng:
A.
cos
. B.
cos
. C.
sin
. D.
sin
.
Hướng dẫn giải
Chọn D.
Biu thc
2003
cos 26 2sin 7 cos1,5 cos cos 1,5 .cot 8
2
A



cos 2sin 0 cos 1,5 cos 1,5 .cot
cos 2sin sin sin .cot
cos 2sin sin cos
sin
.
Câu 32. 
,
th
2
,

,
1
sin
3
,
2
cos
3


sin

.
A.
2 2 10
sin
9

. B.
2 10 2
sin
9


.
C.
5 4 2
sin
9


. D.
5 4 2
sin
9


.
Hướng dẫn giải
Chọn A.
Do
2
,

cos 0
sin 0
.

2
1 2 2
cos 1 sin 1
93

.
2
45
sin 1 cos 1
93

.
Suy ra
1 2 2 2 5 2 2 10
sin sin .cos cos .sin . .
3 3 3 3 9







.
Vy
2 2 10
sin
9

.
Câu 33.   B. 
 B. 
 B. 
ít nhất 

A.  B.  C.  D. 
Hướng dẫn giải
Chọn C.
+) Gi
x
,
y
l tu loi
I
i
II
cu kin
x
,
y
n
+) Vi x tu lou loi II, sn xuc
2 0 1 0xy
kg ch
0,6 1,5xy
kg cht B.
+) S ti mua x tn lon lo
; 4 3,5L x y x y
.
9
Theo gi thi:
20 10 140
0,6 1,5
1
9
00
09
xy
xy
x
y
2 14
2 5 30
00
0
1
9
xy
xy
x
y
Min nghim ca h 
+) Min nghi 
+)
20 14 34LA
;
40 7 47LB
;
40 31,5 71,5LB
10 31,5 41,5LD
T
34L
tring.
Câu 34. Bit
d
ng thm
(1; 2)A
t tia
,x OyO
th t ti
( ;0), (0; )M m N n
sao

OMN
 nht. ng
?mn
A. 6. B. 3. C. 4. D. 1.
Hướng dẫn giải:

( ;0), (0; )M m N n

0m

0n
+
OMN

O

11
.
22
S OM ON mn
OMN

ng thng
d

,MN

:1
xy
d
mn

ng thng
d

A

12
1
mn

+)

12
,
mn

1 2 2
1 2 0 8mn
m n mn
, dn
4S
OMN
4S
OMN

12
1 2 2
1
4
0
0
mn
m
mn
n
m
n


. Vy
6mn
.
Câu 35. 
ABC
th
2
2
tan sin
tan sin
BB
CC
:
A. 
ABC
 B. 
ABC

C. 
ABC
u. D. 
ABC

Hướng dẫn giải
10

2
2 2 2 2
2
tan sin sin sin
tan sin sin tan sin sin
tan sin cos
B B B C
B C B C C B
C C B Ccos
sin sin
sin cosC sin sin2 sin2
cosC
CB
C B B C B
B
cos
cos
sin2 sin2 0 2cos( )sin( ) 0B C B C B C
0
0
cos( ) 0 90
sin( ) 0
0
B C B C
BC
BC



. Vi A.
---------- HẾT ----------
| 1/14
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT PHẠM VĂN ĐỒNG
KIỂM TRA CHẤT LƯỢNG HỌC KỲ II TỔ TOÁN
NĂM HỌC 2018 – 2019
Môn: Toán - Lớp 10 - Chương trình chuẩn ĐỀ CHÍNH THỨC
Thời gian: 90 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên: ……………………………………………. Lớp: ……………........ 158
I. PHẦN TRẮC NGHIỆM (7 ĐIỂM)
Câu 1. Trong mặt phẳng Oxy , cho đường tròn (C) (x − )2 + ( y − )2 : 3
1 =10. Phương trình tiếp tuyến
của (C) tại điểm A(4;4) là
A. x −3y + 5 = 0 .
B. x + 3y −16 = 0 .
C. x + 3y − 4 = 0.
D. x −3y +16 = 0 .
Câu 2. Cho ΔABC có BC =12, AC =15 ,góc  0
C = 60 .Khi đó độ dài cạnh AB là:
A. AB = 6 21
B. AB = 3 21
C. AB = 6 7
D. AB = 3 7 (
 x + 5)(6 − x) > 0
Câu 3. Giải hệ bất phương trình  . 2x +1< 3 A. 5
− < x <1. B. x > 5 − . C. x < 5 − .
D. x <1.
Câu 4. Cho đường tròn (C) (x − )2 + ( y + )2 : 1
3 =10 và đường thẳng ∆ : x + y +1 = 0 biết đường thẳng
∆ cắt (C) tại hai điểm phân biệt A , B . Độ dài đoạn thẳng AB bằng A. 19 . B. 19 . C. 38 . D. 38 . 2 2 2
Câu 5. Chọn khẳng định đúng?
A. sin(π −α ) = −sinα .
B. tan(π −α ) = tanα .
C. cot(π −α ) = cotα .
D. cos(π −α ) = −cosα .
Câu 6. Phương trình nào sau đây là phương trình đường tròn? A. 2 2
4x + y −10x + 4y − 2 = 0 . B. 2 2
x + y − 4x −8y +1 = 0 . C. 2 2
x + 2y − 4x + 6y −1 = 0 . D. 2 2
x + y − 2x −8y + 20 = 0 . Câu 7.  Đường thẳng đi qua ( A 1;
− 2), nhận n = (2; 4
− ) làm vec tơ pháp tuyến có phương trình là:
A. −x + 2y − 4 = 0.
B. x − 2y − 4 = 0.
C. x − 2y + 5 = 0.
D. x + y + 4 = 0.
Câu 8. Phương trình chính tắc của (E) có 5c = 4a , độ dài trục nhỏ bằng 12 là 2 2 2 2 2 2 2 2 A. x y + =1. B. x y + =1. C. x y + =1. D. x y + =1. 100 36 36 25 64 36 25 36
Câu 9. Cung có số đo 250° thì có số đo theo đơn vị là radian là A. 35π . B. 25π . C. 25π . D. 25π . 18 18 12 9
Câu 10. Giải bất phương trình 2x −1≥ 0 . Kết quả tập nghiệm nào sau đây là đúng? A.  1 1   1   1  S = −∞  ;  B. S = ;+∞   C. S = −∞  ;  D. S = − ;+∞    2 2   2   2  Trang 1/4 - Mã đề 158 Câu 11. Cho 3
sinα = . Khi đó, cos 2α bằng 4 A. 1 . B. 7 . C. 1 − . D. 7 − . 8 4 8 4
Câu 12. Tam thức bậc hai f (x) 2
= x −12x −13 nhận giá trị không âm khi và chỉ khi A. x∈( 1; − 13) . B. x∈ \[ 1; − 1 ] 3 . C. x∈[ 1; − 1 ] 3 . D. x∈( ; −∞ − ] 1 ∪[13;+∞).
Câu 13. Đường thẳng ∆ :3x − 2y − 7 = 0 cắt đường thẳng nào sau đây?
A. d :3x + 2y = 0 .
B. d :6x − 4y −14 = 0 . 1 4 C. d : 3
− x + 2y − 7 = 0 .
D. d :3x − 2y = 0. 3 2
Câu 14. Trong tam giác ABC , đẳng thức nào dưới đây luôn đúng?
A. cos A = sin B . B.  π tan A cot B  = +  . 2   
C. cos A+ B = sin C .
D. sin( A+ B) = cosC . 2 2
Câu 15. Chọn điểm A(1;0)làm điểm đầu của cung lượng giác trên đường tròn lượng giác. Tìm điểm cuối π
M của cung lượng giác có số đo 25 . 4
A. M là điểm chính giữa của cung phần tư thứ I .
B. M là điểm chính giữa của cung phần tư thứ IV .
C. M là điểm chính giữa của cung phần tư thứ III .
D. M là điểm chính giữa của cung phần tư thứ II .
Câu 16. Cho đường thẳng d : x − 2y −3 = 0. Tìm tọa độ hình chiếu vuông góc H của điểm M ( 0; ) 1
trên đường thẳng. A. H ( 5; ) 1 . B. H ( 1;− ) 1 .
C. H ( −1;2) .
D. H ( 3;0) . Câu 17. Cho 3 π
sinα = và < α < π . Tính giá trị cosα . 5 2 A. 4 . B. 16 . C. 4 ± . D. 4 − . 5 25 5 5
Câu 18. Trên đường tròn bán kính R = 6 , cung 60° có độ dài bằng bao nhiêu?
A. l = 2π .
B. l = 4π . C. π l = .
D. l = π . 2
Câu 19. Cho hai đường thẳng d : x − y − 2 = 0 và d : 2x + 3y + 3 = 0. Góc tạo bởi đường thẳng d và 1 2 1
d là ( chọn kết quả gần đúng nhất) 2 A. 101 19 ° ′ . B. 78 41 ° ′ . C. 11 19 ° ′ . D. 78 31 ° ′ .
Câu 20. Cho tam giác ABC có độ dài ba cạnh là AB = 2 , BC = 3, CA = 4 . Tính độ dài đường trung
tuyến MA, với M là trung điểm của BC . A. 31 . B. 23 . C. 31 . D. 5 . 4 2 2 2 Trang 2/4 - Mã đề 158
Câu 21. Tìm một vectơ chỉ phương của đường thẳng x = 1 − + 2t d :  . y = 3 − 5t     A. u = ( 3 − ; ) 1 .
B. u = (5;2) . C. u = (2; 5 − ) . D. u = ( 1; − 3) .
Câu 22. Cung nào sau đây có điểm cuối trùng với B’. π π A. k2π
B. − + k2π
C. π + kπ
D. + k2π 2 2
Câu 23. Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d :x − 2y +1= 0 và điểm M (2;3).
Phương trình đường thẳng ∆ đi qua điểm M và vuông góc với đường thẳng d là
A. x + 2y −8 = 0.
B. 2x + y − 7 = 0 .
C. 2x − y −1= 0 .
D. x − 2y + 4 = 0 . 3
x − 4y +12 ≥ 0
Câu 24. Miền nghiệm của hệ bất phương trình: x + y −5 ≥ 0 x +1>  0
Là miền chứa điểm nào trong các điểm sau?
A. M (1;−3)
B. N (4;3) C. P ( 1; − 5) D. Q ( 2 − ; 3 − )
Câu 25. Phương trình chính tắc của (E) có độ dài trục lớn bằng 8, trục nhỏ bằng 6 là 2 2 2 2 2 2 A. x y + =1. B. 2 2
9x +16y =1. C. x y + = 1. D. x y + =1. 16 9 9 16 64 36
Câu 26. Cho góc α thỏa mãn và π < α < π . Tính sinα + 2cosα = 1
− . Tính giá trị sin 2α . 2 A. 2 6 . B. 24 . C. 2 6 − . D. 24 − . 5 25 5 25
Câu 27. Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9kg chất
B . Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6kg
chất B . Từ mỗi tấn nguyên liệu loại II giá 3,5 triệu đồng, có thể chiết suất được 10kg chất A và 1,5kg
chất B . Hỏi chi phí mua nguyên vật liệu ít nhất bằng bao nhiêu, biết rằng cơ sở cung cấp nguyên
liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II?
A. 47 triệu đồng.
B. 34 triệu đồng.
C. 31,5 triệu đồng
D. 31 triệu đồng. 2
Câu 28. Cho tam giác ABC thỏa mãn tan B sin B = thì: 2 tan C sin C
A. Tam giác ABC vuông.
B. Tam giác ABC cân.
C. Tam giác ABC đều.
D. Tam giác ABC vuông hoặc cân.
Câu 29. Cho các góc α , β thỏa mãn π < α , β < π , 1 sinα = , 2
cos β = − . Tính sin (α + β ) . 2 3 3 A. (α − + β ) 5 + 4 2 sin = . B. (α + β ) 5 4 2 sin = . 9 9 C. (α + + β ) 2 10 − 2 sin = . D. (α + β ) 2 2 10 sin = − . 9 9 Trang 3/4 - Mã đề 158
Câu 30. Biết d là đường thẳng đi qua điểm A(1; 2) và cắt tia Ox,Oy thứ tự tại M( ;
m 0), N(0; n) sao
cho tam giác OMN có diện tích nhỏ nhất. Khi đó tổng m + n = ? A. 1. B. 3. C. 4. D. 6.
Câu 31. Biểu thức:  π A (α π ) (α π ) 2003 cos 26 2sin 7 cos1,5π cos α  = + − − − − +
+ cos(α −1,5π ).cot (α −   8π )  2 
có kết quả thu gọn bằng: A. −cosα . B. −sinα . C. sinα . D. cosα .
Câu 32. Bất phương trình 2x + 7 <1 có bao nhiêu nghiệm nguyên dương? x − 4 A. 4 . B. 3. C. 14. D. 0 .
Câu 33. Điều kiện của bất phương trình 2x + 3 2
+ 2x − 3x +1 > 0 là: 5 − xx ≥ 1 1  ≤ x ≤ 5 1  ≤ x < 5 1  ≤ x < 5 A.   1 B. C. D.   x ≤ 1 x ≤ 1 x ≤ 1 x ≤  2  2  2  2
Câu 34. Tìm m để (m + ) 2
1 x + mx + m < 0; x ∀ ∈  ? A. m > 1 − . B. 4 m > . C. 4 m < − . D. m < 1 − . 3 3
Câu 35. Tìm tất cả các giá trị thực của tham số m để phương trình 2 x + 2(m + )
1 x + 9m − 5 = 0 có hai nghiệm âm phân biệt?
A. m < 6.
B. 5 < m <1 hoặc m > 6. 9
C. 1< m < 6 .
D. m >1.
II. PHẦN TỰ LUẬN (3 ĐIỂM)
Câu 36. (1đ) a) Giải bất phương trình sau 1−3x ≤ 7;
b) Bằng cách lập bảng xét dấu, giải bất phương trình (2x −1)(3− x) > 0. 2 x − 5x + 4 Câu 37. (1đ) a) Cho 2  π cos a , α π  = − < <  . Tính sinα . 3  2 
b) Trong mặt phẳng với hệ tọa độ Oxy , viết phương trình của đường thẳng d biết d vuông góc
với đường thẳng ∆ : 2x − y +1= 0 và cắt đường tròn 2 2
(C) : x + y + 2x − 4y − 4 = 0 theo một dây cung có độ dài bằng 6.
Câu 38. (1đ) Giải phương trình: 10 −9 −1 + 4 − 14 −1 x x x = . x
-------------- HẾT -------------- Trang 4/4 - Mã đề 158
ĐÁP ÁN CÁC MÃ ĐỀ
------------------------ Mã đề [158] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 B B A D D B C A B B C D A C A B D A 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B C C B B B A D B D D D C B C C B Mã đề [291] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 C D A A B A B B C B B B B D A C B B 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 D B D C C C C C D D D D D A D D A Mã đề [348] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 B C C D C A B B C A D B C D A B C D 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 A A A C D A D D A C D C B B B C A Mã đề [470] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 B C C A D B D B D D D B B C C A D D 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B D B A B C A C A C C B A A D B D
Lời giải phần tự luận Câu 36.
a) Giải bất phương trình sau 1 3x  7 ;
+) Ta có 13x  7  7
 13x  7 (0,25đ) 8  8   3
x  6   x  2  (0,25đ) 3
(2x 1)(3  x)
b) Bằng cách lập bảng xét dấu, giải bất phương trình  0. 2 x  5x  4 Bảng xét dấu: 1 x  1 3 4  2 2x 1  0  |  |  |  3  x  |  |  0 - | -  0  2
x  5x  4 + | + 0 - | - 0 + VT  0  || - 0 + || -
Lập được bảng xét dấu đúng (0,25đ)  1 
Vậy tập nghiệm của bất phương trình là S  ; 1    3; 4 .(0,25đ)  2  Câu 37. (1đ) 2    a) Cho cos a   ,     .   Tính sin . 3  2  1 2   +) Ta có 2 5 5 2 sin   1    sin  .   (0,25đ)  3  9 3  +) Vì     5
nên sin  0  sin  . (0,25đ) 2 3
b) Trong mặt phẳng với hệ tọa độ Oxy , viết phương trình của đường thẳng d biết d vuông góc với
đường thẳng  : 2x y 1  0 và cắt đường tròn 2 2
(C) : x y  2x  4y  4  0 theo một dây cung có độ dài bằng 6. Hướng dẫn giải: I d B H A
+) Đường tròn có tâm I  1
 ;2, bán kính R  3 nên ta có 2 2 2 2 2
IH R HB  3  3  0  I H .(0,25đ)
+) Đường thẳng d vuông góc với  nên có phương trình dạng x  2y c  0 .
d qua điểm I. Suy ra 1
  2.2 c  0  c  3
 . Vậy d : x  2y  3  0. (0,25đ) 10x  9 
Câu 38. (1đ) Giải phương trình: 1
x  4  14x 1  . x Hướng dẫn giải +) ĐKXĐ: 9 x (0,25đ) 10
Với ĐKXĐ, phương trình tương đương với: 2
x  4x x 14x 1  10x 9 1 0  (
x x  3)  x 14x 1  (x 1)  10x  9  0
x (x 3)  14x 1   (x 1)  10x 9  0   (0,25đ) 2 2
x  6x 9 14x 1 x  2x 110x 9  x     0
x  3 14x 1  
x 1 10x  9     x 1  2
x  8x 10     0 (0,25đ)
x  3 14x 1
x 1 10x  9   (vì 9 x x  nên  0 và 1  0) 2
x 8x 10  0 10
x  3  14x 1
x 1 10x  9
x  4 6 (thỏa mãn ĐKXĐ).
Vậy phương trình có tập nghiệm S  4 6; 4 6 (0,25đ).
CÂU HỎI TRẮC NGHIỆM x  1   2t 2 2 Câu 1. x y
Tìm một vectơ chỉ phương của đường thẳng d :  u  2; 5    1. y  3 5t 9 16 A. .
B. u  5; 2 . C. u   1  ;3. D. u   3  ;  1 . Hướng dẫn giải Chọn A.
Một vectơ chỉ phương của đường thẳng d là u  2; 5   .
Câu 2. Hướng dẫn giải bất phương trình 2x 1 0 . Kết quả tập nghiệm nào sau đây là đúng? 2  1   1  1   1 A. S = ;
B. S =  ;  C. S = ; D. S = ;          2   2  2   2
Câu 3. Phương trình chính tắc của E có độ dài trục lớn bằng 8 , trục nhỏ bằng 6 là 2 2 x y 2 2 x y A.  1. B. . C. 2 2
9x 16y  1. D.  1. 64 36 16 9 Hướng dẫn giải Chọn B. 2a  8 a  4 Ta có:    . 2b  6 b   3 2 2 x y
Vậy phương trình chính tắc của  E  :  1 16 9
Câu 4. Chọn điểm A1;0làm điểm đầu của cung lượng giác trên đường tròn lượng giác. Tìm điểm 
cuối M của cung lượng giác có số đo 25 . 4
A. M là điểm chính giữa của cung phần tư thứ I .
B. M là điểm chính giữa của cung phần tư thứ II .
C. M là điểm chính giữa của cung phần tư thứ III .
D. M là điểm chính giữa của cung phần tư thứ IV . Hướng dẫn giải Chọn A.   Theo giả thiết ta có: 25 AM
  6 , suy ra điểm M là điểm chính giữa của cung phần tư thứ 4 4 3
x  4y 12  0 
Câu 5. Miền nghiệm của hệ bất phương trình: x y  5  0 x 1 0 
Là miền chứa điểm nào trong các điểm sau? A. P  1  ;5
B. N 4;3 C. Q  2  ; 3  
D. M 1; 3
Câu 6. Tam thức bậc hai f x 2
x 12x 13 nhận giá trị không âm khi và chỉ khi A. x  \  1  ;1  3 . B. x  1  ;1 
3 . C. x  ;    1 13;  . D. x  1  ;13 .
Câu 7. Cung có số đo 250 thì có số đo theo đơn vị là radian là 25 25 25 35 A. . B. . C. . D. . 12 18 9 18 Hướng dẫn giải Chọn B.   Ta có: 25 250  .250  . 180 18
Câu 8. Cung nào sau đây có điểm cuối trùng với B’.   A.   k2
B. k 2 C. k2 D.   k 2 2
Câu 9. Trên đường tròn bán kính R  6 , cung 60 có độ dài bằng bao nhiêu? A. l  .
B. l  4 .
C. l  2 . D. l   . 2 Hướng dẫn giải Chọn C.  60  rad. 3
Ta có: cung có số đo  rad của đường tròn có bán kính R có độ dài l R . 3 
Do đó cung 60 có độ dài bằng l  6.  2 . 3
Câu 10. Chọn khẳng định đúng?
A. tan     tan .
B. sin     sin .
C. cot     cot .
D. cos     cos . Hướng dẫn giải Chọn D.
tan     tan sai vì tan      tan ; sin     sin sai vì sin     sin ;
cot     cot sai vì cot      cot .
Câu 11. Trong tam giác ABC , đẳng thức nào dưới đây luôn đúng?
A. sin  A B  cosC .
B. cos A  sin B .    A B C
C. tan A  cot B    . D. cos  sin .  2  2 2 Hướng dẫn giải Chọn D.     Ta có A B C C cos  cos   sin   2  2 2  . 2  Câu 1 3 2. Cho sin   và
    . Tính giá trị cos . 5 2 16 4 4 4 A. . B. . C.  . D.  . 25 5 5 5 Hướng dẫn giải Chọn D.  Với     thì 4 2
cos   1 sin    . 2 5 Câu 13. 3 Cho sin  . Khi đó, cos 2 bằng 4 1 7 7 1 A.  . B. . C.  . D. . 8 4 4 8 Hướng dẫn giải Chọn A. 2 3 1 2 cos 2 1 2sin      1 2.     .  4  8
Câu 14. Phương trình chính tắc của E có 5c  4a , độ dài trục nhỏ bằng 12 là 2 2 x y 2 2 x y 2 2 x y 2 2 x y A.  1. B.  1. C.  1. D.  1. 25 36 64 36 100 36 36 25 Hướng dẫn giải Chọn C.  4 e  5  c  4a 2 2 25c 16a   2 2 a b  2 25 16aa 10 Ta có:  5         .  b   6   b   6  b 6   2b  12 b 6 2 2 x y
Vậy phương trình của  E  :  1. 100 36
Câu 15. Cho ΔABC có BC 12, AC 15 ,góc 0
C  60 .Khi đó độ dài cạnh AB là:
A. AB  6 7
B. AB  3 7
C. AB  3 21 D. AB  6 21 4
Câu 16. Cho tam giác ABC có độ dài ba cạnh là AB  2 , BC  3, CA  4 . Tính độ dài đường trung
tuyến MA , với M là trung điểm của BC . 5 31 23 31 A. . B. . C. . D. . 2 2 2 4
Câu 17. Đường thẳng đi qua ( A 1
 ;2), nhận n  (2; 4
 ) làm vec tơ pháp tuyến có phương trình là:
A. x  2y  4  0.
B. x  2y  4  0.
C. x  2y  5  0.
D. x y  4  0. Hướng dẫn giải. Chọn C.
Phương trình đường thẳng cần tìm là: 2(x 1)  4(y  2)  0
 2x  4y 10  0  x  2y 5  0.
Câu 18. Trong mặt phẳng với hệ tọa độ Oxy cho đường thẳng d :x  2y 1  0 và điểm M 2;3 .
Phương trình đường thẳng  đi qua điểm M và vuông góc với đường thẳng d là
A. x  2y  8  0 .
B. x  2y  4  0 .
C. 2x y 1  0 .
D. 2x y  7  0 . Hướng dẫn giải Chọn D.
 vuông góc d :x  2y 1  0   có VTPT là n  2  ;1 .
 qua M 2;3 nên có phương trình là 2x  2  y 3  0  2x y 7  0 .
Câu 19. Đường thẳng  : 3x  2y  7  0 cắt đường thẳng nào sau đây?
A. d : 3x  2y  0 .
B. d : 3x  2y  0 . 1 2 C. d : 3
x  2y  7  0. D. d : 6x  4y 14  0 . 3 4 Hướng dẫn giải Chọn A.
Xét đường thẳng  : 3x  2y  7  0 và d : 3x  2y  0 có 3 2  . Vậy  cắt d . 1 3 2 1
Câu 20. Cho hai đường thẳng d : x y  2  0 và d : 2x  3y  3  0 . Góc tạo bởi đường thẳng d 1 2 1
và d là ( chọn kết quả gần đúng nhất) 2 A. 11 1  9 . B. 78 4  1 . C. 101 1  9 . D. 78 3  1 . Hướng dẫn giải Chọn B.
d : x y  2  0 có 1 vectơ pháp tuyến là n  1; 1 . 1   1
d : 2x  3y  3  0 có 1 vectơ pháp tuyến là n  2;3 . 2   2
Gọi góc tạo bởi đường thẳng d và d là  . 1 2 n .n 2  3 Ta có 1 2 26 cos      78 4  1. n . n 1   2 2 2 2  26 1 2 1 . 2 3
Câu 21. Phương trình nào sau đây là phương trình đường tròn? A. 2 2
x y  4x  8y 1  0 . B. 2 2
4x y 10x  4y  2  0 . C. 2 2
x y  2x  8y  20  0 . D. 2 2
x  2y  4x  6y 1  0 . Hướng dẫn giải Chọn A.
Xét phương trình C: 2 2
x y  4x  8y 1  0 . Ta có: 2 2 2 2
a b c  2  4 1  19  0.
Vậy C  là phương trình đường tròn.
Câu 22. Cho đường thẳng d : x  2y 3  0. Tìm tọa độ hình chiếu vuông góc H của điểm M  0;  1 trên đường thẳng.
A. H  1;2 . B. H  5;  1 .
C. H  3;0 .
D. H  1;   1 . Hướng dẫn giải 5 Chọn D.
  d   : 2x y m  0 , mà M  0; 
1  : 2.0 1 m  0  m  1
   : 2x y 1 0 .
2x y 1  0 x 1
Tọa độ điểm H là nghiệm của hệ:   
. Vậy H  1; 1 .
x  2y  3  0 y  1  Câu 23. 2 2
Trong mặt phẳng Oxy , cho đường tròn C :  x  3   y   1
10. Phương trình tiếp tuyến của
C tại điểm A4;4 là
A. x  3y 16  0 .
B. x  3y  4  0 .
C. x  3y  5  0 .
D. x  3y 16  0 . Hướng dẫn giải Chọn A.
Đường tròn C có tâm I 3 
;1 . Điểm A4; 4 thuộc đường tròn.
Tiếp tuyến của C  tại điểm A4; 4 có véctơ pháp tuyến là IA  1;3 nên tiếp tuyến d có phương
trình dạng x  3y c  0 .
d đi qua A4;4 nên 4  3.4  c  0  c  1  6.
Vậy phương trình của d : x  3y 16  0 . Câu 24. 2 2
Cho đường tròn C : x  
1   y  3 10 và đường thẳng  : x y 1  0 biết đường thẳng
 cắt C tại hai điểm phân biệt A , B . Độ dài đoạn thẳng AB bằng 19 19 38 A. . B. 38 . C. . D. . 2 2 2 Hướng dẫn giải Chọn B.
Đường tròn C có tâm I 1; 3
  và bán kính R IA  10 .
Gọi H là trung điểm dây cung AB. 1 3 1 Ta có: 1 IH d   . I ; 11 2 1 38
Tam giác AIH vuông tại H nên AH  10   . 2 2
Độ dài đoạn thẳng AB  2AH  38 . 
 x  56  x  0
Câu 25. Hướng dẫn giải hệ bất phương trình  . 2x 1 3 A. 5   x 1.
B. x  1. C. x  5  . D. x  5  . Hướng dẫn giải Chọn A.   x  5 
6 x  0   1  . 2x 1 3  2
+) bất phương trình  
1 có tập nghiệm S  5  ;6 . 1  
+) bất phương trình 2 : x 1 bất phương trình 2 có tập nghiệm S   ;1  . 2  
Vậy tập nghiệm của hệ đã cho là S S S  5  ;1 . 1 2    Câu 26. x
Bất phương trình 2
7 1 có bao nhiêu nghiệm nguyên dương? x  4 A. 14 . B. 3 . C. 0 . D. 4 . Hướng dẫn giải Chọn B. 2x  7 x 11 1   0  1  1 x  4 . x  4 x  4 6
Vậy bất phương trình đã cho có 3 nghiệm nguyên dương lần lượt là 1;2;  3 .
Câu 27. Tìm m để m   2
1 x mx m  0; x   ? 4 4 A. m  . B. m  1  . C. m   . D. m  1  . 3 3 Hướng dẫn giải Chọn C.
Đặt f x  m   2
1 x mx m
Xét m 1 0  m  1
 khi đó f x  x 1 0  x  1
  không thỏa mãn yêu cầu bài toán m 1 0 
Xét m 1 0  m  1
 khi đó f x  0, x     2
  m  4m  m 1  0 m  1  m 1 0     4 4 
  m    m   . m
 3m  4  0 3  3 m  0
Câu 28. Tìm tất cả các giá trị thực của tham số m để phương trình 2
x  2m  
1 x  9m  5  0 có hai
nghiệm âm phân biệt? 5 A.
m 1 hoặc m  6. B. 1 m  6 . 9
C. m  6 . D. m  1. Hướng dẫn giải Chọn A.  m  6   0  2
m  7m  6  0  m 1    5   m 1
Phương trình có hai nghiệm phân biệ b
t khi   0  m 1  0  m  1   9 . a     9m  5  0    5 m 6 c   m  0   9 a  
Câu 29. Cho góc  thỏa mãn và
    . Tính sin  2cos  1
 . Tính giá trị sin 2 . 2 24 2 6 24 2 6 A.  . B.  . C. . D. . 25 5 25 5 Hướng dẫn giải Chọn A. sin  2cos  1   sin  1   2cos . Ta có cos  0 
sin   cos   1  cos    1   2cos 2 2 2 2 2
1  5cos   4cos  0  4  cos    5  Vì  thỏa mãn     nên 4 3 cos    sin  . 2 5 5
Do đó, sin 2  2sin.cos  24  25  Câu 30. 2x 3
Điều kiện của bất phương trình 2
 2x  3x 1  0 là: 5  x 7 1   x  5 x  1 1   x  5 1   x  5  A.    1  B. 1 C. 1 D.  1 x  x  x x    2  2  2  2 Hướng dẫn giải: x  5  1   x  5 5   x  0  
Hàm số xác định khi và chỉ khi x 1      1 . 2 
2x  3x 1  0  1    x x    2  2
Câu 31. Biểu thức:    A          2003 cos 26 2sin 7  cos1,5  cos    cos  
 1,5 .cot 8   2 
có kết quả thu gọn bằng: A. cos . B. cos . C. sin . D. sin . Hướng dẫn giải Chọn D. Biểu thức    A          2003 cos 26 2sin 7  cos1,5  cos    cos  
 1,5 .cot 8   2 
 cos  2sin   0cos 1,5   cos 1,5 .cot  cos  2sin sin sin.cot
 cos  2sin sin cos  sin .  Câu 32. 1 2
Cho các góc  ,  thỏa mãn
  ,    , sin  , cos    . Tính sin     . 2 3 3   A.     2 2 10 sin   . B.     2 10 2 sin  . 9 9   C.     5 4 2 sin  . D.     5 4 2 sin  . 9 9 Hướng dẫn giải Chọn A.  cos  0 Do   ,      . 2 s  in   0 1 2 2 4 5 Ta có 2
cos   1 sin    1   . 2
sin   1 cos   1  . 9 3 9 3      Suy ra     1 2 2 2 5 2 2 10 sin
 sin.cos   cos.sin   .      .     . 3  3  3 3 9    Vậy     2 2 10 sin   . 9
Câu 33. Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9kg chất B. Từ
mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6kg chất B. Từ mỗi
tấn nguyên liệu loại II giá 3,5 triệu đồng, có thể chiết suất được 10kg chất A và 1,5kg chất B. Hỏi chi phí
mua nguyên vật liệu ít nhất bằng bao nhiêu, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp
không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II?
A. 31 triệu đồng
B. 31,5 triệu đồng
C. 34 triệu đồng. D. 47 triệu đồng. Hướng dẫn giải Chọn C.
+) Gọi x , y lần lượt là số tấn nguyên liệu loại I và loại II cần dùng. Điều kiện x , y nguyên dương.
+) Với x tấn nguyên liệu loại I và y tấn nguyên liệu loại II, sản xuất được 20x 10 y kg chất A và
0, 6x 1,5y kg chất B.
+) Số tiền để mua x tấn loại I và y tấn loại II là L  ;
x y  4x  3,5y . 8
20x 10y  140
2x y 14  
0,6x 1,5y  9
2x  5y  30
Theo giả thiết ta có hệ:    0  x  10  0  x  10  0  y  9 0  y  9
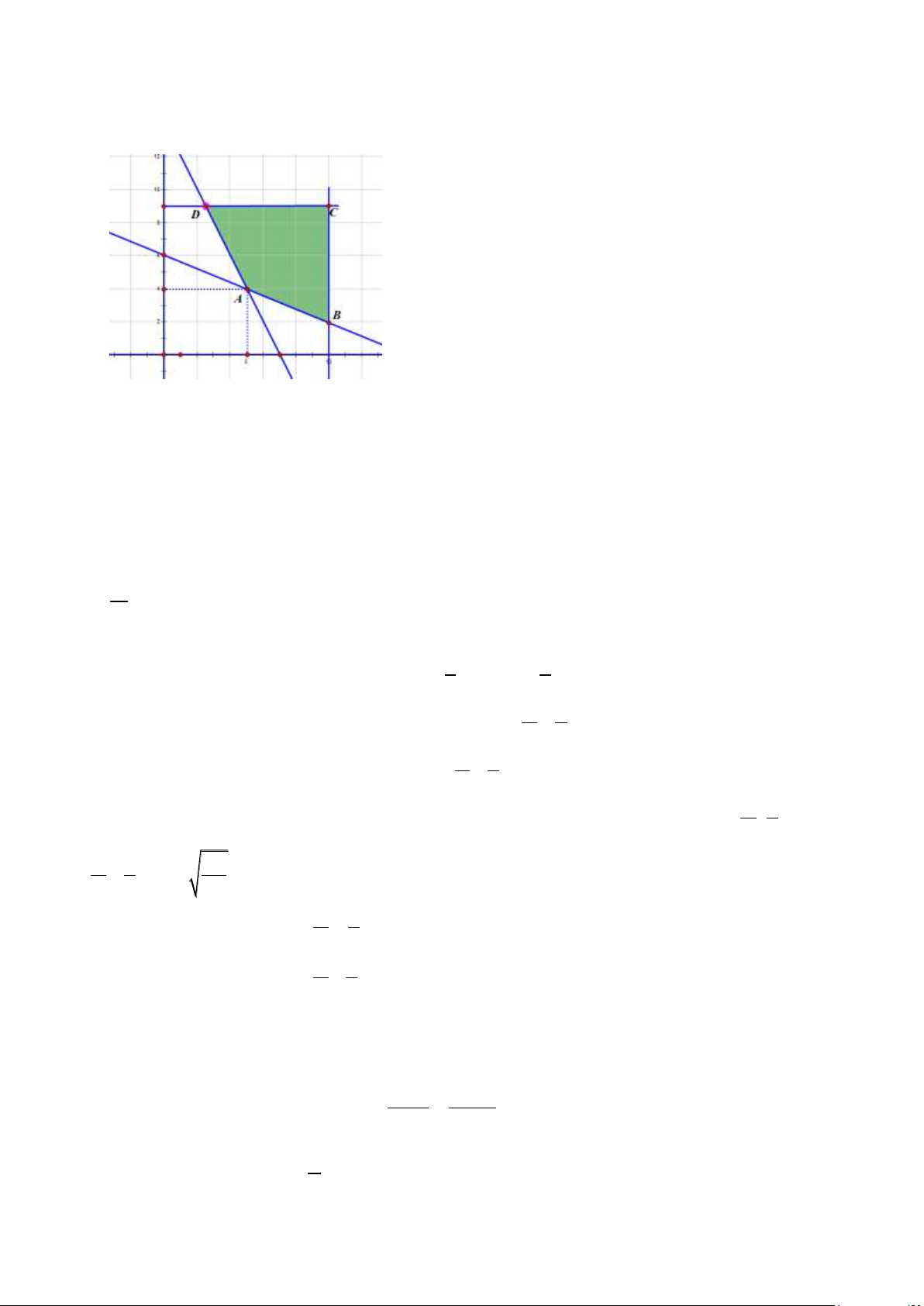
Miền nghiệm của hệ trên là
+) Miền nghiệm là tứ giác ABCD với A(5; 4), B(10; 2) C(10; 9) và D(5/2; 9).
+) L A  20 14  34 ; LB  40  7  47 ;
L B  40  31,5  71,5
L D 10  31,5  41,5
Tại A(5; 4) thì L  34 triệu đồng.
Câu 34. Biết d O
là đường thẳng đi qua điểm A(1; 2) và cắt tia ,
x Oy thứ tự tại M ( ; m 0), N(0; ) n sao
cho tam giác OMN có diện tích nhỏ nhất. Khi đó tổng m n  ? A. 6. B. 3. C. 4. D. 1. Hướng dẫn giải: +) Gọi M ( ; m 0), N(0; )
n thì m  0 và n  0
+) Tam giác OMN vuông ở O nên 1 1 S
OM.ON mn O  MN 2 2 +) Đườ x y
ng thẳng d c ng đi qua hai điểm M , N nên d :  1 m n
Do đường thẳng d đi qua điểm A nên ta có: 1 2  1 m n
p dụng BĐT giữa trung bình cộng và trung bình nhân (BĐT Côsi) cho 2 số dương 1 2 , ta có +) m n 1 2 2  1 2
 0  mn  8 , dẫn đến S  4 O  MN m n mn  1 2  m n   1 2 m  2 S  4       O 1  MN khi và chỉ khi  . Vậy m n 6 . m n  n  4 m  0  n  0 2 Câu 35. tan B sin B
Cho tam giác ABC thỏa mãn  thì: 2 tan C sin C
A. Tam giác ABC cân. B. Tam giác ABC vuông.
C. Tam giác ABC đều. D. Tam giác ABC vuông hoặc cân. Hướng dẫn giải 9 2 +) Ta có tan B sin B sin B sin C 2 2 2 2 
 tan Bsin C  sin B tan C  sin C  sin B 2 tan C sin C co B s cos C sin C sin B  
 sin C cosC  sin Bco B
s  sin 2C  sin 2B co B s cosC
 sin 2B sin 2C  0  2cos(B C)sin(B C)  0 0
cos(B C)  0
B C  90     0
sin(B C)  0
B C  0 . Vậy tam giác ABC vuông hoặc cân tại A.
---------- HẾT ---------- 10
Document Outline

  • Made 158
  • Dap an TN và TL mon toan hk 2 lop 10 2018 2019