Đề thi HK2 Toán 10 năm học 2016 – 2017 trường THPT Đầm Dơi – Cà Mau

SỞ GD&ĐT CÀ MAU
KỲ THI HỌC KỲ II - NĂM HỌC 2016 - 2017
TRƯỜNG THPT ĐẦM DƠI Môn: TOÁN 10
Thời gian làm bài: 90 phút, không kể thời gian giao đề (Đề có 3 trang) Mã đề 121
Họ tên :...................................................... Số báo danh : ...............
I. PHẦN TRẮC NGHIỆM (20 câu; 4,0 điểm).
Câu 1: Tìm giá trị của tham số m để phương trình 2
x  3mx  m  5  0 có nghiệm x  2  . 1 1 A. m   . B. m  . C. m  5 . D. m  5  . 5 5
Câu 2: Tìm tập nghiệm S của bất phương trình (x  2)(x  3)  0 . A. S  ( ;  3  )  (2;) . B. S  ( 3  ;2) .
C. S  3;2.
D. S   ;    3 2; .
Câu 3: Cho tam giác ABC có 1 a  5c ,
m c  9c , m cosC  
. Tính độ dài đường cao h hạ từ 10 a
A của tam giác ABC . A. 462 h  cm . B. 462 h  cm . a 40 a 10 21 11 21 11 C. h  cm . D. h  cm . a 40 a 10 4 3
Câu 4: Cho sin x   với   x 
. Tính giá trị của biểu thức P  cos x  sin x . 5 2 A. 11 P   . B. 9 P   . C. 1 P   . D. 7 P   . 25 25 5 5
Câu 5: Tìm tập nghiệm T của bất phương trình 2
x  3x  4  x  2 . 7  7  7 A.    T  ; 4  .
B. T   ;
 24; . C. T   ;  4; 
. D. T  2; . 2    2     2  
Câu 6: Tìm tập hợp các giá trị của tham số m để phương trình 2
x  2(m  2)x  m 14  0 vô nghiệm. A.  2;  5 . B. ( ;  2  )  (5;) . C. ( 2  ;7) . D.  ;
 27;. Trang 1/3 - Mã đề 121
Câu 7: Tìm tập các giá trị của tham số m để phương trình 2x  x  3  m  0 có nghiệm. 47 47 47 A. m  6 . B.  m  6 . C. m  . D.  m  6 . 8 8 8
Câu 8: Tìm tập hợp các giá trị của x để bất phương trình 2 2
(x  3) x  4  x  9 vô nghiệm.  5  5  5 A.     3;  B.   3;   . C. ;     D.  ;3   . 6     6   6  x  2  t
Câu 9: Trong mặt phẳng với hệ tọa độ Oxy , cho 2 đường thẳng d :  (t  ) , 1 y  3  t
d : 2x  y  5  0 . Tìm tọa độ giao điểm M của d và d . 2 1 2 A. M ( 1  ; 3  ). B. M (3;1) . C. M (1;3) . D. M (3; 3  ) . x  2   3t
Câu 10: Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng d :  (t  ) . Vectơ y  1 5t
nào dưới đây là vectơ chỉ phương của d ?     A. u  ( 2  ;1) . B. u  (3; 5  ) .
C. u  (1;2) .
D. u  (5;3) .
Câu 11: Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn (C) : 2 2
x  y  2x  2y  2  0 và
đường thẳng d : 3x  4y  4  0 . Tìm phương trình đường thẳng  song song với d cắt (C) tại 2 điểm ,
A B sao cho độ dài đoạn AB  2 3 .
A.  : 3x  4y  4  0 .
B.  : 4x  3y  6  0 .
C.  : 3x  4y  6  0 .
D.  : 4x  3y  6  0 .
Câu 12: Cho tam giác ABC có BC  a, AC  ,
b AB  c . Tìm khẳng định SAI. A. 2 2 2
c  a  b  2ab cosC . B. 2 2 2
b  a  c  2ac cos B . C. 2 2 2
a  b  c  2bc cos B . D. 2 2 2
a  b  c  2bc cos A. 1
Câu 13: Tìm điều kiện xác định bất phương trình 3 x   2  0 . x  2 A. x ( ;  2  ) 3; . B. x  2;  3. C. x  2;  3 . D. x  ;  2  3; .
Câu 14: Tìm tất cả các giá trị của tham số m để phương trình 2
x  2(m 1)x  m  2  0 có 2 nghiệm trái dấu. A. m  2 . B. m  1  . C. m  2 . D. m  1  .
Câu 15: Với điều kiện xác định. Tìm đẳng thức nào đúng ? 1 A. 2 1 cot x  . B. 2 2
sin x  cos x  1. 2 cos x 1
C. tan x  cot x  1. D. 2 1 tan x   . 2 sin x Trang 2/3 - Mã đề 121
Câu 16: Tìm tập nghiệm S của bất phương trình 2
x  4x  5  0 . A. S  ( ;  1
 )  (5;) . B. S  ( ;  5
 )  (1;) . C. S  ( 1  ;5) . D. S  ( 5  ;1) . 2  
Câu 17: Tìm tập nghiệm x 4x 3
S của bất phương trình  0 . x 1
A. S   ;    1 1;  3 . B. S   1;   1 3; . C. S  ( 1  ;1) 3; . D. S  ( ;  1  ) 1;  3 .
Câu 18: Cho tam thức 2
f (x)  (1 m)x  2(m 1)x  m  3. Tìm tập hợp các giá trị của tham số
m để bất phương trình f (x)  0 vô nghiệm. A. 1;2 . B. 2; . C.   ;1  . D. 1;2 .
Câu 19: Trong mặt phẳng với hệ tọa độ Oxy , cho 2 điểm ( A 1  ;1) , B(5; 3
 ) . Viết phương trình
đường tròn đường kính AB . A. 2 2
(x  2)  ( y 1)  13 . B. 2 2
(x  2)  ( y 1)  5 . C. 2 2
(x  2)  ( y 1)  13 . D. 2 2
(x  2)  ( y 1)  5 .
Câu 20: Cho tam giác ABC có  120o B 
, cạnh AC  2 3cm . Tìm bán kính R của đường tròn
ngoại tiếp tam giác ABC .
A. R  3cm .
B. R  1cm .
C. R  4cm .
D. R  2cm .
II. PHẦN TỰ LUẬN (6,0 điểm)
Câu 1 (1,5 điểm). Giải các bất phương trình sau: 2   a). 2(x 1) 1 1 2
(x  7x 12)(5  x)  0 , b).   0 . 2 x  x  6 2
Câu 2 (1,5 điểm). Cho phương trình 2
x  2(m  3)x  5  m  0 (*) với m là tham số.
a). Giải phương trình (*) khi m  1.
b). Tìm tất cả các giá trị của tham số m để phương trình (*) có 2 nghiệm phân biệt x , x 1 2
thỏa x  x 1. 1 2 8 
Câu 3 (1,0 điểm). Cho cos x   và  x   . Tính giá trị của sin x, cot . x 9 2
Câu 4 (2,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có đỉnh (1 A ; 2) và
phương trình đường trung tuyến BM : 2x  y 1  0 , M  AC .
a). Viết phương trình đường thẳng d qua A và vuông góc với đường thẳng BM .
b). Viết phương trình đường tròn (C) có tâm A và tiếp xúc với đường thẳng BM .
c). Tìm tọa độ điểm B , biết CD : x  y 1  0 là phương trình đường phân giác trong của góc C . ------ HẾT ------ Trang 3/3 - Mã đề 121
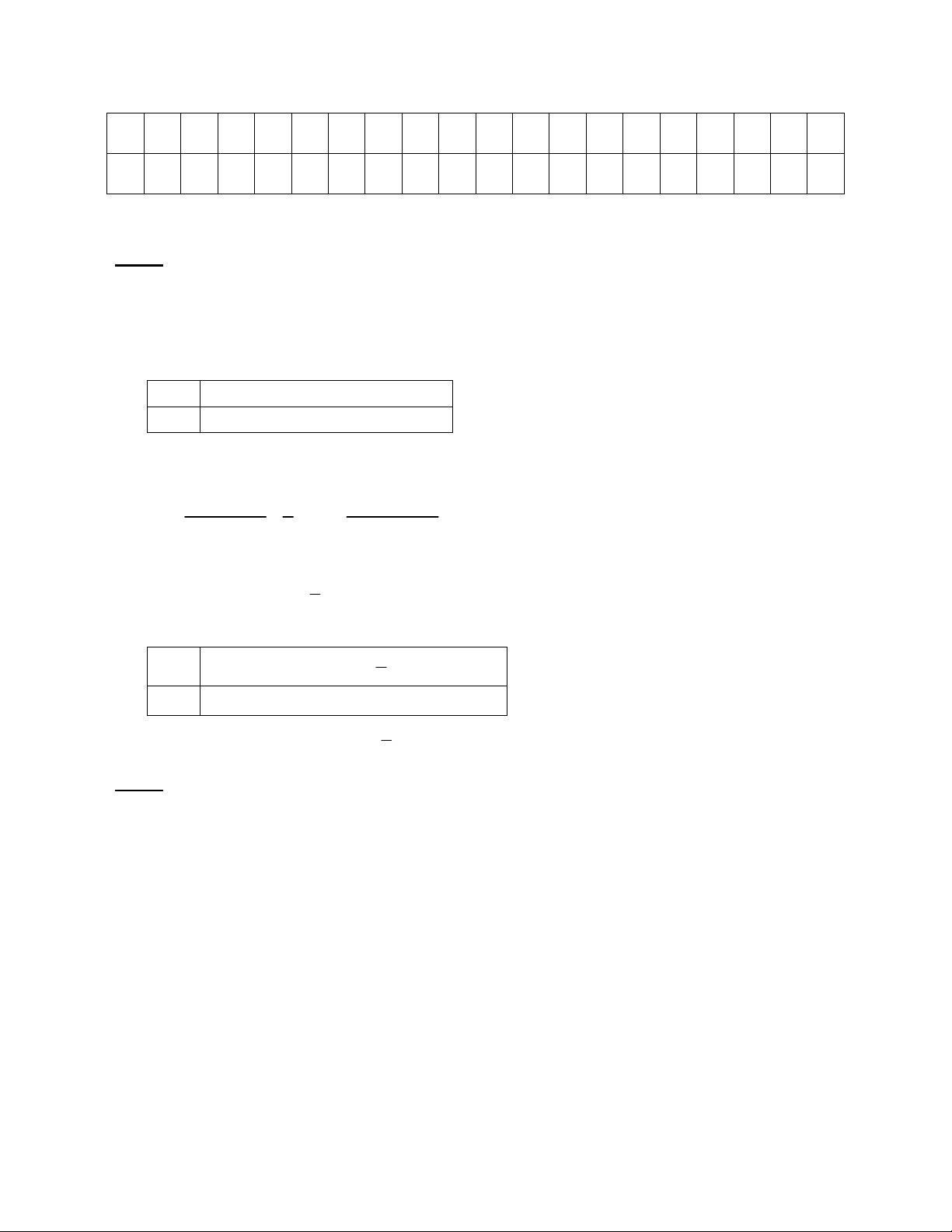
I. PHẦN TRẮC NGHIỆM (20 câu; 4,0 điểm). 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20
B D D D A A C D C B C C B C B C D A A D
II. PHẦN TỰ LUẬN (6,0 điểm)
Câu 1 (1,5 điểm). Giải các bất phương trình sau: a). 2
(x  7x 12)(5  x)  0 x  3 Ta có 2
x  7x 12  0  ; 
5  x  0  x  5 x  4 BXD : x  3 4 5  VT  0  0  0 
Vậy BPT có nghiệm: x  ;3   4;5 2 2    b). 2(x 1) 1 1 5x 9x   0   0. 2 2 x  x  6 2 2x  2x 12 x  0 x  3 Ta có 2 5x 9x 0     9 ; 2      2x 2x 12 0 x   x  2   5 BXD : x  2  0 9 3  5 VT
 ||  0  0  ||  Vậy BPT có nghiệm:   x   9 2;0  ;3   5 
Câu 2 (1,5 điểm). Cho phương trình 2
x  2(m  3)x  5  m  0 (*) với m là tham số.
a). Giải phương trình (*) khi m  1.
Khi m  1, ta có PT : 2
x  4x  4  0  x  2 
b). Tìm tất cả các giá trị của tham số m để phương trình (*) có 2 nghiệm phân biệt x , x 1 2
thỏa x  x 1. 1 2 Ta có / 2
  m  5m  4 m 1
Để PT có 2 nghiệm phân biệt / 2
   0  m  5m  4  0    1; m  4
x  x  2  0 
2(m  3)  2  0 Do 1 2
x  x  1    1 2 
x x  x  x 1  0 5 
  m  2(m  3) 1  0 1 2  1 2 2m  8  0    m  4 2  3  m 12  0 Trang 4/3 - Mã đề 121 Từ  
1 và 2 ta có m 1 thì PT có 2 nghiệm phân biệt x , x thỏa x  x 1. 1 2 1 2 
Câu 3 (1,0 điểm). Cho 8 cos x   và
 x   . Tính giá trị của sin x, cot . x 9 2 17  17 Ta có 2 2 2 2
sin x  cos x  1 sin x  1 cos x 
; Do  x    sin x  81 2 9 cos x 8 17 Mặt khác cot x    sin x 17
Câu 4 (2,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có đỉnh (1 A ; 2) và
phương trình đường trung tuyến BM : 2x  y 1  0 , M  AC .
a). Viết phương trình đường thẳng d qua A và vuông góc với đường thẳng BM .
Ta có: - Đường thẳng d qua (1 A ; 2) 
- Do d  BM  d có VTCP a  2;  1 x 1 2t  d có PTTS: 
 y  2  t
b). Viết phương trình đường tròn (C) có tâm A và tiếp xúc với đường thẳng BM .
Ta có: - Đường tròn (C) có tâm (1 A ; 2)  
- Do (C) tiếp xúc với BM  R  d  A BM  2.1 2 1 ;   5 5
 (C) có PT: x  2   y  2 1 2  5
c). Tìm tọa độ điểm B , biết CD : x  y 1  0 là phương trình đường phân giác trong của góc C .
- Gọi M a; 2  a   1  BM
- M là trung điểm của AC  C 2a 1; 4  a  4 A M   3;  5
- C CD  2a   1   4
 a  4 1  0  a  3    C   7;  8 M D - B  ; b 2  b  
1  BM , B  M  I  CM CD 7 cos ;    5 2 B C      CB CD 3b 16 cos ;   2 
2 5b  50b 130
- Theo đề bài, ta có: cosCM ;CD  cosCB;CD b  3  l 7 3b 16 2 20b 50b 30 0         1 2 5 2
2 5b  50b 130 b  n  2  1   B ; 2     2  ------ HẾT ------ Trang 5/3 - Mã đề 121