
Preview text:
SỞ GD&ĐT NINH BÌNH
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG HỌC KỲ II
TRƯỜNG THPT NHO QUAN C NĂM HỌC 2016-2017 MÔN TOÁN LỚP 10
Thời gian làm bài 90 phút (không kể thời gian giao đề) ĐỀ SỐ 101 I. TRĂC NGHIỆM (3 đ)
Câu 1 : Nghiệm của bất phương trình 2x 1 x 1là. 2 2 2 A. x . B. x 0 .
C. x 0 hoặc x . D. x 0 . 3 3 3 2x 3
Câu 2: : Cho biểu thức f x
. Mệnh đề nào dưới đây là sai? 2 4x 2x 12 U U
A. f x 0, x 2; .
B. f x 3
0, x 2,x . 2
C. f x 3 0, x .
D. f x 0, x 2 . 2
Câu 3: Cho biểu thức f ( x) có bảng xét dấu hình bên dưới. x ∞ 1 2 3 +∞ f(x) + 0 +
Tập nghiệm của bất phương trình f (x) ≤ 0 là: A. ( ; −∞ ) 1 ∪[2;3) B. [1; 2]∪[3; +∞) [1;2]∪(3;+∞) D. ( ) ;1 −∞ C. 1 π
Câu 4: Cho sin a = với
< a < π . tính cos a 3 2 2 2 2 2 2 ± 2 8 A. cos a = B. cos a = − C. cos a = D. cos a = 3 3 3 9
Câu 5: Cho đường thẳng d : 3x − y +1 = 0 . Véc tơ chỉ phương của đường thẳng d là: A. u = (1;3) B. u = (3; ) 1 C. u = (3; − ) 1 D. u = ( 1 − ;3).
Câu 6: Phương trình tham số của đường thẳng đi qua điểm I(-1; 2) và vuông góc với đường thẳng có
phương trình 2x – y + 4 = 0 là: x =1+ 2t x = t x = 1 − + 2t x = 1 − + 2t A. . B. . C. . D. . y = 2 − t y = 4 + 2t y = 2 − t y = 2 + t II. TỰ LUẬN ( 7 đ)
Câu 1: (2,0 điểm) Giải các bất phương trình sau: a). 2 − x − 4 > 0 ;
b). 2x −1 + 2 > x . 3
Câu 2: 2,0 điểm) Cho 900< α <1800 và sinα = . Tính cosα , tanα , cotα , cos3α P P P P 4 và tan 3α
Câu 3: (2,0 điểm) Trong mặt phẳng Oxy cho A(-1; 2), B(3; 1) và đường thẳng (
a). Viết phương trình tham số của đường thẳng AB.
b). Viết phương trình đường tròn tâm A và tiếp xúc với đường thẳng (∆).
Câu 4.(1 điểm) Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng cho thuê mỗi căn
hộ với giá 2.000.000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ tăng thêm giá cho
thuê mỗi căn hộ 100.000 đồng một tháng thì sẽ có hai căn hộ bị bỏ trống. Hỏi muốn có thu
nhập cao nhất thì công ty đó phải cho thuê mỗi căn hộ với giá bao nhiêu một tháng. ---Hết---
Thí sinh không được sử dụng tài liệu, cán bộ coi thi không giải thích gì thêm
Họ và tên học sinh:…………………………………. Số báo danh…………………….
Chữ ký của giám thị: Giám thị 1:................................ Giám thị 2:...................................
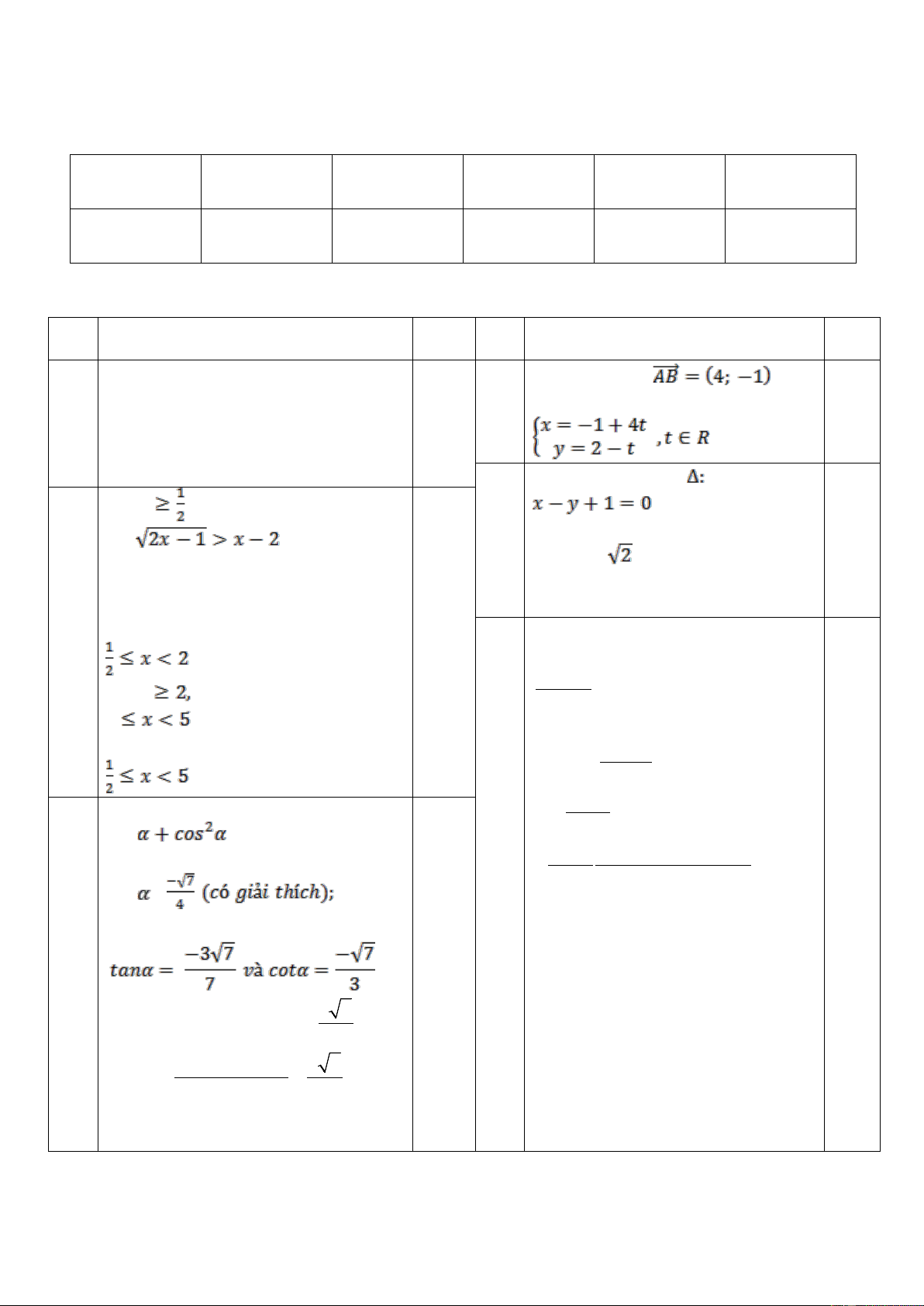
ĐÁP ÁN HKII TOÁN 10 NĂM 2016 - 2017 I.PHẦN TRẮC NGHIỆM Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 C D A B A C II.TỰ LUẬN Câu Nội dung Điểm Câu Nội dung Điểm câu câu Tìm đúng tđộ: 0.5 1.a. Giải đúng x< -2 và KL 1,0 3.a Ptts của đt AB: 0,5 3.b Viết đúng pttq của 0.25 Đk: x
và biến đổi BPT đã cho 0.25
Viết đúng CT khoảng cách và tính 0.25 1.b về: đúng R= Viết đúng ptđtr: 0.5 (x+1)2 +(y – 2)2 = 2 P P P P
Nếu x < 2, KL đúng n của BPT: 0.25 câu Gọi x (đồng) là số tiền tăng thêm R0R 4
Suy ra số căn hộ bị bỏ trống là 2x 0,25 Nếu x giải đúng n của BPT: 0.25 R0R (căn) 100000 2
Số thu nhập trong 1 tháng là
KL: Tập n của BPT đã cho là: 0.25 2x R0R 1đ T =(50− )(2000000 + x) 100000 0,25 1
câu Viết đúng công thức: 0.25 =
(2500000 − x)(2000000 + x) 2 50000 2. sin =1 P P R R 2 1 (2500000 + 2000000) Tính đúng: ≤ 50000 4 cos = 0.25 Dấu bằng sảy ra khi Tính đúng: 0,25 2500000 - x = 2000000 + x 0.5 Suy ra x = 250000 đồng 5 7 3 0,5
Vậy muốn có thu nhập cao nhất thi
cos 3α = 4 cos α − 3cosα = 0,25 16
công ty phải cho thuê mỗi căn hộ 3 3 tan α − tan α 9 7 với giá 2250000 đồng tan 3α = = 2 1− 3 tan α 35 0,5 Chú ý:
Mọi cách làm khác đúng và lập luận chặt chẽ vẫn cho điểm tối đa và chia thang điểm tương ứng.




