
Preview text:
ỦY BAN NHÂN DÂN QUẬN 7
ĐỀ KIỂM TRA HỌC KỲ II
TRƯỜNG THCS NGUYỄN HỮU THỌ Năm học 2019 – 2020 MÔN: TOÁN 7 ĐỀ CHÍNH THỨC
Thời gian: 90 phút (không kể thời gian giao đề) (Đề có 01 trang)
Bài 1: (2 điểm) Điểm kiểm tra Toán (1 tiết) của học sinh lớp 7A được bạn lớp trưởng ghi lại ở bảng sau: 3 6 6 7 7 2 9 6 4 7 5 8 10 9 8 7 7 7 6 6 5 7 2 8 8 6 2 4 7 7 6 8 5 8 6 3 8 8 4 7
a) Dấu hiệu ở đây là gì? Lớp 7A có bao nhiêu học sinh làm bài kiểm tra?
b) Lập bảng tần số và tính số trung bình cộng của dấu hiệu.
c) Tìm mốt của dấu hiệu. 1
Bài 2: (2 điểm) Cho đơn thức: A xy z .2x y z2 3 2 4 3 2 a) Thu gọn đơn thức A
b) Tìm hệ số, phần biến và bậc của đơn thức A
c) Tính giá trị của A tại x = 1; y = - 1; z = 2.
Bài 3: (2 điểm) Cho hai đa thức: P(x)= x2 + 3x3 -6x+12 Q(x)= x2-x+2 + 3x3 170m
a) Tính P(x)+Q(x) và P(x)-Q(x)
b) Tìm nghiệm của đa thức A(x)= P(x)-Q(x)
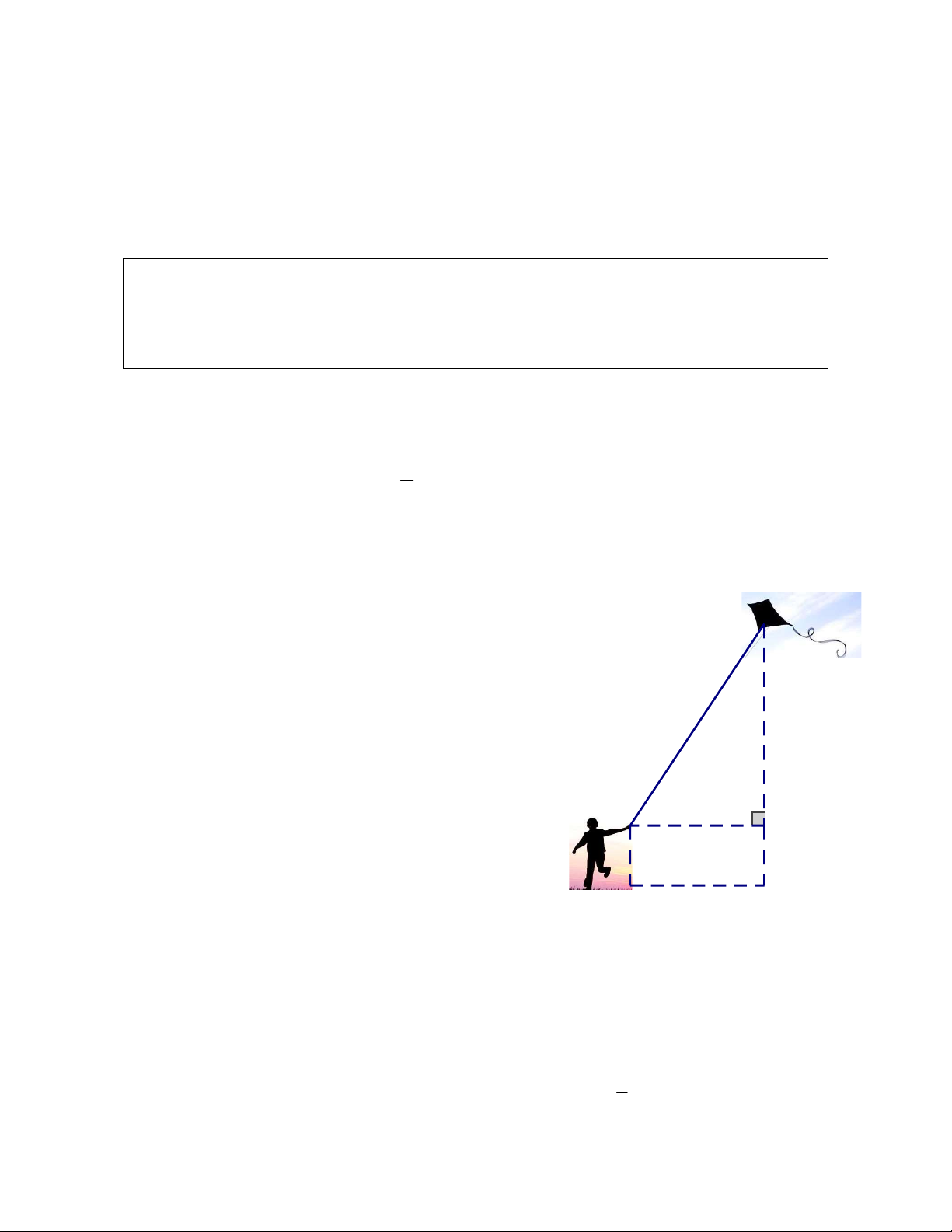
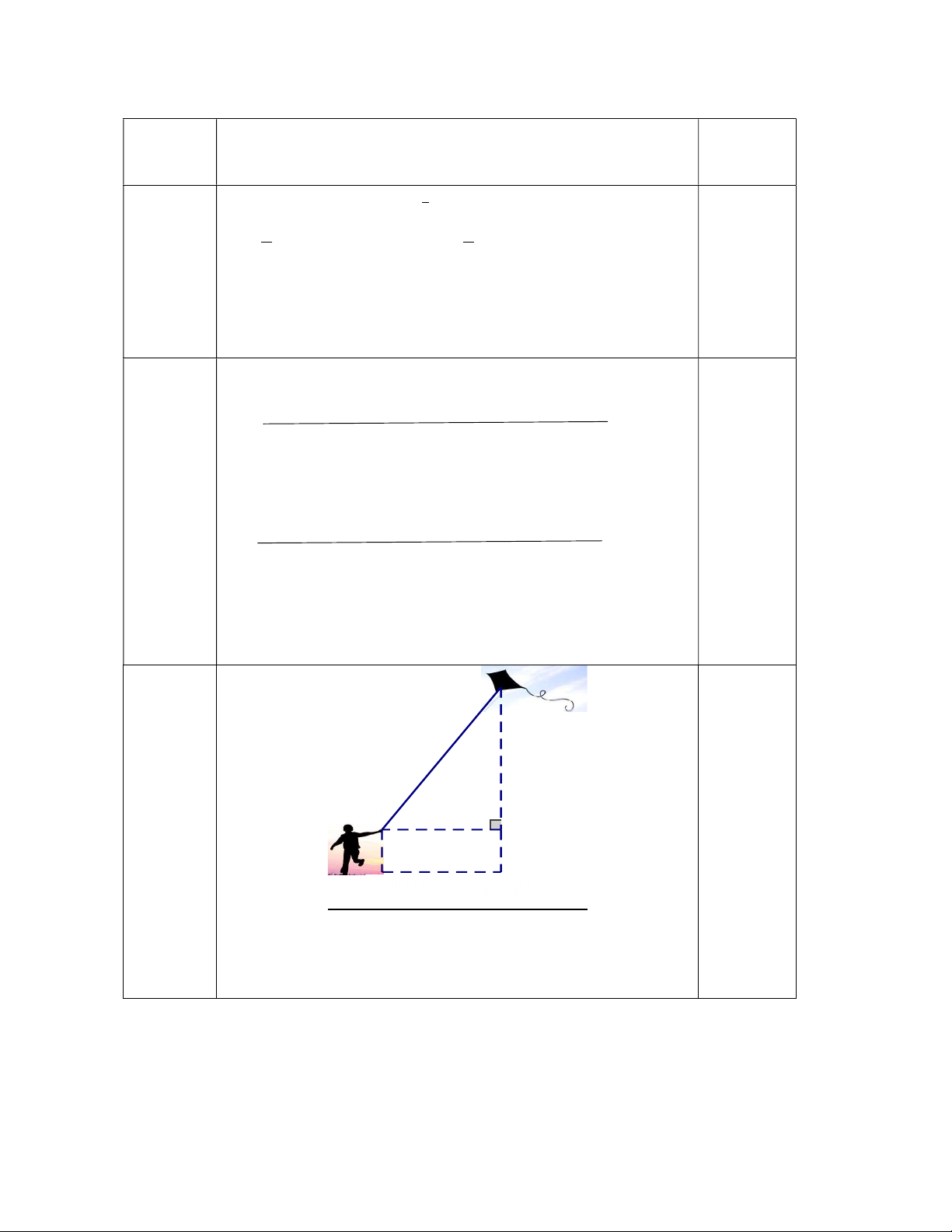
Bài 4: (1 điểm) Một bạn học sinh thả diều ngoài đồng,
cho biết đoạn dây diều từ tay bạn đến diều dài 170m và 80m
bạn đứng cách nơi diều được thả lên theo phương thẳng
đứng là 80m. Tính độ cao của con diều so với mặt đất, 2m
biết tay bạn học sinh cách mặt đất 2m.
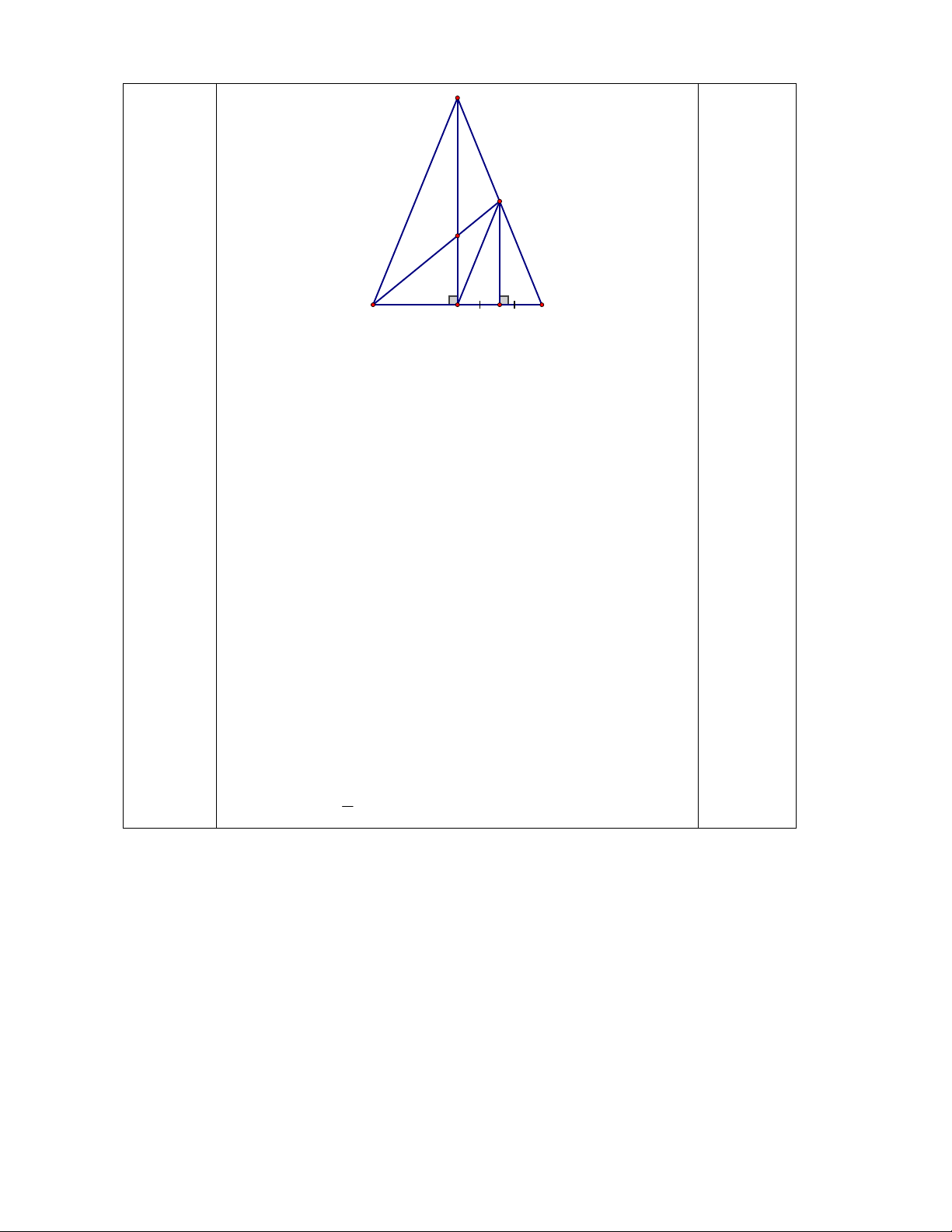
Bài 5: (3 điểm) Cho tam giác ABC cân tại A (AB = AC, Â nhọn). Vẽ AH BC (H BC).
a) Chứng minh AHB = AHC.
b) Gọi M là trung điểm CH. Từ M vẽ đường thẳng vuông góc với BC cắt AC tại D. Chứng
minh DMC = DMH và HD // AB.
c) BD cắt AH tại G. Chứng minh G là trọng tâm ABC và 2 (AH BD) AB . 3 ---HẾT--- GỢI Ý ĐÁP ÁN TOÁN 7 Bài 1.
a) Dấu hiệu ở đây là gì? Lớp 7A có bao nhiêu học sinh? 0,5 (2 đ)
b) Lập bảng tần số và tính số trung bình cộng của dấu hiệu, 0,5x2
c) Tìm mốt của dấu hiệu: 0,5 Bài 2:
a) Thu gọn đơn thức 𝐴 = 𝑥𝑦 𝑧 . (−2𝑥 𝑦 𝑧) 0,25x4 (2 đ) 1 1 𝐴 =
𝑥𝑦 𝑧 . (−2) 𝑥 𝑦 𝑧 =
. 4. 𝑥𝑥 𝑦 𝑦 𝑧 𝑧 2 2 = 2𝑥 𝑦 𝑧
b) Hệ số: 2; Phần biến: 0,5 𝑥 𝑦 𝑧 ; Bậc: 22
c) A = 2𝑥 𝑦 𝑧 = 2.19.(-1)9.24 = 2.1.(-1).16 = - 32. 0,5 Bài 3: a) Tính P(x)+Q(x) 0,25x3 (2 đ) P(x)= 3x3 + x2 – 6x + 12 + Q(x)= 3x3 + x2 – x +2
P(x)+Q(x) = 6x3 + 2x2 – 7x + 14 b/. Tính P(x) – Q(x) 0,25x3 P(x)= 3x3 + x2 – 6x + 12 - Q(x)= 3x3 + x2 – x + 2 P(x) – Q(x) = - 5x + 10
c/. Tìm nghiệm của A(x)= P(x) – Q(x) = -5x+10 0,5
Ta cho -5x + 10 =0 → -5x= -10 →x =2
Vậy x=2 là nghiệm của A(x) Bài 4: (1 đ) B 170m A 80m C 2m H K
∆ABC vuông tại C nên AB2 = AC2 + BC2 (Pytago) 0,25x4 Tính được BC = 150m
BK = BC + CK = 150 + 2 = 152 m
Vậy độ cao của con diều so với mặt đất là 152m Bài 5: A (3,0đ) D G B H M C a)Xét AHB và A HC có: 0,25x4 AB AC ( do A BC cân tại A) AH là cạnh chung 0 ˆ ˆ B H A C H A 90 ( do AH BC ) A HB A
HC ( cạnh huyền – cạnh góc vuông) b) Xét D MC và DMH có: 0,25x4
MH MC ( do M là trung điểm của HC) DM là cạnh chung 0 ˆ ˆ H M D C M D 90 ( do DM HC ) D MC D
MH ( 2 cạnh góc vuông) ˆ H C D ˆ C H D ( hai góc tương ứng) (1) Mà ˆC B A ˆ B C A ( do A BCcân tại A) (2) Từ (1) và (2) ˆ C B A ˆ C H D
Mà 2 góc này ở vị trí đồng vị AB // HD c)Chứng minh: AD=HD 0,25x4
Chứng minh: D là trung điểm của AC H là trung điểm của BC
Từ đó G là trọng tâm A BC
*Chứng minh: 2 (AH BD) AB 3




