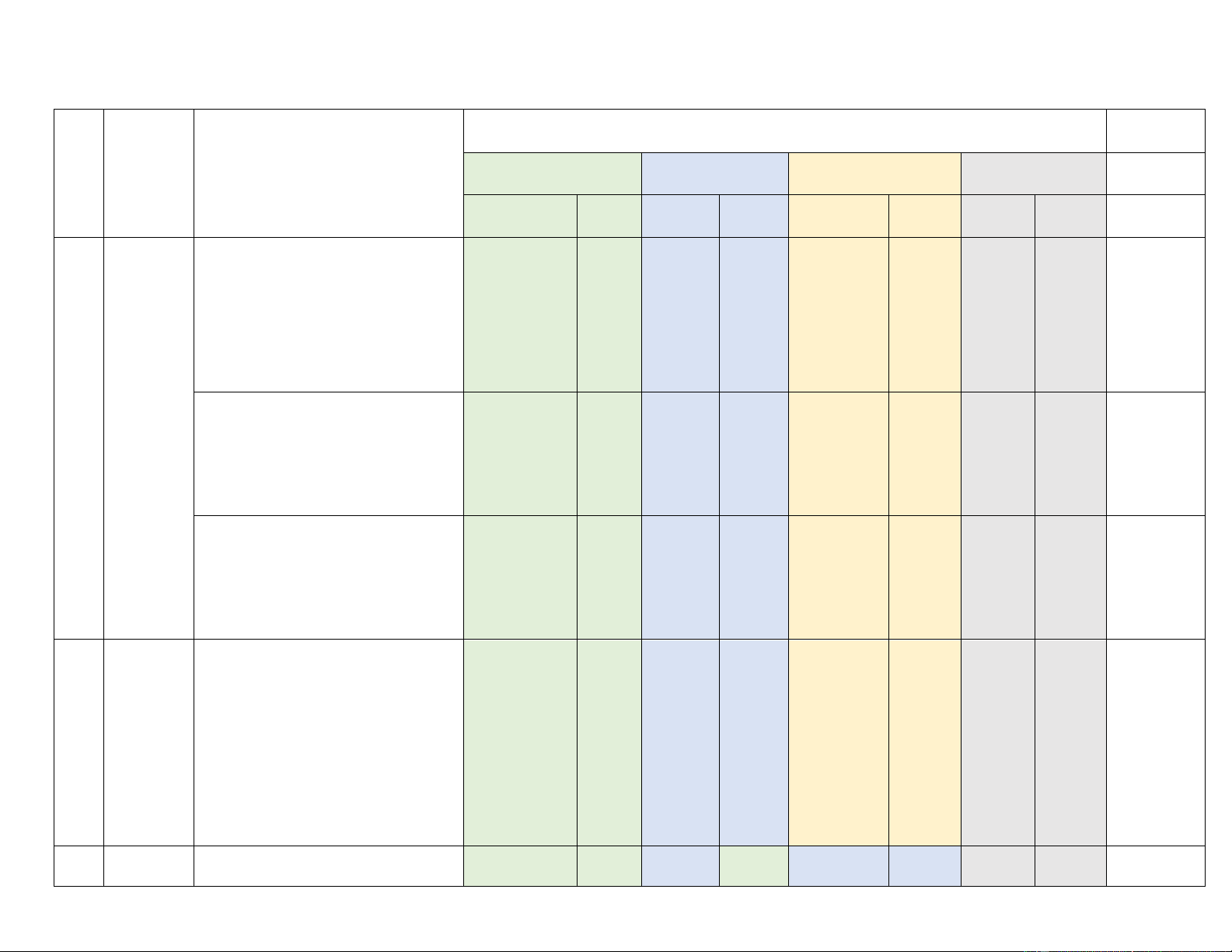
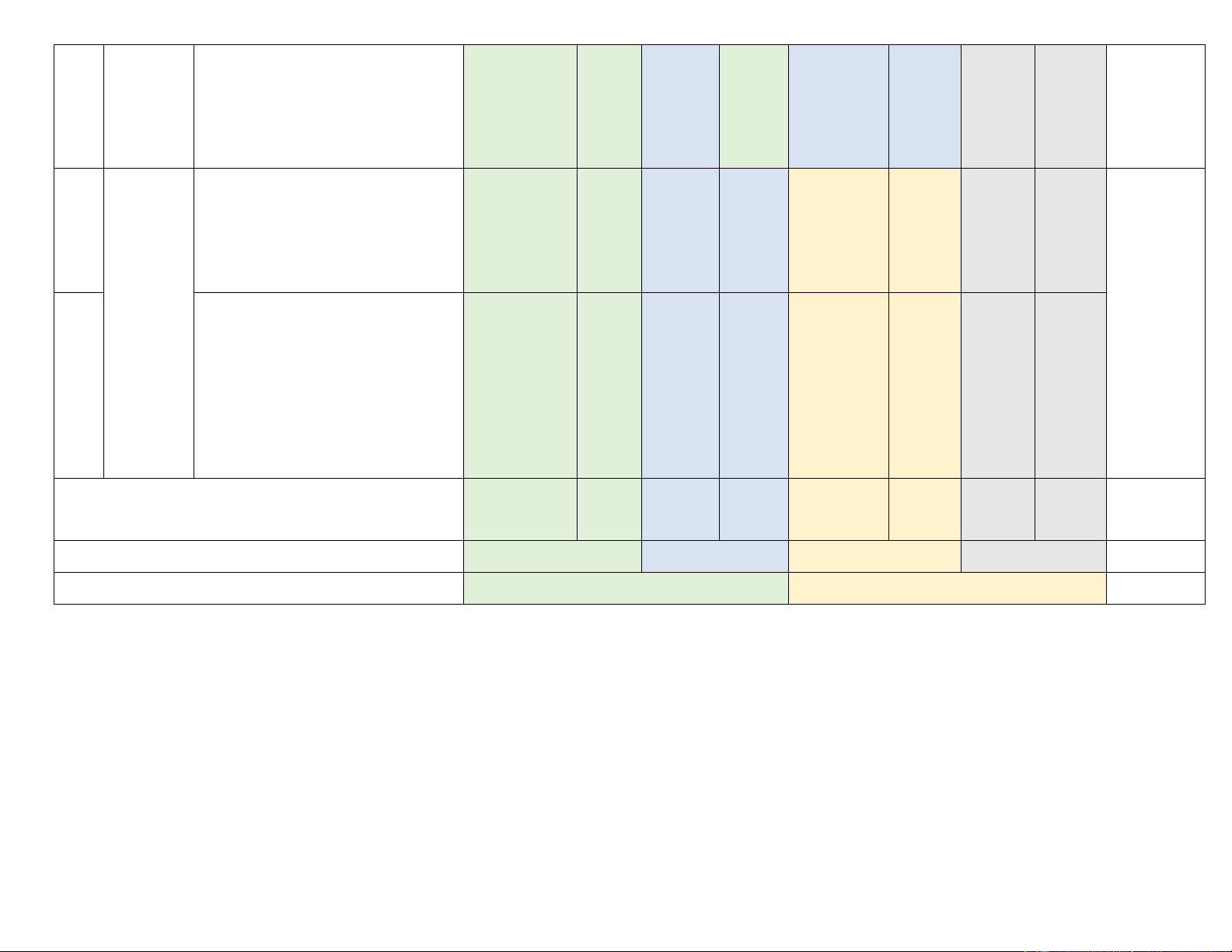
KHUNG MA TRẬN ĐỀ KIỂM TRA CUỐI HKI. MÔN TOÁN – LỚP 8 Tổng %
Mức độ đánh giá điểm Chương/ Nhận biết Thông hiểu Vận dụng Vận dụng cao TT
Nội dung/đơn vị kiến thức Chủ đề TNKQ TL TNKQ TL TNKQ TL TNKQ TL 1 1 1 2 1
Đa thức nhiều biến. Các phép (TN1) TL2.a (TN2,3) TL1a
toán cộng, trừ, nhân, chia các (0,25đ) (0,5đ) (0,5đ) (0,5đ) 1,75 đa thức nhiều biến Biểu 1 1 1 thức đại số (TN4) TL2.b TL1b
Hằng đẳng thức đáng nhớ 1,25 (0,25đ) (0,5đ) (0,5đ) ( 36 tiết) 2 1 1 1
Phân thức đại số. Tính chất cơ
bản của phân thức đại số. Các (TN5,7) (TN6) TL1c TL4,6 2,25
phép toán cộng, trừ, nhân, chia (0,5đ) (0,25đ) (0,5đ) (1đ) các phân thức đại số 2 Các 2 1 2 hình (TN8,9) TL3a (TN10,11) khối (0,5đ) (0,5đ) (0,5đ) trong
Hình chóp tam giác đều, hình 1,5 thực chóp tứ giác đều tiễn (4 tiết) 3
Định lí Định lí Pythagore 0,5 Pythagore 1 TL3b ( 4 tiết ) (0,5đ) 1 1 TL5a (TN12) Tứ giác (1đ) (0,25đ) 4 Tứ giác 1 2,75 (20 tiết ) TL5b,c
Tính chất và dấu hiệu nhận (1,5đ)
biết các tứ giác đặc biệt Tổng số câu 6 3 4 4 2 3 1 23 Số điểm 1,5đ 2đ 1đ 2,0đ 0,5đ 2đ 1đ Tỉ lệ % 35% 30% 25% 10% 100% Tỉ lệ chung 65% 35% 100%
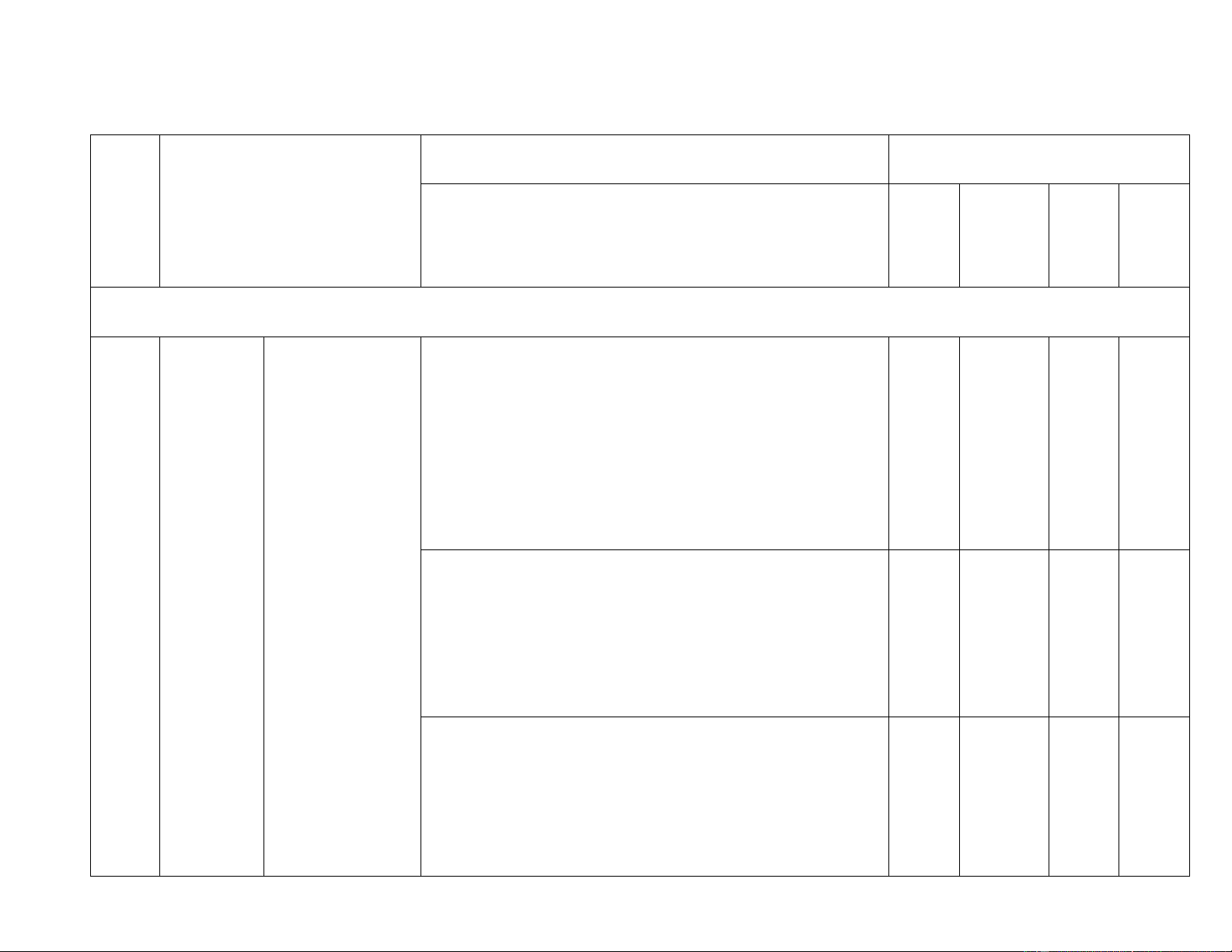
BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI HKI. MÔN TOÁN – LỚP 8
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức TT Chủ đề Vận Nhận Thông Vận dụng biết hiểu dụng cao SỐ VÀ ĐẠI SỐ Nhận biết: 1.TN
– Nhận biết được các khái niệm về đơn thức, đa thức (TN1) nhiều biến. TL2.a (0,5đ) Đa thức nhiều biến. Các phép 2.TN Thông hiểu:
Biểu thức toán cộng, trừ, (2,3), 1 1.TL1.2 đại số
nhân, chia các đa – Tính được giá trị của đa thức khi biết giá trị của các 1 thức nhiều biến biến. TL1a (0,5đ) Vận dụng:
– Thực hiện được việc thu gọn đơn thức, đa thức.
– Thực hiện được phép nhân đơn thức với đa thức và
phép chia hết một đơn thức cho một đơn thức.
– Thực hiện được các phép tính: phép cộng, phép trừ,
phép nhân các đa thức nhiều biến trong những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa thức cho một
đơn thức trong những trường hợp đơn giản. 1.TN4 Nhận biết: 1
– Nhận biết được các khái niệm: đồng nhất thức, hằng TL2.b
đẳng thức. (0,5đ) 1 Thông hiểu: TL1b
– Mô tả được các hằng đẳng thức: bình phương của Hằng đẳng thức (0,5đ)
tổng và hiệu; hiệu hai bình phương; lập phương của
tổng và hiệu; tổng và hiệu hai lập phương. Vận dụng:
– Vận dụng được các hằng đẳng thức để phân tích đa
thức thành nhân tử ở dạng: vận dụng trực tiếp hằng đẳng thức;
– Vận dụng hằng đẳng thức thông qua nhóm hạng tử và đặt nhân tử chung.
Phân thức đại số. Nhận biết: 2.TN5,7
Tính chất cơ bản – Nhận biết được các khái niệm cơ bản về phân thức của phân thức
đại số: định nghĩa; điều kiện xác định; giá trị của phân
đại số. Các phép thức đại số; hai phân thức bằng nhau. toán cộng, trừ, nhân, chia các phân thức đại số Thông hiểu: 1.TN6
– Mô tả được những tính chất cơ bản của phân thức đại số. 1 TL1c (0,5đ) 1 Vận dụng: TL4,6
– Thực hiện được các phép tính: phép cộng, phép trừ, (1đ)
phép nhân, phép chia đối với hai phân thức đại số.
– Vận dụng được các tính chất giao hoán, kết hợp, phân
phối của phép nhân đối với phép cộng, quy tắc dấu
ngoặc với phân thức đại số đơn giản trong tính toán. 2 Nhận biết 2.TN8, – 9
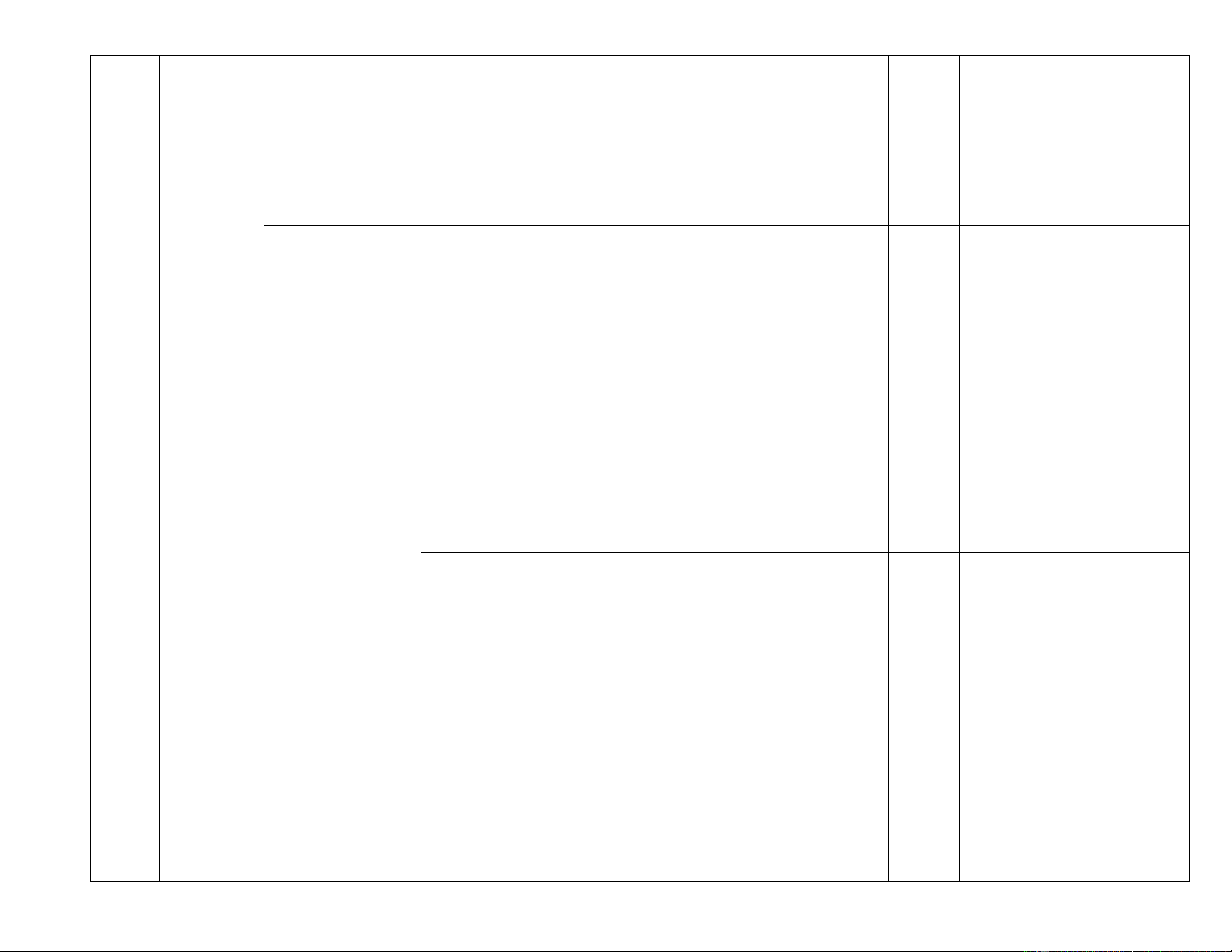
Mô tả (đỉnh, mặt đáy, mặt bên, cạnh bên) được hình
chóp tam giác đều và hình chóp tứ giác đều.
Các hình Hình chóp tam 1 Thông hiểu khối giác đều, hình TL3a trong
chóp tứ giác đều – Tạo lập được hình chóp tam giác đều và hình chóp tứ (0,5đ) thực tiễn giác đều.
– Tính được diện tích xung quanh, thể tích của một
hình chóp tam giác đều và hình chóp tứ giác đều.
– Giải quyết được một số vấn đề thực tiễn (đơn giản,
quen thuộc) gắn với việc tính thể tích, diện tích xung
quanh của hình chóp tam giác đều và hình chóp tứ giác
đều (ví dụ: tính thể tích hoặc diện tích xung quanh của
một số đồ vật quen thuộc có dạng hình chóp tam giác
đều và hình chóp tứ giác đều,...). Vận dụng 2. TN 10,11
– Giải quyết được một số vấn đề thực tiễn gắn với việc
tính thể tích, diện tích xung quanh của hình chóp tam
giác đều và hình chóp tứ giác đều. 3 Thông hiểu:
– Giải thích được định lí Pythagore. 1 Vận dụng: Đị TL3b nh lí Đị
– Tính được độ dài cạnh trong tam giác vuông bằng nh lí (0,5đ) Pythagore
cách sử dụng định lí Pythagore. Pythagore Vận dụng cao:
– Giải quyết được một số vấn đề thực tiễn gắn với việc
vận dụng định lí Pythagore (ví dụ: tính khoảng cách
giữa hai vị trí). 1 Nhận biết: TL5a 4 Tứ giác Tứ giác
– Mô tả được tứ giác, tứ giác lồi. (1đ) Thông hiểu:
– Giải thích được định lí về tổng các góc trong một tứ 1.TN12
giác lồi bằng 3600. Nhận biết:
– Nhận biết được dấu hiệu để một hình thang là hình
thang cân (ví dụ: hình thang có hai đường chéo bằng nhau là hình thang cân).
– Nhận biết được dấu hiệu để một tứ giác là hình bình
hành (ví dụ: tứ giác có hai đường chéo cắt nhau tại
trung điểm của mỗi đường là hình bình hành).
– Nhận biết được dấu hiệu để một hình bình hành là
hình chữ nhật (ví dụ: hình bình hành có hai đường chéo
Tính chất và dấu bằng nhau là hình chữ nhật). hiệu nhận biết các tứ giác đặc
– Nhận biết được dấu hiệu để một hình bình hành là biệt
hình thoi (ví dụ: hình bình hành có hai đường chéo
vuông góc với nhau là hình thoi).
– Nhận biết được dấu hiệu để một hình chữ nhật là hình
vuông (ví dụ: hình chữ nhật có hai đường chéo vuông
góc với nhau là hình vuông). 1 Thông hiểu TL5b,c
– Giải thích được tính chất về góc kề một đáy, cạnh (1,5đ)
bên, đường chéo của hình thang cân.
– Giải thích được tính chất về cạnh đối, góc đối, đường
chéo của hình bình hành.
– Giải thích được tính chất về hai đường chéo của hình chữ nhật.
– Giải thích được tính chất về đường chéo của hình thoi.
– Giải thích được tính chất về hai đường chéo của hình vuông.
ĐỀ KIỂM TRA HỌC KỲ I – TOÁN 8
I. TRẮC NGHIỆM KHÁCH QUAN: (3,0 điểm)
Hãy chọn đáp án đúng nhất trong các đáp án sau:
Câu 1 Kết quả của phép tính 2x(x+2) là: 2 A x + 2 B x + 2 2 .2 2 .2 4x . C 2x +4 . D 2x +2x −2 1
Câu 2 Giá trị của đa thức 2 2 2 2
2x y + 3xy − 2yx − 2y x + 3 tại x = ; y = là 3 2 17 − 17 19 − 19 A. B. C. D. 6 6 6 6
Câu 3 Giá trị của biểu thức 3x + y tại x = -1 ; y = -2 là: A. 1 B. 5 C. - 5 D. - 6 Câu 4 Biểu thức 2 2
x −2xy + y viết gọn là : A. 2 2 x + y B. 2 2 x − y C. 2 (x − y) D. 2 (x + y) 4x +1 1− 3x
Câu 5 Kết quả của phép tính − bằng: 2 2 7x 7x 1 7x − 2 7 1 A. B. C. D. 7x 2 7x x x 5x + 2 10x + 4
Câu 6 Kết quả của phép tính : là: 2 2 3xy x y 6y 6y x x A. 2 x B. x C. 6y D. 2 9y a −1 3 − a
Câu 7 Kết quả của phép tính + bằng: a +1 a +1 2 2 + 2a a 2a A. B. C. D. a +1 a +1 a +1 a +1
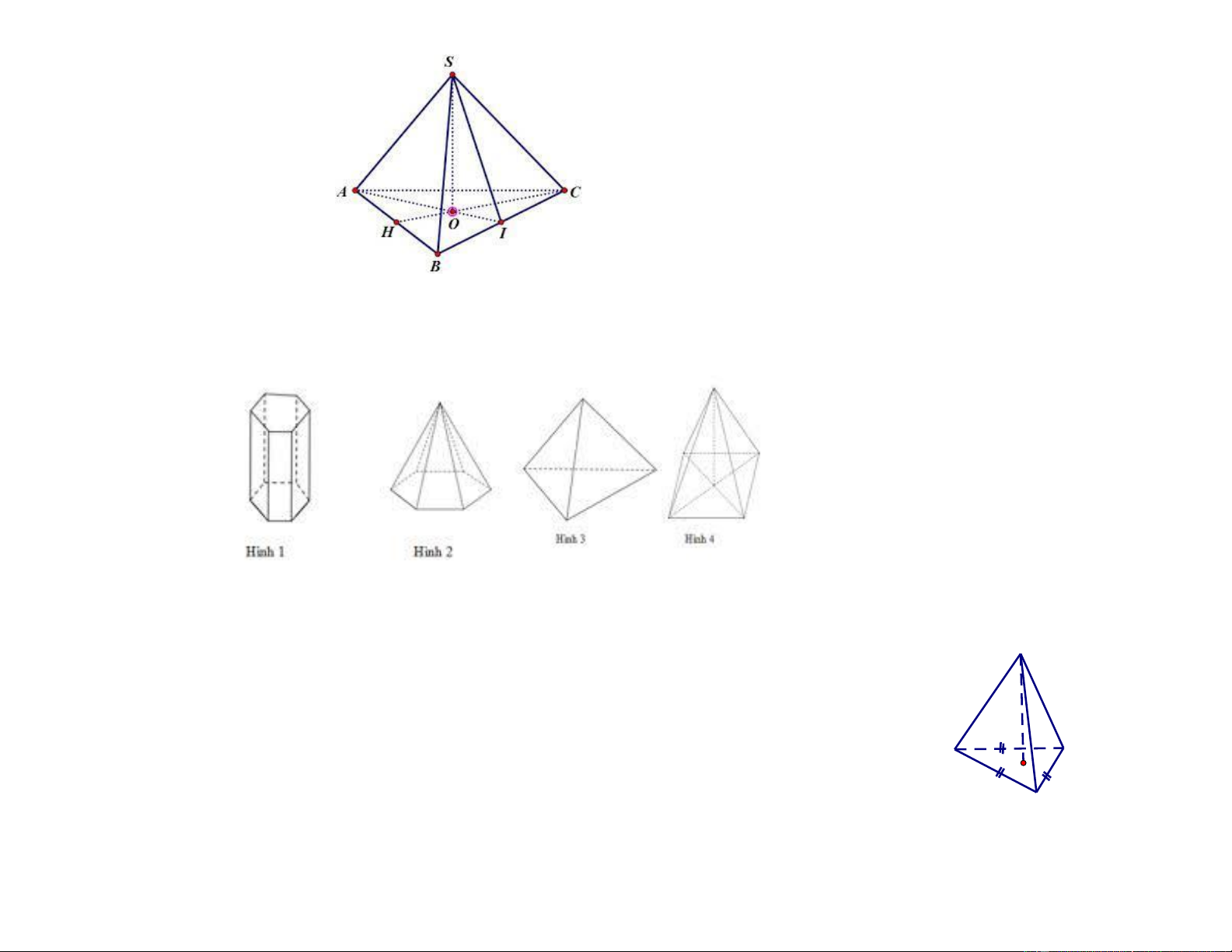
Câu 8 Cho hình chóp tam giác đều sau, chiều cao của hình chóp là: A. SA B. SI C. SO D. SH
Câu 9 Trong những hình sau, hình nào là chóp tứ giác đều: A. Hình 4 B. Hình 3 C. Hình 2 D. Hình 1 M
Câu 10 Cho hình chóp tam giác đều như hình sau . Đỉnh của hình chóp tam giác đều là : A. O B. M C. N D. Q Q N O
Câu 11 Hình chóp tam giác đều có bao nhiêu mặt bên? P A. 1 B. 2 C. 3 D. 4
Câu 12 Tổng các góc trong một tứ giác bằng bao nhiêu? 0 0 A. 180 B. 360 0 0 C. 100 D. 380
II. TỰ LUẬN : (7,0 điểm)
Câu 1. (1,5 điểm) Rút gọn a) + 2
(x 1) − x(x − 2) (0,5đ)
b) (4x + 5)2 – 2(4x + 5) (x + 5) + (x + 5)2 (0,5đ) x − 2y x + 2y c) + (0,5đ) 2 x + 2 xy x + xy
Câu 2. (1 điểm) Phân tích đa thức thành nhân tử a) 2 2x + 4x (0,5đ)
b) 2(x − y) + a(y − x) (0,5đ)
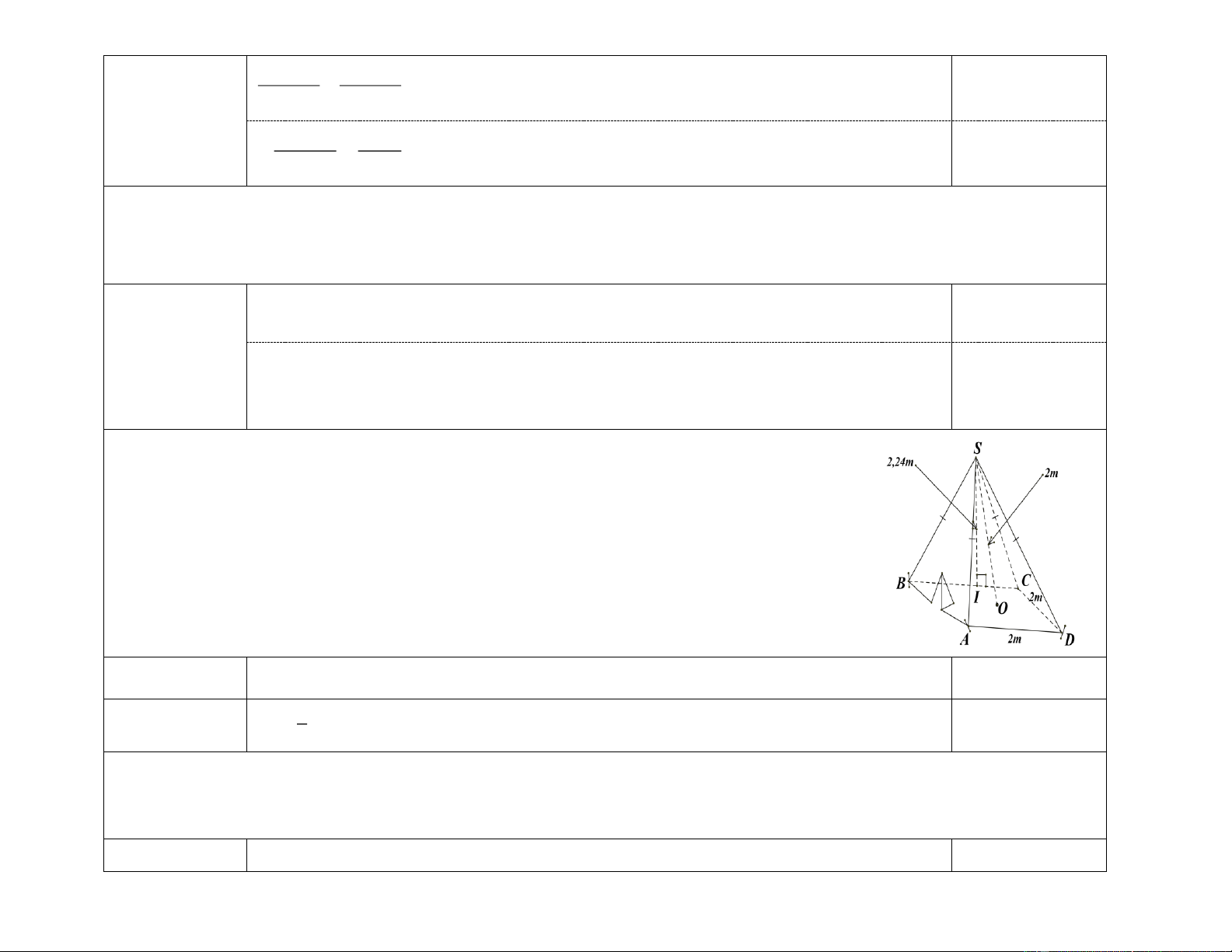
Câu 3. (1 điểm) Hình bên là một cái lều ở một trại hè của học sinh tham gia cắm trại có dạng hình
chóp tứ giác đều theo các kích thước như hình vẽ:
a) Diện tích xung quanh của cái lều đó. (0,5đ)
b) Thể tích không khí bên trong lều là bao nhiêu ? (0,5đ)
Câu 4. (0,5 điểm) Một chiếc xe đò chạy từ Sài Gòn về Bạc Liêu với vận tốc (9x + 5)km/giờ trong thời gian (x + 2) giờ.
Tính quãng đường đi được khi x = 2
Câu 5: Cho ΔABC vuông ở A (ABsong song với AB cắt BC và AC lần lượt ở M và N. (2,5 điểm)
a) Tứ giác ABDM là hình gì?(1đ) b) Chứng mih: BD DC(1đ)
c) Gọi I là trung điểm của MC. Chứng minh: (0,5đ)  1 2
5 − x  1− 2x
Câu 6: Cho biểu thức B = + − :   (0,5đ) 2 2
1− x x +1 1− x  x −1
Tìm giá trị nguyên của x để giá trị của biểu thức B là số nguyên
………………………………….. Hết ……………………………………
ĐÁP ÁN VÀ BIỂU ĐIỂM
I. TRẮC NGHIỆM ( 3 điểm) 1 2 3 4 5 6 7 8 9 10 11 12 B B C C D C A C A B C B
II. TỰ LUẬN (7,0 điểm) Nội dung Điểm Câu 1(1,5 điểm) Đề + 2 (x 1) − x(x − 2) a) = 2 + + − 2 x 2x 1 x + 2x 0,25 điểm = 4x + 1 0,25 điểm
(4x + 5)2 – 2(4x + 5) (x + 5) + (x + 5)2 0,25 điểm = (4x + 5) −(x + 5) 2  b)  = ( x)2 2 3 = 9x 0,25 điểm x − 2y x + 0,25 điểm + 2y 2 2 c) x + xy x + xy 0,25 điểm = 2x = 2 2 x + xy x + y Câu 2. (1 điểm) Đề a) 2 2x + 4x (0,5đ)
b) 2(x − y) + a(y − x) (0,5đ) a) 2x2 + 4x 0,5 điểm = 2x(x + 2) b) 2(x - y) + a(y - x) 0,5 điểm = 2(x - y) - a(x - y) = (2 - a)(x - y) Câu 3. (1 điểm)
Đề Hình bên là một cái lều ở một trại hè của học sinh tham gia cắm trại có dạng hình
chóp tứ giác đều theo các kích thước như hình vẽ:
a) Diện tích xung quanh của cái lều đó. (0,5đ)
b) Thể tích không khí bên trong lều là bao nhiêu ? (0,5đ) a S = 2 8, 96 m 0,5 điểm 8 b V = 3 m 0,5 điểm 3 Câu 4. (0,5 điểm)
Đề Một chiếc xe đò chạy từ Sài Gòn về Bạc Liêu với vận tốc (9x + 5)km/giờ trong thời gian (x + 2) giờ.
Tính quãng đường đi được khi x = 2 2
S = 9.2 + 23.2 +10 = 92 0,5 điểm Câu 5: (2,5 điểm) a 1 điểm b 1 điểm c 0,5 điểm Câu 6: (0,5 điểm) Cho biểu thức B =  1 2
5 − x  1− 2x + − :   (0,5đ) 2 2
1− x x +1 1− x  x −1
Tìm giá trị nguyên của x để giá trị của biểu thức B là số nguyên Đkxđ: x   1  1 2
5 − x  1− 2x
1+ x + 2(1− x) − 5 (x −1)(x +1) 2 − B = + − : = . =     2 2
1− x x +1 1− x  x −1  (1− x)(1+ x)  1− 2x 2x −1
B có giá trị nguyên khi x là số nguyên thì −2 có giá trị nguyên 2x −1 0,5 điểm  2x −1 = 1 x =1   − = − =  2x 1 1 x 0 2x – 1 là Ư(2)      2x −1 = 2 x =1,5   2x −1 = 2 − x = 1 −
Đối chiếu Đkxđ thì chỉ có x = 0 thoả mãn
Document Outline

• Câu 5: Cho ΔABC vuông ở A (AB