Đề thi học kì 2 môn Toán 10 năm 2022 - 2023 sách Chân trời sáng tạo | Đề 3

SỞ GD&ĐT ……..
ĐỀ KIỂM TRA HỌC KỲ II
TRƯỜNG THPT…………….. NĂM HỌC 2022-2023
(Đề thi gồm có 03 trang)
Môn: Toán 10 Chân trời sáng tạo
Thời gian làm bài: 90 phút, không kể thời gian giao đề
Câu 1. (1,5 điểm) Giải các phương trình sau: a) 2 2
x − x − 2 = −x + 2x + 3 ; b) ( x − ) 2 2 2
2x + 4 = x − 4
Câu 2. (1,0 điểm) Giải bất phương trình 1 1 − +1  0 . x −1 x
Câu 3. (1,0 điểm) Tìm tất cả tham số m để f (x) 2 2
= x − 2mx + m − m luôn dương với mọi x thuộc .
Câu 4. (1,5 điểm) Có 3 cuốn sách lý, 4 cuốn sách sinh, 5 cuốn sách địa. Hỏi có bao
nhiêu cách sắp xếp các cuốn sách trên vào giá sách hàng ngang nếu: a) Sắp xếp tùy ý ?
b) Các cuốn sách cùng môn học đứng cạnh nhau ? 5   Câu 5. 1 (1, 5 điểm) Cho 2 3 4 5 1− x
= a + a x + a x + a x + a x + a x   . 0 1 2 3 4 5  2 
a) Tìm hệ số lớn nhất trong tất cả hệ số a , a , ..., a . 0 1 5
b) Tính tổng a + a + a + a + a + a . 0 1 2 3 4 5
Câu 6. (1, 5 điểm) Cho họ đường tròn (C ) 2 2
: x + y + 4mx + 2(m + ) 1 y −1 = 0 . m
a) Tìm m để (C
đi qua điểm A(1;0) . m )
b) Chứng minh rằng (C
luôn là đường tròn với mọi số thực m. Tìm bán kính m )
bé nhất của đường tròn (C . m ) x = t
Câu 7. (1,0 điểm) Cho hai đường thẳng d : 
, d : x + y + 3 = 0 . Viết 1 2 y = 2 − + 2t
phương trình tham số đường thẳng d qua điểm M (3;0) , đồng thời cắt hai
đường thẳng d , d tại hai điểm A, B sao cho M là trung điểm của đoạn 1 2 AB.
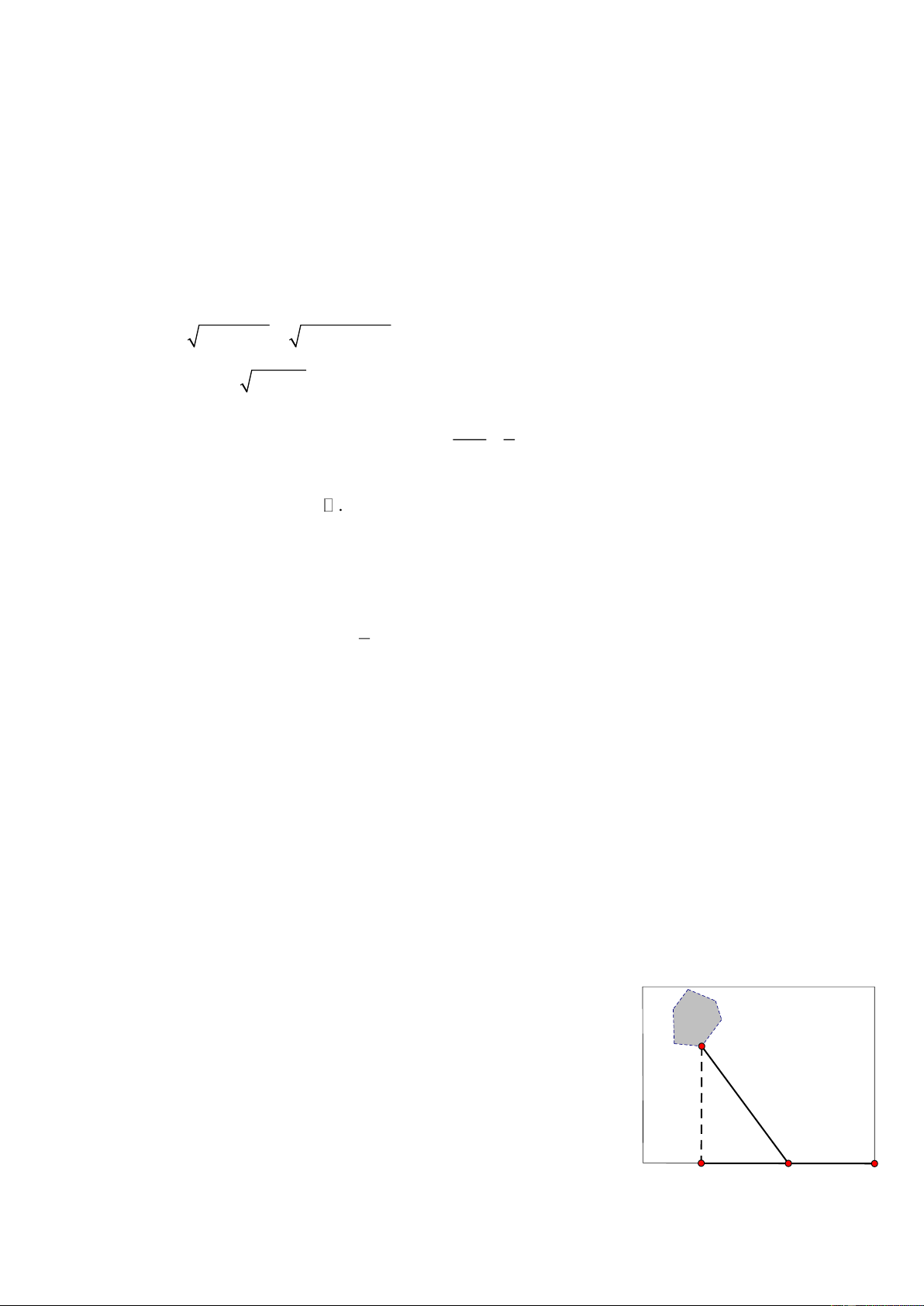
Câu 8. (1,0 điểm) Một công ty muốn làm một đường ống dẫn từ
một điểm A trên bờ đến một điểm B trên một hòn đảo đảo
theo lộ trình từ A đến C (đường bờ biển) rồi từ C đến B B
(dưới nước) như hình vẽ. Hòn đảo cách bờ biển 6 km. biển
Giá để xây đường ống trên bờ là 50000 USD mỗi km, giá để 6km
xây đường ống dưới nước là 130 000 USD mỗi
km; B là điểm trên bờ biển sao cho BB vuông góc
với bờ biển. Khoảng cách từ A đến B là 9 km. Biết C B' x km (9 - x)km A bờ biển
rằng chi phí làm đường ống này là 1170 000 USD. Hỏi vị trí C cách vị trí A bao nhiêu km?
HƯỚNG DẪN ĐÁP ÁN
Câu 1. (1,5 điểm) Giải các phương trình sau: a) 2 2
x − x − 2 = −x + 2x + 3 ; b) ( x − ) 2 2 2
2x + 4 = x − 4 Hướng dẫn giải:
a) Bình phương hai vế phương trình: 5 2 2 2
x − x − 2 = −x + 2x + 3  2x − 3x − 5 = 0  x = −1 x = . 2 5
Thay các giá trị x = 1
− , x = vào phương trình đã cho, ta thấy chúng đều thỏa 2 mãn.  5 
Vậy tập nghiệm phương trình là: S =  1; −  .  2  b) Ta có: (x − ) 2 2 2
2x + 4 = x − 4  − =  =  ( x x x − 2) 2 0 2 2
2x + 4 = ( x − 2)( x + 2)     . 2 2
 2x + 4 = x + 2
 2x + 4 = x + 2 Xét phương trình 2
2x + 4 = x + 2 (1). x = 0
Bình phương hai vế (1), ta được: 2 2 2
2x + 4 = x + 4x + 4  x − 4x = 0   . x = 4
Thay lần lượt x = 0, x = 4 vào phương trình (1), ta thấy chúng đều thỏa mãn.
Vậy tập nghiệm phương trình là: S = 0; 2;  4 .
Câu 2. (1,0 điểm) Giải bất phương trình 1 1 − +1  0 . x −1 x Hướng dẫn giải: x  0 Điều kiện:  . Ta có: x  1 1 1 x − ( x − ) 1 + x ( x − ) 2 1 x − x +1 − +1  0     x −1 x (x − ) 0 0 2 1 x x − . x a =1  0  1 Dễ thấy 2
x − x +1  0, x   vì  .  =  (− )2 1 − 4.1.1  0
Vì vậy bất phương trình trở thành 2 x − x  0 . Tam thức bậc hai 2
x − x có hai nghiệm x = 0, x = 1 và a = 1  0 nên 1 2 2 x  0 2
x − x  0   . x  1
Vậy tập nghiệm của bất phương trình đã cho là S = (−;0)  (1; + ) .
Câu 3. (1,0 điểm) Tìm tất cả tham số m để f (x) 2 2
= x − 2mx + m − m luôn dương với mọi x thuộc . Hướng dẫn giải: Ta có: 2 a = 1, b = 2 − ,
m c = m − m . Theo giả thiết: (luôn đúng)      f ( x) 1 0 a 0  0, x         0 ( 2 − m  ) . 2 − 4  ( 2 m − m)  0 2 2
 4m − 4m + 4m  0  m  0 . Vậy với m  0 thì f (x)  0, x   .
Câu 4. (1,5 điểm) Có 3 cuốn sách lý, 4 cuốn sách sinh, 5 cuốn sách địa. Hỏi có bao
nhiêu cách sắp xếp các cuốn sách trên vào giá sách hàng ngang nếu: a) Sắp xếp tùy ý ?
b) Các cuốn sách cùng môn học đứng cạnh nhau ? Hướng dẫn giải:
a) Số cách xếp tùy ý 12 cuốn sách lên giá là 12! (cách).
b) Gọi L là nhóm 3 sách lý, S là nhóm 4 sách sinh, Đ là nhóm 5 sách địa.
Số cách xếp trong L là 3!; số cách xếp trong S là 4!; số cách xếp trong Đ là
5!; số cách xếp L, S, Đ với nhau: 3!.
Vậy số cách xếp thỏa mãn đề bài là: 3!4!5!3! = 103680 (cách). 5   Câu 5. 1 (1, 5 điểm) Cho 2 3 4 5 1− x
= a + a x + a x + a x + a x + a x   . 0 1 2 3 4 5  2 
a) Tìm hệ số lớn nhất trong tất cả hệ số a , a , ..., a . 0 1 5
b) Tính tổng a + a + a + a + a + a . 0 1 2 3 4 5 Hướng dẫn giải: a) Ta có: 5 2 3 4 5  1   1   1   1   1   1  0 1 2 3 4 5 1− x
= C + C − x + C − x + C − x + C − x + C − x   5 5   5   5   5   5    2   2   2   2   2   2  5 5 5 5 1 2 3 4 5
=1− x + x − x + x − x 2 3 4 5
= a + a x + a x + a x + a x + a x (*). 2 2 4 16 32 0 1 2 3 4 5 5 5 5 5 1
Suy ra: a = 1, a = − , a = , a = − , a = , a = − . 0 1 2 3 2 2 4 4 5 16 32 5
Ta thấy hệ số lớn nhất tìm được là a = . 2 2 5  1 
b) Thay x = 1 vào (*), ta được: 1−
= a + a + a + a + a + a   . 0 1 2 3 4 5  2  1
Vậy a + a + a + a + a + a = . 0 1 2 3 4 5 32
Câu 6. (1, 5 điểm) Cho họ đường tròn (C ) 2 2
: x + y + 4mx + 2(m + ) 1 y −1 = 0 . m
a) Tìm m để (C
đi qua điểm A(1;0) . m )
b) Chứng minh rằng (C
luôn là đường tròn với mọi số thực m. Tìm bán kính m )
bé nhất của đường tròn (C . m ) Hướng dẫn giải: a) (C
đi qua điểm A(1;0) nên 2 2 1 + 0 + 4 . m 1+ 2(m + )
1 .0 −1 = 0  m = 0 . m )
Vậy m = 0 thỏa mãn đề bài. 4m 2(m + ) 1 b) Đặt a = = 2 − , m b = = −(m + ) 1 , c = 1 − . 2 − 2 −
Ta có : a + b − c = m + (m + )2 2 2 2 4 1 +1  0, m
  nên (C luôn là đường m ) tròn với mọi m. Bán kính đường tròn là : 2  1  9 9 2 2 2
R = a + b − c = 5m + 2m + 2 = 5 m + +    .  5  5 5 9
Vậy bán kính nhỏ nhất của đườn tròn R = ; khi đó 1 m = − . min 5 5 x = t
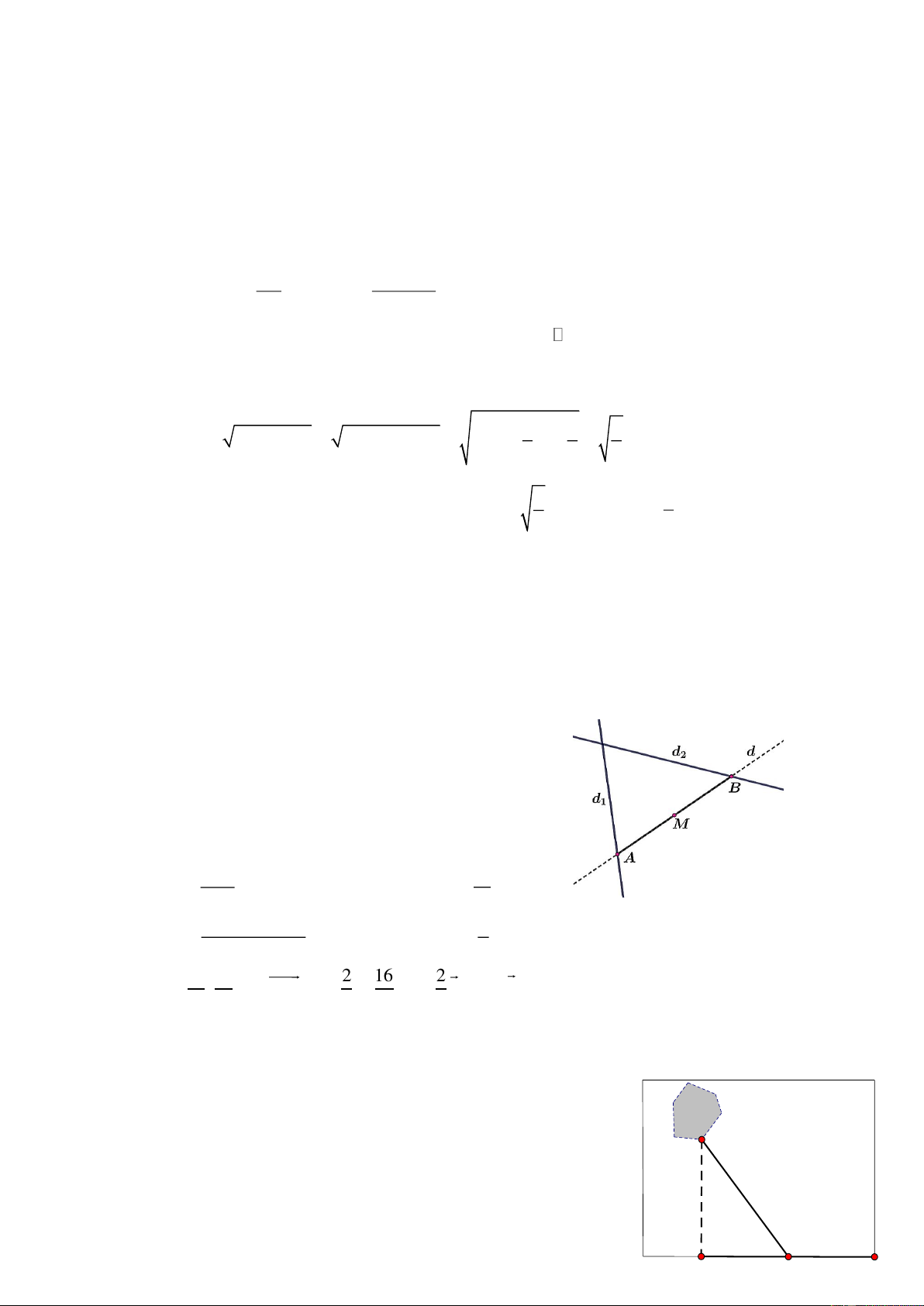
Câu 7. (1,0 điểm) Cho hai đường thẳng d : 
, d : x + y + 3 = 0 . Viết phương 1 2 y = 2 − + 2t
trình tham số đường thẳng d qua điểm M (3;0) , đồng thời cắt hai đường thẳng
d , d tại hai điểm A, B sao cho M là trung điểm của đoạn AB. 1 2 Hướng dẫn giải:
Xét đường thẳng d : x + y + 3 = 0 ; thay x = t  y = 3
− − t, ta có phương trình 2 x = t tham số d :  . 2 y = 3 − − t
Gọi A = d  d  A t ; − 2 + 2t ; gọi 1 ( )
B = d  d  B t; − 3 − t . 2 ( )
Vì M (3;0) là trung điểm của đoạn AB nên  t + t  11 3 =  =  t  +  =  2 t t 6   3     . Ta có 2
− + 2t − 3− t 
2t − t = 5 7 0 =   =  t  2  3 11 16   2 16  2 A ;  AM = − ;− = − u    
với u = (1;8) là một vectơ chỉ phương  3 3   3 3  3 của d. x = 3+ t
Phương trình tham số của d là  . y = 8t
Câu 8. (1,0 điểm) Một công ty muốn làm một đường ống dẫn từ đảo
một điểm A trên bờ đến một điểm B trên một hòn đảo theo lộ B
trình từ A đến C (đường bờ biển) rồi từ C đến B (dưới nước)
như hình vẽ. Hòn đảo cách bờ biển 6 km. Giá để xây đường biển 6km C B' x km (9 - x)km A bờ biển
ống trên bờ là 50000 USD mỗi km, giá để xây đường ống dưới nước là 130000
USD mỗi km; B là điểm trên bờ biển sao cho BB vuông góc với bờ biển.
Khoảng cách từ A đến B là 9 km. Biết rằng chi phí làm đường ống này là
1170 000 USD. Hỏi vị trí C cách vị trí A bao nhiêu km? Hướng dẫn giải: Gọi x = B C
 ( 0  x  9), khi đó: 2 BC = x + 36 .
Số tiền xây đường ống trên bờ: (9 − x)50000 ; số tiền xây đường ống dưới biển: 2 130 000 x + 36 .
Tổng chi phí bỏ ra để làm đường ống là: ( − x) 2 9
50000 +130000 x + 36 .
Theo giả thiết: ( − x) 2 9
.50000 +130000 x + 36 = 1170000  ( − x) 2 5 9 +13 x + 36 =117 2
13 x + 36 = 5x + 72  72 5  x + 72  0  x  − 5      x = . 169  ( 5 2 x + 36) 2
= 25x + 720x + 5184 2  2 14
 4x − 720x + 900 = 0 Ta có B C
 = 2,5 km  AC = 9 − 2,5 = 6,5 km . Vậy, ví trí C cách vị trí A một khoảng bằng 6,5 km.