Đề thi học kì 2 Toán 10 năm 2019 – 2020 trường THPT Phan Đình Phùng – Hà Nội

Đề thi học kì 2 Toán 10 năm 2019 – 2020 trường THPT Phan Đình Phùng – Hà Nội được biên soạn theo dạng trắc nghiệm kết hợp với tự luận, trong đó phần trắc nghiệm gồm 12 câu, phần tự luận gồm 04 câu, mời các bạn đón xem

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 10

Môn: Toán 10

Thông tin:

12 trang 6 tháng trước

Tác giả:

Profile Thanh Tâm
Trang 1/2 - Mã đề 652
TRƯỜNG THPT PHAN ĐÌNH PHÙNG ĐỀ KIỂM TRA HỌC KÌ II - NĂM HỌC 2019-2020
TỔ TOÁN – TIN MÔN TOÁN LỚP 10
Thời gian làm bài: 90 phút
Họ và tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . .
PHẦN 1: TRẮC NGHIỆM (Thời gian làm bài: 25 phút) (3 điểm)
Câu 1. Điều kiện cần và đủ của tham số
m
để biểu thức
( )
22
2 45f x x mx m m=− +−+
nhận giá trị dương
với mọi
x ∈
là
A.
5
4
m <
. B.
5
4
m ≤
. C.
5
4
m >
. D.
5
4
m ≥
.
Câu 2. Thống kê điểm thi của
30
em học sinh đứng đầu kì thi học sinh giỏi Toán (thang điểm là
20
),
kết quả được cho trong bảng sau đây
.
Mốt của bảng phân bố đã cho là
A.
19
. B.
3
. C.
. D.
11
.
Câu 3. Trong mặt phẳng toạ độ
Oxy
, một véc tơ chỉ phương của đường thẳng
d
đi qua hai điểm
( )
2; 3A
và
( )
3;1B
là
A.
( )
2; 1u = −
. B.
( )
1; 2u = −
. C.
( )
2;1u =
. D.
( )
1; 2u =
.
Câu 4. Tập nghiệm của bất phương trình
22xx− >−
là
A.
( )
;5−∞
. B.
( )
;2−∞
. C.
(
]
;2−∞
. D.
(
]
;5−∞
.
Câu 5. Một cung tròn có số đo là
120°
. Số đo theo đơn vị radian của cung tròn đó là
A.
6
π
. B.
2
3
π
. C.
5
6
π
. D.
4
3
π
.
Câu 6. Nhị thức
32x−−
nhận giá trị dương khi
A.
3
2
x <−
. B.
2
3
x >−
. C.
2
3
x <−
. D.
3
2
x >−
.
Câu 7. Với điều kiện tồn tại của các biểu thức, khẳng định nào sau đây sai?
A.
( )
cos cos
πα α
+=−
. B.
( )
sin sin
πα α
−=
.
C.
tan cot
2
π
αα

−=


. D.
( )
tan tan
πα α
+=−
.
Câu 8. Trong mặt phẳng toạ độ
Oxy
, khoảng cách từ điểm
( )
2;2I
đến đường thẳng
:12 5 –10 0d xy+=
là
A.
24
13
. B.
34
13
. C.
43
13
. D.
42
13
.
Mã đề 652
Trang 2/2 - Mã đề 652
Câu 9. Trong mặt phẳng toạ độ
Oxy
, cho ba điểm
( )
4;0A
,
( )
0;2B
,
8 16
C;
55



. Bán kính đường tròn
ngoại tiếp
ABC∆
bằng
A.
5.
B.
5
. C.
5
2
. D.
2 5.
Câu 10. Trong mặt phẳng tọa độ
Oxy
, cho điểm
( )
1; 2A
,
( )
2;3B −
,
( )
2;1C −
.Điểm
( )
,M a b Oy∈
sao
cho:
MA MB MC++
  
nhỏ nhất, khẳng định nào sau đây đúng?
A.
2b <−
. B.
03b<<
. C.
20b−< <
. D.
3b >
.
Câu 11. Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A như sau:
Điểm
3
4
5
6
7
8
9
10
Cộng
Số học sinh
2
3
7
18
3
2
4
1
40
Số trung vị
( )
e
M
của bảng số liệu trên là
A.
8
e
M =
. B.
5
e
M =
. C.
7
e
M =
. D.
6
e
M =
.
Câu 12. Tam thức
2
23xx−−
nhận giá trị không âm khi
A.
–1 3x≤≤
. B.
–1x ≤
hoặc
3x ≥
. C.
–1 3x<<
. D.
–1x <
hoặc
3x >
.
PHẦN 2: TỰ LUẬN (Thời gian làm bài: 65 phút) (7 điểm)
Câu 1 (1 điểm): Tìm tập xác định của hàm số
a)
21
3
x
y
x
+
=
−
. b)
2
23
4 12 9
x
y
xx
−
=
−+
.
Câu 2: (1,5 điểm) Giải bất phương trình:
a)
23
2
2
x
x
−−
>
+
. b)
(
)
22
3 1 2. 6 8 0xx x x x−+−− − +<
.
Câu 3. (2,5 điểm)
a) Cho tam thức bậc
2
:
( )
2
2 4 53f x x mx m= − −+
với
m
là tham số thực. Tìm
m
để
( )
fx
nhận
giá trị không âm với mọi
x ∈
.
b) Cho
3
sin
5
a =
với
2
a
π
π
<<
. Tính
tan
3
a
π

−


.
c) Rút gọn biểu thức:
( ) ( ) ( )
3 2019 3
cos 2020 2sin 7 cos cos cos
.cot 8
22 2
A
π ππ
α π απ α α απ

= + − −− − + + − −


Câu 4. (2,0 điểm)
Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
G
là trọng tâm và tọa độ các đỉnh
( )
1;1A −
,
( )
1; 7B
,
( )
3; 2C −
.
a) Viết phương trình đường tròn tâm
G
và tiếp xúc với cạnh
AC
.
b) Tính góc giữa hai đường thẳng
AB
và
AC
.
c) Cho điểm
( )
,M mn
thay đổi thỏa mãn
2MG =
và số thực
p
thay đổi.Tìm giá trị nhỏ nhất của
biểu thức
( ) ( )
22
1E mp n= − ++
.
----------HẾT----------
Trang 1/2 - Mã đề 653
TRƯỜNG THPT PHAN ĐÌNH PHÙNG ĐỀ KIỂM TRA HỌC KÌ II - NĂM HỌC 2019-2020
TỔ TOÁN – TIN MÔN TOÁN LỚP 10
Thời gian làm bài: 90 phút
PHẦN 1: TRẮC NGHIỆM (Thời gian làm bài: 25 phút) (3 điểm)
Câu 1. Trong mặt phẳng toạ độ
Oxy
, một véc tơ chỉ phương của đường thẳng
d
đi qua hai điểm
( )
2; 3A
và
( )
3;1B
là
A.
( )
2; 1u = −
. B.
( )
1; 2u =
. C.
( )
2;1u =
. D.
( )
1; 2u = −
.
Câu 2. Thống kê điểm thi của
30
em học sinh đứng đầu kì thi học sinh giỏi Toán (thang điểm là
20
),
kết quả được cho trong bảng sau đây
.
Mốt của bảng phân bố đã cho là
A.
19
. B.
11
. C.
. D.
3
.
Câu 3. Trong mặt phẳng toạ độ
Oxy
, cho ba điểm
( )
4;0A
,
( )
0;2B
,
8 16
C;
55



. Bán kính đường tròn
ngoại tiếp
ABC∆
bằng
A.
5
2
. B.
5
. C.
5.
D.
2 5.
Câu 4. Một cung tròn có số đo là
120°
. Số đo theo đơn vị radian của cung tròn đó là
A.
5
6
π
. B.
2
3
π
. C.
6
π
. D.
4
3
π
.
Câu 5. Tam thức
2
23xx−−
nhận giá trị không âm khi
A.
–1 3x<<
. B.
–1x ≤
hoặc
3x ≥
.
C.
–1 3x≤≤
. D.
–1x <
hoặc
3x >
.
Câu 6. Trong mặt phẳng tọa độ
Oxy
, cho điểm
( )
1; 2A
,
( )
2;3B −
,
( )
2;1C −
.Điểm
( )
,M a b Oy∈
sao
cho:
MA MB MC++
  
nhỏ nhất, khẳng định nào sau đây đúng?
A.
2b <−
. B.
20b−< <
. C.
3b >
. D.
03b<<
.
Câu 7. Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A như sau:
Điểm
3
4
5
6
7
8
9
10
Cộng
Số học sinh
2
3
7
18
3
2
4
1
40
Số trung vị
( )
e
M
của bảng số liệu trên là
A.
7
e
M =
. B.
5
e
M =
. C.
8
e
M =
. D.
6
e
M =
.
Câu 8. Điều kiện cần và đủ của tham số
m
để biểu thức
22
() 2 4 5f x x mx m m=− +−+
nhận giá trị
dương với mọi
x ∈
là
A.
5
4
m <
. B.
5
4
m >
. C.
5
4
m ≤
. D.
5
4
m ≥
.
Mã đề 653
Họ và tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . .
Trang 2/2 - Mã đề 653
Câu 9. Nhị thức
32x−−
nhận giá trị dương khi
A.
2
3
x <−
. B.
3
2
x <−
. C.
3
2
x >−
. D.
2
3
x >−
.
Câu 10. Trong mặt phẳng toạ độ
Oxy
, khoảng cách từ điểm
( )
2;2I
đến đường thẳng
:12 5 –10 0d xy+=
là
A.
43
13
. B.
24
13
. C.
42
13
. D.
34
13
.
Câu 11. Tập nghiệm của bất phương trình
22xx− >−
là
A.
(
]
;2−∞
. B.
( )
;5−∞
. C.
(
]
;5−∞
. D.
( )
;2−∞
.
Câu 12. Với điều kiện tồn tại các biểu thức, khẳng định nào sau đây sai?
A.
tan cot
2
π
αα

−=


. B.
( )
cos cos
πα α
+=−
.
C.
( )
tan tan
πα α
+=−
. D.
( )
sin sin
πα α
−=
.
PHẦN 2: TỰ LUẬN (Thời gian làm bài: 65 phút) (7 điểm)
Câu 1 (1 điểm): Tìm tập xác định của hàm số
a)
21
3
x
y
x
+
=
−
.
b)
2
23
4 12 9
x
y
xx
−
=
−+
.
Câu 2: (1,5 điểm) Giải bất phương trình:
a)
23
2
2
x
x
−−
>
+
.
b)
(
)
22
3 1 2. 6 8 0xx x x x−+−− − +<
.
Câu 3. (2,5 điểm)
a) Cho tam thức bậc
2
:
( )
2
2 4 53f x x mx m= − −+
với
m
là tham số thực. Tìm
m
để
( )
fx
nhận
giá trị không âm với mọi
x ∈
.
b) Cho
3
sin
5
a =
với
2
a
π
π
<<
. Tính
tan
3
a
π

−


.
c) Rút gọn biểu thức:
( ) ( ) ( )
3 2019 3
cos 2020 2sin 7 cos cos cos
.cot 8
22 2
A
π ππ
α π απ α α απ

= + − −− − + + − −


Câu 4. (2,0 điểm)
Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
G
là trọng tâm và tọa độ các đỉnh
( )
1;1A −
,
( )
1; 7B
,
( )
3; 2C −
.
a) Viết phương trình đường tròn tâm
G
và tiếp xúc với cạnh
AC
.
b) Tính góc giữa hai đường thẳng
AB
và
AC
.
c. Cho điểm
( )
,M mn
thay đổi thỏa mãn
2MG =
và số thực
p
thay đổi.Tìm giá trị nhỏ nhất của
biểu thức
( ) ( )
22
1E mp n= − ++
.
----------HẾT----------
Trang 1/2 - Mã đề 654
TRƯỜNG THPT PHAN ĐÌNH PHÙNG ĐỀ KIỂM TRA HỌC KÌ II - NĂM HỌC 2019-2020
TỔ TOÁN – TIN MÔN TOÁN LỚP 10
Thời gian làm bài: 90 phút
PHẦN 1: TRẮC NGHIỆM (Thời gian làm bài: 25 phút) (3 điểm)
Câu 1. Một cung tròn có số đo là
120°
. Số đo theo đơn vị radian của cung tròn đó là
A.
4
3
π
. B.
2
3
π
. C.
5
6
π
. D.
6
π
.
Câu 2. Trong mặt phẳng toạ độ
Oxy
, cho ba điểm
( )
4;0A
,
( )
0;2B
,
8 16
C;
55



. Bán kính đường tròn
ngoại tiếp
ABC∆
bằng
A.
2 5.
B.
5
. C.
5
2
. D.
5.
Câu 3. Tập nghiệm của bất phương trình
22xx− >−
là
A.
(
]
;5−∞
. B.
( )
;2−∞
. C.
(
]
;2−∞
. D.
( )
;5−∞
.
Câu 4. Với điều kiện tồn tại của các biểu thức, khẳng định nào sau đây sai?
A.
( )
tan tan
πα α
+=−
. B.
( )
sin sin
πα α
−=
.
C.
tan cot
2
π
αα

−=


. D.
( )
cos cos
πα α
+=−
.
Câu 5. Trong mặt phẳng toạ độ
Oxy
, khoảng cách từ điểm
( )
2;2I
đến đường thẳng
:12 5 –10 0d xy+=
là
A.
42
13
. B.
34
13
. C.
43
13
. D.
24
13
.
Câu 6. Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A như sau:
Điểm
3
4
5
6
7
8
9
10
Cộng
Số học sinh
2
3
7
18
3
2
4
1
40
Số trung vị
( )
e
M
của bảng số liệu trên là
A.
6
e
M =
. B.
5
e
M =
. C.
7
e
M =
. D.
8
e
M =
.
Câu 7. Trong mặt phẳng tọa độ
Oxy
, cho điểm
( )
1; 2A
,
( )
2;3B −
,
( )
2;1C −
.Điểm
( )
,M a b Oy∈
sao
cho:
MA MB MC++
  
nhỏ nhất, khẳng định nào sau đây đúng?
A.
03b<<
. B.
3b >
. C.
2b <−
. D.
20b−< <
.
Câu 8. Tam thức
2
23xx−−
nhận giá trị không âm khi
A.
–1x <
hoặc
3x >
. B.
–1 3x≤≤
. C.
–1x ≤
hoặc
3x ≥
. D.
–1 3x<<
.
Câu 9. Điều kiện cần và đủ của tham số
m
để biểu thức
( )
22
2 45f x x mx m m=− +−+
nhận giá trị dương
với mọi
x ∈
là
A.
5
4
m ≥
. B.
5
4
m ≤
. C.
5
4
m >
. D.
5
4
m <
.
Mã đề 654
Họ và tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . .
Trang 2/2 - Mã đề 654
Câu 10. Nhị thức
32x−−
nhận giá trị dương khi
A.
3
2
x >−
. B.
3
2
x <−
. C.
2
3
x >−
. D.
2
3
x <−
.
Câu 11. Thống kê điểm thi của
30
em học sinh đứng đầu kì thi học sinh giỏi Toán (thang điểm là
20
) ,
kết quả được cho trong bảng sau đây
.
Mốt của bảng phân bố đã cho là
A.
3
. B.
17
. C.
11
. D.
19
.
Câu 12. Trong mặt phẳng toạ độ
Oxy
, một véc tơ chỉ phương của đường thẳng
d
đi qua hai điểm
( )
2; 3A
và
( )
3;1B
là
A.
( )
1; 2u = −
. B.
( )
2;1u =
. C.
( )
1; 2u =
. D.
( )
2; 1u = −
.
PHẦN 2: TỰ LUẬN (Thời gian làm bài: 65 phút) (7 điểm)
Câu 1 (1 điểm): Tìm tập xác định của hàm số
a)
21
3
x
y
x
+
=
−
.
b)
2
23
4 12 9
x
y
xx
−
=
−+
.
Câu 2: (1,5 điểm) Giải bất phương trình:
a)
23
2
2
x
x
−−
>
+
.
b)
(
)
22
3 1 2. 6 8 0xx x x x−+−− − +<
.
Câu 3. (2,5 điểm)
a) Cho tam thức bậc
2
:
( )
2
2 4 53f x x mx m= − −+
với
m
là tham số thực. Tìm
m
để
( )
fx
nhận
giá trị không âm với mọi
x ∈
.
b) Cho
3
sin
5
a =
với
2
a
π
π
<<
. Tính
tan
3
a
π

−


.
c) Rút gọn biểu thức:
( ) ( )
( )
3 2019 3
cos 2020 2sin 7 cos cos cos
.cot 8
22 2
A
π ππ
α π απ α α απ

= + − −− − + + − −


Câu 4. (2,0 điểm)
Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
G
là trọng tâm và tọa độ các đỉnh
( )
1;1A −
,
( )
1; 7B
,
( )
3; 2C −
.
a) Viết phương trình đường tròn tâm
G
và tiếp xúc với cạnh
AC
.
b) Tính góc giữa hai đường thẳng
AB
và
AC
.
c) Cho điểm
( )
,M mn
thay đổi thỏa mãn
2MG =
và số thực
p
thay đổi.Tìm giá trị nhỏ nhất của
biểu thức
( ) ( )
22
1E mp n= − ++
.
----------HẾT----------
Trang 1/2 - Mã đề 655
TRƯỜNG THPT PHAN ĐÌNH PHÙNG ĐỀ KIỂM TRA HỌC KÌ II - NĂM HỌC 2019-2020
TỔ TOÁN – TIN MÔN TOÁN LỚP 10
Thời gian làm bài: 90 phút
PHẦN 1: TRẮC NGHIỆM (Thời gian làm bài: 25 phút) (3 điểm)
Câu 1. Với điều kiện tồn tại của các biểu thức, khẳng định nào sau đây sai?
A.
( )
tan tan
πα α
+=−
. B.
( )
cos cos
πα α
+=−
.
C.
( )
sin sin
πα α
−=
. D.
tan cot
2
π
αα

−=


.
Câu 2. Trong mặt phẳng toạ độ
Oxy
, khoảng cách từ điểm
( )
2;2I
đến đường thẳng
:12 5 –10 0d xy+=
là
A.
42
13
. B.
24
13
. C.
34
13
. D.
43
13
.
Câu 3. Nhị thức
32x−−
nhận giá trị dương khi
A.
3
2
x >−
. B.
3
2
x <−
. C.
2
3
x >−
. D.
2
3
x <−
.
Câu 4. Tập nghiệm của bất phương trình
22xx− >−
là
A.
(
]
;5−∞
. B.
( )
;5−∞
. C.
( )
;2−∞
. D.
(
]
;2−∞
.
Câu 5. Trong mặt phẳng toạ độ
Oxy
, một véc tơ chỉ phương của đường thẳng
d
đi qua hai điểm
( )
2; 3A
và
( )
3;1B
là
A.
( )
1; 2u = −
. B.
( )
2;1u =
. C.
( )
1; 2u =
. D.
( )
2; 1u = −
.
Câu 6. Điều kiện cần và đủ của tham số
m
để biểu thức
22
() 2 4 5f x x mx m m=− +−+
nhận giá trị
dương với mọi
x ∈
là
A.
5
4
m ≥
. B.
5
4
m ≤
. C.
5
4
m >
. D.
5
4
m <
.
Câu 7. Tam thức
2
23xx−−
nhận giá trị không âm khi
A.
–1x <
hoặc
3x >
. B.
–1 3x≤≤
. C.
–1x ≤
hoặc
3x ≥
. D.
–1 3x<<
.
Câu 8. Trong mặt phẳng toạ độ
Oxy
, cho ba điểm
( )
4;0A
,
( )
0;2B
,
8 16
C;
55



. Bán kính đường tròn
ngoại tiếp
ABC∆
bằng
A.
2 5.
B.
5.
C.
5
. D.
5
2
.
Câu 9. Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A như sau:
Điểm
3
4
5
6
7
8
9
10
Cộng
Số học sinh
2
3
7
18
3
2
4
1
40
Số trung vị
( )
e
M
của bảng số liệu trên là
A.
8
e
M =
. B.
5
e
M =
. C.
7
e
M =
. D.
6
e
M =
.
Mã đề 655
Họ và tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . .
Trang 2/2 - Mã đề 655
Câu 10. Một cung tròn có số đo là
120°
. Số đo theo đơn vị radian của cung tròn đó là
A.
6
π
. B.
2
3
π
. C.
5
6
π
. D.
4
3
π
.
Câu 11. Trong mặt phẳng tọa độ
Oxy
, cho điểm
( )
1; 2A
,
( )
2;3B −
,
( )
2;1C −
.Điểm
( )
,M a b Oy∈
sao
cho:
MA MB MC++
  
nhỏ nhất, khẳng định nào sau đây đúng?
A.
20b−< <
. B.
2b <−
. C.
3b >
. D.
03b<<
.
Câu 12. Thống kê điểm thi của
30
em học sinh đứng đầu tham dự kì thi học sinh giỏi Toán (thang điểm
là
20
), kết quả được cho trong bảng sau đây
Mốt của bảng phân bố đã cho là
A.
17
. B.
11
. C.
19
. D.
3
.
PHẦN 2: TỰ LUẬN (Thời gian làm bài: 65 phút) (7 điểm)
Câu 1 (1 điểm): Tìm tập xác định của hàm số
a)
21
3
x
y
x
+
=
−
. b)
2
23
4 12 9
x
y
xx
−
=
−+
.
Câu 2: (1,5 điểm) Giải bất phương trình:
a)
23
2
2
x
x
−−
>
+
. b)
(
)
22
3 1 2. 6 8 0xx x x x−+−− − +<
.
Câu 3. (2,5 điểm)
a) Cho tam thức bậc
2
:
( )
2
2 4 53f x x mx m= − −+
với
m
là tham số thực. Tìm
m
để
( )
fx
nhận
giá trị không âm với mọi
x ∈
.
b) Cho
3
sin
5
a =
với
2
a
π
π
<<
. Tính
tan
3
a
π

−


.
c) Rút gọn biểu thức:
( ) ( ) ( )
3 2019 3
cos 2020 2sin 7 cos cos cos
.cot 8
22 2
A
π ππ
α π απ α α απ

= + − −− − + + − −


Câu 4. (2,0 điểm)
Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
G
là trọng tâm và tọa độ các đỉnh
( )
1;1A −
,
( )
1; 7B
,
( )
3; 2C −
.
a) Viết phương trình đường tròn tâm
G
và tiếp xúc với cạnh
AC
.
b) Tính góc giữa hai đường thẳng
AB
và
AC
.
c) Cho điểm
( )
,M mn
thay đổi thỏa mãn
2MG =
và số thực
p
thay đổi.Tìm giá trị nhỏ nhất của
biểu thức
( ) ( )
22
1E mp n= − ++
.
----------HẾT----------
Trang 1/4 – Đề chính thức
TRƯỜNG THPT PHAN ĐINH PHÙNG
TỔ TOÁN – TIN
KIỂM TRA HỌC KÌ II – NĂM HỌC 2019 - 2020
MÔN TOÁN LỚP 10
Thời gian làm bài : 90 Phút.
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
A. ĐÁP ÁN TRẮC NGHIỆM:
MĐ
Câu
ĐA
MĐ
Câu
ĐA
MĐ
Câu
ĐA
MĐ
Câu
ĐA
652
1
A
653
1
D
654
1
B
655
1
A
652
2
C
653
2
C
654
2
D
655
2
B
652
3
B
653
3
C
654
3
B
655
3
D
652
4
B
653
4
B
654
4
A
655
4
C
652
5
B
653
5
B
654
5
D
655
5
A
652
6
C
653
6
D
654
6
A
655
6
D
652
7
D
653
7
D
654
7
A
655
7
C
652
8
A
653
8
A
654
8
C
655
8
B
652
9
A
653
9
A
654
9
D
655
9
D
652
10
B
653
10
B
654
10
D
655
10
B
652
11
D
653
11
D
654
11
B
655
11
D
652
12
B
653
12
C
654
12
A
655
12
A
B. HƯỚNG DẪN CHẤM PHẦN TỰ LUẬN
CÂU
NỘI DUNG
ĐIỂM
Câu 1
(1,0đ)
1a.(0,5đ) Tìm tập xác định của hàm số
21
3
x
y
x
.
Điều kiện xác định:
3 0 3xx
.
KL: Tập xác định:
\3D
.
0,25đ
0,25đ
1b.0,5đ) Tìm tập xác định của hàm số
2
23
4 12 9
x
y
xx

Điều kiện xác định:
2
4 12 9 0xx
2
2
3
4 12 9 0 2 3 0
2
x x x x
.
KL: Tập xác định:
3
\
2
D



.
0,25đ
0,25đ
Câu 2
1,5(đ)
2a.(1,0đ) Giải bất phương trình
23
2
2
x
x

.
Đk:
2x 
*
.
BPT
2 3 4 7
2 0 0
22
xx
xx

.
Lập bảng xét dấu
x
2
7
4
47x
+
+
0
2x
0
+
+
47
2
x
x

||
+
0
0,25
0,5
Theo bảng ta có
4 7 7
0 2;
24
x
x
x




.
0,25
Trang 2/4 – Đề chính thức
2b.(0,5đ) Giải bất phương trình
22
3 1 2 . 6 8 0x x x x x
.
Bất phương trình tương đương với
2
2
6 8 0
3 1 2
xx
x x x
2
;2 4; 1
3 1 2 2
x
x x x

Xét
2
:
2
22
20
3 1 2
3 1 4 4
x
x x x
x x x x

2
2
1
2 5 3 0 ;3
2
x
x x x




1
;3
2
x



.
Kết hợp nghiệm ta được
1
;2
2
x




.
0,25
0,25
Câu 3
(2,5đ)
3a.(0,5đ) Cho tam thức bậc 2:
2
2 4 5 3f x x mx m
với
m
là tham số thực.
Tìm
m
để
fx
nhận giá trị không âm với mọi
x
.
Điều kiện đề bài
2
20
0
0
4 8 5 3 0
a
mm



0,25
2
1
16 40 24 0 3;
2
m m m



.
0,25
3b.(1,0đ) Cho
3
sin
5
a
với
2
a

. Tính
tan
3
a



.
Có
22
3
sin
5
sin cos 1
: cos 0
2
a
aa
aa

4
cos
5
a
0,5
Khi đó:
3
tan
4
a 
.
Ta có
3
tan tan
3
4 3 3
3
4
tan
3
3 3 4 3 3
1 tan .tan
1
3
4
a
a
a



0,25
0,25
3c.(1,0đ) Rút gọn biểu thức:
3 2019
cos 2020 2sin 7 cos cos
22
A




3
cos .cot 8
2



3
cos 2020 2sin 8 cos cos 1010
22




cos 2 .cot 8
2



0,25
Trang 3/4 – Đề chính thức
cos 2sin cos cos .cot
22

cos 2sin cos cos .cot
22

cos
cos 2sin sin sin .
sin
sin
.
0,25
0,25
0,25đ
Câu 4
(2,0đ)
Câu 4.(2,0đ) Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
G
là trọng tâm
và tọa độ các đỉnh
1;1A
,
1;7B
,
3; 2C
.
4a.(1,0đ) Viết phương trình đường tròn tâm
G
và tiếp xúc với cạnh
AC
.
Ta có đường thẳng
AC
đi qua
(1;2)A
và nhận
(4; 3)AC 
làm VTCP nên nhận
(3;4)n
là VTPT.
Phương trình tổng quát đường thẳng
AC
:
3( 1) 4( 1) 0xy
3 4 1 0xy
Tính được
(1;2)G
( ; ) 2d G AC
.
Vậy phương trình đường tròn tâm
G
và tiếp xúc với cạnh
AC
là:
22
( 1) ( 2) 4xy
C
.
0,25đ
0,25đ
0,25đ
0,25đ
4b.(0,5đ) Tính góc giữa 2 đường thẳng
AB
và
AC
.
Ta có:
(2;6)AB
;
(4; 3)AC 
.
Gọi
là góc giữa hai đường thẳng
AB
và
AC
.
2
2 2 2
2.3 6 3
1
cos cos( , )
10
2 6 3 4
AB AC

o
71 33

.
0,25đ
0,25đ
4c.(0,5đ)Cho điểm
,M m n
thay đổi thỏa mãn
2MG
và số thực
p
thay
đổi.Tìm giá trị nhỏ nhất của biểu thức
22
1E m p n
.
Với
,M m n
,
;1Np
. Nhận xét :
,M m n C
,
;1N p d
:
1y 
và
22
1E m p n
.
Bài toán thành: Tìm điểm
MC
,
Nd
sao cho
MN
nhỏ nhất.
0,25đ
Trang 4/4 – Đề chính thức
min
, 3 2 1MN d G d R
khi
1, 1N
( Hình chiếu của
G
trên
d
) và
1;0M
.
( Không chỉ ra tọa độ điểm
M
,
N
vẫn có thể cho điểm tối đa).
0,25đ
Lưu ý:Tổ chấm có thể thống nhất lại hướng dẫn chấm cho phù hợp. Thí sinh làm cách khác mà
đúng thì vẫn cho điểm tối đa.
-------------HẾT------------
| 1/12
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT PHAN ĐÌNH PHÙNG
ĐỀ KIỂM TRA HỌC KÌ II - NĂM HỌC 2019-2020 TỔ TOÁN – TIN MÔN TOÁN LỚP 10
Thời gian làm bài: 90 phút
Họ và tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . Mã đề 652
PHẦN 1: TRẮC NGHIỆM (Thời gian làm bài: 25 phút) (3 điểm) Câu 1.
Điều kiện cần và đủ của tham số m để biểu thức f (x) 2 2
= x − 2mx + m − 4m + 5 nhận giá trị dương
với mọi x ∈  là 5 5 5 5 A. m < . B. m ≤ . C. m > . D. m ≥ . 4 4 4 4 Câu 2.
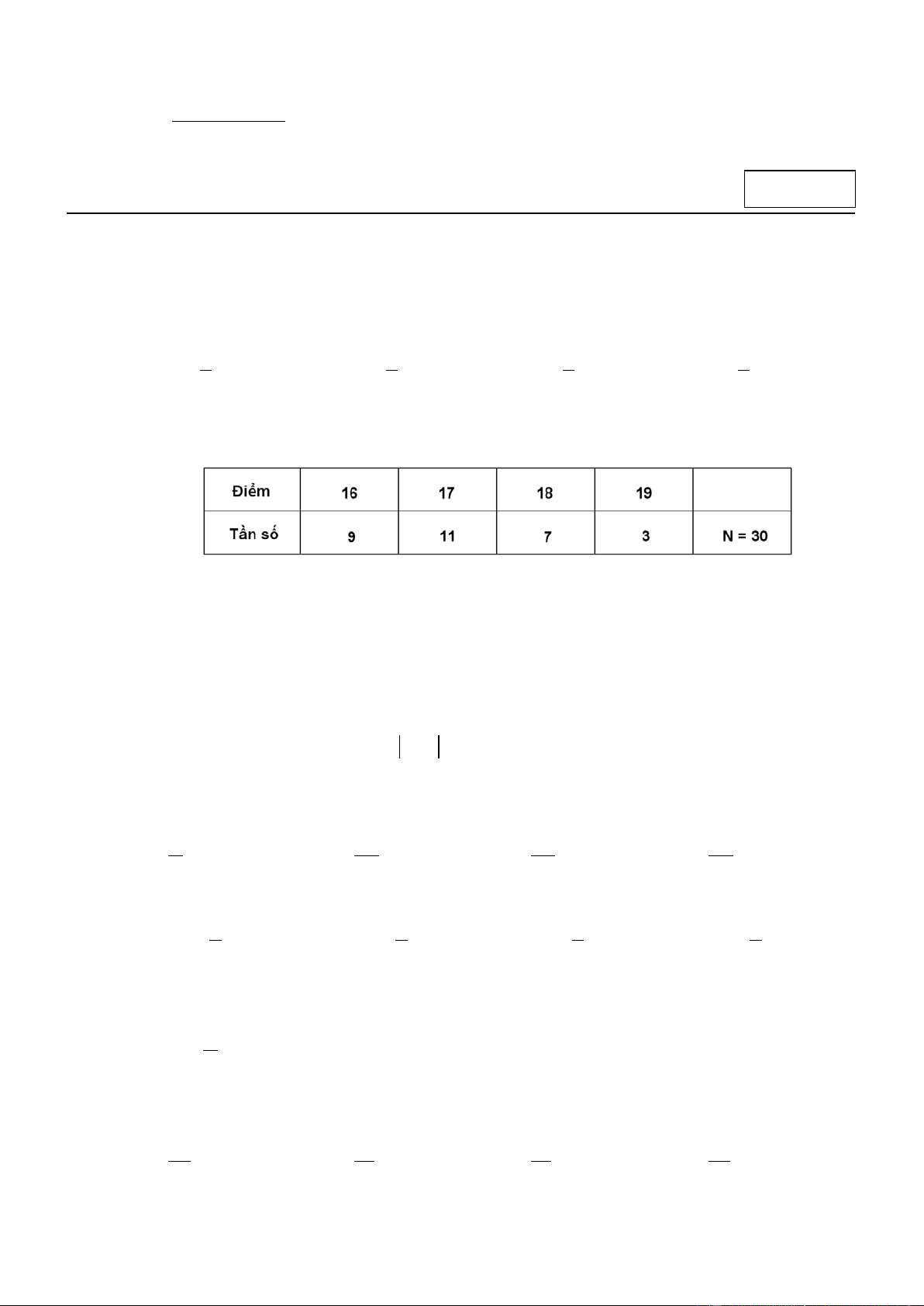
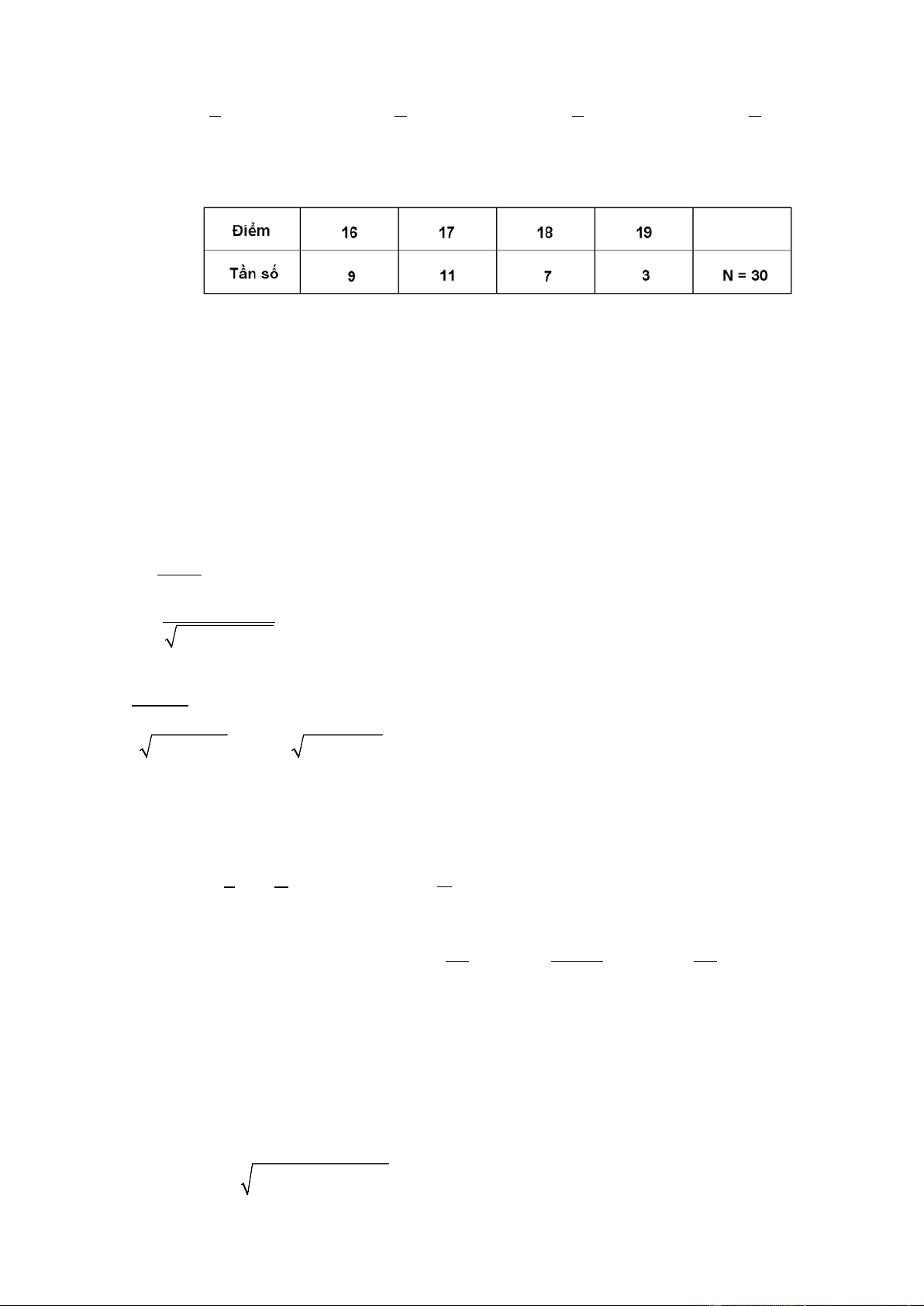
Thống kê điểm thi của 30 em học sinh đứng đầu kì thi học sinh giỏi Toán (thang điểm là 20 ),
kết quả được cho trong bảng sau đây .
Mốt của bảng phân bố đã cho là A. 19 . B. 3 . C. 17 . D. 11. Câu 3.
Trong mặt phẳng toạ độ Oxy , một véc tơ chỉ phương của đường thẳng d đi qua hai điểm
A(2; 3) và B(3; ) 1 là     A. u = (2; − ) 1 . B. u = (1; 2 − ) . C. u = (2; ) 1 . D. u = (1; 2) . Câu 4.
Tập nghiệm của bất phương trình 2 − x > x − 2 là A. ( ; −∞ 5) . B. ( ; −∞ 2) . C. ( ; −∞ 2] . D. ( ; −∞ 5]. Câu 5.
Một cung tròn có số đo là 120° . Số đo theo đơn vị radian của cung tròn đó là π 2π 5π 4π A. . B. . C. . D. . 6 3 6 3 Câu 6. Nhị thức 3
− x − 2 nhận giá trị dương khi 3 2 2 3 A. x < − . B. x > − .
C. x < − . D. x > − . 2 3 3 2 Câu 7.
Với điều kiện tồn tại của các biểu thức, khẳng định nào sau đây sai?
A. cos (π + α ) = − cosα .
B. sin (π −α ) = sinα .  π  C. tan −α = cotα   .
D. tan (π + α ) = − tanα .  2  Câu 8.
Trong mặt phẳng toạ độ Oxy , khoảng cách từ điểm I (2; 2) đến đường thẳng d :12x + 5y –10 = 0 là 24 34 43 42 A. . B. . C. . D. . 13 13 13 13
Trang 1/2 - Mã đề 652  8 16  Câu 9.
Trong mặt phẳng toạ độ Oxy , cho ba điểm A(4;0) , B (0; 2) , C ; 
 . Bán kính đường tròn  5 5  ngoại tiếp A ∆ BC bằng 5 A. 5. B. 5 . C. . D. 2 5. 2
Câu 10. Trong mặt phẳng tọa độ Oxy , cho điểm A(1; 2) , B ( 2; − 3) , C ( 2; − )
1 .Điểm M (a,b) ∈Oy sao
  
cho: MA + MB + MC nhỏ nhất, khẳng định nào sau đây đúng? A. b < 2 − .
B. 0 < b < 3 . C. 2 − < b < 0 . D. b > 3 .
Câu 11. Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A như sau: Điểm 3 4 5 6 7 8 9 10 Cộng Số học sinh 2 3 7 18 3 2 4 1 40
Số trung vị (Me ) của bảng số liệu trên là A. M = 8 M = M = M = e . B. 5 e . C. 7 e . D. 6 e . Câu 12. Tam thức 2
x − 2x − 3 nhận giá trị không âm khi
A. –1 ≤ x ≤ 3 .
B. x ≤ –1 hoặc x ≥ 3 . C. –1 < x < 3 .
D. x < –1 hoặc x > 3 .
PHẦN 2: TỰ LUẬN (Thời gian làm bài: 65 phút) (7 điểm)
Câu 1 (1 điểm): Tìm tập xác định của hàm số 2x +1 2x − 3 a) y = . b) y = . x − 3 2 4x −12x + 9
Câu 2: (1,5 điểm) Giải bất phương trình: 2 − x − 3 a) > 2 . b) ( 2
x − x + − x − ) 2 3 1
2 . x − 6x + 8 < 0 . x + 2 Câu 3. (2,5 điểm)
a) Cho tam thức bậc 2 : f ( x) 2
= 2x − 4mx − 5m + 3 với m là tham số thực. Tìm m để f (x) nhận
giá trị không âm với mọi x ∈  . 3 π  π  b) Cho sin a = với
< a < π . Tính tan −  a . 5 2  3  c) Rút gọn biểu thức: π  π   π A (α + π ) − (α − π ) 3 2019 3  = cos 2020 2 sin 7 − cos − cos α + + cos α − .cot     (α −8π ) 2  2   2  Câu 4. (2,0 điểm)
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có G là trọng tâm và tọa độ các đỉnh A( 1 − ; ) 1 , B(1;7) , C (3; 2 − ) .
a) Viết phương trình đường tròn tâm G và tiếp xúc với cạnh AC .
b) Tính góc giữa hai đường thẳng AB và AC . c) Cho điểm M ( ,
m n) thay đổi thỏa mãn MG = 2 và số thực p thay đổi.Tìm giá trị nhỏ nhất của 2 2
biểu thức E = (m − p) + (n + ) 1 .
----------HẾT----------
Trang 2/2 - Mã đề 652
TRƯỜNG THPT PHAN ĐÌNH PHÙNG
ĐỀ KIỂM TRA HỌC KÌ II - NĂM HỌC 2019-2020 TỔ TOÁN – TIN MÔN TOÁN LỚP 10
Thời gian làm bài: 90 phút
Họ và tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . Mã đề 653
PHẦN 1: TRẮC NGHIỆM (Thời gian làm bài: 25 phút) (3 điểm) Câu 1.
Trong mặt phẳng toạ độ Oxy , một véc tơ chỉ phương của đường thẳng d đi qua hai điểm
A(2; 3) và B(3; ) 1 là     A. u = (2; − ) 1 . B. u = (1; 2) . C. u = (2; ) 1 . D. u = (1; 2 − ) . Câu 2.
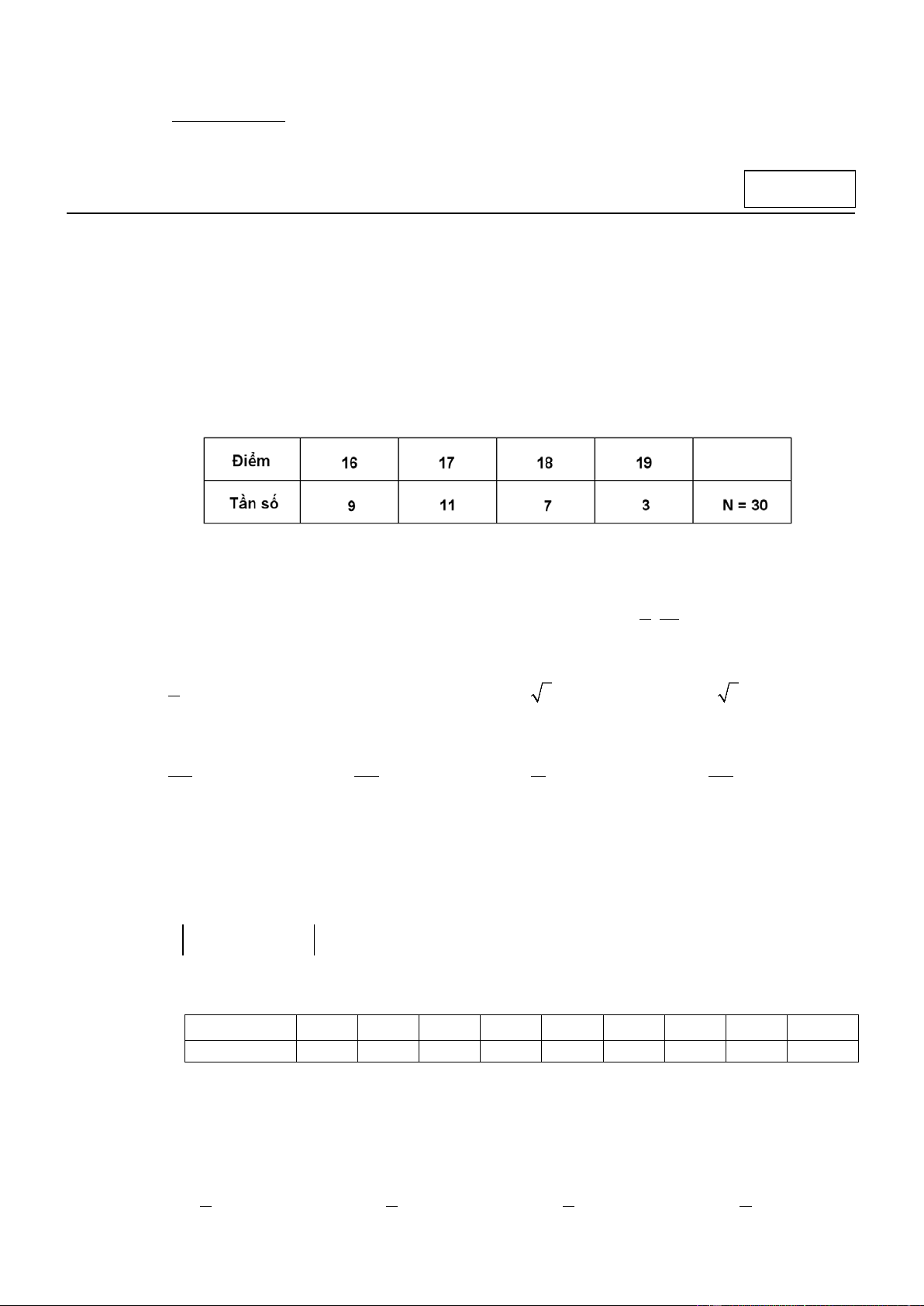
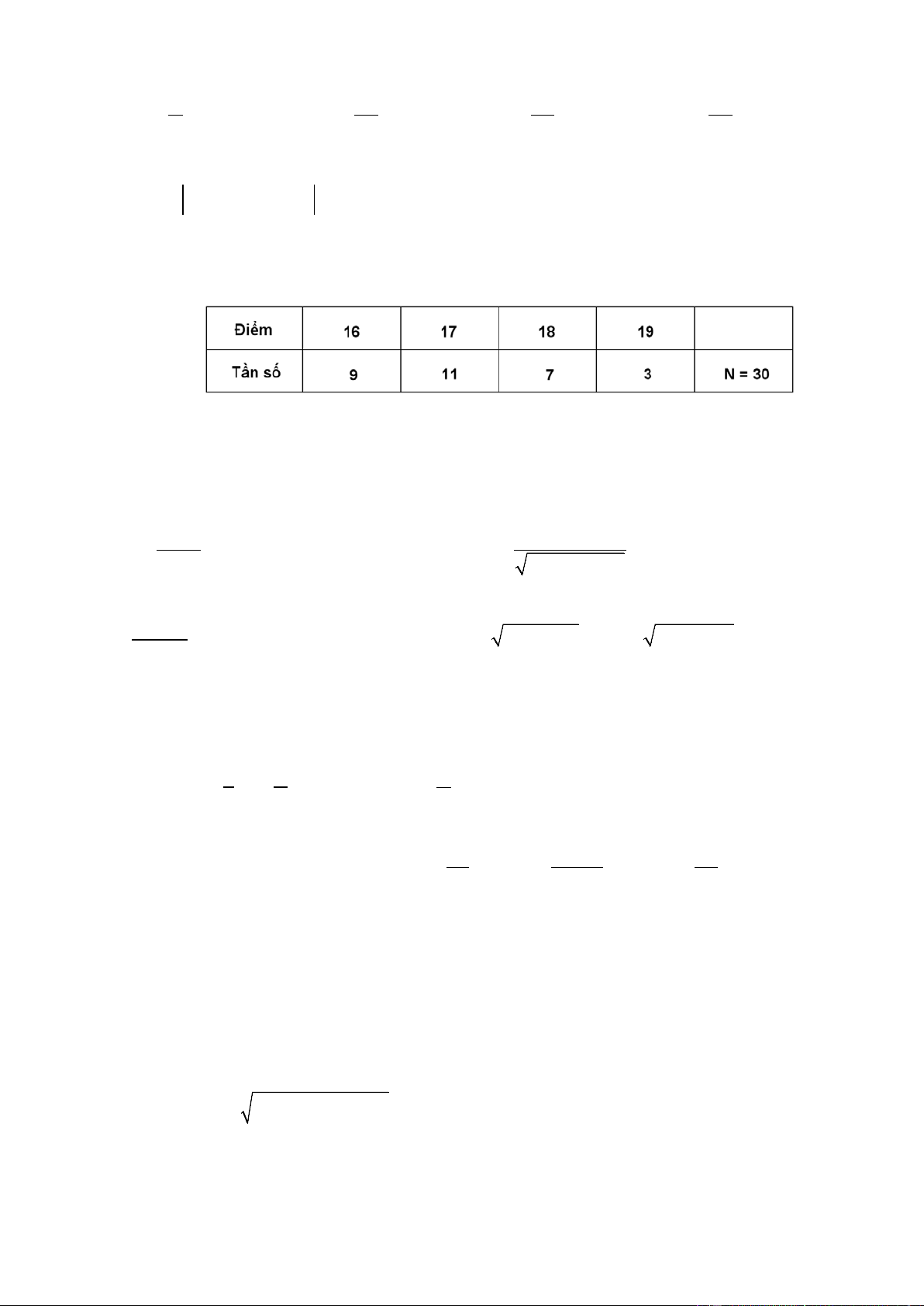
Thống kê điểm thi của 30 em học sinh đứng đầu kì thi học sinh giỏi Toán (thang điểm là 20 ),
kết quả được cho trong bảng sau đây .
Mốt của bảng phân bố đã cho là A. 19 . B. 11. C. 17 . D. 3 .  8 16  Câu 3.
Trong mặt phẳng toạ độ Oxy , cho ba điểm A(4;0) , B (0; 2) , C ; 
 . Bán kính đường tròn  5 5  ngoại tiếp A ∆ BC bằng 5 A. . B. 5 . C. 5. D. 2 5. 2 Câu 4.
Một cung tròn có số đo là 120° . Số đo theo đơn vị radian của cung tròn đó là 5π 2π π 4π A. . B. . C. . D. . 6 3 6 3 Câu 5. Tam thức 2
x − 2x − 3 nhận giá trị không âm khi
A. –1 < x < 3 .
B. x ≤ –1 hoặc x ≥ 3 .
C. –1 ≤ x ≤ 3 .
D. x < –1 hoặc x > 3 . Câu 6.
Trong mặt phẳng tọa độ Oxy , cho điểm A(1; 2) , B ( 2; − 3) , C ( 2; − )
1 .Điểm M (a,b) ∈Oy sao
  
cho: MA + MB + MC nhỏ nhất, khẳng định nào sau đây đúng? A. b < 2 − . B. 2 − < b < 0 . C. b > 3 .
D. 0 < b < 3 . Câu 7.
Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A như sau: Điểm 3 4 5 6 7 8 9 10 Cộng Số học sinh 2 3 7 18 3 2 4 1 40
Số trung vị (Me ) của bảng số liệu trên là A. M = 7 M = M = M = e . B. 5 e . C. 8 e . D. 6 e . Câu 8.
Điều kiện cần và đủ của tham số m để biểu thức 2 2
f (x) = x − 2mx + m − 4m + 5 nhận giá trị
dương với mọi x∈ là 5 5 5 5 A. m < . B. m > . C. m ≤ . D. m ≥ . 4 4 4 4
Trang 1/2 - Mã đề 653 Câu 9. Nhị thức 3
− x − 2 nhận giá trị dương khi 2 3 3 2
A. x < − . B. x < − . C. x > − . D. x > − . 3 2 2 3
Câu 10. Trong mặt phẳng toạ độ Oxy , khoảng cách từ điểm I (2; 2) đến đường thẳng d :12x + 5y –10 = 0 là 43 24 42 34 A. . B. . C. . D. . 13 13 13 13
Câu 11. Tập nghiệm của bất phương trình 2 − x > x − 2 là A. ( ; −∞ 2] . B. ( ; −∞ 5) . C. ( ; −∞ 5]. D. ( ; −∞ 2) .
Câu 12. Với điều kiện tồn tại các biểu thức, khẳng định nào sau đây sai?  π  A. tan −α = cotα   .
B. cos (π + α ) = − cosα .  2 
C. tan (π + α ) = − tanα .
D. sin (π −α ) = sinα .
PHẦN 2: TỰ LUẬN (Thời gian làm bài: 65 phút) (7 điểm)
Câu 1 (1 điểm): Tìm tập xác định của hàm số 2x +1 a) y = . x − 3 2x − 3 b) y = . 2 4x −12x + 9
Câu 2: (1,5 điểm) Giải bất phương trình: 2 − x − 3 a) > 2 . x + 2 b) ( 2
x − x + − x − ) 2 3 1
2 . x − 6x + 8 < 0 . Câu 3. (2,5 điểm)
a) Cho tam thức bậc 2 : f ( x) 2
= 2x − 4mx − 5m + 3 với m là tham số thực. Tìm m để f (x) nhận
giá trị không âm với mọi x ∈  . 3 π  π  b) Cho sin a = với
< a < π . Tính tan −  a . 5 2  3  c) Rút gọn biểu thức: π  π   π A (α + π ) − (α − π ) 3 2019 3  = cos 2020 2 sin 7 − cos − cos α + + cos α − .cot     (α −8π ) 2  2   2  Câu 4. (2,0 điểm)
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có G là trọng tâm và tọa độ các đỉnh A( 1 − ; ) 1 , B(1;7) , C (3; 2 − ) .
a) Viết phương trình đường tròn tâm G và tiếp xúc với cạnh AC .
b) Tính góc giữa hai đường thẳng AB và AC . c. Cho điểm M ( ,
m n) thay đổi thỏa mãn MG = 2 và số thực p thay đổi.Tìm giá trị nhỏ nhất của 2 2
biểu thức E = (m − p) + (n + ) 1 .
----------HẾT----------
Trang 2/2 - Mã đề 653
TRƯỜNG THPT PHAN ĐÌNH PHÙNG
ĐỀ KIỂM TRA HỌC KÌ II - NĂM HỌC 2019-2020 TỔ TOÁN – TIN MÔN TOÁN LỚP 10
Thời gian làm bài: 90 phút
Họ và tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . Mã đề 654
PHẦN 1: TRẮC NGHIỆM (Thời gian làm bài: 25 phút) (3 điểm) Câu 1.
Một cung tròn có số đo là 120° . Số đo theo đơn vị radian của cung tròn đó là 4π 2π 5π π A. . B. . C. . D. . 3 3 6 6  8 16  Câu 2.
Trong mặt phẳng toạ độ Oxy , cho ba điểm A(4;0) , B (0; 2) , C ; 
 . Bán kính đường tròn  5 5  ngoại tiếp A ∆ BC bằng 5 A. 2 5. B. 5 . C. . D. 5. 2 Câu 3.
Tập nghiệm của bất phương trình 2 − x > x − 2 là A. ( ; −∞ 5]. B. ( ; −∞ 2) . C. ( ; −∞ 2] . D. ( ; −∞ 5) . Câu 4.
Với điều kiện tồn tại của các biểu thức, khẳng định nào sau đây sai?
A. tan (π + α ) = − tanα .
B. sin (π −α ) = sinα .  π  C. tan −α = cotα   .
D. cos (π + α ) = − cosα .  2  Câu 5.
Trong mặt phẳng toạ độ Oxy , khoảng cách từ điểm I (2; 2) đến đường thẳng d :12x + 5y –10 = 0 là 42 34 43 24 A. . B. . C. . D. . 13 13 13 13 Câu 6.
Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A như sau: Điểm 3 4 5 6 7 8 9 10 Cộng Số học sinh 2 3 7 18 3 2 4 1 40
Số trung vị (Me ) của bảng số liệu trên là A. M = 6 M = M = M = e . B. 5 e . C. 7 e . D. 8 e . Câu 7.
Trong mặt phẳng tọa độ Oxy , cho điểm A(1; 2) , B ( 2; − 3) , C ( 2; − )
1 .Điểm M (a,b) ∈Oy sao
  
cho: MA + MB + MC nhỏ nhất, khẳng định nào sau đây đúng?
A. 0 < b < 3 . B. b > 3 . C. b < 2 − . D. 2 − < b < 0 . Câu 8. Tam thức 2
x − 2x − 3 nhận giá trị không âm khi
A. x < –1 hoặc x > 3 . B. –1 ≤ x ≤ 3 .
C. x ≤ –1 hoặc x ≥ 3 . D. –1 < x < 3 . Câu 9.
Điều kiện cần và đủ của tham số m để biểu thức f (x) 2 2
= x − 2mx + m − 4m + 5 nhận giá trị dương
với mọi x ∈  là 5 5 5 5 A. m ≥ . B. m ≤ . C. m > . D. m < . 4 4 4 4
Trang 1/2 - Mã đề 654 Câu 10. Nhị thức 3
− x − 2 nhận giá trị dương khi 3 3 2 2 A. x > − . B. x < − . C. x > − . D. x < − . 2 2 3 3
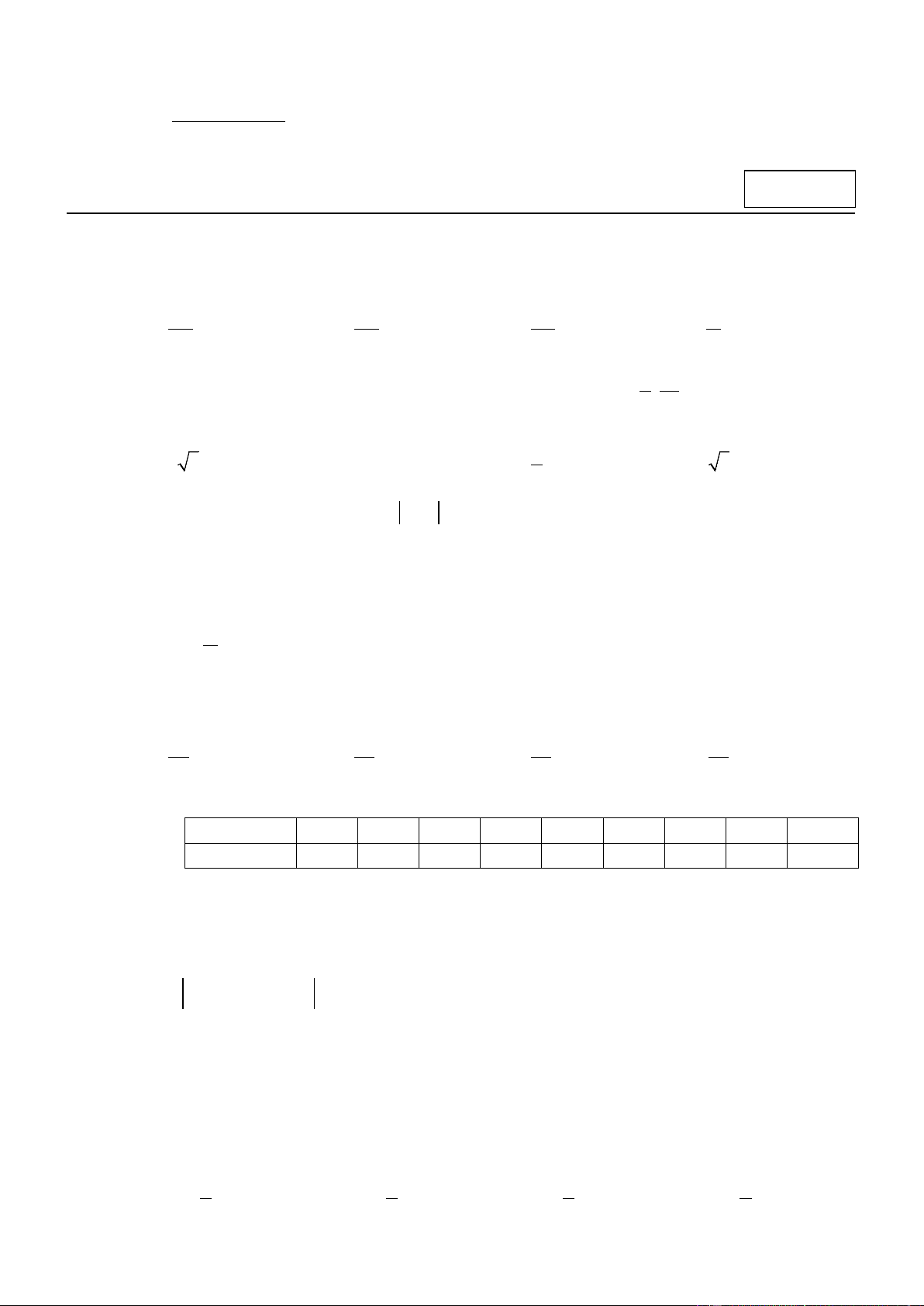
Câu 11. Thống kê điểm thi của 30 em học sinh đứng đầu kì thi học sinh giỏi Toán (thang điểm là 20 ) ,
kết quả được cho trong bảng sau đây .
Mốt của bảng phân bố đã cho là A. 3 . B. 17 . C. 11. D. 19 .
Câu 12. Trong mặt phẳng toạ độ Oxy , một véc tơ chỉ phương của đường thẳng d đi qua hai điểm
A(2; 3) và B(3; ) 1 là     A. u = (1; 2 − ) . B. u = (2; ) 1 . C. u = (1; 2) . D. u = (2; − ) 1 .
PHẦN 2: TỰ LUẬN (Thời gian làm bài: 65 phút) (7 điểm)
Câu 1 (1 điểm): Tìm tập xác định của hàm số 2x +1 a) y = . x − 3 2x − 3 b) y = . 2 4x −12x + 9
Câu 2: (1,5 điểm) Giải bất phương trình: 2 − x − 3 a) > 2 . x + 2 b) ( 2
x − x + − x − ) 2 3 1
2 . x − 6x + 8 < 0 . Câu 3. (2,5 điểm)
a) Cho tam thức bậc 2 : f ( x) 2
= 2x − 4mx − 5m + 3 với m là tham số thực. Tìm m để f (x) nhận
giá trị không âm với mọi x ∈  . 3 π  π  b) Cho sin a = với
< a < π . Tính tan −  a . 5 2  3  c) Rút gọn biểu thức: π  π   π A (α + π ) − (α − π ) 3 2019 3  = cos 2020 2 sin 7 − cos − cos α + + cos α − .cot     (α −8π ) 2  2   2  Câu 4. (2,0 điểm)
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có G là trọng tâm và tọa độ các đỉnh A( 1 − ; ) 1 , B(1;7) , C (3; 2 − ) .
a) Viết phương trình đường tròn tâm G và tiếp xúc với cạnh AC .
b) Tính góc giữa hai đường thẳng AB và AC . c) Cho điểm M ( ,
m n) thay đổi thỏa mãn MG = 2 và số thực p thay đổi.Tìm giá trị nhỏ nhất của 2 2
biểu thức E = (m − p) + (n + ) 1 .
----------HẾT----------
Trang 2/2 - Mã đề 654
TRƯỜNG THPT PHAN ĐÌNH PHÙNG
ĐỀ KIỂM TRA HỌC KÌ II - NĂM HỌC 2019-2020 TỔ TOÁN – TIN MÔN TOÁN LỚP 10
Thời gian làm bài: 90 phút
Họ và tên: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . Mã đề 655
PHẦN 1: TRẮC NGHIỆM (Thời gian làm bài: 25 phút) (3 điểm) Câu 1.
Với điều kiện tồn tại của các biểu thức, khẳng định nào sau đây sai?
A. tan (π + α ) = − tanα .
B. cos (π + α ) = − cosα .  π 
C. sin (π −α ) = sinα . D. tan −α = cotα   .  2  Câu 2.
Trong mặt phẳng toạ độ Oxy , khoảng cách từ điểm I (2; 2) đến đường thẳng d :12x + 5y –10 = 0 là 42 24 34 43 A. . B. . C. . D. . 13 13 13 13 Câu 3. Nhị thức 3
− x − 2 nhận giá trị dương khi 3 3 2 2 A. x > − . B. x < − . C. x > − . D. x < − . 2 2 3 3 Câu 4.
Tập nghiệm của bất phương trình 2 − x > x − 2 là A. ( ; −∞ 5]. B. ( ; −∞ 5) . C. ( ; −∞ 2) . D. ( ; −∞ 2]. Câu 5.
Trong mặt phẳng toạ độ Oxy , một véc tơ chỉ phương của đường thẳng d đi qua hai điểm
A(2; 3) và B(3; ) 1 là     A. u = (1; 2 − ) . B. u = (2; ) 1 . C. u = (1; 2) . D. u = (2; − ) 1 . Câu 6.
Điều kiện cần và đủ của tham số m để biểu thức 2 2
f (x) = x − 2mx + m − 4m + 5 nhận giá trị
dương với mọi x∈ là 5 5 5 5 A. m ≥ . B. m ≤ . C. m > . D. m < . 4 4 4 4 Câu 7. Tam thức 2
x − 2x − 3 nhận giá trị không âm khi
A. x < –1 hoặc x > 3 . B. –1 ≤ x ≤ 3 .
C. x ≤ –1 hoặc x ≥ 3 . D. –1 < x < 3 .  8 16  Câu 8.
Trong mặt phẳng toạ độ Oxy , cho ba điểm A(4;0) , B (0; 2) , C ; 
 . Bán kính đường tròn  5 5  ngoại tiếp A ∆ BC bằng 5 A. 2 5. B. 5. C. 5 . D. . 2 Câu 9.
Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A như sau: Điểm 3 4 5 6 7 8 9 10 Cộng Số học sinh 2 3 7 18 3 2 4 1 40
Số trung vị (Me ) của bảng số liệu trên là A. M = 8 M = M = M = e . B. 5 e . C. 7 e . D. 6 e .
Trang 1/2 - Mã đề 655
Câu 10. Một cung tròn có số đo là 120° . Số đo theo đơn vị radian của cung tròn đó là π 2π 5π 4π A. . B. . C. . D. . 6 3 6 3
Câu 11. Trong mặt phẳng tọa độ Oxy , cho điểm A(1; 2) , B ( 2; − 3) , C ( 2; − )
1 .Điểm M (a,b) ∈Oy sao
  
cho: MA + MB + MC nhỏ nhất, khẳng định nào sau đây đúng? A. 2 − < b < 0 . B. b < 2 − . C. b > 3 .
D. 0 < b < 3 .
Câu 12. Thống kê điểm thi của 30 em học sinh đứng đầu tham dự kì thi học sinh giỏi Toán (thang điểm
là 20 ), kết quả được cho trong bảng sau đây
Mốt của bảng phân bố đã cho là A. 17 . B. 11. C. 19 . D. 3 .
PHẦN 2: TỰ LUẬN (Thời gian làm bài: 65 phút) (7 điểm)
Câu 1 (1 điểm): Tìm tập xác định của hàm số 2x +1 2x − 3 a) y = . b) y = . x − 3 2 4x −12x + 9
Câu 2: (1,5 điểm) Giải bất phương trình: 2 − x − 3 a) > 2 . b) ( 2
3x − x +1 − x − 2) 2
x − x + < . x . 6 8 0 + 2 Câu 3. (2,5 điểm)
a) Cho tam thức bậc 2 : f ( x) 2
= 2x − 4mx − 5m + 3 với m là tham số thực. Tìm m để f (x) nhận
giá trị không âm với mọi x ∈  . 3 π  π  b) Cho sin a = với
< a < π . Tính tan −  a . 5 2  3  c) Rút gọn biểu thức: π  π   π A (α + π ) − (α − π ) 3 2019 3  = cos 2020 2 sin 7 − cos − cos α + + cos α − .cot     (α −8π ) 2  2   2  Câu 4. (2,0 điểm)
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có G là trọng tâm và tọa độ các đỉnh A( 1 − ; ) 1 , B(1;7) , C (3; 2 − ) .
a) Viết phương trình đường tròn tâm G và tiếp xúc với cạnh AC .
b) Tính góc giữa hai đường thẳng AB và AC . c) Cho điểm M ( ,
m n) thay đổi thỏa mãn MG = 2 và số thực p thay đổi.Tìm giá trị nhỏ nhất của 2 2
biểu thức E = (m − p) + (n + ) 1 .
----------HẾT----------
Trang 2/2 - Mã đề 655
TRƯỜNG THPT PHAN ĐINH PHÙNG
KIỂM TRA HỌC KÌ II – NĂM HỌC 2019 - 2020 TỔ TOÁN – TIN MÔN TOÁN LỚP 10
Thời gian làm bài : 90 Phút.
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
A. ĐÁP ÁN TRẮC NGHIỆM: MĐ Câu ĐA MĐ Câu ĐA MĐ Câu ĐA MĐ Câu ĐA 652 1 A 653 1 D 654 1 B 655 1 A 652 2 C 653 2 C 654 2 D 655 2 B 652 3 B 653 3 C 654 3 B 655 3 D 652 4 B 653 4 B 654 4 A 655 4 C 652 5 B 653 5 B 654 5 D 655 5 A 652 6 C 653 6 D 654 6 A 655 6 D 652 7 D 653 7 D 654 7 A 655 7 C 652 8 A 653 8 A 654 8 C 655 8 B 652 9 A 653 9 A 654 9 D 655 9 D 652 10 B 653 10 B 654 10 D 655 10 B 652 11 D 653 11 D 654 11 B 655 11 D 652 12 B 653 12 C 654 12 A 655 12 A
B. HƯỚNG DẪN CHẤM PHẦN TỰ LUẬN CÂU NỘI DUNG ĐIỂM
1a.(0,5đ) Tìm tập xác định của hàm số 2x 1 y  . x  3
Điều kiện xác định: x  3  0  x  3. 0,25đ
KL: Tập xác định: D  \  3 . 0,25đ
1b.0,5đ) Tìm tập xác định của hàm số 2x  3 y Câu 1 2 4x 12x  9
(1,0đ) Điều kiện xác định: 2
4x 12x  9  0 0,25đ 2
x x     x  2 3 4 12 9 0 2 3  0  x  . 2 KL: Tập xác định: 3 D \    . 2   0,25đ
2a.(1,0đ) Giải bất phương trình 2x  3  2 . x  2 Đk: x  2   * . 0,25 BPT  2x  3 4x  7  2  0   0 . x  2 x  2 Lập bảng xét dấu 7 Câu 2 x 2  1,5(đ) 4 4  x  7 + + 0  x  2  0 + + 4x  7 0,5 x  || + 0   2 Theo bảng ta có 4  x  7  7 0 x  2;       . 0,25 x 2 4    
Trang 1/4 – Đề chính thức
2b.(0,5đ) Giải bất phương trình  2x x   x  2 3 1
2 . x  6x 8  0 . 2
x  6x  8   0
Bất phương trình tương đương với  2
 3x x 1  x  2 x  ;  2 4;  1    0,25 2
 3x x 1  x  2  2 x  2  0 Xét 2 : 2
3x x 1  x  2   2 2 3
x x 1 x  4x  4 x  2   1     x     ;3 . 0,25 2  1 2x 5x 3 0 x ;3           2    2 
Kết hợp nghiệm ta được 1 x  ;2    . 2   
3a.(0,5đ) Cho tam thức bậc 2: f x 2
 2x  4mx 5m 3 với m là tham số thực.
Tìm m để f x nhận giá trị không âm với mọi x  . a  0 2  0 Điều kiện đề bài     0,25  0      4m  2 8 5  m  3  0 2 1 16m 40m 24 0 m  3;          . 0,25 2   3b.(1,0đ)   Cho 3 
sin a  với  a   . Tính tan  a  . 5 2 3     3 sin a   5  Có  2 2 s 4
 in a  cos a  1  cos a   0,5  5 
  a   : cos a  0  2 Câu 3 (2,5đ) Khi đó: 3 tan a   . 4 0,25  3 tan  tan a 3    Ta có  3 4 4 3  3 tan  a      3    3 3 4  3 3 1 tan .tan a 0,25 1 3  4
3c.(1,0đ) Rút gọn biểu thức:    A       3 2019 cos 2020 2sin 7 cos cos          2  2     3 cos     .cot     8   2   0,25        3   cos 2020 2sin 8 cos cos   1010           2 2      cos  2     .cot     8   2 
Trang 2/4 – Đề chính thức     
cos 2sin    cos  cos             .cot  2   2  0,25      cos 2sin    cos  cos             .cot 0,25  2   2  cos
 cos  2sin  sin  sin.  sin . 0,25đ sin
Câu 4.(2,0đ) Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có G là trọng tâm
và tọa độ các đỉnh A 1  ; 
1 , B1;7 , C 3; 2   .
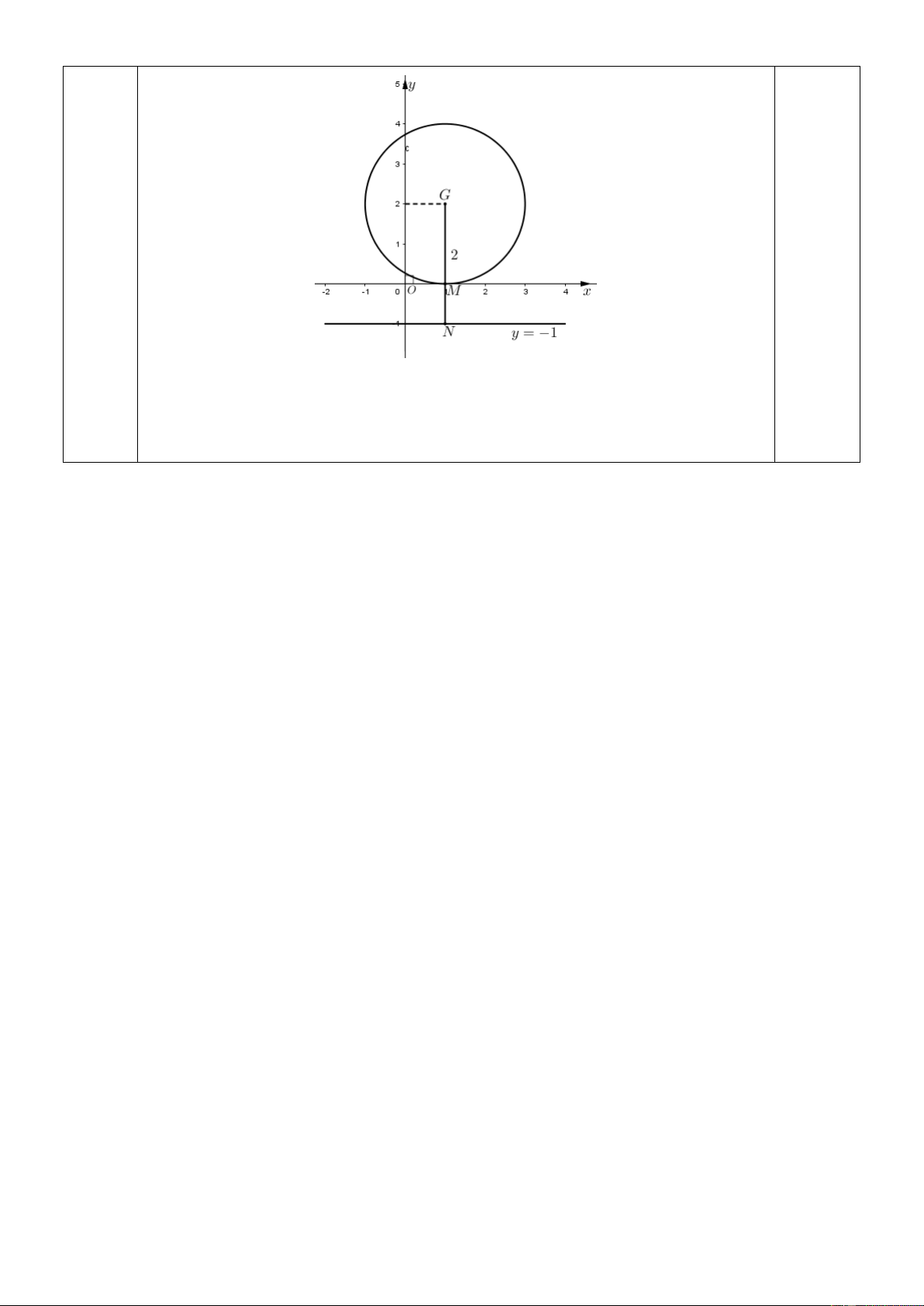
4a.(1,0đ) Viết phương trình đường tròn tâm G và tiếp xúc với cạnh AC .
Ta có đường thẳng AC đi qua (
A 1;2) và nhận AC  (4; 3  ) làm VTCP nên nhận n  (3;4) là VTPT. 0,25đ
Phương trình tổng quát đường thẳng AC :
3(x 1)  4(y 1)  0
 3x  4y 1 0 Tính được G(1;2) 0,25đ d( ; G AC)  2 . 0,25đ
Vậy phương trình đường tròn tâm G và tiếp xúc với cạnh AC là: 0,25đ 2 2
(x 1)  (y  2)  4 C.
4b.(0,5đ) Tính góc giữa 2 đường thẳng AB và AC . Câu 4 Ta có:
(2,0đ) AB  (2;6) ; AC  (4; 3  ) . 0,25đ
Gọi  là góc giữa hai đường thẳng AB và AC . 2.3 6 3   1
cos  cos(AB, AC)   o    71 33. 0,25đ 2 2 2    2 10 2 6 3 4
4c.(0,5đ)Cho điểm M  ,
m n thay đổi thỏa mãn MG  2 và số thực p thay
đổi.Tìm giá trị nhỏ nhất của biểu thức E  m p2  n  2 1 . Với M  , m n , N  ; p  
1 . Nhận xét : M  ,
m nC , N  ; p   1 d : y  1  và
E  m p2  n  2 1 .
Bài toán thành: Tìm điểm M C , N d sao cho MN nhỏ nhất. 0,25đ
Trang 3/4 – Đề chính thức 0,25đ
MN d G,d R  3 2 1 khi N 1, 
1 ( Hình chiếu của G trên d ) và min   M 1;0.
( Không chỉ ra tọa độ điểm M , N vẫn có thể cho điểm tối đa).
Lưu ý:Tổ chấm có thể thống nhất lại hướng dẫn chấm cho phù hợp. Thí sinh làm cách khác mà
đúng thì vẫn cho điểm tối đa.
-------------HẾT------------
Trang 4/4 – Đề chính thức
Document Outline

  • 001_652
  • 001_653
  • 001_654
  • 001_655
  • H (1)