Đề thi học kì 2 Toán 10 năm 2019 – 2020 trường THPT Thủ Đức – TP HCM

Nhằm giúp các em học sinh lớp 10 ôn tập, chuẩn bị cho đợt kiểm tra cuối học kỳ 2 môn Toán lớp 10 sắp tới, xin giới thiệu đến các em đề thi học kì 2 Toán 10 năm học 2019 – 2020 trường THPT THPT Thủ Đức, thành phố Hồ Chí Minh, đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 10

Môn: Toán 10

Thông tin:

3 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
TRƯỜNG THPT THỦ ĐỨC ĐỀ KIỂM TRA HỌC KỲ II - KHỐI 10
NĂM HỌC: 2019 - 2020 Môn: TOÁN - Thời gian: 90 phút.
--------
ĐỀ CHÍNH THỨC
-----------------
Câu 1. (3,5 điểm)
Giải các bất phương trình sau
a)
2
3 4 2 0x x x
b)
2
2
3 2
0
30
x x
x x
c)
2
2
3 2
1
4
x x
x
Câu 2. (1,0 điểm)
Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 1 3 7 0x m x m
có hai nghiệm
dương phân biệt.
Câu 3. (2,5 điểm)
a) Cho
1
sin
3
x
. Tính
2
cos2 1 cotA x x
.
b) Rút gọn biểu thức
sin 7 cos4 sin
cos7 sin 4 cos
x x x
B
x x x
.
c) Chứng minh giá trị biểu thức
5 tan 2
cot 2 2tan 1
x
C
x x
không phụ thuộc vào biến
x
.
Câu 4. (2,0 điểm)
Trong mặt phẳng với hệ tọa độ
Oxy
, cho 3 điểm
1;1A
,
2;5B
và
3;0M
.
a) Viết phương trình tổng quát của đường thẳng
AB
. Tính khoảng cách từ điểm
M
đến đường
thẳng
AB
.
b) Viết phương trình đường tròn đi qua điểm
M
, tiếp xúc với đường thẳng
AB
và có tâm nằm
trên trục
Ox
.
Câu 5. (1,0 điểm)
a) Trong mặt phẳng với hệ tọa độ
Oxy
, viết phương trình chính tắc của Elip biết một tiêu điểm
1
4;0F
và độ dài trục lớn bằng 10.
b) Ông Nam có một mảnh vườn hình Elip có độ
dài trục lớn là 12m và độ dài trục nhỏ là 8m. Giữa vườn
là một cái giếng hình tròn có bán kính 0,6m và nhận
trục lớn, trục bé của Elip làm trục đối xứng (tham khảo
hình vẽ bên). Ông Nam muốn trồng hoa và rau trên
phần đất còn lại (phần tô đậm trên hình). Kinh phí cho
việc trồng hoa và rau là 180000 đồng/1m
2
. Hỏi ông
Nam cần bao nhiêu tiền để trồng hoa và rau trên dải
đất đó (số tiền được làm tròn đến hàng nghìn)?
Biết rằng diện tích của Elip được tính bằng công thức
πS ab
trong đó
a
là nửa độ dài trục lớn,
b
là nửa độ dài trục bé của Elip. Diện tích hình tròn được tính bằng công thức
2
πS R
trong đó
R
là bán kính đường tròn.
------Hết------
ĐÁP ÁN ĐỀ KIỂM TRA MÔN TOÁN KHỐI 10 HỌC KỲ II – NĂM HỌC 2019 – 2020
Câu ĐÁP ÁN
1a
(1,5
điểm)
Giải các bất phương trình sau
a)
2
3 4 2 0x x x
Cho
2
1
3 4 0
4
x
x x
x
,
2 0 2x x
. (0,25đx2)
BXD: (0,5đ)
Vậy tập nghiệm là
4;1 2;S
.
(0,5đ)
1b
(1,0
điểm)
b)
2
2
3 2
0
30
x x
x x
.
Cho
2
1
3 2 0
2
x
x x
x
,
2
6
30 0
5
x
x x
x
.
(0,25đx2)
BXD: (0,25đ)
Vậy tập nghiệm là
5;1 2;6S
.
(0,25đ)
1c
(1,0
điểm)
c)
2
2
3 2
1
4
x x
x
2
3 2
0
4
x
x
(0,25đ)
Cho
3 2 0x
2
3
x
,
2
4 0x
2
2
x
x
.
(0,25đ)
BXD: (0,25đ)
Vậy tập nghiệm là
2
; 2 ;2
3
S

. (0,25đ)
2
(1,0
điểm)
Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 1 3 7 0
x m x m
có hai nghiệm dương phân biệt.
Phương trình có hai nghiệm dương phân biệt khi
0
0
0
S
P
(0,25đ)
2
6 0
2 1 0
3 7 0
m m
m
m
3
3
2
1
m
m
m
m
(0,25đx3)
3a
(1,0
điểm)
a) Cho
1
sin
3
x
. Tính
2
cos2 1 cotA x x
.
2
2
1
1 2sin
sin
A x
x
1
1 2. 9 7
9
(0,25đx4)
MA TRẬN ĐỀ
3b
(0,75
điểm)
b) Rút gọn biểu thức
sin 7 cos 4 sin
cos7 sin 4 cos
x x x
B
x x x
.
2cos4 sin 3 cos 4
2sin 4 sin 3 sin 4
x x x
B
x x x
2cos 4 sin3 1
2sin 4 sin 3 1
x x
x x
cot 4
x
. (0,25đx3)
3c
(0,75
điểm)
c) Chứng minh giá trị biểu thức
5 tan 2
cot 2 2tan 1
x
C
x x
không phụ thuộc vào
biến
x
.
5 tan 2
1
2 tan 1
2
tan
x
C
x
x
5tan tan 2
1 2 tan 2 tan 1
x x
x x
4 tan 2
2
1 2 tan
x
x
. (0,25đx3)
4a
(1,5
điểm)
Trong mặt phẳng với hệ tọa độ
Oxy
, cho 3 điểm
1;1
A ,
2;5
B và
3;0
M .
a) Viết phương trình tổng quát của đường thẳng
AB
. Tính khoảng cách từ điểm
M
đến đường thẳng
AB
.
3;4
AB
: 4 3 7 0
AB x y
.(0,5đx2),
4.3 3.0 7
19
,
5
16 9
d M AB
(0,5đ)
4b
(0,5
điểm)
b) Viết phương trình đường tròn đi qua điểm
M
, tiếp xúc với đường thẳng
AB
và có tâm nằm trên trục
Ox
.
Gọi tâm
;0
I a
,
4 7
,
5
a
d I AB
,
3;0 3
MI a IM a
.
Ta có
,
d I AB IM R
4 7
3
5
a
a
22
8
9
a
a
. (0,25đ)
2
2
1 1
22 22;0 : 22 361
a I C x y
2
2
2 2
8 8 8 361
;0 :
9 9 9 81
a I C x y
(0,25đ)
5a
(0,5
điểm)
a) Trong mặt phẳng với hệ tọa độ
Oxy
, viết phương trình chính tắc của Elip biết
một tiêu điểm
1
4;0
F và độ dài trục lớn bằng 10.
1
4;0 4
F c
,
2 10 5
a a
,
2 2 2
9
b a c
. (0,25đ)
Vậy
E
:
2 2
1
25 9
x y
. (0,25đ)
5a
(0,b
điểm)
Ta có
6, 4
a b
diện tích elip
1
24
π
S
. (0,25đ)
Diện tích hình tròn
2
2
π0,6 0,36π
S .
Số tiền cần là:
24
π 0,36π 180000 13 368 000
đồng. (0,25đ)
| 1/3
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT THỦ ĐỨC
ĐỀ KIỂM TRA HỌC KỲ II - KHỐI 10 NĂM HỌC: 2019 - 2020
Môn: TOÁN - Thời gian: 90 phút. -------- ----------------- ĐỀ CHÍNH THỨC Câu 1. (3,5 điểm)
Giải các bất phương trình sau 2 x  3x  2 2 x  3x  2 a)  2
x  3x  4 x  2  0 b)  0 c) 1 2 x  x  30 2 x 4  Câu 2. (1,0 điểm)
Tìm tất cả các giá trị của tham số m để phương trình 2 x  2m  
1 x  3m  7  0 có hai nghiệm dương phân biệt. Câu 3. (2,5 điểm) 1 a) Cho sin x  . Tính A  x  2 cos 2 1 cot x. 3 sin 7x  cos 4x  sin x
b) Rút gọn biểu thức B  . cos 7x  sin 4x  cos x 5 tan x  2
c) Chứng minh giá trị biểu thức C  
không phụ thuộc vào biến x . cot x  2 2 tan x 1 Câu 4. (2,0 điểm)
Trong mặt phẳng với hệ tọa độ Oxy , cho 3 điểm A 1  ; 
1 , B 2;5 và M 3;0 .
a) Viết phương trình tổng quát của đường thẳng AB . Tính khoảng cách từ điểm M đến đường thẳng AB .
b) Viết phương trình đường tròn đi qua điểm M , tiếp xúc với đường thẳng AB và có tâm nằm trên trục Ox . Câu 5. (1,0 điểm)
a) Trong mặt phẳng với hệ tọa độ Oxy , viết phương trình chính tắc của Elip biết một tiêu điểm
F 4; 0 và độ dài trục lớn bằng 10. 1  
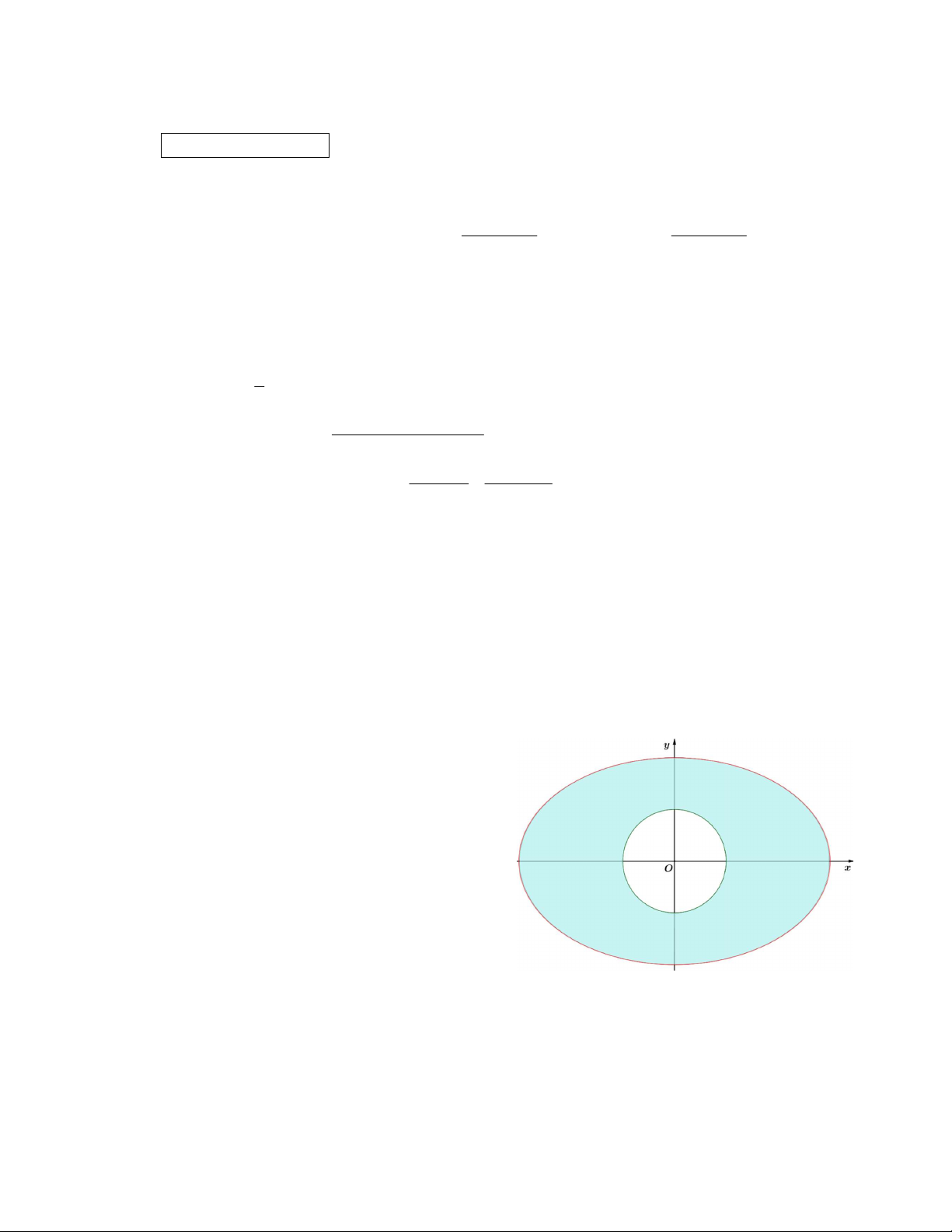
b) Ông Nam có một mảnh vườn hình Elip có độ
dài trục lớn là 12m và độ dài trục nhỏ là 8m. Giữa vườn
là một cái giếng hình tròn có bán kính 0,6m và nhận
trục lớn, trục bé của Elip làm trục đối xứng (tham khảo
hình vẽ bên). Ông Nam muốn trồng hoa và rau trên
phần đất còn lại (phần tô đậm trên hình). Kinh phí cho
việc trồng hoa và rau là 180000 đồng/1m2. Hỏi ông
Nam cần bao nhiêu tiền để trồng hoa và rau trên dải
đất đó (số tiền được làm tròn đến hàng nghìn)?
Biết rằng diện tích của Elip được tính bằng công thức S  πab trong đó a là nửa độ dài trục lớn,
b là nửa độ dài trục bé của Elip. Diện tích hình tròn được tính bằng công thức 2 S  πR trong đó R
là bán kính đường tròn. ------Hết------
ĐÁP ÁN ĐỀ KIỂM TRA MÔN TOÁN KHỐI 10 HỌC KỲ II – NĂM HỌC 2019 – 2020 Câu ĐÁP ÁN
Giải các bất phương trình sau a)  2
x  3x  4 x  2  0 x  1 1a Cho 2 x  3x  4  0  
, x  2  0  x  2 . (0,25đx2) x  4  (1,5 điểm) BXD: (0,5đ)
Vậy tập nghiệm là S  4;  1  2;. (0,5đ) 2 x  3x  2 b)  0 . 2 x  x  30 x 1 x  6 Cho 2 x  3x  2  0   , 2 x  x  30  0   . (0,25đx2) 1b x  2 x  5  (1,0 BXD: (0,25đ) điểm)
Vậy tập nghiệm là S   5  ;  1 2;6 . (0,25đ) 2 x  3x  2 3x  2 c) 1   0 (0,25đ) 2 x 4  2 x  4 x  2 Cho 3x  2  2 0  x   , 2 x  4  0  . (0,25đ) 3  x  2  1c BXD: (0,25đ) (1,0 điểm)  
Vậy tập nghiệm là S     2 ; 2   ; 2   . (0,25đ)  3 
Tìm tất cả các giá trị của tham số m để phương trình 2 x  2m   1 x  3m  7  0
có hai nghiệm dương phân biệt.   0  2
Phương trình có hai nghiệm dương phân biệt khi S  0 (0,25đ) (1,0 P  0  điểm) 2 m  m  6  0 m  3   2m   1  0  m  2   m  3 (0,25đx3) 3  m 7  0   m  1  1 a) Cho sin x  . Tính A  x  2 cos 2 1 cot x. 3a 3 (1,0 1   điểm) A   2 1 1 2sin x  1 2. 9  7 (0,25đx4) 2   sin x  9  sin 7x  cos 4x  sin x  3b b) Rút gọn biểu thức B . cos 7x  sin 4x  cos x (0,75 2cos 4x sin 3x  cos 4x 2cos 4x sin 3x   1 điểm) B    cot 4x . (0,25đx3) 2  sin 4xsin 3x  sin 4x 2  sin 4xsin 3x   1 5 tan x  2
c) Chứng minh giá trị biểu thức C   không phụ thuộc vào cot x  2 2 tan x 1 3c biến x . (0,75 5 tan x  2 5 tan x tan x  2 4 tan x  2 điểm) C       2  . (0,25đx3) 1 2 tan x 1  2 1 2 tan x 2 tan x 1 1 2 tan x tan x
Trong mặt phẳng với hệ tọa độ Oxy , cho 3 điểm A 1  ; 
1 , B2;5 và M 3;0 . 4a
a) Viết phương trình tổng quát của đường thẳng AB . Tính khoảng cách từ điểm (1,5
M đến đường thẳng AB . điểm)   
AB  3;4  AB : 4x  3y  7  0 .(0,5đx2), d M AB 4.3 3.0 7 19 ,   (0,5đ) 16  9 5
b) Viết phương trình đường tròn đi qua điểm M , tiếp xúc với đường thẳng AB
và có tâm nằm trên trục Ox . a   Gọi tâm I  ; a 0 , d I AB 4 7 , 
, MI  a  3;0  IM  a  3 . 5 4b   4a  7 a 22 (0,5
Ta có d I, AB  IM  R   a  3   8 . (0,25đ) điểm) 5 a   9
a  22  I 22;0  C  :  x  222 2  y  361 1 1 2 8  8    a   I ; 0    C  8 361 2 : x   y  (0,25đ) 2 2   9  9   9  81
a) Trong mặt phẳng với hệ tọa độ Oxy , viết phương trình chính tắc của Elip biết một tiêu điểm F 4
 ;0 và độ dài trục lớn bằng 10. 1   5a (0,5 F 4
 ;0  c  4 , 2a 10  a  5 , 2 2 2
b  a  c  9 . (0,25đ) 1   điểm) 2 2 x y Vậy E :  1. (0,25đ) 25 9
Ta có a  6,b  4  diện tích elip S  24π . (0,25đ) 5a 1 (0,b Diện tích hình tròn 2 S  π0,6  0,36π . 2 điểm)
Số tiền cần là: 24π  0,36π180000 13 368 000 đồng. (0,25đ) MA TRẬN ĐỀ