Đề thi học kì 2 Toán 10 năm 2019 – 2020 trường THPT Trần Khai Nguyên – TP HCM

SỞ GIÁO DỤC & ĐÀO TẠO TP HCM
ĐỀ THI HKII, KHỐI 10, NĂM HỌC 2019-2020
TRƯỜNG THPT TRẦN KHAI NGUYÊN Môn : TOÁN n p t n t n o
Họ và Tên:………………………………...........Số báo danh:…………………………….Mã đề: 101
Câu 1: [2,5 điểm] Giải các bất phương trình
 2x 4x4x2 a)  0
b) x  2  2 x  1  2 9  x
Câu 2: [1 điểm] Tìm tập xác định của hàm số 2
y  5  4x  x .
Câu 3: [1 điểm] Định m để bất phương trình 2
x  2mx  3m  2  0 nghiệm đúng với mọi x  Câu 4: [1,5 điểm] 5 3 Cho cos  và    2 . 3 2
a) Tính sin  , tan  và cot  . cos  2 2  tan  
b) Tính giá trị biểu thức A  . 3 sin 
Câu 5: [1 điểm] Chứng minh  x  x2 2 2 sin 3 sin 5
 (cos3x  cos5x)  4cos x
Câu 6: [2 điểm] Trong mặt phẳng tọa độ Oxy , cho tam giác ABC với A1;2 , B  2
 ;3 và C 2;  1 .
a) Viết phương trình cạnh AB và đường trung tuyến BM của tam giác ABC .
b) Viết phương trình đường cao CH và tìm tọa độ điểm H với H là chân đường cao kẻ từ C của tam giác ABC ?
Câu 7: [1 điểm] Một người thợ mộc đóng một cái bàn với mặt bàn là hình tam giác có chu vi bằng 480cm và
độ dài cạnh lớn nhất là 220cm . Để chia mặt bàn thành 2 tam giác nhỏ có diện tích bằng nhau, người thợ
mộc đã kẻ đường trung tuyến ứng với cạnh lớn nhất và đo được độ dài đường trung tuyến này là 70cm .
Hãy tính diện tích mặt bàn và cho biết mặt bàn có dạng tam giác vuông, tam giác nhọn hay tam giác tù? Vì sao? HẾT
Mã đề : 101 - Môn : TOÁN.
SỞ GIÁO DỤC & ĐÀO TẠO TP HCM
ĐỀ THI HKII, KHỐI 10, NĂM HỌC 2019-2020
TRƯỜNG THPT TRẦN KHAI NGUYÊN Môn : TOÁN n p t n t n o
Họ và Tên:………………………………...........Số báo danh:…………………………….Mã đề: 102
Câu 1: [2,5 điểm] Giải các bất phương trình
 2x 6x9x3 a)  0
b) x  2  2 x  5 2 4  x
Câu 2: [1 điểm] Tìm tập xác định của hàm số 2
y  5x  4x 1 .
Câu 3: [1 điểm] Định m để bất phương trình 2
x  2mx  4m  3  0 nghiệm đúng với mọi x  Câu 4: [1,5 điểm] 2 3 Cho sin    và     . 3 2
a) Tính cos, tan và cot  . sin  2 2  cot  
b) Tính giá trị biểu thức A  . 3 cos 
Câu 5: [1 điểm] Chứng minh  x  x2 2 2 sin 7 sin 5
 (cos7x  cos5x)  4sin x
Câu 6: [2 điểm] Trong mặt phẳng tọa độ Oxy , cho tam giác ABC với A1; 2   , B 2
 ;3 và C 3;  1 .
a) Viết phương trình cạnh AC và đường trung tuyến CM của tam giác ABC .
b) Viết phương trình đường cao BH và tìm tọa độ điểm H với H là chân đường cao kẻ từ B của tam giác ABC ?
Câu 7: [1 điểm] Một người thợ mộc đóng một cái bàn với mặt bàn là hình tam giác có chu vi bằng 720cm và
độ dài cạnh lớn nhất là 340cm . Để chia mặt bàn thành 2 tam giác nhỏ có diện tích bằng nhau, người thợ
mộc đã kẻ đường trung tuyến ứng với cạnh lớn nhất và đo được độ dài đường trung tuyến này là 90cm .
Hãy tính diện tích mặt bàn và cho biết mặt bàn có dạng tam giác vuông, tam giác nhọn hay tam giác tù? Vì sao? HẾT 2 MA TRẬN ĐỀ Vận dụng Cộng Chủ đề Nhận biết Thông hiểu Thấp Cao DẤU NHỊ Giải bất G ả bất p ươn THỨC, BẤT phương trìn có á trị PHƯƠNG trình dạng tuyệt ố TRÌNH BẬC tích, thương NHẤT các nhị thức Số câu 1 1 2 Số m 1,25 1,25 2,5 DẤU TAM Tìm tập xác Tìm u ện củ
THỨC BẬC 2, ịn vớ t m số bất PHƯƠNG u ện t m t ức bậc 2 TRÌNH BẤT ả bất t oả mãn u PHƯƠNG p ươn ện v dấu
TRÌNH BẬC 2 trìn bậc 2 Số câu 1 1 2 Số m 1,0 1,0 2,0 GIÁ TRỊ LG
Tính các giá C ứn m n C ứn m n b u CỦA MỘT trị lượn ẳn t ức lượn t ức lượn ác CUNG ác củ 1 giác cung Số câu 1 1 1 3 Số m 0,75 0,75 1,0 3,0 HỆ THỨC Bài toán t ực tế LƯỢNG TRONG TAM GIÁC, GIẢI TAM GIÁC Số câu 1 Số m 1,0 PHƯƠNG
V ết p ươn V ết p ươn trìn TRÌNH trìn ư n ư n t ẳn ĐƯỜNG t ẳn THẲNG Số câu 1 1 2 Số m 1,0 1,0 2,0 ổn số câu 3 4 2 1 10 ổn số m 3,0 4.25 2,25 0,75 10.0 3
HƯỚNG DẪN CHẤM TOÁN 10_ĐỀ 101 Câu 1a[A]
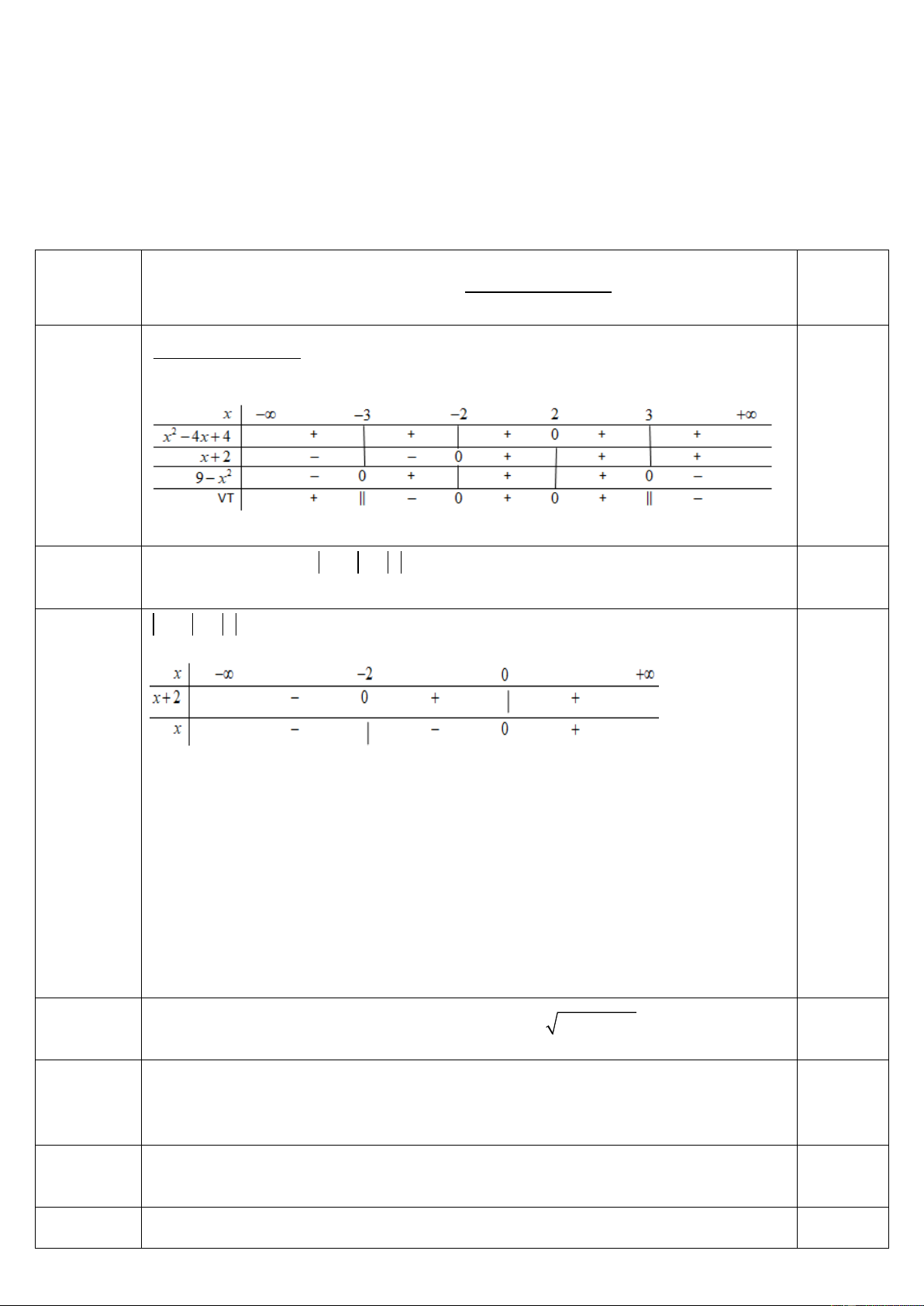
 2x 4x4x2 Điểm chi Giải bất phương trình  0 tiết 2 9  x
 2x 4x4x2 (1,25 điểm)  0 * 2   9  x Bảng xét dấu
Vậy: *  x  3
 hay  2  x  3    
Câu 1b [A] Giải bất phương trình x 2 2 x 1 Điểm chi tiết
x  2  2 x  1  * (1,25 điểm) Bảng xét dấu: TH1: x  2 
*  x  2 2x  1   x  1
So điều kiện: x  2  TH2: 2   x  0
*  x  2 2x  1   3x  3   x  1  So điều kiện: 2   x  1  TH3: x  0
*  x  2 2x  1   x  3   x  3
So điều kiện: x  3
Vậy nghiệm của bất phương trình là: x  1  hay x  3 Câu 2 [A]
Tìm tập xác định của hàm số 2 Điểm chi
y  5  4x  x . tiết    (1 điểm) Hàm số xác định khi 2 5 4x x 0  5   x  1
Hàm số có tập xác định D   5   ;1 Câu 3 [A]
Định m để bất phương trình 2
x  2mx  3m  2  0 nghiệm đúng với mọi x Điểm chi tiết (1 điểm) 4 a  0 2
x  2mx  3m  2  0, x    '0 1   0    1 m  2 2
m  3m  2  0 Vậy: m 1;2 Câu 4[A] 5 3 Điểm chi Cho cos  và    2 . 3 2 tiết
a) Tính sin  , tan  và cot  . cos  2 2  tan  
b) Tính giá trị biểu thức A  . 3 sin  5 4 (1,5 điểm) 2 2
sin   1 cos   1  9 9 2   3 sin    vì    2 3 2 0,25 2  sin  2  5 3 tan     0,25 cos 5 5 3 5 cos 5 3 cot      sin  2 2  0,25 3 5  4  2    3  5  63 5 A    3  2  20     3  Câu 5 [A] Chứng minh  x  x2 2 2 sin 3 sin 5
 (cos3x  cos5x)  4cos x Điểm chi tiết (1 điểm)
VT  sin 3x  sin 5x2 2
 (cos3x  cos5x) 2 2 2 2
 sin 3x  2sin 3xsin 5x  sin 5x  cos 3x  2cos3x cos5x  cos 5x
 2  2(cos3x cos5x  sin 3xsin 5x)  2  2cos 2x 2 2
 2  2(2cos x 1)  4cos x  VP  Câu 6 [A]
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC với A1;2 , B  2;3 và C 2;  1 . Điểm chi
a) Viết phương trình cạnh AB và đường trung tuyến BM của tam giác ABC . tiết
b) Viết phương trình đường cao CH và tìm tọa độ điểm H với H là chân
đường cao kẻ từ C của tam giác ABC ? a) (2 điểm) Phương trình cạnh AB: AB   3  ;  1
Chọn n  1;3 làm VTPT của cạnh AB. 5 qua A  1;2 Khi đó AB:  có PTTQ là: VT  PT : n   1;3 1 x  
1  3 y  2  0
 x  3y  7  0
Phương trình trung tuyến BM: M là trung điểm AC  x  x 1 2 3 A C x     M  2 2 2  3 3     M ;   y  y 2 1 3   2 2  A C y    M  2 2 2  7 3   BM  ;    2 2  Chọn n
 3;7 làm VTPT của BM. BM  qua B   2  ;3 Khi đó BM:  có PTTQ là V  TPT : n   3;7 BM 
3 x  2  7  y  3  0
 3x  7y 15  0
b) Ta có CH  AB  Chọn n  AB   3  ;  1 làm VTPT của CH. CH qua C  2;  1 Khi đó CH:  có PTTQ là: V  TPT : n    3  ;  1 CH 3
 x  2 1 y   1  0  3
 x  y  5  0
 3x  y  5  0
Ta có: H  AB  CH nên tọa độ điểm H là nghiệm của hệ phương trình  11 x 
x  3y  7  0  5    3
 x  y  5  0 8 y   5   Vậy 11 8 H ;    5 5 
Một người thợ mộc đóng một cái bàn với mặt bàn là hình tam giác có chu vi bằng Câu 7 [A] Điểm chi
480cm và độ dài cạnh lớn nhất là 220cm . Để chia mặt bàn thành 2 tam giác nhỏ có tiết
diện tích bằng nhau, người thợ mộc đã kẻ đường trung tuyến ứng với cạnh lớn nhất
và đo được độ dài đường trung tuyến này là 70cm . Hãy tính diện tích mặt bàn và cho
biết mặt bàn có dạng tam giác vuông, tam giác nhọn hay tam giác tù? Vì sao? (1 điểm)
Gọi tên các đỉnh của mặt bàn lần lượt là ,
A B,C và giả sử cạnh lớn nhất là cạnh BC  220cm .
Gọi M là trung điểm BC , theo đề bài ta có AM  70cm .
Chu vi của tam giác ABC bằng 480cm nên ta có
AB  BC  AC  480
 AB  480  BC  AC  480  220  AC  260  AC 6 AM  70 2 2 2 AB  AC BC 2    70 2 4 2 2 AB  AC  17000 2 2 2
 AB  AC  34000
Thay AB  260  AC , ta có 260 AC2 2  AC  34000 2
 2AC  520AC  33600  0
AC 140  AB 120  AC 120   AB 140
Vậy ba cạnh của mặt bàn có độ dài là 120c , m 140c , m 220cm   Nửa chu vi: 120 140 220 p   240 2 Diện tích: S           2 240 240 120 240 140 240 220 2400 10 cm 
Góc BAC là góc có số đo lớn nhất của tam giác ABC 2 2 2 120 140  220 3 cos BAC     0 2.120.140 7  BAC là góc tù.
Vậy mặt bàn là một tam giác tù. 7
HƯỚNG DẪN CHẤM TOÁN 10_ĐỀ 102
 2x 6x9x3 Câu 1a [B] Điểm Giải bất phương trình  0 2 4  x chi tiết
 2x 6x9x3 (1,25 điểm)  0 * 2   4  x Bảng xét dấu: Vậy: 3
  x  2 hay x  2 Câu 1b [B]
Giải bất phương trình x  2  2 x  5 Điểm chi tiết
x  2  2 x  5 * (1,25 điểm) Bảng xét dấu: TH1: x  0
*  x  2 2x  5  3
 x  3  x  1  So điều kiện: 1   x  0 TH2: 0  x  2
*  x  2 2x  5  x  3
So điều kiện: 0  x  2 TH3: x  2   7
*  x  2  2x  5  3x  7  x  3 So điều kiện: 7 2  x  3
Vậy nghiệm của bất phương trình là: 7 1   x  3 Câu 2 [B]
Tìm tập xác định của hàm số 2 Điểm
y  5x  4x 1 . chi tiết (1,0 điểm)    Hàm số xác định khi 2 5x 4x 1 0  1 x     5  x  1  1
Hàm số có tập xác định D  ;   1;    .  5 Câu 3 [B]
Định m để bất phương trình 2
x  2mx  4m  3  0 nghiệm đúng với mọi x Điểm chi tiết 8   (1 điểm) a 0 2
x  2mx  4m  3  0, x      '  0 1   0    1 m  3 2
m  4m  3  0 Vậy: m 1;3 2 3 Câu 4 [B] Cho sin    và     . Điểm 3 2 chi tiết
a) Tính cos, tan và cot  . sin  2 2  cot  
b) Tính giá trị biểu thức A  . 3 cos  4 5 (1,5 điểm) 2 2
cos   1 sin   1  9 9 5   3 cos   vì     3 2 2  sin  2 5 3 tan     cos 5 5  3 5  cos 5 3 cot     sin  2 2  3 2  5   2    3  4  27 5 A   3   50 5    3   Câu 5 [B] Chứng minh  x  x2 2 2 sin 7 sin 5
 (cos7x  cos5x)  4sin x Điểm chi tiết (1 điểm)
VT  sin 7x  sin 5x2 2
 (cos 7x  cos5x) 2 2 2 2
 sin 7x  2sin 7xsin 5x  sin 5x  cos 7x  2cos 7x cos5x  cos 5x
 2  2(cos 7x cos5x  sin 7xsin 5x)  2  2cos 2x 2 2
 2  2(1 2sin x)  4sin x  VP   Câu 6 [B]
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC với A1; 2 , B  2;3 và C 3;  1 Điểm . chi tiết
a) Viết phương trình cạnh AC và đường trung tuyến CM của tam giác ABC .
b) Viết phương trình đường cao BH và tìm tọa độ điểm H với H là chân đường
cao kẻ từ B của tam giác ABC ? a) (2 điểm) Phương trình cạnh AC: AC  2;  1
Chọn n  1; 2
  làm VTPT của cạnh AC. 9 qua A1; 2    Khi đó AC:  có PTTQ là: V  TPT : n   1; 2   1 x  
1  2  y  2  0
 x  2y  5  0
Phương trình trung tuyến CM: M là trung điểm AB  x  x 1 2 1 A B x      M  2 2 2  1 1     M  ;   y  y 2   3 1   2 2  A B y    M  2 2 2  7 3   CM   ;    2 2  Chọn n
 3;7 làm VTPT của CM. CM 
qua C 3;   1 Khi đó CM:  có PTTQ là V  TPT : n   3;7 CM 
3 x  3  7  y   1  0
 3x  7y  2  0
b) Ta có BH  AC  Chọn n
 AC  2;  1 làm VTPT của BH. BH qua B   2  ;3 Khi đó BH:  có PTTQ là: V  TPT : n   2;  1 BH
2  x  2 1 y  3  0
 2x  y 1  0
Ta có: H  AC  BH nên tọa độ điểm H là nghiệm của hệ phương trình  3 x 
x  2y  5  0  5   
2x  y 1  0 11 y    5   Vậy 3 11 H ;     5 5  Câu 7 [B]
Một người thợ mộc đóng một cái bàn với mặt bàn là hình tam giác có chu vi bằng Điểm
720cm và độ dài cạnh lớn nhất là 340cm . Để chia mặt bàn thành 2 tam giác nhỏ có chi tiết
diện tích bằng nhau, người thợ mộc đã kẻ đường trung tuyến ứng với cạnh lớn nhất và
đo được độ dài đường trung tuyến này là 90cm . Hãy tính diện tích mặt bàn và cho biết
mặt bàn có dạng tam giác vuông, tam giác nhọn hay tam giác tù? Vì sao? (1 điểm)
Gọi tên các đỉnh của mặt bàn lần lượt là ,
A B, C và giả sử cạnh lớn nhất là cạnh BC  340cm .
Gọi M là trung điểm BC , theo đề bài ta có AM  90cm .
Chu vi của tam giác ABC bằng 720cm nên ta có
AB  BC  AC  720
 AB  720  BC  AC  720  340  AC  380  AC 10 AM  90 2 2 2 AB  AC BC 2    90 2 4 2 2 AB  AC   37000 2 2 2
 AB  AC  74000
Thay AB  380  AC , ta có 380 AC2 2  AC  74000 2
 2AC  760AC  70400  0
AC  220  AB 160  AC 160   AB  220
Vậy ba cạnh của mặt bàn có độ dài là 160c , m 220c , m 340cm   Nửa chu vi: 160 220 340 p   360 2 Diện tích: S           2 360 360 160 360 220 360 340 2400 35 cm 
Góc BAC là góc có số đo lớn nhất của tam giác ABC 2 2 2 160  220  340 13 cos BAC     0 2.160.220 22  BAC là góc tù.
Vậy mặt bàn là một tam giác tù. 11