Đề thi học kì 2 Toán 10 năm 2019 – 2020 trường THPT Võ Văn Kiệt – TP HCM

Giới thiệu đến quý thầy, cô giáo cùng các em học sinh lớp 10 đề thi học kì 2 Toán 10 năm học 2019 – 2020 trường THPT Võ Văn Kiệt, thành phố Hồ Chí Minh; đề thi có đáp án / lời giải chi tiết, mời các bạn đón xem

14 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 10

Môn: Toán 10

Thông tin:

4 trang 6 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA HỌC KỲ 2
THÀNH PHỐ HỒ CHÍ MINH MÔN :TOÁN - KHỐI : 10
TRƯỜNG THPT VÕ VĂN KIỆT Thời gian làm bài : 90 phút
Ngày kiểm tra : 23 / 06 /2020
ĐỀ CHÍNH THỨC
Câu 1: (1,5 điểm) Giải các bất phương trình:
2
a/
3 3 2 0
x x x
2
3
b/ 0
1
x x
x
Câu 2: (3,5 điểm) Giải các bất phương trình và hệ bất phương trình sau:
2
a/ 1 2 5
x x x
2
b/ 2
x x x
3
c/ 2
2
x
x
2
2 4 12
1
d/
3
3 2 2 1
x x
x
x x
Câu 3: (1,5 điểm)
a/ Chứng minh :
cos 1
tan
1 sin cos
x
x
x x
.
b/ Cho
tan 2
x
. Tính giá trị của biểu thức:
2
2 2
sin 4sin .cos 1
2cos 3sin 2
x x x
P
x x
Câu 4: (2,0 điểm) Trong mặt phẳng tọa độ
Oxy
a/ Cho
ABC
với
1;4 , 2; 1 , 6;2
A B C . Viết phương trình tổng quát của đường thẳng chứa
cạnh BC và phương trình tổng quát của đường thẳng chứa đường cao AH.
b/ Lập phương trình tổng quát của đường thẳng d đi qua
( 2;0)
E
và tạo với đường thẳng
: 3 3 0
x y
một góc bằng
0
45 .
Câu 5: (1.5 điểm) Trong mặt phẳng tọa độ
Oxy
a/ Lập phương trình của đường tròn có đường kính
AB
với
1;3
A
,
5;7
B
b/ Lập phương trình của đường tròn tiếp xúc với hai trục toạ độ Ox, Oy và đi qua điểm
M(2;1).
---------------------------------------------------------HẾT ----------------------------------------------------------
Lưu ý:
1/ Thí sinh được sử dụng máy tính có chức năng tương đương máy tính fx- 570VN-PLUS,
fx- 580VNX,..
2/ Họ và tên thí sinh: Số báo danh: Lớp:
3/ Các em nhớ ghi lớp vào giấy làm bài.
SỞ GD-ĐT TP.HCM ĐÁP ÁN KIỂM TRA HỌC KỲ 2
TRƯỜNG: THPT VÕ VĂN KIỆT NĂM HỌC: 2019-2020
MÔN: TOÁN –KHỐI 10
Thời gian làm bài: 90 phút
ĐÁP ÁN CỦA ĐỀ CHÍNH THỨC
NỘI DUNG
ĐIỂM
CÂU 1
(1,5 điểm)
a/
2
(1)
3 3 2 0x x
x
2
3 0 3
3 2 0 1 2
x x
x x x x
Bảng xét dấu
x
1
3
f(x)
-
0 + 0
-
0 +
Vậy tập nghiệm của bất phương trình là
( ;1 2;3 .
S

] [ ]
b/ b/
2
3
0
1
x x
x
2
0
3 0
3
1 0 1
x
x x
x
x x
BXD:
x

-1 0 3
VT
+ || - 0 + 0 -
Vậy Tập nghiệm của bất phương trình là
; 1 0;3
S 
0,25x3
0,25x3
CÂU 2
(3,5 điểm)
2
2
2
2
2
1 2 5
a/ 1 2 5
1 5 2
6 0
1 4
1 4
3 4 0
x x x
x x x
x x x
x x x R
x
x
x x
2
b/ 2
x x x
2
2
2
0
2 0
2
x x
x
x x x
1 v 0
2
4
3
x x
x
x
0
x
3
c/ 2
2
x
x
3 5 4
4
2 0
2 v
4
2 2
4
5
3 4
5
2 4
2 0
2 2
x x
x x
x x
x
x x
x
x x
0,25x4
0,25x4
0,25x3
0,25x4
0,25x4
0,25x3
2 2
2 4 12 2 3 9
3
1 0
d/ 3 3
3 3
3
3 2 2 1 3
x x x x
x
x
x x
x
x x x
0,25x3
Câu 3
(1,5 điểm)
a/ Chứng minh đẳng thức:
cos 1
tan
1 sin cos
x
x
x x
Ta có:
cos 1 cos sin 1
tan
1 sin cos 1 sin cos cos
x x x
x
x x x x x
2 2 2 2
cos 1 sin cos cos
x x x x
( đúng )
b/
2
2 2
sin 4sin .cos 1
2cos 3sin 2
x x x
P
x x
2
2 2
2 2 2
2 2
2 2
2 2 2
sin 4sin .cos 1
tan 4 tan 1 tan
9
cos cos cos
2cos 3sin 2
4
2 3tan 2 1 tan
cos cos cos
x x x
x x x
x x x
x x
x x
x x x
0.25x3
0.25x3
Câu 4
(2,0 điểm)
a/ Cho
ABC
với
1;4 , 2; 1 , 6;2
A B C
. Viết pttq đường thẳng chứa
cạnh BC và pttq đường thẳng chứa đường cao AH.
BC: qua
2; 1
B
VTCP
(4;3)
BC
(3; 4)
VTPT n
BC:
3( 2) 4 1 0
x y
3 4 10 0
x y
AH qua
1,4
A
(4;3)
VTPT n
AH:
4( 1) 3 4 0
x y
4 3 16 0
x y
b/ Gọi
( ; )
n a b
là VTPT của d
2 2
( 0)
a b
.
Vì
( 2;0)
E d
nên PTTQ của d có dạng
2a 0
ax by
.
Ta có
0
2
cos( , ) cos45
2
d
2 2
2 2 2 2
2 2 2 2 2 2
3
2
3 5
2
1 3
6 9 5 5 4 6 4 0
a b
a b a b
a b
a ab b a b a ab b
0.25x4
0.25x4
Chọn
1
b
, khi đó ta được
2
2
4 6 4 0
1
2
a
a a
a
+ Với
2, 1
a b
, ta có PTTQ của
: 2 4 0
d x y
+ Với
1
, 1
2
a b
, ta có PTTQ của
1
: 1 0
2
d x y
2 2 0
x y
Vậy phương trình đường thẳng d cần tìm là
: 2 4 0
: 2 2 0
d x y
d x y
.
Câu 5
(1,5 điểm)
a/ Lập phương trình đường tròn có đường kính
AB
với
1;3
A
,
5;7
B
Tâm
3;5
I
Bán kính
8
R IA
Phương trình đường tròn:
2 2
3 5 8
x y
b/ Lập phương trình đường tròn tiếp xúc với hai trục toạ độ Ox, Oy và đi
qua điểm M(2;1).
Gọi
;
I a a
là tâm và bán kính
R a
(C):
2 2
2
x a y a a
2 2
2
2;1 2 1
M C a a a
2
1
6 5 0
5
a
a a
a
2 2
1 : 1 1 1
a C x y
2 2
5 : 5 5 25
a C x y
0.25x4
0.25x2
Lưu ý: Mọi cách làm khác đúng , giám khảo cho thang điểm tương ứng
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA HỌC KỲ 2 THÀNH PHỐ HỒ CHÍ MINH MÔN :TOÁN - KHỐI : 10
TRƯỜNG THPT VÕ VĂN KIỆT
Thời gian làm bài : 90 phút
Ngày kiểm tra : 23 / 06 /2020 ĐỀ CHÍNH THỨC
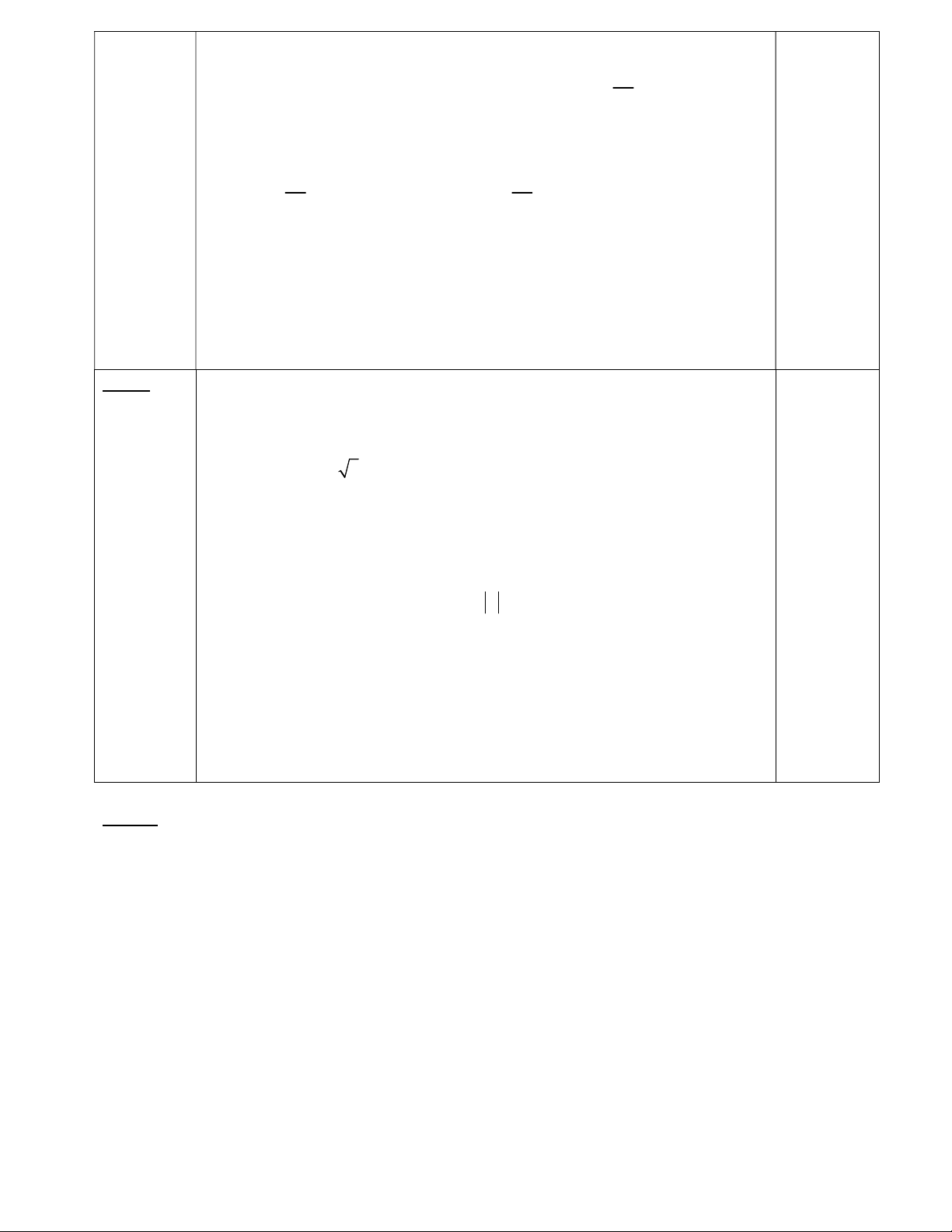
Câu 1: (1,5 điểm) Giải các bất phương trình: x   2 a/ 3 x  3x  2  0 2 x  3x b/  0 x 1
Câu 2: (3,5 điểm) Giải các bất phương trình và hệ bất phương trình sau: 2
a/ x  x 1  2x  5 2 b/ x  x  x  2 2 3x 2x  4x 12   1 c/  2 d/   x  2 3 x 3  x  2  2x 1 Câu 3: (1,5 điểm) a/ Chứng minh : cos x 1  tan x  . 1 sin x cos x 2 sin x  4sin . x cos x 1
b/ Cho tan x  2 . Tính giá trị của biểu thức: P  2 2 2cos x  3sin x  2
Câu 4: (2,0 điểm) Trong mặt phẳng tọa độ Oxy
a/ Cho ABC với A1;4, B2; 
1 ,C 6;2 . Viết phương trình tổng quát của đường thẳng chứa
cạnh BC và phương trình tổng quát của đường thẳng chứa đường cao AH.
b/ Lập phương trình tổng quát của đường thẳng d đi qua E( 2
 ;0) và tạo với đường thẳng
 : x  3y  3  0 một góc bằng 0 45 .
Câu 5: (1.5 điểm) Trong mặt phẳng tọa độ Oxy
a/ Lập phương trình của đường tròn có đường kính AB với A1;3 , B5;7
b/ Lập phương trình của đường tròn tiếp xúc với hai trục toạ độ Ox, Oy và đi qua điểm M(2;1).
---------------------------------------------------------HẾT ---------------------------------------------------------- Lưu ý:
1/ Thí sinh được sử dụng máy tính có chức năng tương đương máy tính fx- 570VN-PLUS, fx- 580VNX,..
2/ Họ và tên thí sinh: Số báo danh: Lớp:
3/ Các em nhớ ghi lớp vào giấy làm bài.
SỞ GD-ĐT TP.HCM ĐÁP ÁN KIỂM TRA HỌC KỲ 2
TRƯỜNG: THPT VÕ VĂN KIỆT NĂM HỌC: 2019-2020 MÔN: TOÁN –KHỐI 10
Thời gian làm bài: 90 phút
ĐÁP ÁN CỦA ĐỀ CHÍNH THỨC NỘI DUNG ĐIỂM CÂU 1 a/  x  3 2 x  3x  2  0 (1) (1,5 điểm) x  3  0  x  3 2
x  3x  2  0  x  1 x  2 Bảng xét dấu 0,25x3 x 1 3 f(x) - 0 + 0 - 0 +
Vậy tập nghiệm của bất phương trình là S  ( ;  1][2;3 .] 2 x  3x b/ b/  0 x 1 x  0 2 x  3x  0   x  3 x 1  0  x  1  BXD: x  -1 0 3  0,25x3 VT + | - 0 + 0 -
Vậy Tập nghiệm của bất phương trình là S   ;    1  0;3 CÂU 2 2
x  x 1 2x  5 2
(3,5 điểm) a/ x  x 1  2x  5   2  0,25x4 0,25x4
x  x 1  5  2x 2 x  x  6  0 x  R      1   x  4 2 x  3x  4  0 1   x  4    2 x  x  0 x  1  v x  0   2 
b/ x  x  x  2  x  2  0  x  2  x  0   x  x   x  22 2 4 x   0,25x4 0,25x4  3  3x 5x  4 3x 2   0  4 c/  2  x  2  x  2 x  2  v  x 4 x  2       5    x  4 3x x  4 5   2   0 2  x  4  x  2  x  2 0,25x3 0,25x3 2 2 2x  4x 12 2x  3x  9   1   0 x  3 d/  3  x   3  x    3   x  3   x  3  3  x  2  2x 1 x  3 0,25x3 Câu 3
a/ Chứng minh đẳng thức: cos x 1  tan x  (1,5 điểm) 1 sin x cos x Ta có: cos x 1 cos x sin x 1  tan x     1 sin x cos x 1 sin x cos x cos x 0.25x3 2 2 2 2
 cos x  1 sin x  cos x  cos x ( đúng ) 2 sin x  4sin . x cos x 1 b/ P  2 2 2cos x  3sin x  2 2 sin x 4sin . x cos x 1   2 tan x  4 tan x   2 2 2 2 1 tan x x x x  9 cos cos cos     2 2 2 2cos x 3sin x 2 2  3 tan x  2 2 1 tan x 4 0.25x3   2 2 2 cos x cos x cos x Câu 4 a/ Cho A
 BC với A1;4, B2; 
1 ,C 6;2 . Viết pttq đường thẳng chứa
(2,0 điểm) cạnh BC và pttq đường thẳng chứa đường cao AH. BC: qua B 2;  1  
VTCP BC  (4;3)  VTPT n  (3; 4  )
BC: 3(x  2)  4 y  
1  0  3x  4 y 10  0 0.25x4 AH qua A1,4  VTPT n  (4;3)
AH: 4(x 1)  3 y  4  0  4x  3y 16  0 
b/ Gọi n  (a;b) là VTPT của d 2 2 (a  b  0) . Vì E( 2
 ;0)d nên PTTQ của d có dạng ax  by  2a  0. Ta có 0 2 cos(d,)  cos 45  2 a  3b 2 2 2    a  3b  5 a  b 2 2 2 2 a  b 1  3 2 0.25x4 2 2 2 2 2 2
 a  6ab  9b  5a  5b  4a  6ab  4b  0 a  2
Chọn b  1, khi đó ta được 2 4a 6a 4 0       1 a   2
+ Với a  2, b  1, ta có PTTQ của d : 2x  y  4  0 1 1  + Với a 
,b  1, ta có PTTQ của d : x  y 1  0 2 2  x  2y  2  0 d : 2x  y  4  0
Vậy phương trình đường thẳng d cần tìm là  . d : x  2y  2  0 Câu 5
a/ Lập phương trình đường tròn có đường kính AB với A1;3 , B5;7 (1,5 điểm) 0.25x4 Tâm I 3;5 Bán kính R  IA  8
Phương trình đường tròn:  x  2   y  2 3 5  8
b/ Lập phương trình đường tròn tiếp xúc với hai trục toạ độ Ox, Oy và đi qua điểm M(2;1). Gọi I  ;
a a là tâm và bán kính R  a
(C):   2    2 2 x a y a  a  0.25x2 a  1 M 
C    a2    a2 2 2;1 2 1  a 2
 a  6a  5  0   a  5
a   C   x  2   y  2 1 : 1 1  1
a   C   x  2   y  2 5 : 5 5  25
Lưu ý: Mọi cách làm khác đúng , giám khảo cho thang điểm tương ứng