Đề thi học kì 2 Toán 9 năm 2023 – 2024 trường THCS Trưng Vương – Hà Nội
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề kiểm tra cuối học kì 2 môn Toán 9 năm học 2023 – 2024 trường THCS Trưng Vương, thành phố Hà Nội; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!
Preview text:
TRƯỜNG THCS TRƯNG VƯƠNG
BÀI KIỂM TRA HỌC KÌ II
NĂM HỌC 2023 – 2024 ĐÁP ÁN Môn thi : TOÁN LỚP 9
Thời gian làm bài : 90 phút HƯỚNG DẪN CHUNG
- Điểm toàn bài để lẻ đến 0,25.
- Các cách làm khác nếu đúng vẫn cho điểm tương ứng với biểu điểm của hướng dẫn chấm. Bài Đáp án Điểm I ý 1 x A (0,5đ) Thay
= 1 (tmđkxđ) vào biểu thức A ta có = −3. 0,5 1 2 2 x B = + − x − 2
x + 2 ( x − 2).( x + 0,25 2)
( x +2)+2( x −2)−2 x B = 0,25 I ý 2
( x −2).( x +2) (1,0đ) x − B = 2 ( 0,25
x + 2).( x − 2) B = 1
với x 0;x 4. 0,25 x + 2 x − 4 1 x − 2 2 P = . AB = . = = 1 − I ý 3 x x + 2 x x 0,25
(0,5đ) Lập luận ta có: P nguyên suy ra x N, x N và x U(2) x {1;4}.
Vậy x = 1(tm) thì P có giá trị nguyên. 0,25
Gọi số sản phẩm làm trong một ngày theo kế hoạch là : x (sản phẩm) ( x 0 ) 1200 0,25
+ Số ngày cần để hoàn thành theo kế hoạch: (ngày) x
+ Số sản phẩm làm trong một ngày thực tế là: x +100 (sản phẩm) 1200 0,25
+ Số ngày thực tế hoàn thành công việc là: II ý 1 x + (ngày) 100
(1,5đ) Vì số ngày thực tế hoàn thành sớm hơn so với kế hoạch là 2 ngày nên ta có 1200 1200 − = 0,25 2 x x + 100 Biến đổi về pt: 2
x +100x − 6000 = 0 . 0,25
Giải pt bậc hai ta được: x = 200(tm); x = 3 − 00(ktm). 0,25
Vậy theo kế hoạch, mỗi ngày tổ sản xuất phải làm 200 sản phẩm. 0,25
Thể tích của bình nước là: 2 2 3 V = R .h = .
41 .280 1477935,2mm 0,25 II ý 2 (0,5đ) =
Vậy bình đựng tối đa được: 3 3 V 1477935, 2mm 1,5dm 1,5 lít. 0,25
(lưu ý: bt yêu cầu làm tròn đến chữ số thập phân thứ nhất nên kq chuẩn 1,5l)
Đkxđ: x 0. (hs thiếu hoặc sai trừ 0,25đ) 0,25 x = 6 − (l) III ý 1 pt ...
x = 1(tm). (1đ) x =1(tm) 0,5
Lưu ý: + Hs giải bằng phương pháp phân tích phải có bước tách (thiếu – 0,25đ)
+ Hs phải đặt ẩn phụ đưa về pt bậc hai mới được sử dụng công thức nghiệm (thiếu -0,5đ)
Vậy tập nghiệm S = 1 . 0,25
+ Xét phương trình hoành độ giao điểm: III 2 0,25 x = ( m − ) 2 2
1 x + 2 x − (2m − ) 1 x − 2 = 0. (1) ý 2a
(0,75đ) + Lập luận chỉ ra được pt (1) luôn có hai nghiệm phân biệt với mọi giá trị m. 0,25
+ Kết luận: đường thẳng (d ) cắt parabol (P) tại hai điểm phân biệt. 0,25
+ Ta có: x + x = 2m −1; x x = 2
− 0 x , x trái dấu. 1 2 1 2 1 2 2 2 x x x + x 0,25 + 1 2 1 2 + = 2 = 2. (2) III x x x .x 2 1 1 2 ý 2b
(0,75đ) + Nx: (2) x .x 0 x 0 và x , x trái dấu nên x 0 x = −x . 1 2 2 1 2 1 1 1 0,25 pt
( x + x )2 = ( m − )2 1 (2) 0 2 1
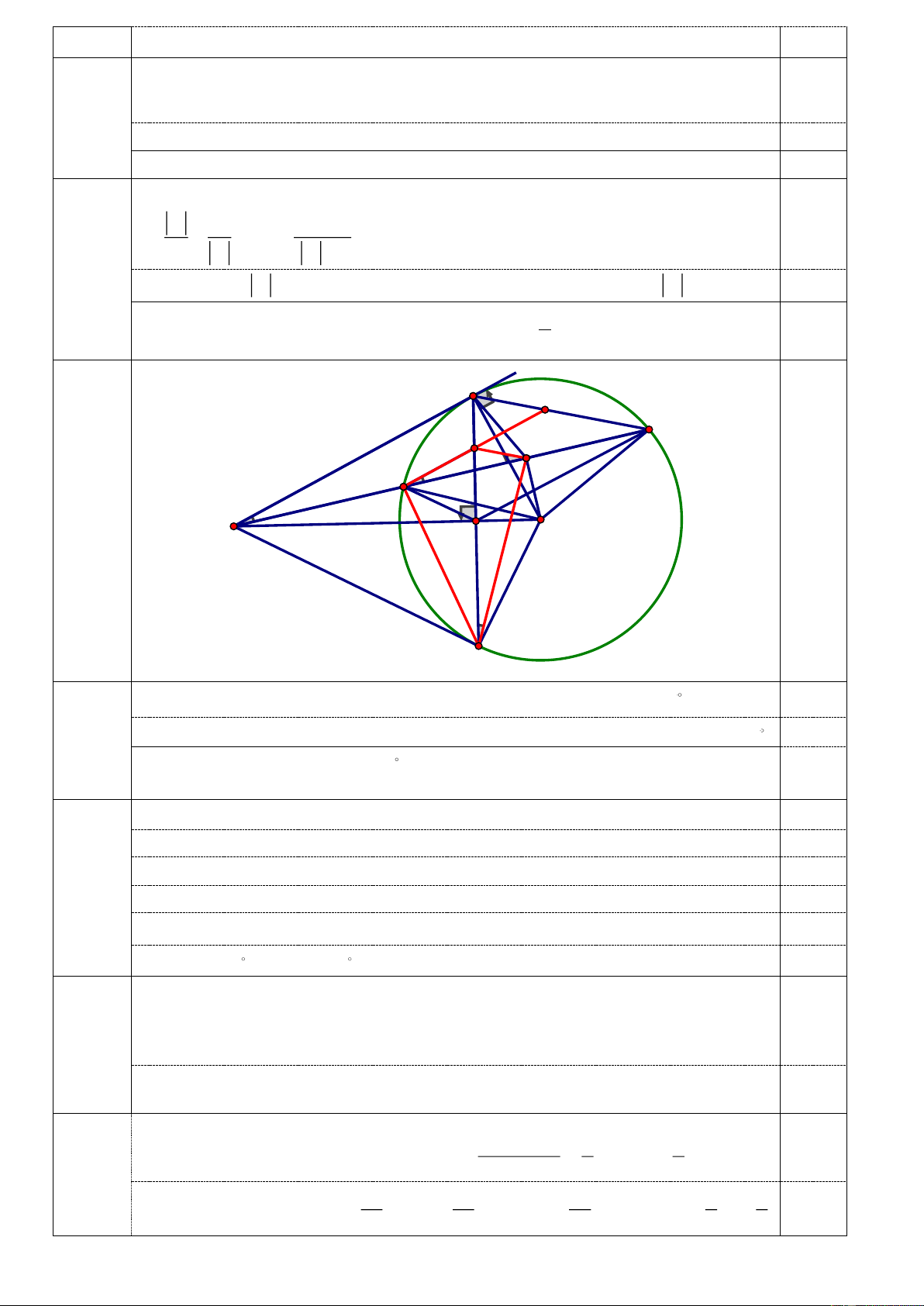
= 0 m = (tm). 1 2 0,25 + 2 A P C IV N Phần 2 B K (0,25đ) M (Vẽ 0,25 H O hình đến ý a) D
+ Chỉ ra: MA là tiếp tuyến của (O) tại tiếp điểm A nên OMA = 90 0,25 IV ý 1
+ K là trung điểm dây cung BC nên OK vuông góc với BC nên OKM = 90 0,25
(0,75đ) + Tứ giác MAKO có OMA = 90 = OKM , hai góc cùng nhìn cạnh . MO 0,25
Nên Tứ giác MDNI nội tiếp (dhnb)
+ Chỉ ra △MBA đồng dạng với △MAC (g- g) suy ra 2 MA = M . B MC 0,25
+ Chỉ ra △MAO vuông tại A có AH là đường cao nên 2
MA = MH .MO . 0,25 IV + Từ đó 2 M .
B MC = MA = MH .MO 0,25 ý 2 (1,5đ)
+ Chỉ ra △MBH đồng dạng với △MOC (c – g – c) suy ra BHOC nội tiếp 0,25
+ Chỉ ra CHO = CBO = BCO = BHM CHO = BHM 0,25
+ Suy ra: 90 − CHO = 90 − BHM BHA = CHA HA: phân giác BHC. 0,25
+ Nối NK. Kẻ tiếp tuyến MD của (O) tại D thì ,
A H , D thẳng hàng và năm IV điểm M , ,
A K,O, D thuộc một đường tròn. 0,25 ý 3
+ Tg BKND nội tiếp NKB = BDA = ACB do đó NK song song với AC.
(0,5đ) + △BPC có: K là trung điểm của BC và NK song song với AC. 0,25
suy ra N là trung điểm của . BP ( b + c)2 2 3 1 1 + = Bài V Giả thiết: 0 2b 3c 1 6bc 2 . b 3c 6bc . 0,25 4 4 4 (0,5đ) 1 − 1 − −1 1 1
M = a(2b + 3c) − 6bc 0 + M . Gtnn M = tại a = 0,b = , c = . 0,25 4 4 4 4 6
Document Outline
- de-hoc-ki-2-toan-9-nam-2023-2024-truong-thcs-trung-vuong-ha-noi
- de
- TRƯNG VƯƠNG