Đề thi học kỳ 2 Toán 10 năm 2017 – 2018 trường THPT chuyên Hà Nội – Amsterdam

Đề thi học kỳ 2 Toán 10 năm học 2017 – 2018 trường THPT chuyên Hà Nội – Amsterdam được biên soạn theo hình thức trắc nghiệm kết hợp với tự luận, thời gian làm bài 120 phút, đề thi có đáp án và lời giải chi tiết , mời các bạn đón xem

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 10

Môn: Toán 10

Thông tin:

9 trang 6 tháng trước

Tác giả:

Profile Thanh Tâm
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987
1
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
I. Câu hỏi trắc nghiệm (4,0 điểm). Chọn phương án đúng (Học sinh ghi đáp án vào giấy làm bài thi)
Câu 1. Nếu
,a b c d
thì bất đẳng thức nào sau đây luôn đúng?
A.
.ac bd
B.
.a c b d
C.
.a b c d
D.
.a c b d
Câu 2. Các giá trị của tham số
m
để bất phương trình
2
( 1) 0m x m
có nghiệm là:
A.
.m
B.
.m 
C.
\ 1 .m 
D.
1.m 
Câu 3. Tập hợp nghiệm của bất phương trình
là:
A.
1
2; .
2



B.
1
;2 .
2


C.
1
2; .
2


D.
1
;2 .
2


Câu 4. Tập hợp nghiệm của hệ bất phương trình
2
2
6 5 0
8 12 0
xx
xx
là:
A.
2;5 .


B.
1;6 .


C.
2;5 .
D.
1;2 5;6 .
Câu 5. Các giá trị của tham số
m
để bất phương trình
2
2 1 0mx mx
vô nghiệm là:
A.
.m 
B.
1.m 
C.
1 0.m
D.
1 0.m
Câu 6. Khi thống kê điểm môn Toán trong một kỳ thi của 200 em học sinh thì thấy có 36 bài được điểm
bằng 5. Tần suất của giá trị
5
i
x
là:
A.
2,5%.
B.
36%.
C.
18%.
D.
10%.
Câu 7. Chọn hệ thức sai trong các hệ thức sau:
A.
3
.
2
tan x cot x




B.
(3 ) .sin x sin x

C.
(3 ) .cos x cos x

D.
( ) .cos x cos x
Câu 8. Cho
1
3
sin
với
0.
2

Giá trị của
3
cos



bằng:
A.
26
.
26
B.
6 3.
C.
1
3.
6
D.
1
6.
2
Câu 9. Nếu
1
2
sin x cos x
thì giá trị của
2sin x
là:
A.
1
.
2
B.
1
.
2
C.
1
.
4
D.
1
.
4
Câu 10. Trong mặt phẳng tọa độ Oxy, cho ba đường thẳng
12
( ) : 3 4 7 0,( ) : 5 4 0d x y d x y
và
3
( ) : (1 ) 3 0.d mx m y
Để ba đường thẳng này đồng quy thì giá trị của tham số
m
là:
A.
2.m
B.
2.m 
C.
0,5.m
D.
0,5.m 
Câu 11. Trên mặt phẳng tọa độ Oxy, cho hai điểm
( 2;3)A
và
(4; 1).B
Phương trình nào sau đây là
phương trình đường thẳng AB?
A.
3 0.xy
B.
C.
41
.
64
xy
D.
13
.
12
xt
yt


TRƯỜNG THPT CHUYÊN
HÀ NỘI – AMSTERDAM
TỔ TOÁN - TIN
ĐỀ KIỂM TRA HỌC KỲ II
MÔN TOÁN LỚP 10
Năm học 2017 – 2018
(Thời gian làm bài: 120 phút (không kể thời gian phát đề)
ĐỀ CHÍNH THỨC
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987
2
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Câu 12. Một elip có diện tích hình chữ nhật cơ sở là 80, độ dài tiêu cự là 6. Tâm sai của elip đó là:
A.
4
.
5
e
B.
3
.
4
e
C.
3
.
5
e
D.
4
.
3
e
Câu 13. Trên mặt phẳng tọa độ Oxy, cho các điểm
(1; 1)A
và
(3;4).B
Giả sử
()d
là một đường thẳng
bất kỳ luôn đi qua điểm B. Khi khoảng cách từ A đến đường thẳng
()d
đạt giá trị lớn nhất, đường thẳng
()d
có phương trình nào sau đây?
A.
1 0.xy
B.
3 4 25.xy
C.
5 2 7 0.xy
D.
2 5 26 0.xy
Câu 14. Trên mặt phẳng tọa độ Oxy, gọi
()d
là đường thẳng đi qua điểm
(1;1)A
và tạo với đường thẳng
có phương trình
3 2 0xy
một góc bằng
0
45 .
Đường thẳng
()d
có phương trình là:
A.
2 1 0.xy
B.
C.
2 1 0.xy
D.
3 4 0.xy
Câu 15. Trên mặt phẳng tọa độ Oxy, cho các điểm
(3;0)A
và
(0;4).B
Đường tròn nội tiếp tam giác OAB
có phương trình là:
A.
22
1.xy
B.
22
4 4 0.x y x
C.
22
2.xy
D.
22
( 1) ( 1) 1.xy
Câu 16. Trên mặt phẳng tọa độ Oxy, cho điểm
( 3; 2)P 
và đường tròn
22
( ) : ( 3) ( 4) 36.C x y
Từ điểm P kẻ các tiếp tuyến PM và PN tới đường tròn
()C
, với M và N là các tiếp điểm. Phương trình
đường thẳng MN là:
A.
1 0.xy
B.
1 0.xy
C.
1 0.xy
D.
1 0.xy
II. Tự luận (6,0 điểm – 6,0 điểm).
Bài 1. (1,5 điểm – 1,5 điểm).
a) Giải bất phương trình sau trên tập số thực:
2 1 2 4 .xx
b) Giải hệ bất phương trình sau trên tập số thực:
2
3
0
2 3 2 1
3 3 1
xx
xx
xx


Bài 2. (1,5 điểm – 2,0 điểm).
a) Chứng minh đẳng thức:
2 2 2
22
1
12
1
cos x tan x
sin x
cos x sin x tan x


khi các biểu thức đề xác định.
b) Tìm các giá trị của tham số
m
để hệ bất phương trình
2
2
45
( 1) 0
xx
x m x m

có nghiệm.
Bài 3. (2,5 điểm – 2,5 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai đường tròn
12
( ),( )CC
có
phương trình lần lượt là
22
( 1) ( 2) 9xy
và
22
( 2) ( 2) 4.xy
a) Tìm tọa độ tâm, bán kính của hai đường tròn và chứng minh hai đường tròn tiếp xúc với nhau.
b) Viết phương trình đường thẳng đi qua gốc tọa độ và tạo với đường thẳng nối tâm của hai đường tròn
một góc bằng 45°.
c) Cho elip (E) có phương trình
22
16 49 1.xy
Viết phương trình đường tròn (C) có bán kính gấp đôi
độ dài trục lớn của elip (E) và (C) tiếp xúc với hai đường tròn
12
( ),( )CC
.
Bài 4. (0,5 điểm – 0 điểm). (Chỉ dành cho các lớp 10 Tin, L
1
, L
2
, H
1
, H
2
)
Cho ba số thực
,,a b c
thỏa mãn điều kiện
2 2 2
3.a b c
Tìm giá trị nhỏ nhất của biểu thức sau:
3 3 3
1 1 1
.
1 8 1 8 1 8
P
a b c
-------------------------------- Hết --------------------------------
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987
3
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
GỢI Ý ĐÁP ÁN.
I. Câu hỏi trắc nghiệm (4,0 điểm). Chọn phương án đúng (Học sinh ghi đáp án vào giấy làm bài thi)
Câu 1. Nếu
,a b c d
thì bất đẳng thức nào sau đây luôn đúng?
A.
.ac bd
B.
.a c b d
C.
.a b c d
D.
.a c b d
Giải thích đáp án.
Dễ thấy đây là quy tắc cộng 2 bất đẳng thức cùng chiều: Khi
ab
a c b d
cd
Chọn D.
Câu 2. Các giá trị của tham số
m
để bất phương trình
2
( 1) 0m x m
có nghiệm là:
A.
.m
B.
.m 
C.
\ 1 .m 
D.
1.m 
Giải thích đáp án.
- Khi
1 0 1 0m
(thỏa mãn).
- Khi
1 0 1 0m
(vô lí)
- Khi
2
1
1
m
mx
m
(thỏa mãn).
Vậy bất phương trình có nghiệm khi và chỉ khi
1m 
hay
\1m
Chọn C.
Câu 3. Tập hợp nghiệm của bất phương trình
là:
A.
1
2; .
2



B.
1
;2 .
2


C.
1
2; .
2


D.
1
;2 .
2


Giải thích đáp án.
Dễ thấy
1 2 2 1 1 1
0 0 2 2;
4 8 2 2
42
xx
xS
x
x



Chọn C.
Câu 4. Tập hợp nghiệm của hệ bất phương trình
2
2
6 5 0
8 12 0
xx
xx
là:
A.
2;5 .


B.
1;6 .


C.
2;5 .
D.
1;2 5;6 .
Giải thích đáp án.
Ta có:
2
2
6 5 0 1 5
2 5 2;5
8 12 0 2 6
x x x
xS
x x x
Chọn C.
Câu 5. Các giá trị của tham số
m
để bất phương trình
2
2 1 0mx mx
vô nghiệm là:
A.
.m 
B.
1.m 
C.
1 0.m
D.
1 0.m
Câu
1
2
3
4
5
6
7
8
Đáp án
D
C
C
C
C
C
C
A
Câu
9
10
11
12
13
14
15
16
Đáp án
A
A
D
C
D
B
D
D
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987
4
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Giải thích đáp án.
Áp dụng ĐL về dấu tam thức bậc hai ta thấy
( ) 0fx
nên BPT vô nghiệm
0
0a

2
0
0
10
10
0
m
mm
m
m
m




Chọn C.
Câu 6. Khi thống kê điểm môn Toán trong một kỳ thi của 200 em học sinh thì thấy có 36 bài được điểm
bằng 5. Tần suất của giá trị
5
i
x
là:
A.
2,5%.
B.
36%.
C.
18%.
D.
10%.
Giải thích đáp án.
Vì có 36 bài được điểm 5 nên tần số của điểm 5 là
36.
i
n
Vậy tần suất của giá trị
5
i
x
là:
36
100 100 18%
200
i
i
n
f
N
Chọn C.
Câu 7. Chọn hệ thức sai trong các hệ thức sau:
A.
3
.
2
tan x cot x




B.
(3 ) .sin x sin x

C.
(3 ) .cos x cos x

D.
( ) .cos x cos x
Giải thích đáp án.
- Dễ thấy
3
22
tan x tan x cot x

(vì tan tuần hoàn chu kỳ π ). A đúng.
- Và
(3 ) ( )sin x sin x sin x

(vì sin tuần hoàn chu kỳ 2π). B đúng.
- Và
(3 ) ( )cos x cos x cos x

(vì cos tuần hoàn chu kỳ 2π)
Chọn C.
Lưu ý. Với học sinh không nắm rõ chu kỳ và giá trị lượng giác của các góc bù, phụ, đối. Có thể lấy sử
dụng máy tính CASIO ở chế độ R và lấy x bất kỳ thay vào để thử đáp án.
Câu 8. Cho
1
3
sin
với
0.
2

Giá trị của
3
cos



bằng:
A.
26
.
26
B.
6 3.
C.
1
3.
6
D.
1
6.
2
Giải thích đáp án.
Ta thấy
2
1
11
6
3
3
0 1( 0 )
2
cos sin
cos
cos do



Mà
6 1 1 3 1 1 2 6
..
3 3 3 3 2 2 2
3 6 2 6
cos cos cos sin sin



Chọn A.
Lưu ý. Ta có thể sử dụng Casio đổi ra góc α thấy thuộc khoảng (0;π/2), lấy KQ tính cos(Ans+π/3) lưu lại
là X. Sau đó lấy X trừ đi kết quả ở các đáp án để thử.
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987
5
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Câu 9. Nếu
1
2
sin x cos x
thì giá trị của
2sin x
là:
A.
1
.
2
B.
1
.
2
C.
1
.
4
D.
1
.
4
Giải thích đáp án.
Ta thấy
2
1 1 1
1 2 2
2 2 2
sin x cos x sin xcos x si n x
Chọn A.
Câu 10. Trong mặt phẳng tọa độ Oxy, cho ba đường thẳng
12
( ) : 3 4 7 0,( ) : 5 4 0d x y d x y
và
3
( ) : (1 ) 3 0.d mx m y
Để ba đường thẳng này đồng quy thì giá trị của tham số
m
là:
A.
2.m
B.
2.m 
C.
0,5.m
D.
0,5.m 
Giải thích đáp án.
Bấm máy giải hệ phương trình tạo bởi phương trình của
12
( )&( )dd
ta được tọa độ giao điểm
1;1 .M
Để ba đường thẳng đồng quy (tại M) thì M phải thuộc
3
( ) 1 3 0 2d m m m
Chọn A.
Câu 11. Trên mặt phẳng tọa độ Oxy, cho hai điểm
( 2;3)A
và
(4; 1).B
Phương trình nào sau đây là
phương trình đường thẳng AB?
A.
3 0.xy
B.
C.
41
.
64
xy
D.
13
.
12
xt
yt


Giải thích đáp án.
Để đơn giản ta cứ thay tọa độ của A và B vào kiểm tra thấy ngay A,B,C sai
Chọn D.
Câu 12. Một elip có diện tích hình chữ nhật cơ sở là 80, độ dài tiêu cự là 6. Tâm sai của elip đó là:
A.
4
.
5
e
B.
3
.
4
e
C.
3
.
5
e
D.
4
.
3
e
Giải thích đáp án.
Diện tích hình chữ nhật cơ sở là:
2 .2 80 20a b ab
mà
2 2 2 2 2
93a b c a b doc
Ta được
2
2
2
2
22
42
2
2
400
400
20
5
3
400 4
9
5
9 400 0
9
b
ab
a
b
c
a
e
a
b
ab
a
aa
a
a



Chọn C.
Câu 13. Trên mặt phẳng tọa độ Oxy, cho các điểm
(1; 1)A
và
(3;4).B
Giả sử
()d
là một đường thẳng
bất kỳ luôn đi qua điểm B. Khi khoảng cách từ A đến đường thẳng
()d
đạt giá trị lớn nhất, đường thẳng
()d
có phương trình nào sau đây?
A.
1 0.xy
B.
3 4 25.xy
C.
5 2 7 0.xy
D.
2 5 26 0.xy
Giải thích đáp án.
Gọi
22
( ) : ( 3) ( 4) 0 3 4 0 0d a x b y hayax by a b a b
Khi đó
22
2 2 2 2 2 2
4 25
3 4 2 5
( ( )) 29
Bunhiacopxki
ab
a b a b a b
d A d
a b a b a b

Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987
6
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Khi đó
2
( ) : 2 5 26 0
2 5 5
a b a
hay d x y
b
Chọn D.
Câu 14. Trên mặt phẳng tọa độ Oxy, gọi
()d
là đường thẳng đi qua điểm
(1;1)A
và tạo với đường thẳng
có phương trình
3 2 0xy
một góc bằng
0
45 .
Đường thẳng
()d
có phương trình là:
A.
2 1 0.xy
B.
C.
2 1 0.xy
D.
3 4 0.xy
Giải thích đáp án.
Gọi
22
( ) : ( 1) ( 1) 0 0 0d a x b y hayax by a b a b
Vì
2
0 2 2
3 2 0
22
3 2 0
;
13
45 , 3 5 5
3;1
2
10.
d
d x y
xy
u b a
ba
cos cos u u a b a b
u
ab


Hay
1
; 1;2 ( ) : 2 3 0
2
2 2 0
2 ; 2; 1 ( ) : 2 1 0
a
a b d x y
b
a b a b
a
a b d x y
b
Chọn B.
Câu 15. Trên mặt phẳng tọa độ Oxy, cho các điểm
(3;0)A
và
(0;4).B
Đường tròn nội tiếp tam giác OAB
có phương trình là:
A.
22
1.xy
B.
22
4 4 0.x y x
C.
22
2.xy
D.
22
( 1) ( 1) 1.xy
Giải thích đáp án.
Tâm I là giao của 3 đường phân giác trong của ∆OAB mà A và B lần
lượt nằm trên Ox và Oy nên phân giác của góc AOB chính là phân giác
góc phần tư thứ I và III có phương trình:
.yx
Gọi
;I m m
là tâm đường tròn nội tiếp ta có:
( ) ( )
:0
: 1 4 3 12 0
34
d I OA d I AB
OA x
xy
AB x y
Hay
7 12
7 12 5 6
12 7 5 1
5
m
m m m
m
m m m
Chọn D.
Lưu ý. Nếu tinh ý ta có thể thấy tâm đường tròn nội tiếp, gốc tọa độ và hình chiếu của tâm lên 2 trục Ox
và Oy lập thành một hình vuông cạnh bằng bán kính đường tròn nội tiếp(bằng 1) nên ta có ngay phương
trình
22
( 1) ( 1) 1.xy
Câu 16. Trên mặt phẳng tọa độ Oxy, cho điểm
( 3; 2)P 
và đường tròn
22
( ) : ( 3) ( 4) 36.C x y
Từ điểm P kẻ các tiếp tuyến PM và PN tới
đường tròn
()C
, với M và N là các tiếp điểm. Phương trình đường thẳng
MN là:
A.
1 0.xy
B.
1 0.xy
C.
1 0.xy
D.
1 0.xy
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987
7
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Giải thích đáp án.
Dễ thấy tứ giác OMPN (O(3;4) là tâm đường tròn) là hình vuông nên (MN) nhận
6; 6 1;1OP 
làm vectơ pháp tuyến và đi qua trung điểm
0;1K
của OP.
Vậy
( ) : 0 1 0 1 0M N x y h ay x y
Chọn D.
II. Tự luận (6,0 điểm – 6,0 điểm).
Bài 1. (1,5 điểm – 1,5 điểm).
a) Giải bất phương trình sau trên tập số thực:
2 1 2 4 .xx
b) Giải hệ bất phương trình sau trên tập số thực:
2
3
0
2 3 2 1
3 3 1
xx
xx
xx


Giải.
a) Ta có BPT
1
2 1 0
13
2
2 3 4 3
22
3
2
;.
1
2
2 1 0
1
2
2 1 4 1
2
6
x
x
x
xx
x
S
x
x
x
xx
x












b) Điều kiện:
2 3 0
31
,
2 1 0
22
x
xx
x


HBPT
2
2 2 2
33
3 2 1 2 3
83
82
00
1
2 1 2 3 2 1 2 3
2
1
11
3
1
1
3 1 3
33
4
3 1 6 9 4 3 1 0
1
4
x
x x x x
x
x x x x
x
x
xx
x
x x x
x x x x x
x






Kết hợp nghiệm ta được:
1
;.
4
S




Bài 2. (1,5 điểm – 2,0 điểm).
a) Chứng minh đẳng thức:
2 2 2
22
1
12
1
cos x tan x
sin x
cos x sin x tan x


khi các biểu thức đề xác định.
b) Tìm các giá trị của tham số
m
để hệ bất phương trình
2
2
45
( 1) 0
xx
x m x m

có nghiệm.
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987
8
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Giải.
a) Ta có:
2 2 2 2 2 2 2
2
2
2
11
1
sin x
cos x sin xcos x
VP
cos x sin x sin x cos x sin x cos x sin x
cos x
2
12
sin x cos x
sin xcos x sin x cos x
cos x sin x
sin x cos x cos x sin x sin x cos x cos x sin x


(1)
Mà
22
2 2 2
2
12
2
cos x
cosx sinx cosx sinx
cos x sin x cosx sinx
VT
sin x cosx sinx
cos x sin x sinxcosx
cosx sinx




(2)
Từ (1) và (2) ta được
VT VP
ĐPCM.
b) Ta có
2
2
5
5
5
45
1
( 1) 0
1
10
1
x
x
m
xm
xx
x
x m x m
x
x x m
m
xm






Vậy với
1
5
m
m

thì hệ bất phương trình luôn có nghiệm.
Bài 3. (2,5 điểm – 2,5 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai đường tròn
12
( ),( )CC
có
phương trình lần lượt là
22
( 1) ( 2) 9xy
và
22
( 2) ( 2) 4.xy
a) Tìm tọa độ tâm, bán kính của hai đường tròn và chứng minh hai đường tròn tiếp xúc với nhau.
b) Viết phương trình đường thẳng đi qua gốc tọa độ và tạo với đường thẳng nối tâm của hai đường tròn
một góc bằng 45°.
c) Cho elip (E) có phương trình
22
16 49 1.xy
Viết phương trình đường tròn (C) có bán kính gấp đôi
độ dài trục lớn của elip (E) và (C) tiếp xúc với hai đường tròn
12
( ),( )CC
.
Giải.
a) Ta thấy đường tròn
1
()C
có tâm
1
1; 2I 
và bán kính
1
3.R
Đường tròn
2
()C
có tâm
2
2;2I
và
bán kính
2
2.R
Khi đó:
22
1 2 1 2
5 2 1 2 2 5R R I I
1
()C
và
2
()C
tiếp xúc
nhau.
b) Ta có
12
3;4II
gọi vectơ chỉ phương của đường thẳng cần lập là
;.u a b
22
0
12
22
22
1 3 4 1 9 24 16
45 ,
2
25 25
2
5
a b a ab b
cos cos I I u
ab
ab
22
; 7;1 7 0
7 48 7 0
; 1; 7 7 0
a b x y
a ab b
a b x y
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987
9
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
c) Ta có
22
22
22
16 49 1 1
11
47
xy
xy
Độ dài trục lớn của (E) là
11
2 2. .
42
a 
Vậy bán kính đường tròn
()C
cần lập là
1.R
Khi đó xét
12
II I
ta có:
11
12
22
3 1 4
2 1 3
II R R
II I
II R R

vuông tại I.
Gọi
;I a b
ta có:
22
12
22
22
2
2 1 2 2 0
60
.0
4 4 1 0
3
2 2 9
a a b b
a b a
II II
a b a b
II
ab


22
2
1
71 22
53
3 4 5
; ( )
25 25
4
60
25 46 71 0
1;2 ( )
a
ab
I tm
b
a b a
aa
I I loai







Vậy phương trình đường tròn cần lập là:
22
71 22
( ) : 1
25 25
C x y
.
Bài 4. (0,5 điểm – 0 điểm). (Chỉ dành cho các lớp 10 Tin, L
1
, L
2
, H
1
, H
2
)
Cho ba số thực
,,a b c
thỏa mãn điều kiện
2 2 2
3.a b c
Tìm giá trị nhỏ nhất của biểu thức sau:
3 3 3
1 1 1
.
1 8 1 8 1 8
P
a b c
Giải.
Ta có
2
3 2 2
1 2 1 2 4
1 8 1 2 1 2 4 1 2
2
AM GM
a a a
a a a a a
Tương tự vai trò cho
3
18b
và
3
18c
ta được:
2 2 2
1 1 1
1 2 1 2 1 2
P
a b c
Mặt khác:
2 2 2 2
2
2 2 2
1 1 1 2 1 2 1 1 2 2 1 5 2
2.
9 9 9 9 9 9
1 2 1 2 1 2
Cauchy
a a a a
a
a a a
Khi đó
2 2 2
2 2 2
15 2
5 2 5 2 5 2 15 2.3
1
9 9 9 9 9
a b c
a b c
P
. Vậy
1M in P
.
Dấu “=” xảy ra
2 2 2
2
2
2
3
1 2 1 2 4
1 1 2
9
12
a b c
a a a
a
a

và vai trò
,,a b c
như nhau hay
; ; 1;1;1a b c
.
-------------------------------- Hết --------------------------------
| 1/9
| | Tải xuống

Có thể bạn quan tâm:

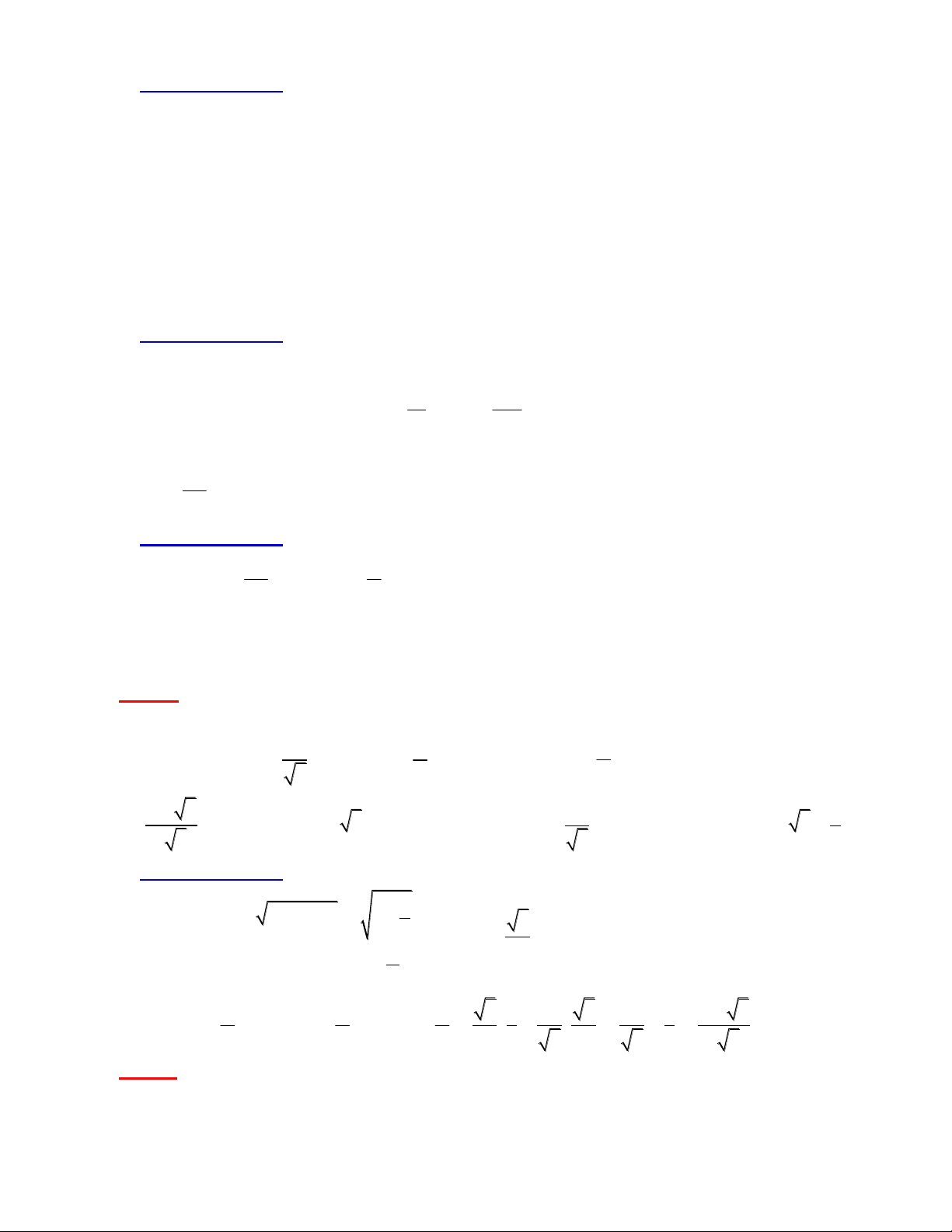
Preview text:

Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987 TRƯỜNG THPT CHUYÊN
ĐỀ KIỂM TRA HỌC KỲ II HÀ NỘ I – AM STERD AM MÔN TOÁN LỚP 10 TỔ TOÁN - TIN
Năm học 2017 – 2018 ĐỀ CHÍNH THỨC
(Thời gian làm bài: 120 phút (không kể thời gian phát đề)
I. Câu hỏi trắc nghiệm (4,0 điểm). Chọn phương án đúng (Học sinh ghi đáp án vào giấy làm bài thi)
Câu 1. Nếu a  ,
b c d thì bất đẳng thức nào sau đây luôn đúng?
A. ac bd.
B. a c b d.
C. a b c d.
D. a c b d.
Câu 2. Các giá trị của tham số m để bất phương trình 2
(m  1)x m  0 có nghiệm là: A. m  .  B. m  . 
C. m   \   1 . D. m  1.  1  2x
Câu 3. Tập hợp nghiệm của bất phương trình  0 là: 4x  8  1  1   1 1  A. 2  ; .   B.   ;2 .  C.  2  ; .  D. ;2  . 2   2   2   2   2 x
  6x  5  0
Câu 4. Tập hợp nghiệm của hệ bất phương trình  là: 2
x  8x  12  0  A. 2  ;5.   B. 1  ;6.   C. 2;5.  D. 1  ;2  5  ;6.    
Câu 5. Các giá trị của tham số m để bất phương trình 2
mx  2mx  1  0 vô nghiệm là: A. m  .  B. m  1.  C. 1   m  0. D. 1   m  0.
Câu 6. Khi thống kê điểm môn Toán trong một kỳ thi của 200 em học sinh thì thấy có 36 bài được điểm
bằng 5. Tần suất của giá trị x  5 là: i A. 2, 5%. B. 36%. C. 18%. D. 10%.
Câu 7. Chọn hệ thức sai trong các hệ thức sau:  3  A. tan
x   cot x. B. sin(3  x)  sin x.
C. cos (3  x)  cos x.
D. cos ( x  )  cos x. 2   1    
Câu 8. Cho sin   với 0   
. Giá trị của cos    bằng: 3 2 3   2  6 1 1 A. . B. 6  3. C.  3. D. 6  . 2 6 6 2 1
Câu 9. Nếu sin x cos x
thì giá trị của sin 2x là: 2 1 1 1 1 A. . B.  . C. . D.  . 2 2 4 4
Câu 10. Trong mặt phẳng tọa độ Oxy, cho ba đường thẳng (d ) : 3x  4y  7  0,(d ) : 5x y  4  0 và 1 2
(d ) : mx  (1  m)y  3  0. Để ba đường thẳng này đồng quy thì giá trị của tham số m là: 3 A. m  2. B. m  2.  C. m  0,5. D. m  0  ,5.
Câu 11. Trên mặt phẳng tọa độ Oxy, cho hai điểm ( A 2  ;3) và ( B 4; 1
 ). Phương trình nào sau đây là
phương trình đường thẳng AB? x  4 y  1 x   1  3t
A. x y  3  0.
B. y  2x  1. C.  . D.  . 6 4  y  1  2t  1
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987
Câu 12. Một elip có diện tích hình chữ nhật cơ sở là 80, độ dài tiêu cự là 6. Tâm sai của elip đó là: 4 3 3 4 A. e  . B. e  . C. e  . D. e  . 5 4 5 3
Câu 13. Trên mặt phẳng tọa độ Oxy, cho các điểm ( A 1; 1  ) và (
B 3;4). Giả sử (d) là một đường thẳng
bất kỳ luôn đi qua điểm B. Khi khoảng cách từ A đến đường thẳng (d) đạt giá trị lớn nhất, đường thẳng
(d) có phương trình nào sau đây?
A. x y  1  0.
B. 3x  4y  25.
C. 5x  2y  7  0.
D. 2x  5y  26  0.
Câu 14. Trên mặt phẳng tọa độ Oxy, gọi (d) là đường thẳng đi qua điểm (
A 1;1) và tạo với đường thẳng
có phương trình x  3y  2  0 một góc bằng 0
45 . Đường thẳng (d)có phương trình là:
A. 2x y  1  0.
B. 2x y  1.
C. x  2y  1  0.
D. 3x y  4  0.
Câu 15. Trên mặt phẳng tọa độ Oxy, cho các điểm ( A 3;0) và (
B 0;4). Đường tròn nội tiếp tam giác OAB có phương trình là: A. 2 2 x y  1. B. 2 2
x y  4x  4  0. C. 2 2 x y  2. D. 2 2
(x  1)  (y  1)  1.
Câu 16. Trên mặt phẳng tọa độ Oxy, cho điểm P( 3  ; 2  ) và đường tròn 2 2
(C) : (x  3)  (y  4)  36.
Từ điểm P kẻ các tiếp tuyến PM và PN tới đường tròn (C ) , với M và N là các tiếp điểm. Phương trình đường thẳng MN là:
A. x y  1  0.
B. x y  1  0.
C. x y  1  0.
D. x y  1  0.
II. Tự luận (6,0 điểm – 6,0 điểm).
Bài 1. (1,5 điểm – 1,5 điểm).
a) Giải bất phương trình sau trên tập số thực:
2x  1  2  4x.  x  3 x    0
b) Giải hệ bất phương trình sau trên tập số thực:
2x  3 2x  1 2
x  3  3x  1 
Bài 2. (1,5 điểm – 2,0 điểm). cos 2x 2 1 tan x
a) Chứng minh đẳng thức:  
khi các biểu thức đề xác định. 2 2 2 1 sin 2x cos x sin x 1  tan x 2 x   4x  5
b) Tìm các giá trị của tham số m để hệ bất phương trình  có nghiệm. 2
x  (m  1)x m  0 
Bài 3. (2,5 điểm – 2,5 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai đường tròn (C ),(C ) có 1 2
phương trình lần lượt là 2 2
(x  1)  (y  2)  9 và 2 2
(x  2)  (y  2)  4.
a) Tìm tọa độ tâm, bán kính của hai đường tròn và chứng minh hai đường tròn tiếp xúc với nhau.
b) Viết phương trình đường thẳng đi qua gốc tọa độ và tạo với đường thẳng nối tâm của hai đường tròn một góc bằng 45°.
c) Cho elip (E) có phương trình 2 2
16x  49y  1. Viết phương trình đường tròn (C) có bán kính gấp đôi
độ dài trục lớn của elip (E) và (C) tiếp xúc với hai đường tròn (C ),(C ) . 1 2
Bài 4. (0,5 điểm – 0 điểm). (Chỉ dành cho các lớp 10 Tin, L1, L2, H1, H2) Cho ba số thực , a ,
b c thỏa mãn điều kiện 2 2 2
a b c  3. Tìm giá trị nhỏ nhất của biểu thức sau: 1 1 1 P    . 3 3 3 1  8a 1  8b 1  8c
-------------------------------- Hết -------------------------------- 2
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987 GỢI Ý ĐÁP ÁN.
I. Câu hỏi trắc nghiệm (4,0 điểm). Chọn phương án đúng (Học sinh ghi đáp án vào giấy làm bài thi) Câu 1 2 3 4 5 6 7 8 Đáp án D C C C C C C A Câu 9 10 11 12 13 14 15 16 Đáp án A A D C D B D D
Câu 1. Nếu a  ,
b c d thì bất đẳng thức nào sau đây luôn đúng?
A. ac bd.
B. a c b d.
C. a b c d.
D. a c b d.
Giải thích đáp án. a   b
Dễ thấy đây là quy tắc cộng 2 bất đẳng thức cùng chiều: Khi 
a c b d Chọn D. c d 
Câu 2. Các giá trị của tham số m để bất phương trình 2
(m  1)x m  0 có nghiệm là: A. m  .  B. m  . 
C. m   \   1 . D. m  1. 
Giải thích đáp án.
- Khi m  1  0  1  0 (thỏa mãn). - Khi m  1   0  1  0(vô lí) m - Khi m  1   x  (thỏa mãn). 2 1  m
Vậy bất phương trình có nghiệm khi và chỉ khi m  1
 hay m   \  1  Chọn C. 1  2x
Câu 3. Tập hợp nghiệm của bất phương trình  0 là: 4x  8  1  1   1 1  A. 2  ; .   B.   ;2 .  C.  2  ; .  D. ;2  . 2   2   2   2  
Giải thích đáp án. 1  2x 2x 1 1  1  Dễ thấy  0 
    x   S     Chọn C. x  4 x  2 0 2 2; 4 8 2 2   2 x
  6x  5  0
Câu 4. Tập hợp nghiệm của hệ bất phương trình  là: 2
x  8x  12  0  A. 2  ;5.   B. 1  ;6.   C. 2;5.  D. 1  ;2  5  ;6.    
Giải thích đáp án. 2 x
  6x  5  0  1  x  5 Ta có: 
 2  x  5  S  2;5  Chọn C. 2  x 8x 12 0 2 x 6        
Câu 5. Các giá trị của tham số m để bất phương trình 2
mx  2mx  1  0 vô nghiệm là: A. m  .  B. m  1.  C. 1   m  0. D. 1   m  0. 3
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987
Giải thích đáp án.     0
Áp dụng ĐL về dấu tam thức bậc hai ta thấy f (x)  0 nên BPT vô nghiệm  a  0  2 m   m  0 m   0      1
  m  0  Chọn C. m  0 m  1  0  
Câu 6. Khi thống kê điểm môn Toán trong một kỳ thi của 200 em học sinh thì thấy có 36 bài được điểm
bằng 5. Tần suất của giá trị x  5 là: i A. 2, 5%. B. 36%. C. 18%. D. 10%.
Giải thích đáp án.
Vì có 36 bài được điểm 5 nên tần số của điểm 5 là n  36. i n 36
Vậy tần suất của giá trị x  5 là: i f  100 
100  18%  Chọn C. i i N 200
Câu 7. Chọn hệ thức sai trong các hệ thức sau:  3  A. tan
x   cot x. B. sin(3  x)  sin x.
C. cos (3  x)  cos x.
D. cos ( x  )  cos x. 2  
Giải thích đáp án.  3    
- Dễ thấy tan
x   tan   x   cot x (vì tan tuần hoàn chu kỳ π ). A đúng. 2 2    
- Và sin (3  x)  sin (  x)  sin x (vì sin tuần hoàn chu kỳ 2π). B đúng.
- Và cos (3  x)  cos (  x)  c
os x (vì cos tuần hoàn chu kỳ 2π)  Chọn C.
Lưu ý. Với học sinh không nắm rõ chu kỳ và giá trị lượng giác của các góc bù, phụ, đối. Có thể lấy sử
dụng máy tính CASIO ở chế độ R và lấy x bất kỳ thay vào để thử đáp án. 1    
Câu 8. Cho sin   với 0   
. Giá trị của cos    bằng: 3 2 3   2  6 1 1 A. . B. 6  3. C.  3. D. 6  . 2 6 6 2
Giải thích đáp án.  1 2 c
os   1  sin   1   6 Ta thấy 3   cos    3
0  cos  1(do 0    )  2      6 1 1 3 1 1 2  6 Mà cos  
  coscossin sin  .  .     Chọn A. 3 3 3 3 2 2 2   3 6 2 6
Lưu ý. Ta có thể sử dụng Casio đổi ra góc α thấy thuộc khoảng (0;π/2), lấy KQ tính cos(Ans+π/3) lưu lại
là X. Sau đó lấy X trừ đi kết quả ở các đáp án để thử. 4
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987 1
Câu 9. Nếu sin x cos x
thì giá trị của sin 2x là: 2 1 1 1 1 A. . B.  . C. . D.  . 2 2 4 4
Giải thích đáp án.
Ta thấy sin x cos x 2 1 1 1
  1 2sin xcos x  sin 2x   Chọn A. 2 2 2
Câu 10. Trong mặt phẳng tọa độ Oxy, cho ba đường thẳng (d ) : 3x  4y  7  0,(d ) : 5x y  4  0 và 1 2
(d ) : mx  (1  m)y  3  0. Để ba đường thẳng này đồng quy thì giá trị của tham số m là: 3 A. m  2. B. m  2.  C. m  0,5. D. m  0  ,5.
Giải thích đáp án.
Bấm máy giải hệ phương trình tạo bởi phương trình của (d )&(d ) ta được tọa độ giao điểm M  1  ;  1 . 1 2
Để ba đường thẳng đồng quy (tại M) thì M phải thuộc (d )  m
  1  m  3  0  m  2  Chọn A. 3
Câu 11. Trên mặt phẳng tọa độ Oxy, cho hai điểm ( A 2  ;3) và ( B 4; 1
 ). Phương trình nào sau đây là
phương trình đường thẳng AB? x  4 y  1 x   1  3t
A. x y  3  0.
B. y  2x  1. C.  . D.  . 6 4  y  1  2t 
Giải thích đáp án.
Để đơn giản ta cứ thay tọa độ của A và B vào kiểm tra thấy ngay A,B,C sai  Chọn D.
Câu 12. Một elip có diện tích hình chữ nhật cơ sở là 80, độ dài tiêu cự là 6. Tâm sai của elip đó là: 4 3 3 4 A. e  . B. e  . C. e  . D. e  . 5 4 5 3
Giải thích đáp án.
Diện tích hình chữ nhật cơ sở là: 2 .
a 2b  80  ab  20 mà 2 2 2 2 2
a b c a b  9doc  3  400 2 b      400 2 ab 20      2 b a   5 c 3 Ta được a 2      a    e    2 2 Chọn C. a b  9 400 b  4 2 4 2 a 5  a    9 a
  9a  400  0  2 a  
Câu 13. Trên mặt phẳng tọa độ Oxy, cho các điểm ( A 1; 1  ) và (
B 3;4). Giả sử (d) là một đường thẳng
bất kỳ luôn đi qua điểm B. Khi khoảng cách từ A đến đường thẳng (d) đạt giá trị lớn nhất, đường thẳng
(d) có phương trình nào sau đây?
A. x y  1  0.
B. 3x  4y  25.
C. 5x  2y  7  0.
D. 2x  5y  26  0.
Giải thích đáp án. Gọi d a x   b y
hayax by a b   2 2 ( ) : ( 3) ( 4) 0 3 4
0 a b  0
a b  3a  4b
2a  5 Bunhiacopxki b 4  25 2 2 a b
Khi đó d(A  (d))     29 2 2 2 2 2 2 a b a b a b 5
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987 a b a 2 Khi đó  hay
 (d) : 2x  5y  26  0  Chọn D. 2 5 b 5
Câu 14. Trên mặt phẳng tọa độ Oxy, gọi (d) là đường thẳng đi qua điểm (
A 1;1) và tạo với đường thẳng
có phương trình x  3y  2  0 một góc bằng 0
45 . Đường thẳng (d)có phương trình là:
A. 2x y  1  0.
B. 2x y  1.
C. x  2y  1  0.
D. 3x y  4  0.
Giải thích đáp án. Gọi d a x
b y   hayax by a b   2 2 ( ) : ( 1) ( 1) 0
0 a b  0 u   d    ;b a   1 3b a Vì                 cos
cos ud uxy  a b a b ux y 3;  45  ,   3 2 0 2 2 3 2 0 5 5 2 2 3 2 0 1 2 10. a ba 1
   a;b  1;2  (d) : x  2y  3  0
Hay  a ba bb 2 2 2  0   Chọn B. a   2
  a;b  2; 1
   (d) : 2x y  1  0 b
Câu 15. Trên mặt phẳng tọa độ Oxy, cho các điểm ( A 3;0) và (
B 0;4). Đường tròn nội tiếp tam giác OAB có phương trình là: A. 2 2 x y  1. B. 2 2
x y  4x  4  0. C. 2 2 x y  2. D. 2 2
(x  1)  (y  1)  1.
Giải thích đáp án.
Tâm I là giao của 3 đường phân giác trong của ∆OAB mà A và B lần
lượt nằm trên Ox và Oy nên phân giác của góc AOB chính là phân giác
góc phần tư thứ I và III có phương trình: y x. Gọi I  ;
m m là tâm đường tròn nội tiếp ta có:
d(I O )A d(I AB) OA : x  0  x y AB  : 
 1  4x  3y  12  0  3 4 7m  12
7m  12  5m m  6 Hay m     Chọn D. 5
12  7m  5m m  1 
Lưu ý. Nếu tinh ý ta có thể thấy tâm đường tròn nội tiếp, gốc tọa độ và hình chiếu của tâm lên 2 trục Ox
và Oy lập thành một hình vuông cạnh bằng bán kính đường tròn nội tiếp(bằng 1) nên ta có ngay phương trình 2 2
(x  1)  (y  1)  1.
Câu 16. Trên mặt phẳng tọa độ Oxy, cho điểm P( 3  ; 2  ) và đường tròn 2 2
(C) : (x  3)  (y  4)  36. Từ điểm P kẻ các tiếp tuyến PM và PN tới
đường tròn (C ), với M và N là các tiếp điểm. Phương trình đường thẳng MN là:
A. x y  1  0.
B. x y  1  0.
C. x y  1  0.
D. x y  1  0. 6
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987
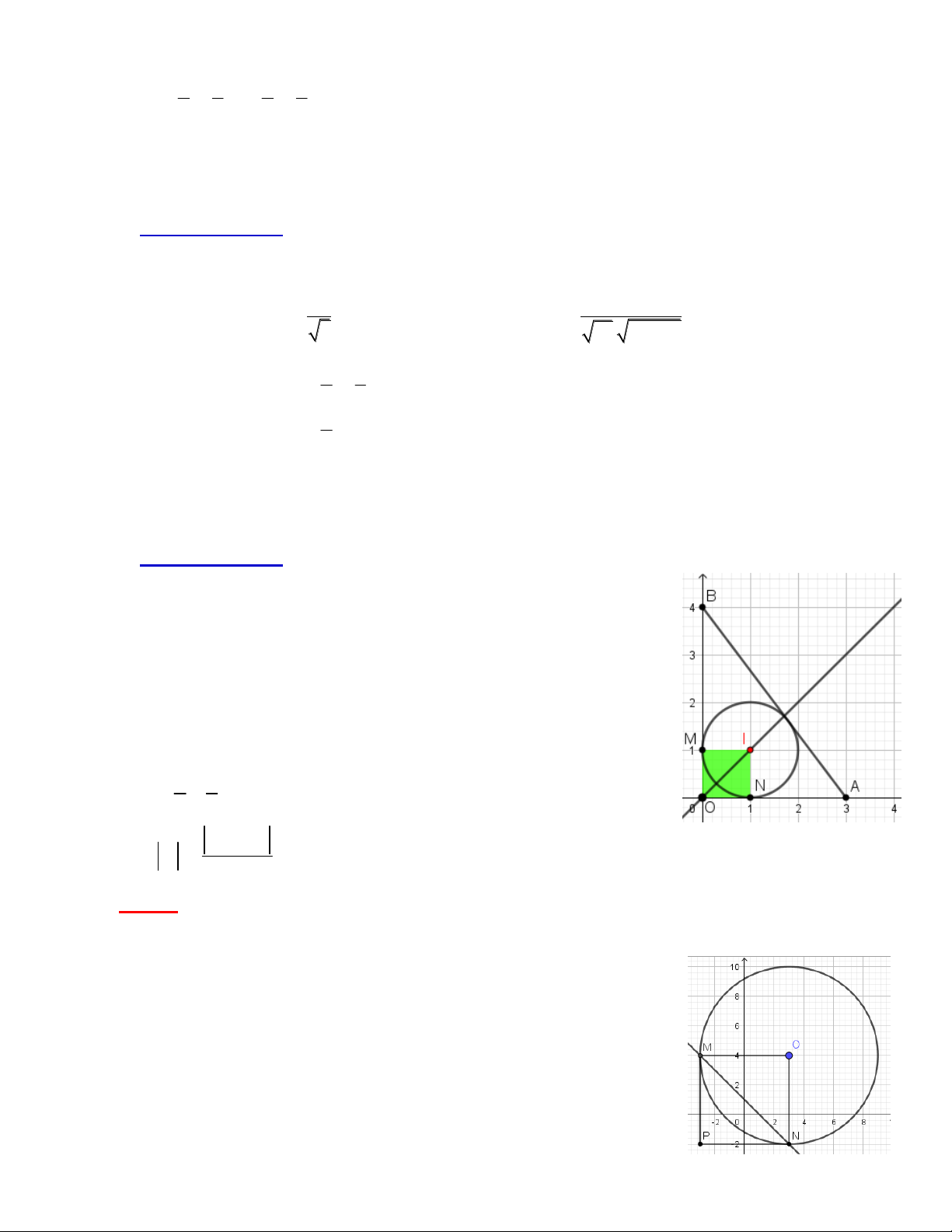
Giải thích đáp án. 
Dễ thấy tứ giác OMPN (O(3;4) là tâm đường tròn) là hình vuông nên (MN) nhận OP   6  ; 6    1;  1
làm vectơ pháp tuyến và đi qua trung điểm K 0;  1 của OP.
Vậy (MN ) : x  0  y 1  0 hay x y  1  0  Chọn D.
II. Tự luận (6,0 điểm – 6,0 điểm).
Bài 1. (1,5 điểm – 1,5 điểm).
a) Giải bất phương trình sau trên tập số thực:
2x  1  2  4x.  x  3 x    0
b) Giải hệ bất phương trình sau trên tập số thực:
2x  3 2x  1 2
x  3  3x  1   Giải.   1  2   1  0 x x    1 3 2       x  2x  3  4x 3  2 2  x      3  2  a) Ta có BPT   S     ;  .   1 2    2   1  0 x x    1  2     x    2
x  1  4x 1 2  x     6 2  x  3  0 3 1 b) Điều kiện:   x  ,x  2x  1  0 2 2    
x   x    x x   3 3 3 2 1 2 3 8x  3   x  8 2        
2x  12x  3 0
2x 12x  3 0 1 x     2  HBPT    1 x  1 1     3 x    x    1 2
x  3  1  3x   3   3   x   1  x    2 2 2  4 x
  3  1  6x  9x
4x  3x  1  0   1   x         4  1 
Kết hợp nghiệm ta được: S    ;   . 4  
Bài 2. (1,5 điểm – 2,0 điểm). cos 2x 2 1 tan x
a) Chứng minh đẳng thức:  
khi các biểu thức đề xác định. 2 2 2 1 sin 2x cos x sin x 1  tan x 2 x   4x  5
b) Tìm các giá trị của tham số m để hệ bất phương trình  có nghiệm. 2
x  (m  1)x m  0  7
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987 Giải. 2sin x cos x 2 1 1 sin xcos x a) Ta có: VP     2 2 2 2 2 2 2 cos x sin x sin x cos x sin x cos x sin x 1  2 cos xsin xcos x   2 1 2 sin x cos x sin x cos x     (1)
sin x cos x cos x sin x  sin x cos x cos x sin x cos x sin x 2 2 cos 2x
cosx sinxcosx sinx cos x sin xcosx sinx Mà VT     (2) 2 2 1 sin 2x
cos x sin x  2sinxcosx
cosx sinx2 cosx sinx
Từ (1) và (2) ta được VT VP  ĐPCM.  x   5  x   5   m  5 2 x   4x  5   x m  b) Ta có   x  1    2 
x  (m  1)x m  0          x  x mx 1 1 0       m  1   x m  m   1  Vậy với 
thì hệ bất phương trình luôn có nghiệm. m  5 
Bài 3. (2,5 điểm – 2,5 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai đường tròn (C ),(C ) có 1 2
phương trình lần lượt là 2 2
(x  1)  (y  2)  9 và 2 2
(x  2)  (y  2)  4.
a) Tìm tọa độ tâm, bán kính của hai đường tròn và chứng minh hai đường tròn tiếp xúc với nhau.
b) Viết phương trình đường thẳng đi qua gốc tọa độ và tạo với đường thẳng nối tâm của hai đường tròn một góc bằng 45°.
c) Cho elip (E) có phương trình 2 2
16x  49y  1. Viết phương trình đường tròn (C) có bán kính gấp đôi
độ dài trục lớn của elip (E) và (C) tiếp xúc với hai đường tròn (C ),(C ) . 1 2  Giải.
a) Ta thấy đường tròn (C ) có tâm I 1  ; 2 
và bán kính R  3. Đường tròn (C ) có tâm I 2;2 và 2   1   1 1 2 2 2
bán kính R  2. Khi đó: 5  R R I I  2  1  2  2
 5  (C )và (C ) tiếp xúc 1 2 1 2     2 1 2 nhau.  
b) Ta có I I  3; 4 gọi vectơ chỉ phương của đường thẳng cần lập là u a;b. 1 2   1   a b a ab b
cos 45  cos I I ,u 2 2 3 4 1 9 24 16 0    1 2 2 2 2 2 2 2 5 a b 25a  25b
a;b  7;1  7x y  0 2 2    
 7a  48ab  7b  0  a;b  1; 7  x 7y  0 8
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).
Teacher: Trinh Hao Quang – Phone: 0972.805.357 – Facebook: https://www.facebook.com/Pi81987 2 2 x y 1 1 c) Ta có 2 2
16x  49y  1  
 1  Độ dài trục lớn của (E) là 2a  2.  . 2 2  1   1  4 2     4 7    
Vậy bán kính đường tròn (C ) cần lập là R  1. II
  R R  3  1  4 Khi đó xét III ta có: 1 1   III vuông tại I. 1 2 1 2
II R R  2  1  3  2 2    II  .II  0 a 2 
a  1  b 2b 2 2 2  0 a
 b a  6  0
Gọi I a;b ta có: 1 2      II  3  a 2  2  b 22 2 2  9
a b  4a  4b  1  0 2   5  3a   71 22 
3a  4b  5  b   I   ;  (tm)     4  25 25 2 2
a b a  6  0    2  2
 5a  46a  71  0 I     1
 ;2  I (loai) 1 2 2  71   22 
Vậy phương trình đường tròn cần lập là: (C ) : x    y    1. 25 25    
Bài 4. (0,5 điểm – 0 điểm). (Chỉ dành cho các lớp 10 Tin, L1, L2, H1, H2) Cho ba số thực , a ,
b c thỏa mãn điều kiện 2 2 2
a b c  3. Tìm giá trị nhỏ nhất của biểu thức sau: 1 1 1 P    . 3 3 3 1  8a 1  8b 1  8cGiải. AM G
M 1  2a  1  2a  4a Ta có 1  8a
12a12a  4a  2 3 2 2   1  2a 2 1 1 1 Tương tự vai trò cho 3 1  8b và 3
1  8c ta được: P    2 2 2 1  2a 1  2b 1  2c 2 2 Cauchy 2 2 1 1 1  2a 1  2a 1 1  2a 2 1 5  2a Mặt khác: 2     2 .  a   2 2 2 1  2a 1  2a 9 9 1  2a 9 9 9 9      2 2 2 2 2 2 15 2 5 2 5 2 5 2
a b c a b c  152.3 Khi đó P     
 1. Vậy Min P  1 . 9 9 9 9 9  2 2 2 a
  b c  3  Dấu “=” xảy ra 2  1
  2a  1  2a  4a và vai trò , a ,
b c như nhau hay a; ; b c  1;1;  1 .  2 1 1  2a   2 1  2a 9
-------------------------------- Hết -------------------------------- 9
Gợi ý đáp án đề thi HKII trường THPT Chuyên Hà Nội - Amsterdam (năm học 2017-2018).