Đề thi học kỳ 2 Toán 10 năm 2018 – 2019 trường THPT Thị xã Quảng Trị

Đề thi học kỳ 2 Toán 10 năm 2018 – 2019 trường THPT Thị xã Quảng Trị được biên soạn theo dạng đề tự luận với 6 bài toán, đề gồm 1 trang, thời gian học sinh làm bài 90 phút, đề thi có lời giải chi tiết và thang điểm, mời các bạn đón xem

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 10

Môn: Toán 10

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GIÁO DỤC – ĐÀO TẠO QUẢNG TRỊ
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ THI HỌC KỲ II NĂM HỌC 2018 - 2019
Môn: Toán khối 10
(Thời gian làm bài: 90 phút)
ĐỀ SỐ 1
Câu 1 (2,0đ): Giải các bất phương trình sau:
1)
2
5 6 0xx
.
2)
2
4 3 1 x x x
.
Câu 2 (2,5đ): Cho
2
( ) 2( 1) 4 7 f x x m x m
.
1) Tìm m để phương trình
( ) 0fx
có hai nghiệm dương phân biệt.
2) Tìm m để bất phương trình
( ) 0fx
có tập nghiệm R.
Câu 3 (2,0đ):
1) Cho
4
sin ,
52
aa
. Tính cosα, cos2α.
2) Chứng minh đẳng thức:
22
sin sin cos cos . x y x y y x
Câu 4 (2,0đ): Trong mặt phẳng tọa độ Oxy, cho
(3;2)I
và
:3 4 8 0 d x y
.
1) Viết phương trình đường tròn (C) có tâm
và bán kính
2R
.
2) Tìm tọa độ điểm M trên (C) và tọa độ điểm N trên d để đoạn thẳng MN có
độ dài nhỏ nhất.
Câu 5 (1,0đ): Viết phương trình chính tắc của elip, biết elip có một tiêu điểm
(1;0)F
và có tâm sai
1
.
2
e
Câu 6 (0,5đ): Cho
ABC
có G là trọng tâm. Đặt
, , .GAB GBC GCA
Chứng minh rằng:
2 2 2
3 a b c
cot cot cot
4S

.
-------------------Hết------------------------
Họ và tên .......................................................SBD.................Lớp.......
ĐỀ CHÍNH THỨC
SỞ GIÁO DỤC – ĐÀO TẠO QUẢNG TRỊ
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ THI HỌC KỲ II NĂM HỌC 2018 - 2019
Môn: Toán khối 10(phần tự luận)
(Thời gian làm bài: 90 phút)
ĐỀ SỐ 2
Câu 1 (2,0đ): Giải các bất phương trình sau:
1)
2
4 3 0xx
.
2)
2
6 5 1 x x x
.
Câu 2 (2,5đ): Cho
2
( ) 2( 1) 5 f x x m x m
.
1) Tìm m để phương trình
( ) 0fx
có hai nghiệm dương phân biệt.
2) Tìm m để
( ) 0,f x x R
.
Câu 3 (2,0đ):
1) Cho
43
cos ,
52
aa
. Tính
sin ,cos2

.
2) Chứng minh đẳng thức:
22
sin sin sin sin . x y x y x y
Câu 4 (2,0đ): Trong mặt phẳng tọa độ Oxy, cho
(2;3)I
và
:4 3 13 0 d x y
.
1) Viết phương trình đường tròn (C) có tâm
và bán kính
5R
.
2) Tìm tọa độ điểm M trên (C) và điểm N trên d để đoạn thẳng MN có độ dài
nhỏ nhất.
Câu 5 (1,0đ): Viết phương trình chính tắc của elip, biết elip có một tiêu điểm
( 1;0)F
và một đỉnh
0;2B
.
Câu 6 (0,5đ): Cho
ABC
có G là trọng tâm. Đặt
, , .GAB GBC GCA
Chứng minh rằng:
2 2 2
3 a b c
cot cot cot
4S

.
-------------------Hết------------------------
Họ và tên thí sinh.......................................................SBD................Lớp......
ĐỀ CHÍNH THỨC
SỞ GD&ĐT QUẢNG TRỊ ĐÁP ÁN THI HỌC KỲ II NĂM HỌC 2018 - 2019
TRƯỜNG THPT TX QUẢNG TRỊ MÔN TOÁN KHỐI 10 (NC)
ĐỀ SỐ 1
Câu
Lời giải
Điểm
1.1.
1.0đ
2
5 6 0xx
23x
1đ
1.2.
1.0đ
2
2
2
2
10
4 3 0
4 3 1
10
4 3 1
x
xx
x x x
x
x x x

.
1
1
1
1
x
x
x
x
.
0.50đ
0.50đ
2.1.
1.5đ
'0
0
0
ycbt P
S

22
( 1) 4 7 0 6 8 0
4
4 7 0 7 / 4
2
2( 1) 0 1
7 / 4
4
7 / 4 2
m m m m
m
mm
m
mm
m
m
m





0.5đ
0.75đ
0.25đ
2.2.
1.0đ
2
0
'0
6 8 0 2 4
a
ycbt
m m m

0.25đ
0.50đ
0.25
3.1.
1.0đ
Tính đúng cosa = - 3/5
Tính đúng cos2a = -7/25
0.50đ
0.50đ
3.2.
1.0đ
Ta có:
2 2 2 2
1
sin( )sin( ) cos2 cos2
2
1
2cos 1 2cos 1 cos cos
2
x y x y x y
x y y x


0,25đ
0,5
0,25
4.1.
1.0đ
Ta có
22
( ):( 3) ( 2) 4C x y
1.0đ
4.2.
d(I,d) = 5, R = 2
1.00đ
MN =5 – 2 = 3. MN nhỏ nhất khi N là hình chiếu của I trên d và M là giao
điểm của đoạn IN với ( C).
Tìm được N(0;-2)
Tìm được M(9/5;2/5)
0.25đ
0,25
0.5đ
C5.
1.00đ
2 2 2
(1;0) 1
1/ 2 2
3
Fc
ea
b a c

Vậy
22
( ): 1
43
xy
E 
0.25đ
0.25
0.25đ
0.25đ
C6. 0.5đ
2 2 2
22
2 2 2
22
2 2 2
2 2 2
2 2 2
4 2 2
99
4 2 2
99
cot
2 . .sin
3
, 3 .
4
3 a +b +c
cot cot cot
4
a
b
ABG
c b a
AG m
c a b
BG m
AB AG BG
AB BG
c b a
SS
S
S







0.25
0.25
ĐỀ SỐ 2
Câu
Lời giải
Điểm
C1.1.
1.00đ
2
4 3 0xx
1
3
x
x
1.0
C1.2.
1.00đ
2
2
22
1
6 5 0
6 5 1
1
6 5 2 1
1
1.
1
1
x
xx
x x x
x
x x x x
x
x
x
x

.
0.50đ
0.50đ
C2.1.
1.50đ
'0
0
0
ycbt P
S


22
( 1) 5 0 3 4 0
5 0 5
2( 1) 0 1
4
m m m m
mm
mm
m






0.5đ
0.75đ
0.25
C2.2.
1.00đ
0
( ) 0,
'0
a
f x x R

2
10
14
3 4 0
m
mm
0.25đ
0.50đ
0.25
C3.1.
1.00đ
Tính đúng sinα = -3/5
Tính đúng cos2α = 7/25
0.50đ
0.50đ
C3.2.
1.00đ
2 2 2 2
1
sin .sin cos2 cos2
2
1
1 2sin 1 2sin sin sin
2
x y x y x y
x y x y


0.5
0.5
C4.1.
1.00đ
Ta có
22
( ):( 2) ( 3) 25C x y
1.00đ
C4.2.
1.00đ
d(I,d) = 6, R = 5 nên MN nhỏ nhất khi N là hình chiếu của I trên d và M là
giao điểm của đoạn IN với đường tròn ( C).
Tìm được N(-14/5; -3/5)
Tìm được M(-2;0)
0.25đ
0.25đ
0.5đ
C5.
1.00đ
F(-1;0) => c = 1, B(0;2) => b = 2
Vậy (E):
22
( ): 1.
54
xy
E 
0.5đ
0.5đ
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC – ĐÀO TẠO QUẢNG TRỊ
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ THI HỌC KỲ II NĂM HỌC 2018 - 2019 Môn: Toán khối 10 ĐỀ CHÍ NH THỨC
(Thời gian làm bài: 90 phút) ĐỀ SỐ 1
Câu 1 (2,0đ): Giải các bất phương trình sau: 1) 2
x  5x  6  0 . 2) 2
x  4x  3  x 1.
Câu 2 (2,5đ): Cho 2
f (x)  x  2(m 1)x  4m  7 .
1) Tìm m để phương trình f (x)  0 có hai nghiệm dương phân biệt.
2) Tìm m để bất phương trình f (x)  0 có tập nghiệm R.
Câu 3 (2,0đ): 4  1) Cho sin a  ,
a   . Tính cosα, cos2α. 5 2
2) Chứng minh đẳng thức:
x y x y 2 2 sin sin  cos y  cos . x
Câu 4 (2,0đ): Trong mặt phẳng tọa độ Oxy, cho I (3;2) và d : 3x  4y  8  0.
1) Viết phương trình đường tròn (C) có tâm I và bán kính R  2 .
2) Tìm tọa độ điểm M trên (C) và tọa độ điểm N trên d để đoạn thẳng MN có độ dài nhỏ nhất.
Câu 5 (1,0đ): Viết phương trình chính tắc của elip, biết elip có một tiêu điểm F(1;0) 1 và có tâm sai e  . 2
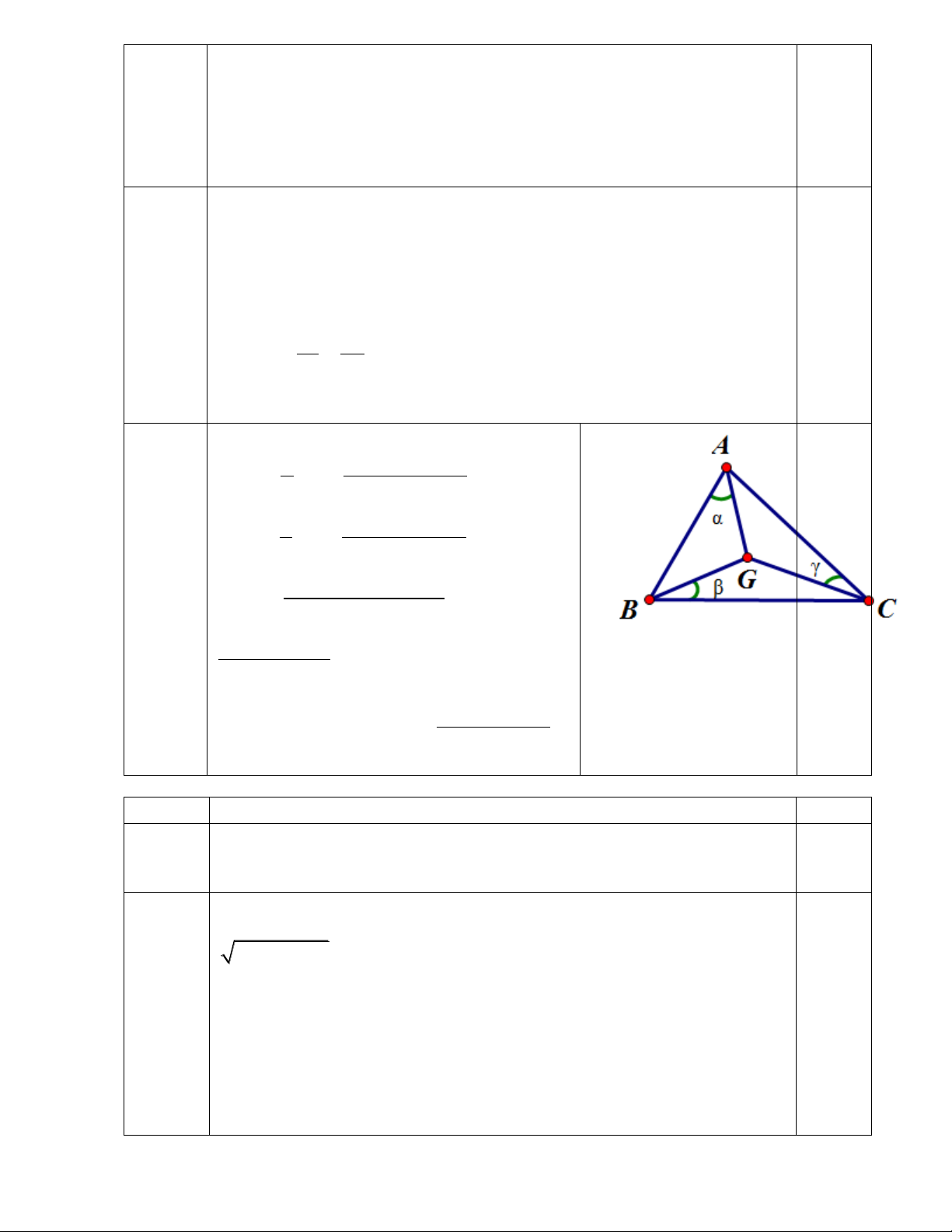
Câu 6 (0,5đ): Cho ABC
có G là trọng tâm. Đặt   
GAB  ,GBC   ,GCA   .  2 2 2 3 a  b  c 
Chứng minh rằng: cot  cot   cot  . 4S
-------------------Hết------------------------
Họ và tên .......................................................SBD.................Lớp.......
SỞ GIÁO DỤC – ĐÀO TẠO QUẢNG TRỊ
TRƯỜNG THPT TX QUẢNG TRỊ ĐỀ THI HỌC KỲ II NĂM HỌC 2018 - 2019
Môn: Toán khối 10(phần tự luận) ĐỀ CHÍ NH THỨC
(Thời gian làm bài: 90 phút) ĐỀ SỐ 2
Câu 1 (2,0đ): Giải các bất phương trình sau: 1) 2
x  4x  3  0 . 2) 2
x  6x  5  x 1.
Câu 2 (2,5đ): Cho 2
f (x)  x  2(m 1)x m  5 .
1) Tìm m để phương trình f (x)  0 có hai nghiệm dương phân biệt.
2) Tìm m để f (x)  0, x  R .
Câu 3 (2,0đ): 4  3 1) Cho cosa  ,  a
. Tính sin,cos2 . 5 2
2) Chứng minh đẳng thức:
x y x y 2 2 sin sin  sin x  sin . y
Câu 4 (2,0đ): Trong mặt phẳng tọa độ Oxy, cho I (2;3) và d : 4x  3y 13  0.
1) Viết phương trình đường tròn (C) có tâm I và bán kính R  5 .
2) Tìm tọa độ điểm M trên (C) và điểm N trên d để đoạn thẳng MN có độ dài nhỏ nhất.
Câu 5 (1,0đ): Viết phương trình chính tắc của elip, biết elip có một tiêu điểm F( 1
 ;0) và một đỉnh B0;2 .
Câu 6 (0,5đ): Cho ABC
có G là trọng tâm. Đặt   
GAB  ,GBC   ,GCA   .  2 2 2 3 a  b  c 
Chứng minh rằng: cot  cot   cot  . 4S
-------------------Hết------------------------
Họ và tên thí sinh.......................................................SBD................Lớp......
SỞ GD&ĐT QUẢNG TRỊ
ĐÁP ÁN THI HỌC KỲ II NĂM HỌC 2018 - 2019
TRƯỜNG THPT TX QUẢNG TRỊ
MÔN TOÁN KHỐI 10 (NC) ĐỀ SỐ 1 Câu Lời giải Điểm 1.1. 2
x  5x  6  0  2  x  3 1.0đ 1đ 1.2. x 1 0 1.0đ  2
x  4x  3  0 0.50đ 2
x  4x  3  x 1   .  x 1  0 
x  4x  3   x  2 2 1 x 1   
x  1  x  1  .  0.50đ x 1 2.1. '  0 1.5đ 0.5đ
ycbt  P  0  S  0  2 2
(m 1)  4m  7  0
m  6m  8  0 m  4    4m  7  0  m  7 / 4  m  2 0.75đ    2(m 1)  0 m  1   m  7 / 4 m  4  0.25đ  7 / 4  m  2 2.2. a  0 0.25đ 1.0đ ycbt   '  0 2  0.50đ
m  6m  8  0  2  m  4 0.25 3.1. Tính đúng cosa = - 3/5 0.50đ 1.0đ 0.50đ Tính đúng cos2a = -7/25 3.2. 1 1.0đ
sin(x y)sin(x y)   cos 2x  cos 2 y 0,25đ 2 Ta có: 1 2 2 2 2    0,5
2cos x 1  2cos y  1  cos y  cos x   2 0,25 4.1. 2 2
Ta có (C) : (x  3)  ( y  2)  4 1.0đ 1.0đ 4.2. d(I,d) = 5, R = 2 1.00đ
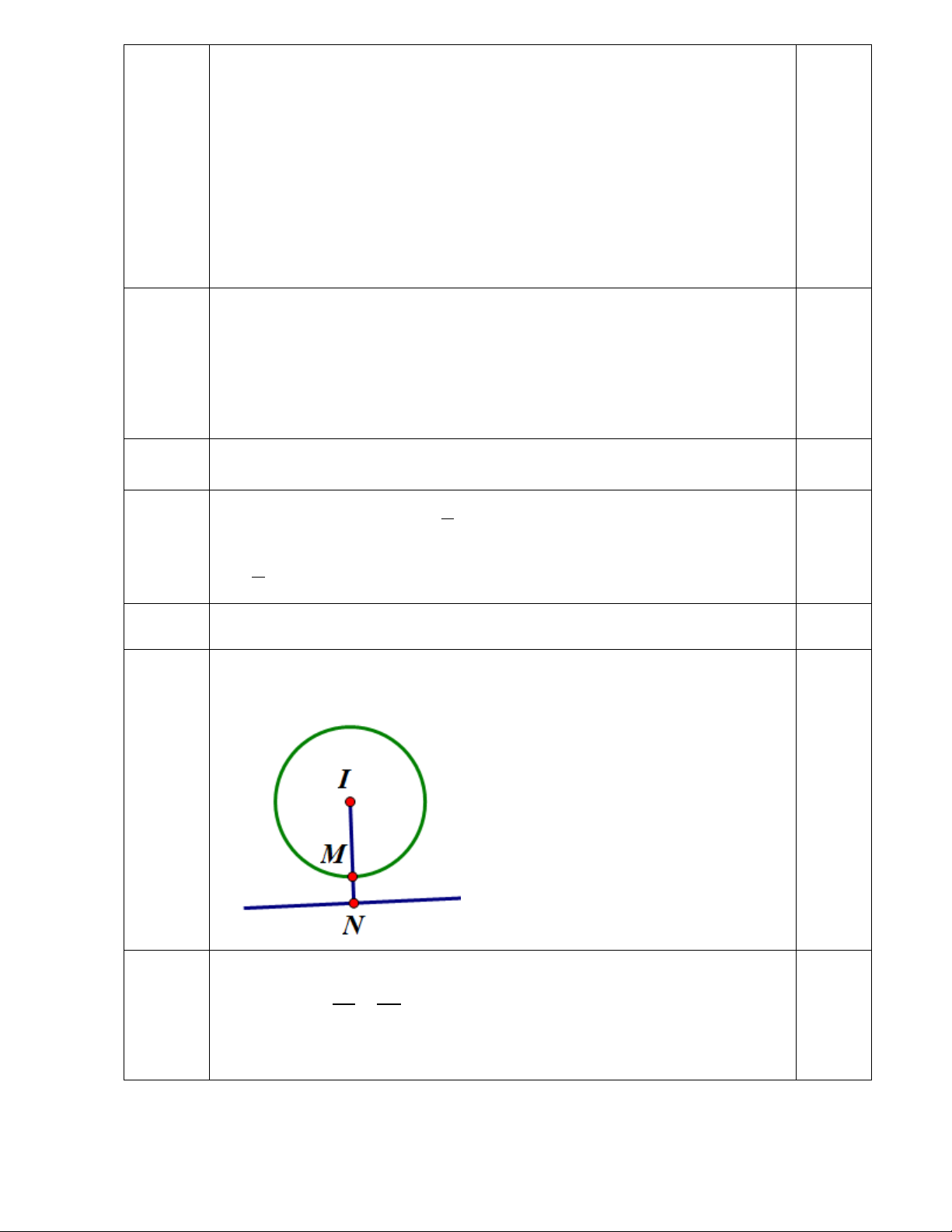
MN =5 – 2 = 3. MN nhỏ nhất khi N là hình chiếu của I trên d và M là giao
điểm của đoạn IN với ( C). 0.25đ 0,25 Tìm được N(0;-2) Tìm được M(9/5;2/5) 0.5đ C5.
F (1;0)  c  1 1.00đ 0.25đ
e  1 / 2  a  2 0.25 2 2 2
b a c  3 0.25đ 2 2 x y Vậy (E) :  1 0.25đ 4 3 C6. 0.5đ 2 2 2 4
2c  2b a 2 2 AG m 9 a 9 2 2 2 4
2c  2a b 2 2 BG m 9 b 9 2 2 2
AB AG BG cot   2 . AB . BG sin 2 2 2
3c b a ,S  3S . 0.25  4 ABG S 3 2 2 2 a +b +c   0.25
cot  cot   cot   4S ĐỀ SỐ 2 Câu Lời giải Điểm C1.1. x 1.00đ 2
x  4x  3  1 0   1.0x  3 C1.2. x 1 1.00đ  2
x  6x  5  0 2 0.50đ
x  6x  5  x  1  x 1   . 2 2
x  6x  5  x  2x 1 x 1   
x  1  x  1.  x 1 0.50đ C2.1. '  0 1.50đ 0.5đ
ycbt  P  0 S  0  2 2
(m 1)  m  5  0
m  3m  4  0    m  5  0  m  5  0.75đ   2(m 1)  0 m  1   0.25 m  4 C2.2. a  0 1.00đ
f (x)  0, x   R   0.25đ '  0 1   0    1   m  4 0.50đ 2
m  3m  4  0 0.25 C3.1. Tính đúng sinα = -3/5 0.50đ 1.00đ Tính đúng cos2α = 7/25 0.50đ C3.2. 1 1.00đ
sin  x y.sin  x y   cos 2x  cos 2y 0.5 2 1 2 2 2 2   0.5 1
  2sin x 1 2sin y  sin x  sin y   2 C4.1. Ta có 2 2
(C) : (x  2)  ( y  3)  25 1.00đ 1.00đ C4.2.
d(I,d) = 6, R = 5 nên MN nhỏ nhất khi N là hình chiếu của I trên d và M là 1.00đ
giao điểm của đoạn IN với đường tròn ( C). 0.25đ Tìm được N(-14/5; -3/5) 0.25đ Tìm được M(-2;0) 0.5đ C5.
F(-1;0) => c = 1, B(0;2) => b = 2 0.5đ 1.00đ 2 2 x y Vậy (E): (E) :  1. 0.5đ 5 4