
Preview text:
UBND QUẬN TÂY HỒ
ĐỀ KIỂM TRA HỌC KỲ II
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Năm học 2023-2024 Môn: Toán 7 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút
(Đề thi gồm có: 02 trang)
PHẦN I: TRẮC NGHIỆM ( 2,0 điểm)
Hãy chọn một chữ cái đứng trước đáp án đúng cho mỗi câu sau.
Câu 1: Điểm kiểm tra môn toán của học sinh trong tổ 1 và tổ 2 của lớp 7A được liệt kê ở bảng sau: 8 9 7 10 5 7 8 7 9 8 6 7 9 6 4 10 7 9 7 8
Số học sinh của hai tổ đó là:
A. 20 học sinh ; B. 15 học sinh; C. 10 học sinh; D. 4 học sinh.
Câu 2: Từ các số 1; 2; 4; 6; 8; 9 ta lấy ngẫu nhiên một số. Xác suất để lấy được một số chẵn là: A. 1
B. 1 C. 1 D. 2 6 3 2 3
Câu 3: Biểu thức đại số nào sau đây biểu thị chu vi hình chữ nhật có chiều dài bằng 5(cm)
và chiều rộng bằng x (cm)?
A. 5 + x
B. (5 − x).2 C. 5.x
D. (5 + x).2
Câu 4: Giá trị của biểu thức 2
x − x tại x = 3 − là: A. 9 B. 12 C. 12 − D. 9 −
Câu 5: Bậc của đa thức 5 2 6
9x − x + x + x −11 là: A. 11 B. 9 C. 6 D. 5
Câu 6: Trong các biểu thức sau, biểu thức nào là đơn thức một biến: A. 1 2 1+ x B. 2 x C. 2
5xy z D. 2x + 3 3
Câu 7: Các tam giác cân trong hình vẽ bên là A A. AB ∆ C; C
∆ AD B. A ∆ BC; A ∆ BD C. AC ∆ ; D AB ∆ D D. A ∆ BD B C D Câu 8: Cho DEF ∆
có trung tuyến DM và trọng tâm G (hình vẽ). Khi đó: A. DG 1 = . B. GM 1 = . D DM 3 DG 2 C. GM 1 = . D. DM = 3DG . G DM 2 E M F
PHẦN II: TỰ LUẬN (8,0 điểm)
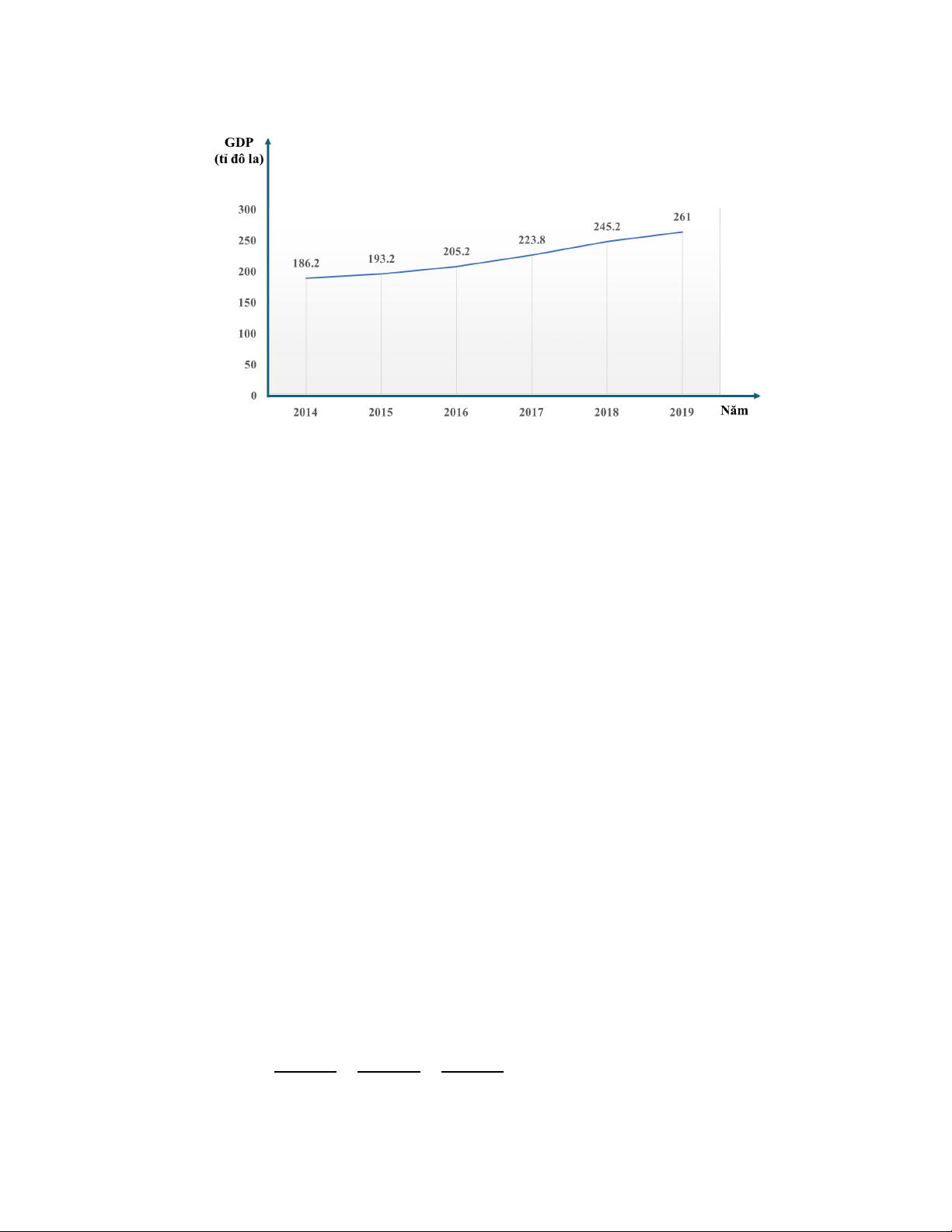
Bài 1 (1,5 điểm). Biểu đồ đoạn thẳng dưới đây biểu diễn tổng sản phẩm quốc nội (GDP)
của nước ta trong giai đoạn từ năm 2014 đến năm 2019.
a) GDP năm 2016 là bao nhiêu?
b) So với năm 2014, GDP năm 2019 đã tăng bao nhiều tỉ đô la.
c) GDP năm 2017 đã tăng bao nhiêu phần trăm so với năm 2015.
Bài 2 (1,5 điểm). Một hộp có 100 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số tự
nhiên từ 1 đến 100, hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ
trong hộp. Tính xác suất của biến cố
a) A: “Số xuất hiện trên thẻ được rút ra là số có một chữ số”.
b) B: “Số xuất hiện trên thẻ được rút ra là số tròn chục”.
c) C: “Số xuất hiện trên thẻ được rút ra là số có tổng các chữ số bằng 10”.
Bài 3 (1,5 điểm) Cho hai đa thức 2
P(x) = 2x + 5x −1 và 2
Q(x) = 2x − 5x −15 a) Tính (
A x) = P(x) + Q(x) và B(x) = P(x) −Q(x).
b) Tìm nghiệm của đa thức ( A x).
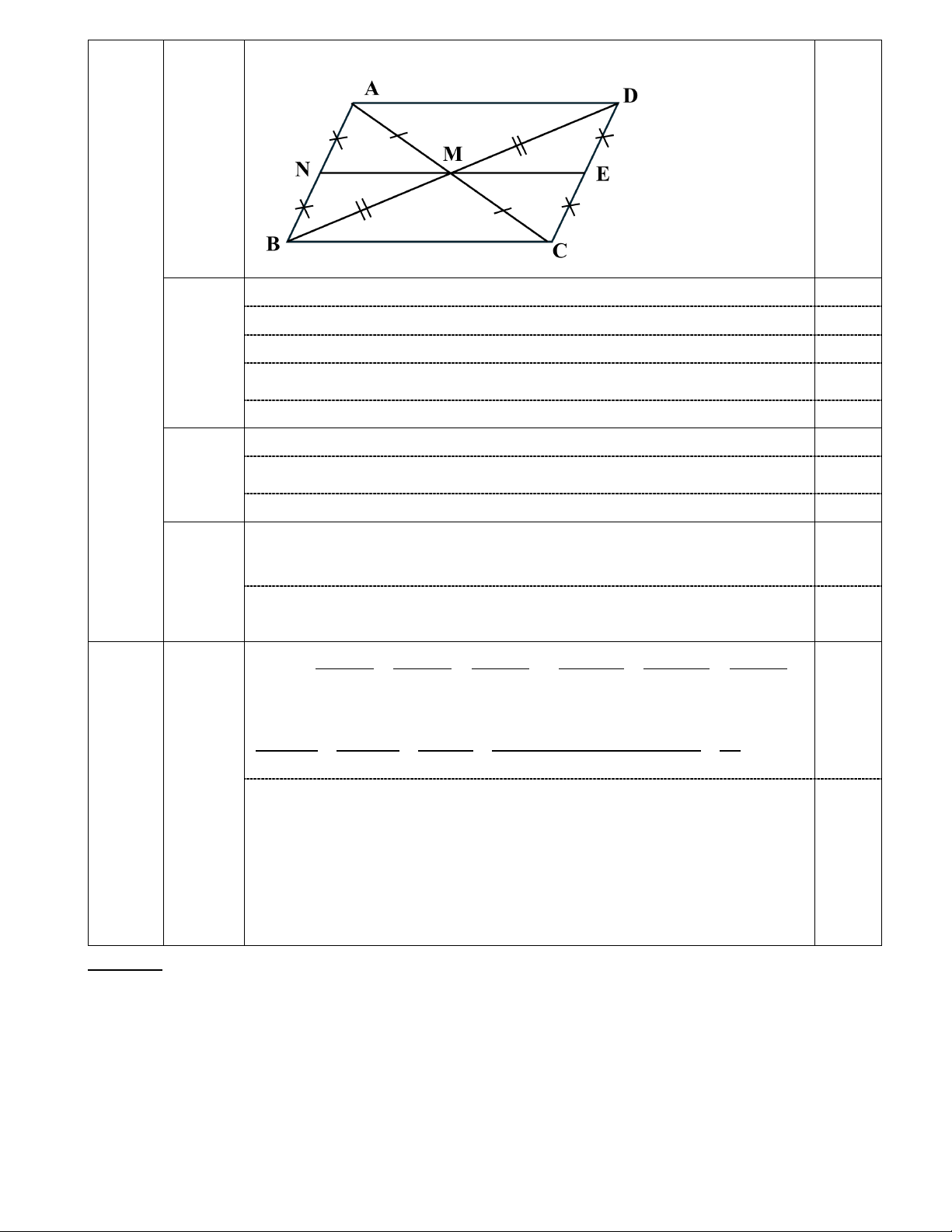
Bài 4 (3,0 điểm). Cho tam giác ABC nhọn. Lấy điểm M là trung điểm của cạnh AC. Trên
tia đối của tia MB lấy điểm D sao cho MB = MD.
a) Chứng minh: ∆AMD = ∆CMB.
b) Chứng minh CD = AB và CD // AB.
c) Lấy điểm N là trung điểm của cạnh AB và điểm E là trung điểm của cạnh CD. Chứng
minh điểm M là trung điểm của đoạn NE.
Bài 5 (0,5 điểm). Tìm tất cả các số nguyên dương x, y, z thỏa mãn:
2z − 4x 3x − 2y 4y − 3z = = và 2 2
200 < y + z < 450. 3 4 2 -----Hết-----
Cán bộ coi thi không giải thích gì thêm!
Họ và tên: …………………………………………….. Số báo danh:…………………….. UBND QUẬN TÂY HỒ HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ II Năm học 2023-2024 Môn Toán 7
(Hướng dẫn chấm gồm 02 trang)
Phần I: Trắc nghiệm (2,0 điểm)
Mỗi ý chọn đúng được 0,25 điểm Câu 1 2 3 4 5 6 7 8 Đáp án A D D B C B A B
Phần II: Tự luận (8,0 điểm) Câu Ý Nội dung Điểm a
GDP năm 2016 là 205,2 tỉ đô la (0,5đ) 0,5 b
So với năm 2014, GDP năm 2019 tăng là: 0,25 1 (0,5đ) (1,5đ)
261 – 186,2 = 74,8 (tỉ đô la) 0,25
Tỉ số phần trăm của GDP năm 2017 so với GDP năm 2015 là: c 223,8.100% ≈115,8% 0,25 (0,5đ) 193,2
So với năm 2015, GDP năm 2017 đã tăng khoảng 15,8% 0,25
Rút ngẫu nhiên 1 thẻ có 100 kết quả có thể xảy ra với số ghi
trên hình thẻ được rút ra là 1;2;….; 99; 100. a
(0,5đ) Có 9 kết quả thuận lợi cho biến cố A là 1;2;3;…; 8; 9. 0,25
Xác suất của biến cố A là 9 0,25 100 2
Có 10 kết quả thuận lợi cho biến cố B là 10; 20; 30;…; 100 0,25 (1,5đ) b
(0,5đ) Xác suất của biến cố B là 10 1 = 0,25 100 10
Có 9 kết quả thuận lợi cho biến cố C là 19; 91; 28; 82; 37; 73; C 46; 64; 55 0,25
(0,5đ) Xác suất của biến cố C là 9 0,25 100
A(x) = P x + Q(x) = ( 2
x + x − ) + ( 2 ( ) 2 5 1
2x − 5x −15) 0,25 a A(x) 2 = 4x −16 0,25 3
(1,0đ) B(x) = P x −Q(x) = ( 2x + x − )−( 2 ( ) 2 5 1
2x − 5x −15) 0,25 (1,5đ)
B(x) =10x +14 0,25 b A(x) 2 = 4x −16 = 0 0,25 (0,5đ) x = 2
± . Vậy nghiệm của A(x) là x = 2 ± 0,25
Vẽ hình đúng đến câu a Vẽ (0,25đ) 0,25 Xét ΔAMD và ΔCMB có 4
MA = MC (M là trung điểm AC) 0,25 a (2,5đ) MB = MD (gt) 0,25 (1,0đ) =
AMD CMB (đối đỉnh) 0,25 Nên ΔAMD = ΔCMB (c.g.c) 0,25
Vì ΔAMB = ΔCMD (c.g.g) nên AB = CD (2 cạnh tương ứng) 0,25 b (0,75đ) Và =
ABM CDM (2 góc tương ứng) 0,25
Mà 2 góc ở vị trí SLT nên AB // CD 0,25
Chứng minh được ΔAMN = ΔCME (c.g.c) c 0,25 Nên ME = MN và = AMN CME
(0,5đ) Từ đó suy ra 3 điểm E,M, N thẳng hàng và ME = MN
Vậy M là trung điểm của NE 0,25
Ta có 2z − 4x 3x − 2y 4y −3z
6z −12x 12x −8y 8y − 6z = = ⇔ = = 3 4 2 9 16 4
Áp dụng tính chất của dãy tỉ số bằng nhau: 0,25
6z −12x 12x −8y 8y − 6z 6z −12x +12x −8y +8y − 6z 0 = = = = = 0 + + 5 9 16 4 9 16 4 29 (0,5đ)
Do đó 6z =12x = 8y
Đặt 6z =12x = 8y = 24k (k > 0) ⇒ ( ;x y; z) = (2k;3k;4k) Theo giả thiết 2 2 2 2
200 < y + z < 450 ⇒ 200 < 9k +16k < 450 0,25 2
⇒ 200 < 25k < 450 ⇒ k ∈{3; } 4
Từ đó tìm được ( ;x y; z)∈ ({6;9;12);(8;12;16)}
*Lưu ý: Nếu học sinh làm cách khác mà đúng vẫn cho điểm tương đương.




