Đề thi học kỳ 2 Toán 9 năm 2023 – 2024 phòng GD&ĐT Bắc Từ Liêm – Hà Nội

UBND QUẬN BẮC TỪ LIÊM
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2023 – 2024 Môn Toán 9 Bài Đáp án Điểm Bài I 2 16  8
1) Thay x =16 (thỏa mãn điều kiện), vào A ta có: A  0.25 đ 16  9 Tính được 12 A  . 7 0.25 đ Vậy x =16 thì 12 A  7 2) x 2 18 B    x  3 x  3 x  9 0.25 đ
x  x  3  2 x  318 B  ( x  3)( x  3) x  3 x  2 x  6 18 x  5 x  24 B   0.25đ ( x  3)( x  3) ( x  3)( x  3) ( x  8)( x  3) B  0.25đ ( x  3)( x  3) x  8 0.25đ B  (đpcm) x  3   3) Tính được x 8 x 8 1 P  A : B  :  x  9 x  3 x  3 0.25đ 1 Từ P  0   0......  x  9 x  3
Kết hợp điều kiện: 0  x  9 và x nguyên tố 0.25đ
Tìm được x 2;3;5;  7 Bài II 2đ
Câu 1 1)Gọi chiểu rộng của mảnh vườn hình chữ nhật là x (m; x >0) 0.25đ
Chiểu dài của mảnh vườn hình chữ nhật đó là x + 7 (m) 0.25 đ
Vì đường chéo của mảnh vườn có chiều dài 17m,
nên ta có pt: x   x  2 2 2 7  17 0.25đ 0.25đ 2 x  7x 120  0 0.25đ
Giải phương trình được x  8 (TMÐK); x  15 ( Loại). 1 2
Vậy chiều rộng của mảnh vườn hình chữ nhật 8 (m) 0.25đ
Chiều dài của mảnh vườn hình chữ nhật 15 (m)
2) Bán kính của hình tròn là: R 64 2 2 S   R  R    64   0.25đ  R  64  8(cm)
Vậy đường kính của hình tròn là: 16 (cm) 0.25đ Bài III  1 3 x  3  1  x  3 1)   y 1  + Điều kiện:  Câu 1 2     y 1 x  3   5  y 1 a  x  3 0.25 đ Đặt  1 b    y 1    Đưa hệ về dạng 3a b 1  a  2b  5  
Giải HPT trên ta được a 1  0.25đ b  2 Giải HPT ta được x  4  0.25đ  1 (TMĐK) y    2 Vậy HPT có nghiệm là    x y 1 ;  4;   0.25đ  2 
Câu 2a) Xét pt hoành độ giao điểm của (d) và (P) ta có: x2 - 2x + m -1 = 0 0.25đ Tính được  = 8 – 4m 0.25đ
Tìm được m = 2 thì (d) tiếp xúc (P). 0.25đ b)
Để đường thẳng (d) cắt (P) tại hai điểm phân biệt 0.25d
thì pt: x2 - 2x + m -1 = 0 có hai nghiệm phân biệt. Tìm được m < 2 x  0
Điều kiện x và 2x xác định 1  1 2 x  0  2 x  x  2 1 2  0.25d x x  m 1 1 2 Theo ĐL Viet ta có:   .......  m 1 x  0  1 x  0  2
Tìm được 𝑥 = và 𝑥 = thay vào tích 𝑥 . 𝑥 = m-1
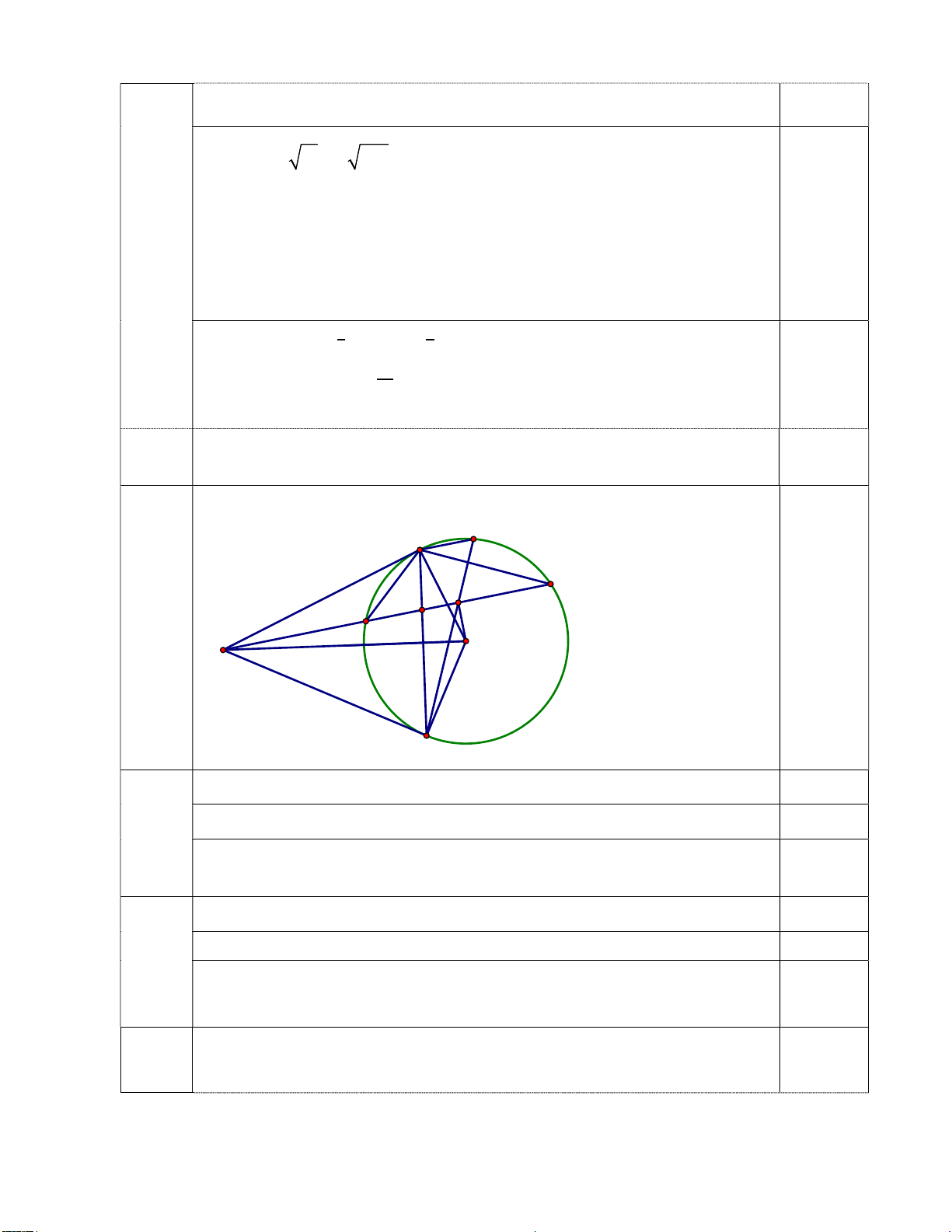
Từ đó tìm được m = ( TMĐK). 0.25đ KL….. Bài IV Hình vẽ đúng câu 1 F B D I E G 0.25đ O A C Chứng minh  ABO   0
ACO  90 ( giải thích rõ lý do) 0.25đ 1 Tứ giác ABOC có  ABO   0
ACO  180 , mà hai góc ở vị trí đối nhau 0.25đ
 Tứ giác ABOC nội tiếp đường tròn 0.25đ
KL bốn điểm A; B; O; C thuộc đường tròn. Chứng minh  ABE  
ADB ( giải thích rõ lý do) 0.25đ
Chứng minh tam giác ABE đồng dạng với tam giác ADB 0.5đ 2 => AB2 = AE.AD 0.25đ 3
Chứng minh I là trung điểm của ED 0.25đ + Chứng minh  ABC   AIC ( =
BFC) ( giải thích rõ lý do)
+ Chứng minh: Tứ giác ABIC nội tiếp đường tròn suy ra 5 điểm A;
B; I; O; C thuộc đường tròn. + Chứng minh  ABO   0
AIO = 90 ( giải thích rõ lý do)  OI  DE 0.25đ
KL: I là trung điểm của DE AD ID Chứng minh  GA GE + Chứng minh  AIC  
ACB từ đó suy ra tam giác ACG đồng dạng 0.25đ
tam giác AIC (g.g) => AC2 = AG.AI.
+ Chứng minh 𝐴𝐵 = 𝐴𝐶2, theo c/m b => AG.AI = AE.AD ( = AC2)
Biến đổi AG.( AD – ID ) = AD .( AG – GE )
 AG.AD – AG.ID = AD .AG – AD.GE  AG.ID = AD.GE 0.25đ AD ID   GA GE Bài V 0.5điểm 1 1 4 M    1 x 1 y 2  x  y x  y2   2 2 2 x  y   2.8 16 0.25đ  x  y  4  2  x  y  6 4 2   2  x  y 3 1   x  1 y
Dấu “=” xảy ra khi và chỉ khi   x  y  2 2 2 x  y  8 0.25đ Vậy GTNN của 2 P   x  y  2 min 3
(Các cách làm đúng khác vẫn cho điểm tối đa)
Document Outline

• Doc1
• ĐÁP ÁN VÀ BIỂU ĐIỂM ĐỀ CHÍNH THỨC TOÁN 9