Đề thi học phần Cấu trúc dữ liệu và thuật toán có đáp án | Trường Đại học Phenikaa

BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI KẾT THÚC HỌC PHẦN
TRƯỜNG ĐẠI HỌC PHENIKAA
(Đối với môn thi tự luận) ĐỀ SỐ: 04
Học phần: Cấu trúc dữ liệu và thuật toán Đề thi gồm có 06 câu; 02 trang Mã học phần:
Đề thi không được sử dụng tài liệu Ngày thi: Giờ thi:
Thời gian làm bài: 90 phút
(Không kể thời gian giao đề)
Họ và tên sinh viên: ………………………………. Số báo danh:…………………… Câu 1 (1 điểm) :
Em hãy cho biết ưu điểm và nhược điểm khi dùng mảng và danh sách liên kết. Câu 2 (1 điểm):
Hàng đợi và ngăn xếp có những điểm nào giống và khác nhau. Câu 3 (3 điểm):
Cho thuật toán sắp xếp có mã giả như sau, trong đó A là mảng số được đánh chỉ số từ 0 đến N-1. Lưu ý: -
0 to D gồm các giá trị [0, 1, …, D] -
Câu lệnh dòng 7 để in số nguyên m_idx -
Câu lệnh dòng 10 để in dãy tất cả phần tử của mảng A 1 Algorithm sort (A, N): 2
for iter from 0 to N - 2 do 3 m_idx = iter; 4
for idx from (iter + 1) to N - 1 do 5
if A[idx] < A[m_idx] then 6 m_idx = idx 7 print(m_idx) 8
if m_idx != iter then 9 swap (A[iter], A[m_idx]) 10 print(A)
Cho mảng A = {11, 4, 2, 14, 5, 9, 3, 17}.
a. Đây là mã giả của thuật toán sắp xếp nào đã học? Sau khi thực hiện xong thuật toán sắp xếp
trên, thu được dãy số có thứ tự như thế nào? (1.0 điểm)
b. Minh họa quá trình sử dụng giải thuật trên để sắp xếp mảng A bằng cách liệt kê các dãy số mà
dòng lệnh thứ 10 in ra (tổng cộng có N - 1 dãy số). (1.5 điểm)
c. Trình bày dãy số mà dòng lệnh thứ 7 in ra sau khi chạy xong hàm sắp xếp trên (dãy số gồm
N - 1 số). (0.5 điểm) Câu 4 (1 điểm):
Cho vector A = {11, 4, 2, 10, 5, 9, 14, 20, 3, 17}.
a. Vector A là vector lưu trữ của một cây nhị phân hoàn chỉnh có 8 nút (kiểm soát các nút trên cây
dựa vào chỉ mục). Vẽ max heap tree T (cây nhị phân mà nút cha lớn hơn 2 nút con) được xây
dựng từ cây nhị phân hoàn chỉnh được biểu diễn bởi A. (0.5 điểm)
b. Với cây T ở phần a, thực hiện đổi chỗ nút gốc với nút cuối, sau đó loại bỏ nút cuối khỏi cây và
cập nhật cây sao cho cây vẫn là max heap tree. Vẽ cây T’ đã được cập nhật (thao tác trên chính
là vòng lặp đầu tiên trong giai đoạn sắp xếp của thuật toán heapsort). (0.5 điểm) Câu 5 (2 điểm):
Cho đồ thị vô hướng gồm 7 đỉnh và 9 cạnh có trọng số được liệt kê dưới đây: 0-1 0.28 1-3 0.16 3-5 0.26 0-4 0.32 2-3 0.58 4-5 0.10 0-6 0.35 2-6 0.93 5-6 0.17
Trong đó, một biểu diễn “0-1 0.28” tức là cạnh nối đỉnh 0 và 1 có độ dài 0.28.
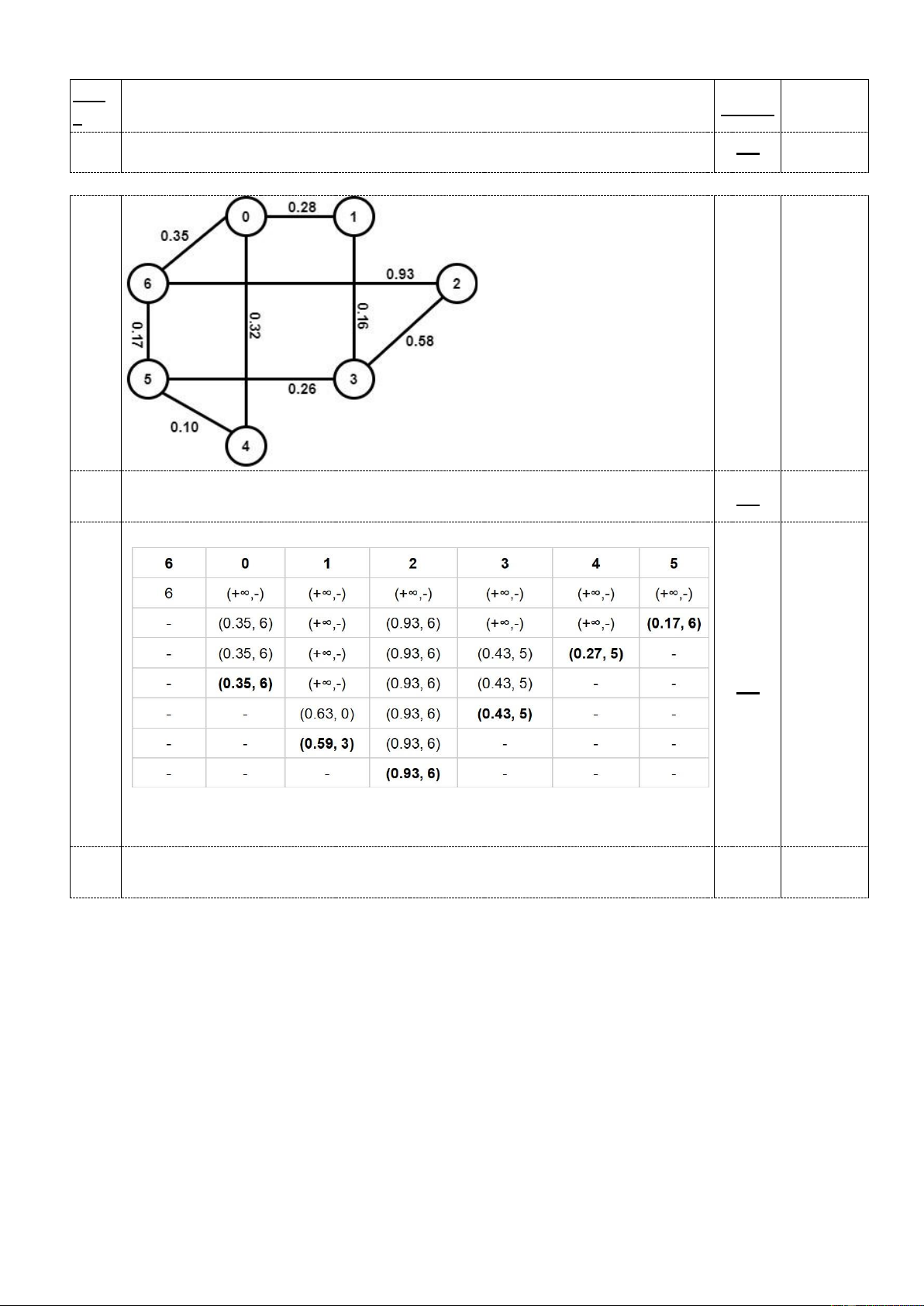
a. Vẽ đồ thị minh họa G. (0.5 điểm)
b. Duyệt đồ thị G theo chiều sâu (DFS) bắt đầu từ đỉnh 3 và liệt kê dãy đỉnh theo thứ tự đã duyệt. (0.5 điểm)
Lưu ý: khi xem xét một đỉnh mà kề với nhiều hơn 1 đỉnh khác, thứ tự lựa chọn thăm sẽ theo
thứ tự tăng dần (Ví dụ: 0 kề với 1, 2, 3 thì duyệt 1 trước rồi đến 2 và cuối cùng là 3).
c. Minh họa các bước sử dụng thuật toán Djikstras để tìm đường đi ngắn nhất từ đỉnh 6 đến đỉnh
3 bằng cách kẻ bảng. Cho biết độ dài đường đi ngắn nhất đó và danh sách các đỉnh của đường
đi. (1 điểm) Câu 6 (2 điểm):
Cho dãy số 11, 4, 2, 10, 5, 15, 20, 17.
a. Xây dựng cây tìm kiếm nhị phân cân bằng T bằng cách chèn lần lượt các số trong dãy vào
cây (Các nút lần lượt được thêm vào cây từ trái qua phải, bắt đầu từ 11 và kết thúc là 17). Vẽ
cây tìm kiếm nhị phân cân bằng ở trạng thái có 3 nút (cây chứa các nút có khóa là 11, 4, 2), 6
nút (cây chứa các nút có khóa là 11, 4, 2, 10, 5, 15) và có đủ 8 nút có khóa là các số của dãy
(tổng cộng cần vẽ 3 cây). (1.25 điểm)
b. Cách duyệt nào (preorder, inorder và postorder) sẽ thu được các khóa trên cây T theo thứ tự tăng dần? (0.25 điểm)
c. Thêm nút có giá trị 18 vào cây T và cập nhật lại cây sao cho đảm bảo cây vẫn là cây tìm kiếm
nhị phân cân bằng. Vẽ cây T’ thu được sau quá trình trên. (0.5 điểm) Tổng: 06 câu
Ghi chú: - Cán bộ coi thi không giải thích gì thêm.
Trưởng Khoa/Bộ môn Giảng viên ra đề TS. Tạ Thúy Anh
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN ĐỀ THI KẾT THÚC HỌC PHẦN
TRƯỜNG ĐẠI HỌC PHENIKAA
Học phần: Cấu trúc dữ liệu và thuật toán Mã học phần: ĐỀ SỐ: 01
Đáp án gồm có 04 trang Chuẩn Câu Nội dung trả lời Điểm đầu ra học phần Câu 1 1 điểm 1.1. Mảng: -
Ưu điểm: Truy cập phần tử dễ dàng, trực tiếp, thông qua chỉ mục; đơn
giảnkhi khai báo, sử dụng. -
Nhược điểm: Kích thước cần khai báo ngay ban đầu, nếu khai báo kích
thướcquá lớn sẽ tốn bộ nhớ, còn nếu khai báo kích thước quá nhỏ thì chương
trình không hoạt động; chèn và xóa không dễ dàng. 1.2. Danh sách liên kết -
Ưu điểm: Kích thước không cố định, có thể xóa hoặc chèn thêm phần tử một. -
Nhược điểm: Thao tác truy cập phần tử mất nhiều thời gian hơn do
khôngtruy cập trực tiếp được, cần tuân theo quy tắc truy cập một cách tuần tự;
cần thêm bộ nhớ để lưu con trỏ.
Câu 2.1. Giống nhau: 2 -
Đều dùng để lưu trữ dữ liệu -
Đều có thể dùng mảng hoặc danh sách liên kết để cài đặt -
Đều cho phép thực hiện các thao tác: xóa, chèn phần tử 1 2.2. Khác nhau: điểm -
Hàng đợi: FIFO, việc chèn và xóa trong hàng đợi diễn ra riêng
biệt ởhai đầu đối diện của danh sách. -
Ngăn xếp: LIFO, việc chèn và xóa trong ngăn xếp đều thực
hiện ở một đầucủa danh sách. Câu 3 3 điểm a.
Đây là mã giả của thuật toán sắp xếp kiểu lựa chọn (selection-sort).
Sau khi thực hiện xong thuật toán, ta thu được dãy số theo thứ tự tăng dần. 1.0 b.
Mảng A: 11, 4, 2, 14, 5, 9, 3, 17
Các dãy số cần liệt kê: 2, 4, 11, 14, 5, 9, 3, 17 2, 3, 11, 14, 5, 9, 4, 17 2, 3, 4, 14, 5, 9, 11, 17 1.5 2, 3, 4, 5, 14, 9, 11, 17 2, 3, 4, 5, 9, 14, 11, 17 2, 3, 4, 5, 9, 11, 14, 17 2, 3, 4, 5, 9, 11, 14, 17 c. Dãy số dòng lệnh 7: 2, 6, 6, 4, 5, 6, 6 0.5 Câu 1 4 điểm a. Max heap tree T
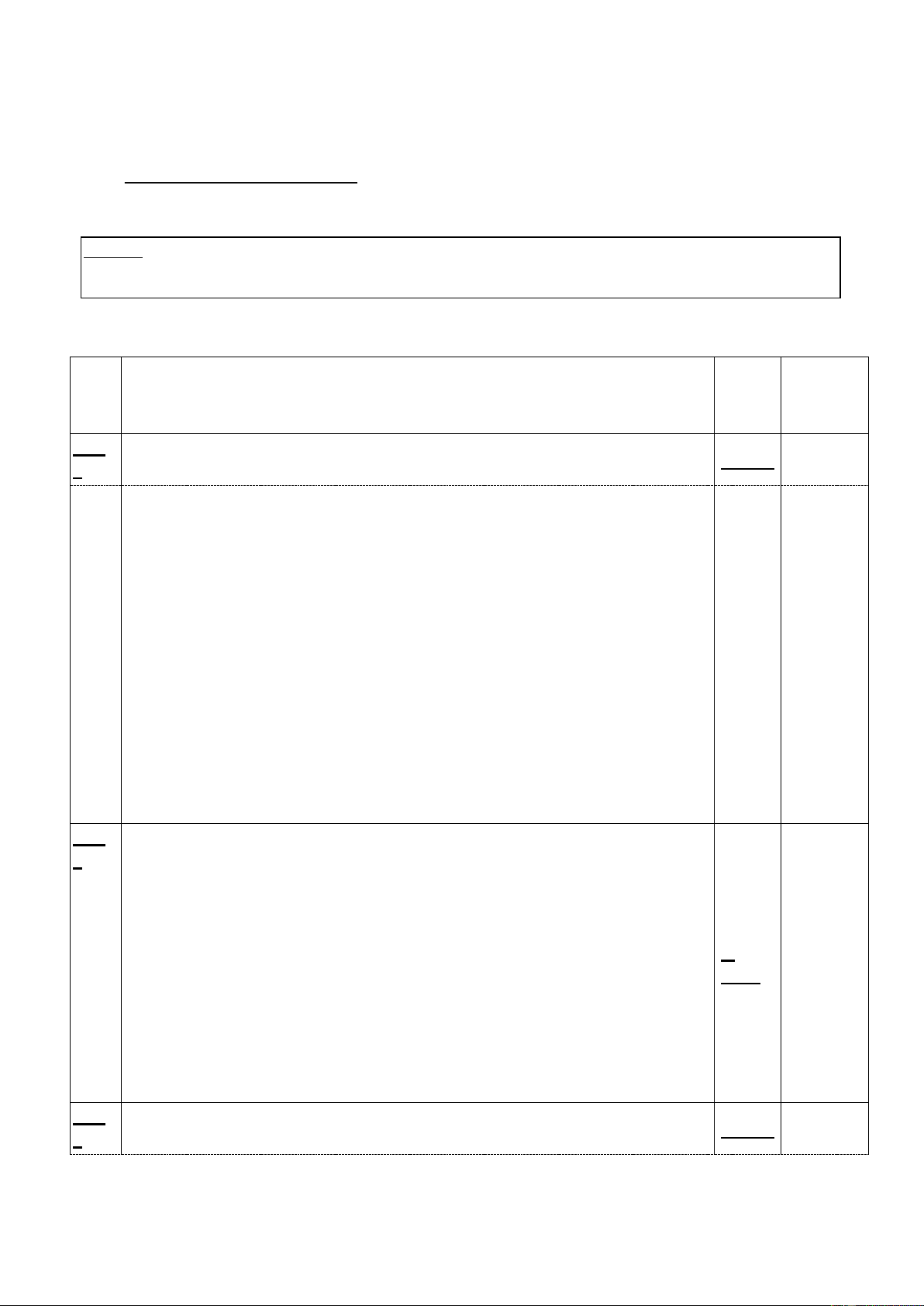
Dãy số: 11, 4, 2, 10, 5, 9, 14, 20, 3, 17 Max heap tree T 0.5 b.
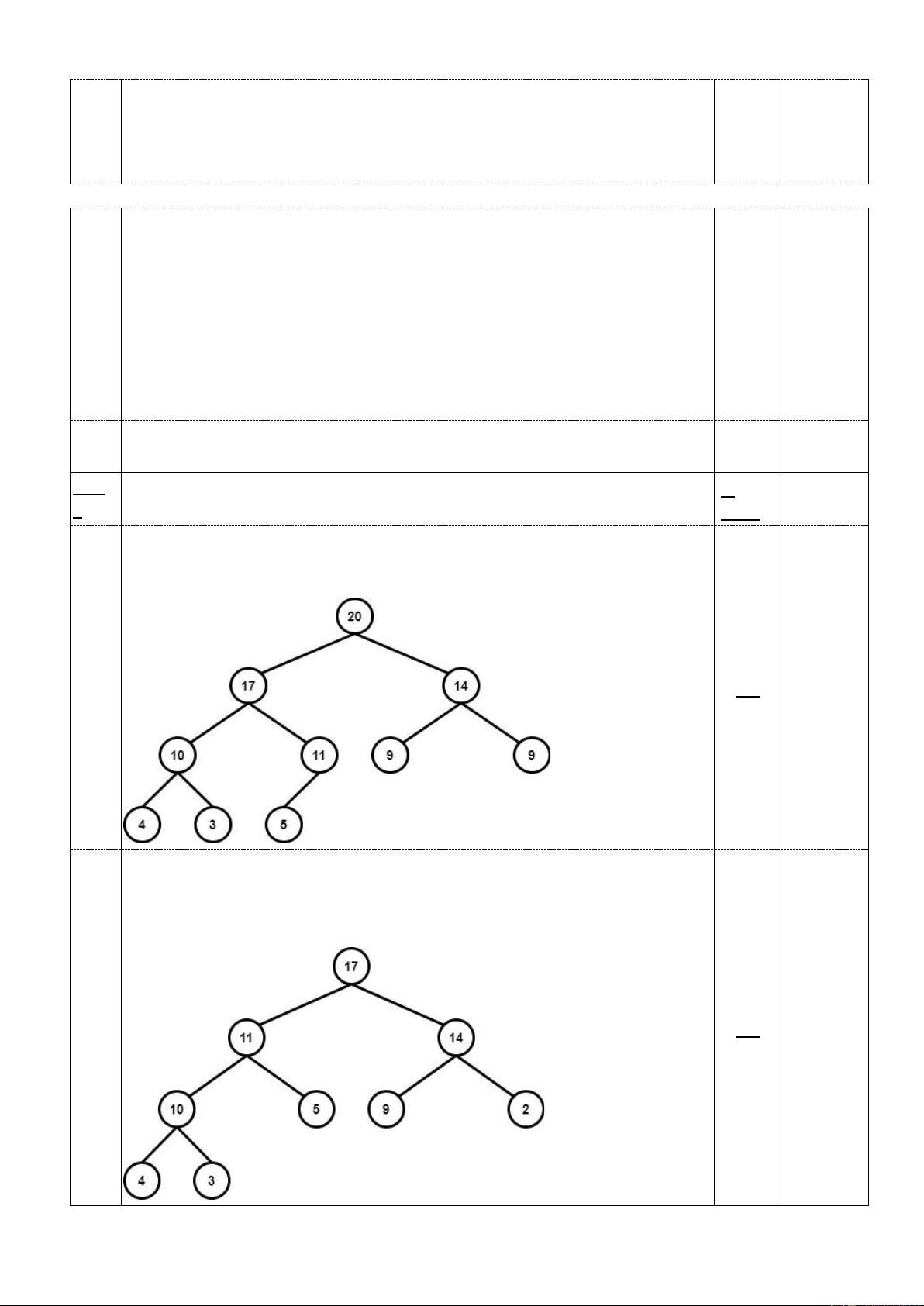
Max heap tree T’ sau khi xóa nút gốc Dãy số:
11, 4, 2, 10, 5, 9, 14, 20, 3, 17 Max heap tree T’ 0.5 Câu 5 1 điểm a. a. Đồ thị minh họa G 0.5 b.
Duyệt độ thị bằng DFS 0.5
Thứ tự duyệt các đỉnh: 3 1 0 4 5 6 2 c. Djikstras 1.0
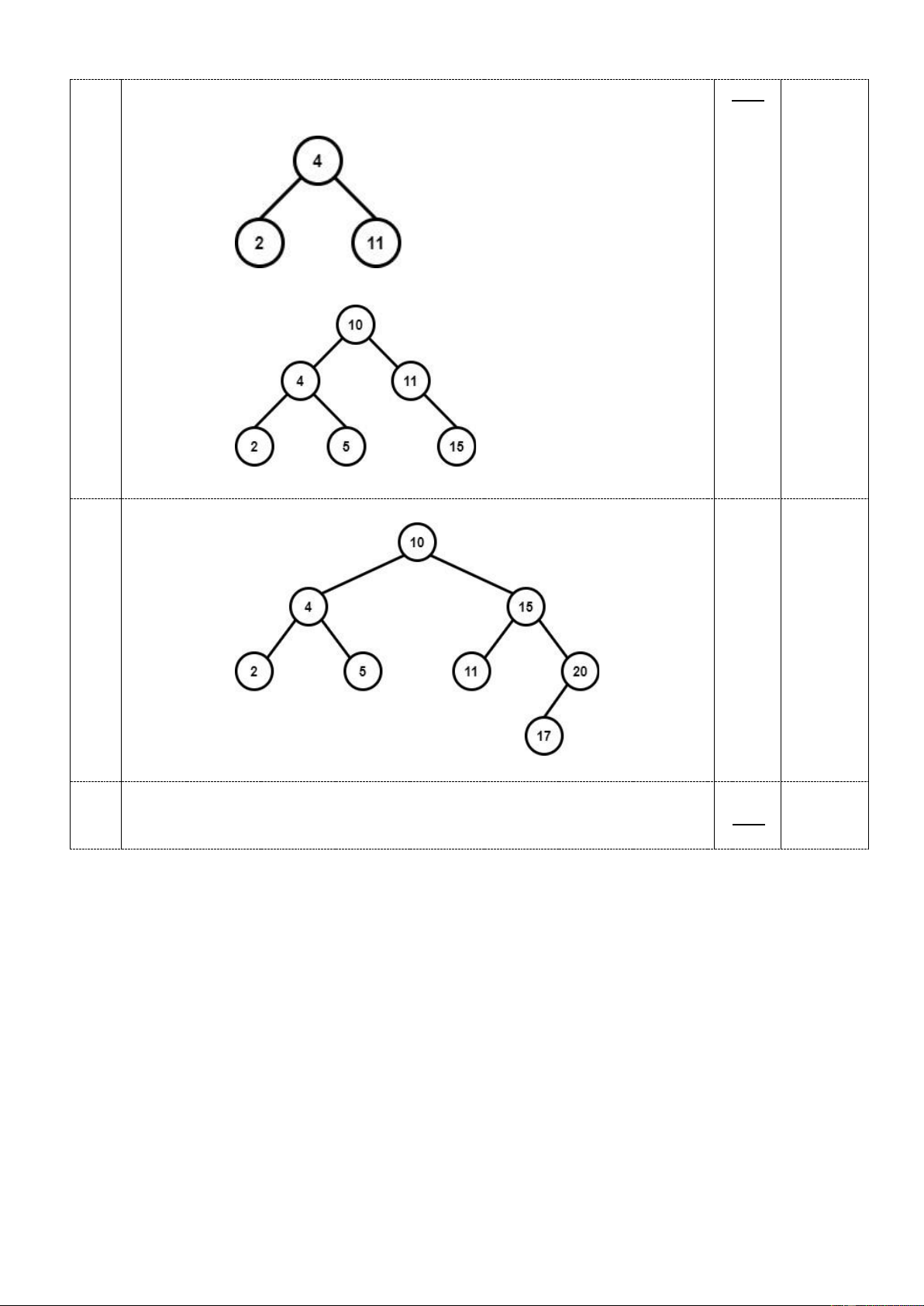
Độ dài đường đi ngắn nhất là 0.43, đường đi 6 -> 5 -> 3 Câu 6 a. a. Các cây cần vẽ: 1.25 - (0.25) Cây có 3 nút: - (0.5) Cây có 6 nút:
- (0.5) Cây có đầy đủ các nút:
b. Để thu được các khóa trên cây T theo thứ tự tăng dần, cần sử dụng cách duyệt preorder 0.25
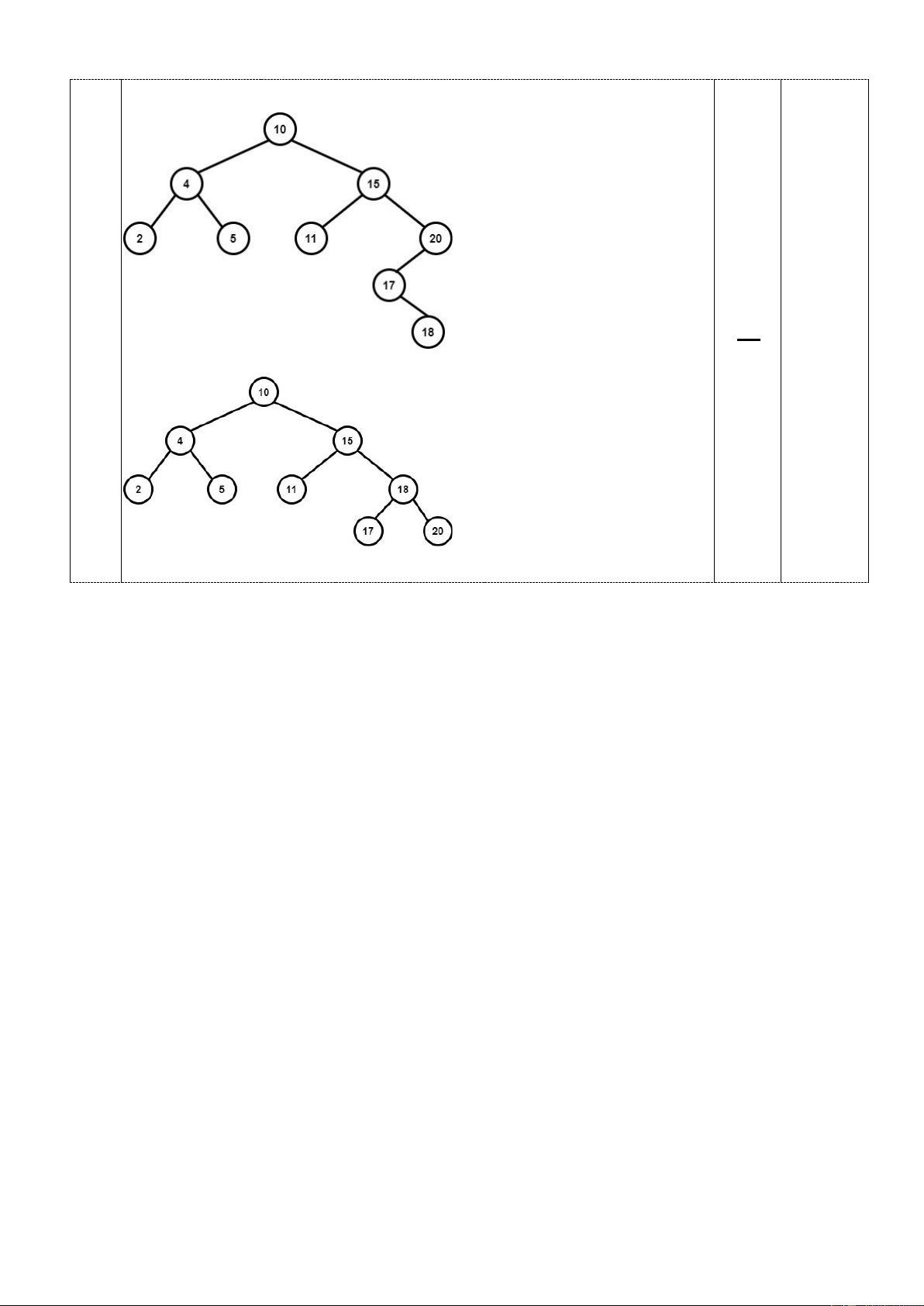
c. Thêm nút 18 vào cây 0.5
Cây sau khi thêm (chưa xoay):
Cây T’ thu được (sau khi xoay):
(Đáp án đề thi phải phù hợp với biểu điểm của đề)
Trưởng Khoa/Bộ môn
Giảng viên làm đáp án TS. Tạ Thúy Anh