Đề thi học sinh giỏi cấp tỉnh Toán 10 năm 2023 – 2024 sở GD&ĐT Hải Dương

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH HẢI DƯƠNG
LỚP 10 THPT NĂM HỌC 2023 - 2024 MÔN THI: TOÁN ĐỀ CHÍNH THỨC Ngày thi: 05/4/2024
Thời gian làm bài: 180 phút, không kể thời gian phát đề
(Đề thi có 01 trang) Câu I. (2,0 điểm)
1) Cho hàm số y = (m − ) 2
2 x + 2mx + m + 2. Tìm tất cả giá trị của tham số m để hàm số đã cho đồng biến trên khoảng ( 2; − +∞) .
2) Trong mặt phẳng toạ độ Oxy cho parabol (P) 2
: y = x − 2mx − 2m − 3, đường thẳng (d ): y = 2x + m .
Tìm tất cả các giá trị của tham số m để (d ) cắt (P) tại hai điểm phân biệt M , N sao cho MN =10 2 . Câu II. (2,0 điểm)
1) Giải phương trình 2
x 2x − x + 3 = 4x − 2 (x∈) .  2
 3x + 6y − 2 = 2y +1
2) Giải hệ phương trình:  (x, y∈). 3 4y + 
(x + )1(xy −3x + y) 3 = x +1
Câu III. (2,0 điểm)
1) Một xưởng cơ khí có hai công nhân là An và Bình. Xưởng sản xuất hai loại sản phẩm I và II . Mỗi
sản phẩm loại I bán lãi 500 nghìn đồng, mỗi sản phẩm loại II bán lãi 400 nghìn đồng. Để sản xuất được một
sản phẩm loại I thì An phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản
phẩm loại II thì An phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể tham gia
làm hai loại sản phẩm tại cùng một thời điểm. Biết rằng trong một tháng An không thể làm việc quá 180 giờ và
Bình không thể làm việc quá 220 giờ. Tính số tiền lãi lớn nhất trong một tháng của xưởng đó.
2) Cho tập hợp A = {1;2;3;4;5; }
6 . Gọi S là tập hợp các số tự nhiên có 3 chữ số và chia hết cho 6 được
lập từ các chữ số thuộc tập A . Tính số phần tử của tập S . Câu IV. (3,0 điểm)
1) Cho tam giác ABC đều cạnh a . Lấy các điểm M , N, P lần lượt nằm trên ba cạnh BC,C , A AB sao cho 1
BM = BC, AC = 2AN, AP = x,0 < x < a . Tính x theo a để AM vuông góc với NP . 3
2) Trong mặt phẳng tọa độ Oxy , cho hình thang ABCD vuông tại A và D , CD = 2AB . Gọi H là hình
chiếu của D trên AC và M là trung điểm HC , K là trực tâm tam giác ADM . Biết điểm D có hoành độ bằng
2 , phương trình đường thẳng DH và BM lần lượt là 2x + y − 6 = 0 và 4x + 7y − 61 = 0 . Tìm tọa độ điểm K .
3) Cho tam giác nhọn ABC nội tiếp đường tròn tâm O bán kính bằng 1. Gọi H, E, K lần lượt là chân
đường cao kẻ từ các đỉnh ,
A B,C . Gọi diện tích các tam giác ABC và HEK lần lượt là S và S . Biết G là trọng 0 −
tâm tam giác ABC và 3 1 S =
S . Tính độ dài đoạn OG . 0 4 Câu V. (1,0 điểm)
Cho 3 số thực a,b,c >1 thỏa mãn 2 2 2
a + b + c ≤ 2(a + b + c) . Tìm giá trị lớn nhất của biểu thức a −1 b −1 c −1 H = + + 2 2 2
a + 4b b + 4c c + 4a
- - - - - - - - - - - - HẾT - - - - - - - - - - - -
(Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh: .................................................... Số báo danh: ................................. Phòng thi: .........
Cán bộ coi thi số 1:.................................................... Cán bộ coi thi số 2:....................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH HẢI DƯƠNG
LỚP 10 THPT NĂM HỌC 2023 – 2024
HƯỚNG DẪN CHẤM MÔN TOÁN DỰ THẢO Câu
1) Cho hàm số y = (m − ) 2
2 x + 2mx + m + 2 ( m là tham số). Tìm tất cả giá trị của m để hàm số I.1(1,0
điểm) đã cho đồng biến trên khoảng ( 2; − +∞) .
Với m = 2 ⇒ y = 4x + 4. Hàm số đồng biến trên  .
Do đó m = 2 thỏa mãn. 0,25
Với m ≠ 2 . Hàm số đồng biến trên khoảng ( 2; − +∞) khi và chỉ khi 0,25 m − 2 > 0  m > 2  −m ⇔ ≤  2  − −m ≤ 2 − m + 4 m − 2 m > 2 ⇔  ⇔ m∈(2;4] 0,25 m ≤ 4 Vậy m∈[2;4] 0,25
2) Trong mặt phẳng Oxy cho Parabol (P) 2
: y = x − 2mx − 2m − 3, đường thẳng (d ): y = 2x + m Câu I.2(1,0
. Tìm tất cả các giá trị của tham số m để (d ) cắt (P) tại hai điểm phân biệt M , N sao cho điểm) MN =10 2 .
Ta có: Hoành độ giao điểm của (d ) và (P) là nghiệm của phương trình: 0,25 2 2
x − 2mx − 2m − 3 = 2x + m ⇔ x − 2(m + )
1 x − 3m − 3 = 0 ( ) 1 .
(d ) cắt (P) tại hai điểm phân biệt M,N ⇔ Phương trình ( ) 1 có 2 nghiệm phân biệt 0,25 m > −
⇔ ∆′ > 0 ⇔ (m + )2 1 2
1 + 3m + 3 > 0 ⇔ m + 5m + 4 > 0 ⇔  m < 4 −
Khi đó gọi x ; x tương ứng là hoành độ các điểm
⇒ M x ;2x + m , N x ;2x + m . 1 2 M ,N ( 1 1 ) ( 2 2 )
Theo hệ thức Vi ét ta có: 0,25
x + x = 2 m +1 1 2 ( )  x x = 3 − m − 3 1 2
MN =10 2 ⇔ (x − x )2 + (2x + m − 2x − m)2 = 200 1 2 1 2 0,25
⇔ (x + x )2 − 4x x = 40 ⇔ 4(m + )2 1 − 4 3 − m − 3 = 40 1 2 1 2 ( ) m =1 2
⇔ 4m + 20m − 24 = 0 ⇔  m = 6 − Vậy m∈{ 6; − } 1 Câu
1) Giải phương trình 2
x 2x − x + 3 = 4x − 2 II.1(1,0 điểm) Ta có 2
x 2x − x + 3 = 4x − 2 0,25  2 ⇔ x
x − x + − (x + ) 2 2 3
1 + x − 3x + 2 = 0   x ≤ 1 − TH1: 2
2x − x + 3 + (x + ) 1 = 0 ⇔  (PTVN) 2 0,25
x − 3x + 2 = 0 TH2: 2
2x − x + 3 + (x + ) 1 ≠ 0 2 PT x − 3x + 2 2 ⇔ . x
+ x − 3x + 2 = 0 0,25 2
2x − x + 3 + x +1 x =1 ⇔ (    2 − 3 + 2) x x x  +1 = 0 ⇔ x = 2 2
 2x − x + 3 + x +1   2
 2x − x + 3 = 1 − − 2x  ( ) 1  1  1 x ≤ − x ≤ −  PT( )  2 5 − − 41 1 ⇔  2 ⇔  ⇔ x = 2 5 − ±   41 4
2x + 5x − 2 = 0 x = 0,25  4 − − 
Vậy phương trình đã cho có tập nghiệm 5 41 S ;1;2 =  4    Câu  2
 3x + 6y − 2 = 2y +1 ( ) 1
II.2(1,0 2) Giải hệ phương trình:  (x, y∈) . điểm) 3 4y + 
(x + )1(xy −3x + y) 3 = x +1 (2) PT ( ) 3
⇔ y + (x + )  y  ( x + ) 3 2 4 1 .
1 − 3x = x +1  0,25 3 ⇔ 4y + . y (x + )2 3 2
1 = x +1+ 3x + 3x 3 ⇔ 4y + . y (x + )2 1 − (x + )3 1 = 0 (3)
TH1: Nếu x +1 = 0 ⇔ x = 1
− ⇒ y = 0 thoả mãn ( ) 1 0,25 Suy ra ( 1;
− 0) là nghiệm của hệ.
TH2: x +1 ≠ 0 ⇔ x ≠ 1
− (*). Chia hai vế của (3) cho (x + )3 1 ta có: 3 ⇔ 4 y  y + −1 = 0,25   0  x +1 x +1 Đặt y t =
. Phương trình trở thành: 3t + t − = ⇔ ( t − ) ( 2t + t + ) 1 4 1 0 2 1 . 2 1 = 0 ⇔ t = . x +1 2 Thay y 1
= ⇔ x +1 = 2y . Thay vào ( ) 1 ta có: x +1 2 x = 1 0,25 x ≥ 2 − − 2
3x 3x 1 x 2  + + = + ⇔  ⇔ 2 3
2x − x − 3 = 0 x =  2 Kết hợp (*) ta được 3 5 x = ⇒ y = . 2 4 Vậy hệ có 2 nghiệm (   − )  3 5 1;0 ,  ;    2 4  
1) Một xưởng cơ khí có hai công nhân là An và Bình. Xưởng sản xuất hai loại sản phẩm I và
II . Mỗi sản phẩm loại I bán lãi 500 nghìn đồng, mỗi sản phẩm loại II bán lãi 400 nghìn
đồng. Để sản xuất được một sản phẩm loại I thì An phải làm việc trong 3 giờ, Bình phải làm Câu
việc trong 1 giờ. Để sản xuất được một sản phẩm loại II thì An phải làm việc trong 2 giờ, Bình
III.1(1,0 phải làm việc trong 6 giờ. Một người không thể tham gia làm hai loại sản phẩm tại cùng một điểm)
thời điểm. Biết rằng trong một tháng An không thể làm việc quá 180 giờ và Bình không thể làm
việc quá 220 giờ. Tính số tiền lãi lớn nhất trong một tháng của xưởng đó.
Gọi x, y lần lượt là số sản phẩm loại I và loại II được sản xuất ra trong một tháng.
Điều kiện x, y ∈ . 3
 x + 2y ≤180 0,25
Ta có hệ bất phương trình sau: x + 6y ≤ 220
x ≥ 0, y ≥  0
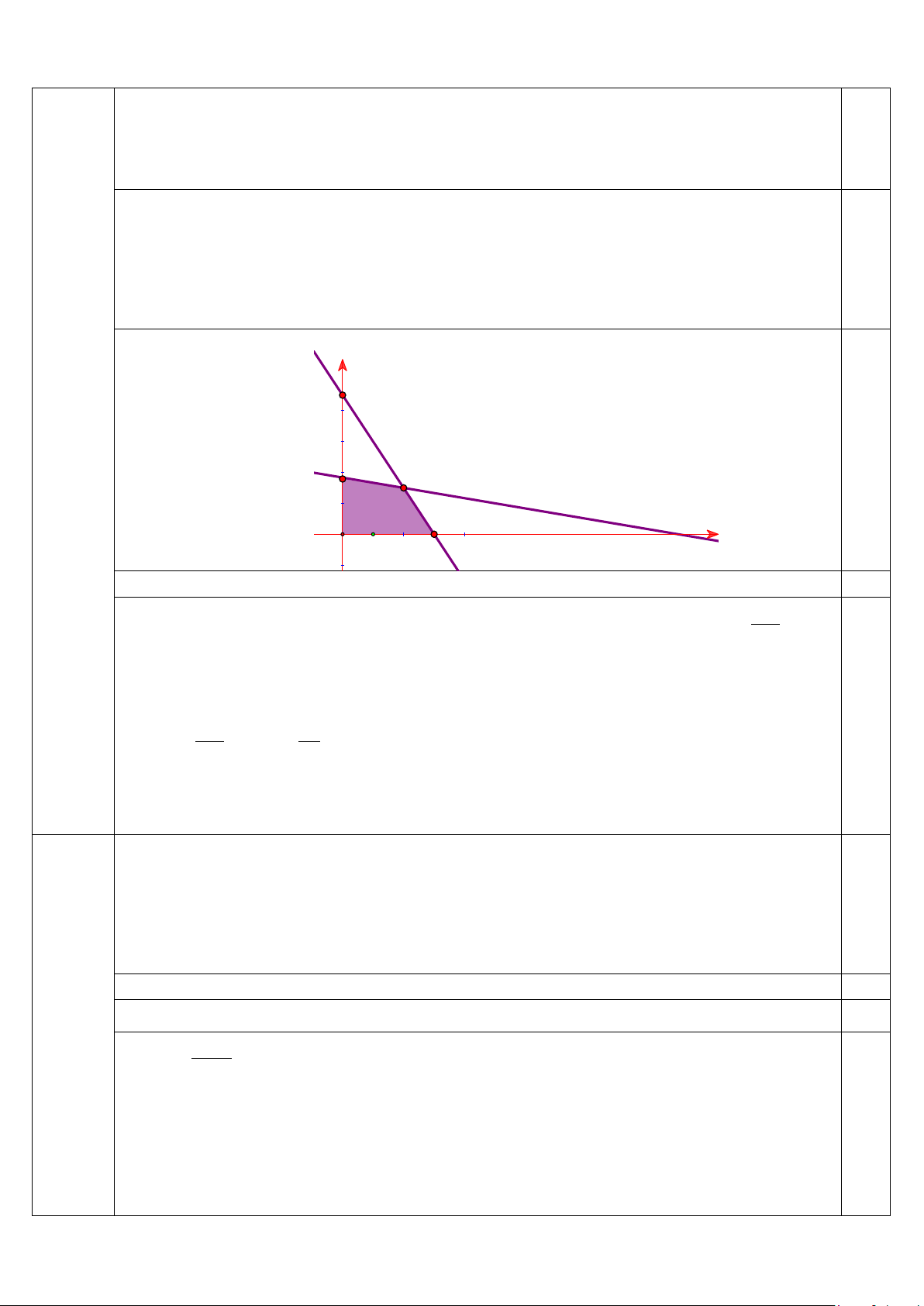
Miền nghiệm của hệ trên là y 90 0,25 B C x O A
Tiền lãi trong một tháng của xưởng là T = 0,5x + 0,4y (triệu đồng) 0,25
Ta thấy T đạt giá trị lớn nhất chỉ tại một trong các điểm A(60;0), B(40;30) , 110 C 0;   . 3    0,25
Tại A(60;0) thì T = 30 triệu đồng.
Tại B(40;30) thì T = 32 triệu đồng. 44 Tại 110 C 0;   thì T = triệu đồng. 3    3
Vậy tiền lãi lớn nhất trong một tháng của xưởng là 32 triệu đồng đạt được khi một tháng
xưởng đó sản xuất 40 sản phẩm loại I và 30 sản phẩm loại II (số sản phẩm là số nguyên thoả mãn).
Cách 2 Gọi x, y lần lượt là số sản phẩm loại I và loại II được sản xuất ra trong một tháng. Điều kiện x, y ∈ . 3
 x + 2y ≤180 0,25
Ta có hệ bất phương trình sau: x + 6y ≤ 220
x ≥ 0, y ≥  0
Tiền lãi trong một tháng của xưởng là T = 0,5x + 0,4y (triệu đồng) 0,25
Ta có 80T = 40x + 32y =13(3x + 2y) + (x + 6y) ≤13.180 + 220 = 2560 0,25 2560 Vậy T ≤ = 32 80
Hay giá trị lớn nhất của T bằng 32 triệu. 0,25 3  x + 2y =180  x = 40
Dấu bằng xảy ra khi x + 6y = 220 ⇔   y = 30 x ≥ 0, y ≥  0
Tức là trong một tháng xưởng đó sản xuất 40 sản phẩm loại I và 30 sản phẩm loại II. Câu
2) Cho tập hợp A = {1;2;3;4;5; }
6 . Gọi S là tập hợp các số tự nhiên có 3 chữ số và chia hết III.2(1,0 điểm)
cho 6 được lập từ các chữ số thuộc tập A. Tính số phần tử của tập S .
Gọi số cần tìm là x = abc
Vì x6 ⇒ c∈{2;4; }
6 và (a + b + c)3 0,25
+) Chọn c có 3 cách.
+) Chọn b có 6 cách. 0,25
Đặt A = 3;6 , A = 1;4 , A = 2;5 0 { } 1 { } 2 { } 0,25
Nếu (b + c) chia 3 dư 1 thì a∈ A , nếu (b + c) chia 3 dư 2 thì a ∈ A , nếu (b + c) chia hết cho 2 1
3 thì a ∈ A . 0
+) Với mỗi cách chọn b,c luôn có 2 cách chọn a
Vậy có 3.6.2 = 36 số thoả mãn. 0,25
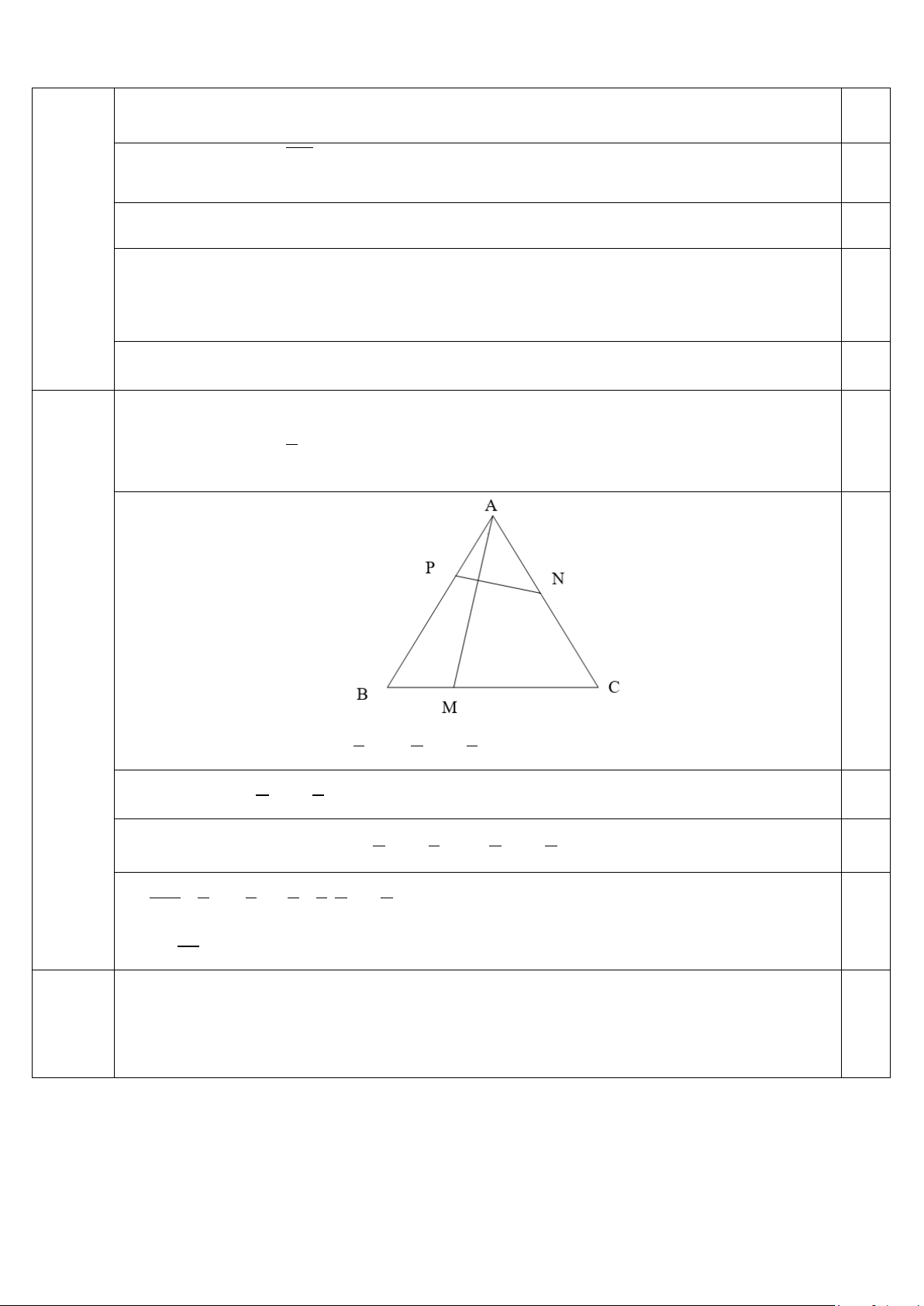
1) Cho tam giác ABC đều cạnh a . Lấy các điểm M , N, P lần lượt nằm trên ba cạnh BC,CA Câu 1
IV.1(1,0 , AB sao cho BM = BC, AC = 2AN, AP = x,0 < x < a . Tính x theo a để AM vuông điểm) 3 góc với NP . 0,25
       Ta có 1 2 1
AM = AB + BM = AB + BC = AB + AC 3 3 3
   x  1 
NP = AP − AN = AB − AC a 2 0,25  
 2  1   x  1  AM NP AM NP = 0 ⇔ AB
AC  AB − AC  ⊥ ⇔ ⊥ + =    0  3 3  a 2  0,25 2xa 1 2 1 1 1 x 1 ⇔ − a − . a . a + . . . a . a = 0 3 6 3 2 3 a 2 2a 0,25 ⇔ x = . 5 Câu
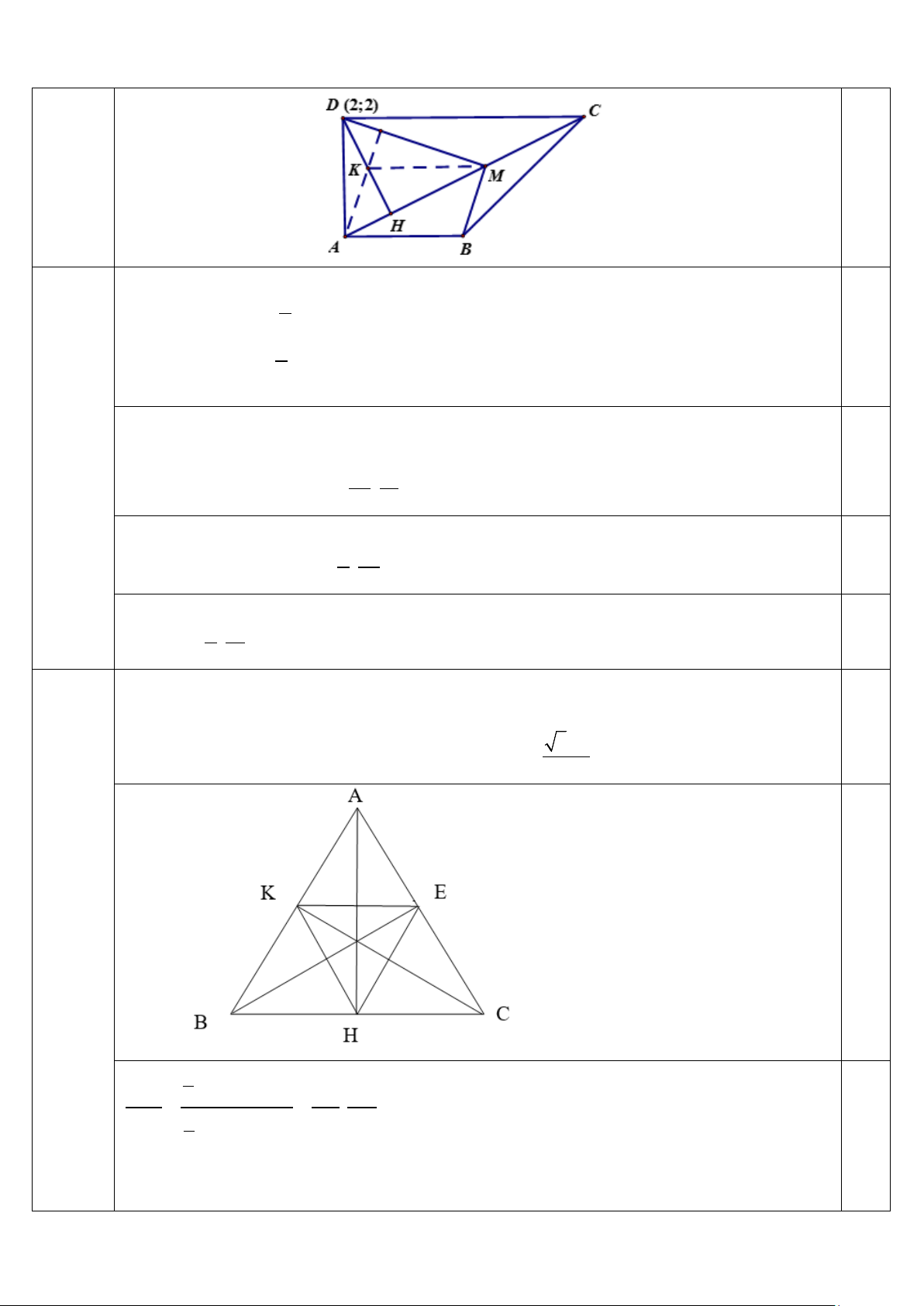
2) Trong mặt phẳng tọa độ Oxy , cho hình thang ABCD vuông tại A và D , CD = 2AB . Gọi
IV.2(1,0 H là hình chiếu của D trên AC và M là trung điểm HC , K là trực tâm tam giác ADM . điểm)
Biết điểm D có hoành độ bằng 2 , phương trình đường thẳng DH và BM lần lượt là
2x + y − 6 = 0 và 4x + 7y − 61 = 0 . Tìm tọa độ điểm K .
Do K là trực tâm A
∆ DM ⇒ KM ⊥ AD ⇒ KM //DC ⇒ KM là đường trung bình trong tam giác CDH 1 ⇒ KM = DC . 2 0,25 Mà 1
AB//DC; AB = DC ⇒ Tứ giác ABMK là hình bình hành⇒ AK //BM 2
Mà AK ⊥ DM ⇒ BM ⊥ DM .
Ta có D ∈ DM ⇒ D(2;2) . Khi đó đường thẳng DM qua D và vuông góc BM có phương
trình là 7x − 4y − 6 = 0 . 0,25 Ta có 22 31 M DM BM M  ;  = ∩ ⇒  . 5 5   
Đường thẳng AC qua M và vuông góc DH có phương trình là x − 2y + 8 = 0. 0,25 Ta có 4 22 H AC DH H  ;  = ∩ ⇒  . 5 5   
KM là đường trung bình trong tam giác CDH nên K là trung điểm của DH 0,25 Suy ra 7 16 K  ;   . 5 5   
3) Cho tam giác nhọn ABC nội tiếp đường tròn tâm O bán kính bằng 1. Gọi H, E, K lần lượt Câu
là chân đường cao kẻ từ các đỉnh ,
A B,C . Gọi diện tích các tam giác ABC và HEK lần lượt là IV.3(1,0 điểm) −
S và S . Biết G là trọng tâm tam giác ABC và 3 1 S =
S . Tính độ dài đoạn OG . 0 0 4 1
AE.AK sin A S AE AK EAK 2 2 = = . = cos . A cos A = cos 1 A S . sin AB AC AB AC A 2 0,25
1 BK.BH.sin B S BK BH KBH 2 2 = = . = cos . B cos B = cos 1 B S . sin BC AB AB BC B 2
1 CH.CE.sinC S CH CE HCE 2 2 = = .
= cosC.cosC = cos 1 C S . sin AC BC AC BC C 2 Ta có S + S + S = S − S EAK KBH HCE 0 5 − 3 S + S + S = S EAK KBH HCE 4 0,25 S S S − − EAK KBH HCE 5 3 2 2 2 5 3 + + =
⇔ cos A + cos B + cos C = S S S 4 4 2 2 2 5 − 3 2 2 2 7 + 3
⇔ 1− sin A +1− sin B +1− sin C =
⇔ sin A + sin B + sin C = 4 4 2 2 2 a b c 7 + 3 2 2 2 ⇔ + + =
⇔ a + b + c = 7 + 3 (Do R =1) 2 2 2 4R 4R 4R 4 0,25
   
Ta có: OA + OB + OC = 3OG
(   
OA + OB + OC)2 2 = 9OG 2 2 2
⇔ OA + OB + OC + ( 2 2 2
OA + OB − AB ) + ( 2 2 2
OA + OC − AC ) + ( 2 2 2
OB + OB − BC ) 2 = 9OG 0,25 2 2 OG R ( 2 2 2 a b c ) 2 3 6 2 9 9 2 3 OG − − ⇔ = − + + = − ⇔ = = 3 6
Cho 3 số thực a,b,c >1 thỏa mãn 2 2 2
a + b + c ≤ 2(a + b + c) . Tìm giá trị lớn nhất của biểu thức Câu V(1,0 a −1 b −1 c −1 H = + + điểm) 2 2 2
a + 4b b + 4c c + 4a Ta có: 2 2 2
a + 4 ≥ 4a ⇔ a ≥ 4a − 4 ⇔ a + 4b ≥ 4a − 4 + 4b > 0 (do a,b >1) Suy ra a −1 a −1 ≤ (do a −1 > 0 ) 2
a + 4b 4a + 4b − 4 0,25 Tương tự b −1 b −1 ≤ 2
b + 4c 4b + 4c − 4 c −1 c −1 ≤ 2
c + 4a 4c + 4a − 4
Dấu bằng trong các bất đẳng thức trên xảy ra khi và chỉ khi a = b = c = 2. Ta chứng minh a −1 b −1 c −1 1 + + ≤
4a + 4b − 4 4b + 4c − 4 4c + 4a − 4 4 a −1 b −1 c −1 ⇔ + + ≤1
a + b −1 b + c −1 c + a −1 0,25 ⇔ 1 b − +1 c − +1 a − ≤1 a + b −1 b + c −1 c + a −1 b c a ⇔ + + ≥ 2
a + b −1 b + c −1 c + a −1
Trước hết ta chứng minh BĐT sau: x y z
(x + y + z)2 2 2 2
Với a,b,c > 0, x, y, z ∈ ta có: + + ≥ a b c a + b + c Thật vậy: x y (x + y)2 2 2 + ≥ ( ) 2 2 2 2
1 ⇔ b x + a y ≥ 2abxy ⇔ (bx − ay)2 ≥ 0 luôn đúng. a b a + b
Dấu bằng xảy ra khi và chỉ khi x y = a b 0,25 x y z
(x + y + z)2 2 2 2 Từ đó áp dụng ( ) 1 ta có + + ≥ a b c a + b + c
Dấu bằng xảy ra khi: x y z = = . a b c Áp dụng ta có: 2 2 2 b c a b c a + + = + + 2 2 2
a + b −1 b + c −1 c + a −1 ab + b − b bc + c − c ca + a − a
(a +b + c)2 ≥ 2 2 2
a + b + c + (ab + bc + ca) −(a + b + c)
Dấu bằng xảy ra khi và chỉ khi 1 1 1 = =
⇔ a = b = c .
a + b −1 b + c −1 c + a −1
Ta chứng minh (a + b + c)2 2 2 2
≥ 2 a + b + c + (ab + bc + ca) − (a + b + c)   0,25 2 2 2
⇔ a + b + c ≤ 2(a + b + c) (luôn đúng)
Vậy giá trị lớn nhất của H bằng 1 khi a = b = c = 2. 4
Thí sinh làm theo cách khác đúng vẫn cho điểm tối đa.