Đề thi học sinh giỏi tỉnh Toán 10 năm 2020 – 2021 sở GD&ĐT Hà Tĩnh

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 10 & 11 THPT HÀ TĨNH NĂM HỌC 2020 - 2021 TOANMATH.com Môn thi: TOÁN LỚP 10
Đề thi có 01 trang - gồm 05 câu
Thời gian làm bài: 180 phút (không kể thời gian phát đề) Câu 1. (5,0 điểm)
a. Giải bất phương trình 2 2
x  2x  x  3x  2x . (x  y)   2 2
x  xy  y  3  3 2 2 x  y   2
b. Giải hệ phương trình  . 2
(y  2) 2x  y 1  (x  5) 3x  2 y  2  x  5x  6  Câu 2. (5,0 điểm) 2 mx  2mx  2m  3
a. Có bao nhiêu giá trị nguyên của tham số m để hệ bất phương trình 2    3 nghiệm 2 x  2x  3
đúng với mọi x   ?
b. Tìm tất cả các giá trị của tham số m để hệ phương trình sau có nghiệm duy nhất: x  y 1 xy   x, y   .
(y  m)x  (2m  3) y  m Câu 3. (5,0 điểm)
a. Cho tam giác ABC có góc  30o A 
, bán kính đường tròn nội tiếp tam giác r  3 và độ dài đường cao kẻ 1 1 1
từ đỉnh A là h thỏa mãn   . Tính giá trị 2 2
T  sin B  cos C và bán kính đường tròn ngoại tiếp 2 2 2 h AB AC tam giác ABC.
b. Trong mặt phẳng tọa độ Oxy, cho A2;3 , B  1
 ;5 và đường thẳng d : 2x  y 1 0. Tìm tọa độ điểm C 5
thuộc đường thẳng d và tọa độ điểm D thuộc đoạn thẳng AC, biết rằng tam giác ABC cân tại B và DC  . 5 Câu 4. (3,0 điểm)
a. Một cửa hàng chuyên kinh doanh xe máy điện với chi phí mua vào là 23 triệu đồng và bán ra với giá 27
triệu đồng mỗi chiếc. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc.
Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe này, chủ cửa hàng dự định giảm giá bán và ước tính
rằng, theo tỉ lệ nếu cứ giảm 100 nghìn đồng mỗi chiếc thì số lượng xe bán ra trong một năm sẽ tăng thêm 20
chiếc. Vậy doanh nghiệp phải bán với giá mới là bao nhiêu để sau khi giảm giá, lợi nhuận thu được sẽ là cao nhất?
b. Tìm tất cả các bộ ba số nguyên dương  ;
x y; p với p là số nguyên tố thỏa mãn 2 2 2
x  p y  6 x  2 p . Câu 5. (2,0 điểm)
Cho các số thực dương x, y, z thỏa mãn xy  yz  zx . Tìm giá trị nhỏ nhất của biểu thức: 4z  2 z  xy  2 2 x  y (2z  x  y) P  . 2 (x  y)z
_______________ HẾT _______________ https://toanmath.com/
Thí sinh không được sử dụng tài liệu và máy tính cầm tay. Giám thị không giải thích gì thêm./.
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . . . . . . LỜI GIẢI TOÁN 10 x  3  2    Đk : x 2x 0    x  0 2  x  3x  0 x  2 
* khi x  3 hay x  0 bpt ®óng Suy ra x  3
 hay x  0 là nghiệm của bpt *khi x  2
bpt  x  2  x  3  2 x  2x 1 2 2 x  x  6  4x  25 2
2 x  x  6  2x-1  8x  25  x  tháa ®k x  2 8 25
Vậy tập nghiệm của bpt S  ( ;  3  ]{0}[ ; ) 8 (1) 3 3
 x  y  x  y   2 2 x  y  3 3 3 3 3
 2  (x 1)  (y 1)
 x 1  y 1  y  x  2
Thế vào phương trình (2) ta được 2
x x 1  (x  5) x  6  x  5x  6 ĐK : x  2  .
BPT  x  x     x   x    2 1 2 ( 5) 6 3  x  9 x  3 x  3  x  (x  5)
 (x  3)(x  3) x 1  2 x  6  3  x x  5   (x  3)   (x  3)  0    x 1  2 x  6  3  x x  5 Ta thấy   (x  3) x 1  2 x  6  3 x 1 x 1 x  5 x  5 1      x 1  2 2 x  6  3 2 x 1  2 (x 1) x 1
(x  5)( x  6 1) 1      0, x   2  x 1  2 x  6  3 x 1  2 1
Suy ra BPT tương đương với x  3. Vậy hệ có nghiệm (3;1) Do 2
x  2x  3  0 x
  nên hệ BPT tương đương với 2
(m 3)x  2(m 3)x  2m  6  0 (1)  2
(m  2)x  2(m  2)x  2m  9  0 (2)
Yêu cầu bài toán tương đương với hệ (1) và (2) nghiệm đúng với mọi x thuộc
Kiểm tra được hai giá trị m  3, m  2  đều thỏa mãn m  3 Với  
thì yêu cầu bài toán tuơng đương với m  2  m  3  0  2
  (m  3)  (m  3)(2m  6)  0 1  m  2  0   2
  (m  2)  (m  2)(2m  9)  0  2 m  3  2 (m  3)  0   m  2   2   m  3 m  2   m  7  Vậy 2
  m  3. Suy ra có 6 giá trị nguyên của m thỏa mãn. y  1
PT đầu tương đương vớ  i  1 y x  
Thế vào PT thứ hai của hệ ta được  1 y 2
(2  m) y  (m 1) y  m  0 (3)
TH1: m  2 . (3) tương đương y  2 . Hệ có nghiệm duy nhất (-3;2)
Suy ra m  2 thỏa mãn
TH2: m  2 . (3) là PT bậc 2. Ta có các khả năng sau 2 2   3
 m  6m 1  0 3  2 3
+) (3) có nghiệm kép khác 1    m 
2  m  m 1 m  0 3
+) (3) có hai nghiệm phân biệt, trong đó có một nghiệm bằng 1 2   3
 m  6m 1  0    m 1
2  m  m 1 m  0 3  2 3
Vậy các giá trị m là m  2; m  1; m  3 2 2 2 1 a 4R 1 1 4R
Ta có ah  2S  bc sin A       a 2 2 2 2 2 2 2 2 2 2 h b c sin A b c b c b c a 2 2 2 2 2
 b  c  4R  sin B  sin C 1 2 2 2 2  sin B 1 o
c s C  1  sin B  o c s C  0
Không mất tính tổng quát, giả sử o
B  C  C  90  cos C  0 . Khi đó: 2 2 B  C  B  C   o sin cos sin cos sin 90  C  o B  90 C   o o
B 90 C 180 Kết hợp với o
B  C  150 ta được o o
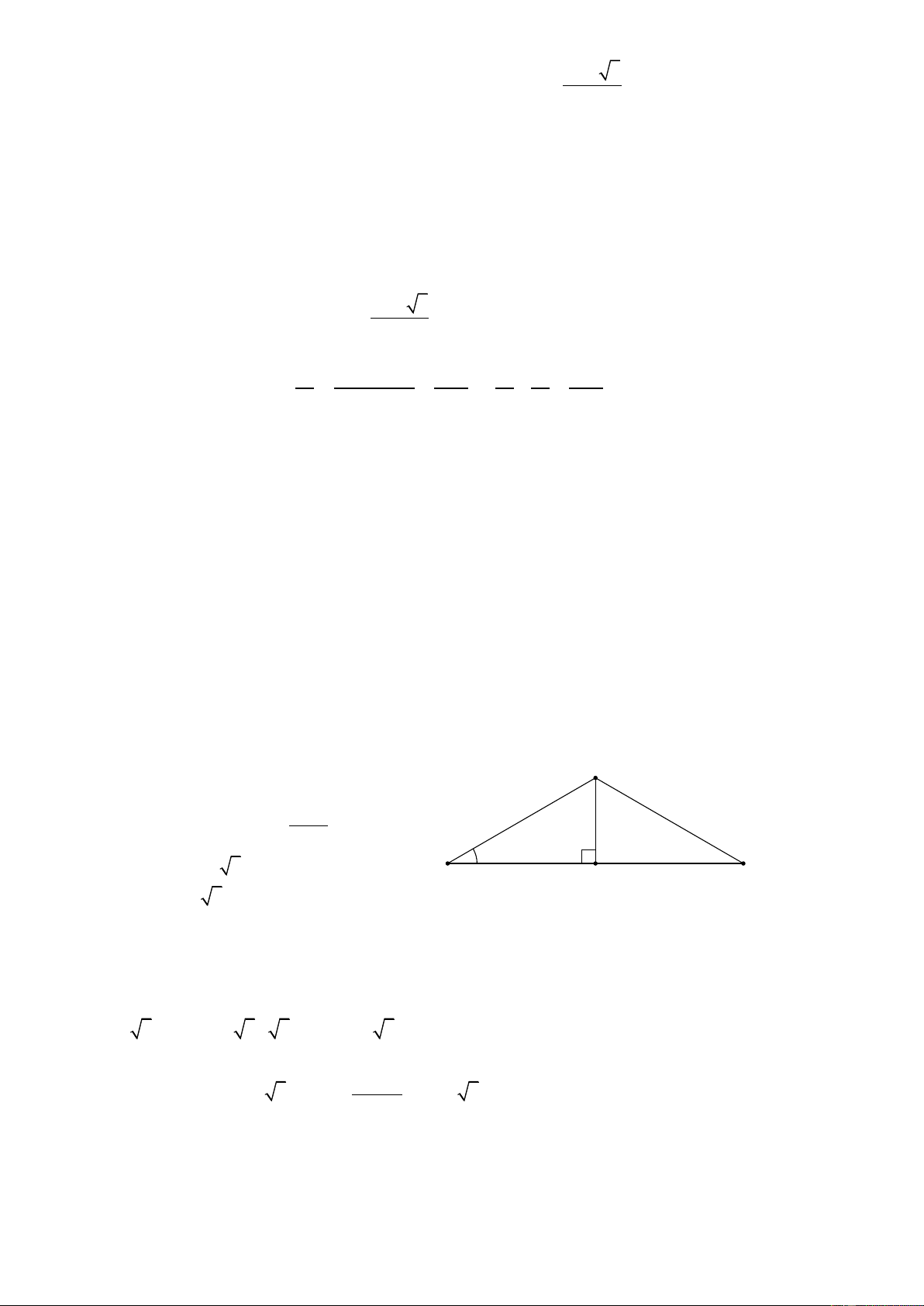
B  120 , C  30  A suy ra tam giác ABC cân tại B . Gọi H là trung điểm B
AC  BH  AC . Đặ BH
t BH  x  BC  AB   2x ; sin A 30°
AH  AB cos A  x 3 ; A H C
AC  2AH  2x 3 .
BH.AC  2S
  AB  BC  CA.r ABC 2
 2x 3  4x  2x 3. 3  x  2 3 BC
Suy ra BC  2x  2(2  3)  R   4  2 3 2 sin A
C  d  C( ; a 2  a 1). 3
Tam giác ABC cân tại B suy ra 2 2 2 2
BC  BA  (a 1)  ( 2
 a  6)  3  2 a  4  2 
 5a  26a  24  0  6   a   . 5 6  7 Suy ra C( 4  ;7), C( ; ) 5 5 Điểm C( 4
 ;7) loại vì với C( 4
 ;7) thì ba điểm A, B, C thẳng hàng. 6  7 Vậy C( ; ). 5 5 8 5 5 Ta có AC  ; DC 
, kết hợp với D thuộc đoạn AC suy ra AC  8DC 5 5  16  6   4   8(  x) x     5 5  5 4  8 Gọi D( ;
x y) . Ta có AC  8DC     . Vậy D( ; ) 8  7 8  5 5 8( y)    y   5 5  5
Giả sử giá bán mỗi chiếc xe giảm x (triệu đồng), 0  x  4 .
Khi đó, số tiền lãi mỗi chiếc xe là 4  x (triệu đồng)
Theo dự kiến, số xe bán ra trong 1 năm là 600  200x (chiếc)
Tổng số tiền lãi là T x    x  x 2 ( ) 4 600 200  2
 00x  200x  2400 (triệu đồng) b  1
T(x) có hệ số của 2
x âm nên T(x) đạt GTLN tại x   (tm) 2a 2
Suy ra cửa hàng cần giảm giá mỗi chiếc xe 500.000 ngàn đồng thì sẽ thu được lợi nhuận cao nhất.
Vậy Giá bán mới là 26500000 đồng.
Từ phương trình đã cho suy ra 2 2 2 x  p y 3. Mặt khác ta thấy  với a  thì 2
a chia 3 dư 0 hoặc 1. Do đó, để 2 2 2 x
p y 3 thì ta phải có 4 2 x và 2 2
p y cùng chia hết cho 3. Suy ra x và py cùng chia hết cho 3.
Đặt x  3a, với a nguyên dương. Khi đó phương trình trở thành 2 2 2
9a  p y  18a 12 p (1) . Do 2 2 2
9a , p y , 18a đều chia hết cho 9 nên 12 p 9  p 3  p  3 . Suy ra, (1) trở thành 2 2 2 2
a  y  2a  4  (a 1)  y  5 Do 2 (a 1)  0 suy ra 2
y  5 . Do y nguyên dương nên y 1, 
2 . Bằng cách thử trực tiếp ta
được các cặp (a, y) là (2,2), (3,1). Vậy có 2 bộ (x, y, p) thỏ mãn là (6, 2,3), (9,1,3). 1 1 1 1 1 4 1 4 x  y
Ta có xy  yz  zx    .       4 z x y Mặt khác x y x  y z x  y z x  y Đặ   t t 4 z . 2 2 2 x  y 2(x  y) 4z (x  y) 2(x  y) 4z
Biến đổi biểu thức đã cho ta được P       2 2 z z x  y 2z z x  y 2 Khi đó, t 4 P 
 2t  , t  4 . 2 t 2 2 2 t 4 t 9t 4 t
2t  9t  4  4 4 t
(t  4)(2t 1) 4 t P   2t            1 2 t 2 4 t 4 4 t 4 4 t 4 Ta có: Vậy 4 t  2 .
1 1; P 1 khit  4. t 4 P
1 khi x  y  2 .z min 5 6
Document Outline

• de-thi-hoc-sinh-gioi-tinh-toan-10-nam-2020-2021-so-gddt-ha-tinh
• LỜI GIẢI TOÁN 10