Đề thi học sinh giỏi Toán 10 cụm trường Sơn Động 2022-2023 (có đáp án)

Đề thi học sinh giỏi Toán 10 cụm trường Sơn Động 2022-2023 theo chương trình chuẩn. Tài liệu được biên soạn dưới dạng file pdf gồm 14 trang chứa nhiều thông tin hay và bổ ích giúp bạn dễ dàng tham khảo và ôn tập đạt kết quả cao. Mời bạn đọc đón xem!

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 10

Môn: Toán 10

Thông tin:

14 trang 8 tháng trước

Tác giả:

Profile hằng phan
SỞ GIÁO DỤC& ĐÀOTẠO BẮC GIANG
CỤM THPT HUYỆN SƠN ĐỘNG
ĐỀ CHÍNH THỨC
Đề thi gồm có 06 trang
ĐỀ THI HỌC SINH GIỎI CẤP CƠ SỞ
NĂM HỌC 2022-2023
MÔN: Toán- Lớp 10
(Thời gian làm bài: 120 phút, không tính thời gian phát đề)
Họ tên thí sinh.....................................................Số báo danh:..................................
A. PHẦN CÂU HỎI TRẮC NGHIỆM: (14,0 điểm)
Câu 1: Hội khỏe Phù Đổng của trường Trần Phú, lớp
10A
có 45 học sinh , trong đó có 25 học sinh thi
điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham
gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
A. 38. B. 45. C. 20. D. 21.
Câu 2: Cho
2
:P y x
và
1
2;
2
A



. Gọi M là một điểm bất kì thuộc
P
. Khoảng cách MA bé nhất là:
A.
. B.
7
2
. C.
2
2
. D.
23
3
.
Câu 3: Cho 2 vectơ
a
và
b
tạo với nhau góc 60°. Biết
6; 3ab
. Tính
a b a b
A.
6 5 3
. B.
3 7 5
. C.
3 7 3
. D.
1
2 3 51
2
.
Câu 4: Tìm tập xác định D của hàm số:
24
35
3
x
y f x x
x
.
A.
3
; \ 3
5
D



. B.
5
; \ 3
3
D



.
C.
5
;
3
D


. D.
\3D
.
Câu 5: Tìm điều kiện của tham số
m
để hàm số
2
2
25
1
xx
y
x m x m

xác định trên
;0
.
A.
0m
. B.
1
0
m
m
. C.
1
0
m
m
. D.
1m
.
Câu 6: Cho tam giác đều
ABC
cạnh
a
. Gọi
M
,
N
là các điểm thỏa mãn
2
3
BM BC
,
1
5
AN AB
.
Gọi
I
là giao điểm của
AM
và
CN
. Tính
a
, biết diện tích của tam giác
IBC
bằng
36 3
7
.
A.
5a
. B.
3a
. C.
4a
. D.
6a
.
Câu 7: Cho hình bình hành
ABCD
. Gọi M, N là các điểm nằm trên cạnh AB và CD sao cho
1
3
AM AB
,
1
2
CN CD
. Gọi G là trọng tâm của
BMN
. Gọi I là điểm xác định bởi
BI mBC
. Xác định m để AI
đi qua G.
A.
11
6
m
. B.
6
11
m
. C.
6
5
m
. D.
18
11
m
.
Mã đề thi:
101
Câu 8: Cho hai lực
12
,FF
. Có điểm đặt tại M. Tìm cường độ lực tổng hợp của chúng biết
1
F
và
2
F
có
cùng cường độ lực là 100N, góc hợp bởi
1
F
và
2
F
là
120
.
A. 100N. B. 50N. C.
50 3
N. D.
100 3
N.
Câu 9: Gọi M là điểm cố định mà parabol
2
: 3 6 1
m
P y x mx m
luôn đi qua với mọi giá trị của
tham số m. Tính tổng khoảng cách từ M đến hai trục tọa độ.
A.
3
. B. 5. C. 7. D. 2.
Câu 10: Biết rằng
fx
là đa thức thỏa mãn:
2
2 1 3 2 5,f x f x x x x
.
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
fx
trên đoạn
4;2
. Giá trị của
34Mm
bằng
A. 147. B. 151. C. 123. D. 119.
Câu 11: Tam giác ABC có
sin 2sin
sin
2cos cos
BC
A
BC
. Kết luận nào sau đây là đúng?
A. Tam giác đều. B. Tam giác có
0
120 .A
C. Tam giác có
0
150 .A
D. Tam giác có
0
90 .A
Câu 12: Cho hệ phương trình:
22
33
3
5
9
x y z
x y z
x y z



.Số nghiệm của hệ phương trình là:
A. 1. B. 2. C. 4. D. 5.
Câu 13: Có bao nhiêu giá trị nguyên của
20;20m
để phương trình:
23
2 2 1 3 2x mx x x
có
hai nghiệm thực phân biệt?
A. 20. B. 23. C. 21. D. 22.
Câu 14: Tam giác
ABC
có đỉnh
1;2A
, trực tâm
3;0H
, trung điểm của
BC
là
6;1M
. Bán kính
đường tròn ngoại tiếp tam giác
ABC
là
A.
5
. B.
5
. C.
3
. D.
4
.
Câu 15: Trong mặt phẳng tọa độ , cho hình thang với hai đáy là và . Biết diện tích
hình thang bằng , đỉnh và trung điểm cạnh là . Đỉnh có hoành độ
dương và nằm trên đường thẳng . Tính
A. B. C. D.
Câu 16: Một chiếc ăng - ten chảo parabol có chiều cao
0,5hm
và đường kính miệng
4dm
. Mặt cắt
qua trục là một parabol dạng
2
y ax
. Biết
m
a
n
, trong đó m, n là các số nguyên dương nguyên tố cùng
nhau. Tính
mn
.
A.
31mn
. B.
31mn
. C.
7mn
. D.
7mn
.
Câu 17: Cho hai tập hợp
2;5P 
và
3;Q 
. Kết quả nào đúng?
A.
2;5PQ
. B.
\ P 3; 2 5;Q 
.
C.
3; 2 5;
Q
CP 
. D.
3;5PQ
.
Câu 18: Trong hệ tọa độ Oxy, cho 3 điểm
2;1 ; 0; 3 ; 3;1A B C
. Tìm tọa độ điểm D để ABCD là
hình bình hành.
Oxy
ABCD
AB
CD
14
1;1A
BC
1
;0
2
H



;D a b
D
:5 1 0d x y
2.ab
2 13.ab
2 35.ab
2 2.ab
2 24.ab
A.
5; 2D
. B.
5;5D
. C.
5; 4D
. D.
1; 4D 
.
Câu 19: Gọi M là giá trị lớn nhất của hàm số
y f x
22
4 2 3 2x x x x
. Tính tích các nghiệm
của phương trình
f x M
.
A.
1
. B. 0. C. 1. D. 2.
Câu 20: Cho hàm số:
2
()y f x ax bx c
với là các tham số,
0a
. Biết rằng
()fx
đồng
biến trên khoảng
2; 
, hãy tìm giá trị lớn nhất của biểu thức
2
22
6
52
a
P
a ab b

.
A.
6
5
. B.
6
29
. C.
3
4
. D.
6
13
.
Câu 21: Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số
2
24y x x m
trên
đoạn
2;1
bằng 4?
A. 2. B. 3. C. 1. D. 4.
Câu 22: Cho hệ bất phương trình
2
3 5 15
0
0
xy
xy
x
y


. Biết miền nghiệm của hệ bất phương trình là một đa
giác. Diện tích của đa giác đó gần với số nào nhất trong các số dưới đây?
A. 7. B. 5,5. C. 6,5. D. 6.
Câu 23: Cho hàm số
y f x
có đồ thị như hình vẽ:
Khi đó phương trình
2
1
2
1f x x

xác định trên tập nào sau đây?
A.
1;2
. B.
0;2
. C.
;2
. D.
2;0
.
Câu 24: Một đường thẳng cắt các cạnh DA, DC và đường chéo DB của hình bình hành ABCD lần lượt tại
các điểm E, F và M. Biết rẳng
DE mDA
,
DF nDC
,0mn
. Hãy biểu diễn
DM
qua
DB
và m, n.
A.
.mn
DM DB
mn
. B.
n
DM DB
mn
. C.
m
DM DB
mn
. D.
.mn
DM DB
mn
.
Câu 25: Cho tập hợp
2
; | 25 6 ; , A x y x y y x y
,
4 ; 3 ; 4 ; 3B
và tập
hợp
M
. Biết
\A B M
, số phần tử của tập hợp
M
là
A.
3
. B.
4
C.
2
. D.
5
.
Câu 26: Một công ty sản xuất bao bì cần sản xuất 3 loại hộp giấy X, Y, Z từ những tấm bìa giống nhau để
đựng ba loại sản phẩm khác nhau. Mỗi tấm bìa có hai cách cắt khác nhau: Cách thứ nhất cắt được 3 hộp X,
,,a b c
1 hộp Y và 6 hộp Z. Cách thứ hai cắt được 2 hộp X, 3 hộp Y và 1 hộp Z. Theo kế hoạch, số hộp mỗi loại X và
Z tối thiểu là 900 hộp; số hộp loại Y tối thiểu là 1000 hộp. Tìm phương án sao cho tổng số tấm bìa phải dùng
là ít nhất?
A. Cắt theo cách một
160
tấm, cắt theo cách hai
220
tấm.
B. Cắt theo cách một
250
tấm, cắt theo cách hai
100
tấm.
C. Cắt theo cách một
150
tấm, cắt theo cách hai
250
tấm.
D. Cắt theo cách một
100
tấm, cắt theo cách hai
300
tấm.
Câu 27: Trong mặt phẳng Oxy, cho
1;2 ; 2;5 2 ; 3;4A m B m C m
. Tìm m để A, B, C thẳng hàng.
A.
1m
. B.
2m
. C.
3m
. D.
2m 
.
Câu 28: Giá trị biểu thức
33
3
8cos 2sin cos
2cos sin
a a a
A
aa

khi
tan 2a
là:
A.
3
2
. B.
3
2
. C.
3
2
. D.
3
2
.
Câu 29: Trong mặt phẳng tọa độ
Oxy
cho ba điểm
1; 2 , 3;2 , 4; 1A B C
. Biết điểm
;E a b
di
động trên đường thẳng
AB
sao cho
23EA EB EC
đạt giá trị nhỏ nhất. Tính
22
ab
.
A.
22
1ab
. B.
22
2
3
ab
. C.
22
3
2
ab
. D.
22
2ab
.
Câu 30: Mệnh đề nào sau đây có mệnh đề đảo sai?
A. Một tứ giác là hình chữ nhật thì nó có
3
góc vuông.
B. Hai góc đối đỉnh thì bằng nhau.
C. Trong tam giác cân, hai góc ở đáy bằng nhau.
D. Một tam giác là vuông thì nó có một góc bằng tổng hai góc còn lại.
Câu 31: Biết tập hợp tất cả các giá trị của tham số m để phương trình
2
44x x x m
có 6 nghiệm
phân biệt là khoảng
;ab
. Tính
ab
.
A.
6ab
. B.
1ab
. C.
2ab
. D.
4ab
.
Câu 32: Cho parabol
22
( ): 2 3 4 3 P y x mx m m
(m là tham số) có đỉnh
I
. Gọi
,AB
là hai điểm
thuộc
Ox
sao cho
2024AB
. Khi đó
IAB
có diện tích nhỏ nhất bằng:
A.
4048
. B.
1012
. C.
506
. D.
2024
.
Câu 33: Cho
ABC
với H, O, G lần lượt là trực tâm, tâm đường tròn ngoại tiếp trọng tâm. Hệ thức nào
sau đây là đúng?
A.
3HO OG
. B.
3
2
OH OG
. C.
1
2
OG GH
. D.
23GO OH
.
Câu 34: ]Cho hai tập hợp
2 1; 2 5M m m
và
1; 7N m m
(với
m
là tham số thực) . Tổng tất
cả các giá trị của
m
để hợp của hai tập hợp
M
và
N
là một đoạn có độ dài bằng 10 là
A. 6. B. 10. C.
2
. D. 4 .
Câu 35: Cho tập hợp
0;A 
và
2
\ 4 3 0B x mx x m
. Tìm m để B có đúng hai tập con
và
BA
.
A.
3m
. B.
0m
. C.
03
4
m
m

. D.
4m
.
Câu 36: Cho tam giác
ABC
vuông tại
B
và điểm
M
trên cạnh
BC
sao cho
2 2 2
MA MB MC
đạt giá
trị nhỏ nhất. Tính tỉ số diện tích
ABM
ABC
S
S
S
.
A.
1
2
. B.
2
3
. C.
1
3
. D.
3
4
.
Câu 37: Cho hàm số
y f x
có đồ thị như hình
bên. Có bao nhiêu giá trị nguyên của tham số
m
để
phương trình
2 f x x m
có bốn nghiệm
phân biệt?
A.
3
B.
1
C.
4
. D.
2
Câu 38: Tính tổng các nghiệm của phương trình:
2
5 2 3 3x x x x
.
A. 3. B.
3
2
. C.
3
. D.
3
2
.
Câu 39: Cho parabol
2
: 2 1
m
P y x mx m
, trong đó m là tham số. Tập hợp các đỉnh của
m
P
khi
m thay đổi là một parabol
P
. Đỉnh của
P
là:
A.
17
;
24
I



. B.
1;3I
C.
13
;
24
I



D.
1;1I
Câu 40: Cho parabol
P
có phương trình
2
2y ax bx
. Có bao nhiêu bộ số
;ab
, biết
P
đi qua
điểm
1;6A
và tung độ của đỉnh là
1
4
.
A. 2 B. 1 C. 4. D. 0
B. PHẦN CÂU HỎI TỰ LUẬN( 6,0 điểm)
Câu 1 (2,5 điểm):
a) Cho hàm số
2
23y x mx m
và hàm số
23yx
. Tìm
m
để hai đồ thị đã cho cắt nhau tại hai
điểm phân biệt
A
và
B
sao cho
45AB
.
b) Giải phương trình:
3 2 3 2 6 x x x x
Câu 2 (2,5 điểm) :
a) Cho hình chữ nhật
ABCD
,
K
là hình chiếu của
B
lên
AC
.
N
là trung điểm cạnh
CD
,
M
là trung
điểm của
AK
.Chứng minh rằng:
BM
vuông góc với
MN
.
b) Cho tam giác nhọn
ABC
, gọi
,,H E K
lần lượt là chân đường cao kẻ từ các đỉnh
,,A B C
. Gọi diện
tích các tam giác
ABC
và
HEK
lần lượt là
ABC
S
và
HEK
S
. Biết rằng
3 10

ABC HEK
SS
, Tính giá trị
biểu thức:
222
sin sin sin T A B C
.
Câu 3 (1,0 điểm) : Cho ba số dương
,,abc
thoả mãn
3
4
abc
. Tìm giá trị nhỏ nhất của
3 3 3
1 1 1
3 3 3
P
a b b c c a
.
------------------ Hết--------------
Họ tên cán bộ coi thi ……………………………………… Chữ ký…………………
SỞ GIÁO DỤC& ĐÀOTẠO BẮC GIANG
CỤM THPT HUYỆN SƠN ĐỘNG
ĐỀ CHÍNH THỨC
Đề thi gồm có 06 trang
ĐỀ THI HỌC SINH GIỎI CẤP CƠ SỞ
NĂM HỌC 2022-2023
MÔN: Toán- Lớp 10
(Thời gian làm bài: 120 phút, không tính thời gian phát đề)
Họ tên thí sinh.....................................................Số báo danh:..................................
A. PHẦN CÂU HỎI TRẮC NGHIỆM: (14,0 điểm)
Câu 1: Một đường thẳng cắt các cạnh DA, DC và đường chéo DB của hình bình hành ABCD lần lượt tại
các điểm E, F và M. Biết rẳng
DE mDA
,
DF nDC
,0mn
. Hãy biểu diễn
DM
qua
DB
và m, n.
A.
.mn
DM DB
mn
. B.
n
DM DB
mn
.
C.
m
DM DB
mn
. D.
.mn
DM DB
mn
.
Câu 2: Cho hình bình hành
ABCD
. Gọi M, N là các điểm nằm trên cạnh AB và CD sao cho
1
3
AM AB
,
1
2
CN CD
. Gọi G là trọng tâm của
BMN
. Gọi I là điểm xác định bởi
BI mBC
. Xác định m để AI
đi qua G.
A.
6
11
m
. B.
11
6
m
. C.
6
5
m
. D.
18
11
m
.
Câu 3: Cho 2 vectơ
a
và
b
tạo với nhau góc 60°. Biết
6; 3ab
. Tính
a b a b
A.
3 7 3
. B.
3 7 5
. C.
6 5 3
. D.
1
2 3 51
2
.
Câu 4: Trong mặt phẳng Oxy, cho
1;2 ; 2;5 2 ; 3;4A m B m C m
. Tìm m để A, B, C thẳng hàng.
A.
1m
. B.
2m
. C.
2m 
. D.
3m
.
Câu 5: Gọi M là giá trị lớn nhất của hàm số
y f x
22
4 2 3 2x x x x
. Tính tích các nghiệm
của phương trình
f x M
.
A.
1
. B. 1. C. 0. D. 2.
Câu 6: Tam giác
ABC
có đỉnh
1;2A
, trực tâm
3;0H
, trung điểm của
BC
là
6;1M
. Bán kính
đường tròn ngoại tiếp tam giác
ABC
là
A.
5
. B.
5
. C.
3
. D.
4
.
Mã đề thi:
102
Câu 7: Cho tam giác đều
ABC
cạnh
a
. Gọi
M
,
N
là các điểm thỏa mãn
2
3
BM BC
,
1
5
AN AB
.
Gọi
I
là giao điểm của
AM
và
CN
. Tính
a
, biết diện tích của tam giác
IBC
bằng
36 3
7
.
A.
5a
. B.
3a
. C.
4a
. D.
6a
.
Câu 8: Cho hàm số
y f x
có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số
m
để
phương trình
2 f x x m
có bốn nghiệm phân biệt?
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 9: Cho hai lực
12
,FF
. Có điểm đặt tại M. Tìm cường độ lực tổng hợp của chúng biết
1
F
và
2
F
có
cùng cường độ lực là 100N, góc hợp bởi
1
F
và
2
F
là
120
.
A. 100N. B. 50N. C.
50 3
N. D.
100 3
N.
Câu 10: Cho hàm số
y f x
có đồ thị như hình vẽ:
Khi đó phương trình
2
1
2
1f x x

xác định trên tập nào sau đây?
A.
;2
. B.
2;0
. C.
0;2
. D.
1;2
.
Câu 11: Trong mặt phẳng tọa độ
Oxy
cho ba điểm
1; 2 , 3;2 , 4; 1A B C
. Biết điểm
;E a b
di
động trên đường thẳng
AB
sao cho
23EA EB EC
đạt giá trị nhỏ nhất. Tính
22
ab
.
A.
22
1ab
. B.
22
2ab
. C.
22
2
3
ab
. D.
22
3
2
ab
.
Câu 12: Cho hệ bất phương trình
2
3 5 15
0
0
xy
xy
x
y


. Biết miền nghiệm của hệ bất phương trình là một đa
giác. Diện tích của đa giác đó gần với số nào nhất trong các số dưới đây?
A. 6. B. 6,5. C. 7. D. 5,5.
Câu 13: Cho hệ phương trình:
22
33
3
5
9
x y z
x y z
x y z



.Số nghiệm của hệ phương trình là:
A. 1. B. 2. C. 4. D. 5.
Câu 14: Có bao nhiêu giá trị nguyên của
20;20m
để phương trình:
23
2 2 1 3 2x mx x x
có
hai nghiệm thực phân biệt?
A. 20. B. 23. C. 21. D. 22.
Câu 15: Cho
2
:P y x
và
1
2;
2
A



. Gọi M là một điểm bất kì thuộc
P
. Khoảng cách MA bé nhất
là:
A.
7
2
. B.
23
3
. C.
5
2
. D.
2
2
.
Câu 16: Cho parabol
2
: 2 1
m
P y x mx m
, trong đó m là tham số. Tập hợp các đỉnh của
m
P
khi
m thay đổi là một parabol
P
. Đỉnh của
P
là:
A.
17
;
24
I



. B.
1;1I
. C.
1;3I
. D.
13
;
24
I



.
Câu 17: Trong mặt phẳng tọa độ , cho hình thang với hai đáy là và . Biết diện tích
hình thang bằng , đỉnh và trung điểm cạnh là . Đỉnh có hoành độ
dương và nằm trên đường thẳng . Tính
A. B. C. D.
Câu 18: Tìm tập xác định D của hàm số:
24
35
3
x
y f x x
x
.
A.
5
; \ 3
3
D



. B.
\3D
.
C.
3
; \ 3
5
D



. D.
5
;
3
D



.
Câu 19: Trong hệ tọa độ Oxy, cho 3 điểm
2;1 ; 0; 3 ; 3;1A B C
. Tìm tọa độ điểm D để ABCD là
hình bình hành.
A.
5; 2D
. B.
5;5D
. C.
5; 4D
. D.
1; 4D 
.
Câu 20: Tìm điều kiện của tham số
m
để hàm số
2
2
25
1
xx
y
x m x m

xác định trên
;0
.
Oxy
ABCD
AB
CD
14
1;1A
BC
1
;0
2
H



;D a b
D
:5 1 0d x y
2.ab
2 24.ab
2 2.ab
2 35.ab
2 13.ab
A.
0m
. B.
1m
. C.
1
0
m
m
. D.
1
0
m
m
.
Câu 21: Cho
ABC
với H, O, G lần lượt là trực tâm, tâm đường tròn ngoại tiếp trọng tâm. Hệ thức nào
sau đây là đúng?
A.
3
2
OH OG
. B.
3HO OG
. C.
1
2
OG GH
. D.
23GO OH
.
Câu 22: Một công ty sản xuất bao bì cần sản xuất 3 loại hộp giấy X, Y, Z từ những tấm bìa giống nhau để
đựng ba loại sản phẩm khác nhau. Mỗi tấm bìa có hai cách cắt khác nhau: Cách thứ nhất cắt được 3 hộp X,
1 hộp Y và 6 hộp Z. Cách thứ hai cắt được 2 hộp X, 3 hộp Y và 1 hộp Z. Theo kế hoạch, số hộp mỗi loại X và
Z tối thiểu là 900 hộp; số hộp loại Y tối thiểu là 1000 hộp. Tìm phương án sao cho tổng số tấm bìa phải dùng
là ít nhất?
A. Cắt theo cách một
250
tấm, cắt theo cách hai
100
tấm.
B. Cắt theo cách một
160
tấm, cắt theo cách hai
220
tấm.
C. Cắt theo cách một
100
tấm, cắt theo cách hai
300
tấm.
D. Cắt theo cách một
150
tấm, cắt theo cách hai
250
tấm.
Câu 23: Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số
2
24y x x m
trên
đoạn
2;1
bằng 4?
A. 1. B. 4. C. 2. D. 3.
Câu 24: Cho tập hợp
2
; | 25 6 ; , A x y x y y x y
,
4 ; 3 ; 4 ; 3B
và tập
hợp
M
. Biết
\A B M
, số phần tử của tập hợp
M
là
A.
3
. B.
4
. C.
2
. D.
5
.
Câu 25: Hội khỏe Phù Đổng của trường Trần Phú, lớp
10A
có 45 học sinh , trong đó có 25 học sinh thi
điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham
gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
A. 38. B. 20. C. 21. D. 45.
Câu 26: ]Cho hai tập hợp
2 1; 2 5M m m
và
1; 7N m m
(với
m
là tham số thực) . Tổng tất
cả các giá trị của
m
để hợp của hai tập hợp
M
và
N
là một đoạn có độ dài bằng 10 là
A.
2
. B. 6. C. 4 . D. 10.
Câu 27: Một chiếc ăng - ten chảo parabol có chiều cao
0,5hm
và đường kính miệng
4dm
. Mặt cắt
qua trục là một parabol dạng
2
y ax
. Biết
m
a
n
, trong đó m, n là các số nguyên dương nguyên tố cùng
nhau. Tính
mn
.
A.
31mn
. B.
31mn
. C.
7mn
. D.
7mn
.
Câu 28: Cho hai tập hợp
2;5P 
và
3;Q 
. Kết quả nào đúng?
A.
2;5PQ
. B.
\ P 3; 2 5;Q 
.
C.
3; 2 5;
Q
CP 
. D.
3;5PQ
.
Câu 29: Giá trị biểu thức
33
3
8cos 2sin cos
2cos sin
a a a
A
aa

khi
tan 2a
là:
A.
3
2
. B.
3
2
. C.
3
2
. D.
3
2
.
Câu 30: Tam giác ABC có
sin 2sin
sin
2cos cos
BC
A
BC
. Kết luận nào sau đây là đúng?
A. Tam giác đều. B. Tam giác có
0
120 .A
C. Tam giác có
0
150 .A
D. Tam giác có
0
90 .A
Câu 31: Mệnh đề nào sau đây có mệnh đề đảo sai?
A. Một tứ giác là hình chữ nhật thì nó có
3
góc vuông.
B. Hai góc đối đỉnh thì bằng nhau.
C. Trong tam giác cân, hai góc ở đáy bằng nhau.
D. Một tam giác là vuông thì nó có một góc bằng tổng hai góc còn lại.
Câu 32: Biết tập hợp tất cả các giá trị của tham số m để phương trình
2
44x x x m
có 6 nghiệm
phân biệt là khoảng
;ab
. Tính
ab
.
A.
6ab
. B.
4ab
. C.
1ab
. D.
2ab
.
Câu 33: Cho parabol
22
( ): 2 3 4 3 P y x mx m m
(m là tham số) có đỉnh
I
. Gọi
,AB
là hai điểm
thuộc
Ox
sao cho
2024AB
. Khi đó
IAB
có diện tích nhỏ nhất bằng:
A.
4048
. B.
1012
. C.
506
. D.
2024
.
Câu 34: Gọi M là điểm cố định mà parabol
2
: 3 6 1
m
P y x mx m
luôn đi qua với mọi giá trị của
tham số m. Tính tổng khoảng cách từ M đến hai trục tọa độ.
A. 7. B.
3
. C. 2. D. 5.
Câu 35: Biết rằng
fx
là đa thức thỏa mãn:
2
2 1 3 2 5,f x f x x x x
.
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
fx
trên đoạn
4;2
. Giá trị của
34Mm
bằng
A. 119. B. 147. C. 123. D. 151.
Câu 36: Cho tập hợp
0;A 
và
2
\ 4 3 0B x mx x m
. Tìm m để B có đúng hai tập con
và
BA
.
A.
3m
. B.
0m
. C.
03
4
m
m

. D.
4m
.
Câu 37: Cho tam giác
ABC
vuông tại
B
và điểm
M
trên cạnh
BC
sao cho
2 2 2
MA MB MC
đạt giá
trị nhỏ nhất. Tính tỉ số diện tích
ABM
ABC
S
S
S
.
A.
1
2
. B.
2
3
. C.
3
4
. D.
1
3
.
Câu 38: Cho hàm số:
2
()y f x ax bx c
với là các tham số,
0a
. Biết rằng
()fx
đồng
biến trên khoảng
2; 
, hãy tìm giá trị lớn nhất của biểu thức
2
22
6
52
a
P
a ab b

.
A.
6
5
. B.
6
29
. C.
3
4
. D.
6
13
.
Câu 39: Cho parabol
P
có phương trình
2
2y ax bx
. Có bao nhiêu bộ số
;ab
, biết
P
đi qua
điểm
1;6A
và tung độ của đỉnh là
1
4
.
A.4. B. 2. C. 1. D. 0.
Câu 40: Tính tổng các nghiệm của phương trình:
2
5 2 3 3x x x x
.
,,a b c
A. 3. B.
3
. C.
3
2
. D.
3
2
.
B. PHẦN CÂU HỎI TỰ LUẬN( 6,0 điểm)
Câu 1 (2,5 điểm):
a) Cho hàm số
2
23y x mx m
và hàm số
23yx
. Tìm
m
để hai đồ thị đã cho cắt nhau tại hai
điểm phân biệt
A
và
B
sao cho
45AB
.
b) Giải phương trình:
3 2 3 2 6 x x x x
Câu 2 (2,5 điểm) :
a) Cho hình chữ nhật
ABCD
,
K
là hình chiếu của
B
lên
AC
.
N
là trung điểm cạnh
CD
,
M
là trung
điểm của
AK
.Chứng minh rằng:
BM
vuông góc với
MN
.
b) Cho tam giác nhọn
ABC
, gọi
,,H E K
lần lượt là chân đường cao kẻ từ các đỉnh
,,A B C
. Gọi diện
tích các tam giác
ABC
và
HEK
lần lượt là
ABC
S
và
HEK
S
. Biết rằng
3 10

ABC HEK
SS
, Tính giá trị
biểu thức:
222
sin sin sin T A B C
.
Câu 3 (1,0 điểm) : Cho ba số dương
,,abc
thoả mãn
3
4
abc
. Tìm giá trị nhỏ nhất của
3 3 3
1 1 1
3 3 3
P
a b b c c a
.
------------------ Hết--------------
Họ tên cán bộ coi thi ……………………………………… Chữ ký…………………
SỞ GIÁO DỤC& ĐÀOTẠO BẮC GIANG
CỤM THPT HUYỆN SƠN ĐỘNG
HD CHẤM ĐỀ THI HỌC SINH GIỎI CẤP CƠ SỞ
NĂM HỌC 2022-2023
MÔN: Toán- Lớp 10
(Thời gian làm bài: 120 phút, không tính thời gian phát đề)
I. TRẮC NGHIỆM
MĐ\CÂU
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
101
D
A
C
B
A
D
B
A
C
C
D
D
D
A
A
C
C
B
A
B
102
A
A
A
B
A
A
D
D
A
B
D
A
D
D
C
D
D
A
B
A
MĐ\CÂU
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
101
A
D
D
A
B
D
B
B
C
B
B
B
C
D
D
C
A
C
C
A
102
C
C
C
B
C
C
C
C
B
D
B
C
B
A
C
D
D
B
B
B
II. TỰ LUẬN
Câu
Nội dung
Điểm
Câu
1
a) Cho hàm số
2
23y x mx m
và hàm số
23yx
. Tìm
m
để hai đồ thị đã
cho cắt nhau tại hai điểm phân biệt
A
và
B
sao cho
45AB
.
b) Giải phương trình:
3 2 3 2 6 x x x x
2,5
điểm
a) Phương trình hoành độ giao điểm của hai đồ thị là:
2
2 3 2 3x mx m x
2
2 1 3 3 0x m x m
(*)
0,5
Hai đồ thị cắt nhau tại hai điểm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt
'0
1
.
4
m
m
Theo Vi-et ta có:
12
12
21
. 3 1
x x m
x x m
0,25
Gọi
1 1 2 2
; 2 3 ; ; 2 3A x x B x x
với
12
;xx
là nghiệm phương trình (*)
Ta có:
2 2 2
1 2 1 2 1 2
5 5 20 . 20 1 60 1AB x x x x x x m m
0,25
22
4 5 20 1 60 1 4 5 1 2 1 4 0AB m m m m
0; 5.mm
So sánh với điều kiện ta được
0; 5. mm
0,5
b)
3 2 3 2 6 x x x x
2x
3 2 6 2 3 x x x x
8x 24
2 x 3
3 x 2 x 6
x 3 0
x3
4
1
3 x 2 x 6 4(*)
3 x 2 x 6


0.5
22
(*) 9 x 2 6 x 4x 12 x 6 16 3 x 4x 12 14 5x
2
2
2
14
x
5
14
14 5x 0
x
11 3 5
5
x
9 x 4x 12 14 5x
2
16x 176x 304 0
11 3 5
x
2



11 3 5
x
2

( thoả mãn điều kiện
2x
).
Vậy phương trình có tập nghiệm
11 3 5
S 3;
2





.
0.5
Câu
2
a) Cho hình chữ nhật
ABCD
,
K
là hình chiếu của
B
lên
AC
.
N
là trung điểm cạnh
CD
,
M
là trung điểm của
AK
.Chứng minh rằng:
BM
vuông góc với
MN
.
1,0
điểm
Gọi
P
là trung điểm
BK
.
Khi đó :
MP
là đường trung bình tam giác
BKA
,
suy ra
//
1
2
MP AB
MP AB
, hay
MP BC
MP CN
.
0,5
Khi đó:
. BM MN BP PM MC CN
. . . BP CN PM MC PM CN
. . . BPCN CN MC PM CN
CN BP MC PM
.0CN BC
.
Vậy
BM
vuông góc với
MN
.
0,5
b) Cho tam giác nhọn
ABC
, gọi
,,H E K
lần lượt là chân đường cao kẻ từ các đỉnh
,,A B C
. Gọi diện tích các tam giác
ABC
và
HEK
lần lượt là
ABC
S
và
HEK
S
. Biết rằng
3 10

ABC HEK
SS
, Tính giá trị biểu thức:
222
sin sin sin T A B C
.
1,5
Đặt
ABC
SS
thì từ giả thiết suy ra
7
10
7
10
EAK KBH HCE
HCE
EAK KBH
S S S S
S
SS
S S S
0,25
2
1
. sin
2
. cos .cos cos
1
. sin
2
EAK
AE AK A
S
AE AK
A A A
S AB AC
AB AC A
2
1
. .sin
2
. cos .cos cos
1
. sin
2
KBH
BK BH B
S
BK BH
B B B
S BC AB
AB BC B
2
1
. .sin
2
. cos .cos cos
1
. sin
2
HCE
CH CE C
S
CH CE
C C C
S AC BC
AC BC C
0,5
222
77
cos cos cos
10 10
HCE
EAK KBH
S
SS
A B C
S S S
0,25
2 2 2 2 2 2
7 23
sin sin sin 3 cos cos cos 3
10 10
T A B C A B C
0,5
Câu
3
Cho ba số dương thoả mãn
3
4
abc
. Tìm giá trị nhỏ nhất của
1 điểm
3 3 3
1 1 1
3 3 3
P
a b b c c a
.
Áp dụng bất đẳng thức Cô si ta có:
3
3
1 1 1 3 1 1 1 9
3 . 9




x y z xyz
x y z x y z x y z
xyz
Khi đó :
3 3 3 3 3 3
1 1 1 9
3 3 3 3 3 3
P
a b b c c a a b b c c a
0,25
Ta có:
3
3 1 1 1
3 3 2
33
ab
a b a b
3
3 1 1 1
3 3 2
33
bc
b c b c
3
3 1 1 1
3 3 2
33
ca
c a c a
0,25
Suy ra:
3 3 3
1
3 3 3 4 4 4 6 3
3
a b b c c a a b c
0,25
Do đó :
3P
. Dấu bằng xảy ra
3
1
4
4
3 3 3
abc
abc
a b b c c a
.
0,25
Lưu ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa.
| 1/14
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC& ĐÀOTẠO BẮC GIANG
ĐỀ THI HỌC SINH GIỎI CẤP CƠ SỞ
CỤM THPT HUYỆN SƠN ĐỘNG NĂM HỌC 2022-2023 MÔN: Toán- Lớp 10 ĐỀ CHÍNH THỨC
(Thời gian làm bài: 120 phút, không tính thời gian phát đề) Đề thi gồm có 06 trang Mã đề thi:
Họ tên thí sinh.....................................................Số báo danh:......... 101 .........................
A. PHẦN CÂU HỎI TRẮC NGHIỆM: (14,0 điểm)
Câu 1: Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh , trong đó có 25 học sinh thi
điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham
gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu? A. 38. B. 45. C. 20. D. 21.  1 
Câu 2: Cho  P 2
: y x và A 2;  
 . Gọi M là một điểm bất kì thuộc  P . Khoảng cách MA bé nhất là:  2  5 7 2 2 3 A. . B. . C. . D. . 2 2 2 3
Câu 3: Cho 2 vectơ a và b tạo với nhau góc 60°. Biết a  6; b  3 . Tính a b a b 1 A. 6 5  
3 . B. 3 7  5 .
C. 3 7  3 . D. 2 3  51. 2 x
Câu 4: Tìm tập xác định D của hàm số: y f x 2 4   3x 5 . x  3 3  5  A. D  ;  \     3 . B. D  ;  \     3 . 5  3  5  C. D  ;    . D. D  \   3 . 3  2 2x x  5
Câu 5: Tìm điều kiện của tham số m để hàm số y  ;  0 . 2
x  m   1 x  xác định trên   mm  1 m  1 A. m  0 . B.  . C.  . D. m  1. m  0 m  0 1
Câu 6: Cho tam giác đều ABC cạnh a . Gọi M , N là các điểm thỏa mãn 2 BM BC , AN AB . 3 5 36 3
Gọi I là giao điểm của AM và CN . Tính a , biết diện tích của tam giác IBC bằng . 7 A. a  5 . B. a  3. C. a  4 . D. a  6 . 1
Câu 7: Cho hình bình hành ABCD . Gọi M, N là các điểm nằm trên cạnh AB và CD sao cho AM AB 3 1 , CN
CD . Gọi G là trọng tâm của B
MN . Gọi I là điểm xác định bởi BI mBC . Xác định m để AI 2 đi qua G. 11 6 6 18 A. m  . B. m  . C. m  . D. m  . 6 11 5 11
Câu 8: Cho hai lực F , F . Có điểm đặt tại M. Tìm cường độ lực tổng hợp của chúng biết F và F có 1 2 1 2
cùng cường độ lực là 100N, góc hợp bởi F và F là 120 . 1 2 A. 100N. B. 50N. C. 50 3 N. D. 100 3 N.
Câu 9: Gọi M là điểm cố định mà parabol  P  2
: y x  3mx  6m 1 luôn đi qua với mọi giá trị của m
tham số m. Tính tổng khoảng cách từ M đến hai trục tọa độ. A. 3 . B. 5. C. 7. D. 2.
Câu 10: Biết rằng f x là đa thức thỏa mãn: f x  f   x 2 2 1
 3x  2x  5, x   .
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x trên đoạn  4  ;2. Giá trị của
3M  4m bằng A. 147. B. 151. C. 123. D. 119. sin B  2sin C
Câu 11: Tam giác ABC có sin A
. Kết luận nào sau đây là đúng? 2cos B  cos C A. Tam giác đều. B. Tam giác có 0 A  120 . C. Tam giác có 0 A  150 . D. Tam giác có 0 A  90 .
x y  3z
Câu 12: Cho hệ phương trình: 2 2
x y  5z .Số nghiệm của hệ phương trình là:  3 3
x y  9zA. 1. B. 2. C. 4. D. 5.
Câu 13: Có bao nhiêu giá trị nguyên của m  2
 0;20 để phương trình: 2 3
2x  2mx 1  3 2x x có
hai nghiệm thực phân biệt? A. 20. B. 23. C. 21. D. 22.
Câu 14: Tam giác ABC có đỉnh A 1
 ;2 , trực tâm H 3;0 , trung điểm của BC là M 6;  1 . Bán kính
đường tròn ngoại tiếp tam giác ABC là A. 5 . B. 5 . C. 3 . D. 4 .
Câu 15: Trong mặt phẳng tọa độ Oxy , cho hình thang ABCD với hai đáy là AB và CD . Biết diện tích  1 
hình thang bằng 14 , đỉnh A1; 
1 và trung điểm cạnh BC là H  ; 0 . Đỉnh D  ;
a b có hoành độ    2 
dương và D nằm trên đường thẳng d : 5x y 1  0. Tính a  2 . b
A. a  2b 13.
B. a  2b  35.
C. a  2b  2.
D. a  2b  24.
Câu 16: Một chiếc ăng - ten chảo parabol có chiều cao h  0,5m và đường kính miệng d  4m . Mặt cắt
qua trục là một parabol dạng 2
y ax . Biết m a
, trong đó m, n là các số nguyên dương nguyên tố cùng n
nhau. Tính m n .
A. m n  31  .
B. m n  31.
C. m n  7  .
D. m n  7 .
Câu 17: Cho hai tập hợp P   2
 ;5 và Q   3;
  . Kết quả nào đúng?
A. P Q  2;5 .
B. Q \ P   3  ; 2  5; .
C. C P   3  ; 2  5; .
D. P Q   3  ;5 . Q
Câu 18: Trong hệ tọa độ Oxy, cho 3 điểm A2  ;1 ; B 0; 3  ;C 3 
;1 . Tìm tọa độ điểm D để ABCD là hình bình hành. A. D 5; 2   .
B. D 5;5 . C. D 5; 4   . D. D  1  ; 4   .
Câu 19: Gọi M là giá trị lớn nhất của hàm số y f x 2 2
 4 x  2x  3  2x x . Tính tích các nghiệm
của phương trình f x  M . A. 1  . B. 0. C. 1. D. 2.
Câu 20: Cho hàm số: 2
y f (x)  ax bx c với a, ,
b c là các tham số, a  0 . Biết rằng f (x) đồng 2 6a biến trên khoảng  2;
  , hãy tìm giá trị lớn nhất của biểu thức P  2 2 5a  2ab  . b 6 6 3 6 A. . B. . C. . D. . 5 29 4 13
Câu 21: Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số 2
y x  2x m  4 trên đoạn 2;  1 bằng 4? A. 2. B. 3. C. 1. D. 4. x y  2 3
x  5y 15
Câu 22: Cho hệ bất phương trình 
. Biết miền nghiệm của hệ bất phương trình là một đa x  0  y  0
giác. Diện tích của đa giác đó gần với số nào nhất trong các số dưới đây? A. 7. B. 5,5. C. 6,5. D. 6.
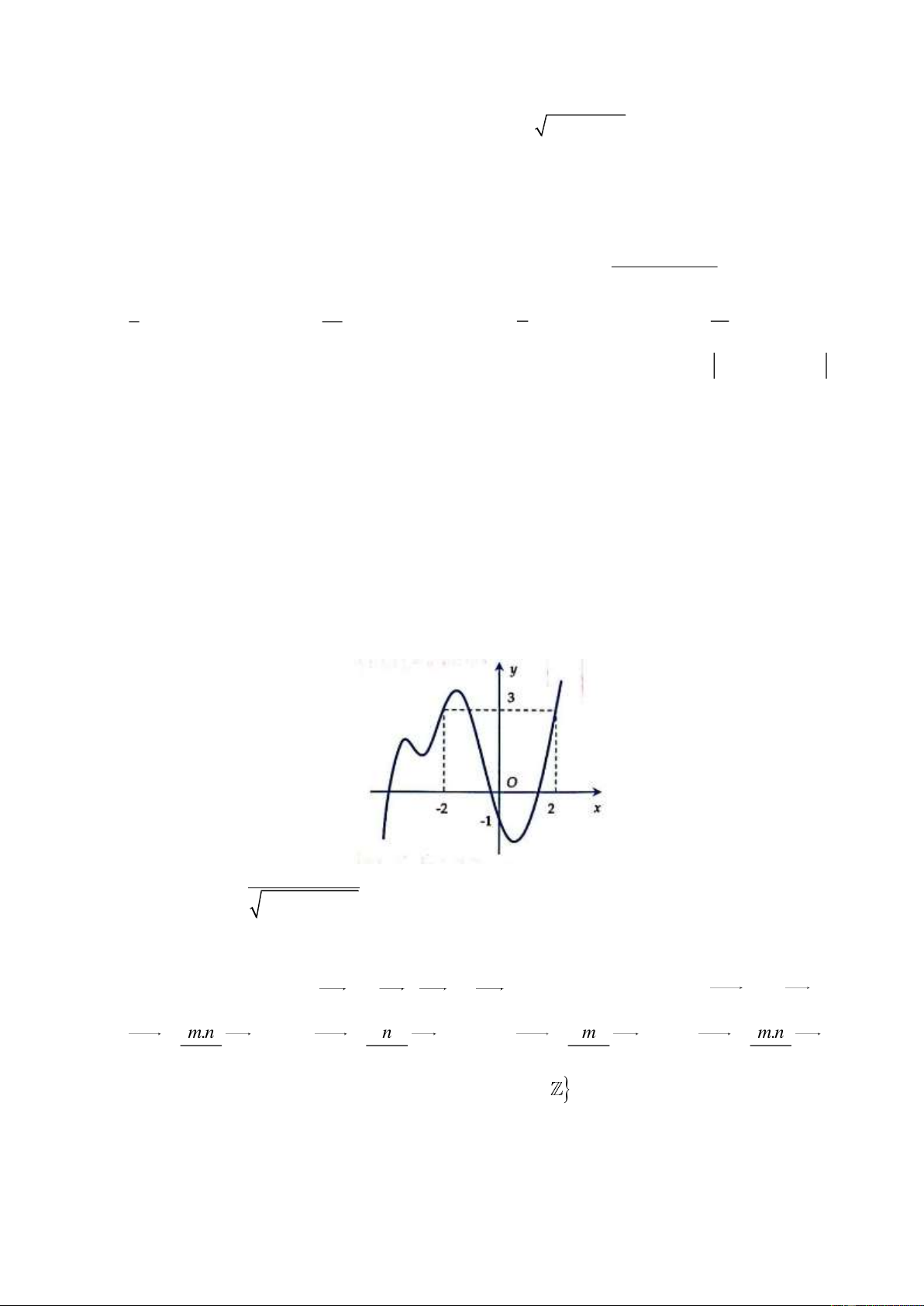
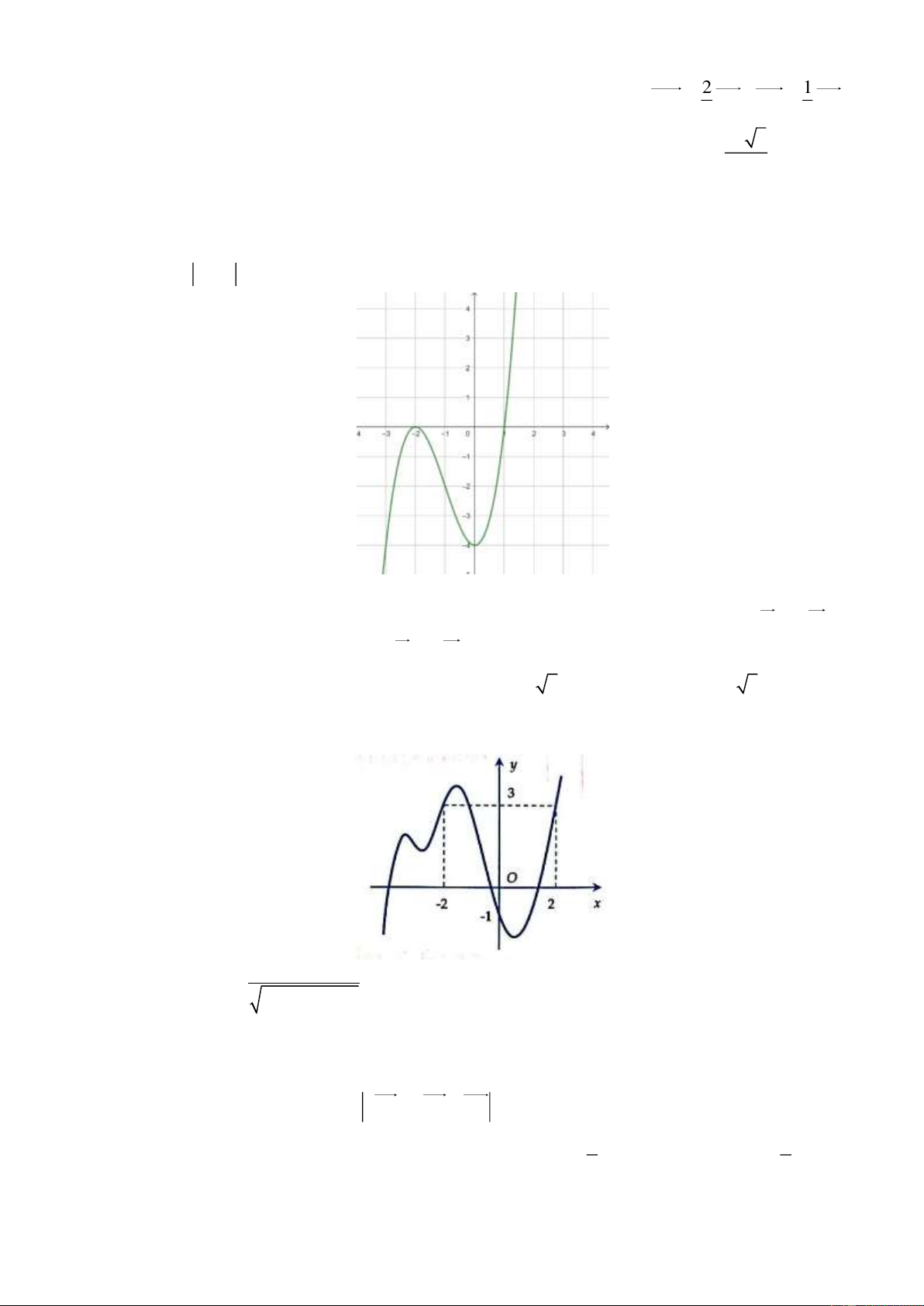
Câu 23: Cho hàm số y f x có đồ thị như hình vẽ: Khi đó phương trình 1
 xác định trên tập nào sau đây? f x 2 2  x 1 A.  1  ;2. B. 0; 2 . C.  ;  2   . D.  2  ;0 .
Câu 24: Một đường thẳng cắt các cạnh DA, DC và đường chéo DB của hình bình hành ABCD lần lượt tại
các điểm E, F và M. Biết rẳng DE mDA , DF nDC  ,
m n  0 . Hãy biểu diễn DM qua DB và m, n. . m n n m . m n A. DM
DB . B. DM DB . C. DM
DB . D. DM DB . m n m n m n m n
Câu 25: Cho tập hợp A    x y 2 ;
| x  25  y y  6; x , y   , B    4 ; 3 ;  4  ; 3 và tập
hợp M . Biết A \ B M , số phần tử của tập hợp M là A. 3 . B. 4 C. 2 . D. 5 .
Câu 26: Một công ty sản xuất bao bì cần sản xuất 3 loại hộp giấy X, Y, Z từ những tấm bìa giống nhau để
đựng ba loại sản phẩm khác nhau. Mỗi tấm bìa có hai cách cắt khác nhau: Cách thứ nhất cắt được 3 hộp X,
1 hộp Y và 6 hộp Z. Cách thứ hai cắt được 2 hộp X, 3 hộp Y và 1 hộp Z. Theo kế hoạch, số hộp mỗi loại X và
Z tối thiểu là 900 hộp; số hộp loại Y tối thiểu là 1000 hộp. Tìm phương án sao cho tổng số tấm bìa phải dùng là ít nhất?
A. Cắt theo cách một 160 tấm, cắt theo cách hai 220 tấm.
B. Cắt theo cách một 250 tấm, cắt theo cách hai 100 tấm.
C. Cắt theo cách một 150 tấm, cắt theo cách hai 250 tấm.
D. Cắt theo cách một 100 tấm, cắt theo cách hai 300 tấm.
Câu 27: Trong mặt phẳng Oxy, cho Am 1; 2; B 2;5  2m;C m  3; 4 . Tìm m để A, B, C thẳng hàng. A. m  1. B. m  2 .
C. m  3 . D. m  2  . 3 3
8cos a  2sin a  cos a
Câu 28: Giá trị biểu thức A  khi tan a  2 là: 3
2 cos a  sin a 3 3 3 3 A. . B.  . C.  . D. . 2 2 2 2
Câu 29: Trong mặt phẳng tọa độ Oxy cho ba điểm A 1  ; 2
 , B3;2,C 4; 
1 . Biết điểm E a;b di
động trên đường thẳng AB sao cho 2EA  3EB EC đạt giá trị nhỏ nhất. Tính 2 2 a b . 2 3 A. 2 2 a b  1. B. 2 2 a b  . C. 2 2 a b  . D. 2 2 a b  2 . 3 2
Câu 30: Mệnh đề nào sau đây có mệnh đề đảo sai?
A. Một tứ giác là hình chữ nhật thì nó có 3 góc vuông.
B. Hai góc đối đỉnh thì bằng nhau.
C. Trong tam giác cân, hai góc ở đáy bằng nhau.
D. Một tam giác là vuông thì nó có một góc bằng tổng hai góc còn lại.
Câu 31: Biết tập hợp tất cả các giá trị của tham số m để phương trình 2 x
x  4 x  4  m có 6 nghiệm
phân biệt là khoảng a;b . Tính a b .
A. a b  6.
B. a b  1.
C. a b  2 .
D. a b  4 . Câu 32: Cho parabol 2 2
(P) : y  x  2mx  3m  4m  3 (m là tham số) có đỉnh I . Gọi , A B là hai điểm
thuộc Ox sao cho AB  2024 . Khi đó IAB có diện tích nhỏ nhất bằng: A. 4048 . B. 1012 . C. 506 . D. 2024 . Câu 33: Cho ABC
với H, O, G lần lượt là trực tâm, tâm đường tròn ngoại tiếp trọng tâm. Hệ thức nào sau đây là đúng? 3 1
A. HO  3OG . B. OH OG . C. OG GH . D. 2GO  3  OH . 2 2
Câu 34: ]Cho hai tập hợp M  2m 1; 2m  5 và N  m 1; m  7 (với m là tham số thực) . Tổng tất
cả các giá trị của m để hợp của hai tập hợp M và N là một đoạn có độ dài bằng 10 là A. 6. B. 10. C. 2 . D. 4 .
Câu 35: Cho tập hợp A  0;  và B   2 x
\ mx  4x m  3  
0 . Tìm m để B có đúng hai tập con và B A . 0  m  3 A. m  3 . B. m  0 . C.  . D. m  4 . m  4
Câu 36: Cho tam giác ABC vuông tại B và điểm M trên cạnh BC sao cho 2 2 2
MA MB MC đạt giá S
trị nhỏ nhất. Tính tỉ số diện tích ABM S   . S ABC  1 2 1 3 A. . B. . C. . D. . 2 3 3 4
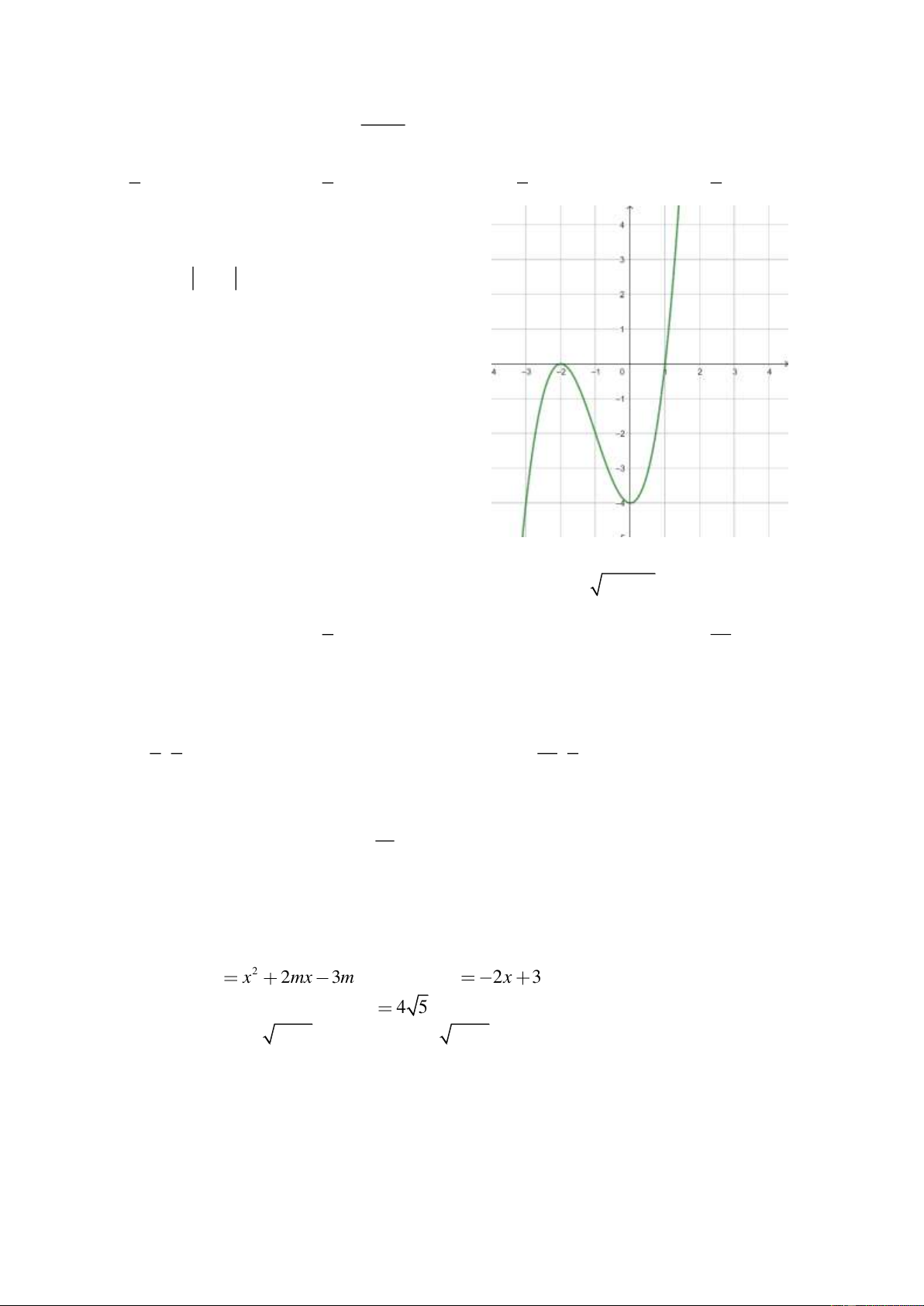
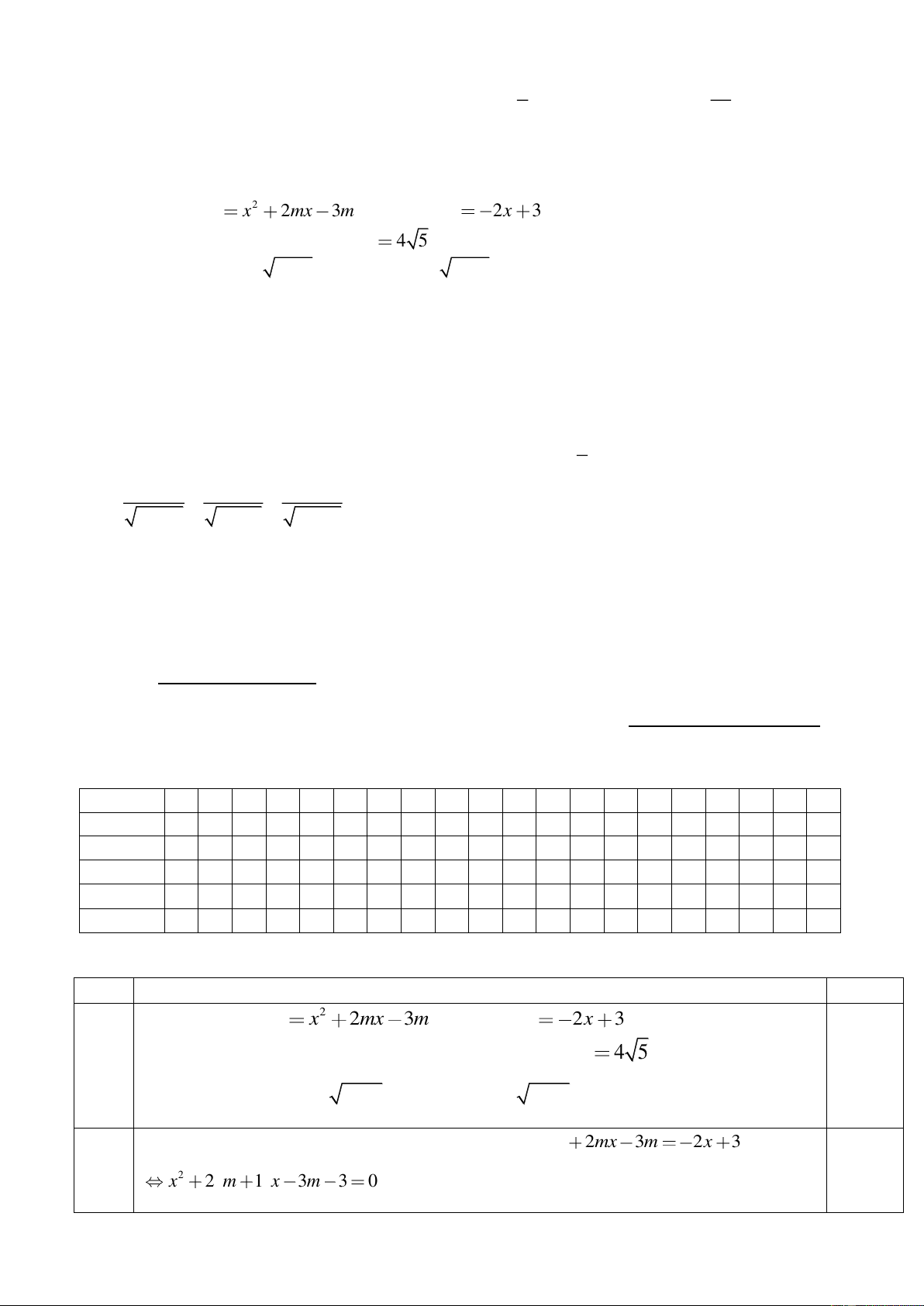
Câu 37: Cho hàm số y f x có đồ thị như hình
bên. Có bao nhiêu giá trị nguyên của tham số m để
phương trình f x  x m  2 có bốn nghiệm phân biệt? A. 3 B. 1 C. 4 . D. 2
Câu 38: Tính tổng các nghiệm của phương trình:  x    x 2 5 2
 3 x  3x . 3 3  A. 3. B. . C. 3  . D. . 2 2
Câu 39: Cho parabol  P  2
: y  x  2mx 1 m , trong đó m là tham số. Tập hợp các đỉnh của  P khi m m
m thay đổi là một parabol  P . Đỉnh của  P là:  1 7   1  3  A. I ;   . B. I 1;3 C. I ;   D. I  1   ;1  2 4   2 4 
Câu 40: Cho parabol  P có phương trình 2
y ax bx  2 . Có bao nhiêu bộ số a;b , biết  P đi qua 
điểm A1;6 và tung độ của đỉnh là 1 . 4 A. 2 B. 1 C. 4. D. 0
B. PHẦN CÂU HỎI TỰ LUẬN( 6,0 điểm) Câu 1 (2,5 điểm): a) Cho hàm số 2 y x 2mx
3m và hàm số y 2x
3 . Tìm m để hai đồ thị đã cho cắt nhau tại hai
điểm phân biệt A và B sao cho AB 4 5 .
b) Giải phương trình: 3 x  2  x  3x  2  x  6 Câu 2 (2,5 điểm) :
a) Cho hình chữ nhật ABCD , K là hình chiếu của B lên AC . N là trung điểm cạnh CD , M là trung
điểm của AK .Chứng minh rằng: BM vuông góc với MN .
b) Cho tam giác nhọn ABC , gọi H , E, K lần lượt là chân đường cao kẻ từ các đỉnh ,
A B,C . Gọi diện
tích các tam giác ABC và HEK lần lượt là S S SS , Tính giá trị ABC  và HEK  . Biết rằng 3 10 ABCHEK biểu thức: 2 2 2
T  sin A  sin B  sin C .
Câu 3 (1,0 điểm) : Cho ba số dương a, , b c thoả mãn 3
a b c
. Tìm giá trị nhỏ nhất của 4 1 1 1 P    . 3 3 3 a  3b b  3c c  3a
------------------ Hết--------------
Họ tên cán bộ coi thi ……………………………………… Chữ ký…………………
SỞ GIÁO DỤC& ĐÀOTẠO BẮC GIANG
ĐỀ THI HỌC SINH GIỎI CẤP CƠ SỞ
CỤM THPT HUYỆN SƠN ĐỘNG NĂM HỌC 2022-2023 MÔN: Toán- Lớp 10 ĐỀ CHÍNH THỨC
(Thời gian làm bài: 120 phút, không tính thời gian phát đề) Đề thi gồm có 06 trang Mã đề thi:
Họ tên thí sinh.....................................................Số báo danh:.................................. 102
A. PHẦN CÂU HỎI TRẮC NGHIỆM: (14,0 điểm)
Câu 1: Một đường thẳng cắt các cạnh DA, DC và đường chéo DB của hình bình hành ABCD lần lượt tại
các điểm E, F và M. Biết rẳng DE mDA , DF nDC  ,
m n  0 . Hãy biểu diễn DM qua DB và m, n. . m n n A. DM DB . B. DM DB . m n m n m . m n C. DM DB . D. DM DB . m n m n 1
Câu 2: Cho hình bình hành ABCD . Gọi M, N là các điểm nằm trên cạnh AB và CD sao cho AM AB 3 1 , CN
CD . Gọi G là trọng tâm của B
MN . Gọi I là điểm xác định bởi BI mBC . Xác định m để AI 2 đi qua G. 6 11 6 18 A. m  . B. m  . C. m  . D. m  . 11 6 5 11
Câu 3: Cho 2 vectơ a và b tạo với nhau góc 60°. Biết a  6; b  3 . Tính a b a b 1
A. 3 7  3 . B. 3 7  5 . C. 6 5  
3 . D. 2 3  51 . 2
Câu 4: Trong mặt phẳng Oxy, cho Am 1; 2; B 2;5  2m;C m  3; 4 . Tìm m để A, B, C thẳng hàng. A. m  1. B. m  2 . C. m  2  .
D. m  3 .
Câu 5: Gọi M là giá trị lớn nhất của hàm số y f x 2 2
 4 x  2x  3  2x x . Tính tích các nghiệm
của phương trình f x  M . A. 1  . B. 1. C. 0. D. 2.
Câu 6: Tam giác ABC có đỉnh A 1
 ;2 , trực tâm H 3;0 , trung điểm của BC là M 6;  1 . Bán kính
đường tròn ngoại tiếp tam giác ABC là A. 5 . B. 5 . C. 3 . D. 4 . 1
Câu 7: Cho tam giác đều ABC cạnh a . Gọi M , N là các điểm thỏa mãn 2 BM BC , AN AB . 3 5
Gọi I là giao điểm của AM và CN . Tính a , biết diện tích của tam giác IBC bằng 36 3 . 7 A. a  5 . B. a  3. C. a  4 . D. a  6 .
Câu 8: Cho hàm số y f x có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số m để
phương trình f x  x m  2 có bốn nghiệm phân biệt? A. 1. B. 4 . C. 2 . D. 3 .
Câu 9: Cho hai lực F , F . Có điểm đặt tại M. Tìm cường độ lực tổng hợp của chúng biết F và F có 1 2 1 2
cùng cường độ lực là 100N, góc hợp bởi F và F là 120 . 1 2 A. 100N. B. 50N. C. 50 3 N. D. 100 3 N.
Câu 10: Cho hàm số y f x có đồ thị như hình vẽ: Khi đó phương trình 1
 xác định trên tập nào sau đây? f x 2 2  x 1 A.  ;  2   . B.  2  ;0 . C. 0; 2 . D.  1  ;2.
Câu 11: Trong mặt phẳng tọa độ Oxy cho ba điểm A 1  ; 2
 , B3;2,C 4; 
1 . Biết điểm E a;b di
động trên đường thẳng AB sao cho 2EA  3EB EC đạt giá trị nhỏ nhất. Tính 2 2 a b . 2 3 A. 2 2 a b  1. B. 2 2 a b  2 . C. 2 2 a b  . D. 2 2 a b  . 3 2 x y  2 3
x  5y 15
Câu 12: Cho hệ bất phương trình 
. Biết miền nghiệm của hệ bất phương trình là một đa x  0  y  0
giác. Diện tích của đa giác đó gần với số nào nhất trong các số dưới đây? A. 6. B. 6,5. C. 7. D. 5,5.
x y  3z
Câu 13: Cho hệ phương trình: 2 2
x y  5z .Số nghiệm của hệ phương trình là:  3 3
x y  9zA. 1. B. 2. C. 4. D. 5.
Câu 14: Có bao nhiêu giá trị nguyên của m  2
 0;20 để phương trình: 2 3
2x  2mx 1  3 2x x có
hai nghiệm thực phân biệt? A. 20. B. 23. C. 21. D. 22.  1 
Câu 15: Cho  P 2
: y x và A 2;  
 . Gọi M là một điểm bất kì thuộc  P . Khoảng cách MA bé nhất  2  là: 7 2 3 5 2 A. . B. . C. . D. . 2 3 2 2
Câu 16: Cho parabol  P  2
: y  x  2mx 1 m , trong đó m là tham số. Tập hợp các đỉnh của  P khi m m
m thay đổi là một parabol  P . Đỉnh của  P là:  1 7   1  3  A. I ;   . B. I  1   ;1 .
C. I 1;3 . D. I ;   .  2 4   2 4 
Câu 17: Trong mặt phẳng tọa độ Oxy , cho hình thang ABCD với hai đáy là AB và CD . Biết diện tích  1 
hình thang bằng 14 , đỉnh A1; 
1 và trung điểm cạnh BC là H  ; 0 . Đỉnh D  ;
a b có hoành độ    2 
dương và D nằm trên đường thẳng d : 5x y 1  0. Tính a  2 . b
A. a  2b  24.
B. a  2b  2.
C. a  2b  35.
D. a  2b 13. x
Câu 18: Tìm tập xác định D của hàm số: y f x 2 4   3x 5 . x  3 5  A. D  ;  \     3 . B. D  \   3 . 3  3  5  C. D  ;  \     3 . D. D  ;    . 5  3 
Câu 19: Trong hệ tọa độ Oxy, cho 3 điểm A2  ;1 ; B 0; 3  ;C 3 
;1 . Tìm tọa độ điểm D để ABCD là hình bình hành. A. D 5; 2   .
B. D 5;5 . C. D 5; 4   . D. D  1  ; 4   . 2 2x x  5
Câu 20: Tìm điều kiện của tham số m để hàm số y  ;  0 . 2
x  m   1 x  xác định trên   mm  1 m  1 A. m  0 . B. m  1. C.  . D.  . m  0 m  0 Câu 21: Cho ABC
với H, O, G lần lượt là trực tâm, tâm đường tròn ngoại tiếp trọng tâm. Hệ thức nào sau đây là đúng? 3 1 A. OH OG .
B. HO  3OG . C. OG GH . D. 2GO  3  OH . 2 2
Câu 22: Một công ty sản xuất bao bì cần sản xuất 3 loại hộp giấy X, Y, Z từ những tấm bìa giống nhau để
đựng ba loại sản phẩm khác nhau. Mỗi tấm bìa có hai cách cắt khác nhau: Cách thứ nhất cắt được 3 hộp X,
1 hộp Y và 6 hộp Z. Cách thứ hai cắt được 2 hộp X, 3 hộp Y và 1 hộp Z. Theo kế hoạch, số hộp mỗi loại X và
Z tối thiểu là 900 hộp; số hộp loại Y tối thiểu là 1000 hộp. Tìm phương án sao cho tổng số tấm bìa phải dùng là ít nhất?
A. Cắt theo cách một 250 tấm, cắt theo cách hai 100 tấm.
B. Cắt theo cách một 160 tấm, cắt theo cách hai 220 tấm.
C. Cắt theo cách một 100 tấm, cắt theo cách hai 300 tấm.
D. Cắt theo cách một 150 tấm, cắt theo cách hai 250 tấm.
Câu 23: Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số 2
y x  2x m  4 trên đoạn 2;  1 bằng 4? A. 1. B. 4. C. 2. D. 3.
Câu 24: Cho tập hợp A    x y 2 ;
| x  25  y y  6; x , y   , B    4 ; 3 ;  4  ; 3 và tập
hợp M . Biết A \ B M , số phần tử của tập hợp M là A. 3 . B. 4 . C. 2 . D. 5 .
Câu 25: Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh , trong đó có 25 học sinh thi
điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham
gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu? A. 38. B. 20. C. 21. D. 45.
Câu 26: ]Cho hai tập hợp M  2m 1; 2m  5 và N  m 1; m  7 (với m là tham số thực) . Tổng tất
cả các giá trị của m để hợp của hai tập hợp M và N là một đoạn có độ dài bằng 10 là A. 2 . B. 6. C. 4 . D. 10.
Câu 27: Một chiếc ăng - ten chảo parabol có chiều cao h  0,5m và đường kính miệng d  4m . Mặt cắt
qua trục là một parabol dạng 2
y ax . Biết m a
, trong đó m, n là các số nguyên dương nguyên tố cùng n
nhau. Tính m n .
A. m n  31.
B. m n  31  .
C. m n  7  .
D. m n  7 .
Câu 28: Cho hai tập hợp P   2
 ;5 và Q   3;
  . Kết quả nào đúng?
A. P Q  2;5 .
B. Q \ P   3  ; 2  5; .
C. C P   3  ; 2  5; .
D. P Q   3  ;5 . Q  3 3
8cos a  2sin a  cos a
Câu 29: Giá trị biểu thức A  khi tan a  2 là: 3
2 cos a  sin a 3 3 3 3 A. . B.  . C.  . D. . 2 2 2 2 sin B  2sin C
Câu 30: Tam giác ABC có sin A
. Kết luận nào sau đây là đúng? 2cos B  cos C A. Tam giác đều. B. Tam giác có 0 A  120 . C. Tam giác có 0 A  150 . D. Tam giác có 0 A  90 .
Câu 31: Mệnh đề nào sau đây có mệnh đề đảo sai?
A. Một tứ giác là hình chữ nhật thì nó có 3 góc vuông.
B. Hai góc đối đỉnh thì bằng nhau.
C. Trong tam giác cân, hai góc ở đáy bằng nhau.
D. Một tam giác là vuông thì nó có một góc bằng tổng hai góc còn lại.
Câu 32: Biết tập hợp tất cả các giá trị của tham số m để phương trình 2 x
x  4 x  4  m có 6 nghiệm
phân biệt là khoảng a;b . Tính a b .
A. a b  6.
B. a b  4 .
C. a b 1.
D. a b  2 . Câu 33: Cho parabol 2 2
(P) : y  x  2mx  3m  4m  3 (m là tham số) có đỉnh I . Gọi , A B là hai điểm
thuộc Ox sao cho AB  2024 . Khi đó IAB có diện tích nhỏ nhất bằng: A. 4048 . B. 1012 . C. 506 . D. 2024 .
Câu 34: Gọi M là điểm cố định mà parabol  P  2
: y x  3mx  6m 1 luôn đi qua với mọi giá trị của m
tham số m. Tính tổng khoảng cách từ M đến hai trục tọa độ. A. 7. B. 3 . C. 2. D. 5.
Câu 35: Biết rằng f x là đa thức thỏa mãn: f x  f   x 2 2 1
 3x  2x  5, x   .
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x trên đoạn  4  ;2. Giá trị của
3M  4m bằng A. 119. B. 147. C. 123. D. 151.
Câu 36: Cho tập hợp A  0;  và B   2 x
\ mx  4x m  3  
0 . Tìm m để B có đúng hai tập con và B A . 0  m  3 A. m  3 . B. m  0 . C.  . D. m  4 . m  4
Câu 37: Cho tam giác ABC vuông tại B và điểm M trên cạnh BC sao cho 2 2 2
MA MB MC đạt giá S
trị nhỏ nhất. Tính tỉ số diện tích ABM S   . S ABC  1 2 3 1 A. . B. . C. . D. . 2 3 4 3
Câu 38: Cho hàm số: 2
y f (x)  ax bx c với a, ,
b c là các tham số, a  0 . Biết rằng f (x) đồng 2 6a biến trên khoảng  2;
  , hãy tìm giá trị lớn nhất của biểu thức P  2 2 5a  2ab  . b 6 6 3 6 A. . B. . C. . D. . 5 29 4 13
Câu 39: Cho parabol  P có phương trình 2
y ax bx  2 . Có bao nhiêu bộ số a;b , biết  P đi qua 
điểm A1;6 và tung độ của đỉnh là 1 . 4 A.4. B. 2. C. 1. D. 0.
Câu 40: Tính tổng các nghiệm của phương trình:  x    x 2 5 2
 3 x  3x . 3 3  A. 3. B. 3  . C. . D. . 2 2
B. PHẦN CÂU HỎI TỰ LUẬN( 6,0 điểm) Câu 1 (2,5 điểm): a) Cho hàm số 2 y x 2mx
3m và hàm số y 2x
3 . Tìm m để hai đồ thị đã cho cắt nhau tại hai
điểm phân biệt A và B sao cho AB 4 5 .
b) Giải phương trình: 3 x  2  x  3x  2  x  6 Câu 2 (2,5 điểm) :
a) Cho hình chữ nhật ABCD , K là hình chiếu của B lên AC . N là trung điểm cạnh CD , M là trung
điểm của AK .Chứng minh rằng: BM vuông góc với MN .
b) Cho tam giác nhọn ABC , gọi H , E, K lần lượt là chân đường cao kẻ từ các đỉnh ,
A B,C . Gọi diện
tích các tam giác ABC và HEK lần lượt là S S SS , Tính giá trị ABC  và HEK  . Biết rằng 3 10 ABCHEK biểu thức: 2 2 2
T  sin A  sin B  sin C .
Câu 3 (1,0 điểm) : Cho ba số dương a, , b c thoả mãn 3
a b c
. Tìm giá trị nhỏ nhất của 4 1 1 1 P    . 3 3 3 a  3b b  3c c  3a
------------------ Hết--------------
Họ tên cán bộ coi thi ……………………………………… Chữ ký…………………
SỞ GIÁO DỤC& ĐÀOTẠO BẮC GIANG
HD CHẤM ĐỀ THI HỌC SINH GIỎI CẤP CƠ SỞ
CỤM THPT HUYỆN SƠN ĐỘNG NĂM HỌC 2022-2023 MÔN: Toán- Lớp 10
(Thời gian làm bài: 120 phút, không tính thời gian phát đề) I. TRẮC NGHIỆM MĐ\CÂU 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 101 D A C B A D B A C C D D D A A C C B A B 102 A A A B A A D D A B D A D D C D D A B A
MĐ\CÂU 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 101 A D D A B D B B C B B B C D D C A C C A 102 C C C B C C C C B D B C B A C D D B B B II. TỰ LUẬN Câu Nội dung Điểm Câu a) Cho hàm số 2 y x 2mx
3m và hàm số y 2x
3 . Tìm m để hai đồ thị đã 1
cho cắt nhau tại hai điểm phân biệt A và B sao cho AB 4 5 . 2,5 điểm
b) Giải phương trình: 3 x  2  x  3 x  2  x  6
a) Phương trình hoành độ giao điểm của hai đồ thị là: 2 x 2mx 3m 2x 3 0,5 2 x 2 m 1 x 3m 3 0 (*)
Hai đồ thị cắt nhau tại hai điểm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt m 1 ' 0 . m 4 x x  2  m 1  1 2   Theo Vi-et ta có:  x .x  3  m 1  1 2   0,25 Gọi A x ; 2x 3 ; B x ; 2x
3 với x ; x là nghiệm phương trình (*) 1 1 2 2 1 2 0,25 2 2 2
Ta có: AB  5 x x  5 x x
 20x .x  20 m 1  60 m 1 1 2   1 2 1 2     AB  
m 2  m    m 2 4 5 20 1 60 1 4 5 1  2m   1  4  0
m  0;m  5  . 0,5
So sánh với điều kiện ta được m  0; m  5  .
b) 3 x  2  x  3 x  2  x  6  x  2  8x  24 3 x  2x
x  6  2 x  3   2x  3 3 x  2  x  6 0.5 x  3  0 x  3   4     1
3 x  2  x  6  4(*) 3 x  2  x  6     2 2 (*) 9 x
2  6 x  4x 12  x  6  16  3 x  4x 12  14  5x  14 x   5 14   1  4  5x  0  x   11  3 5        9
 x  4x 12  14  5x 5 2 x 2  2 2  1  6x 176x  304  0   11  3 5 x  0.5  2 11  3 5  x 
( thoả mãn điều kiện x  2 ). 2  11 3 5 
Vậy phương trình có tập nghiệm S  3  ; .  2   Câu
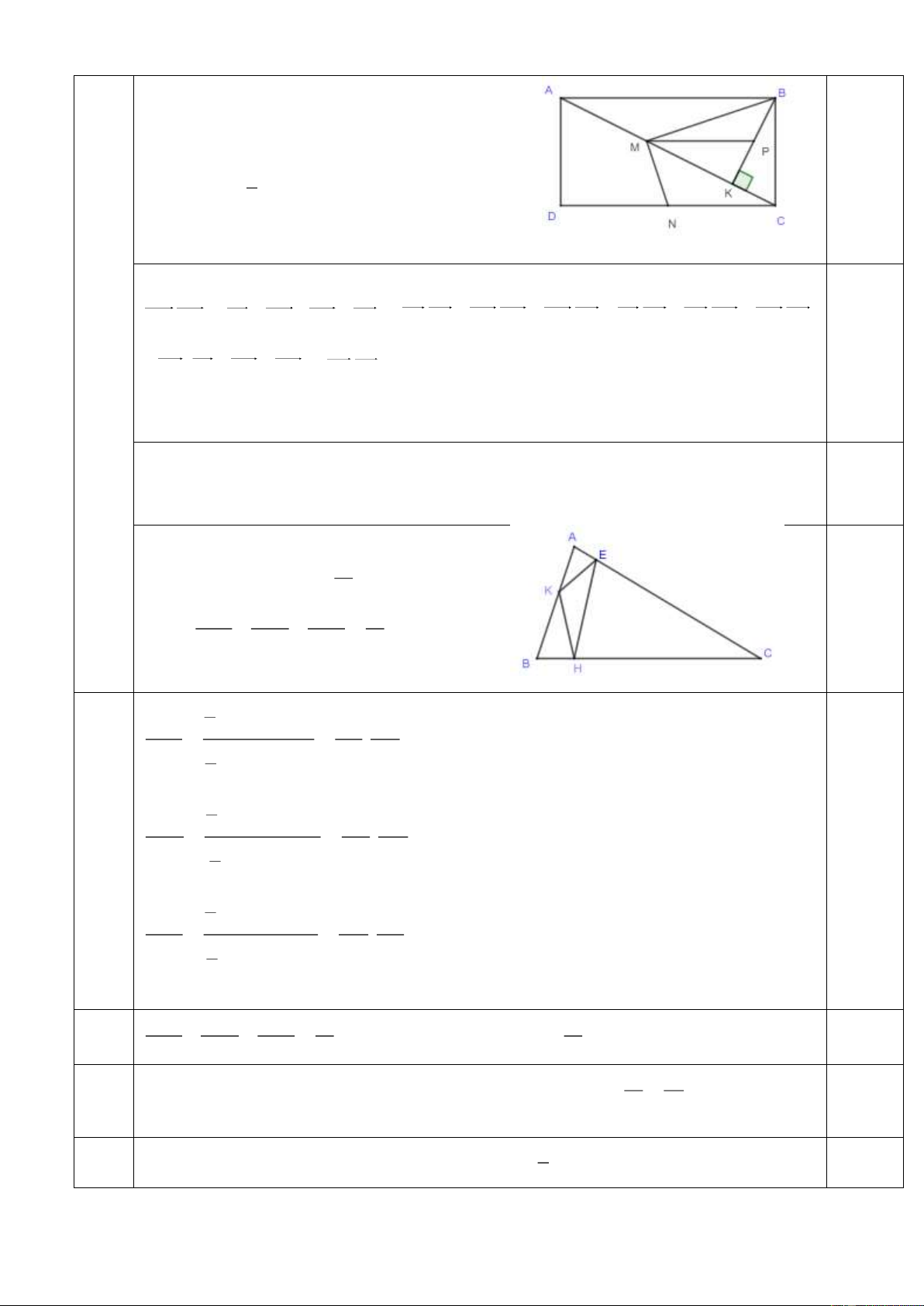
a) Cho hình chữ nhật ABCD , K là hình chiếu của B lên AC . N là trung điểm cạnh 1,0 2 điểm
CD , M là trung điểm của AK .Chứng minh rằng: BM vuông góc với MN .
Gọi P là trung điểm BK .
Khi đó : MP là đường trung bình tam giác BKA , MP / /  ABMP BC suy ra  1 , hay  . MP   AB MP CN 0,5   2 Khi đó:
BM .MN  BP PM MC CN   B .
P CN PM .MC PM .CN B .
P CN CN.MC PM .CN 0,5
CN BP MC PM   CN.BC  0.
Vậy BM vuông góc với MN .
b) Cho tam giác nhọn ABC , gọi H , E, K lần lượt là chân đường cao kẻ từ các đỉnh ,
A B, C . Gọi diện tích các tam giác ABC và HEK lần lượt là S S ABC  và HEK  . Biết rằng 1,5 3S  10 T A B   S
, Tính giá trị biểu thức: 2 2 2 sin sin sin C . ABCHEK Đặt S S
thì từ giả thiết suy ra ABC 7 SSSS EAK KBH HCE 10 S S S 0,25 7
EAK KBH HCE S S S 10
1 AE.AK sin A S AE AK EAK 2 2   .  cos .
A cos A  cos A S 1 AB AC A . B AC sin A 2
1 BK.BH.sin B S BK BH KBH 2 2   .  cos .
B cos B  cos B S 1 BC AB 0,5 A . B BC sin B 2
1 CH.CE.sinC S CH CE HCE 2 2   .
 cosC.cosC  cos C S 1 AC BC
AC.BC sin C 2 S S S 7 7 EAK KBH HCE 2 2 2   
 cos A  cos B  cos C  0,25 S S S 10 10 7 23 2 2 2
T  sin A  sin B  sin C  3   2 2 2
cos A  cos B  cos C   3   10 10 0,5 Câu 3
Cho ba số dương thoả mãn a b c
. Tìm giá trị nhỏ nhất của 1 điểm 3 4 1 1 1 P    . 3 3 3 a  3b b  3c c  3a
Áp dụng bất đẳng thức Cô si ta có:
x y z 1 1 1  3 1 1 1 9 3    3 xyz.  9       3  x y z xyz x y z
x y z 0,25 Khi đó : 1 1 1 9 P     3 3 3 3 3 3 a  3b b  3c c  3a
a  3b b  3c c  3a
a  3b 11 1
Ta có: 3 a  3b
 a  3b  2 3 3
b  3c 11 1 3 b  3c
 b  3c  2 3 3 0,25
c  3a 11 1 3 c  3a
 c  3a  2 3 3 1 Suy ra: 3 3 3
a  3b b  3c c  3a
4a  4b  4c  6  3 0,25 3  3
a b c  Do đó 1
: P  3 . Dấu bằng xảy ra   4
a b c  . 4  0,25
a  3b b  3c c  3a
Lưu ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa.